Первый слайд презентации: Лекция 3. Ортогональные проекции плоскости
Способы задания плоскости Плоскости общего и частного положений Особые линии плоскости Лектор Стриганова Л.Ю.
Слайд 2: ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ
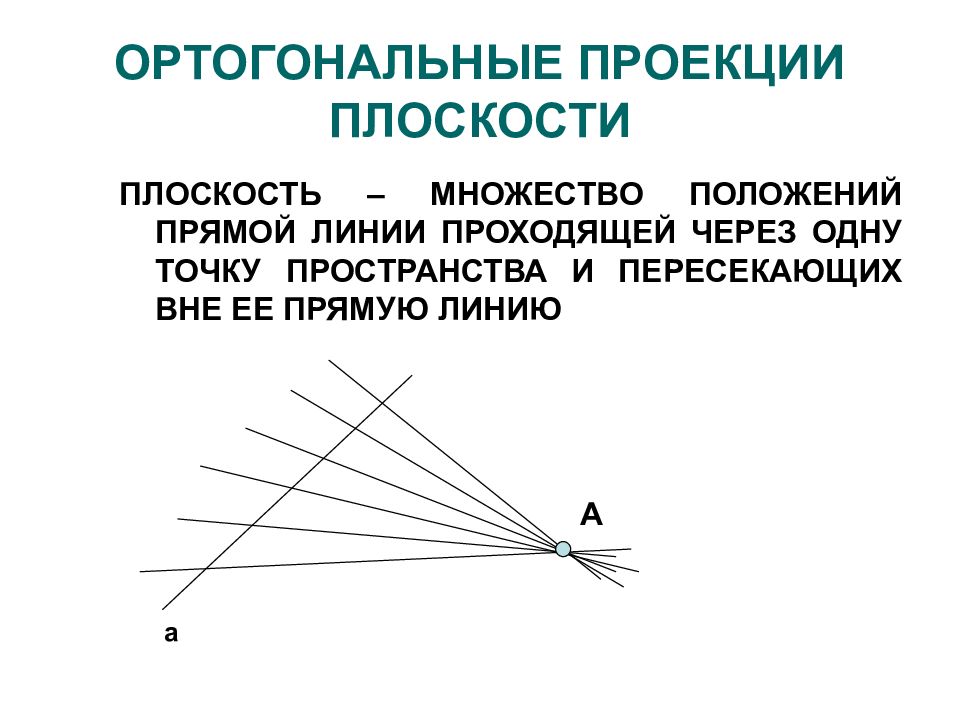
ПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ ЛИНИИ ПРОХОДЯЩЕЙ ЧЕРЕЗ ОДНУ ТОЧКУ ПРОСТРАНСТВА И ПЕРЕСЕКАЮЩИХ ВНЕ ЕЕ ПРЯМУЮ ЛИНИЮ A a
Слайд 3
СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ 1. Аналитический способ А x + By + Cz + D = 0 2. Графические способы
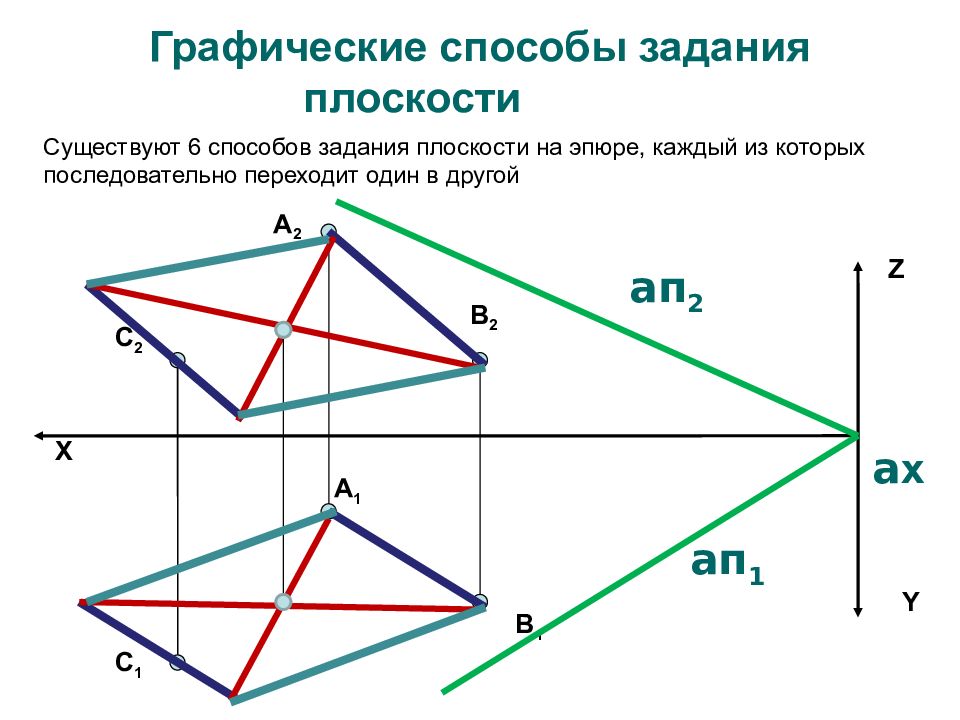
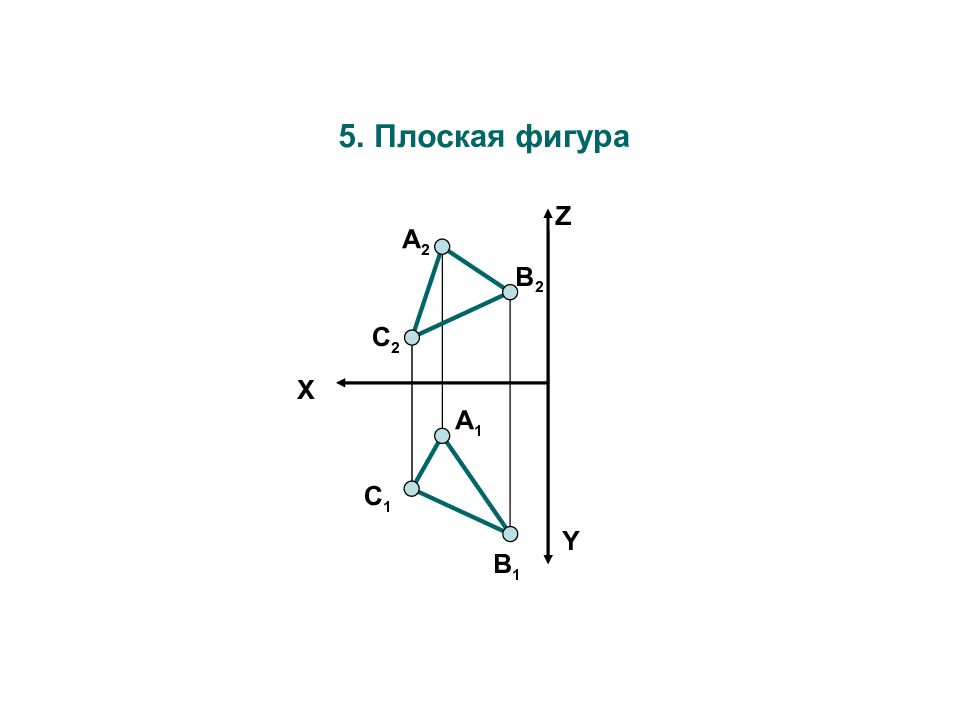
X Z Y А 2 А 1 В 1 C 2 C 1 В 2 Существуют 6 способов задания плоскости на эпюре, каждый из которых последовательно переходит один в другой a x a п 2 a п 1
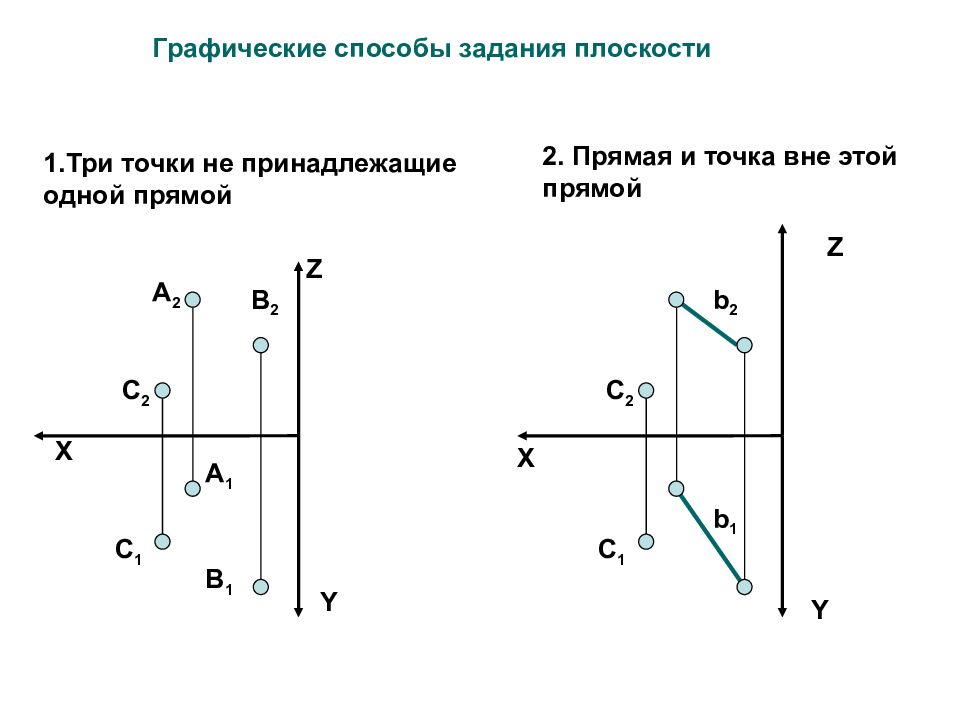
X Z Y А 2 А 1 В 1 C 2 C 1 В 2 X Y b 1 C 2 C 1 b 2 1.Три точки не принадлежащие одной прямой 2. Прямая и точка вне этой прямой Z
Слайд 6
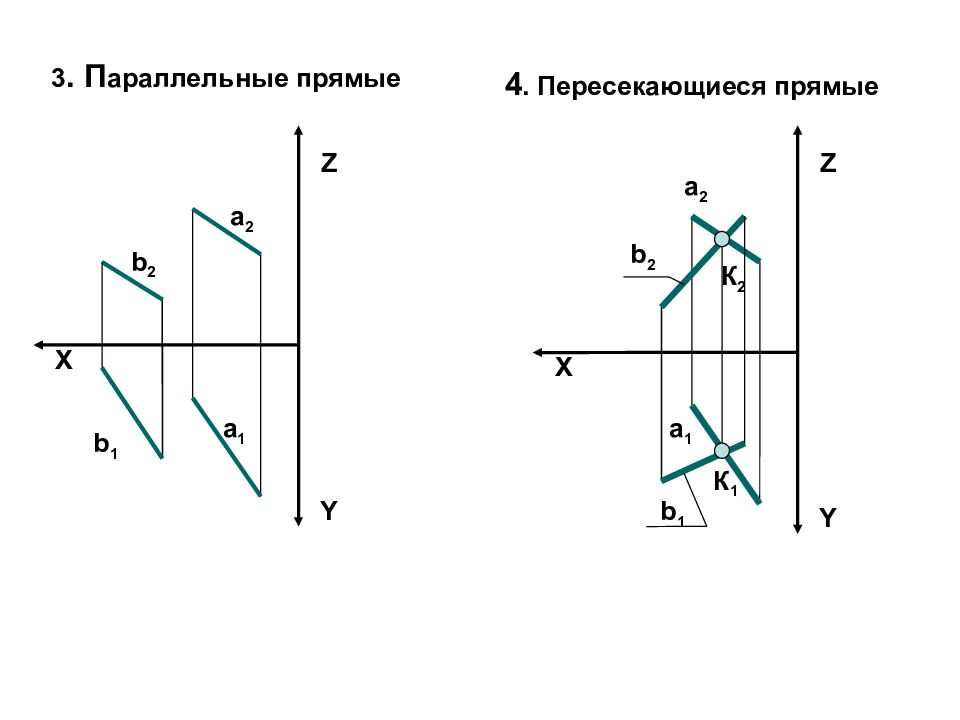
X Z Y а 2 а 1 b 2 b 1 X Z Y a 2 a 1 b 2 b 1 3. П араллельные прямые 4. Пересекающиеся прямые К 1 К 2
Слайд 8
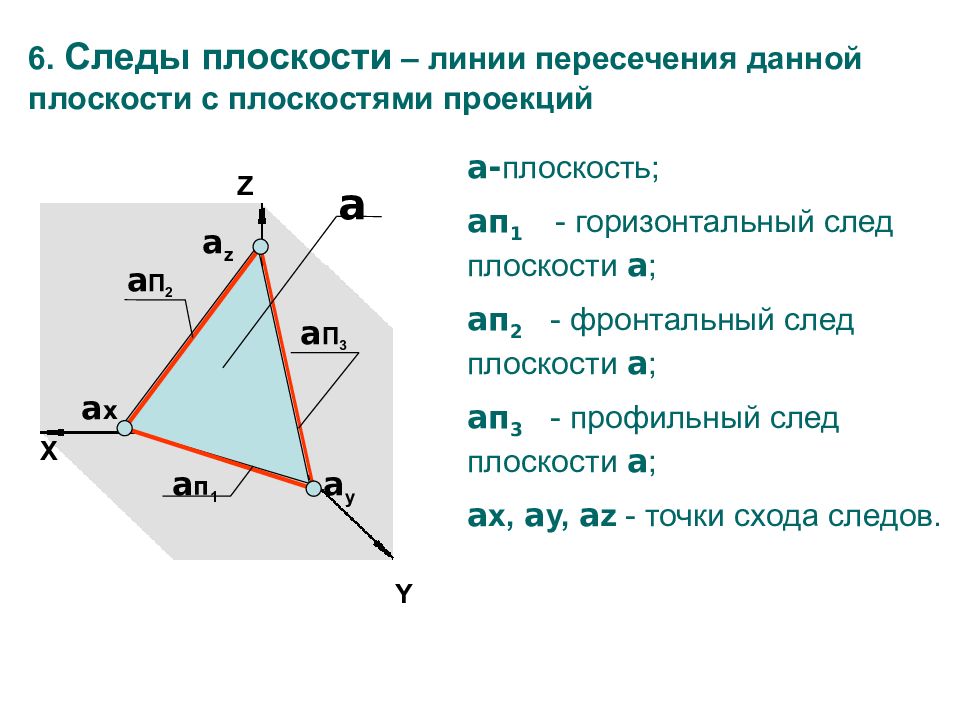
Y Z X a п 1 a П 3 a П 2 a x a y a z 6. Следы плоскости – линии пересечения данной плоскости с плоскостями проекций a a- плоскость ; a п 1 - горизонтальный след плоскости a ; a п 2 - фронтальный след плоскости a ; a п 3 - профильный след плоскости a ; a x, a y, a z - точки схода следов.
Слайд 9
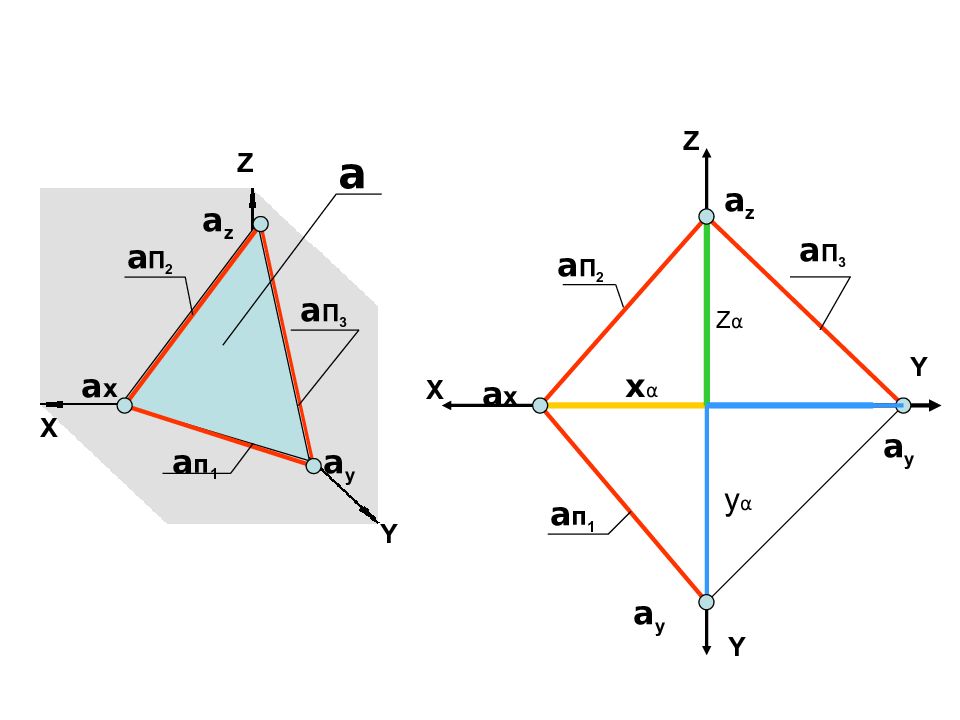
Z X Y Y a П 2 a п 1 a П 3 a x a y a z Z X a п 1 a П 3 a П 2 a x a y a z a a y Y x α y α Z α
Слайд 10: ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
1. Относительно плоскостей проекций плоскости разделяют : • плоскости частного положения • плоскости общего положения 2. Плоскости частного положения разделяют : плоскости параллельные плоскостям проекций – плоскости уровня плоскости перпендикулярные плоскостям проекций – плоскости проецирующие
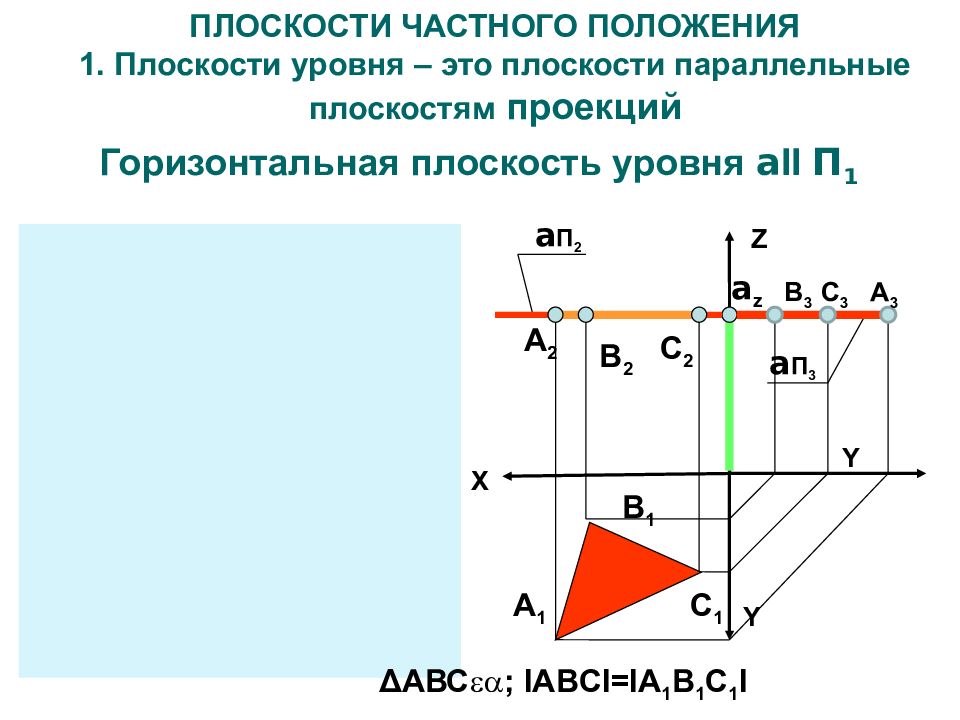
Слайд 11: ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ 1. Плоскости уровня – это плоскости параллельные плоскостям проекций
Горизонтальная плоскость уровня a II П 1 Z X Y Y a П 2 a П 3 a z Y Z X a П 3 a П 2 a z a А 1 В 1 С 1 А 2 В 2 С 2 А 1 С 1 В 1 А 2 В 2 С 2 Δ АВС ; IABCI=IA 1 B 1 C 1 I В 3 С 3 А 3
Слайд 12
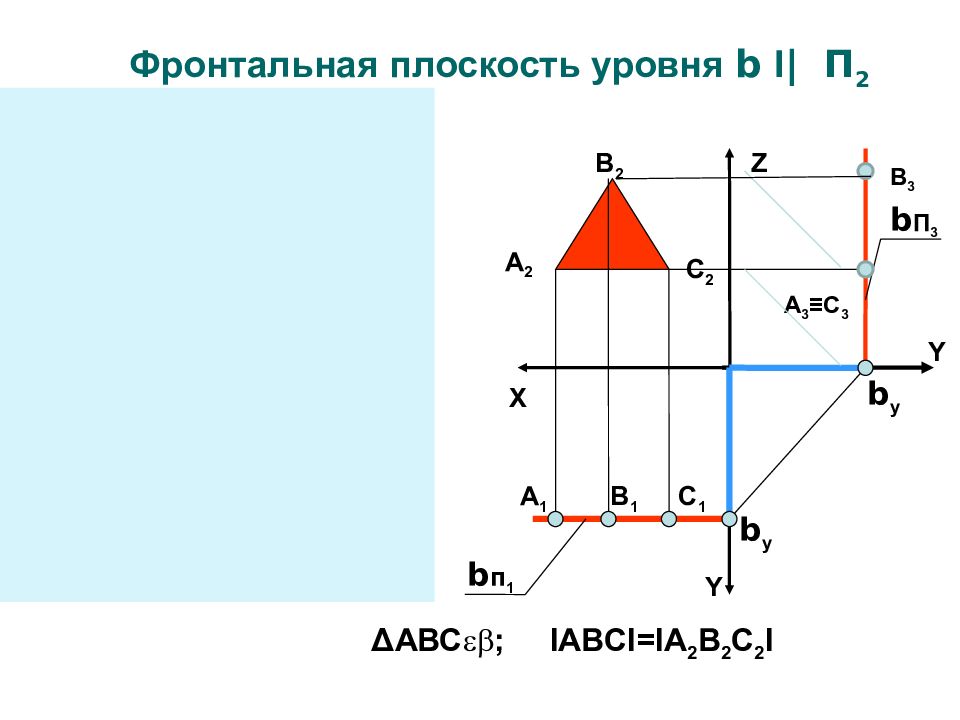
Z X Y Y b п 1 b П 3 b y Y Z X b п 1 b П 3 b y b y Фронтальная плоскость уровня b I | П 2 А 1 В 1 С 1 С 2 В 2 А 2 b Δ АВС ; IABCI=IA 2 B 2 C 2 I А 3 ≡С 3 В 3
Слайд 13
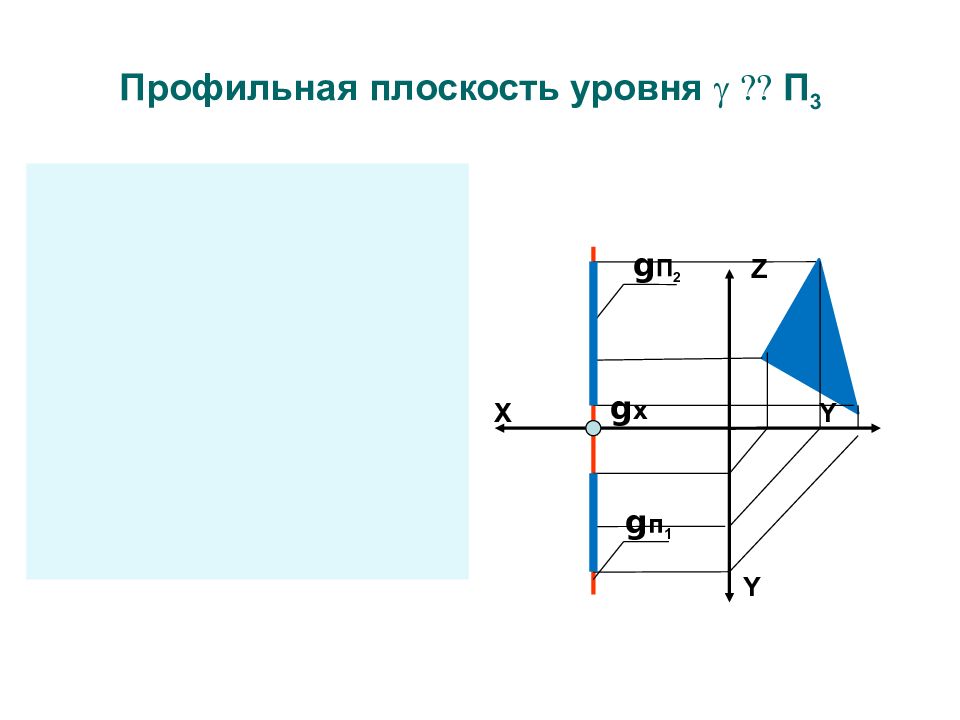
Z X Y Y g П 2 g п 1 g x Z X g п 1 g П 2 g x g Профильная плоскость уровня П 3 Y
Слайд 14: Особенности чертежа плоскостей уровня
Фигуры принадлежащие плоскостям уровня проецируются в натуральную величину на параллельную плоскость проекций На другие плоскости проекций фигуры принадлежащие плоскостям уровня проецируются в прямую линию
Слайд 15
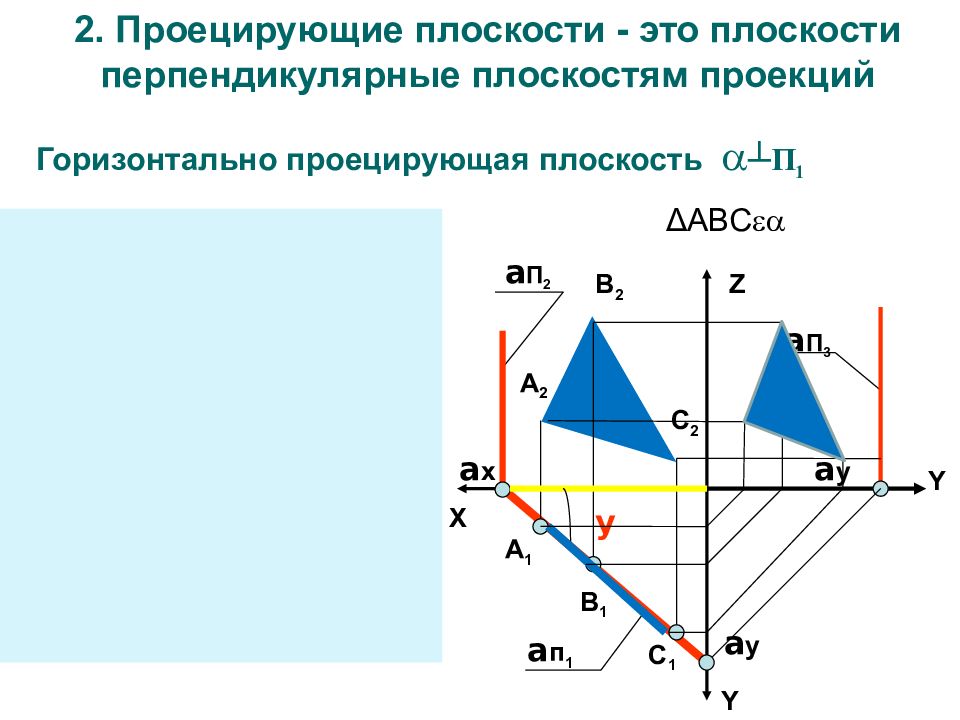
2. Проецирующие плоскости - это плоскости перпендикулярные плоскостям проекций Горизонтально проецирующая плоскость ┴П 1 X Y Y a П 2 a П 3 Z X a п 1 a П 2 a x a x Z a п 1 a П 3 a Y a y y a y a y А 1 В 1 С 1 А 2 В 2 С 2 Δ АВС
Слайд 16
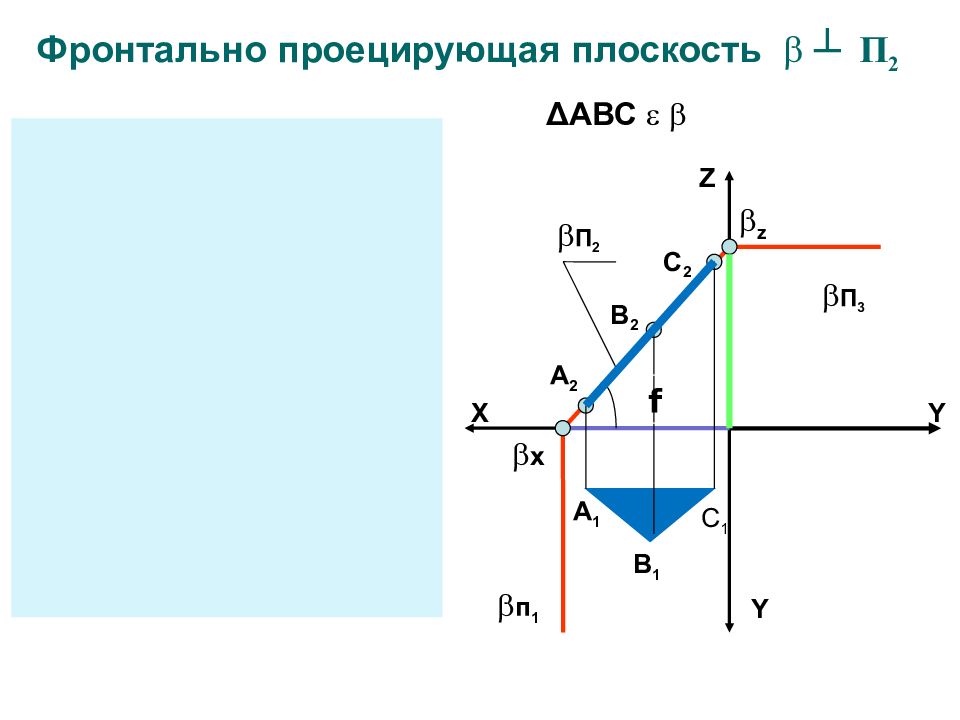
Фронтально проецирующая плоскость ┴ П 2 Z X Y Y П 2 п 1 x Y Z X П 2 z П 3 П 1 П 3 z x А 2 В 2 С 2 А 1 В 1 С 1 f Δ АВС
Слайд 17
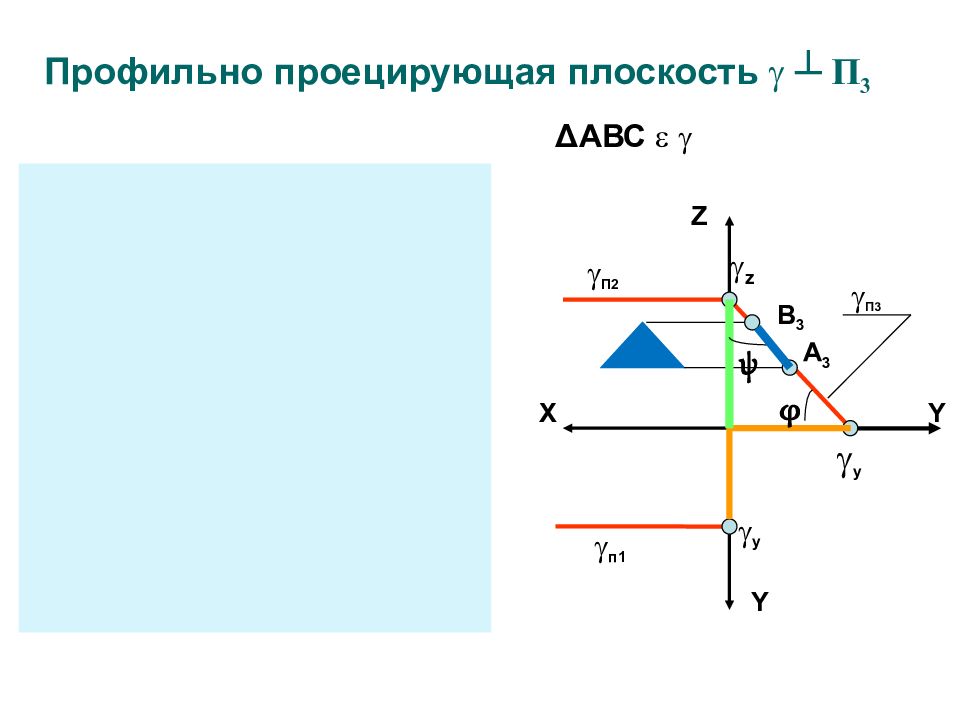
Профильно проецирующая плоскость ┴ П 3 Z X Y Y П 2 п1 Y Z X п1 П 2 П3 П3 z y z y y А 3 В 3 φ ψ Δ АВС
Слайд 18
Фигуры принадлежащие проецирующим плоскостям на перпендикулярную плоскость проекций проецируются в прямую линию (вырожденная проекция) Угол наклона между вырожденной проекцией и осями координат равен углу между заданной плоскостью и плоскостью проекций Особенности чертежа проецирующих плоскостей
Слайд 19: ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
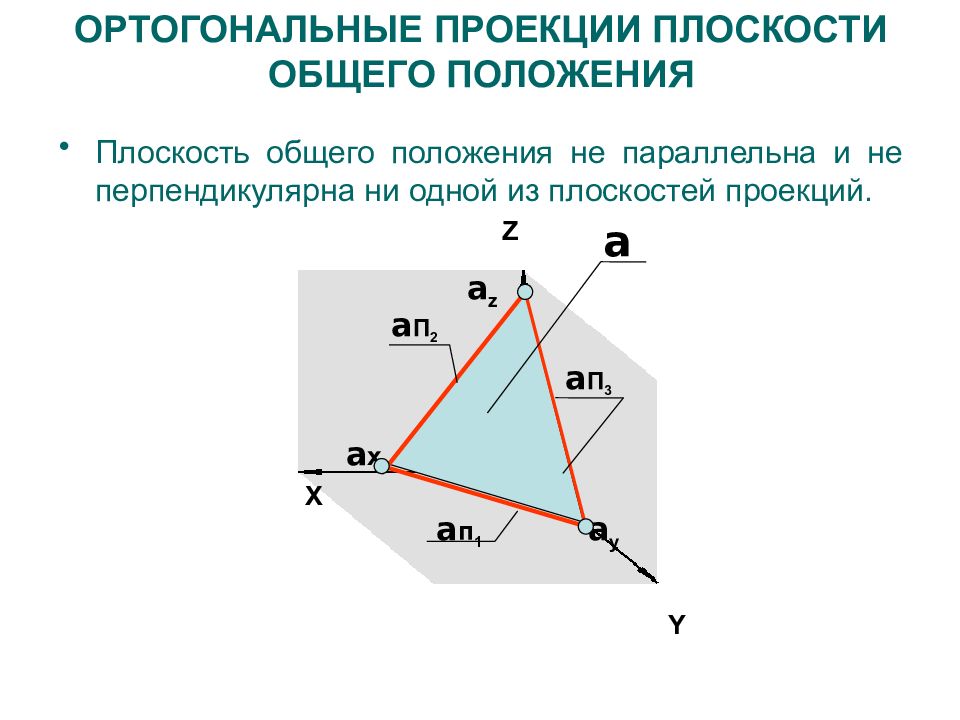
Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций. Y Z X a п 1 a П 3 a П 2 a x a y a z a
Слайд 20
ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ ПЛОСКОСТИ Точка принадлежит плоскости, если она принадлежит прямой в этой плоскости Прямая принадлежит плоскости если она проходит : а) через две точки этой плоскости б) через точку плоскости параллельно какой-либо прямой этой плоскости
Слайд 21
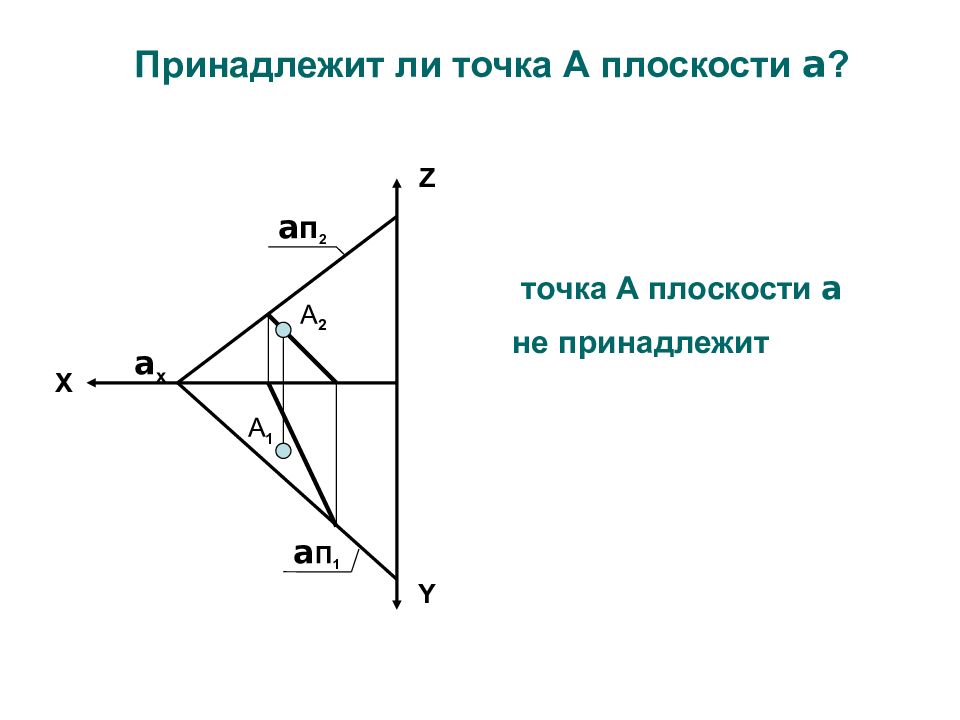
Принадлежит ли точка А плоскости a ? А 2 А 1 a п 2 a П 1 a x Y Z X точка А плоскости a не принадлежит
Слайд 22: ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ
ЛИНИИ УРОВНЯ ПЛОСКОСТИ – линии параллельные плоскостям проекций и принадлежащие данной плоскости ; ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА (ЛНН) ПЛОСКОСТИ – определяют угол наклона данной плоскости к одной из плоскостей проекций. ЛНН перпендикулярны линиям уровня : горизонтали на плоскости П 1 ; фронтали на плоскости П 2.
Слайд 23
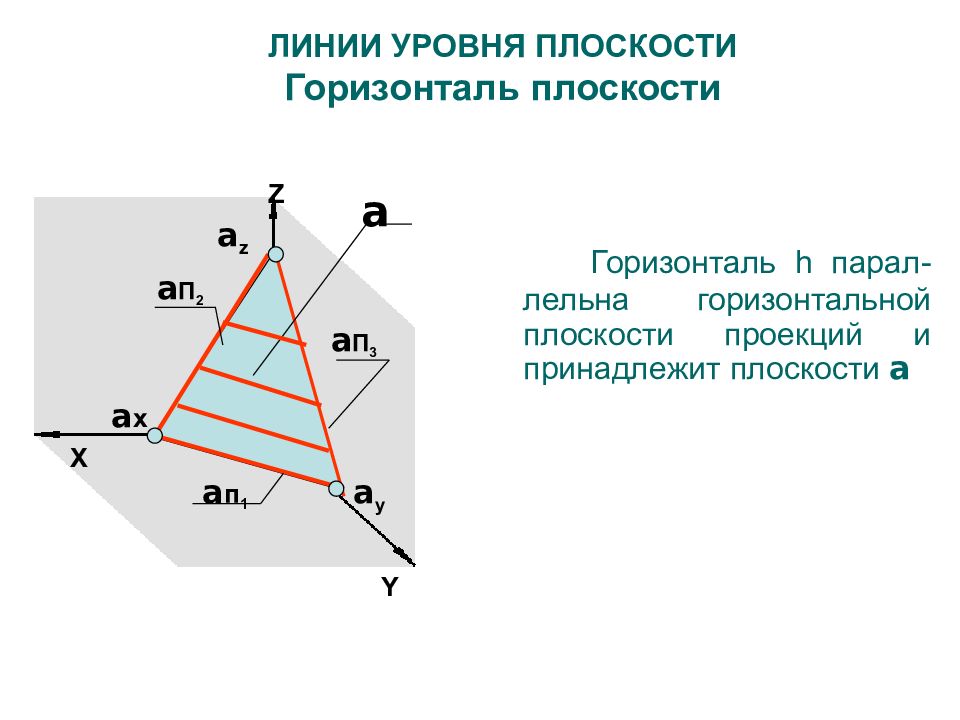
Z X a п 1 a П 3 a П 2 a x a y a z a ЛИНИИ УРОВНЯ ПЛОСКОСТИ Горизонталь плоскости Y Горизонталь h парал-лельна горизонтальной плоскости проекций и принадлежит плоскости a
Слайд 24
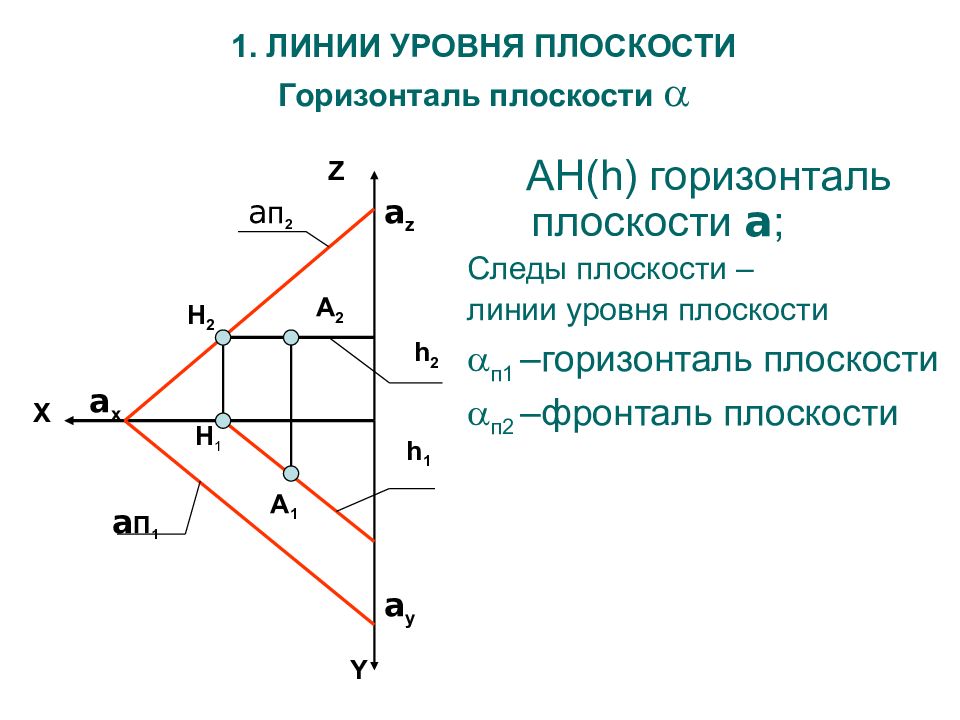
A Н (h) горизонталь плоскости a ; Следы плоскости – линии уровня плоскости п1 –горизонталь плоскости п2 –фронталь плоскости 1. ЛИНИИ УРОВНЯ ПЛОСКОСТИ Горизонталь плоскости a п 2 a П 1 Y Z X a x А 2 А 1 h 2 h 1 Н 2 Н 1 a y a z
Слайд 25
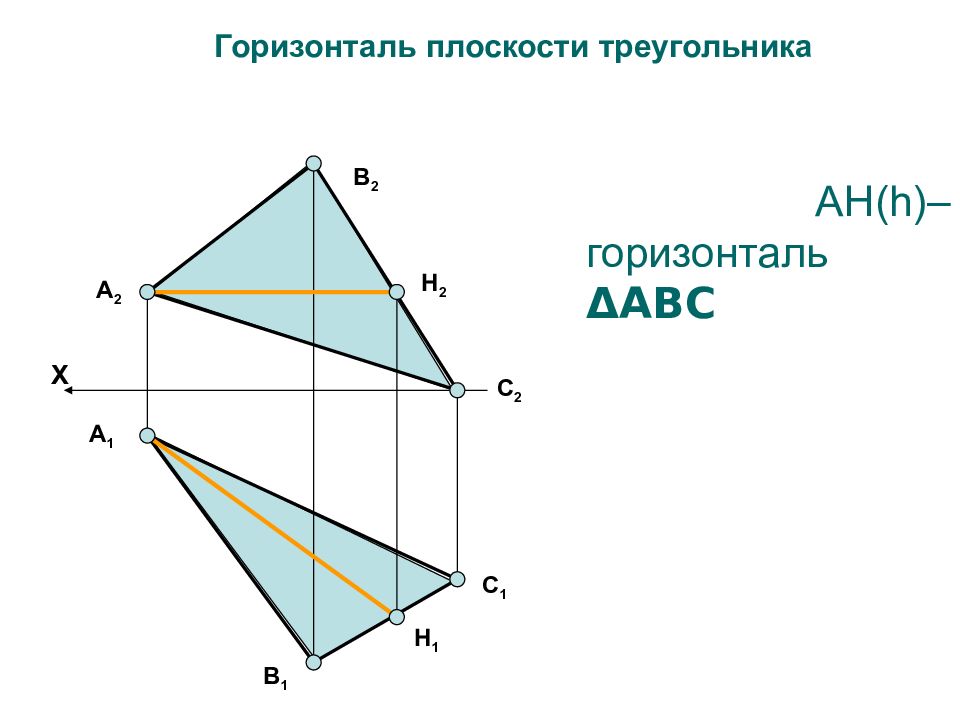
AH(h)– горизонталь Δ АВС Горизонталь плоскости треугольника А 2 В 2 С 2 H 2 В 1 С 1 А 1 H 1 X
Слайд 26
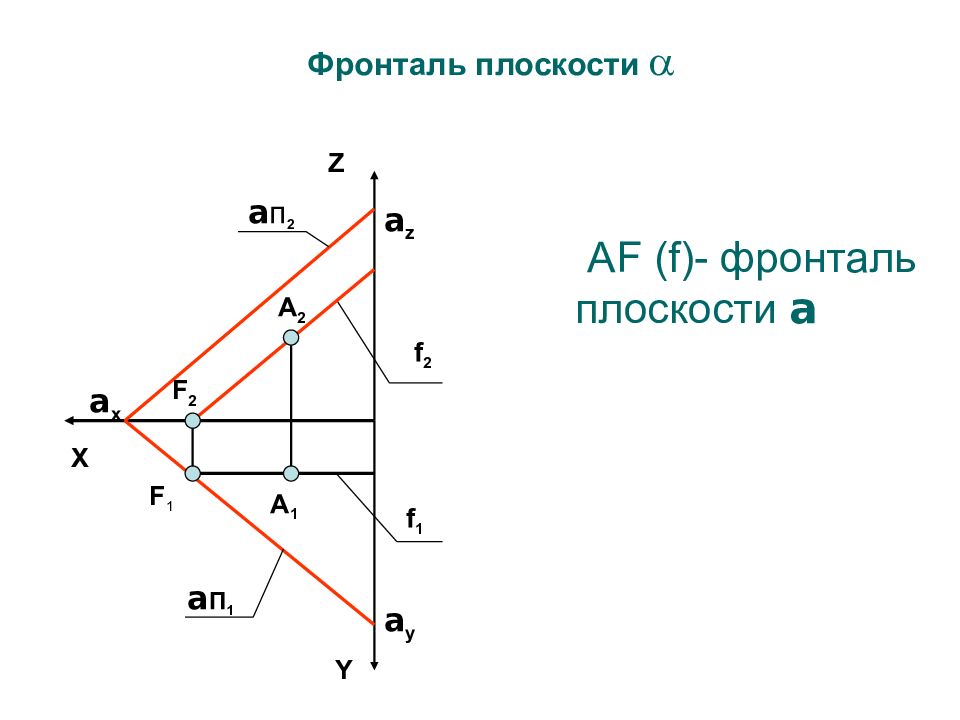
А F (f)- фронталь плоскости a Фронталь плоскости a п 2 a П 1 Y Z a x А 2 А 1 f 2 f 1 F 2 F 1 X a z a y
Слайд 27
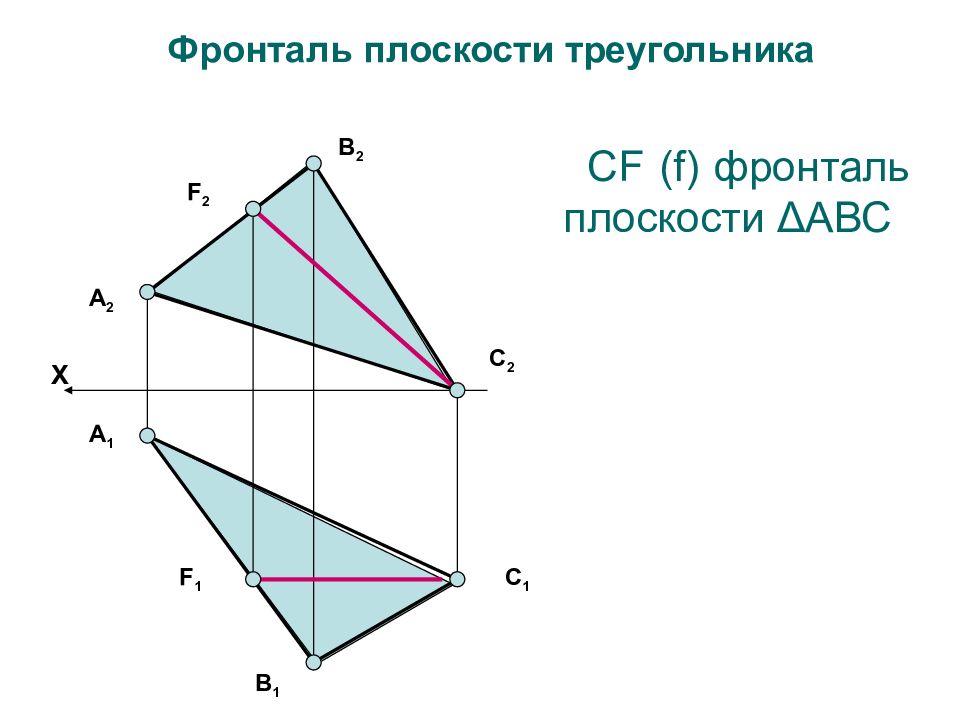
А 2 F 2 В 2 С 2 В 1 С 1 А 1 F 1 Фронталь плоскости треугольника С F (f) фронталь плоскости Δ АВС X
Слайд 28
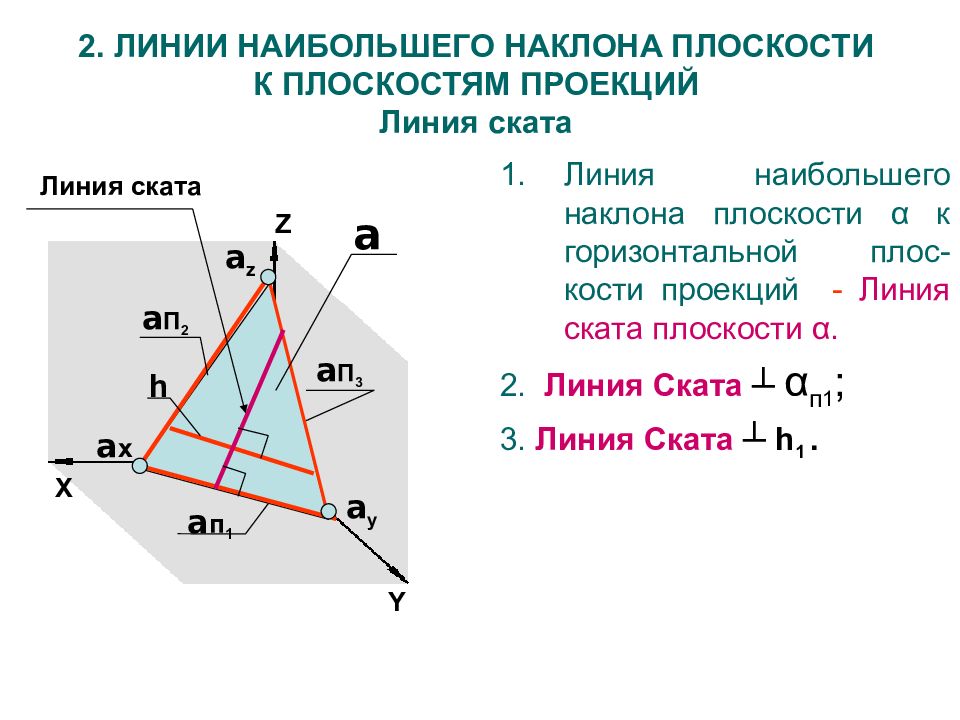
Z X a п 1 a П 3 a П 2 a x a y a z a 2. ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ К ПЛОСКОСТЯМ ПРОЕКЦИЙ Линия ската Линия наибольшего наклона плоскости α к горизонтальной плос-кости проекций - Линия ската плоскости α. 2. Линия Ската ┴ α п 1 ; 3. Линия Ската ┴ h 1. h Y Линия ската
Слайд 29
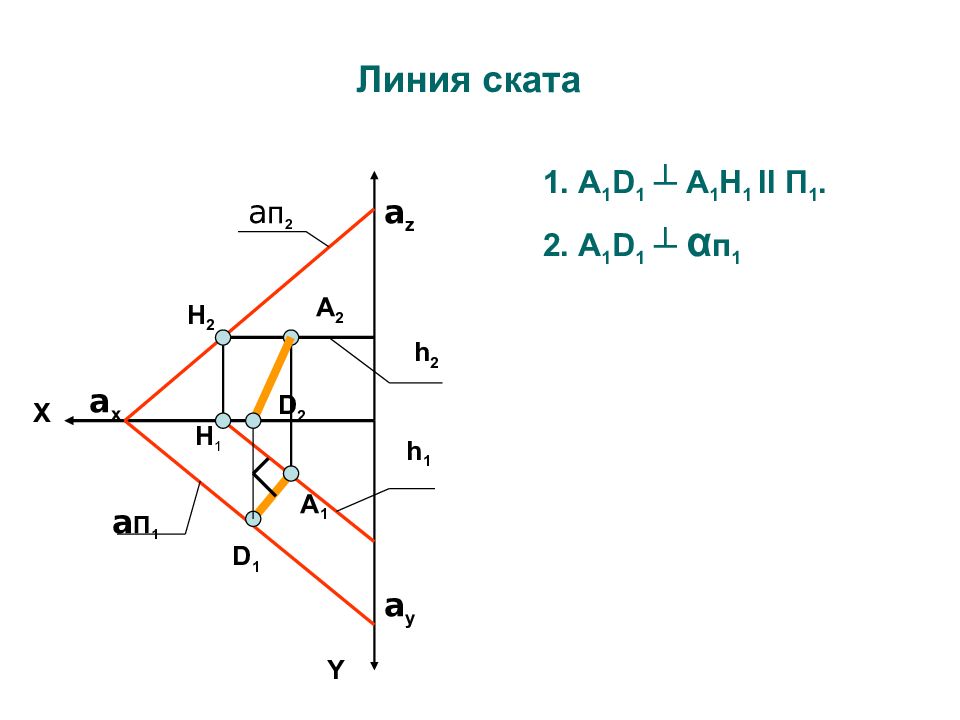
1. А 1 D 1 ┴ А 1 H 1 II П 1. 2. А 1 D 1 ┴ α п 1 Линия ската a п 2 a П 1 Y X a x А 2 А 1 h 2 h 1 H 2 H 1 a y a z D 1 D 2
Слайд 30
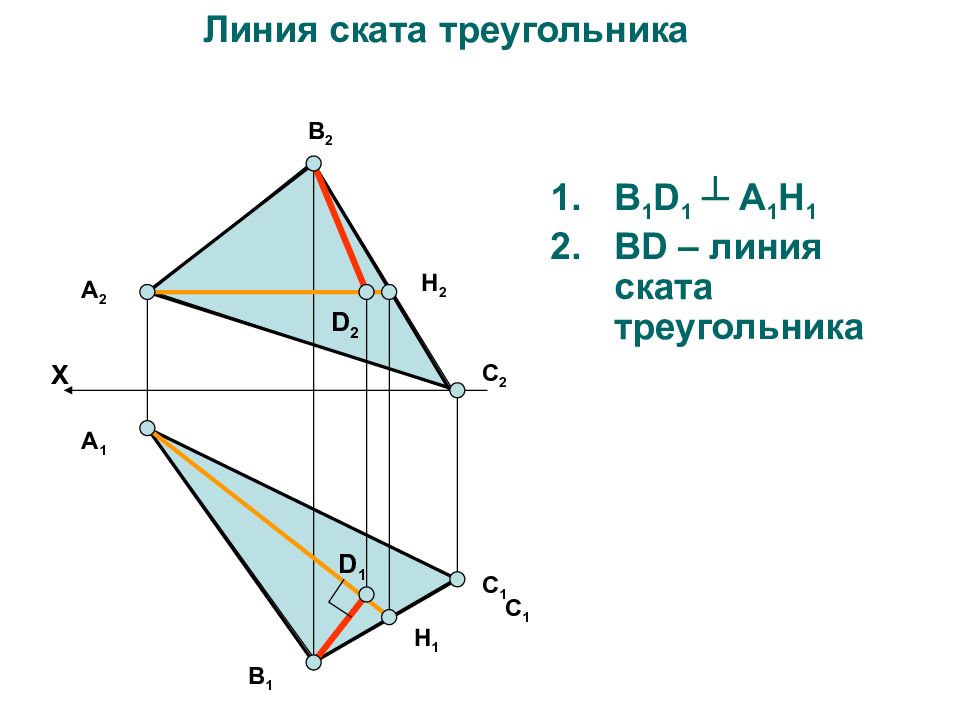
В 1 D 1 ┴ А 1 H 1 В D – линия ската треугольника А 2 В 2 С 2 H 2 В 1 С 1 А 1 H 1 X Линия ската треугольника D 1 D 2 С 1
Слайд 31
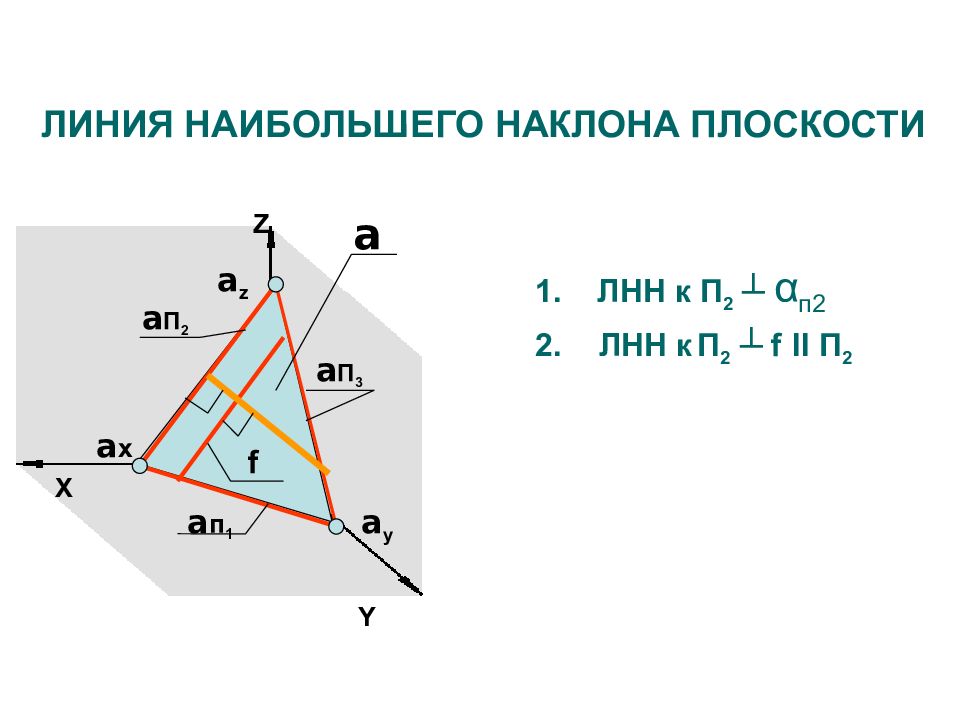
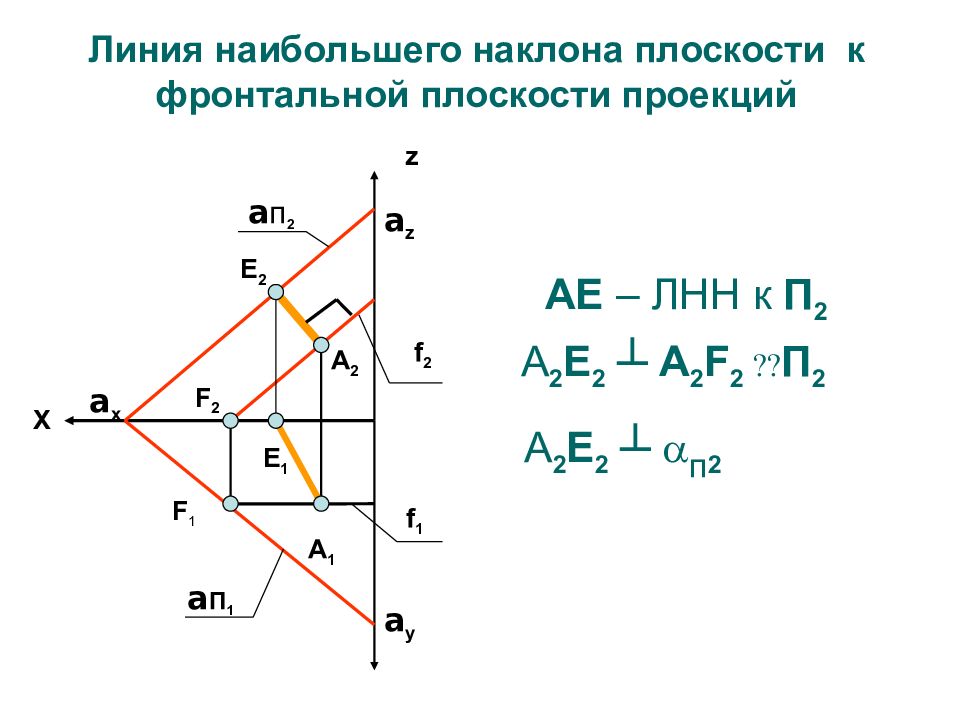
Z X a п 1 a П 3 a П 2 a x a y a z a ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ 1. ЛНН к П 2 ┴ α п2 ЛНН к П 2 ┴ f II П 2 Y f
Слайд 32
АЕ – ЛНН к П 2 A 2 Е 2 ┴ A 2 F 2 П 2 A 2 Е 2 ┴ п 2 a п 2 a П 1 z a x А 2 A 1 f 2 f 1 F 2 F 1 X a z a y Е 1 Е 2 Линия наибольшего наклона плоскости к фронтальной плоскости проекций
Слайд 33
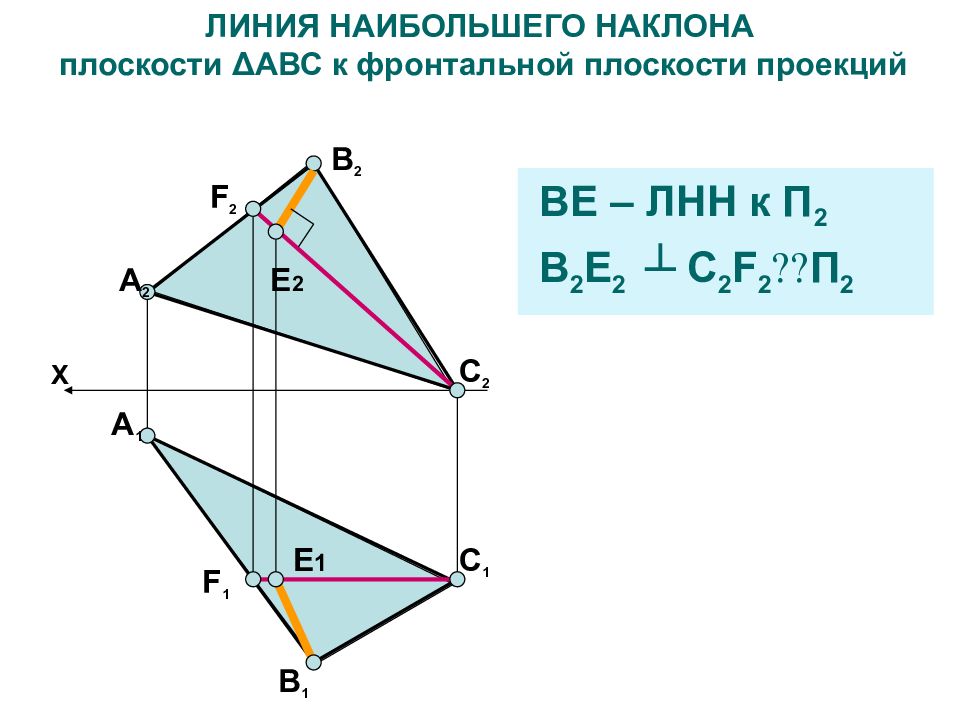
А 2 F 2 В 2 А 1 F 1 ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА плоскости Δ АВС к фронтальной плоскости проекций BE – ЛНН к П 2 В 2 E 2 ┴ C 2 F 2 П 2 X Е 2 Е 1 В 1 С 1 С 2
Слайд 34: НОРМАЛЬ ПЛОСКОСТИ
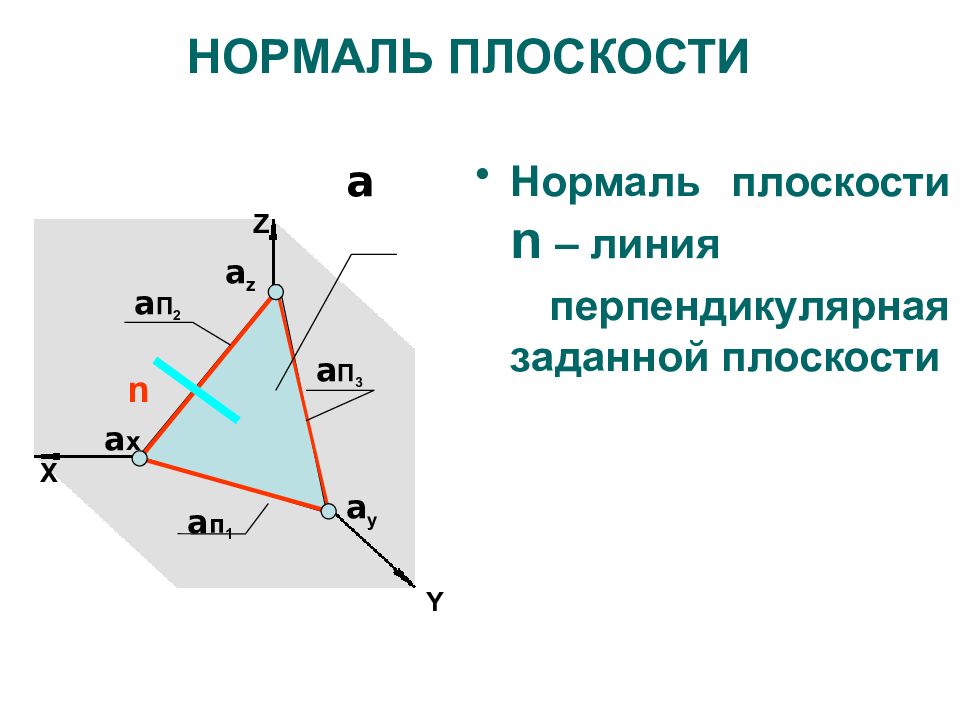
Нормаль плоскости n – линия перпендикулярная заданной плоскости Z X a п 1 a П 3 a П 2 a x a y a z Y a n
Слайд 35
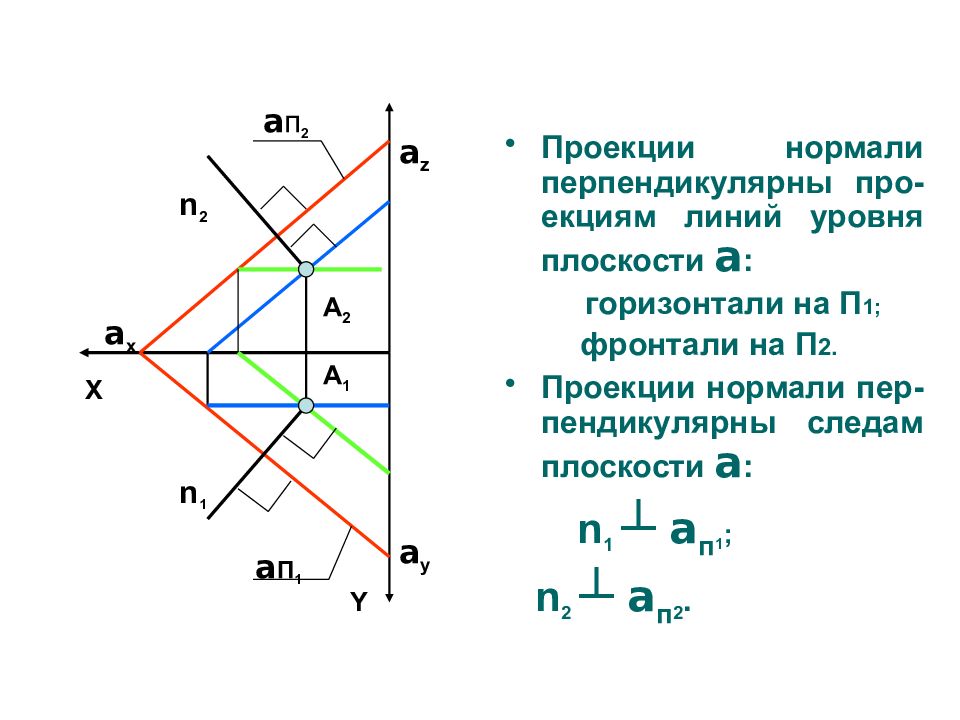
Проекции нормали перпендикулярны про - екциям линий уровня плоскости a : горизонтали на П 1 ; фронтали на П 2. Проекции нормали пер - пендикулярны следам плоскости a : n 1 ┴ a п 1 ; n 2 ┴ a п 2. a П 1 Y a x А 2 А 1 n 2 n 1 X a z a y a п 2
Слайд 36: НОРМАЛЬ ПЛОСКОСТИ ТРЕУГОЛЬНИКА
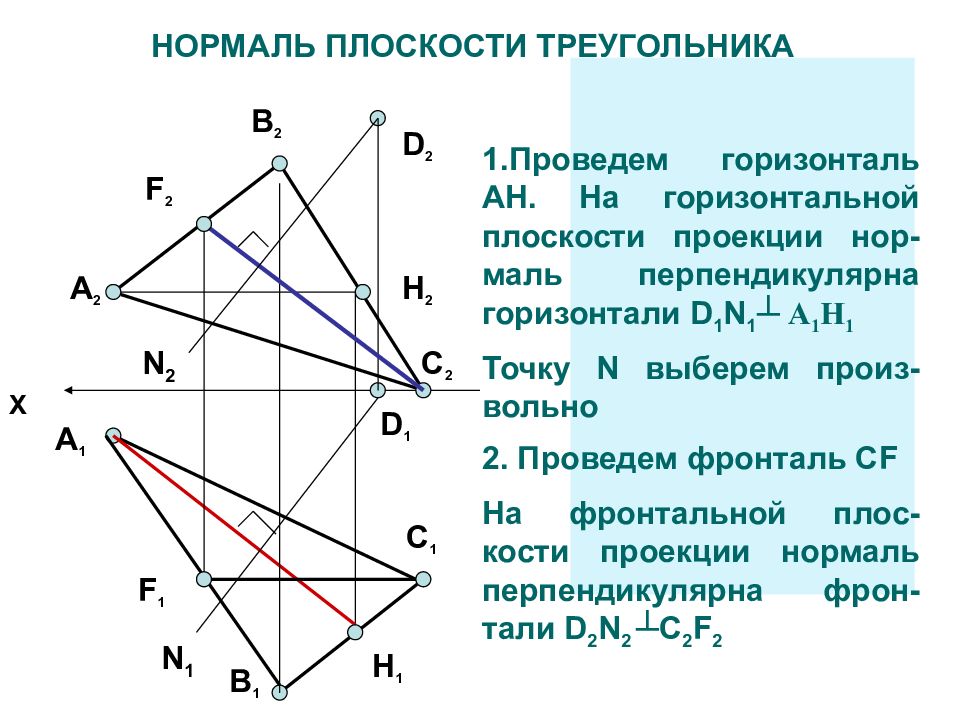
А 2 В 2 А 1 X В 1 С 1 С 2 Через точку D провести перпендикуляр к плоскости треугольника АВС А(80,20,30) В(40,60,60) С(0,40,0) D( 10,0,70) D 2 D 1 1.Проведем горизонталь AH. На горизонтальной плоскости проекции нор-маль перпендикулярна горизонтали D 1 N 1 ┴ А 1 Н 1 Точку N выберем произ-вольно 2. Проведем фронталь CF На фронтальной плос-кости проекции нормаль перпендикулярна фрон-тали D 2 N 2 ┴ C 2 F 2 H 1 H 2 F 1 F 2 НОРМАЛЬ ПЛОСКОСТИ ТРЕУГОЛЬНИКА N 1 N 2
Слайд 39
ПРЯМАЯ ПАРАЛЛЕЛЬНА ПЛОСКОСТИ, ЕСЛИ ОНА ПАРАЛЛЕЛЬНА ЛЮБОЙ ПРЯМОЙ ПРИНАДЛЕЖАЩЕЙ ПЛОСКОСТИ 2. ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫ, ЕСЛИ ДВЕ ПЕРЕ-СЕКАЮЩИЕСЯ ПРЯМЫЕ ОДНОЙ ПЛОСКОСТИ, ПАРАЛЛЕЛЬНЫ ДВУМ ПЕРЕСЕКАЮЩИМСЯ ПРЯ- МЫМ ДРУГОЙ ПЛОСКОСТИ
Слайд 40
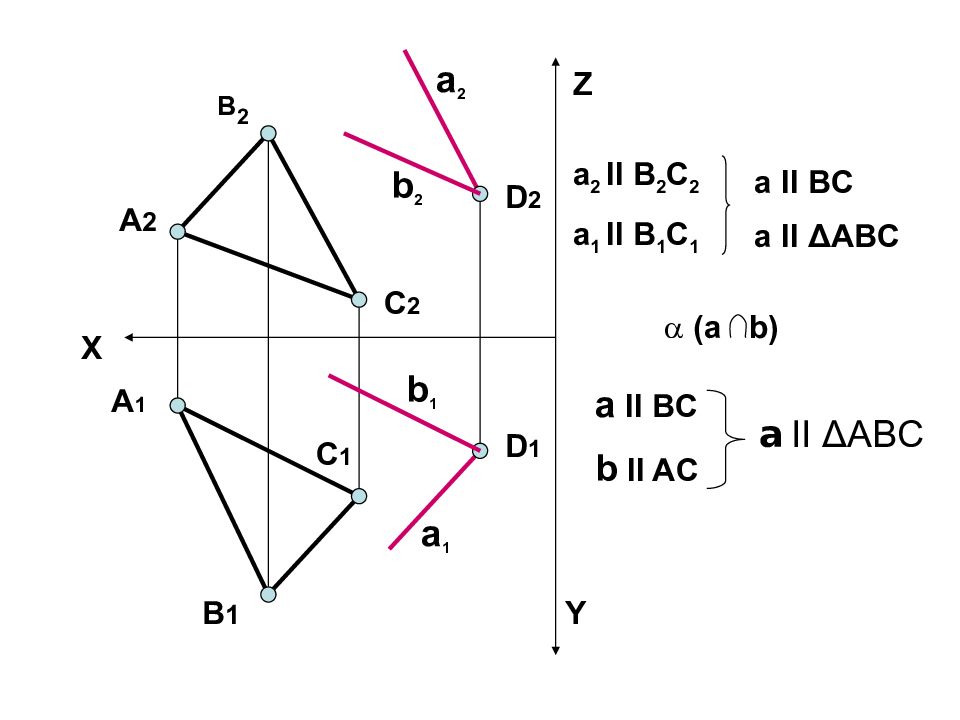
Через точку D провести прямую a параллельную Δ АВС и плоскость α (a ∩ b) параллельную Δ АВС
Слайд 41
X Y Z A 2 B 2 A 1 C 2 C 1 B 1 a 1 a 2 D 2 D 1 a 2 II B 2 C 2 a 1 II B 1 C 1 a II BC a II Δ ABC b 1 b 2 (a b ) a II BC b II AC a II Δ ABC
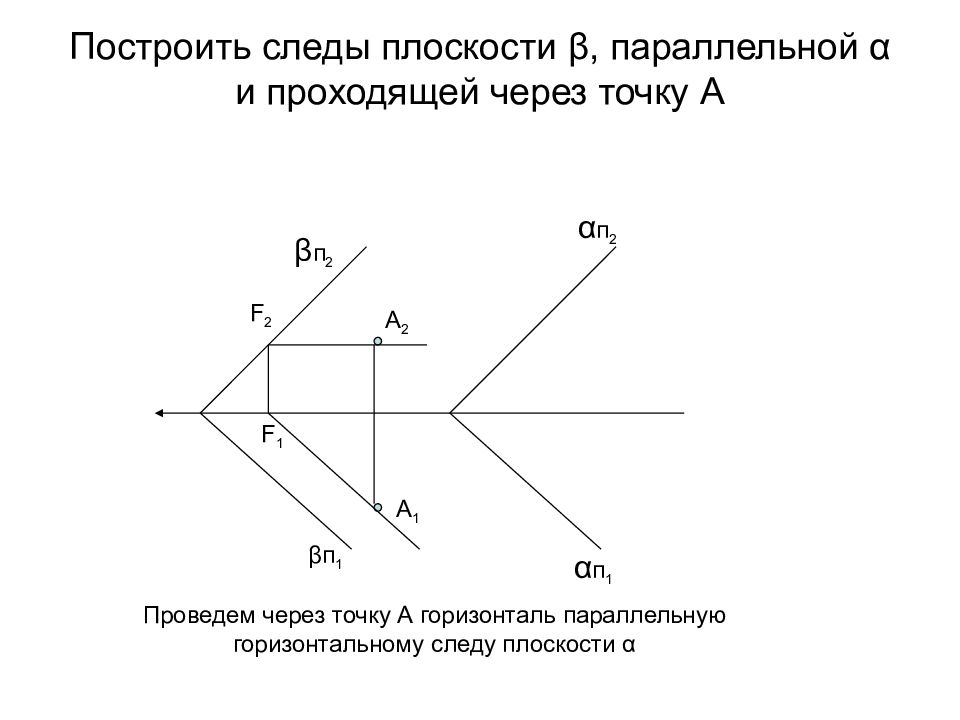
Слайд 42: Построить следы плоскости β, параллельной α и проходящей через точку А
α п 2 α п 1 А 2 А 1 Проведем через точку А горизонталь параллельную горизонтальному следу плоскости α F 1 F 2 β п 2 β п 1
Слайд 43: ПРЯМАЯ ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ, ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
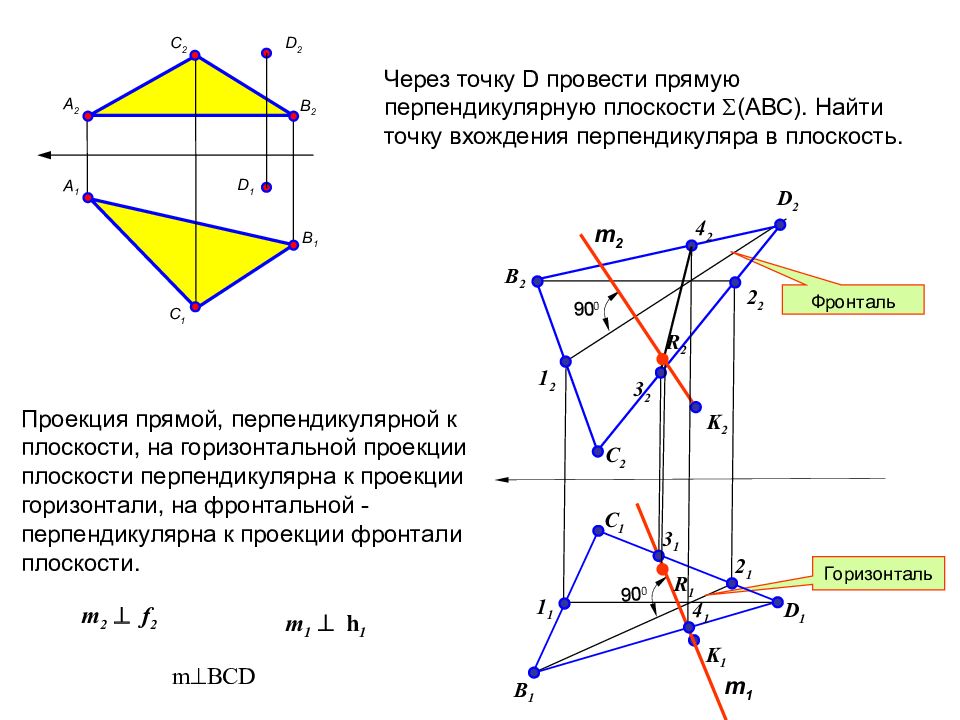
ПРЯМАЯ ПЕРПЕНДИКУЛЯРНА ПЛОСКОСТИ, ЕСЛИ ОНА ПЕРПЕНДИКУЛЯРНА ДВУМ ПЕРЕСЕКАЮЩИМСЯ ПРЯМЫМ ПРИНАДЛЕЖАЩИМ ЭТОЙ ПЛОСКОСТИ В соответствии с теоремой о проекциях прямого угла прямая перпендикулярна плоскости, если она перпендикулярна одноименным проекциям горизонтали и фронтали плоскости · ДВЕ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫ, ЕСЛИ ОДНА ПЛОСКОСТЬ ПРОХОДИТ ЧЕРЕЗ ПЕРПЕНДИКУЛЯР К ДРУГОЙ
Слайд 44: Задача
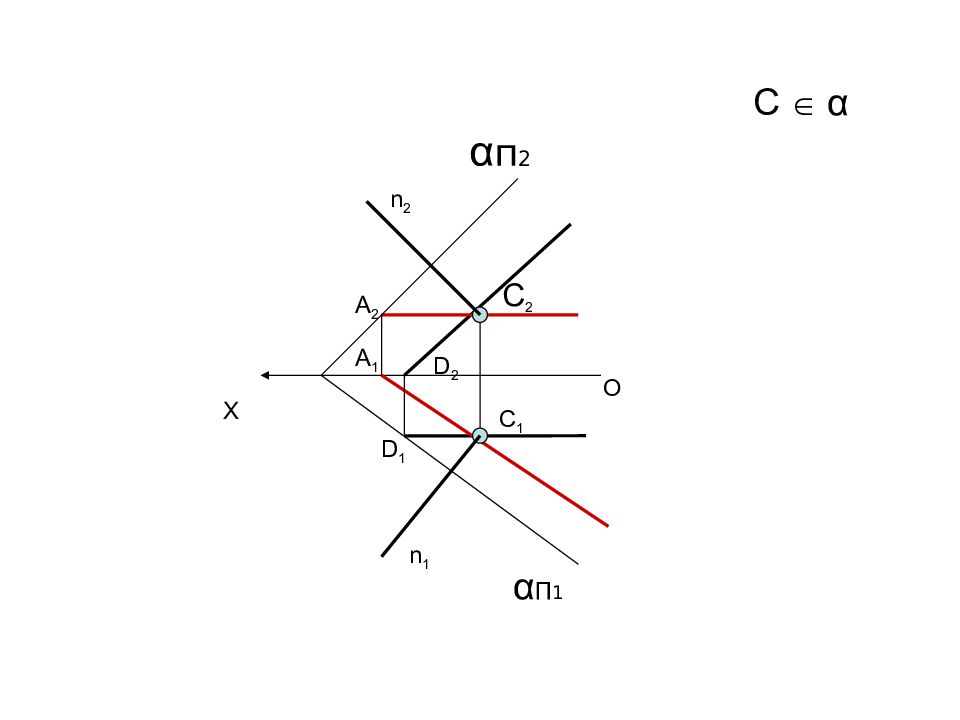
Построить проекции нормали плоскости a, проходящей через точку С плоскости
Слайд 46
Через точку D провести перпендикуляр к плоскости Δ АВС и плоскость α ( n ∩ a) перпендикулярную Δ АВС А(80,10,30) В(40,60,50) С(10,45,0) D(50, 55, 5)
Слайд 47
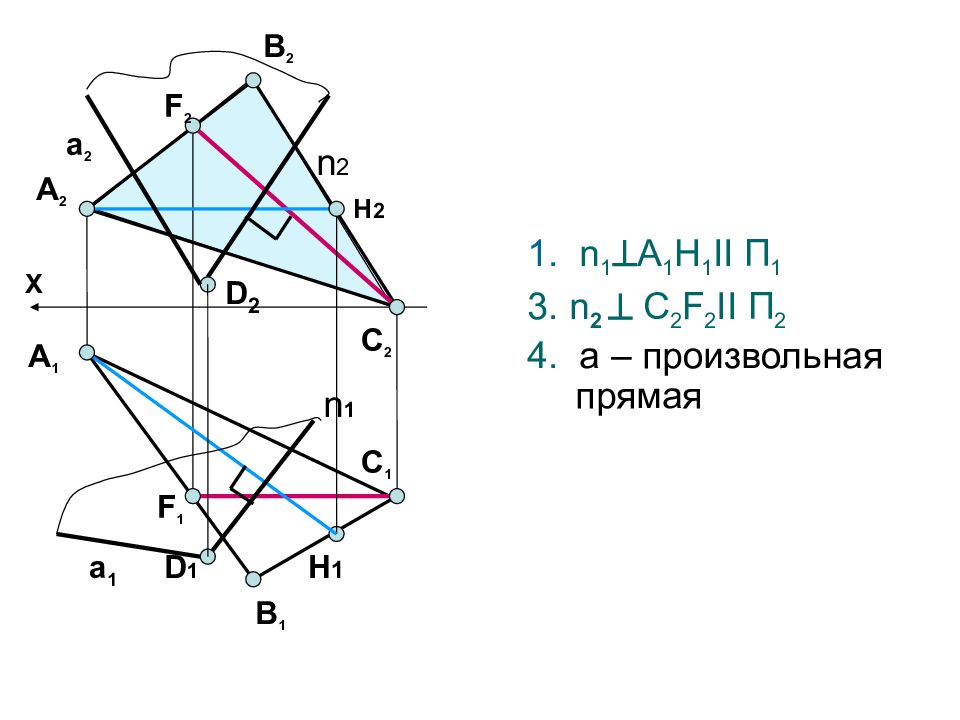
1. n 1 А 1 Н 1 II П 1 3. n 2 С 2 F 2 II П 2 4. а – произвольная прямая А 2 F 2 В 2 А 1 F 1 X H 2 H 1 С 1 С 2 n 2 n 1 В 1 D 2 D 1 a 2 a 1
Слайд 48: ПЕРЕСЕКАЮЩИЕСЯ ПРЯМАЯ И ПЛОСКОСТЬ
ПРЯМАЯ И ПЛОСКОСТЬ ПЕРЕСЕКАЮТСЯ, ЕСЛИ У НИХ ЕСТЬ ОДНА ОБЩАЯ ТОЧКА
Слайд 49
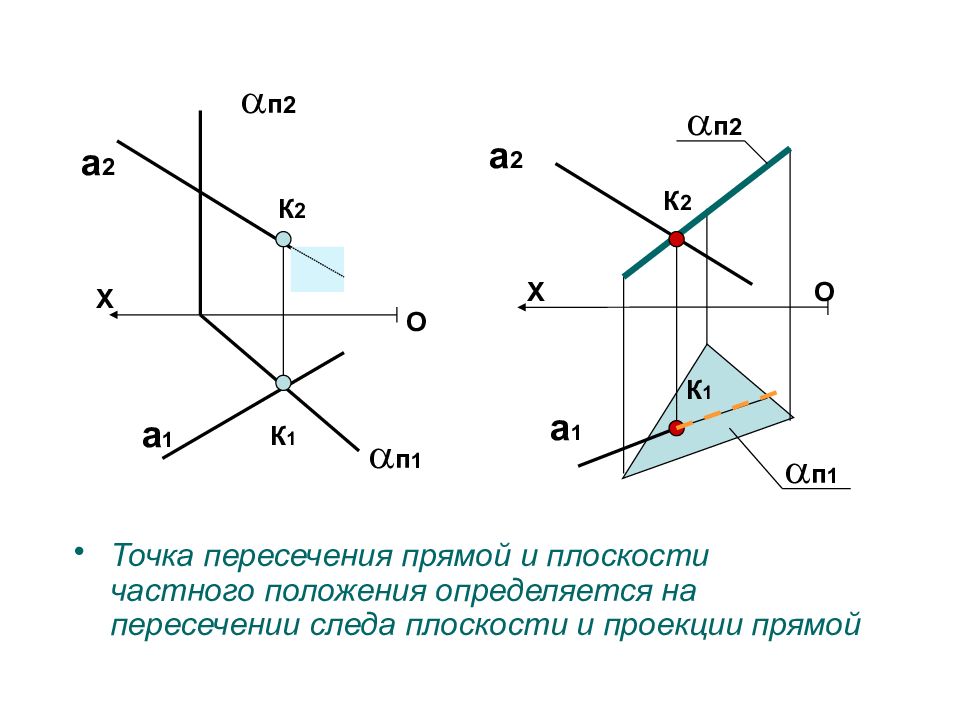
Точка пересечения прямой и плоскости частного положения определяется на пересечении следа плоскости и проекции прямой X O a 1 а 2 п 1 п 2 К 1 К 2 X O a 1 а 2 п 1 п 2 К 1 К 2
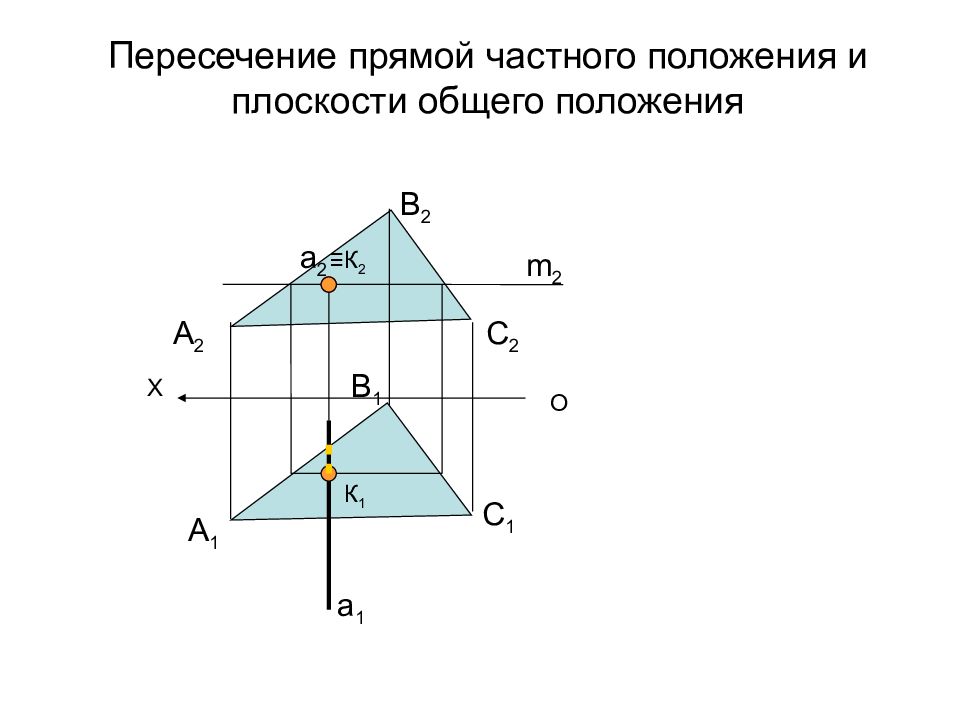
Слайд 50: Пересечение прямой частного положения и плоскости общего положения
О X А 2 В 2 С 2 А 1 В 1 С 1 a 1 a 2 m 2 К 1 ≡К 2
Слайд 51: Пересечение прямой общего положения и плоскости общего положения
СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ 1. Через прямую проводят плоскость частного положения α ┴ П 1. 2. Определяют линию пересечения заданной плоскости и введенной плоскости α. 3. Определяют точку пересечения заданной прямой и построенной линии пересечения. Это искомая точка пересечения заданной плоскости и прямой а. 4. Определяют видимость заданной прямой.
Слайд 52
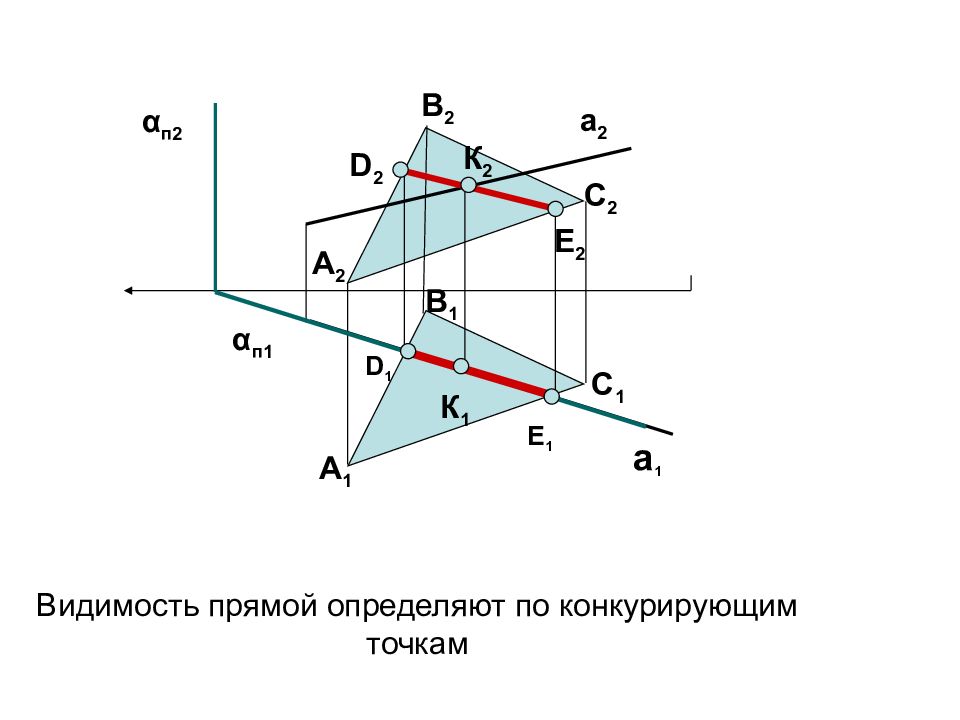
α п 1 C 1 Е 2 A 2 С 2 B 2 A 1 B 1 D 1 E 1 a 1 a 2 D 2 α п 2 К 2 К 1 Видимость прямой определяют по конкурирующим точкам
Слайд 53
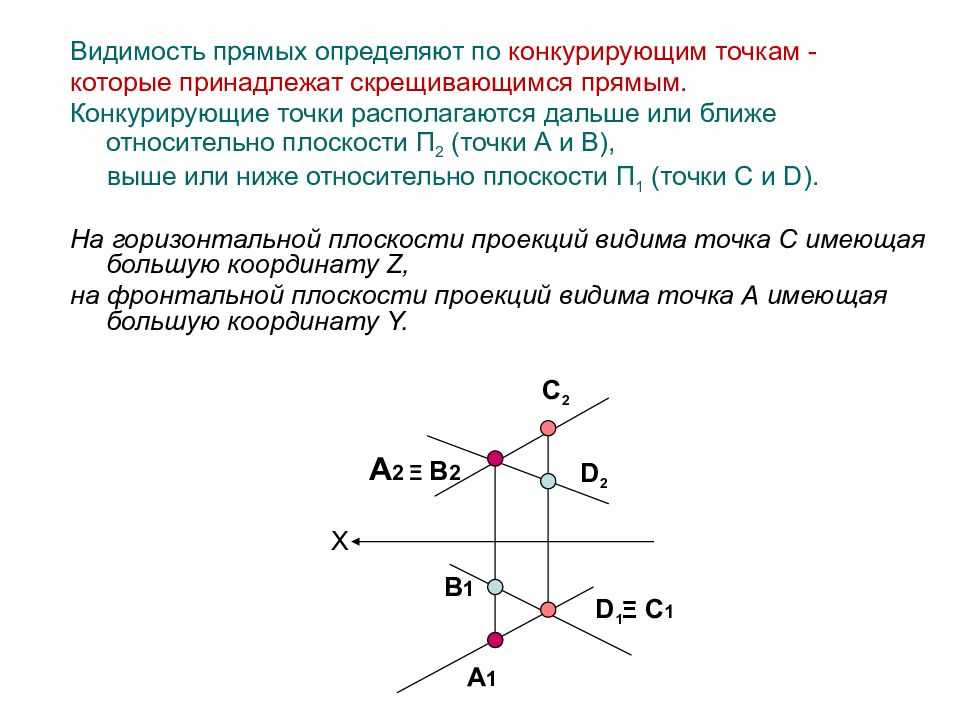
Видимость прямых определяют по конкурирующим точкам - которые принадлежат скрещивающимся прямым. Конкурирующие точки располагаются дальше или ближе относительно плоскости П 2 (точки А и В), выше или ниже относительно плоскости П 1 (точки C и D ). На горизонтальной плоскости проекций видима точка С имеющая большую координату Z, на фронтальной плоскости проекций видима точка А имеющая большую координату Y. А 1 С 2 D 2 D 1 Ξ C 1 В 1 А 2 Ξ В 2 X
Слайд 54
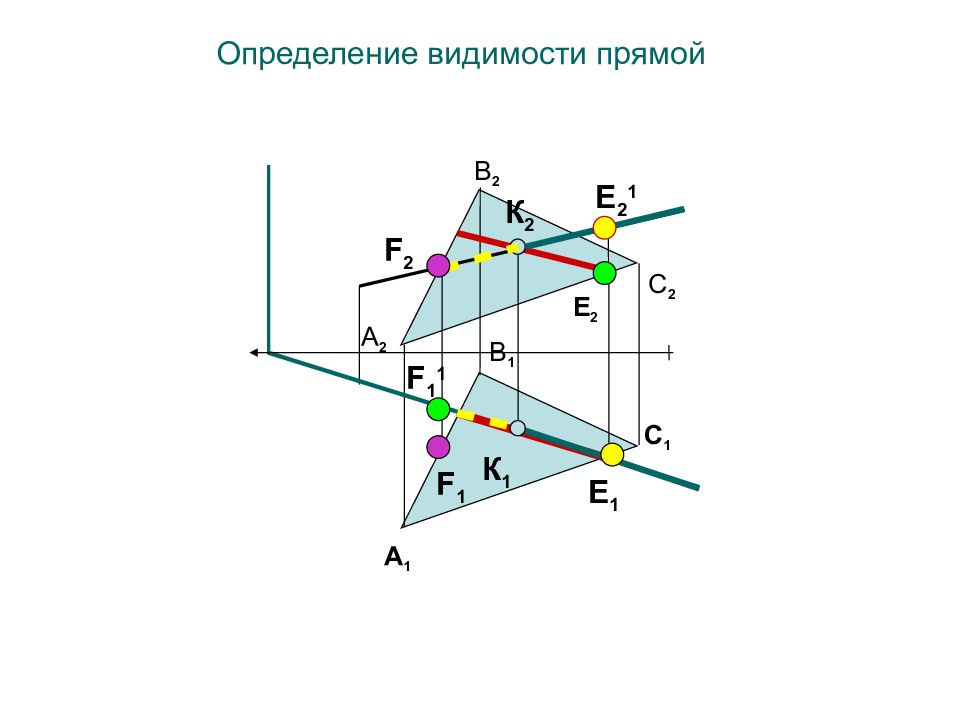
Определение видимости прямой Е 2 F 1 1 E 1 F 2 Е 2 1 F 1 C 1 A 2 С 2 B 2 A 1 B 1 К 1 К 2
Слайд 56
1. ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ, ЕСЛИ У НИХ ЕСТЬ ДВЕ ОБЩИЕ ТОЧКИ 2. ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ ПО ПРЯМОЙ ЛИНИИ, КОТОРАЯ ПРОХОДИТ ЧЕРЕЗ ДВЕ ОБЩИЕ ТОЧКИ ПЛОСКОСТЕЙ
Слайд 57
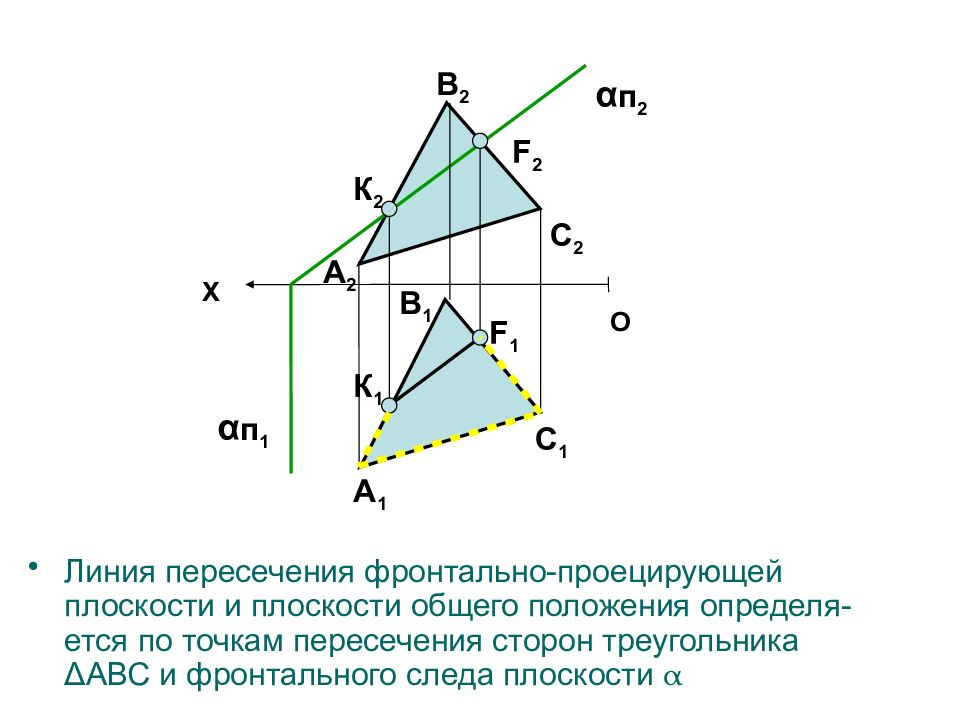
Линия пересечения фронтально-проецирующей плоскости и плоскости общего положения определя-ется по точкам пересечения сторон треугольника Δ АВС и фронтального следа плоскости α X O К 2 F 2 F 1 К 1 A 2 B 2 C 2 B 1 A 1 C 1 α п 1 α п 2
Слайд 58: ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
Для построения линии пересечения плоскостей достаточно определить две общие точки заданных плоскостей ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
Слайд 59: Задача
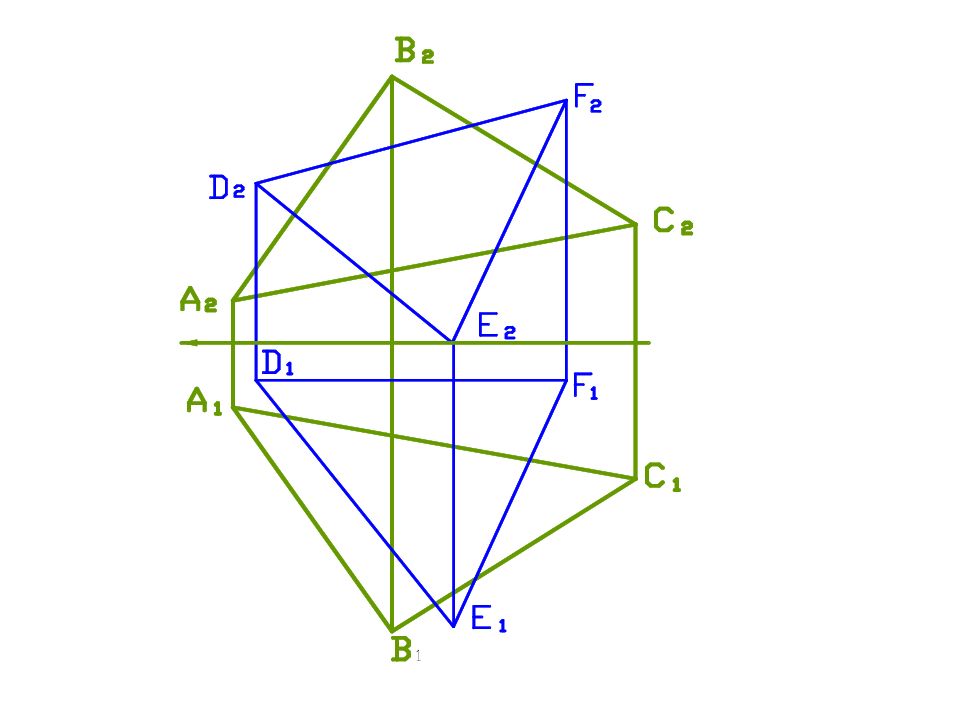
Построить линию пересечения треугольников Δ ABC и Δ DEF. A(100, 20, 20), B(65, 70, 70), C(10, 30, 25 ), D(90, 10, 55), E(45, 70, 0), F(20, 10, 65)
Слайд 62: ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
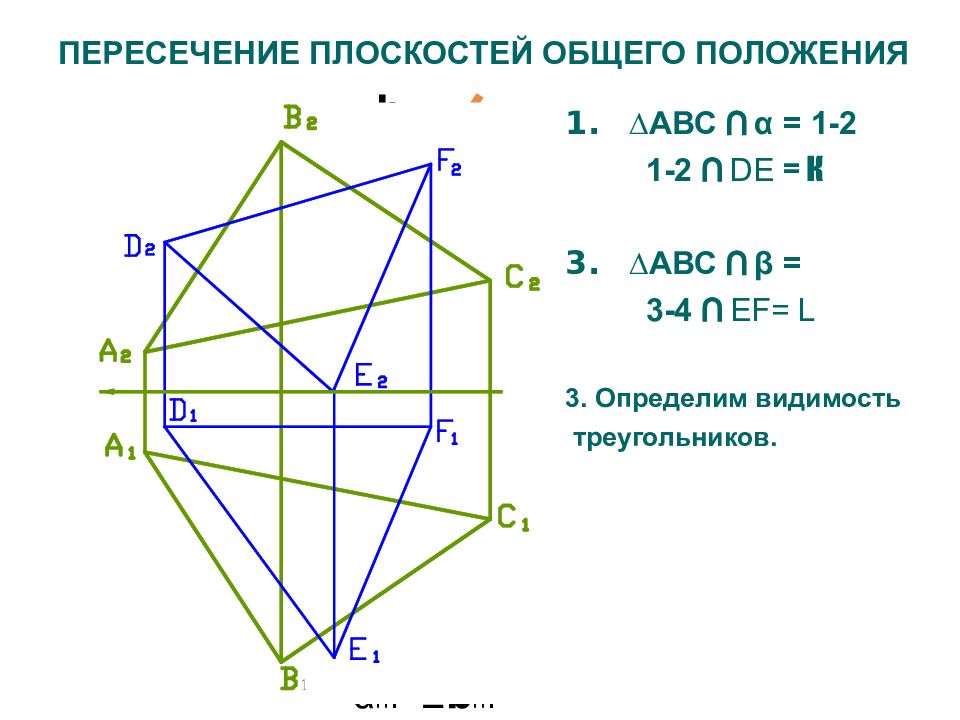
АВС ∩ α = 1-2 1-2 ∩ DE = К АВС ∩ β = 3-4 ∩ EF= L 3. Определим видимость треугольников. α п 2 α п 1 К 1 К 2 b п 2 Ξ b п 1 L 2 L 1 1 2 2 2 1 1 2 1 3 2 4 2 3 1 4 1
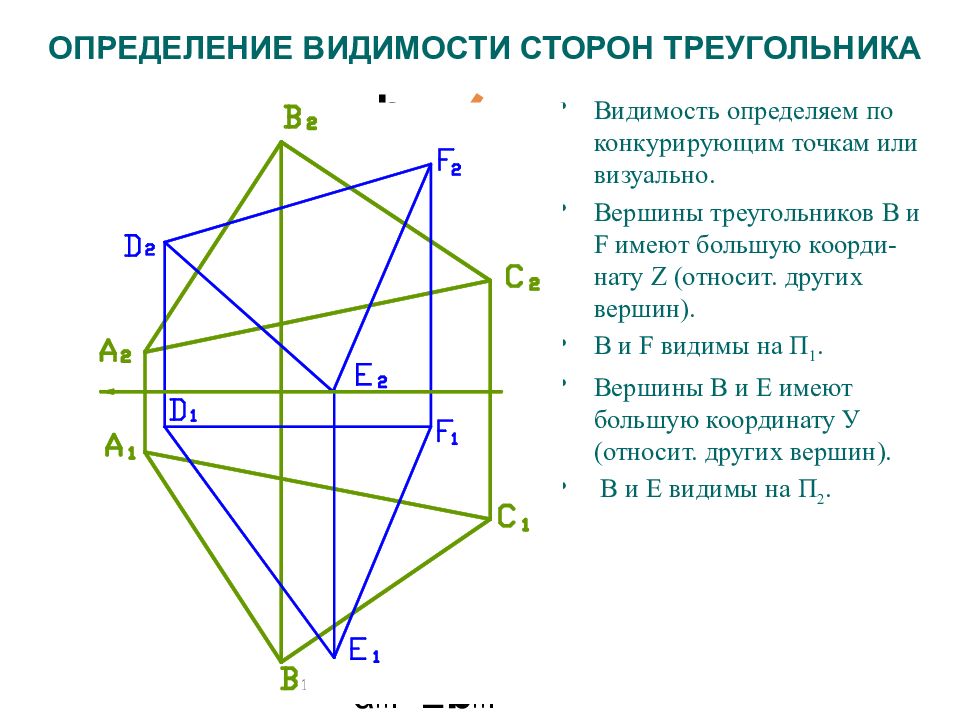
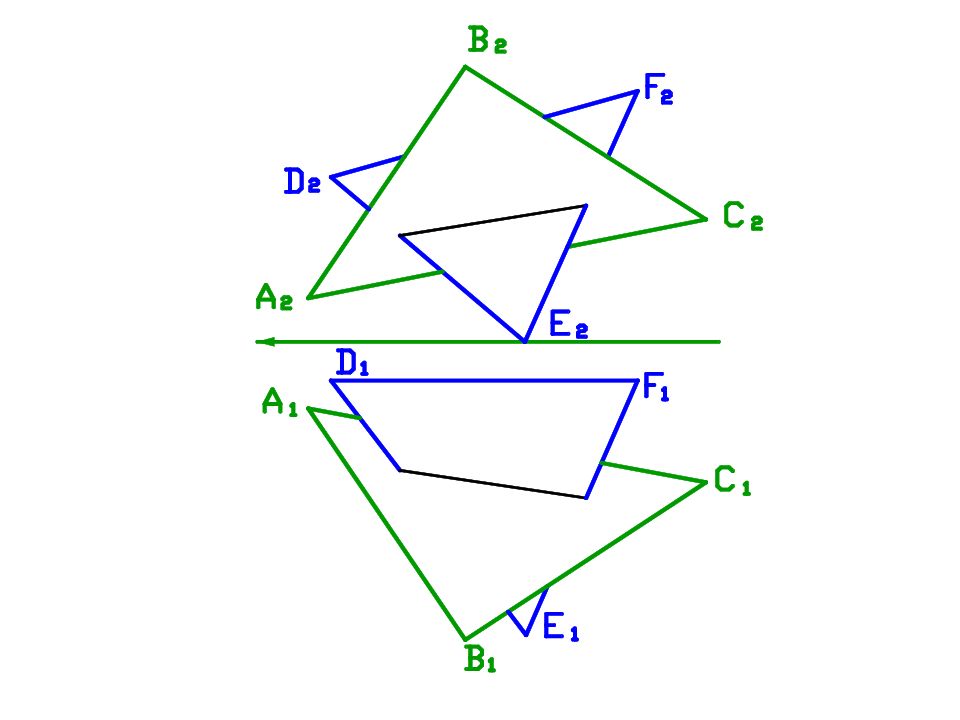
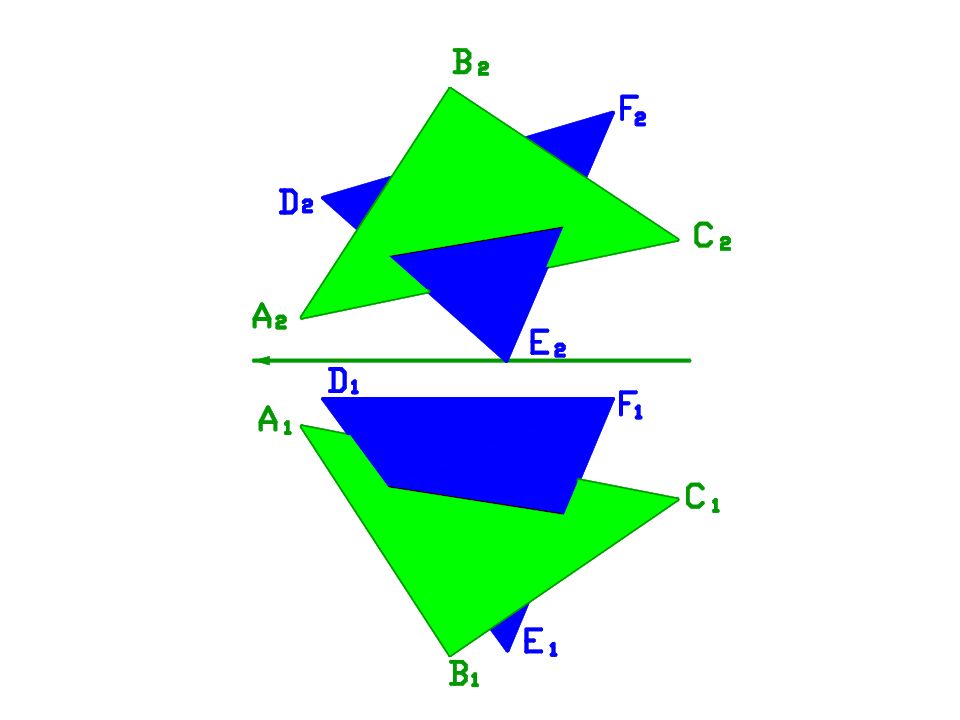
Слайд 63: ОПРЕДЕЛЕНИЕ ВИДИМОСТИ СТОРОН ТРЕУГОЛЬНИКА
Видимость определяем по конкурирующим точкам или визуально. Вершины треугольников В и F имеют большую коорди-нату Z ( относит. других вершин). В и F видимы на П 1. Вершины В и Е имеют большую координату У (относит. других вершин). В и Е видимы на П 2. α п 2 α п 1 К 1 К 2 b п 2 Ξ b п 1 L 2 L 1