1 МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2 Пусть имеем обыкновенное дифференциальное уравнение первого порядка y'= f(x;y) с начальными условиями y(x 0 )=y 0. Будем искать решение этого уравнения на отрезке [ x 0 ; b]. Разобьем этот отрезок на n равных частей. Тогда получим систему равноотстоящих узлов a=x 0, x 1 =x 0 +h, x 2 =x 1 +h, …, x n =b. Здесь h=(b- a )/n – шаг интегрирования. Численные методы дают возможность найти в некотором числе точек x 1, x 2, …, x n приближения y 1, y 2, …, y n для значений точного решения y(x 1 ), y(x 2 ), …, y(x 0 ). Наиболее простым методом решения обыкновенных дифференциальных уравнений и их систем является
3 МЕТОД ЭЙЛЕРА Пусть дано дифференциальное уравнение y'=f(x,y) (1) с начальными условиями y(x 0 )=y 0. Пусть y=y(x) – искомое точное решение. Интегральная кривая проходит через точку (x 0,y 0 ). Найдем приближенные значения функции в точках x 1, x 2, …, x n. Построим систему равноотстоящих точек a= x 0, x 1 =x 0 + h, …, x n =b. Проведём прямые x=x 0, x=x 1, …, x=b.
4 y x x 0 x 1 x 2 b y 2 y 1 y 0 A
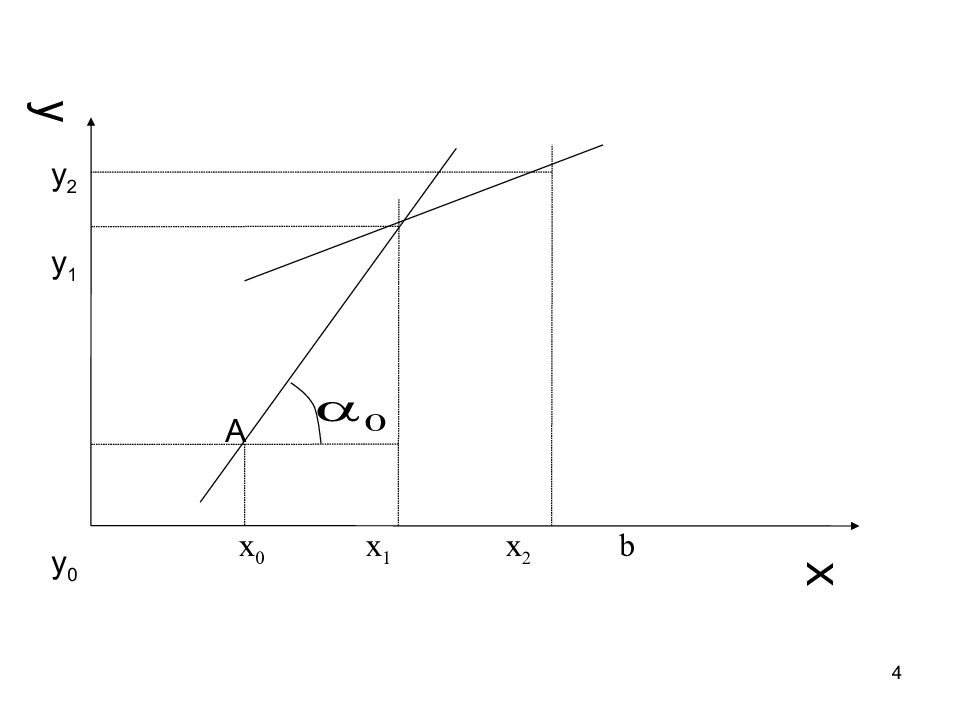
5 Рассмотрим отрезок [x 0,x 1 ]. На этом отрезке есть одна точка, которая принадлежит искомой кривой – это точка А (x 0,y 0 ). Заменим дугу искомой кривой y=y(x) на отрезке [x 0,x 1 ] касательной к ней, проведенной в точке (x 0,y 0 ). В качестве y 1 возьмём ординату точки пересечения прямой x=x 1 к касательной. Очевидно y 1 =y 0 +h•tgα 0. Но tgα 0 =y'(x 0 ), т.е. y 1 =y 0 +h•y'(x 0 ). Но из уравнения (1) следует, что y'(x 0 )=f(x 0,y 0 ). Итак, получаем y 1 =y 0 +h•f( x 0, y 0 ), x 1 = x 0 + h.
6 Предположим теперь, что точка ( x 1, y 1 ) принадлежит искомой кривой. В этой точке опять проведём касательную к графику функции до пересечения с прямой x = x 2. Тогда аналогично: y 2 = y 1 + h f ( x 1, y 1 ); x 2 = x 1 + h. Продолжая и так далее, получим систему значений y 1, y 2,…, y n, которые и будут приближенными значениями функции y = y ( x ) в точках x 1, x 2,… x n. Итак, расчётные формулы метода Эйлера: y m+1 = y m + h f( x m,y m ) x m +1 = x m + h
7 МЕТОД ЭЙЛЕРА-КОШИ Пусть опять решаем уравнение y '= f ( x, y ), y(x 0 )= y 0. Решение ищем на отрезке [ x 0, x n ]. Пусть нам известны координаты некоторой точки, принадлежащей искомому решению ( x m, y m ). Найдём средний тангенс угла наклона касательной для двух точек: ( x m, y m ) и ( x m + h, y m +hf(x m,y m ) ). Последняя точка, есть та самая, которую в методе Эйлера мы обозначаем ( x m +1, y m +1 ), но здесь эта точка будет вспомогательной ( x m +1, ỹ m +1 )/
8 y x x m x m +1 α 2 A L 2 L 1 L ỹ m+1 y m +1 y m α 1
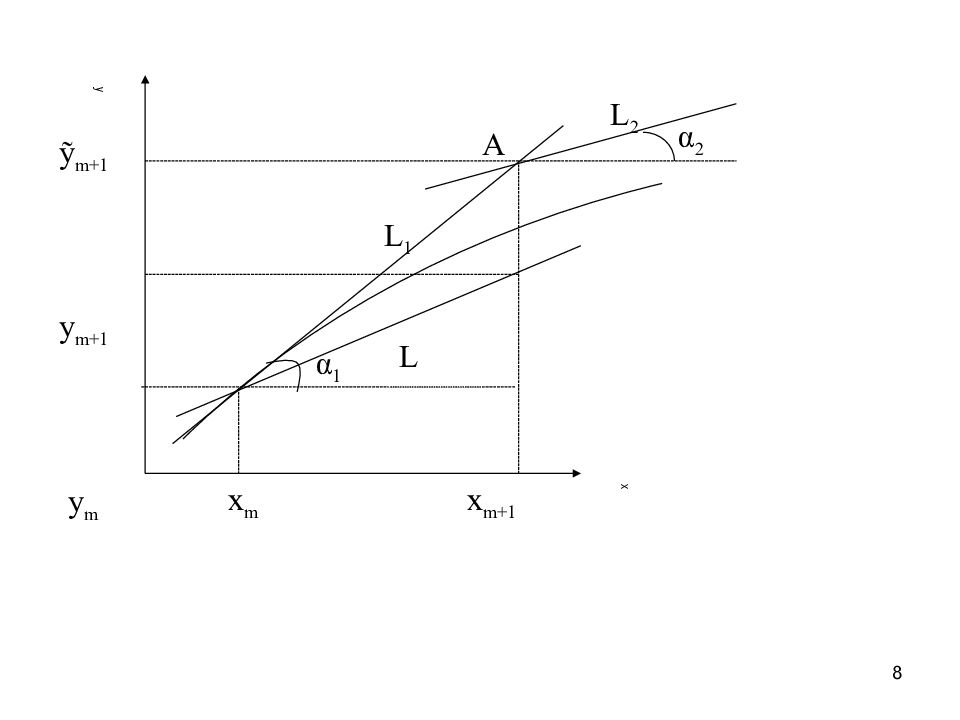
9 Итак, сначала по методу Эйлера находится точка А, лежащая на прямой L 1, тангенс угла наклона которой tg α 1 = f ( x m, y m ). В этой точке снова вычисляется тангенс угла наклона касательной L 2 tgα 2 = f ( x m + h, y m +hf(x m,y m ) ) Затем через точку ( x m, y m ) проводим прямую L, тангенс угла наклона которой равен ( tgα 1 + tgα 2 )/2. Точка, в которой L пересекается с прямой x = x m +1 и будет искомой ( x m +1, y m +1 ). Таким образом, y m +1 есть искомое приближение значений функции на данном шаге интегрирования. Расчетные формулы метода Эйлера-Коши следующие: ỹ m+1 = y m +hf(x m,y m ); y m+1 = y m +(h/2)·[f(x m,y m )+f(x m+1,ỹ m+1 )]; x m +1 = x m + h.
10 МЕТОД РУНГЕ-КУТТА 2-ГО ПОРЯДКА Пусть имеем дифференциальное уравнение y '= f ( x, y ) с начальными условиями у( x 0 )= y 0. Ищем решение на отрезке [ x 0, x n ]. Пусть имеем точку ( x m, y m ), принадлежащему искомому решению. Для того, чтобы найти следующую точку проведем касательную к кривой в точке ( x m, y m ) до пересечения с прямой x = x m +0.5, где x m +0.5 = x m + h /2. Тогда получим координату (по формуле Эйлера) y m+0.5 =y m +h/2·f(x m,y m ).
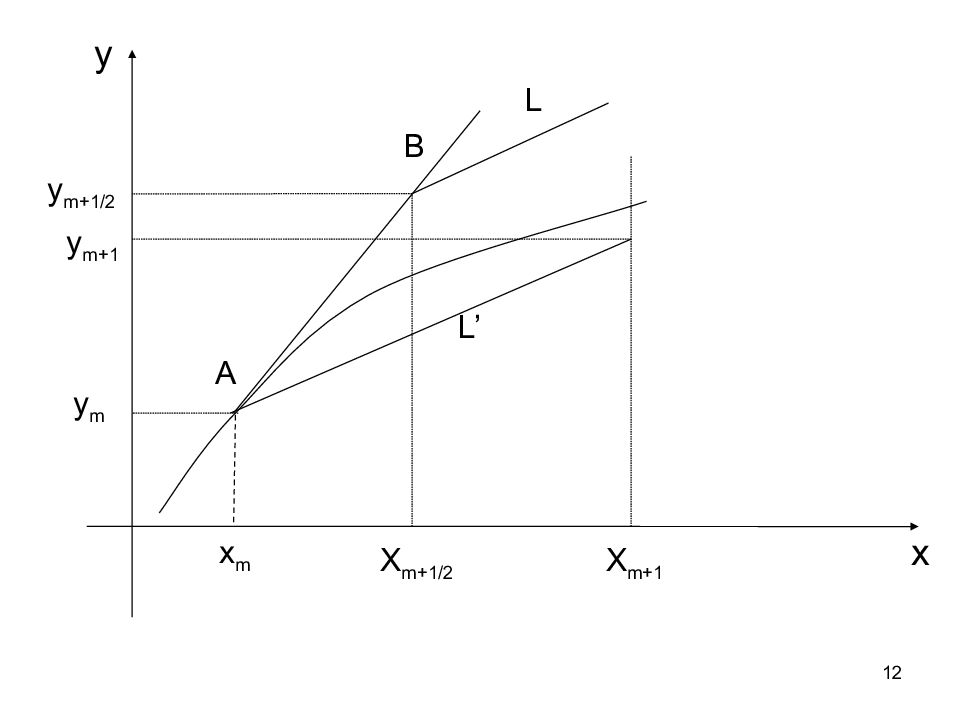
11 Теперь найдём тангенс угла наклона касательной в точке В ( x m +0.5, y m +0.5 ), (прямая L ). Через точку А проведём прямую L '|| L. Ординату точки пересечения прямых L ' и x = x m +1 возьмём в качестве y m +1. Таким образом, y m +0.5 = y m + h /2· f ( x m, y m ), x m +0.5 = x m + h /2 y m+1 = y m +h·f(x m+0.5,y m+0.5 ), x m+1 =x m +h
12 y x X m+1/2 X m+1 x m y m y m+1/2 y m+1 L L’ A B
13 МЕТОД РУНГЕ-КУТТА 4-ГО ПОРЯДКА Этот метод один из самых распространённых методов интегрирования дифференциальных уравнений. Для одиночного дифференциального уравнения y '= f ( x, y ), y ( x 0 )= y 0 расчётные формулы имеют следующий вид: y m+1 = y m +h /6(k 1 +2k 2 +2k 3 +k 4 ), где k 1 = f( x m,y m ); k 2 = f( x m +h /2,y m +hk 1 /2); k 3 = f( x m +h /2,y m +hk 2 /2); k 4 = f(x m +h,y m +hk 3 ); x m +1 = x m + h.
