Слайд 2
2 Понятие производной Определение. Производной функции y = f ( x ) в точке х 0 называется предел при х 0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует). Пример: Вычислить производную функции y = x 2 в точке х = 5.
Слайд 3
3 Если для некоторого значения х 0 выполняется условие то говорят, что в точке х функция имеет бесконечную производную знака «+» или знака « – ». В отличие от бесконечной производной определенную выше производную функции иногда называют конечной производной. или
Слайд 4
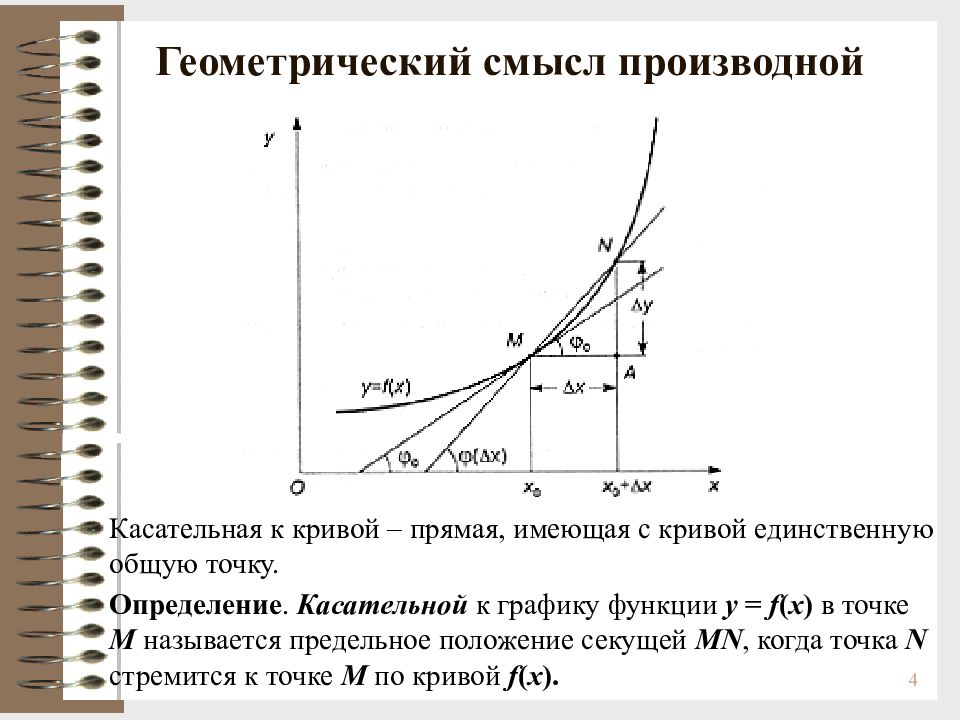
4 Геометрический смысл производной Касательная к кривой – прямая, имеющая с кривой единственную общую точку. Определение. Касательной к графику функции y = f ( x ) в точке М называется предельное положение секущей MN, когда точка N стремится к точке М по кривой f ( x ).
Слайд 5
5 Уравнения касательной и нормали к кривой Для касательной всегда выполнятся Если взять Определение. Нормалью к кривой называется прямая, проходящая через точку касания перпендикулярно касательной. Производная f’ ( x 0 ) равна угловому коэффициенту (тангенсу угла наклона к положительному направлению оси Ох ) касательной к графику функции y = f ( x ) в точке M ( x 0, f ( x 0 )). При этом Для перпендикулярных прямых Уравнение нормали к кривой: Уравнение касательной:
Слайд 6
6 Физический смысл производной Если функция s = f ( t ) описывает закон движения материаль- ной точки по прямой как зависимость пути от времени, то Путь, пройденный за интервал времени D t. Средняя скорость за время D t Мгновенная скорость точки В определенном смысле производную функции y = f ( x ) можно также трактовать как скорость изменения функции: чем больше величина f’ ( x ), тем больше угол наклона касательной к кривой, тем круче график f ( x ) и быстрее растет функция.
Слайд 8
8 Операцию нахождения производной называют дифференцированием. Функция, имеющая производную в точке, называет дифференцируемой в этой точке. Определение. Функция f ( x ) называется дифференцируемой в точке х 0, если ее приращение в этой точке можно представить в виде y = A D x + ( x ) x, где А – некоторое число, не зависящее от х, а ( х ) – функция аргумента х, являющаяся бесконечно малой при х 0, т.е. Теорема Если функция f ( x ) дифференцируема в данной точке х 0, то она и непрерывна в этой точке. Замечание. Обратное утверждение неверно. Например, функция f ( x ) = | x | непрерывна в точке х = 0, но не является дифференцируемой. Таким образом, требование дифференцируемости является более сильным, чем требование непрерывности.
Слайд 9
9 Правила дифференцирования суммы, разности, произведения и частного Теорема. Если функции u = u ( x ) и v = v ( x ) дифференцируемы в точке х, то сумма, разность, произведение и частное этих функций (частное при условии v ( x ) 0) также дифференцируемы в этой точке и имеют место следующие формулы
Слайд 11
11 Теорема о производной обратной функции Пусть функция х = ( у ) является обратной для функции y = f ( x ). Теорема. Если функция y = f ( x ) имеет в точке х 0 производную f ( x ) 0, то обратная функция х = ( у ) также имеет в соответствующей точке у 0 = f ( x 0 ) производную, причем
Слайд 12
12 Доказательство. Учтем, что Перейдем к пределу при у 0. Обратная функция х = ( у ) непрерывна в точке у 0, то х 0 при у 0. Получим Ч.т.д.
Слайд 13
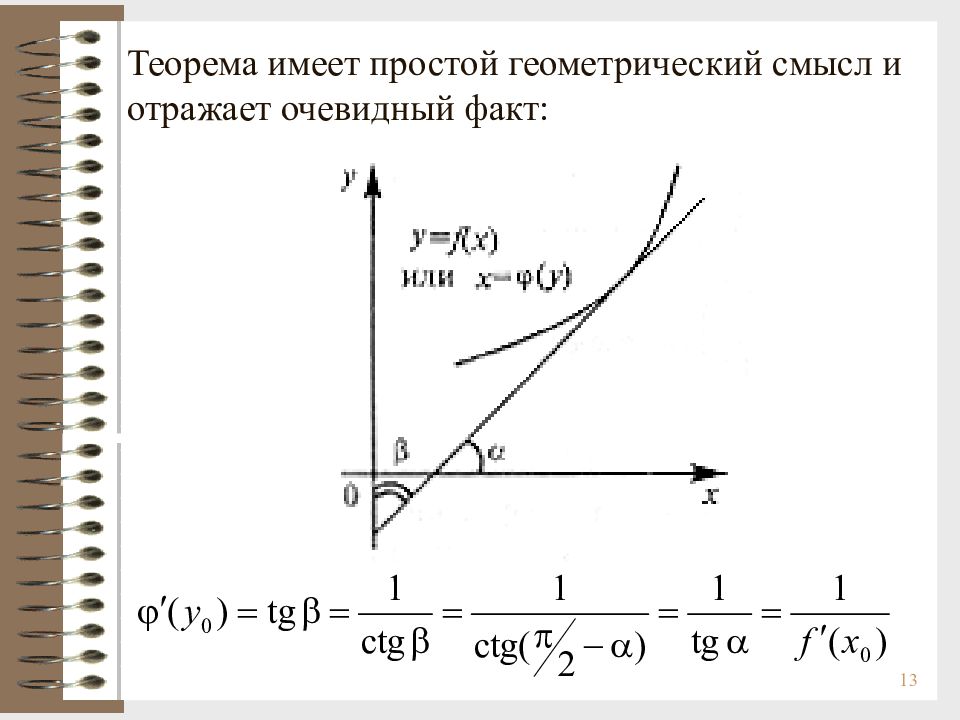
13 Теорема имеет простой геометрический смысл и отражает очевидный факт :
Слайд 14
14 Правило дифференцирования сложной функции Теорема. Если функция u = ( x ) имеет производную в точке x 0, а функция y = f ( u ) имеет производную в соответствующей точке u 0 = ( x 0 ), то сложная функция f [ ( x )] имеет производную в точке x 0 и справедлива следующая формула
Слайд 15
15 Доказательство : т.к. функция y = f ( x ) дифференцируема в точке х 0, то Так как по условию u = ( x ) дифференцируема, то она и непрерывна в точке x 0, следовательно Переходя к пределу в предыдущем равенстве получим при и Замечание. Правило дифференцирования остается тем же, если зависимость более сложная – с двумя, тремя и большим числом промежуточных переменных.
Слайд 16
16 Производные простейших элементарных функций В частности В частности В частности
Слайд 17
17 На основе правил и формул дифференцирования можно сделать вывод : операция дифференцирования не выводит из класса элементарных функций.
Слайд 20
20 Логарифмическая производная Вычислим производную сложной функции которая называется логарифмической производной (знак модуля обычно не записывается). Логарифмическую производную удобно использовать при нахождении производных функций, выражения которых значительно упрощаются при логарифмировании.
Слайд 22
22 Техника нахождения производных Основные правила: Ввести функцию u ( x ), так чтобы y = f ( u ) содержалось в таблице производных Использовать правила дифференцирования Примеры:
Слайд 23
23 Понятие дифференциала функции Пусть функция f ( x ) дифференцируема в точке х 0, тогда её приращение в этой точке можно записать в виде суммы : y =A x + ( x ) x, где Слагаемое ( х ) х при х 0 – бесконечно малая более высокого порядка, чем х. Определение. Дифференциалом функции y= f ( x ) в точке х 0 называется главная, линейная относительно х, часть приращения функции в этой точке : dy = A x Учитывая, что А= f '( x 0 ), формулу можно записать в виде dy = f '( x 0 ) x. Дифференциалом независимой переменной х назовем приращение этой переменной dx = x. Соотношение принимает теперь вид: dy = f '( x 0 ) dx
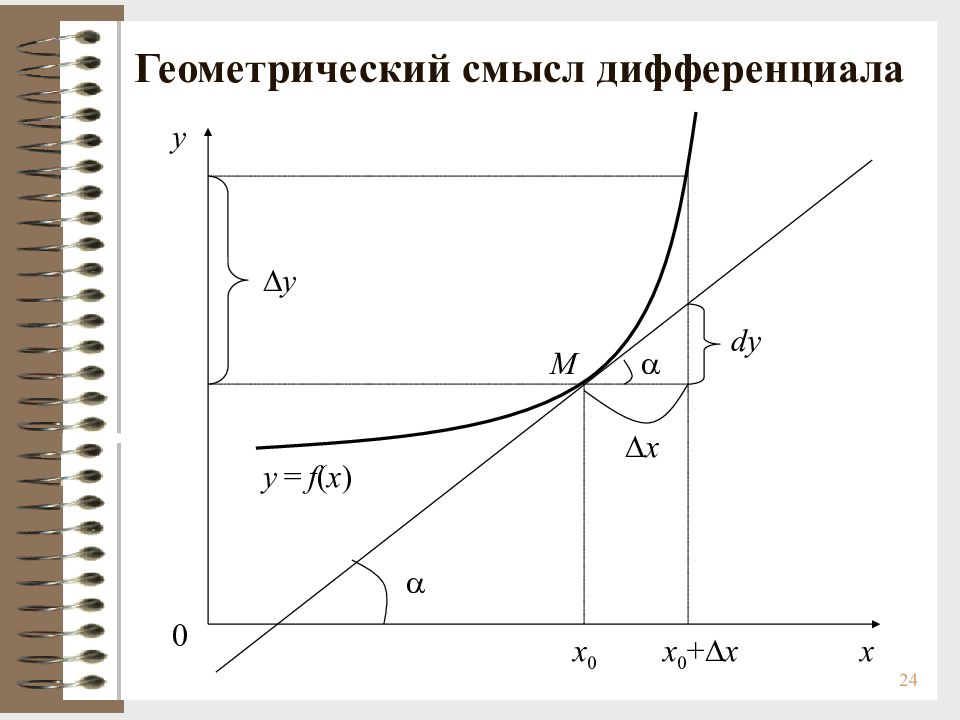
Слайд 24: Геометрический смысл дифференциала
24 Геометрический смысл дифференциала x 0 x 0 + x x y y 0 y = f ( x ) dy M x
Слайд 25
25 Производные высших порядков Производная f '( x ) функции y = f ( x ) сама является некоторой функцией аргумента х. Назовём f '( x ) производной первого порядка функции f ( x ). Производная от производной некоторой функции называется производной 2 -го порядка (или второй производной ) этой функции. Производная от второй производной называется производной 3 -го порядка (или третьей производной ) и т.д.
Слайд 26
26 Производные, начиная со второй, называются производными высших порядков и обозначаются у '', у ''', у (4), …, у ( n), … или f ''( x ), f '''( x ), f (4) ( x ), …, f ( n ) ( x ), … Производная n - го порядка является производной от производной ( n -1)- го порядка : y ( n ) = ( y ( n -1) )'. Если функция y = f ( x ) описывает закон движения материальной точки по прямой линии, то 1-ая производная f '( x ) есть мгновенная скорость точки в момент времени х, а 2-ая производная равна ускорению точки в момент х
Слайд 27
27 Параметрическое задание функции и ее дифференцирование Пусть заданы две функции x = ( t ), y = ( t ) (1) одной независимой переменной t, определенные и непрерывные в одном и том же промежутке. Если x = ( t ) строго монотонна, то обратная функция t = F ( x ) однозначна, также непрерывна и строго монотонна. Поэтому у можно рассматривать как функцию, зависящую от переменной х посредством переменной t, называемый параметром : y = [ F ( x )].
28 В этом случае говорят, что функция у от х задана параметрически с помощью уравнений (1). Предположим, что функции (1) имеют производные, причем ' ( t ) 0 на некотором промежутке. По теореме о производной обратной функции функция F ( x ) имеет производную : а по теореме о производной сложной функции функция y = [ F ( x )] имеет производную : y '( x ) = ' [ F ( x )] F '( x )
29 Найдем вторую производную : y ''( x ) = ( y '( x ))' x =
Слайд 30
30 Производная неявной функции Функция задана неявно, если она имеет вид f ( x, y ) = C. Для нахождения производной y ' x заданной неявно функции нужно продифференцировать обе части уравнения, считая y = y ( x ), а затем из полученного уравнения найти производную y ' x. Можно также воспользоваться свойством дифференциала функции двух переменных: