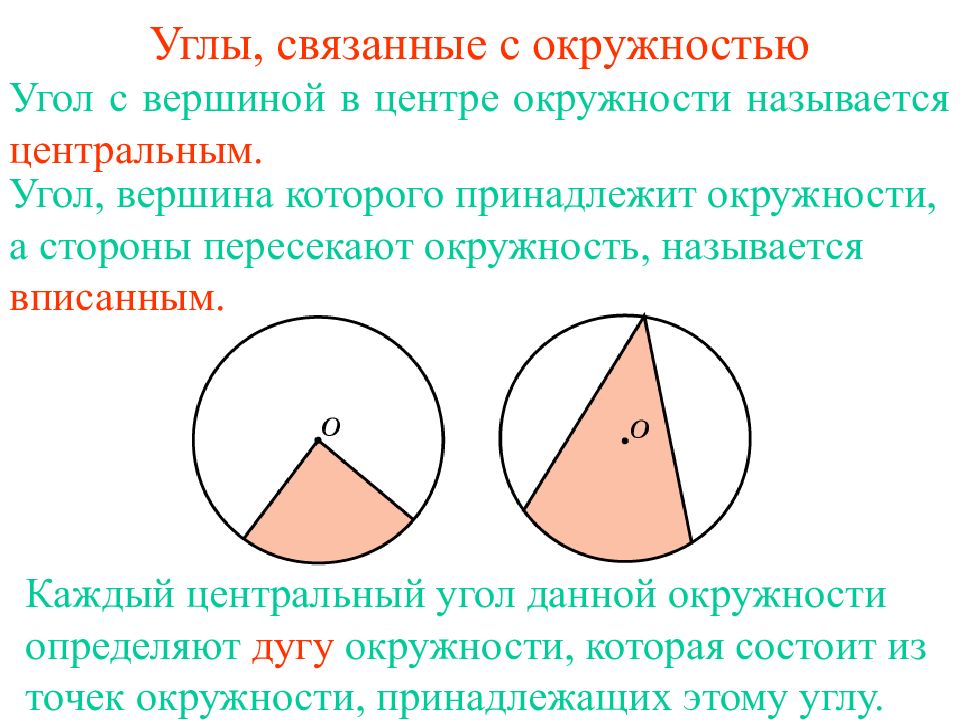
Первый слайд презентации: Углы, связанные с окружностью
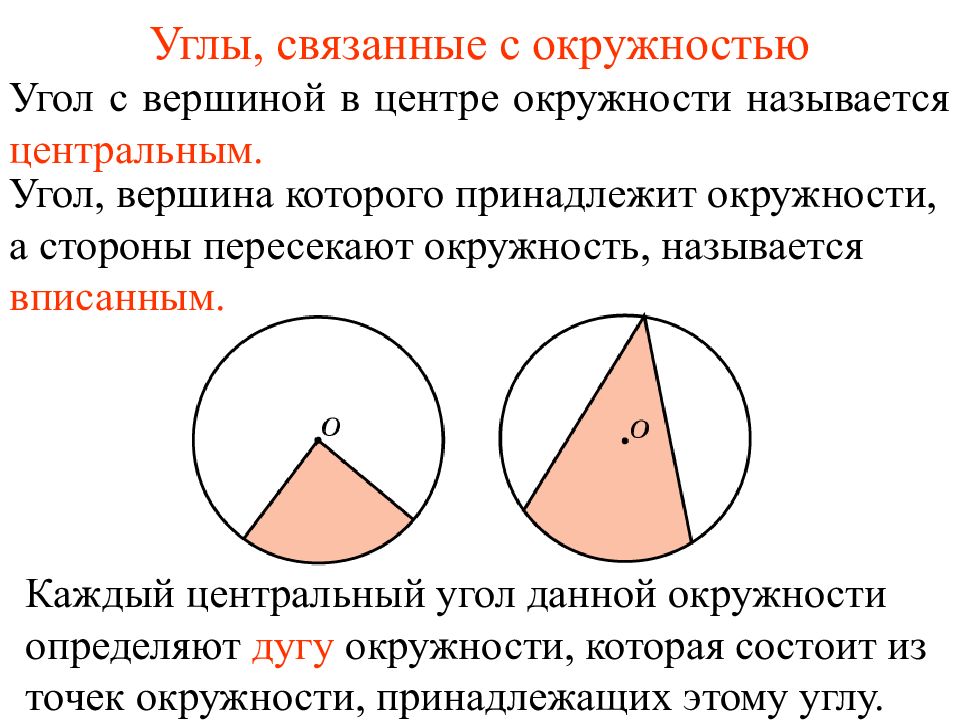
Угол с вершиной в центре окружности называется центральным. Угол, вершина которого принадлежит окружности, а стороны пересекают окружность, называется вписанным. Каждый центральный уг ол данной окружности определяют дуг у окружности, котор ая состо и т из точек окружности, принадлежащих эт ому угл у.
Слайд 2: Теорема о вписанном угле
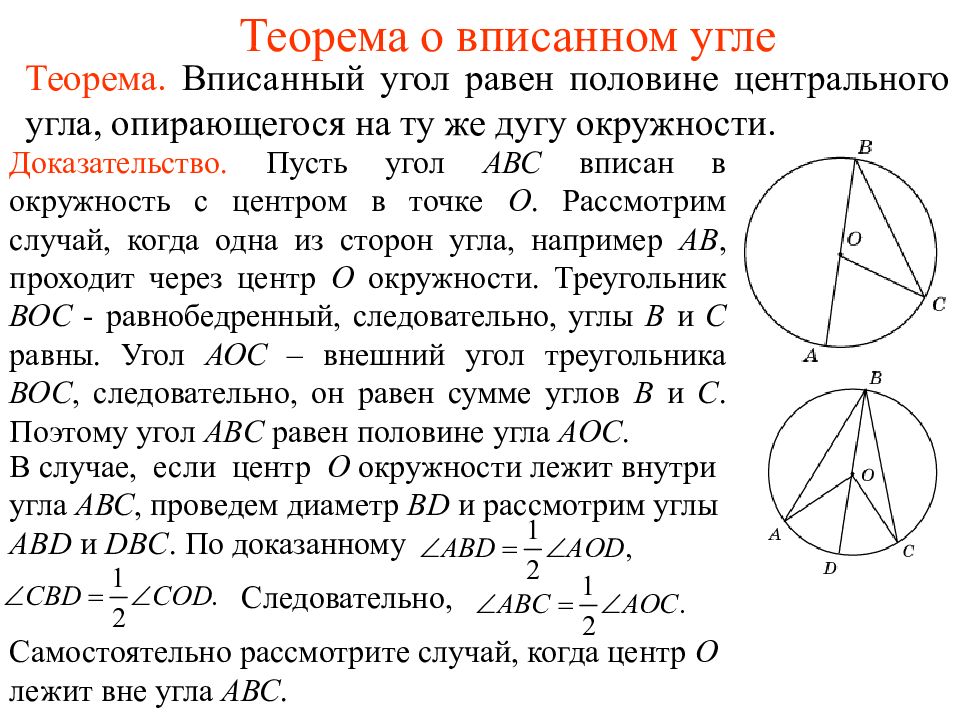
Теорема. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу окружности. Доказательство. Пусть угол АВС вписан в окружность с центром в точке О. Рассмотрим случай, когда одна из сторон угла, например АВ, проходит через центр О окружности. Треугольник ВОС - равнобедренный, следовательно, углы B и C равны. Угол АОС – внешний угол треугольника ВОС, следовательно, он равен сумме углов В и С. Поэтому угол ABC равен половине угла AOC. В случае, если центр О окружности лежит внутри угла АВС, проведем диаметр ВD и рассмотрим углы АВD и DBC. По доказанному Следовательно, Самостоятельно рассмотрите случай, когда центр О лежит вне угла АВС.
Слайд 3: Следствие
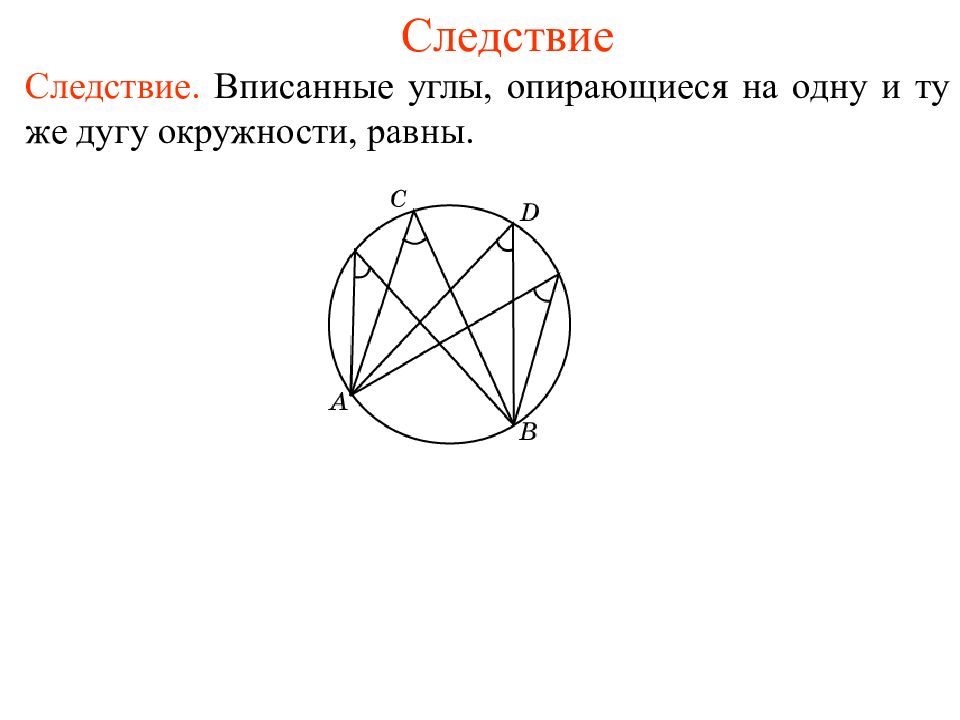
Следствие. Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.
Слайд 4: Вопрос 1
Какой угол называется центральным? Ответ: Центральным называется у гол с вершиной в центре окружности.
Слайд 5: Вопрос 2
Какой угол называется вписанным? Ответ: Вписанным называется у гол, вершина которого принадлежит окружности, а стороны пересекают окружность.
Слайд 6: Вопрос 3
Что называется дугой окружности? Ответ: Дугой окружности называется часть окружности, состоящая из точек окружности, принадлежащих некоторому центральному углу.
Слайд 7: Вопрос 4
Как связаны между собой вписанный и центральный углы, опирающиеся на одну и ту же дугу? Ответ: Вписанный угол равен половине центрального угла, опирающегося на ту же дугу окружности.
Слайд 8: Вопрос 5
Чем измеряются дуги окружности? Ответ: Дуги окружности измеряют ся соответствующими центральными углами.
Слайд 9: Упражнение 1
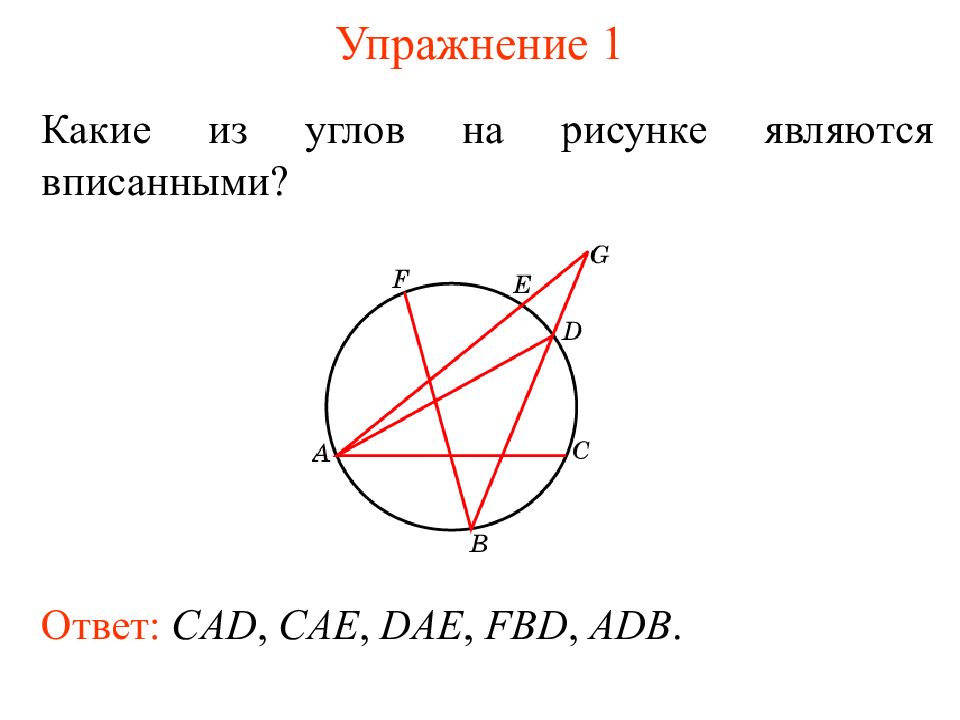
Какие из углов на рисунке являются вписанными? Ответ: CAD, CAE, DAE, FBD, ADB.
Слайд 10: Упражнение 2
Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ: 90 о.
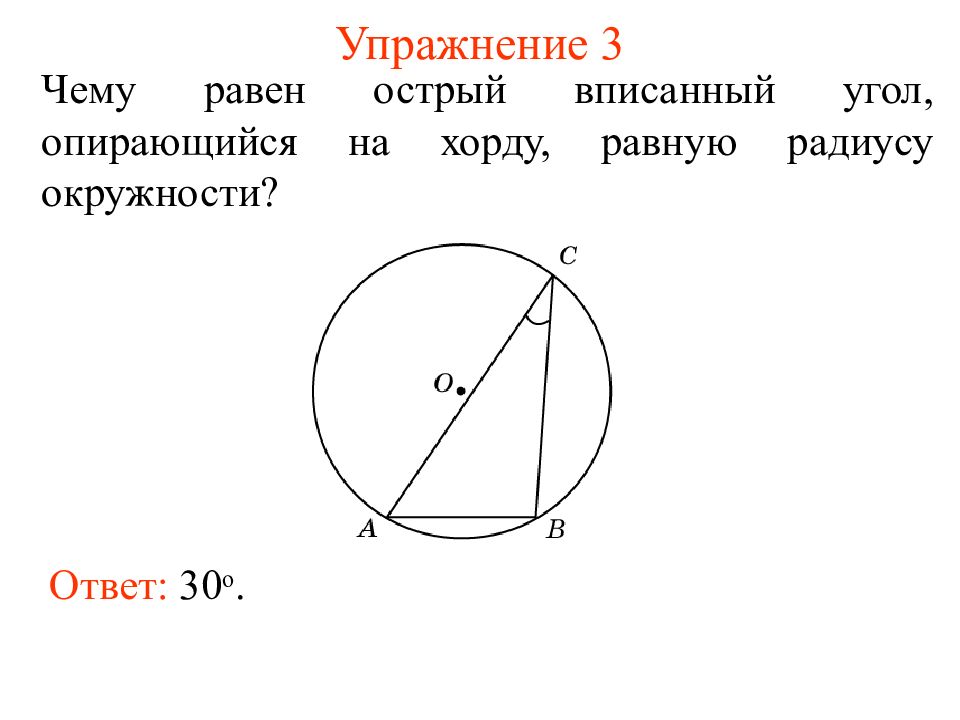
Слайд 11: Упражнение 3
Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ: 30 о.
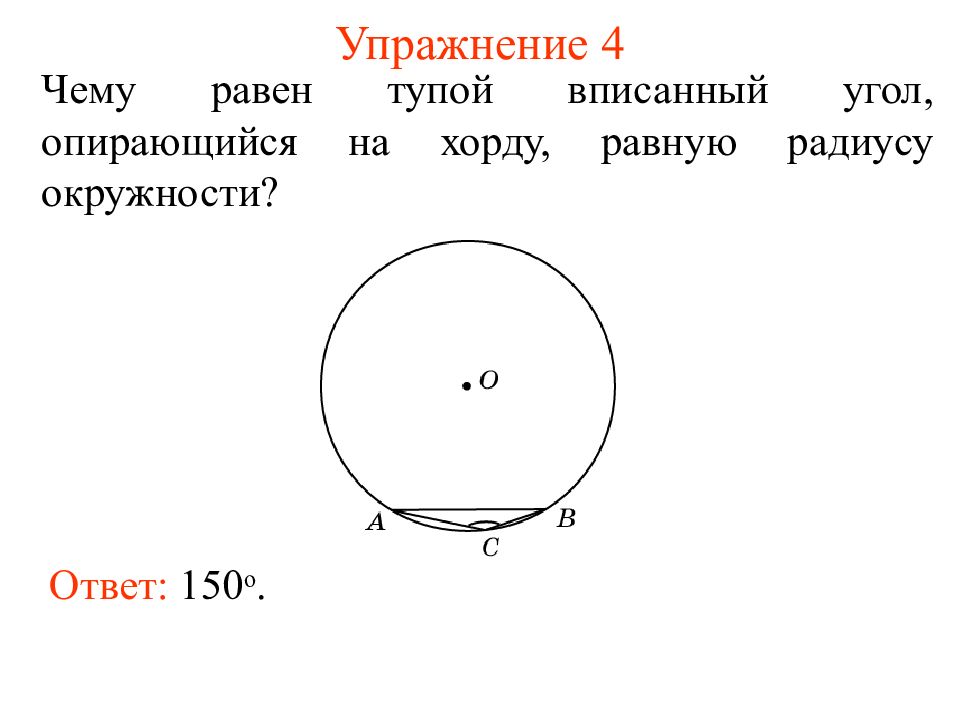
Слайд 12: Упражнение 4
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ: 150 о.
Слайд 13: Упражнение 5
Центральный угол на 35 больше вписанного угла, опирающегося на ту же дугу. Найдите каждый из этих углов. Ответ: 70 о и 35 о.
Слайд 14: Упражнение 6
В окружности с центром O AC и BD – диаметры. Вписанный угол ACB равен 38 о. Найдите центральный угол AOD. Ответ: 104 о.
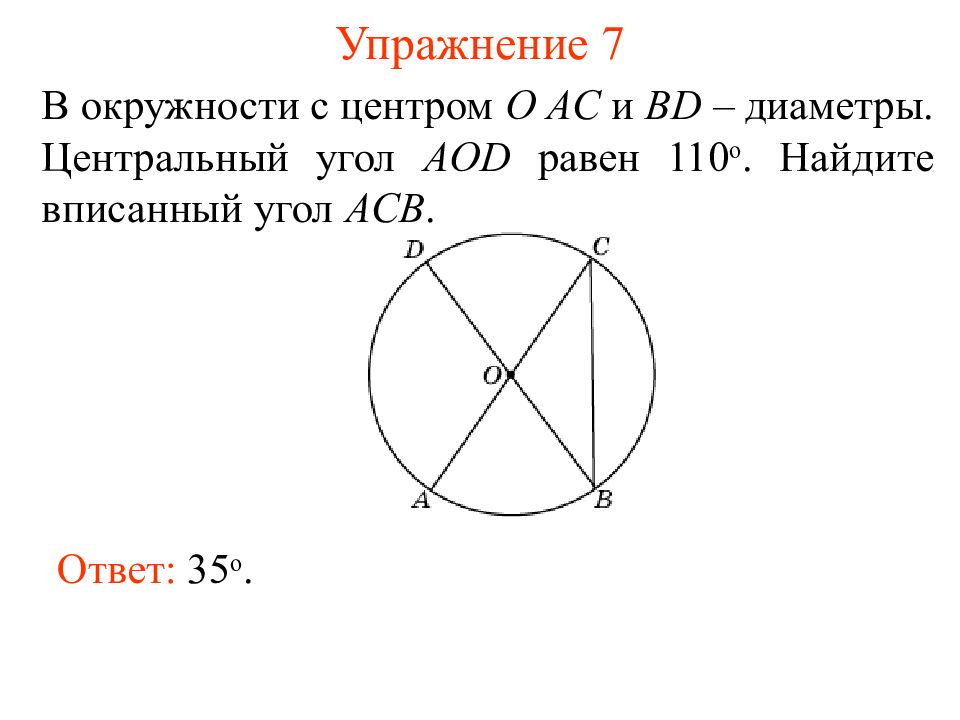
Слайд 15: Упражнение 7
В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 110 о. Найдите вписанный угол ACB. Ответ: 35 о.
Слайд 16: Упражнение 8
Ответ: 3 6 о. Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности.
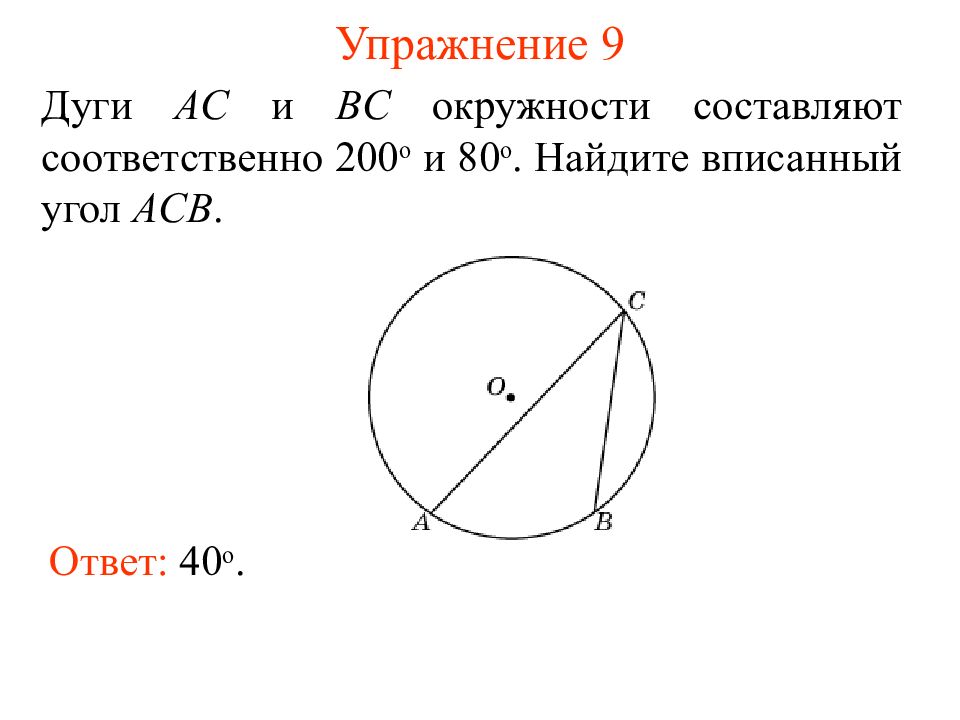
Слайд 17: Упражнение 9
Ответ: 40 о. Дуги AC и BC окружности составляют соответственно 200 о и 80 о. Найдите вписанный угол ACB.
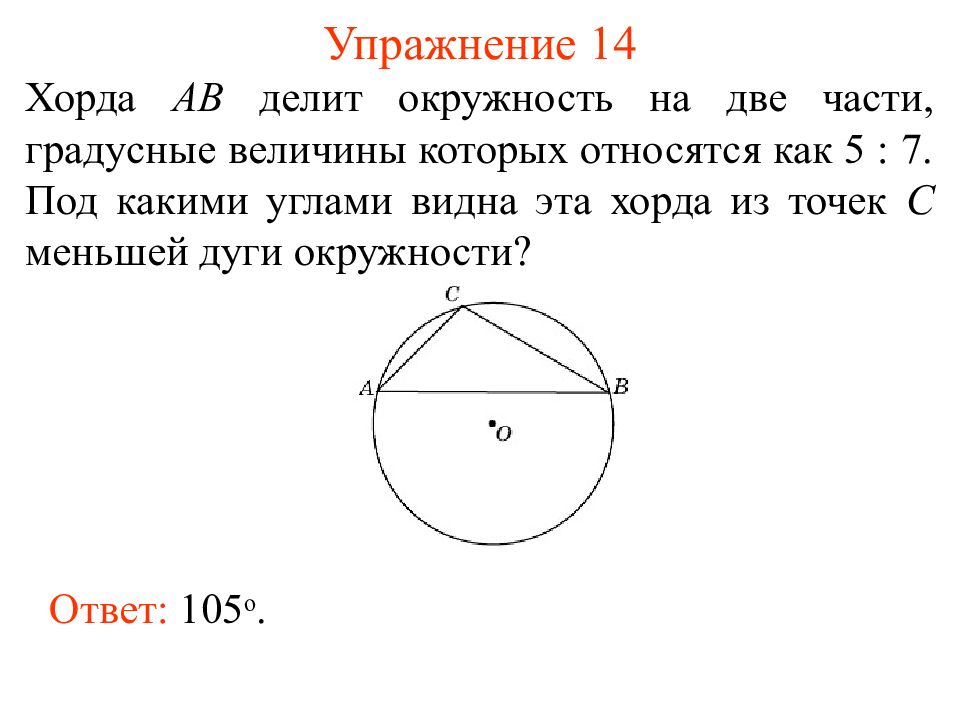
Слайд 22: Упражнение 14
Хорда AB делит окружность на две части, градусные величины которых относятся как 5 : 7. Под какими углами видна эта хорда из точек C меньшей дуги окружности? Ответ: 105 о.
Слайд 23: Упражнение 15
Найдите угол ACO, если его сторона CA касается окружности, а дуга AB окружности, заключенная внутри этого угла, равна 64 о. Ответ: 26 о.
Слайд 24: Упражнение 16
Угол ACO равен 28 о. Его сторона CA касается окружности. Найдите градусную величину дуги AB окружности, заключенной внутри этого угла. Ответ: 52 о.
Слайд 25: Упражнение 17
Найдите угол ACD, если его сторона CA касается окружности, а дуга AD окружности, заключенная внутри этого угла, равна 116 о. Ответ: 26 о.