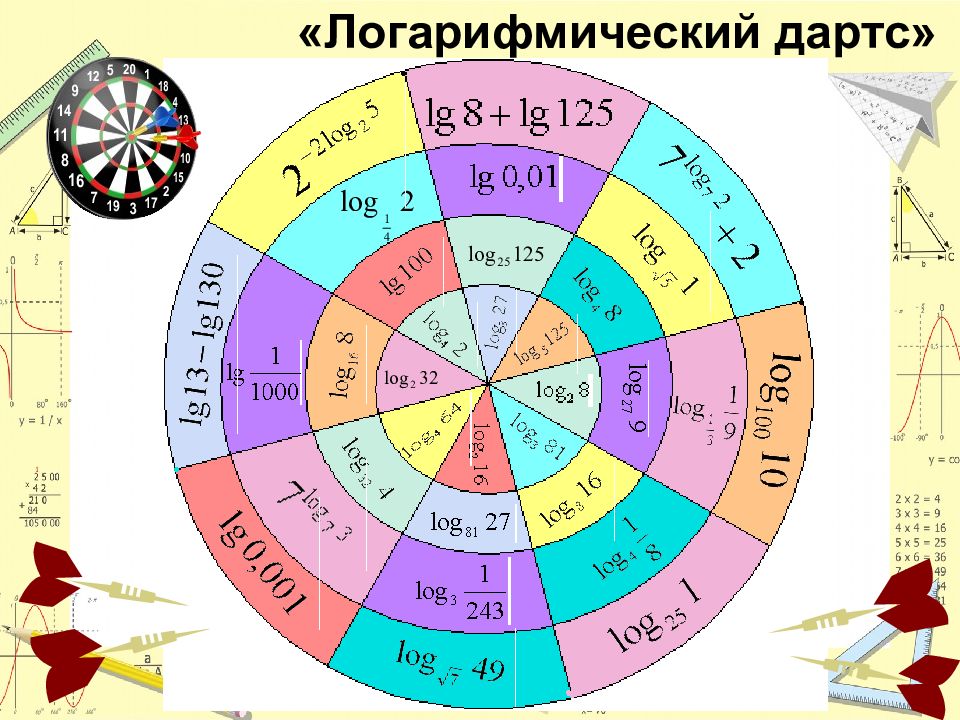
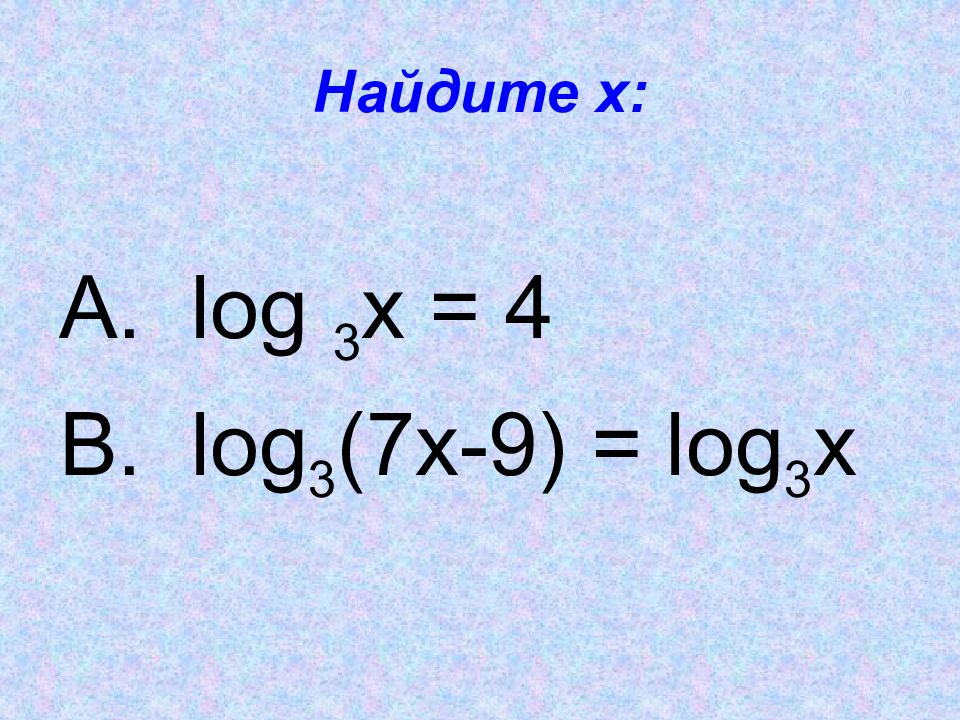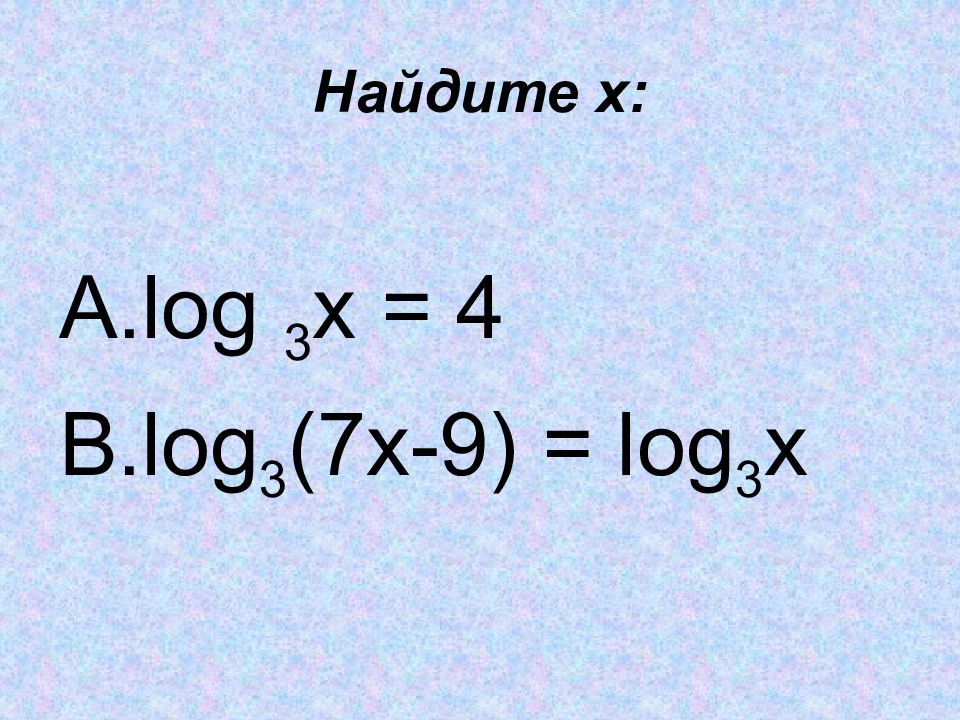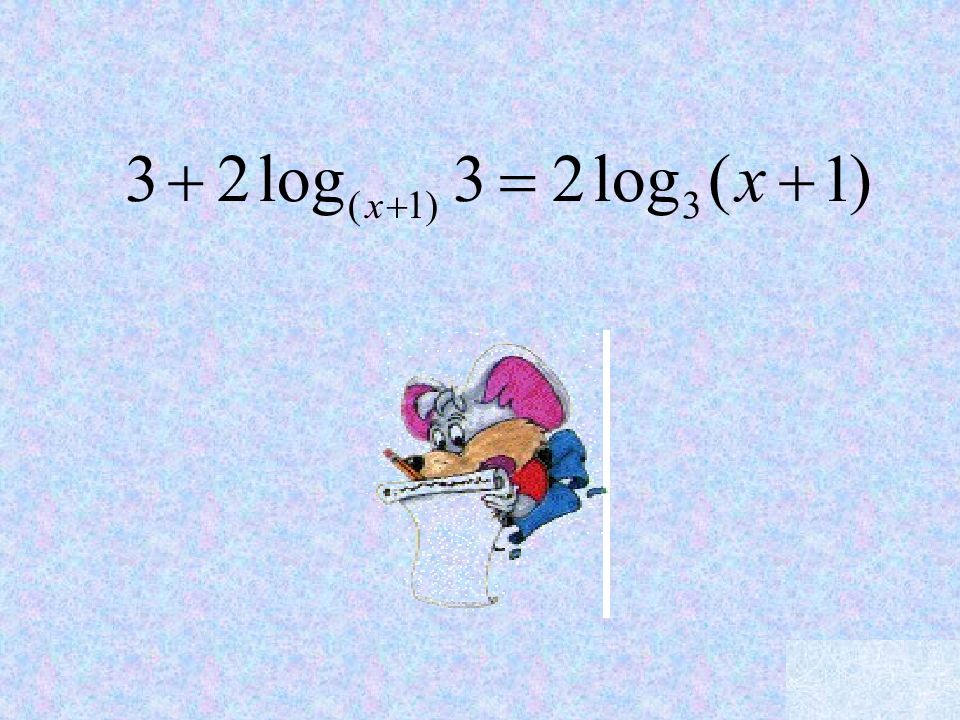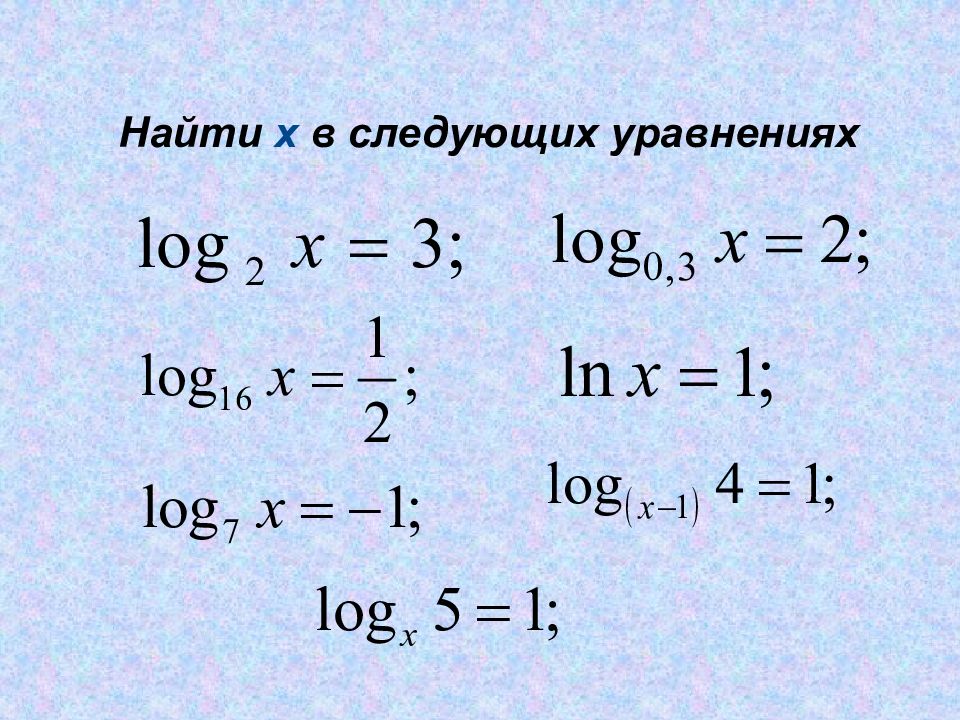Слайд 2: Найдите ошибки:
log 3 24 – log 3 8 = 16 log 3 15 + log 3 3 = log 3 5 log 5 5 3 = 2 log 2 16 2 = 8 3log 2 4 = log 2 (4*3) 3log 2 3 = log 2 27 log 3 27 = 4 log 2 2 3 = 8
Слайд 3: Вычислите:
log 2 11 – log 2 44 log 1/6 4 + log 1/6 9 2log 5 25 +3log 2 64
Слайд 7: Определение
Уравнение, содержащее переменную под знаком логарифма или в основании логарифма, называется логарифмическим Например, или Если в уравнении содержится переменная не под знаком логарифма, то оно не будет являться логарифмическим. Например,
Слайд 8
Определите уравнения являющиеся логарифмическими и не являющимися логарифмическими:
Слайд 10: Методы решения логарифмических уравнений
Решение простейшего логарифмического уравнения основано на применении определения логарифма и решении равносильного уравнения Методы решения логарифмических уравнений 1. По определению логарифма Пример 1
Слайд 11: Методы решения логарифмических уравнений
2. Потенцированием Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их: Решив полученное равенство, следует сделать проверку корней, т.к.применение формул потенцирования расширяет область определения уравнения
Слайд 12: Методы решения логарифмических уравнений
Пример 2 Решите уравнение Если Проверка: . 3 : Ответ Потенцируя, получаем:
Слайд 13: Методы решения логарифмических уравнений
Пример 2 Решите уравнение ОДЗ: является корнем исходного уравнения. Потенцируя, получаем:
Слайд 14
ЗАПОМНИ ! Сладкая парочка! Два в одном! Два берега у одной реки! Два сапога – пара! Близки и неразлучны! Нам не жить друг без друга! Логарифм и ОДЗ вместе трудятся везде! ОН - ЛОГАРИФМ ! ОНА - ОДЗ!
Слайд 15: Методы решения логарифмических уравнений
3. Применение свойств логарифмов Пример 3 Решите уравнение
Слайд 16: Методы решения логарифмических уравнений
4. Введения новой переменной Пример 4 Решите уравнение ОДЗ: x>0 Переходя к переменной х, получим: ; х = 4 удовлетворяют условию х > 0, следовательно, - корни исходного уравнения.
Слайд 17: Методы решения логарифмических уравнений
По определению логарифма 2. Потенцированием 3. Применение свойств логарифмов 4. Введения новой переменной
Слайд 18: Определи метод решения уравнений:
По определению Применяя св-ва логарифмов Потенцированием Введением новой переменной
Слайд 19
Задания №1 Найдите произведение корней уравнения 1) - 1,21 №2 Укажите промежуток, которому принадлежит корень уравнения №3 Найдите сумму корней уравнения 1) 5 1) (- ∞;-2] 2) - 0,9 3) 0, 81 4) 1,21 3) [1;2] 2) [ - 2;1] 4) [2;+∞) 2) 25, 2 3) -25, 2 4) - 5
Слайд 20: Алгоритм решения логарифмических уравнений
Выписать условия, при которых логарифмическое уравнение определено Выбрать метод решения Решить уравнение Для найденных корней проверить выполнение условий пункта 1 При записи ответа исключить посторонние корни
Слайд 27
Логарифмическая функция имеет экстремумы Логарифмическая функция является нечетной Логарифмическая функция будет возрастающей, если ее основание а > 1 Графический диктант "Верно- неверно"
Слайд 28
4. Логарифмическая функция является периодической 5. Логарифмическая функция будет убывающей, если ее основание а < 0 6. log a xy = log a x * log a y Графический диктант "Верно- неверно"
Слайд 29
7. log a b + log a c = log a bc 8. p log a b = log a bp 9. log a (b-c) = log a b - log a c Графический диктант "Верно- неверно"