1 Логические основы компьютеров Логические выражения и операции Диаграммы Преобразование логических выражений Синтез логических выражений Логические элементы компьютера Логические задачи
2 Логические основы компьютеров Тема 1. Логические выражения и операции
3 Булева алгебра Двоичное кодирование – все виды информации кодируются с помощью 0 и 1. Задача – разработать оптимальные правила обработки таких данных. Джордж Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра логики, булева алгебра). Почему "логика"? Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.
4 Логические высказывания Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно. Высказывание или нет ? Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата – 10 сторон и все разные. Красиво! В городе N живут 2 миллиона человек. Который час?
5 Обозначение высказываний A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные) Составные высказывания строятся из простых с помощью логических связок (операций) " и ", " или ", " не ", " если … то ", " тогда и только тогда " и др. Любое высказывание может быть ложно (0) или истинно (1). ! A и B A или не B если A, то B не A и B A тогда и только тогда, когда B Сейчас идет дождь и открыта форточка. Сейчас идет дождь или форточка закрыта. Если сейчас идет дождь, то форточка открыта. Сейчас нет дождя и форточка открыта. Дождь идет тогда и только тогда, когда открыта форточка.
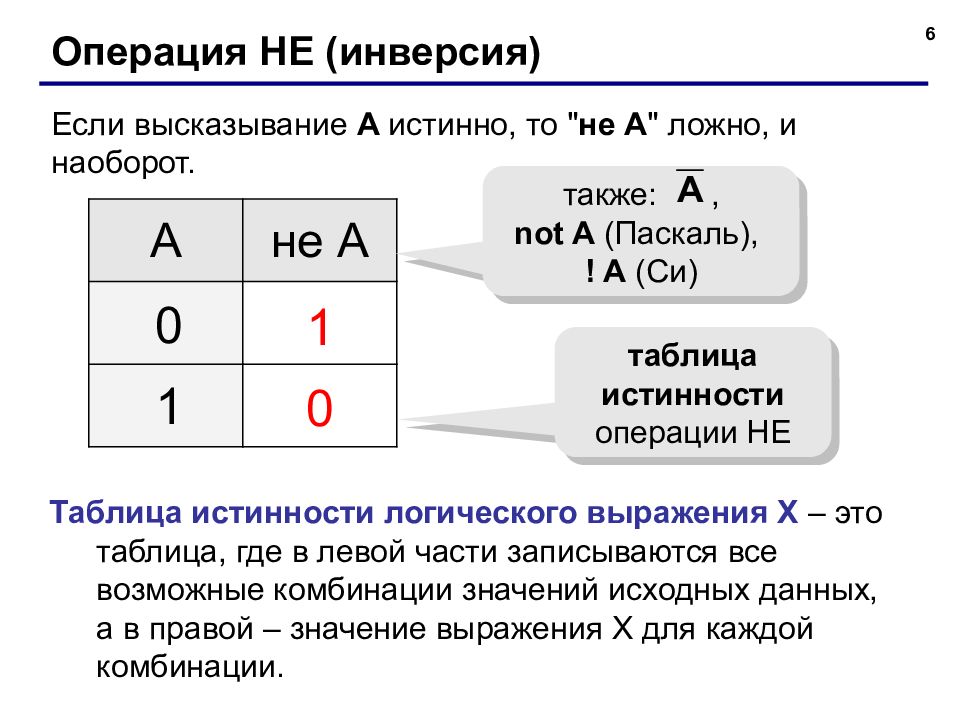
6 Операция НЕ ( инверсия) Если высказывание A истинно, то " не А " ложно, и наоборот. А не А 1 0 0 1 таблица истинности операции НЕ также:, not A ( Паскаль ), ! A ( Си) Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.
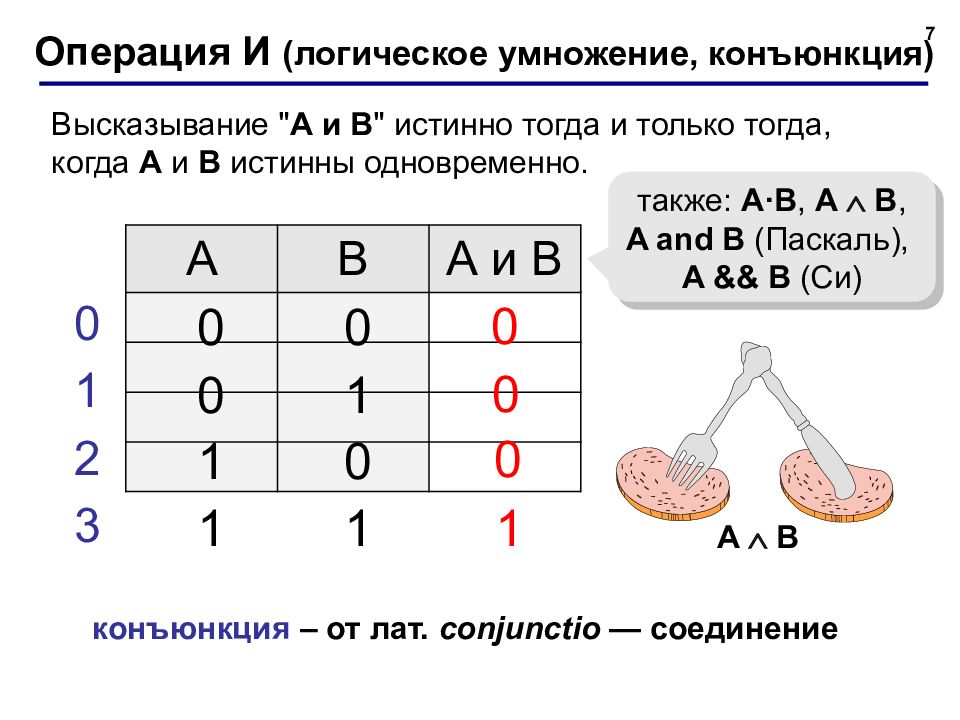
7 Операция И ( логическое умножение, конъюнкция) A B А и B 1 0 также: A·B, A B, A and B ( Паскаль ), A && B ( Си) 0 0 0 1 1 0 1 1 0 1 2 3 0 0 конъюнкция – от лат. conjunctio — соединение A B Высказывание " A и B " истинно тогда и только тогда, когда А и B истинны одновременно.
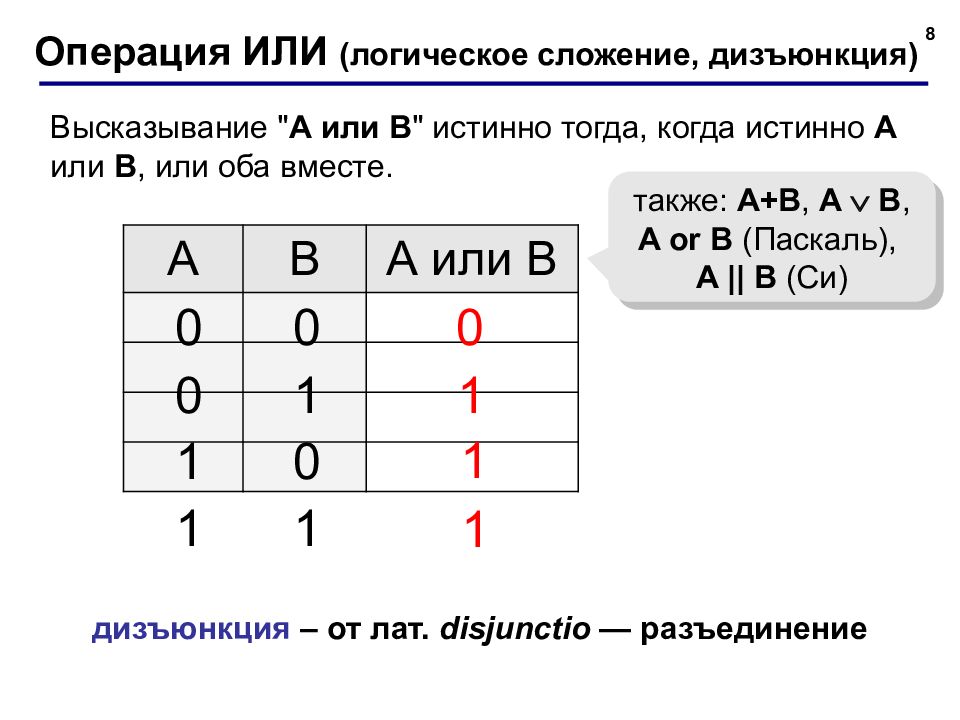
8 Операция ИЛИ ( логическое сложение, дизъюнкция) A B А или B 1 0 также: A + B, A B, A or B ( Паскаль ), A || B ( Си) 0 0 0 1 1 0 1 1 1 1 дизъюнкция – от лат. dis junctio — разъединение Высказывание " A или B " истинно тогда, когда истинно А или B, или оба вместе.
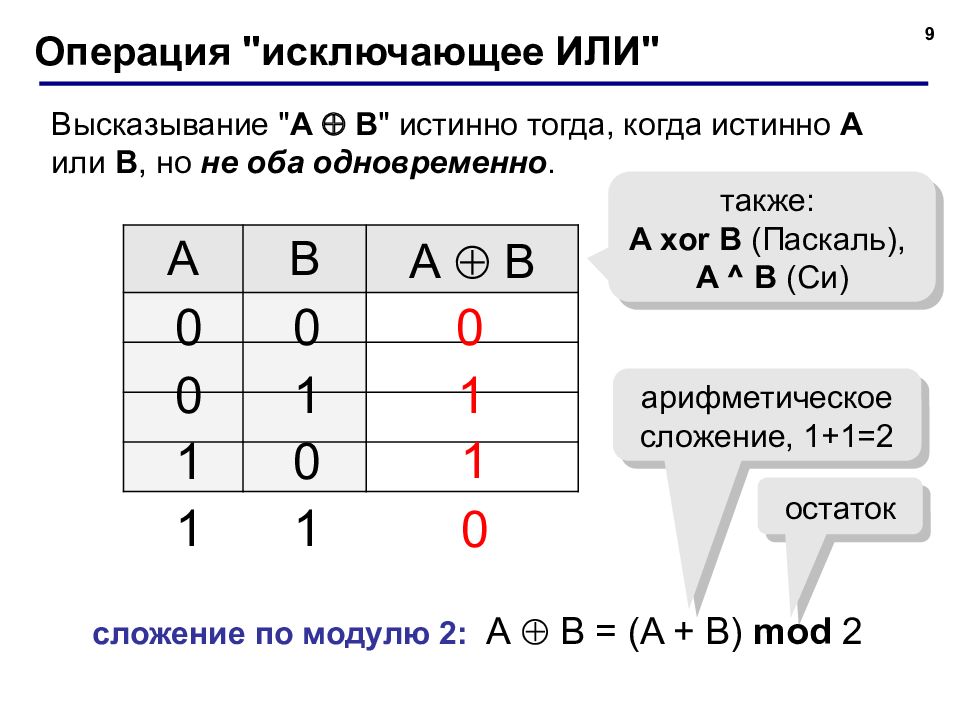
9 Операция " исключающее ИЛИ " Высказывание " A B " истинно тогда, когда истинно А или B, но не оба одновременно. A B А B 0 0 также: A xor B ( Паскаль ), A ^ B ( Си) 0 0 0 1 1 0 1 1 1 1 сложение по модулю 2: А B = ( A + B) mod 2 арифметическое сложение, 1+1=2 остаток
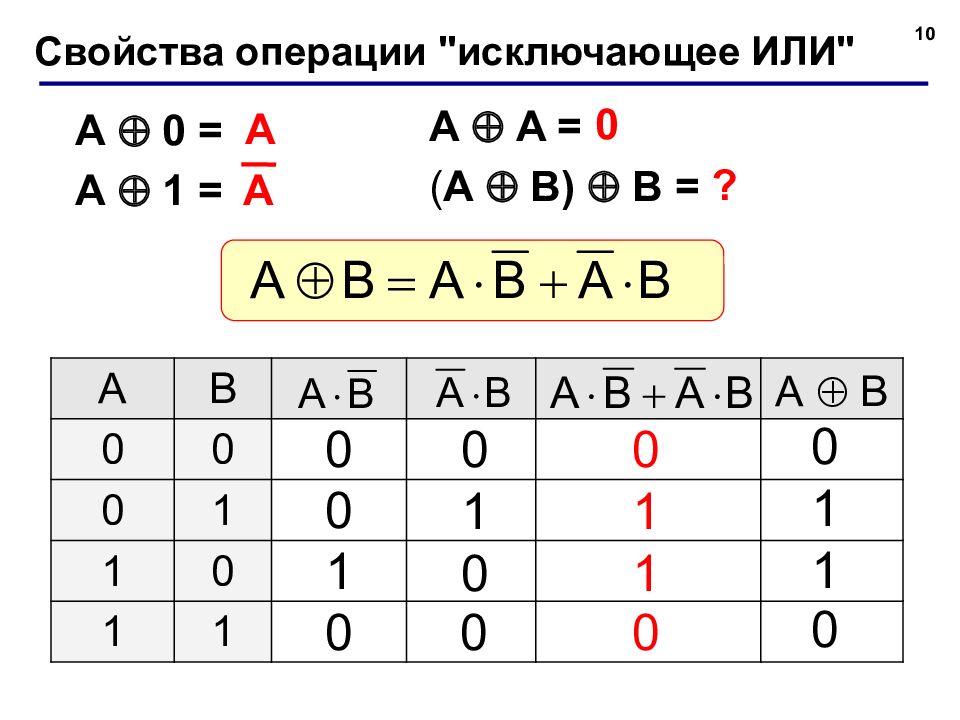
10 A A = ( A B) B = Свойства операции " исключающее ИЛИ " A 0 = A 1 = A 0 ? A B А B 0 0 0 1 1 0 1 1 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 A
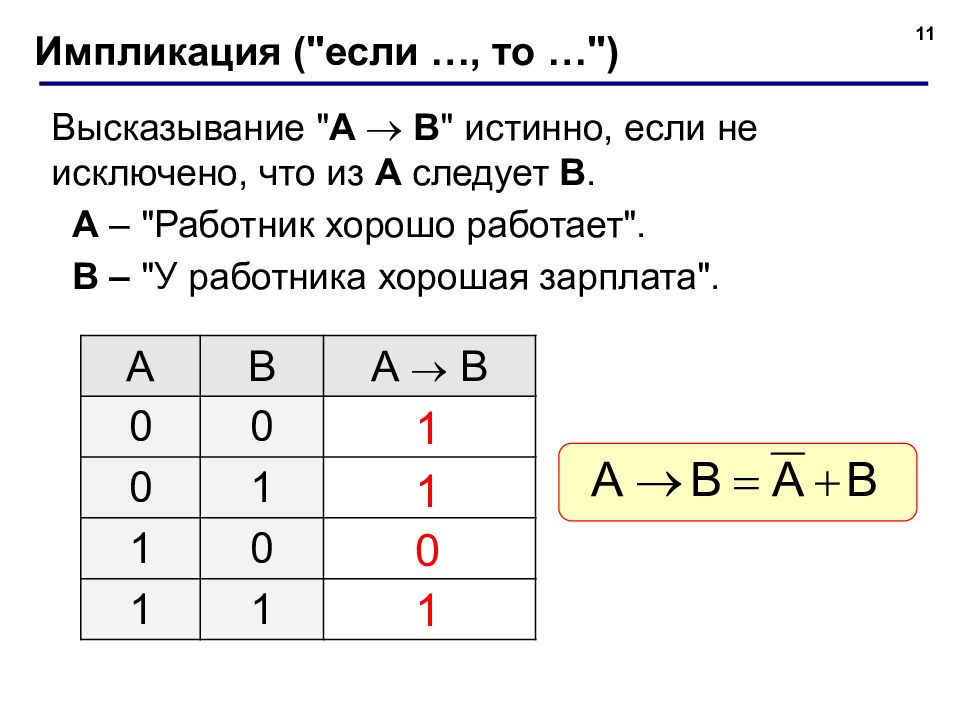
11 Импликация ("если …, то …") Высказывание " A B " истинно, если не исключено, что из А следует B. A – " Работник хорошо работает". B – "У работника хорошая зарплата". A B А B 0 0 0 1 1 0 1 1 1 1 1 0
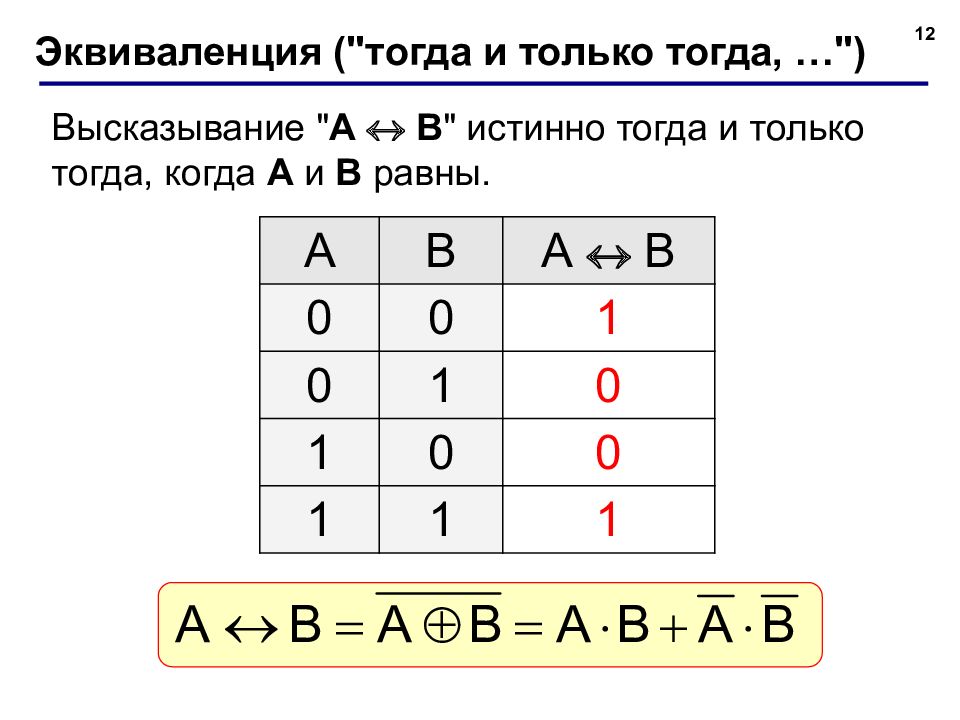
12 Эквиваленция ("тогда и только тогда, …") Высказывание " A B " истинно тогда и только тогда, когда А и B равны. A B А B 0 0 1 0 1 0 1 0 0 1 1 1
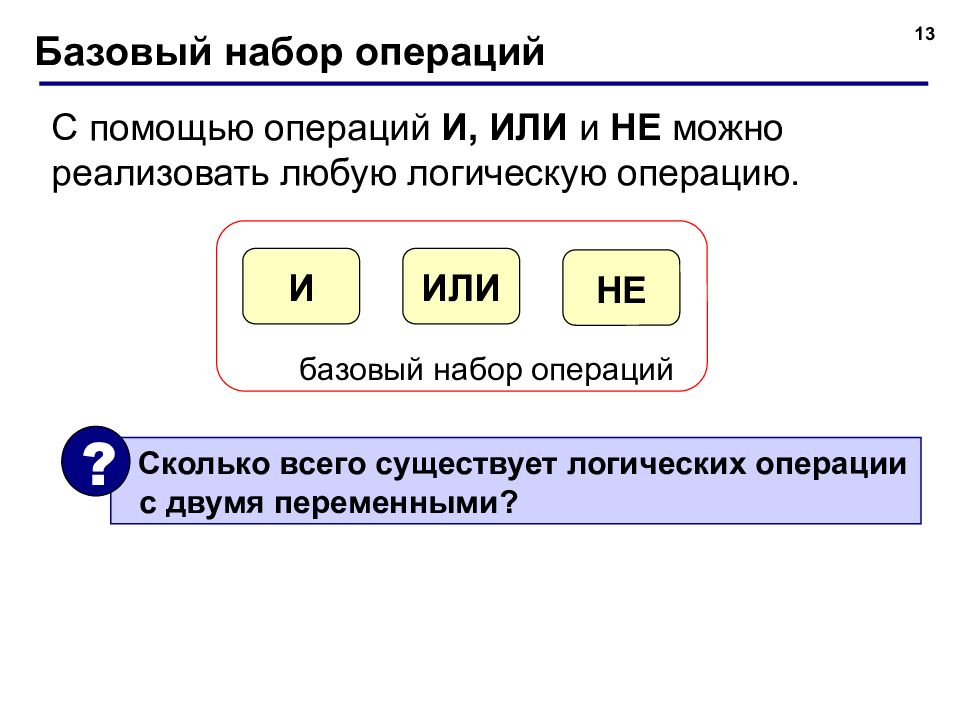
13 Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию. ИЛИ И НЕ базовый набор операций Сколько всего существует логических операции с двумя переменными? ?
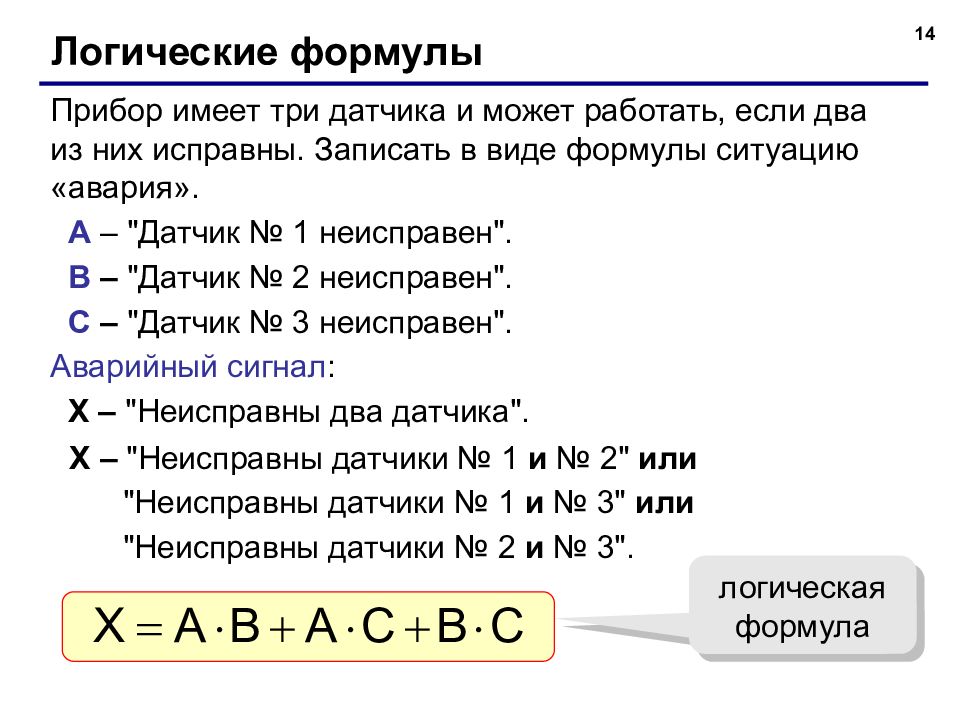
14 Логические формулы Прибор имеет три датчика и может работать, если два из них исправны. Записать в виде формулы ситуацию «авария». A – " Датчик № 1 неисправен". B – "Датчик № 2 неисправен". C – "Датчик № 3 неисправен". Аварийный сигнал : X – "Неисправны два датчика". X – "Неисправны датчики № 1 и № 2" или "Неисправны датчики № 1 и № 3" или "Неисправны датчики № 2 и № 3". логическая формула
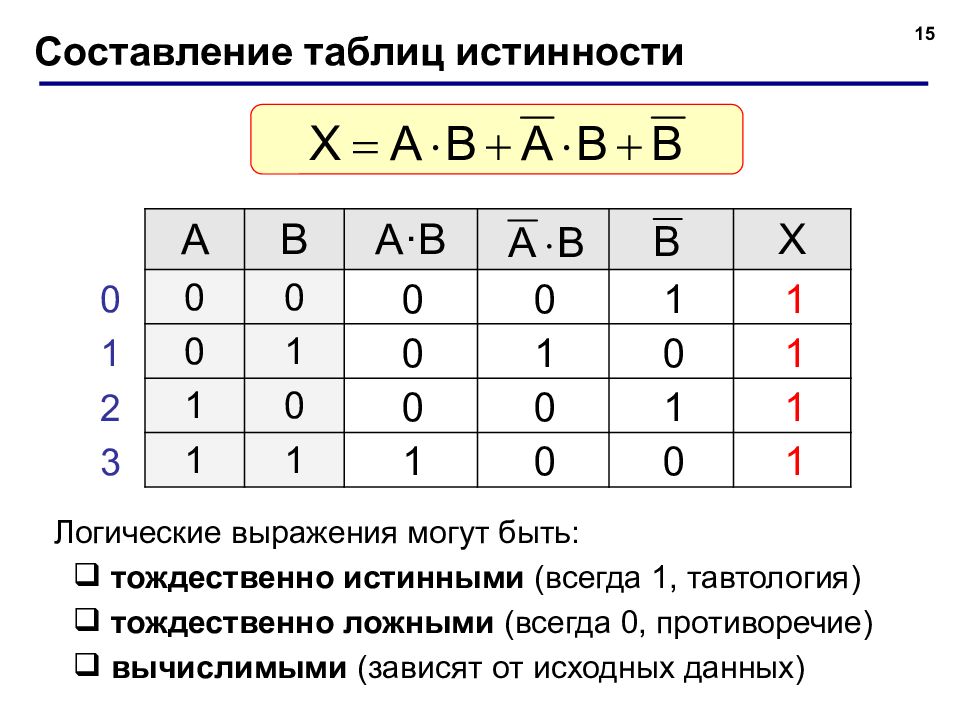
15 Составление таблиц истинности A B A · B X 0 0 0 1 1 0 1 1 0 1 2 3 0 1 0 0 0 0 0 1 1 0 1 0 1 1 1 1 Логические выражения могут быть: тождественно истинными (всегда 1, тавтология) тождественно ложными (всегда 0, противоречие) вычислимыми (зависят от исходных данных)
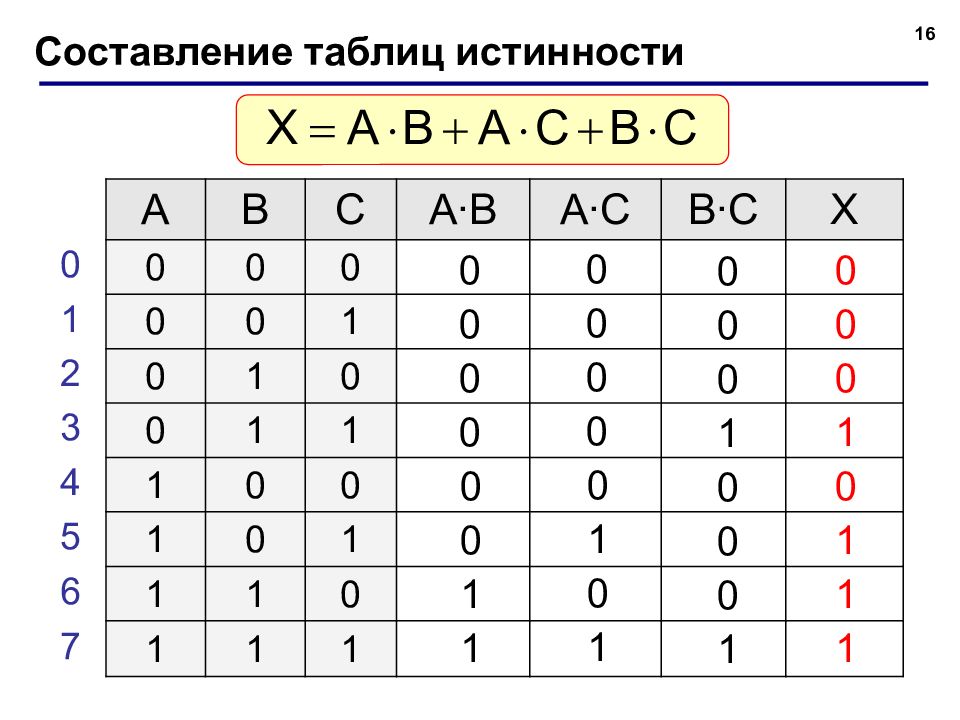
16 Составление таблиц истинности A B C A∙B A∙C B∙C X 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 2 3 4 5 6 7 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 1 1 1
17 Логические основы компьютеров Тема 2. Диаграммы
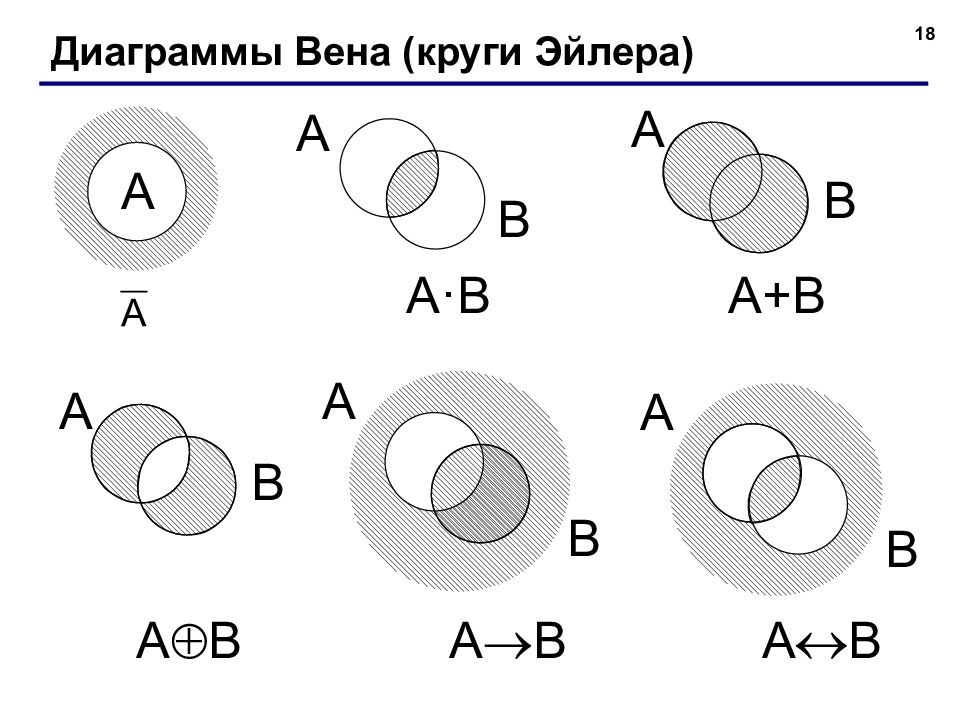
18 A B A B Диаграммы Вена (круги Эйлера) A A · B A B A+B A B A B A B A B A B
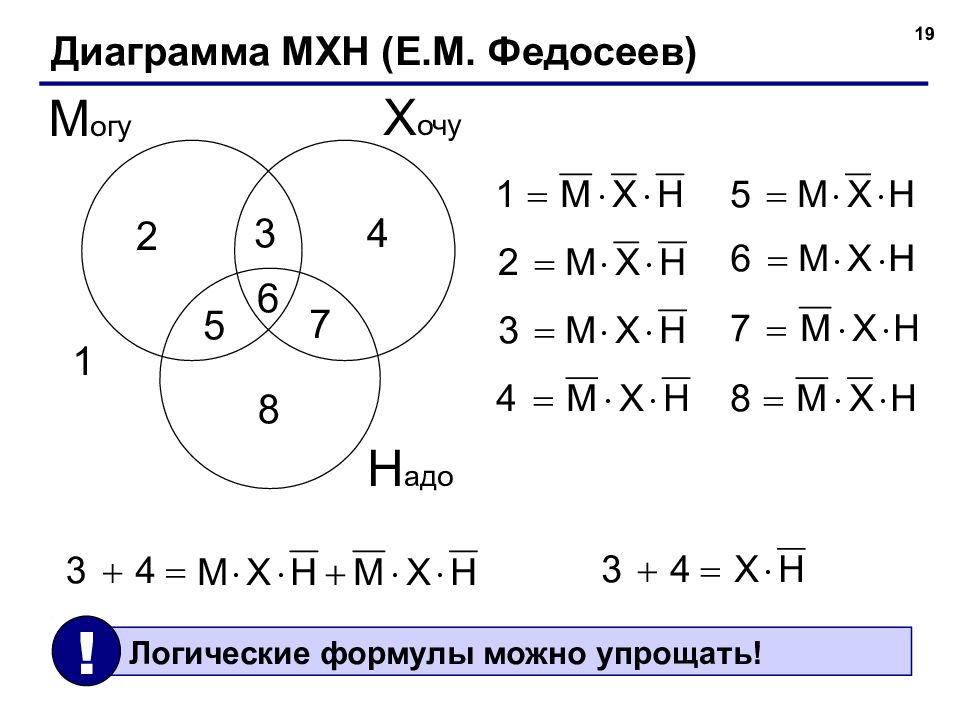
19 Диаграмма МХН (Е.М. Федосеев) Х очу М огу Н адо 1 2 3 4 5 6 7 8 Логические формулы можно упрощать! !
20 Логические основы компьютеров Тема 3. Преобразование логических выражений
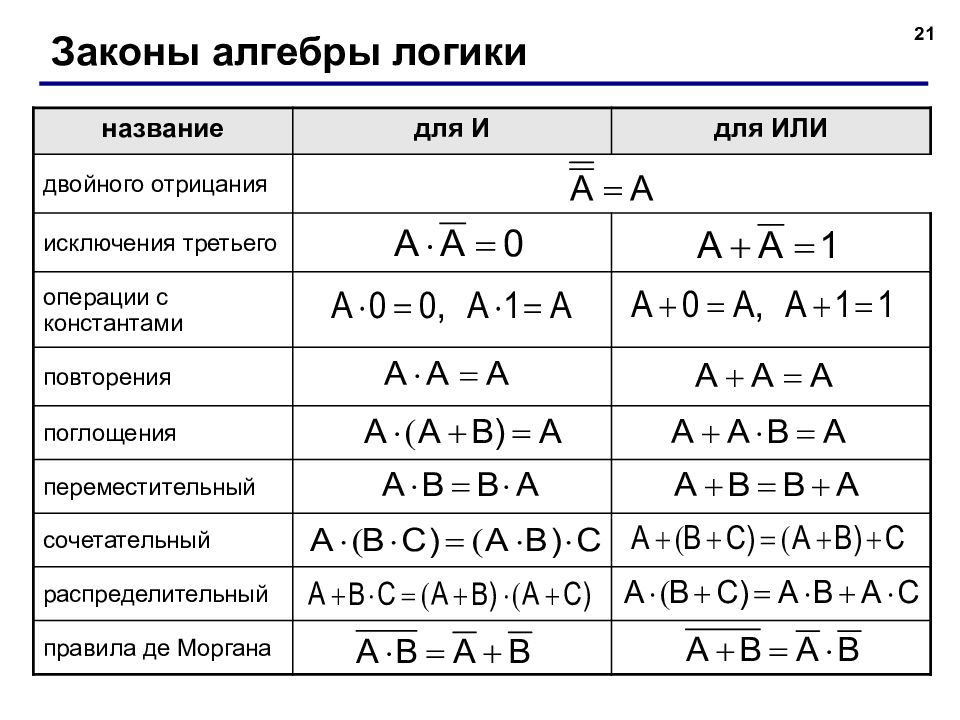
21 Законы алгебры логики название для И для ИЛИ двойного отрицания исключения третьего операции с константами повторения поглощения переместительный сочетательный распределительный правила де Моргана
22 Упрощение логических выражений Шаг 1. Заменить операции на их выражения через И, ИЛИ и НЕ : Шаг 2. Раскрыть инверсию сложных выражений по формулам де Моргана: Шаг 3. Используя законы логики, упрощать выражение, стараясь применять закон исключения третьего.
23 Упрощение логических выражений раскрыли формула де Моргана распределительный исключения третьего повторения поглощения
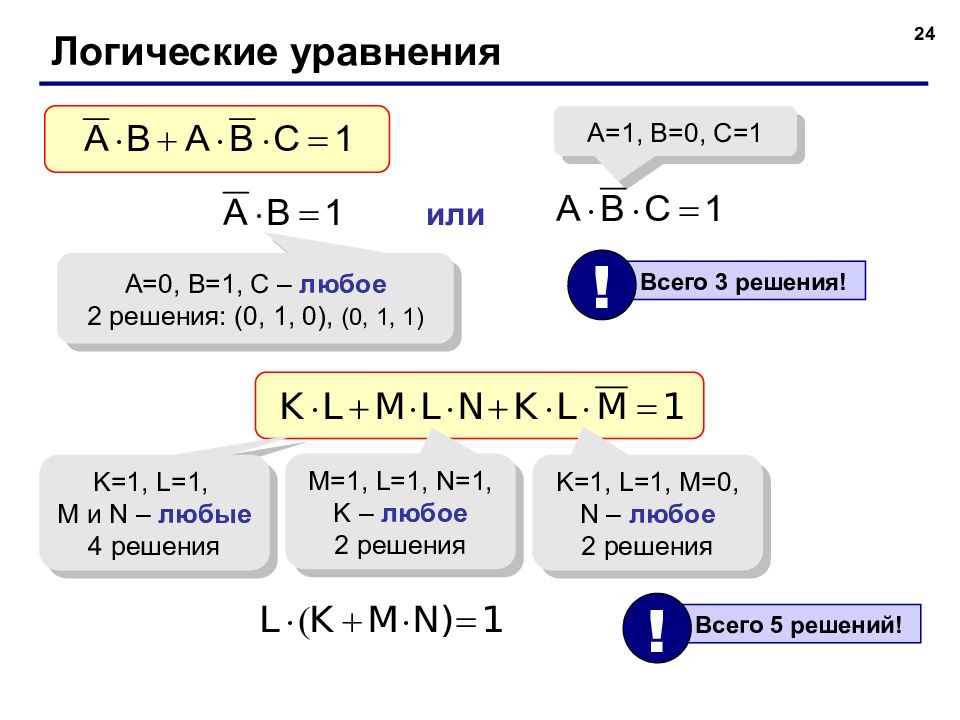
24 Логические уравнения A=0, B=1, C – любое 2 решения: (0, 1, 0), (0, 1, 1) или A= 1, B= 0, C =1 Всего 3 решения! ! K= 1, L=1, M и N – любые 4 решения M=1, L=1, N=1, K – любое 2 решения K=1, L=1, M=0, N – любое 2 решения Всего 5 решений! !
25 Логические основы компьютеров Тема 4. Синтез логических выражений
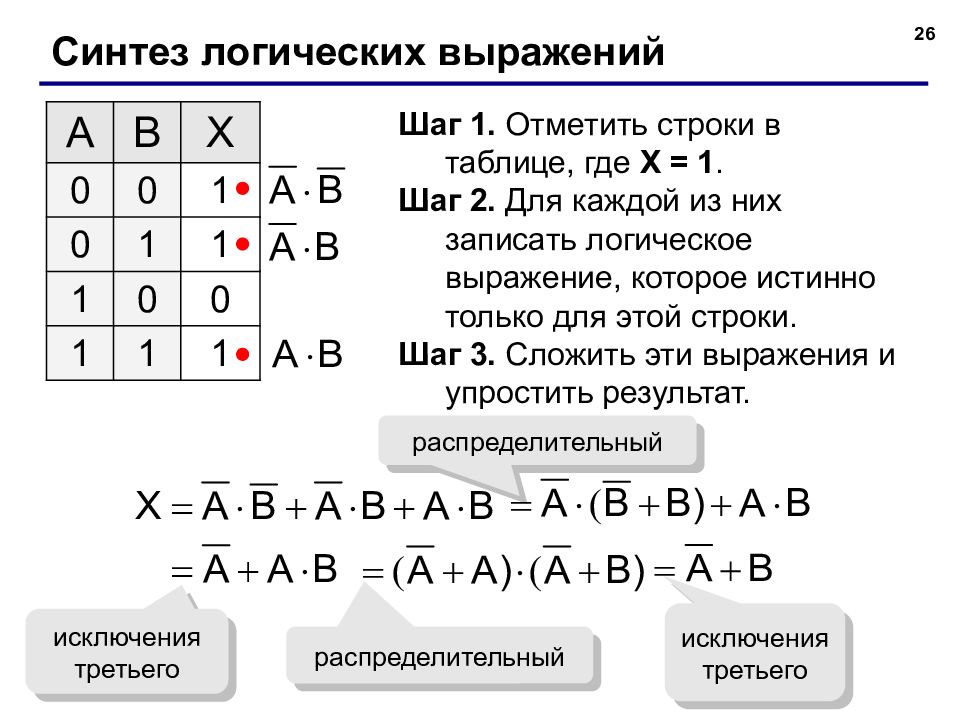
26 Синтез логических выражений A B X 0 0 1 0 1 1 1 0 0 1 1 1 Шаг 1. Отметить строки в таблице, где X = 1. Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки. Шаг 3. Сложить эти выражения и упростить результат. распределительный исключения третьего исключения третьего распределительный
27 Синтез логических выражений (2 способ) A B X 0 0 1 0 1 1 1 0 0 1 1 1 Шаг 1. Отметить строки в таблице, где X = 0. Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки. Шаг 3. Сложить эти выражения и упростить результат, который равен. Шаг 4. Сделать инверсию. Когда удобнее применять 2-ой способ? ?
28 Синтез логических выражений A B C X 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1
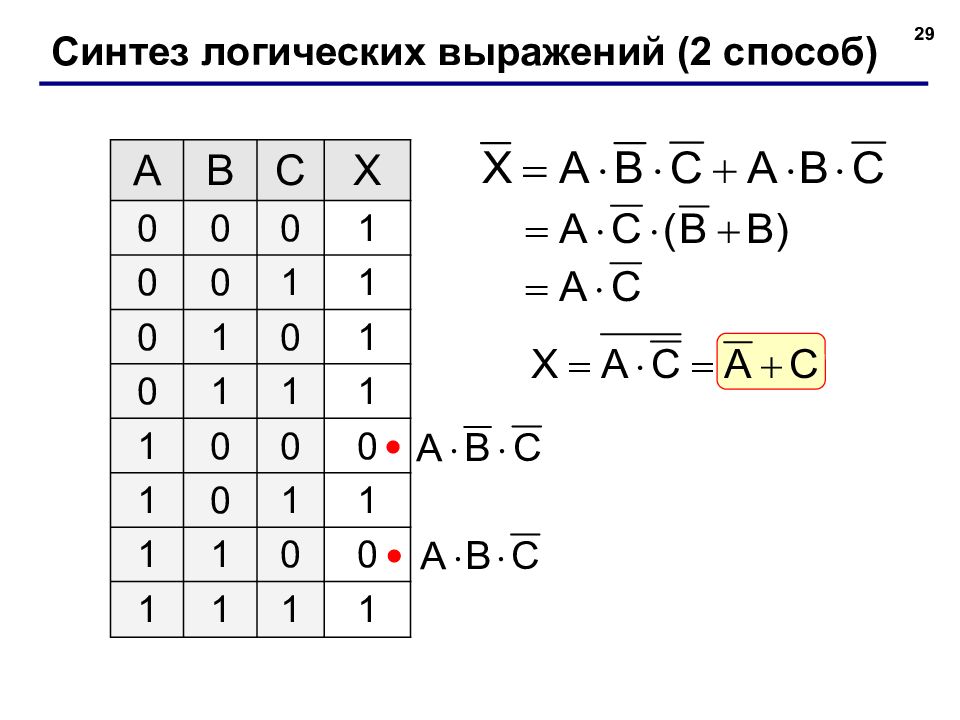
29 Синтез логических выражений (2 способ) A B C X 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1
30 Логические основы компьютеров Тема 5. Логические элементы компьютера
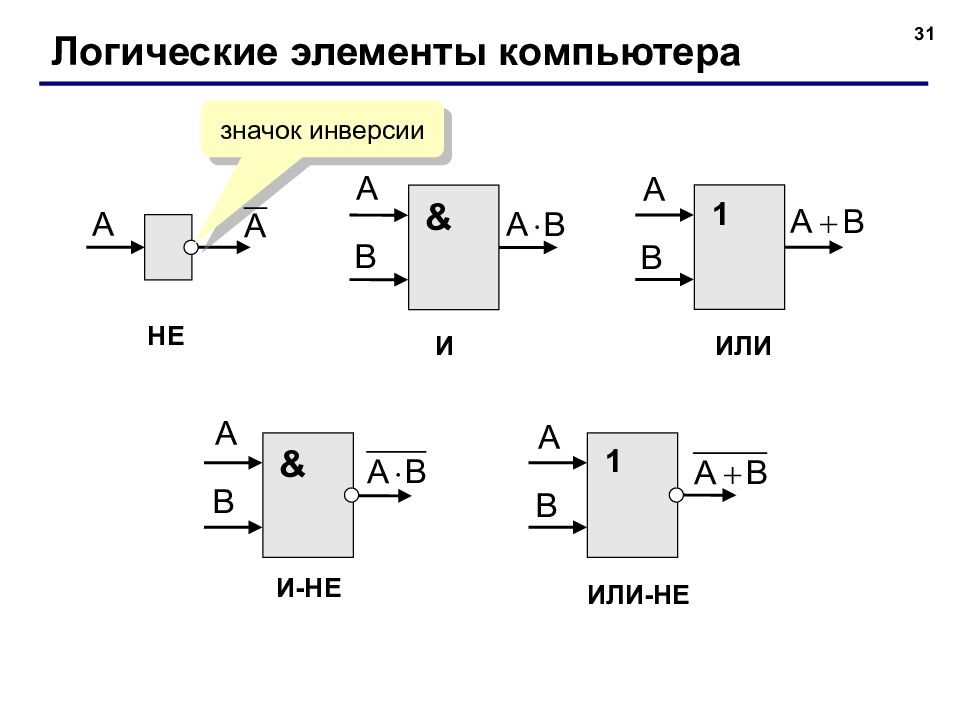
31 Логические элементы компьютера & 1 1 & НЕ И ИЛИ ИЛИ-НЕ И-НЕ значок инверсии
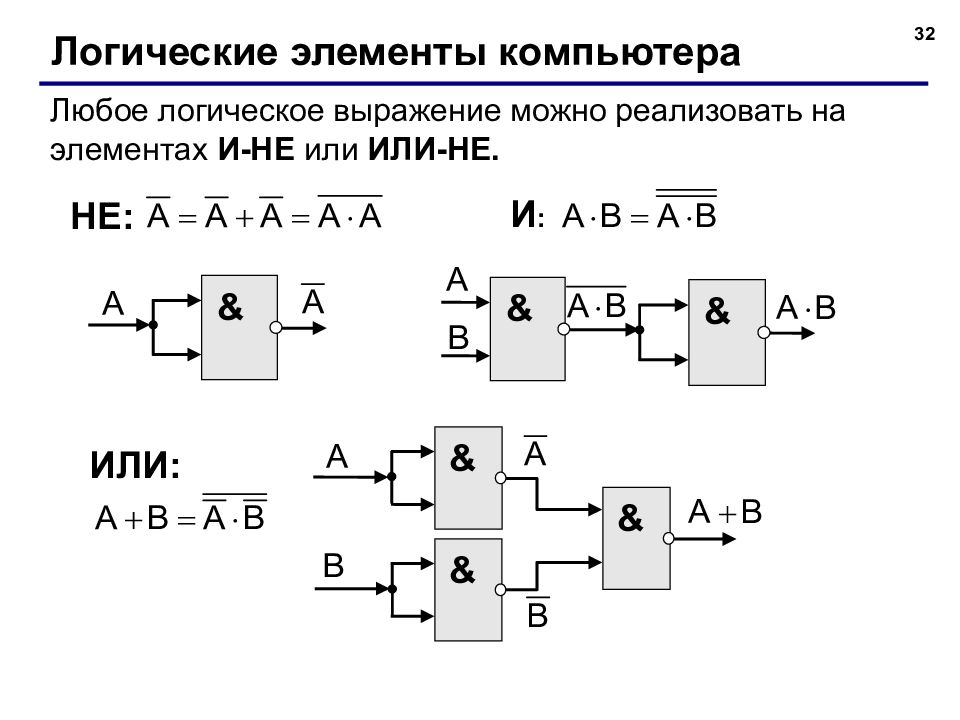
32 Логические элементы компьютера Любое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ. & И : НЕ: & & ИЛИ: & & &
33 Составление схем последняя операция - ИЛИ & 1 & & И
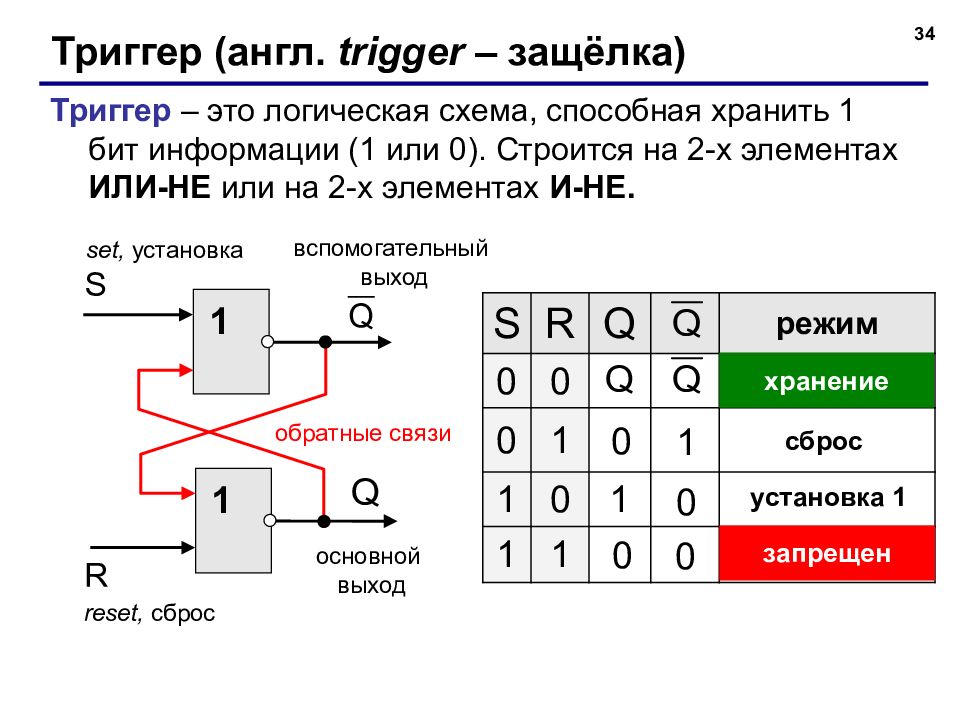
34 Триггер (англ. trigger – защёлка) Триггер – это логическая схема, способная хранить 1 бит информации (1 или 0). Строится на 2-х элементах ИЛИ-НЕ или на 2-х элементах И-НЕ. 1 1 основной выход вспомогательный выход reset, сброс set, установка обратные связи S R Q режим 0 0 0 1 1 0 1 1 хранение запрещен 1 1 0 0 сброс установка 1 0 0
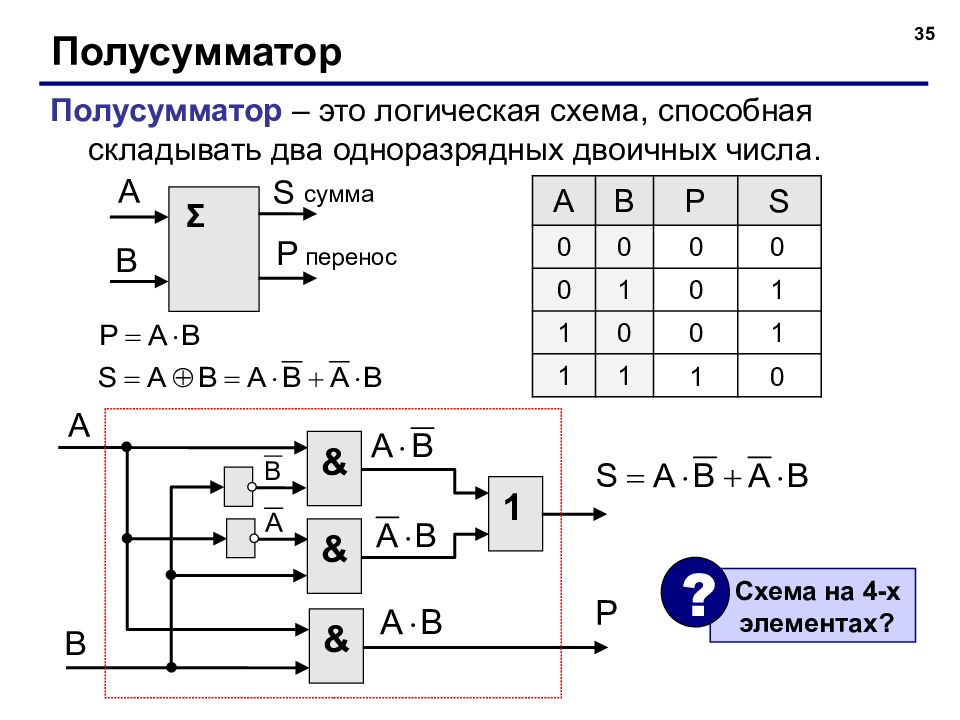
35 Полусумматор Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа. Σ сумма перенос A B P S 0 0 0 1 1 0 1 1 0 0 0 1 0 1 1 0 & 1 & & Схема на 4-х элементах? ?
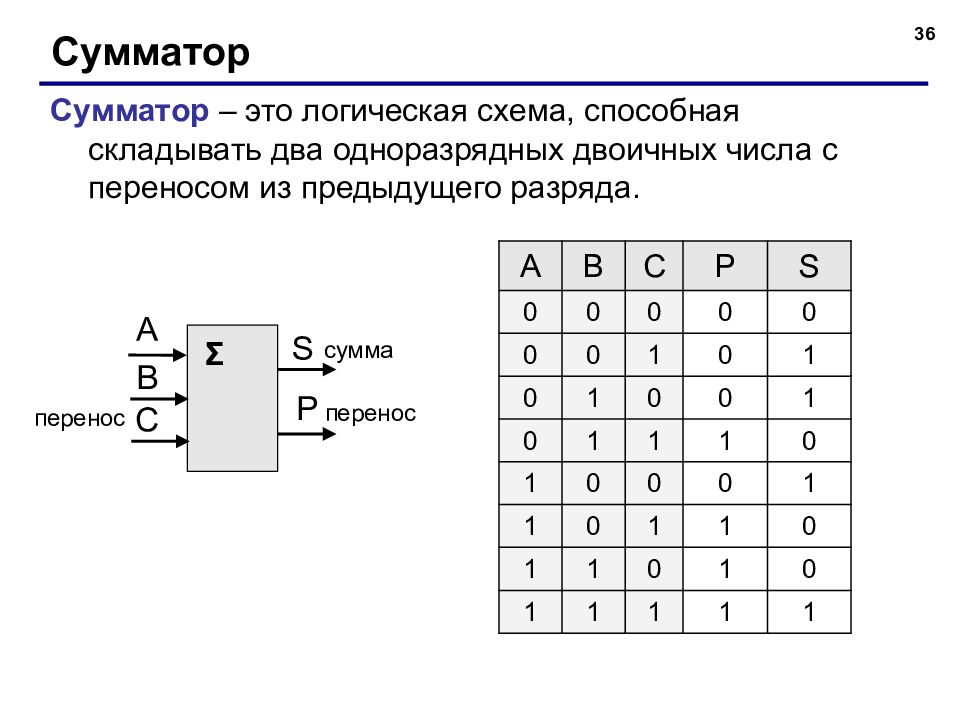
36 Сумматор Сумматор – это логическая схема, способная складывать два одноразрядных двоичных числа с переносом из предыдущего разряда. Σ сумма перенос перенос A B C P S 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1
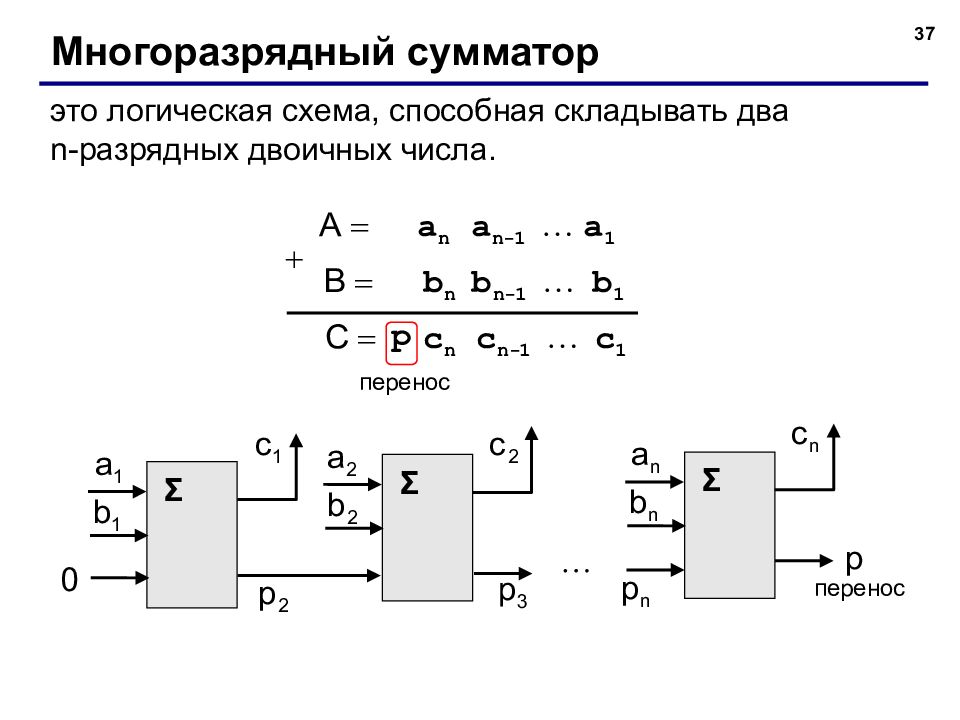
37 Многоразрядный сумматор это логическая схема, способная складывать два n- разрядных двоичных числа. перенос перенос Σ Σ Σ
38 Логические основы компьютеров Тема 6. Логические задачи
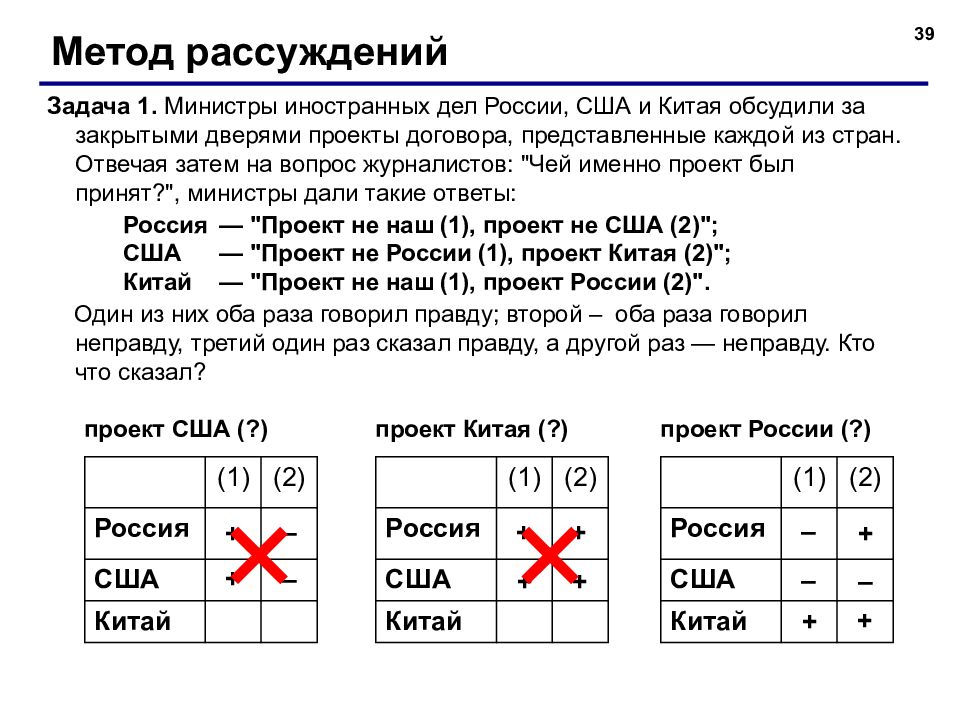
39 Метод рассуждений Задача 1. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты договора, представленные каждой из стран. Отвечая затем на вопрос журналистов: "Чей именно проект был принят?", министры дали такие ответы: Россия — "Проект не наш (1), проект не США (2) "; США — "Проект не России (1), проект Китая (2) "; Китай — "Проект не наш (1), проект России (2) ". Один из них оба раза говорил правду; второй – оба раза говорил неправду, третий один раз сказал правду, а другой раз — неправду. Кто что сказал? (1) (2) Россия США Китай проект России ( ?) – + – – + + (1) (2) Россия США Китай проект США ( ?) + – (1) (2) Россия США Китай проект Китая ( ?) + – + + + +
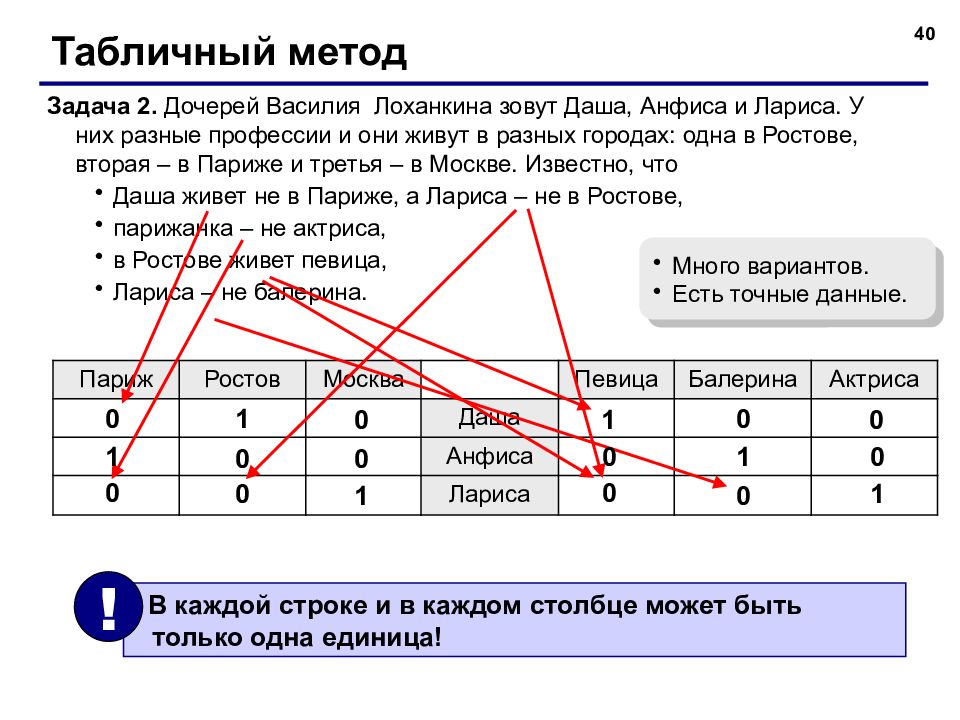
40 Табличный метод Задача 2. Дочерей Василия Лоханкина зовут Даша, Анфиса и Лариса. У них разные профессии и они живут в разных городах: одна в Ростове, вторая – в Париже и третья – в Москве. Известно, что Даша живет не в Париже, а Лариса – не в Ростове, парижанка – не актриса, в Ростове живет певица, Лариса – не балерина. Париж Ростов Москва Певица Балерина Актриса Даша Анфиса Лариса 0 0 0 В каждой строке и в каждом столбце может быть только одна единица! ! 0 1 0 0 0 1 0 0 1 1 0 1 0 0 1 Много вариантов. Есть точные данные.
41 Задача Эйнштейна Условие: Есть 5 домов разного цвета, стоящие в ряд. В каждом доме живет по одному человеку отличной от другого национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит животное. Никто из пяти человек не пьет одинаковые напитки, не курит одинаковые сигареты и не держит одинаковых животных. Известно, что: Англичанин живет в красном доме. Швед держит собаку. Датчанин пьет чай. Зеленой дом стоит слева от белого. Жилец зеленого дома пьет кофе. Человек, который курит Pallmall, держит птицу. Жилец среднего дома пьет молоко. Жилец из желтого дома курит Dunhill. Норвежец живет в первом доме. Курильщик Marlboro живет около того, кто держит кошку. Человек, который содержит лошадь, живет около того, кто курит Dunhill. Курильщик Winfield пьет пиво. Норвежец живет около голубого дома. Немец курит Rothmans. Курильщик Marlboro живет по соседству с человеком, который пьет воду. Вопрос: У кого живет рыба?
42 Использование алгебры логики Задача 3. Следующие два высказывания истинны: 1. Неверно, что если корабль A вышел в море, то корабль C – нет. 2. В море вышел корабль B или корабль C, но не оба вместе. Определить, какие корабли вышли в море. … если корабль A вышел в море, то корабль C – нет. 1. Неверно, что если корабль A вышел в море, то корабль C – нет. 2. В море вышел корабль B или корабль C, но не оба вместе. Решение:
43 Использование алгебры логики Задача 4. Когда сломался компьютер, его хозяин сказал «Память не могла выйти из строя». Его сын предположил, что сгорел процессор, а винчестер исправен. Мастер по ремонту сказал, что с процессором все в порядке, а память неисправна. В результате оказалось, что двое из них сказали все верно, а третий – все неверно. Что же сломалось? Решение: A – неисправен процессор, B – память, C – винчестер хозяин: сын: мастер: Если ошибся хозяин: Если ошибся сын: Если ошибся мастер: В общем случае: Несколько решений! !
44 Конец фильма
