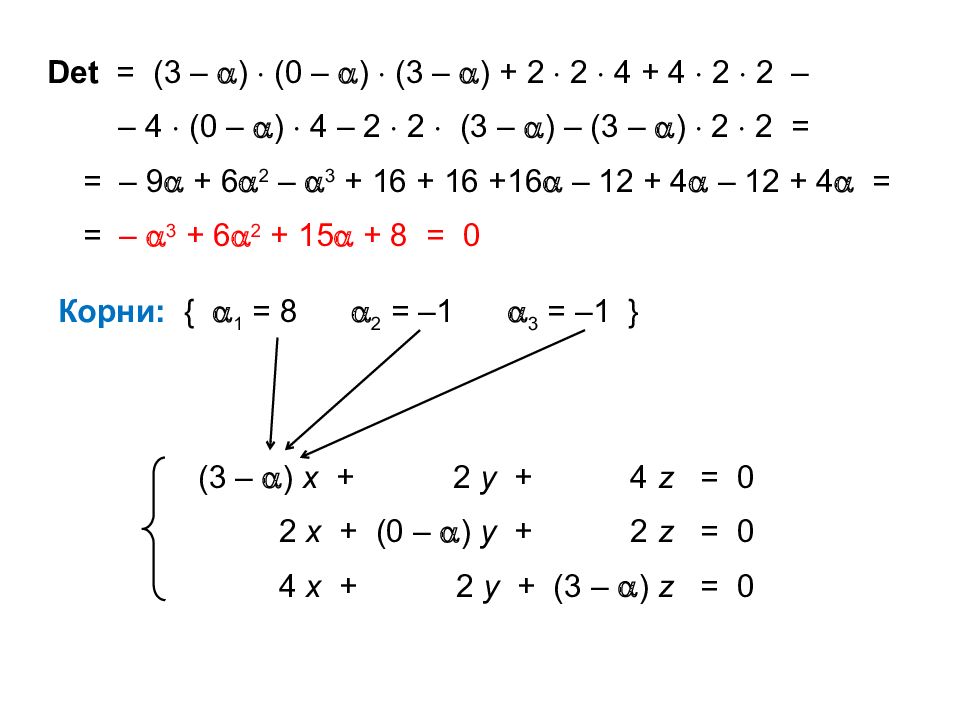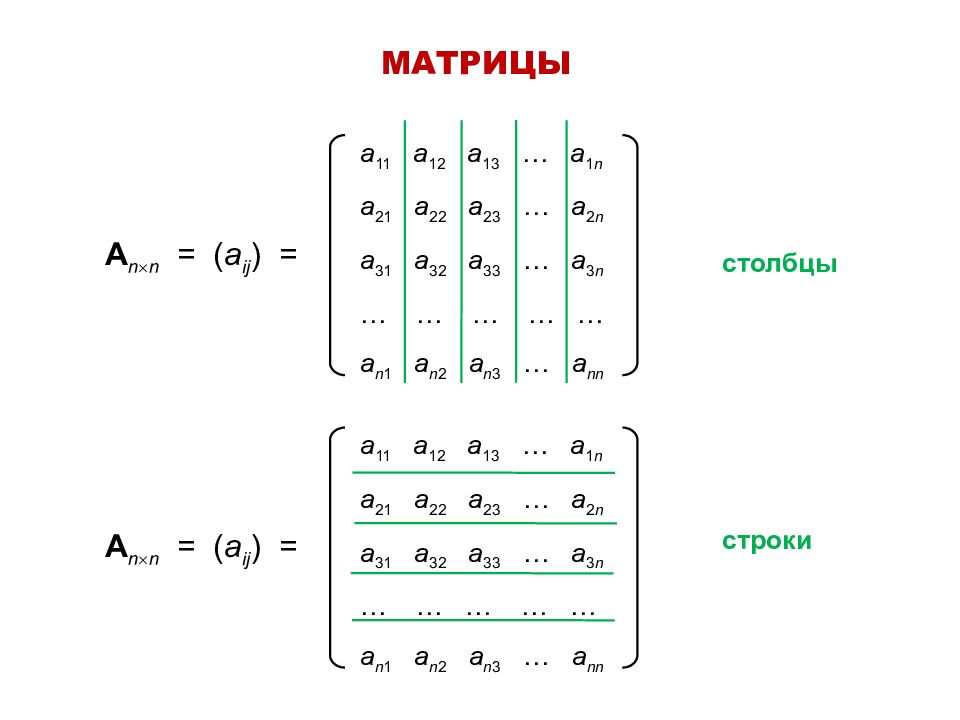
МАТРИЦЫ а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n a 31 a 32 a 33 … a 3 n … … … … … a n 1 a n 2 a n 3 … a nn A n n = ( a ij ) = столбцы а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n a 31 a 32 a 33 … a 3 n … … … … … a n 1 a n 2 a n 3 … a nn A n n = ( a ij ) = строки
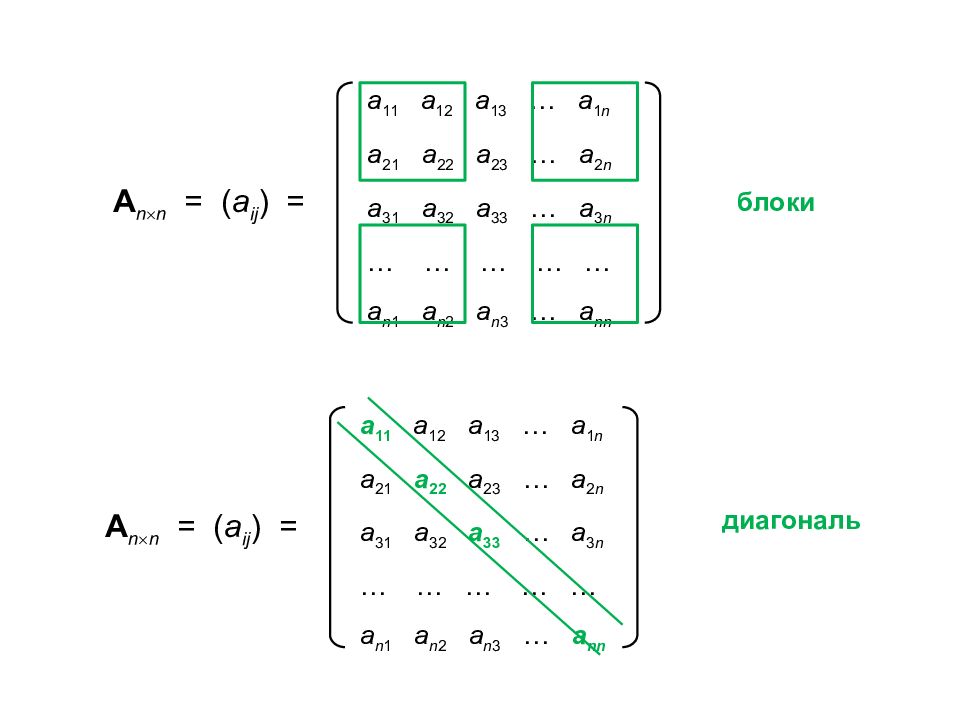
а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n a 31 a 32 a 33 … a 3 n … … … … … a n 1 a n 2 a n 3 … a nn A n n = ( a ij ) = блоки а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n a 31 a 32 a 33 … a 3 n … … … … … a n 1 a n 2 a n 3 … a nn A n n = ( a ij ) = диагональ
Характеристики матриц 1. След Sp = a 11 + a 22 + … + a nn = a ii 2. Определитель (детерминант) Метод разложения по элементам строки (столбца) 1) выбрать в матрице некоторую строку (обычно выбирается та строка, которая содержит наибольшее количество нулей); 2) записать первый элемент выбранной строки и умножить его на вспомогательную матрицу ( минор ), которая получается из исходной посредством вычеркивания строки и столбца, на пересечении которых стоит выписанный элемент;
а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n a 31 a 32 a 33 … a 3 n … … … … … a n 1 a n 2 a n 3 … a nn A n n = ( a ij ) = а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n a 31 a 32 a 33 … a 3 n … … … … … a n 1 a n 2 a n 3 … a nn Det A = = a 11 a 22 a 23 … a 2 n a 32 a 33 … a 3 n … … … … a n 2 a n 3 … a nn + … 3) выполнить описанный выше прием для всех элементов выделенной строки ;
+ a 12 a 21 a 23 … a 2 n a 31 a 33 … a 3 n … … … … a n 1 a n 3 … a nn + … + a 1 n a 21 a 22 … a 2 n–1 a 31 a 32 … a 3 n–1 … … … … a n 1 a n 2 … a nn–1 4) каждое произведение дополнительно умножить на (–1) i+j, где i и j — индексы элемента выделенной строки. В итоге большой определитель представляется в виде линейной комбинации определителей, размерность которых на 1 меньше, чем у исходного.
5) применить описанную процедуру ко всем определителям с размерностью ( n – 1 ), в результате чего каждый из них превратится в линейную комбинацию определителей размерностью ( n – 2). Систематически повторяя процедуру, мы, в конце концов, придем к длинной линейной комбинации определителей с размерностью 1, т.е. обычных чисел. Для завершения процедуры нужно выполнить все перемножения, сложения и вычитания,что даст в итоге единственное число — определитель матрицы А.
Пример Det A = = 2 (5 5 – 7 1) – 4 (3 5 – 7 4) + 8 (3 1 – 5 4) = 2 (25 – 7) – 4 (15 – 28) + 8 (3 – 20) = = 2 (18) – 4 (–13) + 8 (–17) = 36 + 52 – 136 = – 48 Det A = –48 3. Перманент (плюс-определитель) Метод вычисления тот же самый, что и для определителя, но вместо дополнительного множителя (–1) i+j используется множитель (+1) i+j
Пример Per A = = 2 (5 5 + 7 1) + 4 (3 5 + 7 4) + 8 (3 1 + 5 4) = 2 (25 + 7) + 4 (15 + 28) + 8 (3 + 20) = = 2 ( 32 ) + 4 ( 4 3) + 8 ( 23 ) = 6 4 + 172 + 1 84 = 4 20 Per A = 420 Алгебраическое дополнение A ij = минор ( a ij ) (–1) i + j Det A = a i 1 A i 1 + a i 2 A i 2 + … + a in A in
Операции над матрицами 1. Сложение матриц А + В = С 2. Умножение матрицы на число А = D 3. Линейные комбинации А + В + С + … = F А ij + В ij = С ij А ij = D ij А ij + В ij + С ij + … = F ij
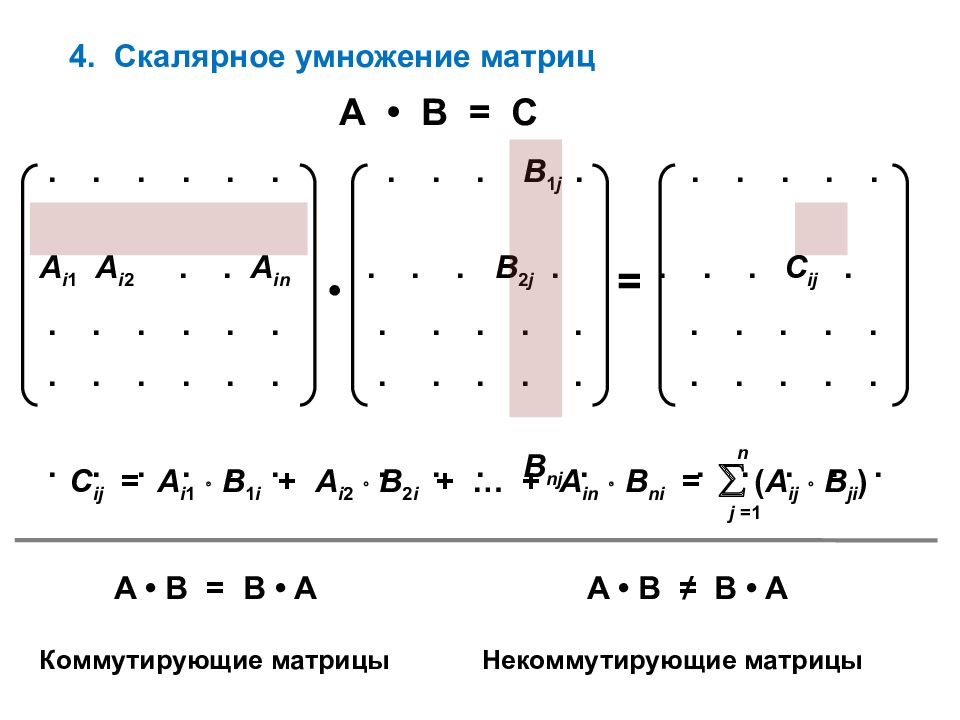
4. Скалярное умножение матриц А • В = С ......... B 1 j...... А i 1 A i 2.. A in... B 2 j.... C ij. ................ ................ ......... B nj...... • = C ij = A i 1 B 1 i + A i 2 B 2 i + … + A in B ni = ( A ij B ji ) j =1 n A • B = B • A A • B ≠ B • A Коммутирующие матрицы Некоммутирующие матрицы
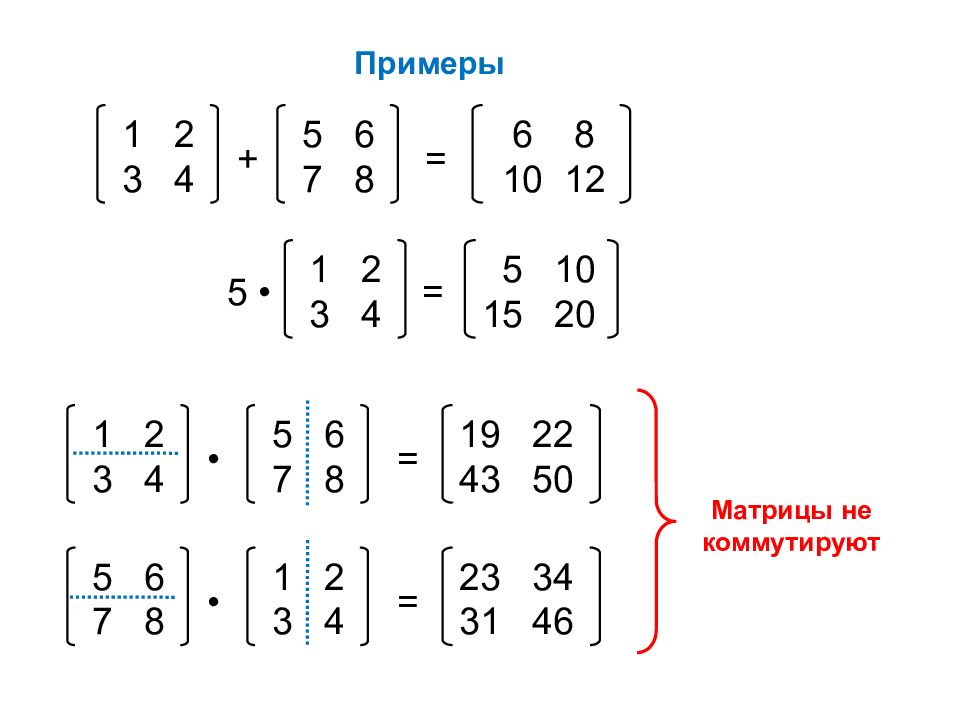
Примеры 1 2 3 4 5 6 7 8 6 8 10 12 + = 1 2 3 4 = 5 • 5 10 15 20 Матрицы не коммутируют 1 2 3 4 5 6 7 8 19 22 43 50 • = 5 6 7 8 1 2 3 4 23 34 31 46 • =
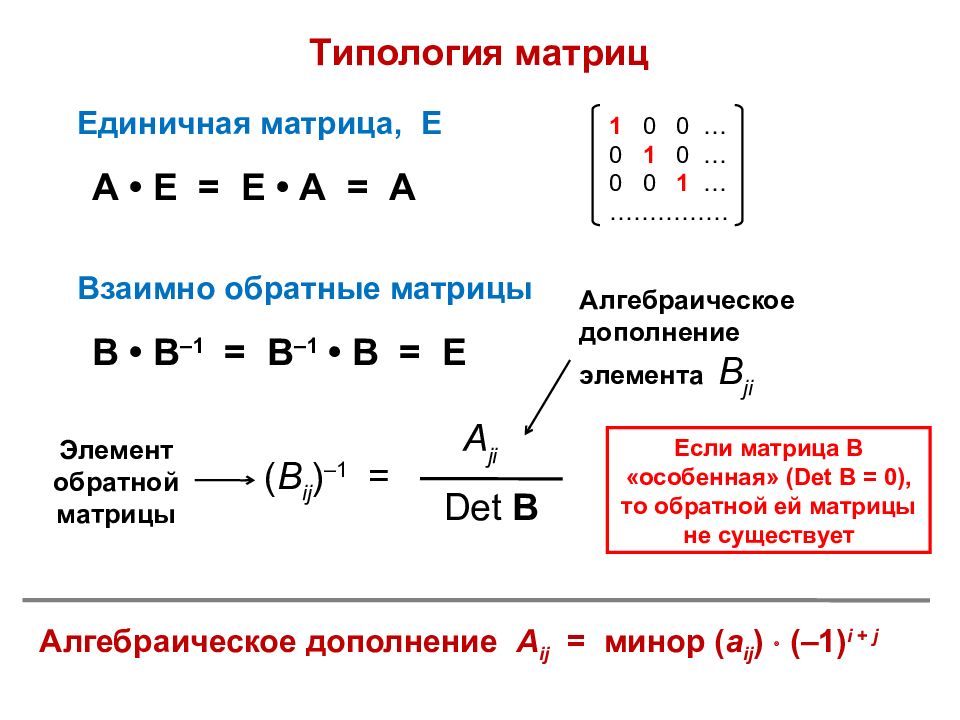
Типология матриц Взаимно обратные матрицы В • В –1 = В –1 • В = Е Если матрица В « особенная» ( Det В = 0), то обратной ей матрицы не существует ( В ij ) –1 = A ji Det В Алгебраическое дополнение элемента В ji Элемент обратной матрицы Единичная матрица, Е А • Е = Е • А = А 1 0 0 … 0 1 0 … 0 0 1 … …………… Алгебраическое дополнение A ij = минор ( a ij ) (–1) i + j
Пример 1 2 3 4 В = А 11 = +4 А 12 = –3 А 21 = –2 А 22 = +1 ( В 11 ) –1 = +4 /–2 = –2 ( В 1 2 ) –1 = – 2/–2 = +1 ( В 2 1 ) –1 = – 3/–2 = +1,5 ( В 22 ) –1 = + 1/–2 = –0,5 Det B = –2 1 2 3 4 – 2 1 1,5 –0,5 • = 1 0 0 1 Проверка: В • В –1 = Е В –1 = А 11 А 21 А 12 А 22 1 = 4 –2 –3 1 1 –2 – 2 1 1,5 –0,5 =
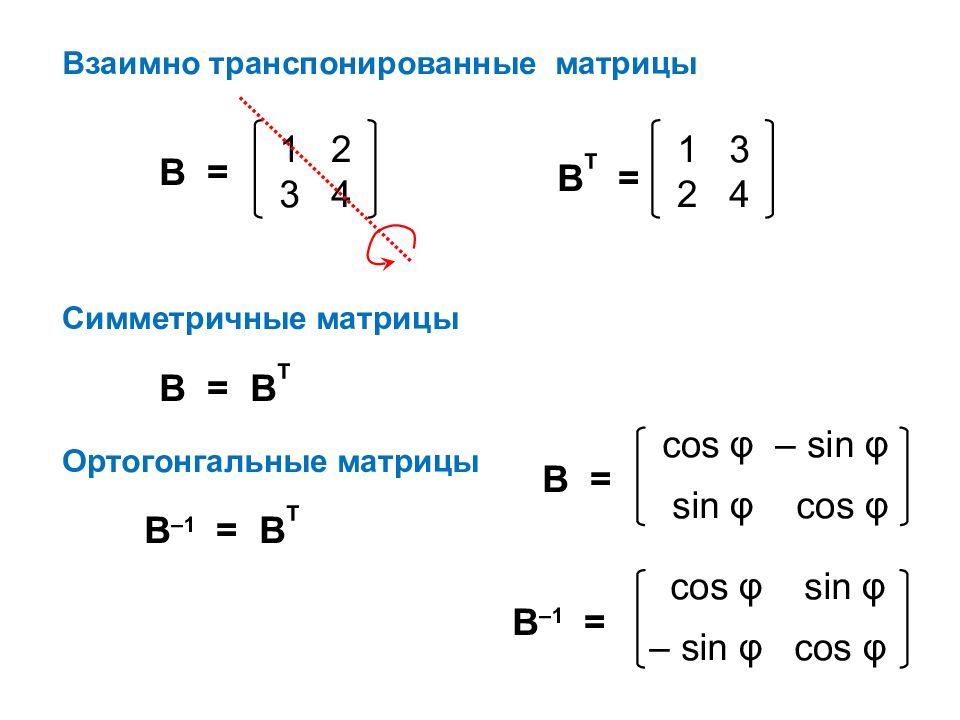
Взаимно транспонированные матрицы 1 2 3 4 В = 1 3 2 4 В Т = Симметричные матрицы В –1 = В Т В = В Т Ортогонгальные матрицы cos φ – sin φ sin φ cos φ В = cos φ sin φ – sin φ cos φ В –1 =
Комплексно сопряженные матрицы 1 + i 2 – i 3 – 2 i 4 В = В = В + Самосопряженные (эрмитовы) матрицы 1 – i 2 + i 3 + 2 i 4 В * = Эрмитово сопряженные матрицы 1 + i 2 – i 3 – 2 i 4 В = 1 – i 3 + 2 i 2 + i 4 В + = В –1 = В + Унитарные матрицы Аналоги симметричных матриц Аналоги ортогональных матриц
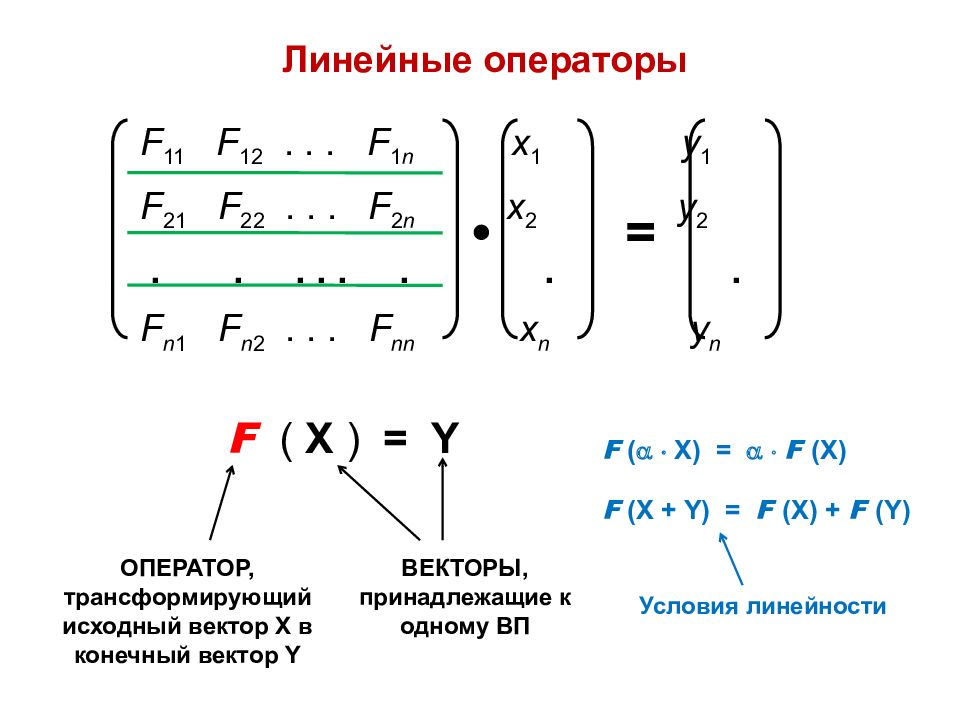
Линейные операторы F 11 F 12... F 1 n x 1 y 1 F 21 F 22... F 2 n x 2 y 2 ........ F n 1 F n 2... F nn x n y n • = F ( X ) = Y ОПЕРАТОР, трансформирующий исходный вектор X в конечный вектор Y ВЕКТОРЫ, принадлежащие к одному ВП F ( X) = F ( X) F ( X + Y) = F ( X) + F (Y) Условия линейности
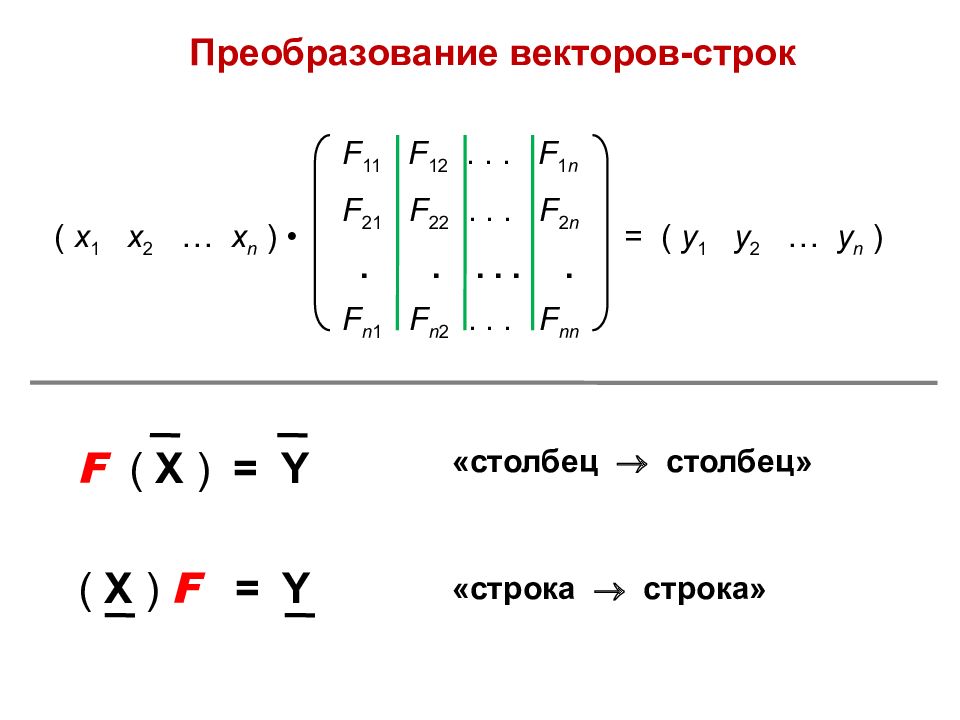
F 11 F 12... F 1 n F 21 F 22... F 2 n ...... F n 1 F n 2... F nn ( x 1 x 2 … x n ) • = ( y 1 y 2 … y n ) Преобразование векторов-строк F ( X ) = Y ( X ) F = Y «столбец столбец» «строка строка»
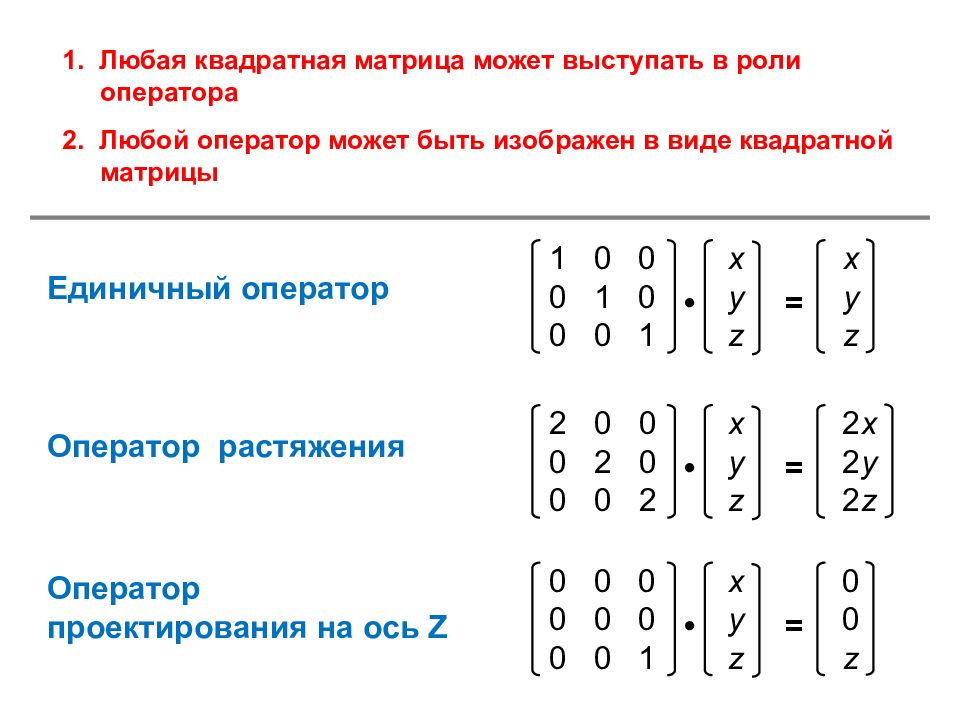
1. Любая квадратная матрица может выступать в роли оператора 2. Любой оператор может быть изображен в виде квадратной матрицы Единичный оператор 1 0 0 x x 0 1 0 y y 0 0 1 z z • = Оператор растяжения 2 0 0 x 2 x 0 2 0 y 2 y 0 0 2 z 2 z • = Оператор проектирования на ось Z 0 0 0 x 0 0 0 0 y 0 0 0 1 z z • =
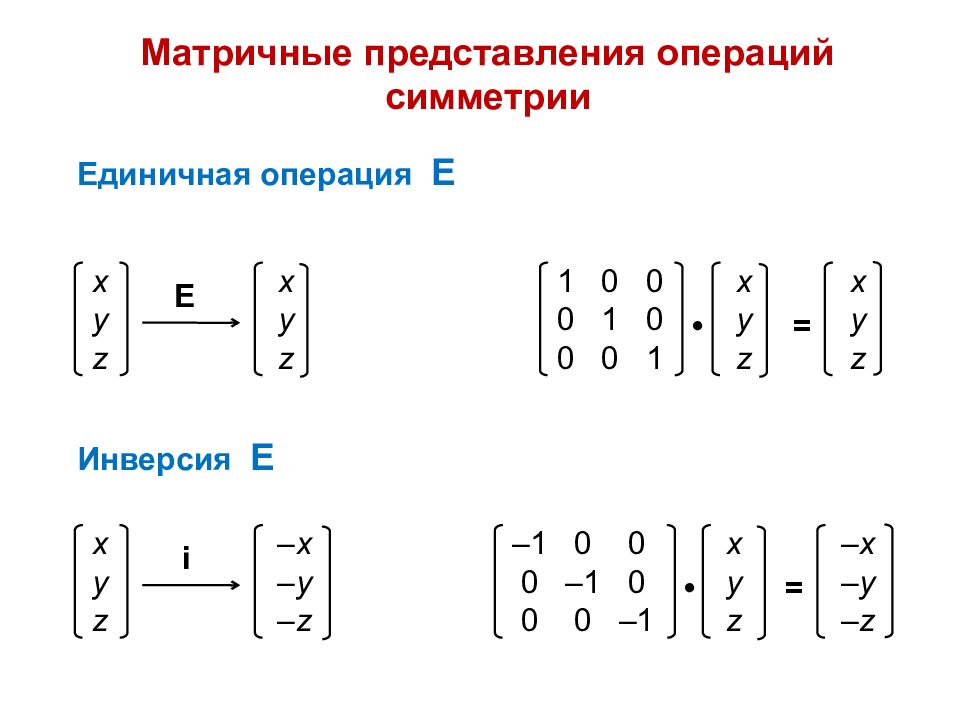
Матричные представления операций симметрии 1 0 0 x x 0 1 0 y y 0 0 1 z z • = Единичная операция E x x y y z z Е Инверсия E – 1 0 0 x – x 0 – 1 0 y – y 0 0 – 1 z – z • = x – x y – y z – z i
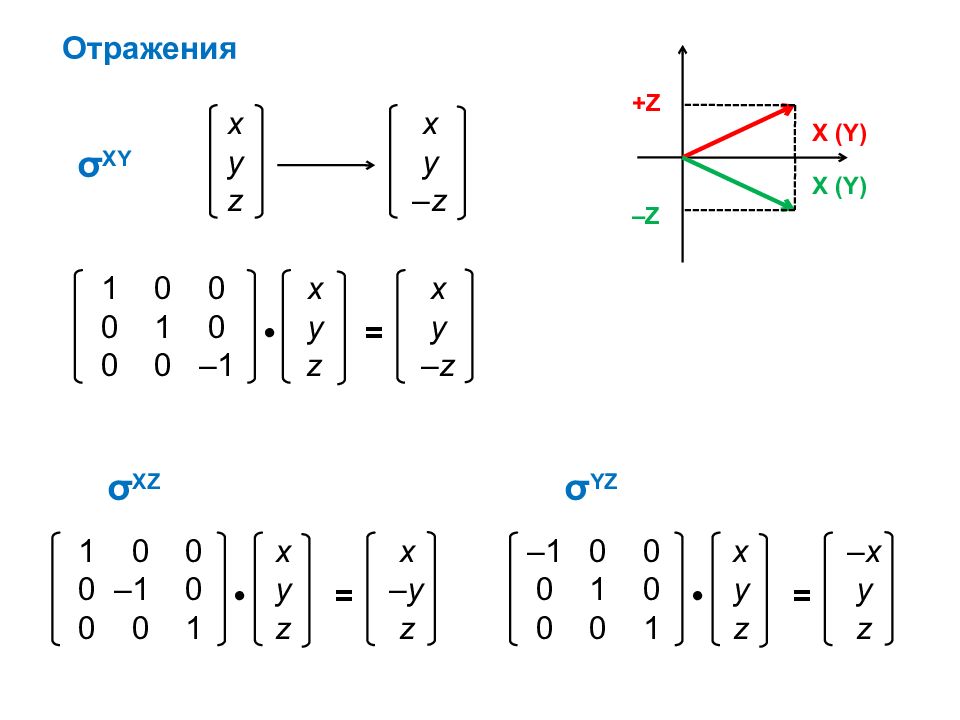
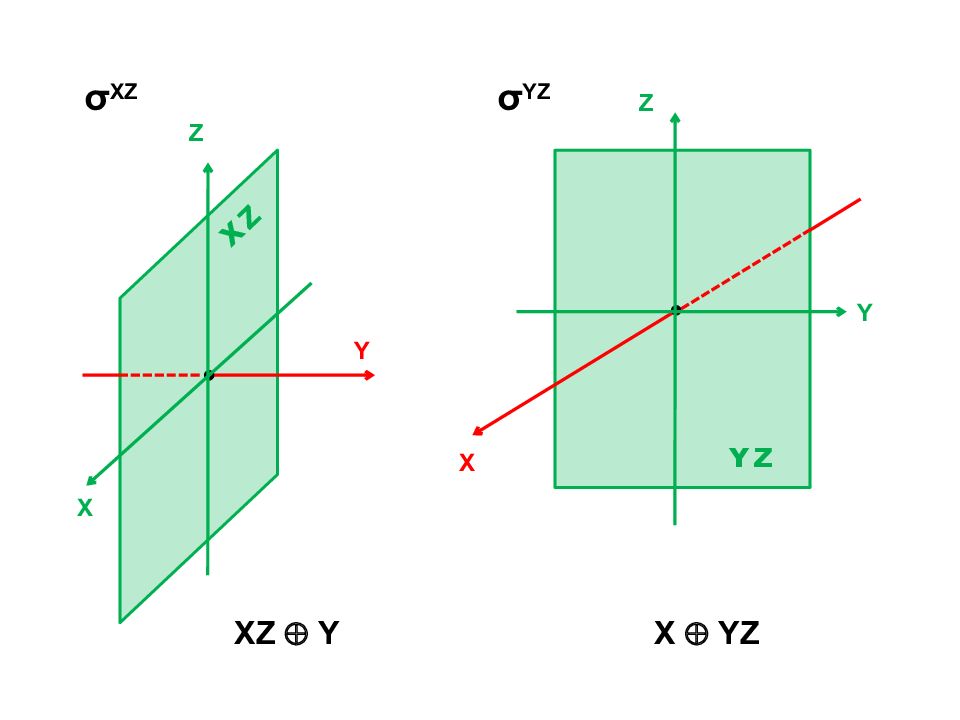
σ XY 1 0 0 x x 0 – 1 0 y – y 0 0 1 z z • = σ XZ Отражения +Z X (Y) –Z X (Y) 1 0 0 x x 0 1 0 y y 0 0 – 1 z – z • = x x y y z – z – 1 0 0 x – x 0 1 0 y y 0 0 1 z z • = σ YZ
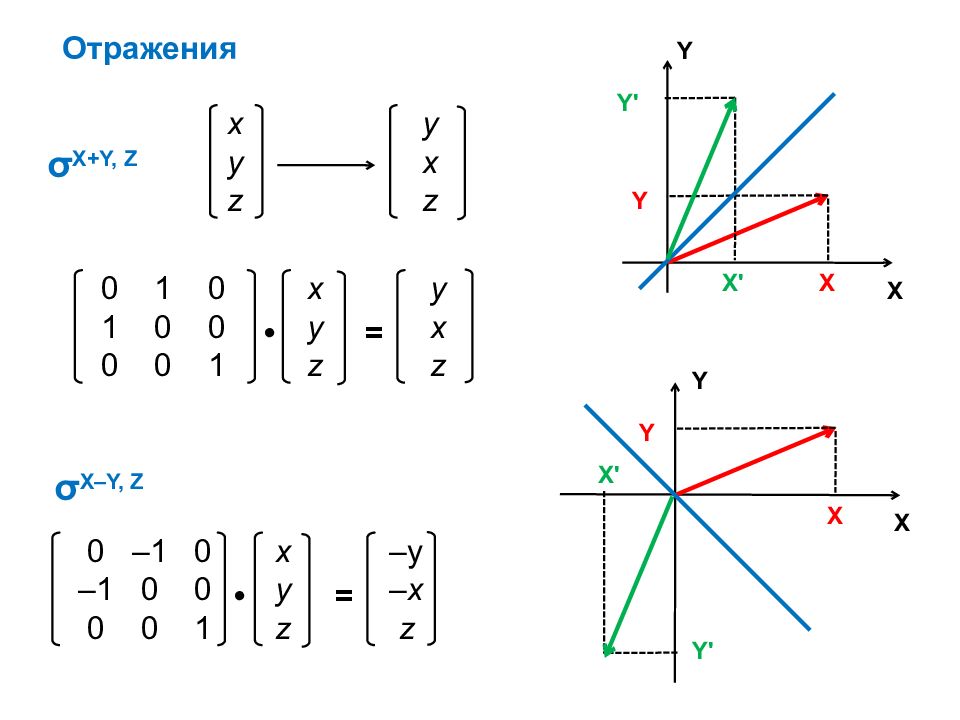
σ X+Y, Z 0 –1 0 x –y –1 0 0 y – x 0 0 1 z z • = σ X–Y, Z Отражения 0 1 0 x y 1 0 0 y x 0 0 1 z z • = x y y x z z X X Y Y X ' Y ' X X Y Y X ' Y '
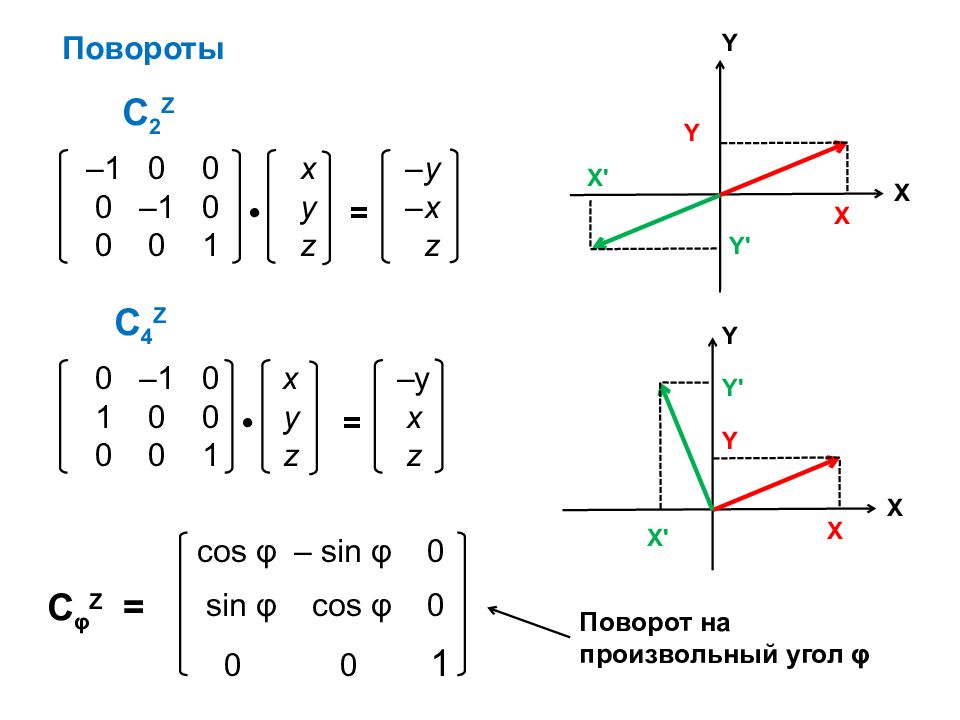
С 2 Z 0 –1 0 x –y 1 0 0 y x 0 0 1 z z • = С 4 Z Повороты –1 0 0 x – y 0 –1 0 y – x 0 0 1 z z • = X X Y Y X ' Y ' X X Y Y X ' Y ' cos φ – sin φ 0 sin φ cos φ 0 0 0 1 С φ Z = Поворот на произвольный угол φ
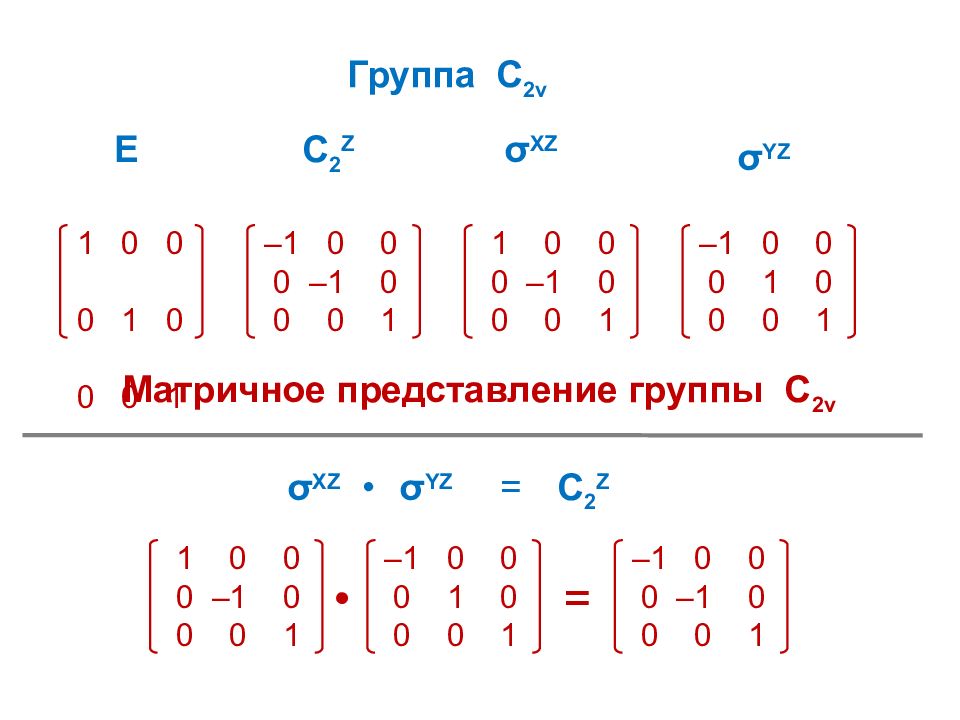
Матричное представление группы С 2 v 1 0 0 0 1 0 0 0 1 – 1 0 0 0 – 1 0 0 0 1 E C 2 Z 1 0 0 0 – 1 0 0 0 1 – 1 0 0 0 1 0 0 0 1 Группа С 2 v σ XZ σ YZ σ XZ σ YZ C 2 Z • = 1 0 0 0 – 1 0 0 0 1 – 1 0 0 0 1 0 0 0 1 – 1 0 0 0 – 1 0 0 0 1 • =
Домашнее задание Задача 3.1. Установить, коммутируют ли между собой заданные операции симметрии, найти коммутатор. 1) найти матричные представления операций F 1 и F 2 ; 2) найти произведения: F 1 • F 2 и F 2 • F 1 ; 3) найти коммутатор: С = F 1 • F 2 – F 2 • F 1
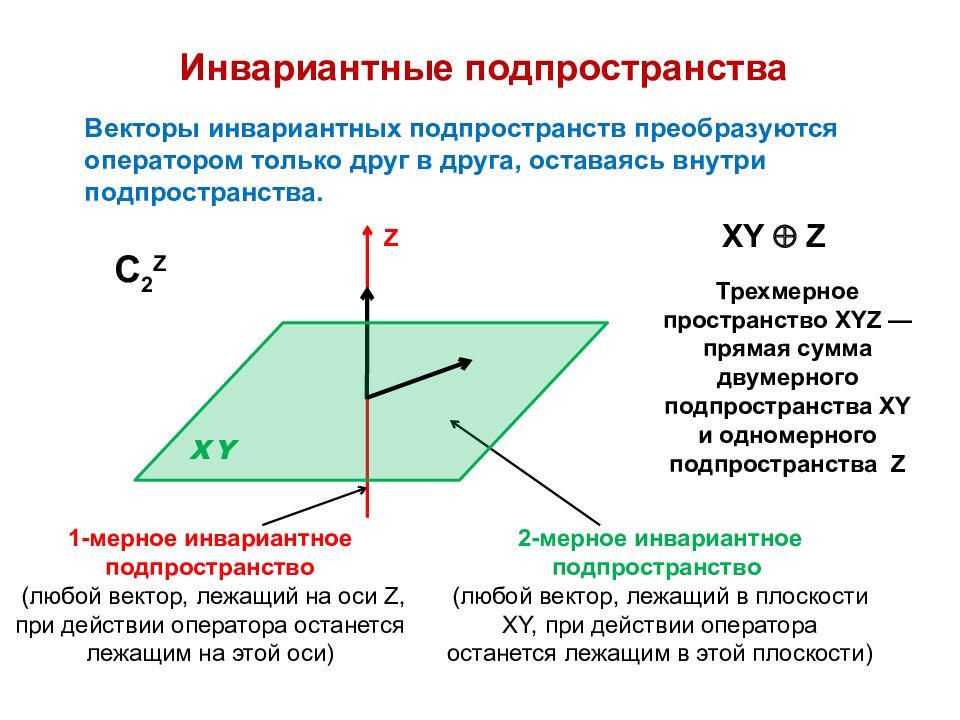
Инвариантные подпространства Векторы инвариантных подпространств преобразуются оператором только друг в друга, оставаясь внутри подпространства. C 2 Z 2-мерное инвариантное подпространство (любой вектор, лежащий в плоскости XY, при действии оператора останется лежащим в этой плоскости) 1-мерное инвариантное подпространство (любой вектор, лежащий на оси Z, при действии оператора останется лежащим на этой оси) X Y Z Z Х Y Трехмерное пространство X Y Z — прямая сумма двумерного подпространства X Y и одно мерного подпространства Z
σ XZ Y XZ XZ Y Z X σ YZ X YZ X Y Z Z Y
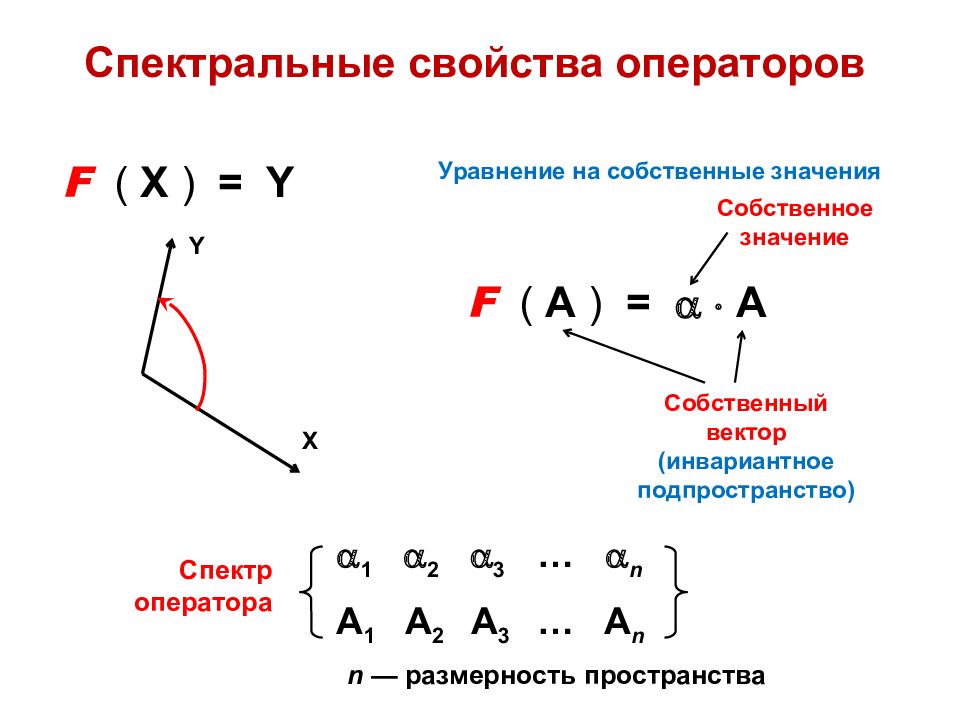
Спектральные свойства операторов F ( X ) = Y F ( А ) = А X Y Собственный вектор (инвариантное подпространство) Собственное значение Уравнение на собственные значения 1 2 3 … n A 1 A 2 A 3 … A n Спектр оператора n — размерность пространства
F ( А ) = А F 11 F 12... F 1 n a 1 a 1 F 21 F 22... F 2 n a 2 a 2 ......... F n 1 F n 2... F nn a n a n • = F 11 а 1 + F 12 а 2 +... + F 1 n а n = a 1 F 21 а 1 + F 22 а 2 +... + F 2 n а n = a 2 .............. F n 1 а 1 + F n 2 а 2 +... + F nn а n = a n
( F 11 – ) а 1 + F 12 а 2 +... + F 1 n а n = 0 F 21 а 1 + ( F 22 – ) а 2 +... + F 2 n а n = 0 .............. F n 1 а 1 + F n 2 а 2 +... + ( F nn – ) а n = 0 Однородная система линейных уравнений Условие разрешимости: Det = 0 ( F 11 – ) F 12... F 1 n F 21 ( F 22 – )... F 2 n .......... F n 1 F n 2... ( F nn – ) = 0
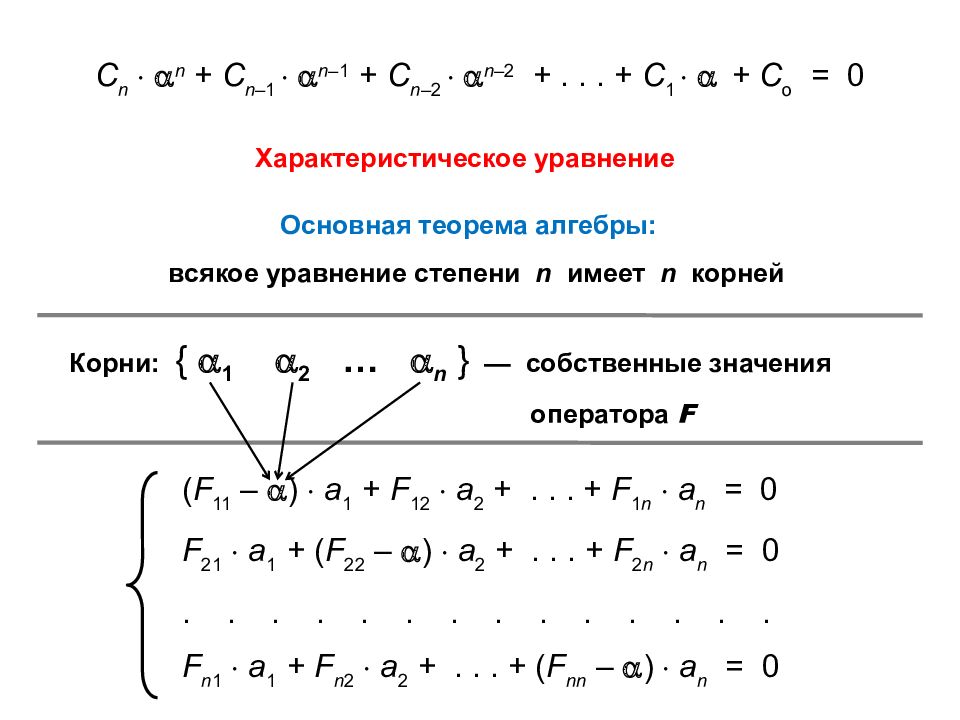
С n n + С n –1 n –1 + С n –2 n –2 +... + С 1 + C o = 0 Характеристическое уравнение Основная теорема алгебры: всякое уравнение степени n имеет n корней Корни: { 1 2 … n } — собственные значения оператора F ( F 11 – ) а 1 + F 12 а 2 +... + F 1 n а n = 0 F 21 а 1 + ( F 22 – ) а 2 +... + F 2 n а n = 0 .............. F n 1 а 1 + F n 2 а 2 +... + ( F nn – ) а n = 0
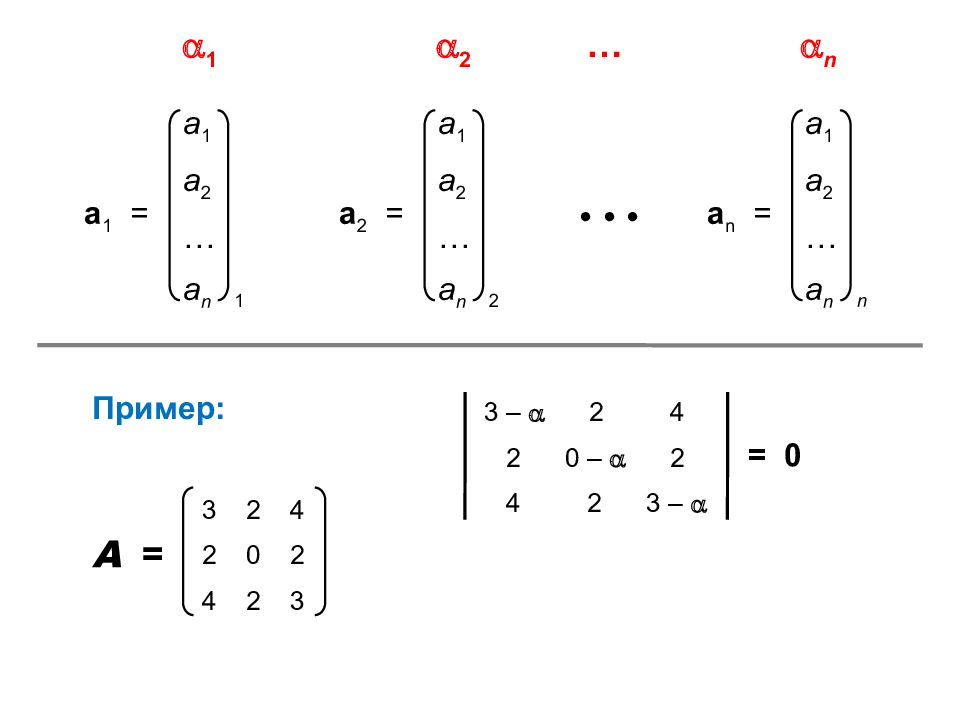
a 1 a 2 … a n a 1 = 1 1 2 … n a 1 a 2 … a n a 2 = 2 a 1 a 2 … a n a n = n • • • 3 2 4 2 0 2 4 2 3 A = Пример: 3 – 2 4 2 0 – 2 4 2 3 – = 0
Det = (3 – ) (0 – ) (3 – ) + 2 2 4 + 4 2 2 – – 4 (0 – ) 4 – 2 2 (3 – ) – (3 – ) 2 2 = = – 9 + 6 2 – 3 + 16 + 16 +16 – 12 + 4 – 12 + 4 = = – 3 + 6 2 + 15 + 8 = 0 Корни: { 1 = 8 2 = –1 3 = –1 } (3 – ) х + 2 y + 4 z = 0 2 x + (0 – ) y + 2 z = 0 4 x + 2 y + (3 – ) z = 0
1 = 8 – 5 х + 2 y + 4 z = 0 2 x – 8 y + 2 z = 0 4 x + 2 y – 5 z = 0 Вычитая третье уравнение из первого, получим: –9 x + 9 z = 0 или x = z. Подставим этот результат во второе уравнение и получим: 4 х – 8 у = 0 или у = х /2. Теперь мы можем выразить все три координаты вектора через одну, например, через х : х = х у = х /2 z = x Решение : x x /2 x 2 1 2 а 1 = = ( х /2)
= –1 4 х + 2 y + 4 z = 0 2 x + 1 y + 2 z = 0 4 x + 2 y + 4 z = 0 Видно, что все три уравнения одинаковы и задают только одно соотношение между тремя неизвестными. Поэтому мы можем произвольно выбрать значения двух неизвестных, а третье уже выразить через эти два. Уравнение 2 x + 1 y + 2 z = 0 определяет некоторую плоскость (двумерное инвариантное подпространство) в трехмерном пространстве. Любой вектор, лежащий на этой плоскости является решением нашей системы и, следовательно, будет собственным для нашего оператора. Экономный способ задать все эти векторы заключается в выборе базиса — двух ортогональных векторов на плоскости.
Первый базисный вектор можно выбрать произвольно. Положим, например, х = 0 и у = 1. Тогда из уравнения плоскости 2 x + 1 y + 2 z = 0 следует, что z = –1/2. Второй базисный вектор должен удовлетворять как уравнению плоскости ( 2 x + 1 y + 2 z = 0 ), так и условию ортогональности: x y z (0, 1, –1/2) = y – 1/2 z = 0 Решая совместно эти два уравнения, получим: у = –2/5 х и z = –4/5 х. 0 1 – 1/ 2 1 –2/5 –4/5 а 2 = a 3 = 0 2 – 1 5 –2 –4 а 2 = a 3 =
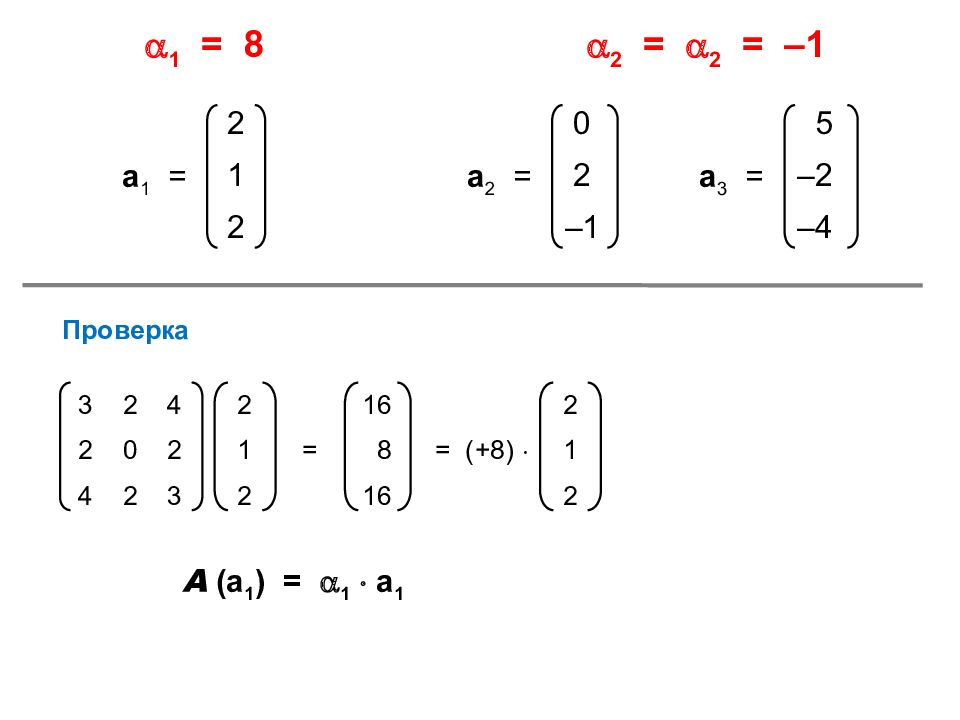
2 1 2 a 1 = 1 = 8 2 = 2 = –1 0 2 –1 a 2 = 5 –2 –4 a 3 = Проверка 3 2 4 2 0 2 4 2 3 2 1 2 16 8 16 2 1 2 = = (+8) А (а 1 ) = 1 а 1
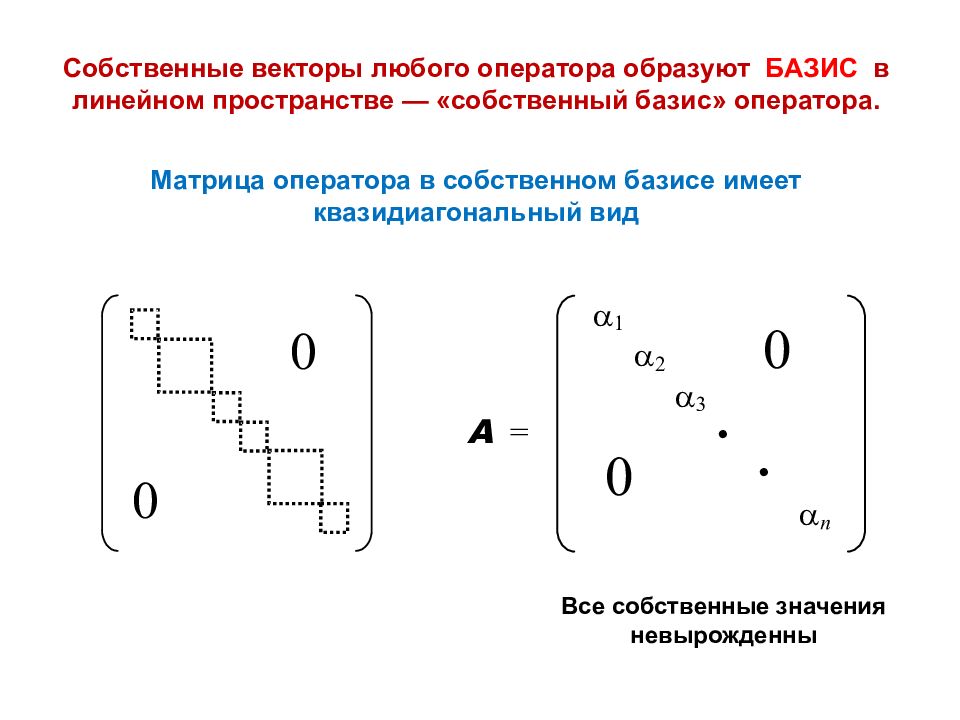
Собственные векторы любого оператора образуют БАЗИС в линейном пространстве — «собственный базис» оператора. Матрица оператора в собственном базисе имеет квазидиагональный вид Все собственные значения невырожденны
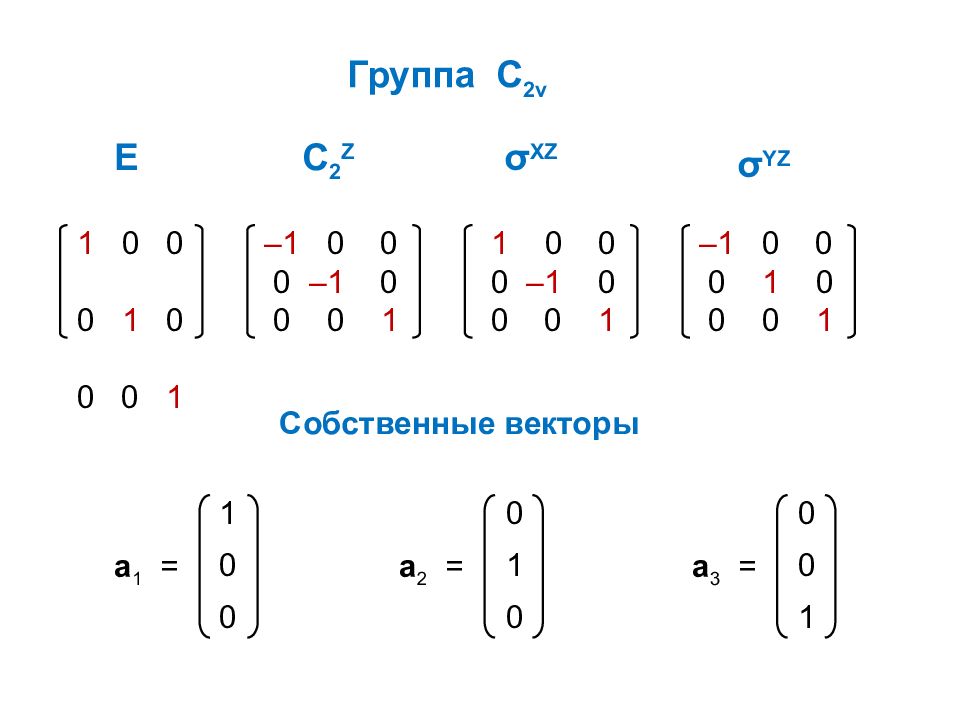
1 0 0 0 1 0 0 0 1 – 1 0 0 0 – 1 0 0 0 1 E C 2 Z 1 0 0 0 – 1 0 0 0 1 – 1 0 0 0 1 0 0 0 1 Группа С 2 v σ XZ σ YZ 1 0 0 a 1 = 0 1 0 a 2 = 0 0 1 a 3 = Собственные векторы
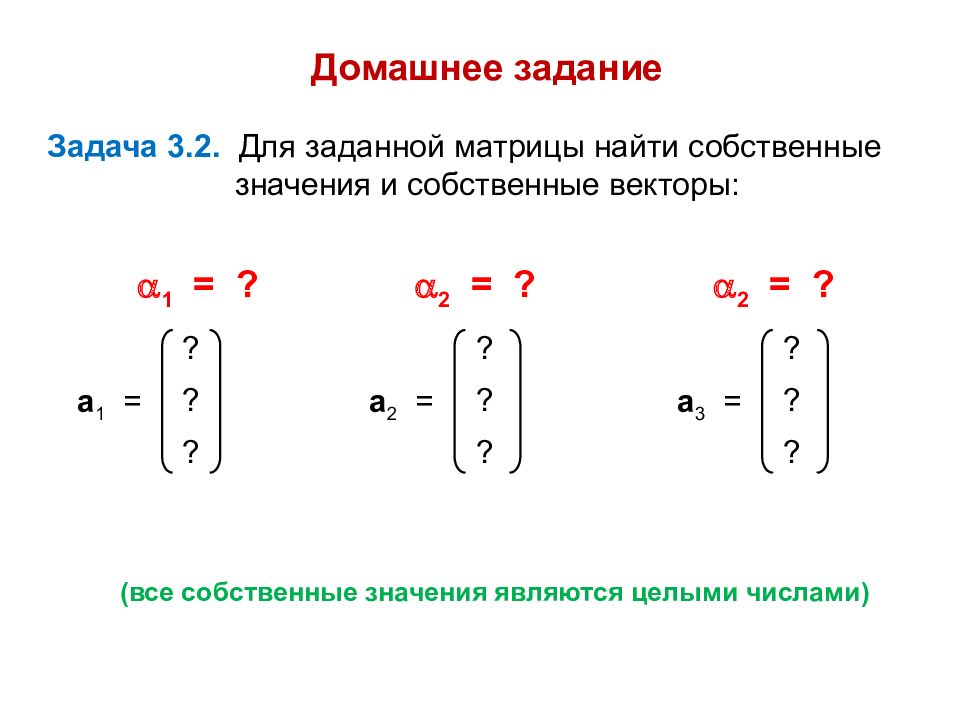
Домашнее задание Задача 3.2. Для заданной матрицы найти собственные значения и собственные векторы: ? ? ? a 1 = ? ? ? a 2 = ? ? ? a 3 = 1 = ? 2 = ? 2 = ? (все собственные значения являются целыми числами)
