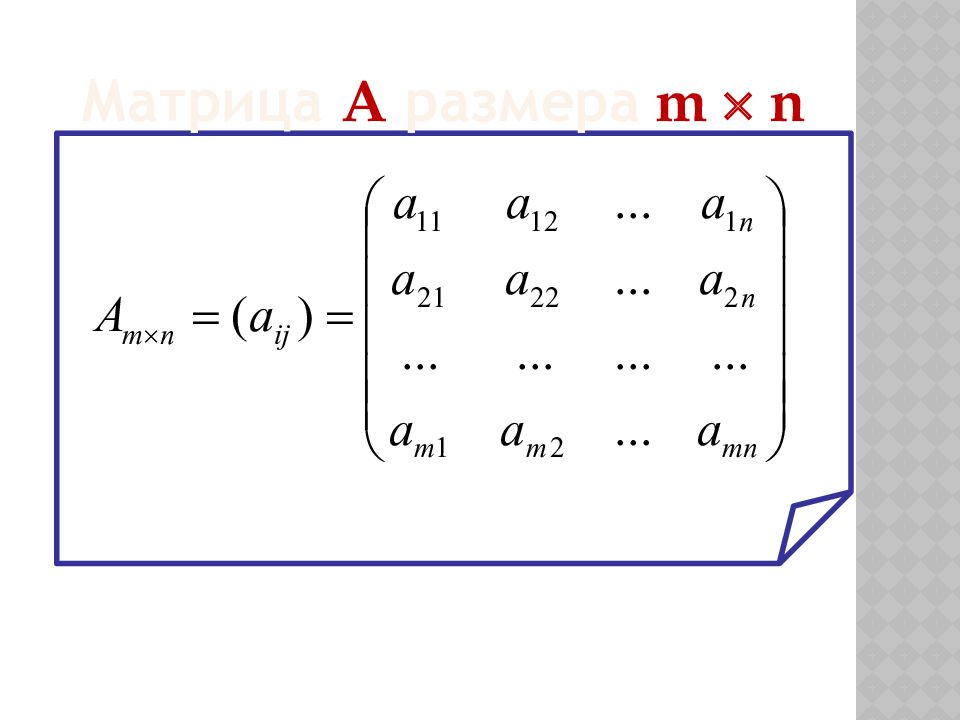
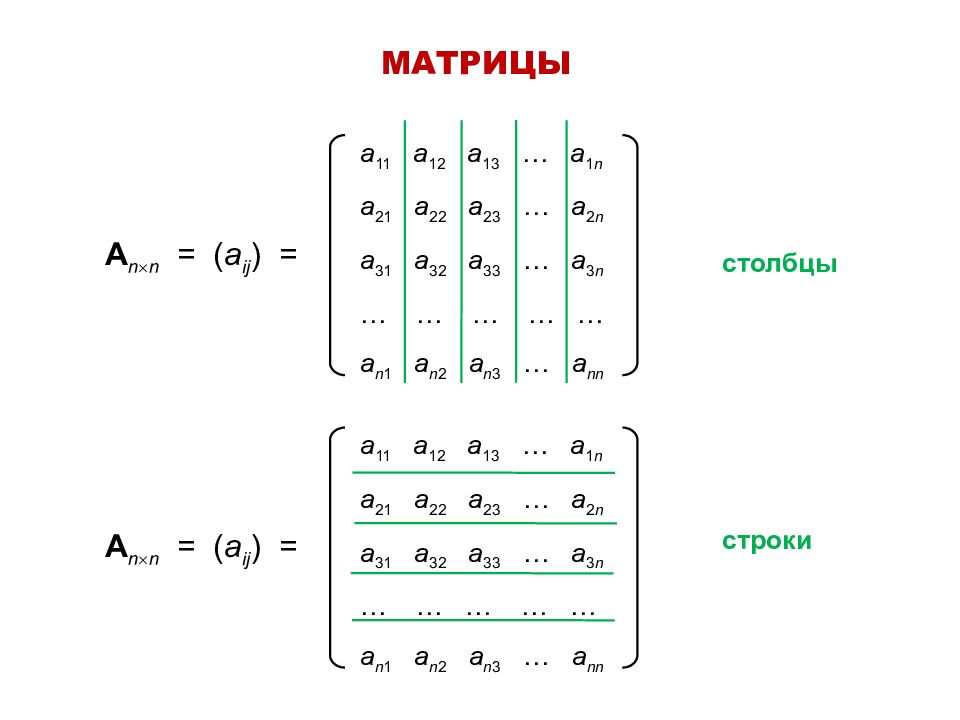
Матрицей А размера m n называется прямоугольная таблица чисел, содержащая m строк ( i ) и n столбцов ( j ). Числа, составляющие матрицу, называются элементами матрицы ( a ij ). 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ Определение:
Матрица А размера m n
матрица размерности m x n ; элемент матрицы i –ой строки и j -го столбца, где i = 1, 2,…, m и j = 1, 2,…, n Матрицы обозначаются прописными буквами латинского алфавита: А, В, С, D и т.д. ; Матрицы обозначаются скобками : ( ) или [ ] ; Обозначения:
Две матрицы называются равными, если у них одинаковая размерность и совпадают строки и столбцы. Если число строк матрицы равно числу ее столбцов, то такая матрица называется квадратной. Определения:
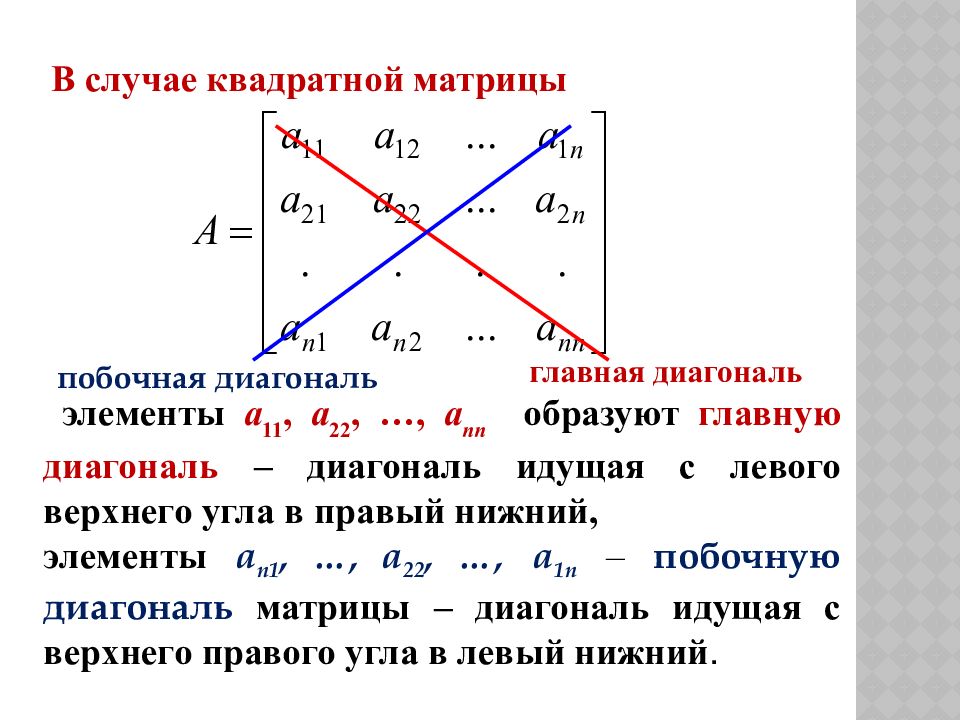
В случае квадратной матрицы элементы a 11, a 22, …, a nn образуют главную диагональ – диагональ идущая с левого верхнего угла в правый нижний, элементы a n1, …, a 2 2, …, a 1n – побочную диагональ матрицы – диагональ идущая с верхнего правого угла в левый нижний. побочная диагональ главная диагональ
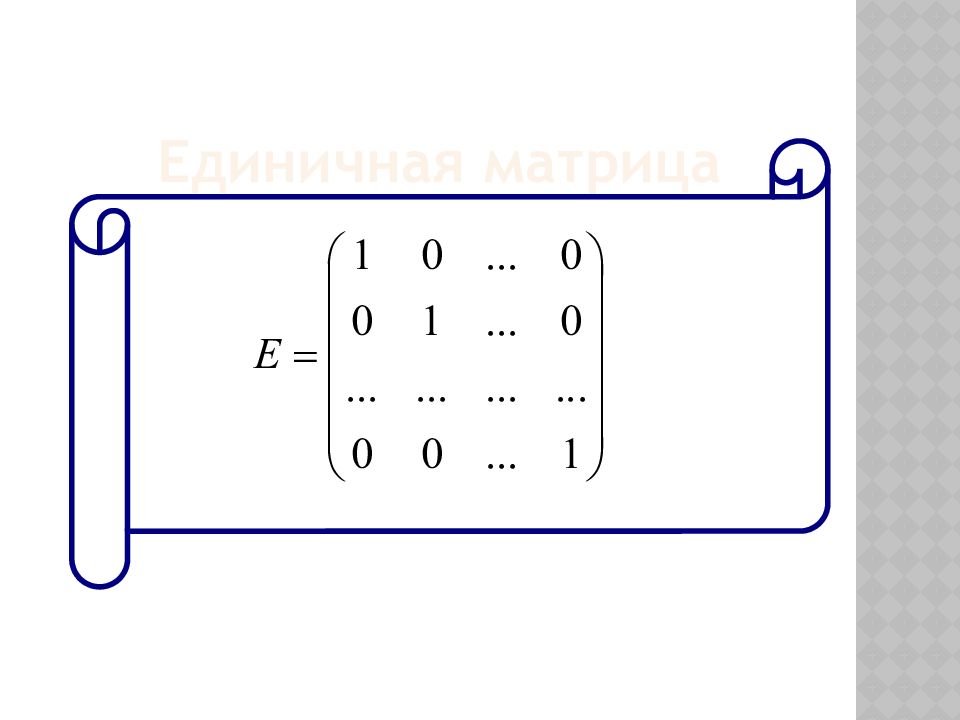
Элементы матрицы a ij, у которых номер столбца совпадает с номером строки, называются диагональными. Если в квадратной матрице все диагональные элементы равны 1, а остальные элементы равны 0, то она называется единичной. Определения:
Матрица, состоящая из одной строки, называется матрицей-строкой. Определение:
Матрица, состоящая из одного столбца, называется матрицей-столбцом. Определение:
- квадратная матрица размера m n = 3 3, где а 11 = 1, а 22 = 4, а 33 = 1 - элементы главной диагонали, а 31 = 0, а 22 = 4, а 13 = -2 - элементы побочной диагонали Примеры:
Единичная матрица
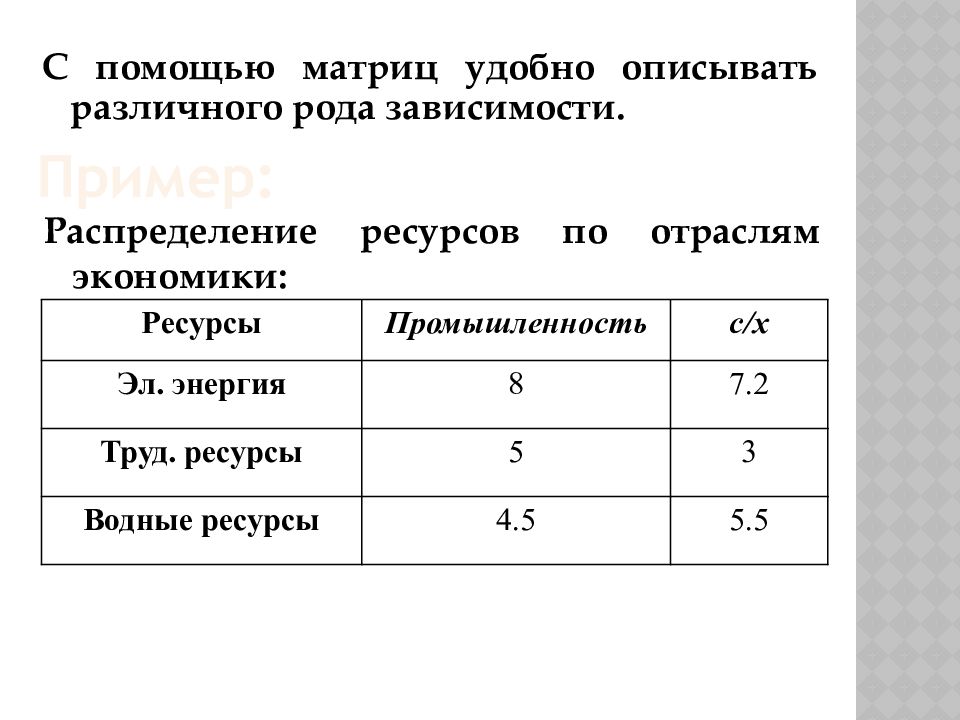
Распределение ресурсов по отраслям экономики: С помощью матриц удобно описывать различного рода зависимости. Ресурсы Промышленность с / х Эл. энергия 8 7.2 Труд. ресурсы 5 3 Водные ресурсы 4.5 5.5 Пример:
Эту зависимость можно представить в виде матрицы: Где элемент a ij показывает сколько i – го ресурса потребляет j – отрасль. Например, a 32 показывает, сколько воды потребляет сельское хозяйство.
Чтобы умножить матрицу на произвольное число ( λ ), надо каждый элемент этой матрицы ( a ij ) умножить на это число. Полученные произведения образуют итоговую матрицу. 1) Умножение матриц на число Действия над матрицами
Пусть дана матрица: Умножаем ее на число λ : Где каждый элемент матрицы: Где: Умножая матрицу на число 2, получим: Пример:
Складываются (вычитаются) матрицы только одинаковой размерности. Получается матрица той же размерности, каждый элемент которой равен сумме (разности) соответствующих элементов исходных матриц: 2) Сложение (вычитание) матриц Где каждый элемент матрицы С :
Найти: 1) сумму и 2) разность матриц: Пример 1 Решение:
Пример 2 Найти: 1) сумму и 2) разность матриц: Решение:
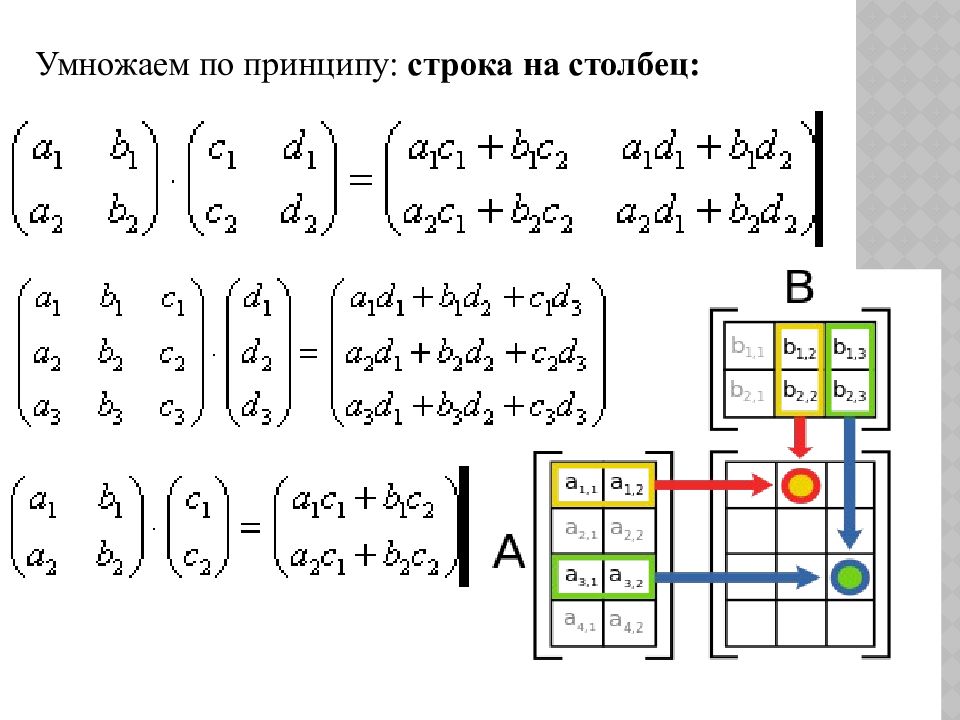
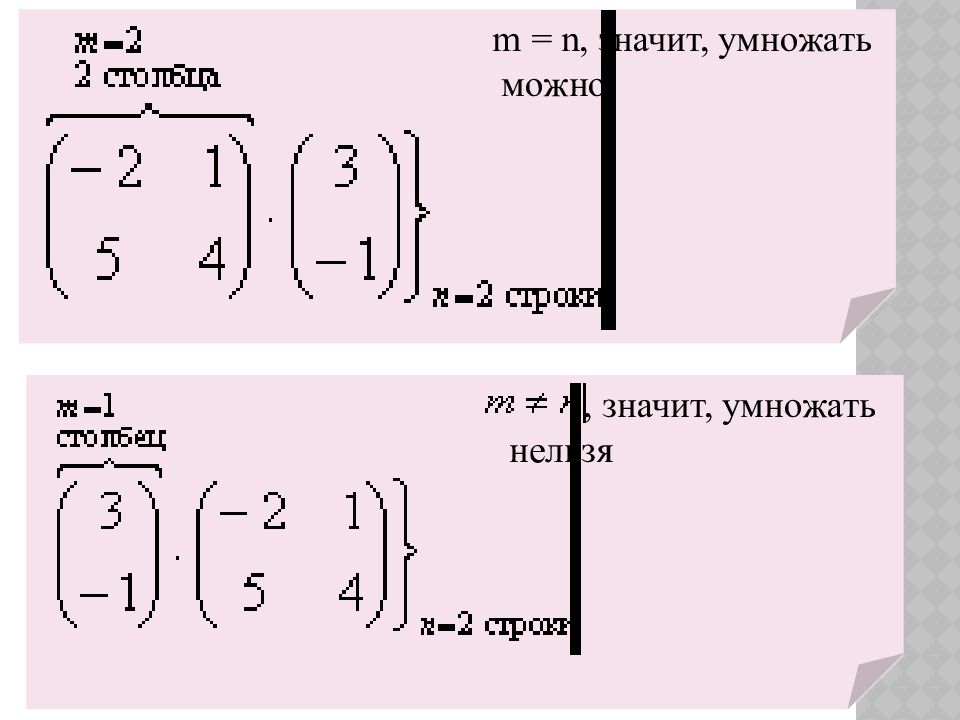
Умножение матриц возможно, если число столбцов первой матрицы равно числу строк второй. Тогда каждый элемент полученной матрицы равен сумме произведений элементов i – ой строки первой матрицы на соответствующие элементы j -го столбца второй. 3) Умножение матриц
Результатом умножения двух матриц является матрица C размера m n, т.е. : где каждый элемент матрицы С, т.е. с ij равен:
Даны две матрицы : и размера m n и n k соответственно. Произведением матрицы А m n на матрицу В n k называется матрица С m k с элементами с ij равными сумме произведений элементов i - ой строки матрицы А на соответствующие элементы j - го столбца матрицы В, т.е. с ij = a i 1 b 1 j + a i 2 b 2 j +…+ a in b nj, где i = 1, 2,..., m ; j = 1, 2,..., k
Умножаем по принципу: строка на столбец:
Найти произведение матриц: Пример 1: Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует: Решение:
Эти две матрицы так же можно перемножить и в обратном порядке, так как число столбцов первой матрицы равно числу строк второй (это исключение, см. свойство 3):
, значит, умножать нельзя m = n, значит, умножать можно
Найти произведение матриц и Пример 2: Решение:
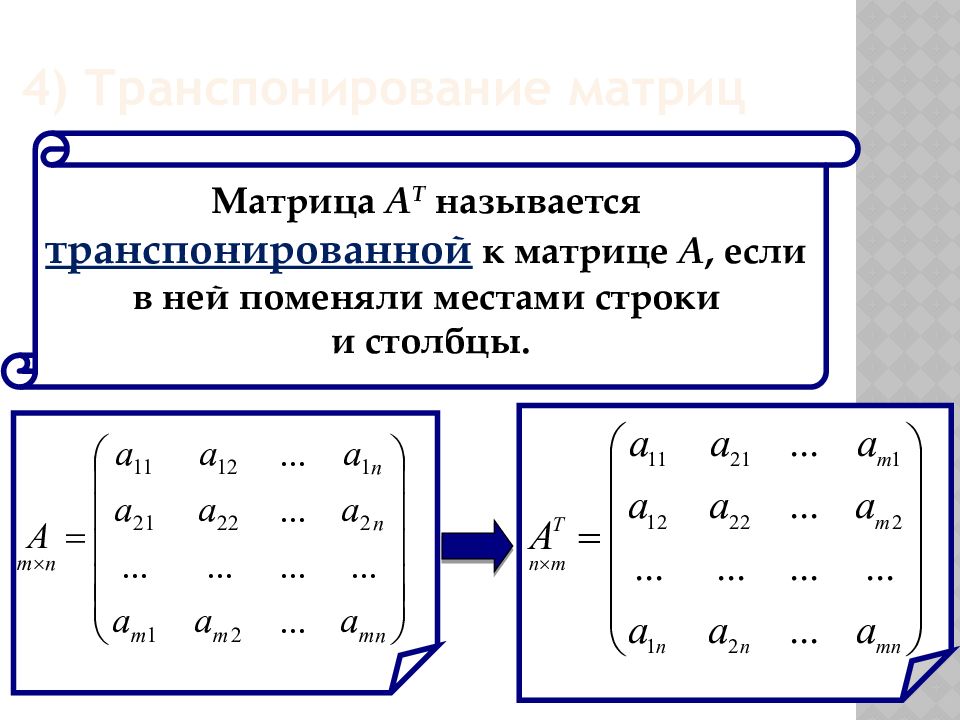
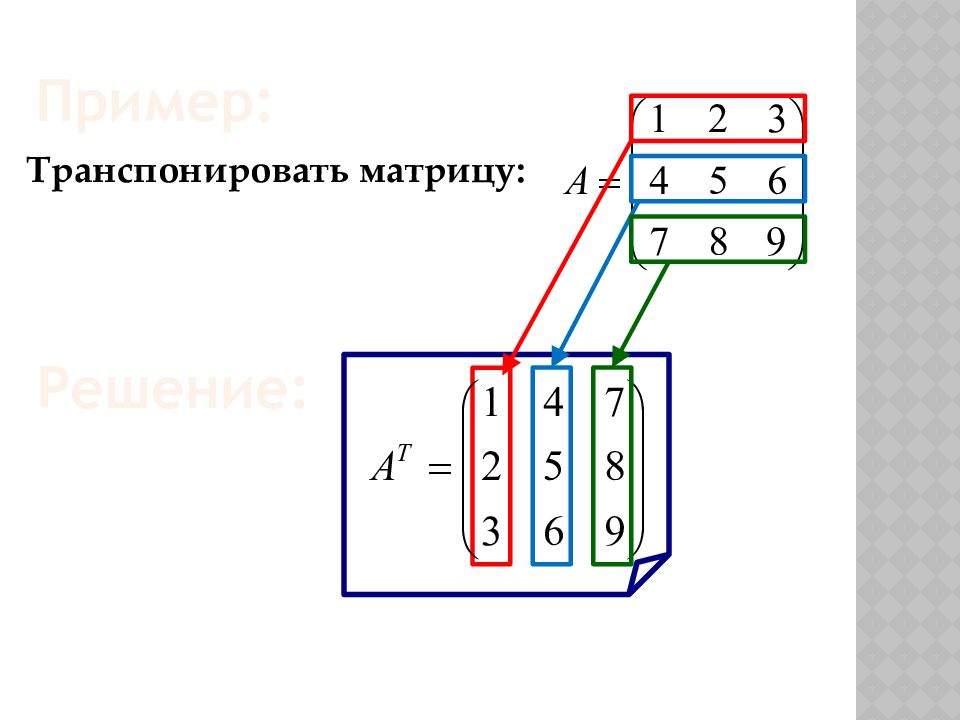
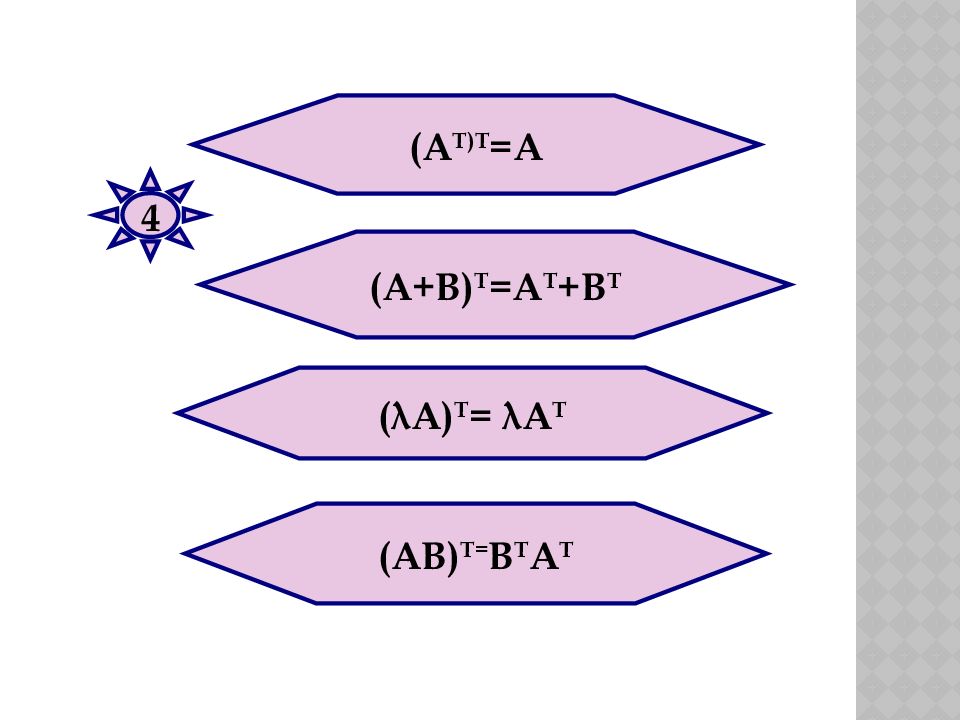
Матрица А Т называется транспонированной к матрице А, если в ней поменяли местами строки и столбцы. 4) Транспонирование матриц
Транспонировать матрицу: Пример: Решение:
5) Возведение матриц в степень Матрица называется k степенью квадратной матрицы А
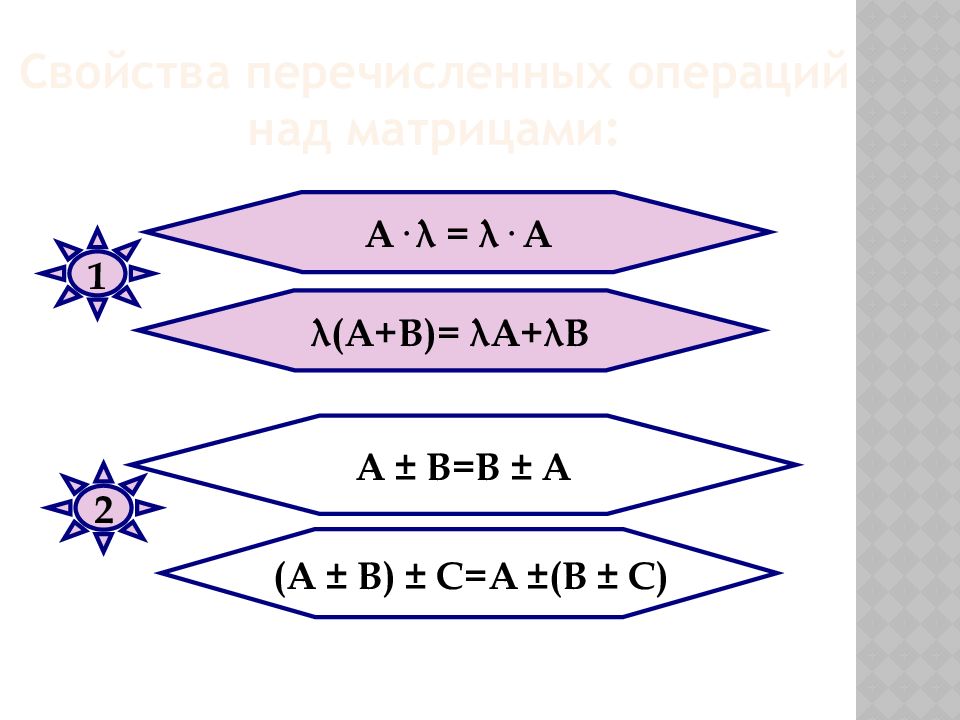
А ± В=В ± А (А ± В) ± С=А ±(В ± С) 1 2 λ (А+В)= λ А+ λ В А· λ = λ · А Свойства перечисленных операций над матрицами:
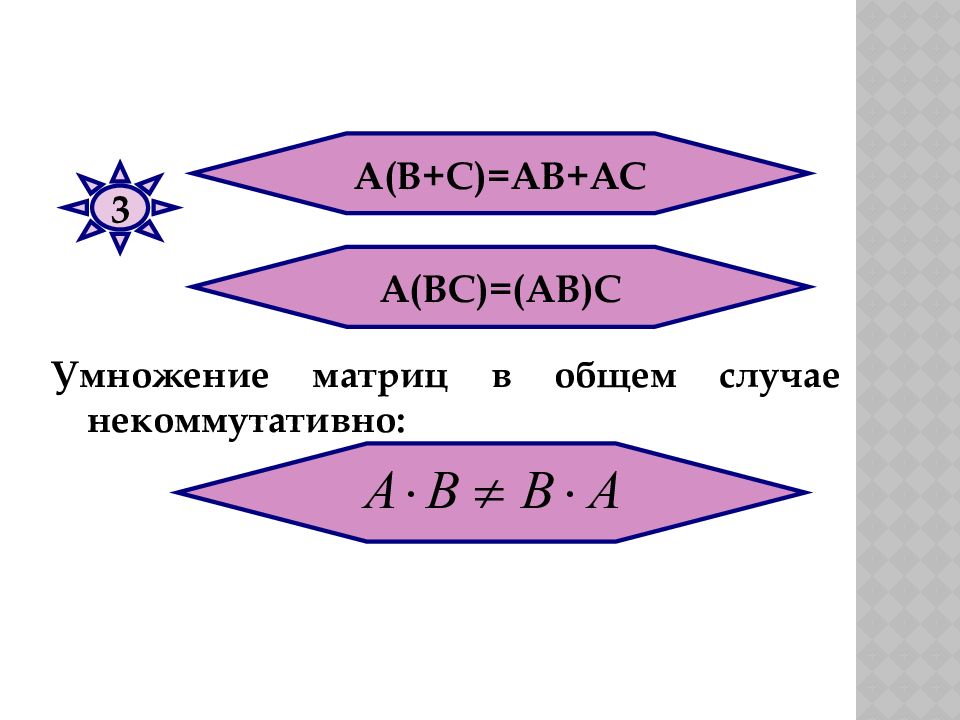
А(В+С)=АВ+АС А(ВС)=(АВ)С 3 Умножение матриц в общем случае некоммутативно:
(А Т)Т =А (А+В) Т =А Т +В Т 4 ( λ А) Т = λ А Т (АВ) Т= В Т А Т
Понятие определителя (детерминанта) матрицы вводится только для квадратных матриц. Определителем или детерминантом (от лат. determinare - определять ) квадратной матрицы А называется некоторое число, которое можно поставить ей в соответствие следуя определённым правилам. 1.2. ОПРЕДЕЛИТЕЛИ И ДЕЙСТВИЯ НАД НИМИ Определение:
Обозначения: , det ( A ), Определители записываются в прямых скобках . Определения: 1) Определителем первого порядка называется число, соответствующее квадратной матрице содержащей один элемент, т.е. А = (а 11 ), которое равно самому элементу = а 11. . Пример: Вычислить определитель для матрицы: А = (5) Решение: = 5.
2) Определителем второго порядка называется число, соответствующее квадратной матрице и вычисленное по следующему правилу: произведение элементов, стоящих по главной диагонали минус произведение элементов, стоящих по побочной диагонали, т.е. = a 11 a 22 - a 12 a 21 – правило диагоналей : Пример:
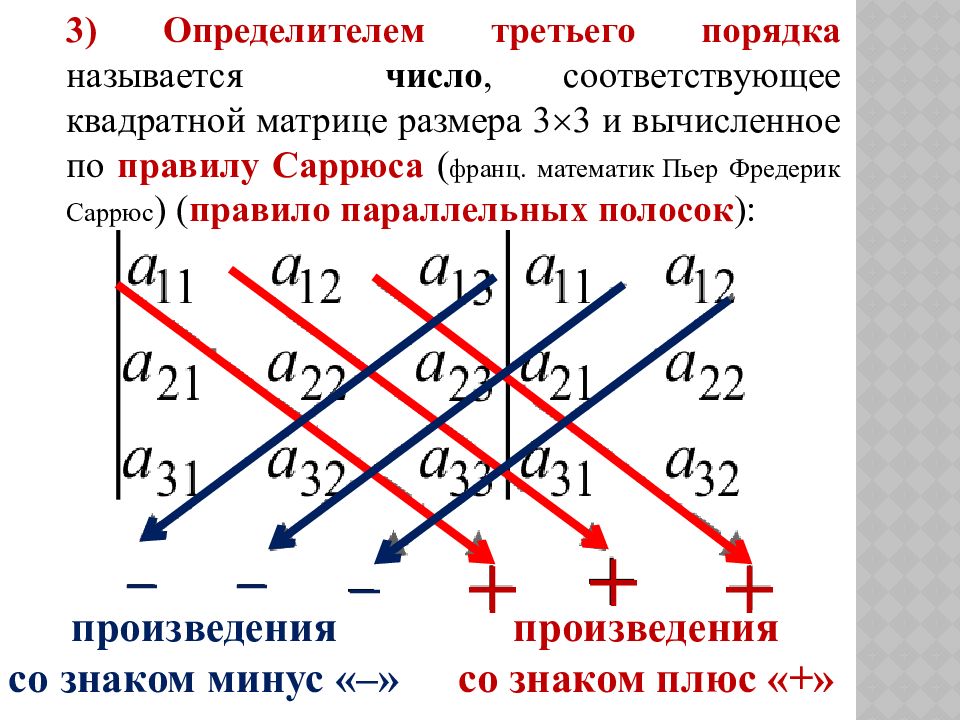
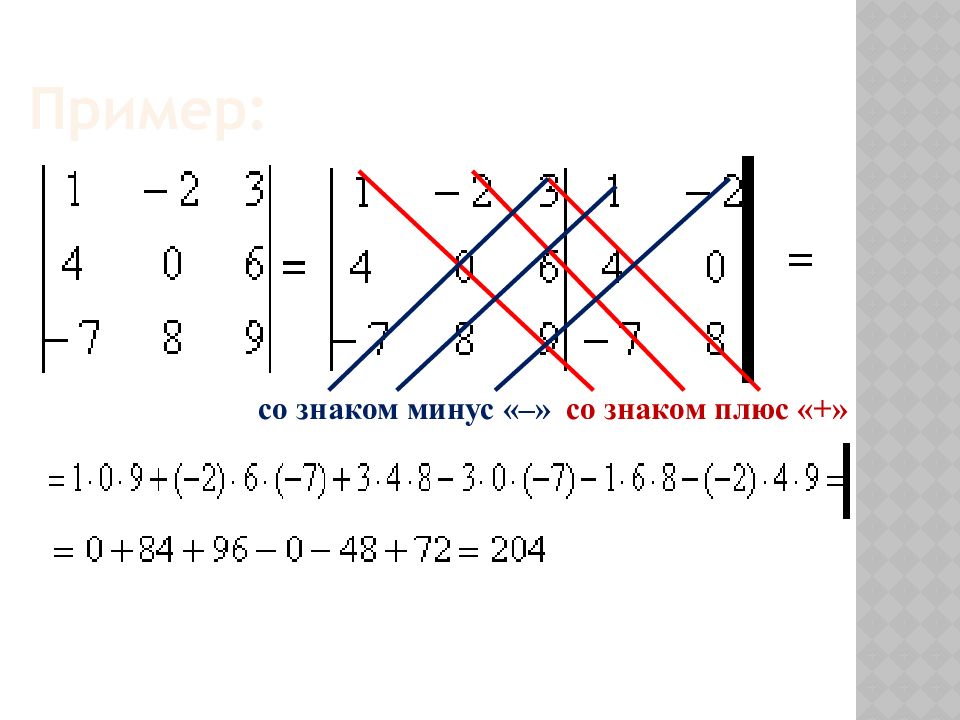
3) Определителем третьего порядка называется число, соответствующее квадратной матрице размера 33 и вычисленное по правилу Саррюса ( франц. математик Пьер Фредерик Саррюс ) ( правило параллельных полосок ): произведения со знаком минус «–» произведения со знаком плюс «+» + + + – – –
Пример: со знаком минус «–» со знаком плюс «+»
Можно свернуть форму вычисления по правилу Саррюса и получить правило треугольников Пример: произведения со знаком минус «–» произведения со знаком плюс «+»
Определение. Определитель, у которого все элементы, находящиеся над (под) главной (боковой) диагональю, равны нулю, называются определителем треугольного вида. Утверждение 1. Приведение любого определителя к треугольному виду всегда возможно. Теорема Гаусса. Определитель треугольного вида равен: по главной диагонали - произведению элементов его главной диагонали. по боковой диагонали - произведению элементов его боковой диагонали со знаком "-" Приведение определителя к треугольному виду:
4) Определителем n- го порядка называется число, соответствующее квадратной матрице размера n n и вычисленное по теореме Лапласа Определитель квадратной матрицы n- го порядка равен сумме попарных произведений элементов любой строки ( столбца ) на их алгебраические дополнения : Разложение по элементам i -й строки: Разложение по элементам j -го столбца:
В квадратной матрице n -го порядка рассмотрим элемент a ij. Вычеркнем i -ю строку и j -ый столбец, на пересечении которых стоит элемент a ij. В результате получается матрица ( n-1 )- го порядка. Алгебраические дополнения и миноры:
Минором М ij к элементу a ij матрицы n -го порядка называется определитель матрицы ( n- 1) -го порядка, полученной из исходной матрицы вычеркиванием i - й строки и j -го столбца. Алгебраическим дополнением А ij к элементу a ij матрицы n -го порядка называется его минор, взятый со знаком «+», если сумма i + j четная, и со знаком «-», если сумма нечетная.
где элемент a ij : 1) a 12 = 1; 2) a 31 = -1
Вычислить определитель разложением по элементам 1-ой строки (т.е. а 1 j ) Пример: Решение: 1-ая строка вычёркиваем для всех А ij вычёркиваем по очереди 1-й 2-й 3-й
