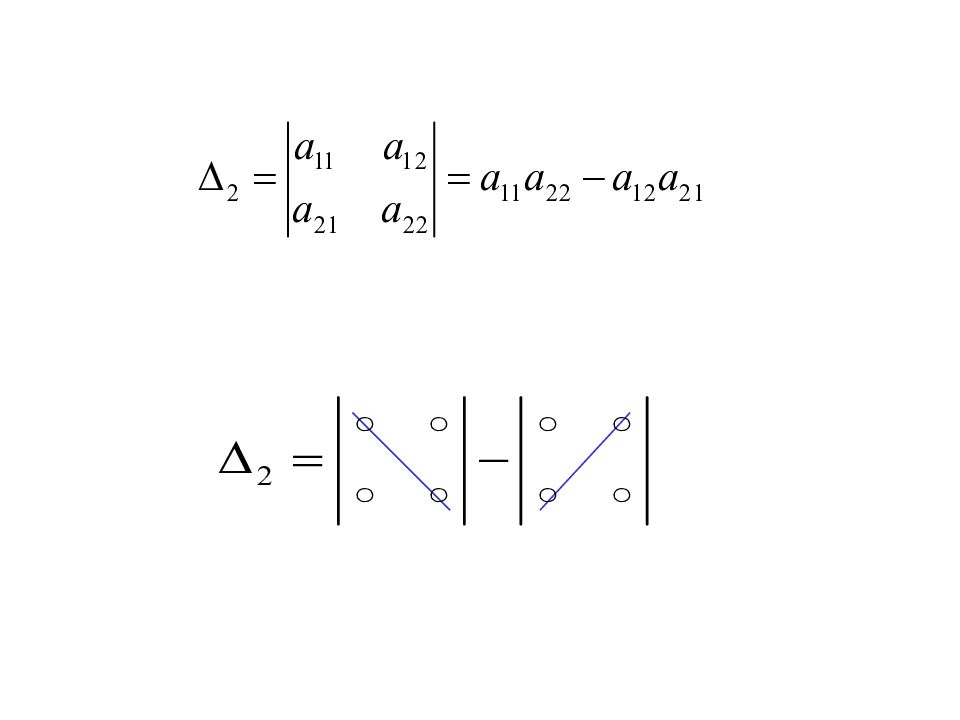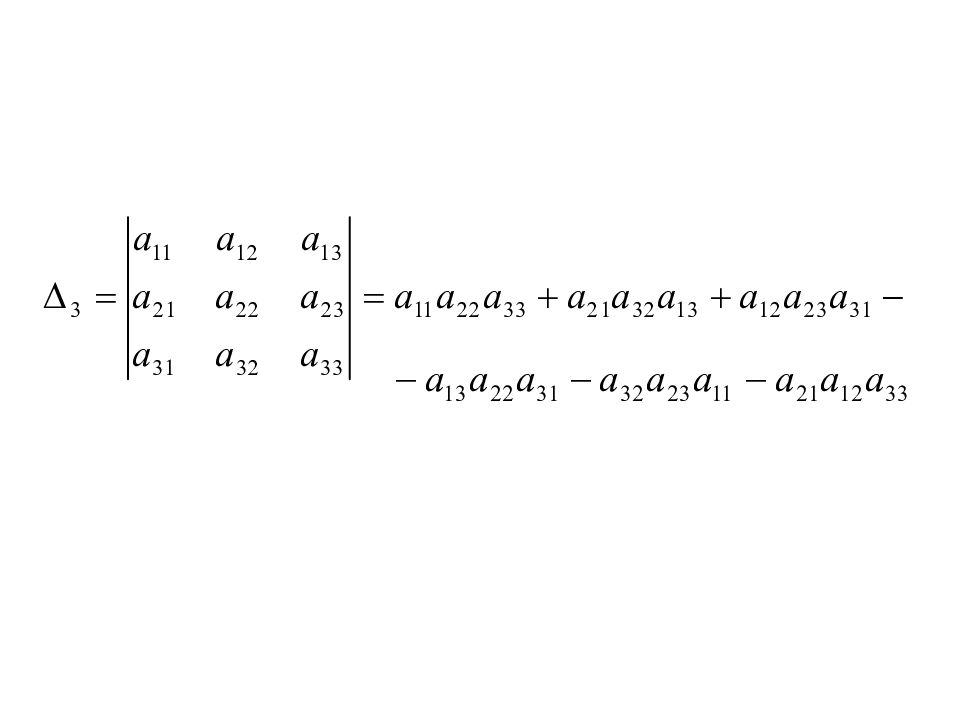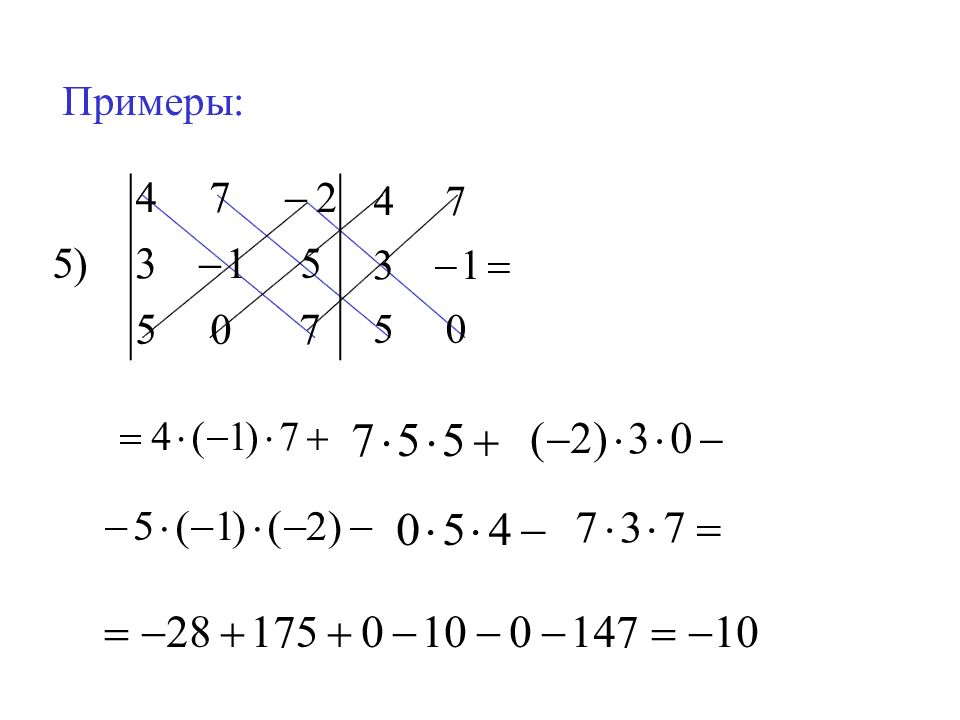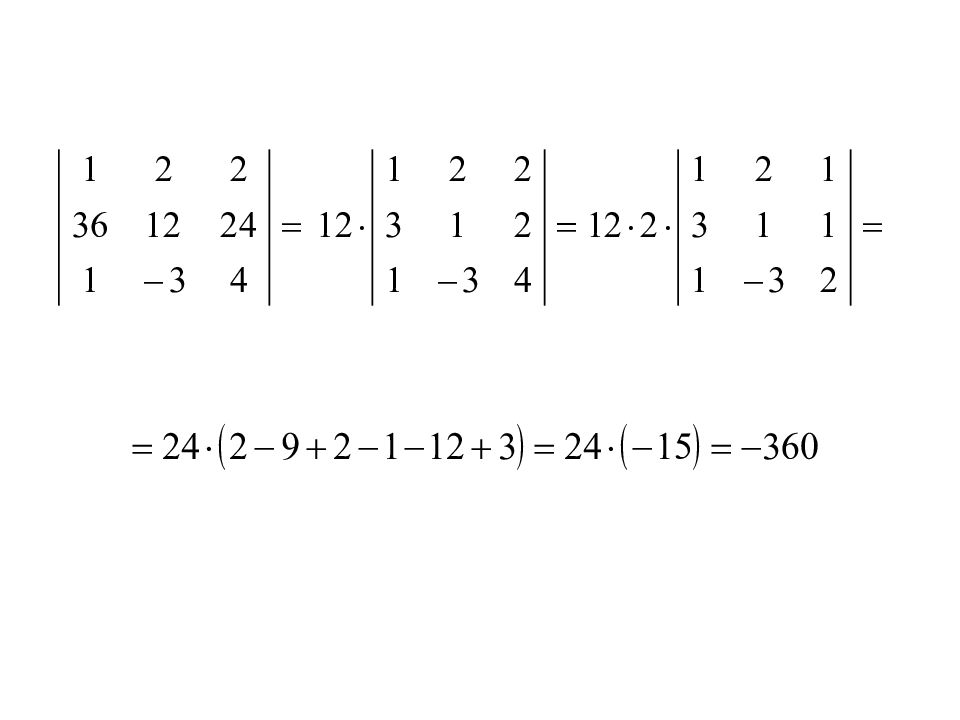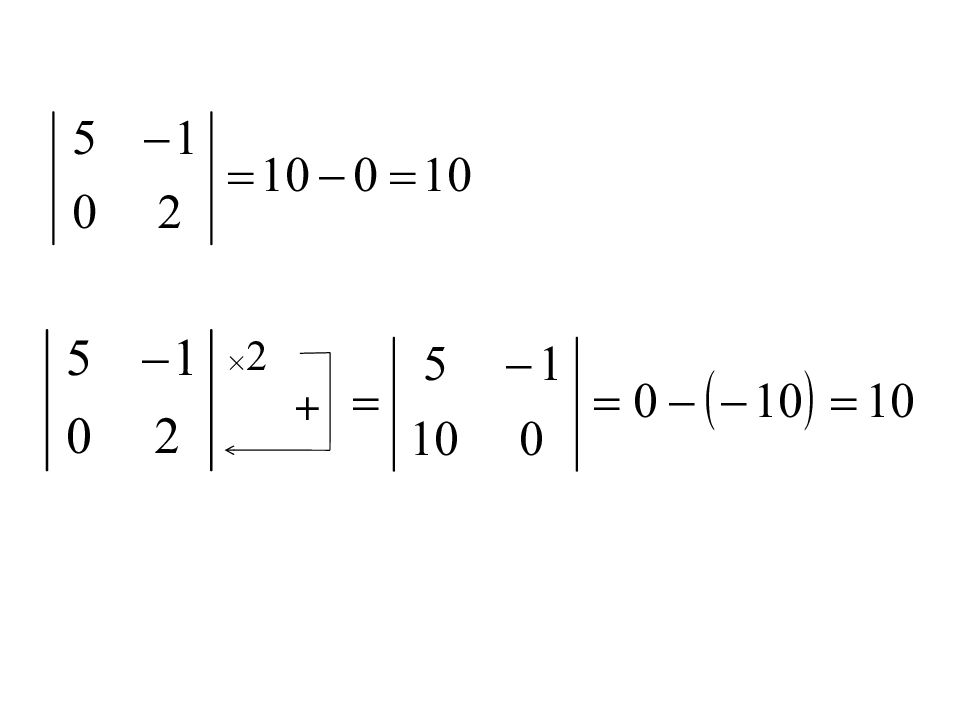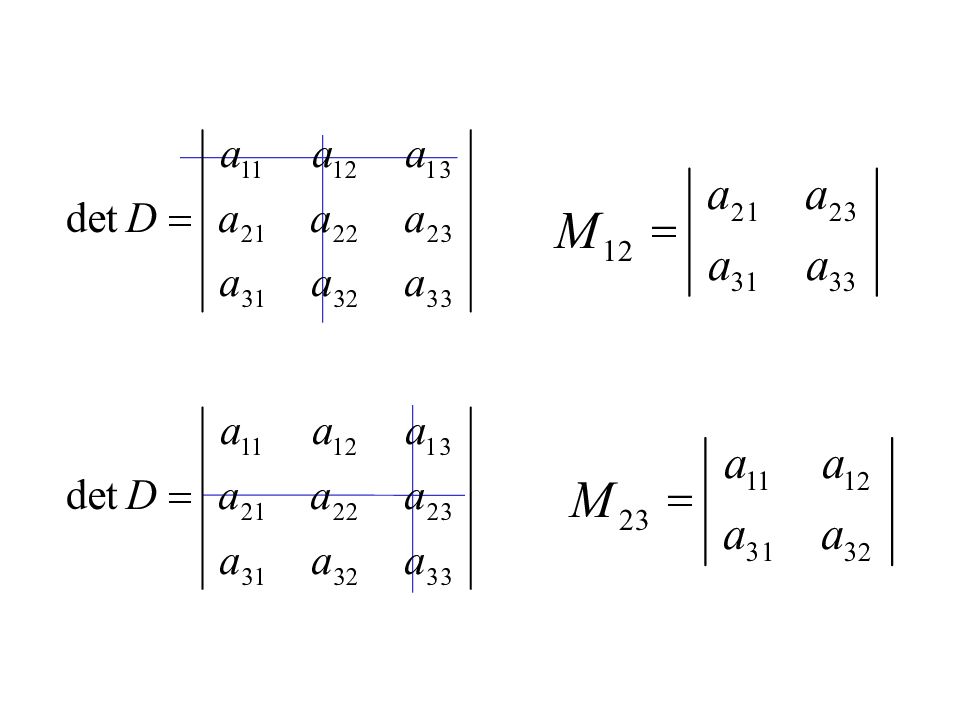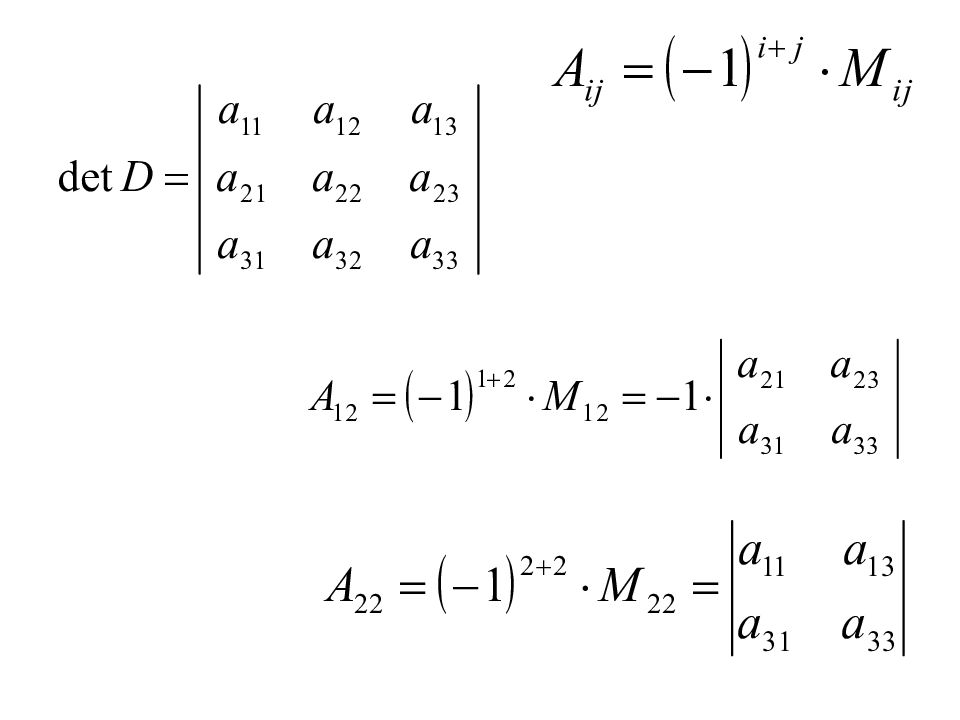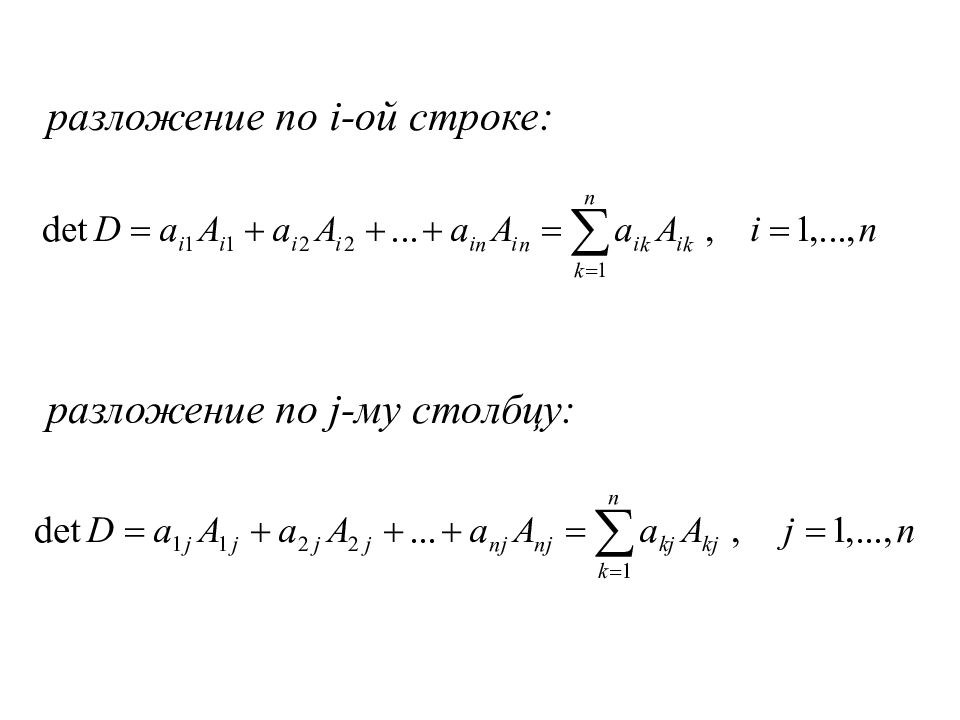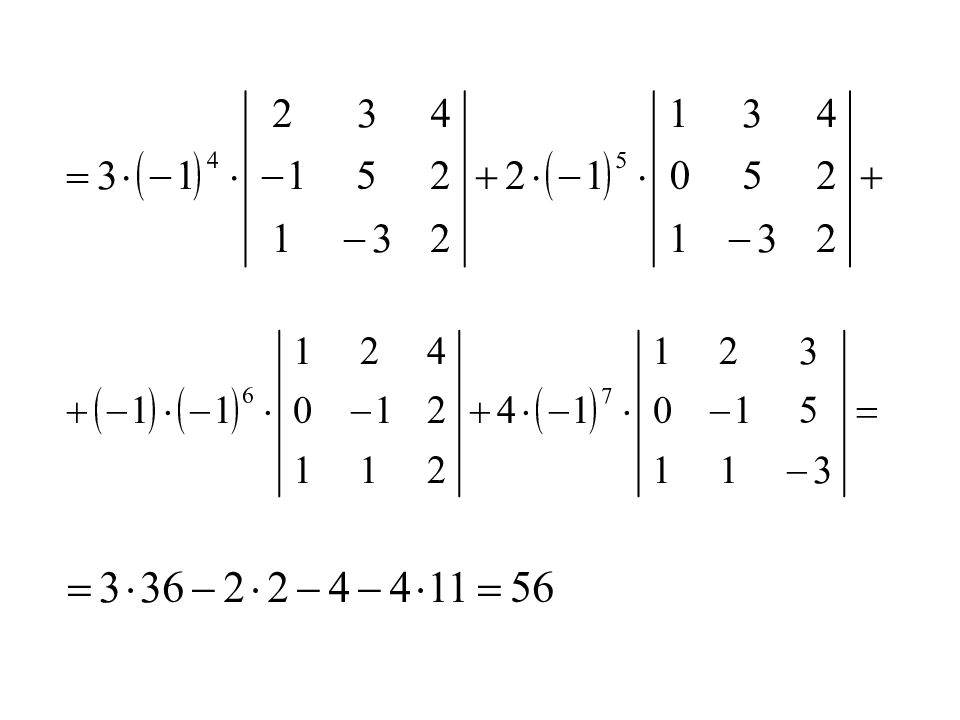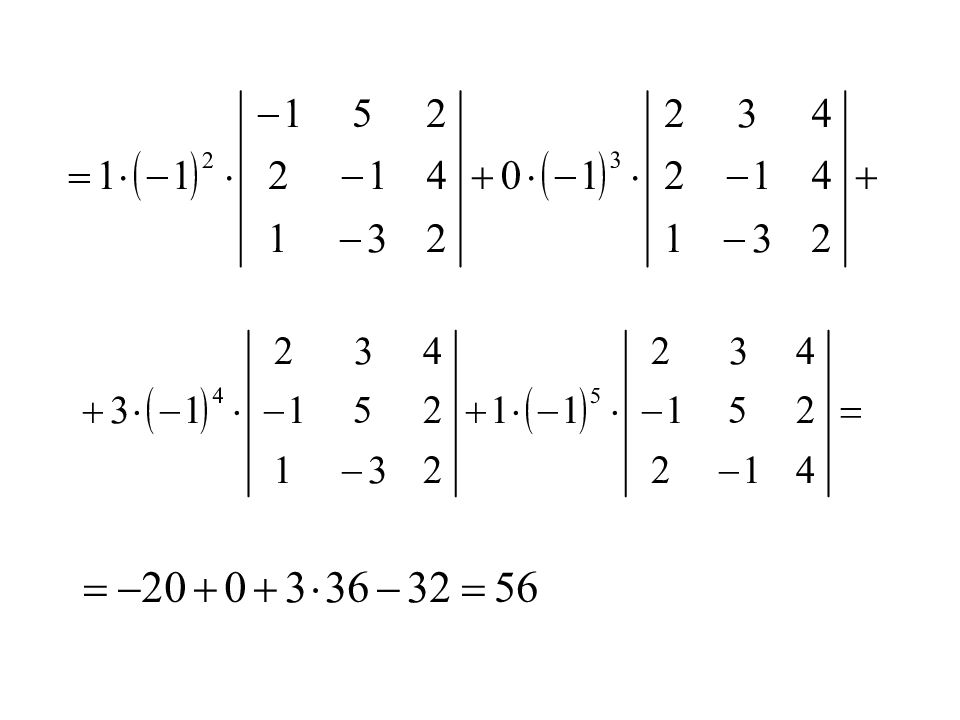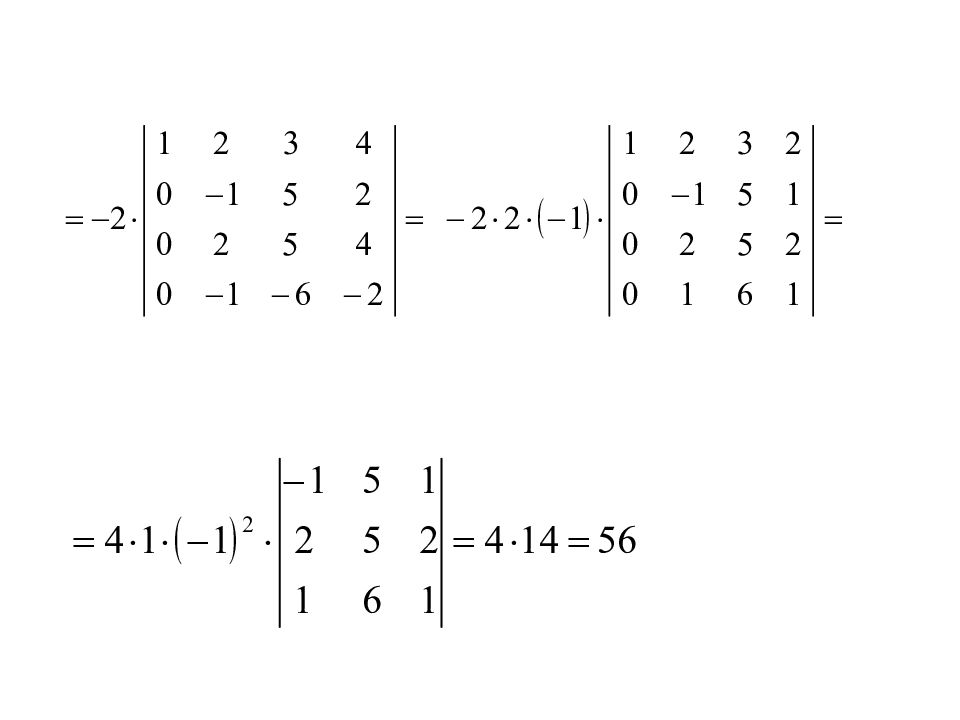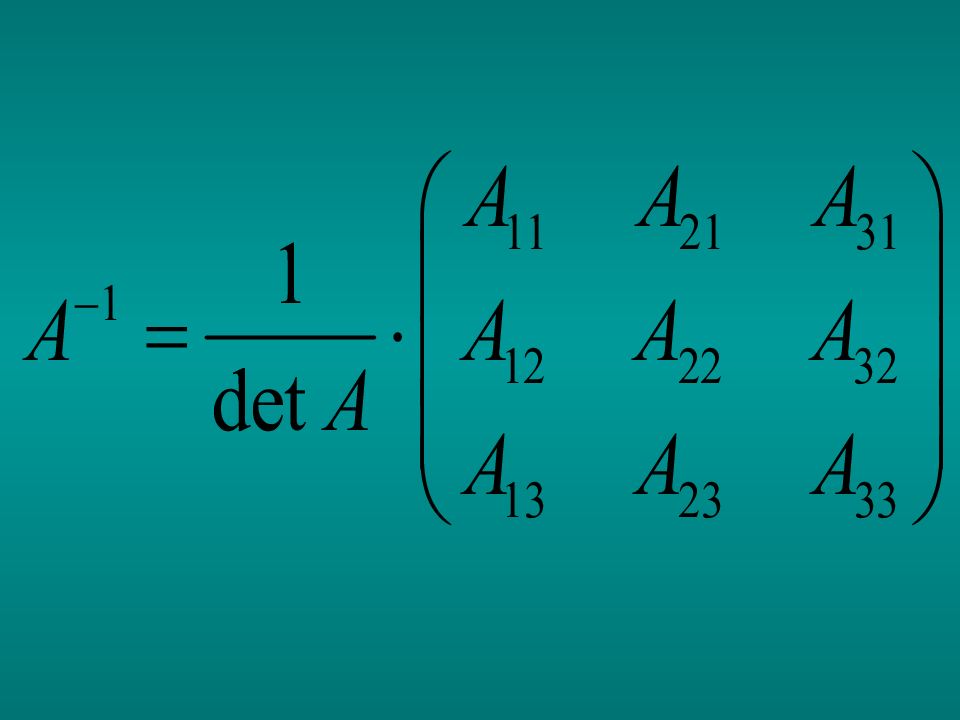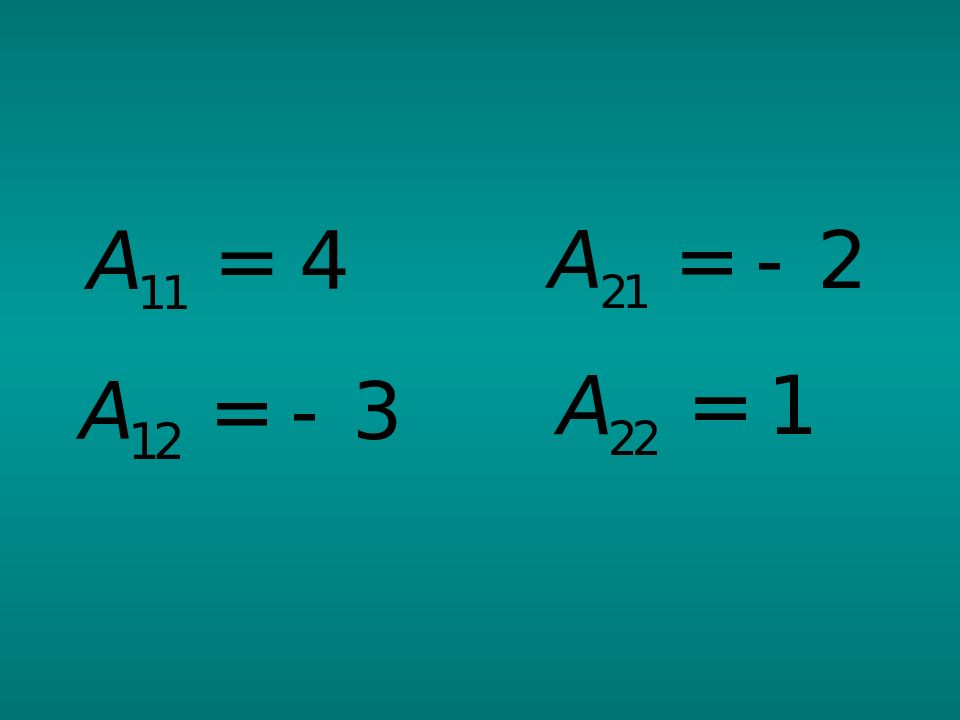Первый слайд презентации: Матрицы и определители
Преподаватель: Мокляк Денис Сергеевич
Слайд 2
МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ Матрицей размера m x n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Слайд 3
Обозначение: где i=1,2…m j=1,2…n - матрица размерности m x n - элемент матрицы i –ой строки и j -го столбца,
Слайд 5
Две матрицы называются равными, если у них одинаковая размерность и совпадают строки и столбцы. Если число строк матрицы равно числу ее столбцов, то такая матрица называется квадратной.
Слайд 7
Элементы матрицы a ij, у которых номер столбца совпадает с номером строки, называются диагональными. Если в квадратной матрице все диагональные элементы равны 1, а остальные элементы равны 0, то она называется единичной.
Слайд 9
Матрица любого размера называется нулевой, если все ее элементы равны 0. нулевая матрица
Слайд 10
Матрица, состоящая из одной строки, называется матрицей-строкой или вектором-строкой. матрица-строка
Слайд 11
Матрица, состоящая из одного столбца, называется матрицей-столбцом или вектором-столбцом. матрица-столбец
Слайд 12
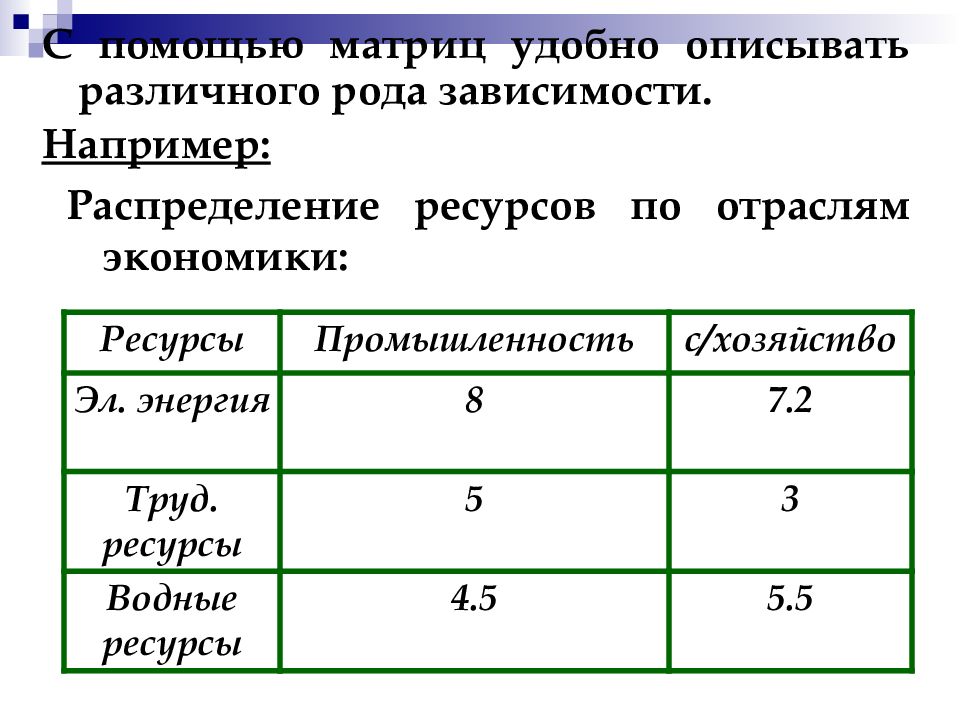
Распределение ресурсов по отраслям экономики: Ресурсы Промышленность с / хозяйство Эл. энергия 8 7.2 Труд. ресурсы 5 3 Водные ресурсы 4.5 5.5 С помощью матриц удобно описывать различного рода зависимости. Например:
Слайд 13
Эту зависимость можно представить в виде матрицы: Где элемент a ij показывает сколько i – го ресурса потребляет j – отрасль. Например, a 32 показывает, сколько воды потребляет сельское хозяйство.
Слайд 14
ДЕЙСТВИЯ НАД МАТРИЦАМИ 1. Умножение матрицы на число Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число. Полученные произведения образуют итоговую матрицу.
Слайд 15
Пусть дана матрица Умножаем ее на число λ : Где каждый элемент матрицы В : Где:
Слайд 17
2. Сложение матриц Складываются матрицы одинаковой размерности. Получается матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов исходных матриц.
Слайд 18
Пусть даны матрицы Складываем их: Где каждый элемент матрицы С : Аналогично проводится вычитание матриц.
Слайд 21
3. Умножение матриц Умножение матриц возможно, если число столбцов первой матрицы равно числу строк второй. Тогда каждый элемент полученной матрицы равен сумме произведений элементов i – ой строки первой матрицы на соответствующие элементы j -го столбца второй.
Слайд 24
Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует: Решение:
Слайд 25
Теперь перемножим матрицы в обратном порядке: Умножение матриц в общем случае некоммутативно:
Слайд 26
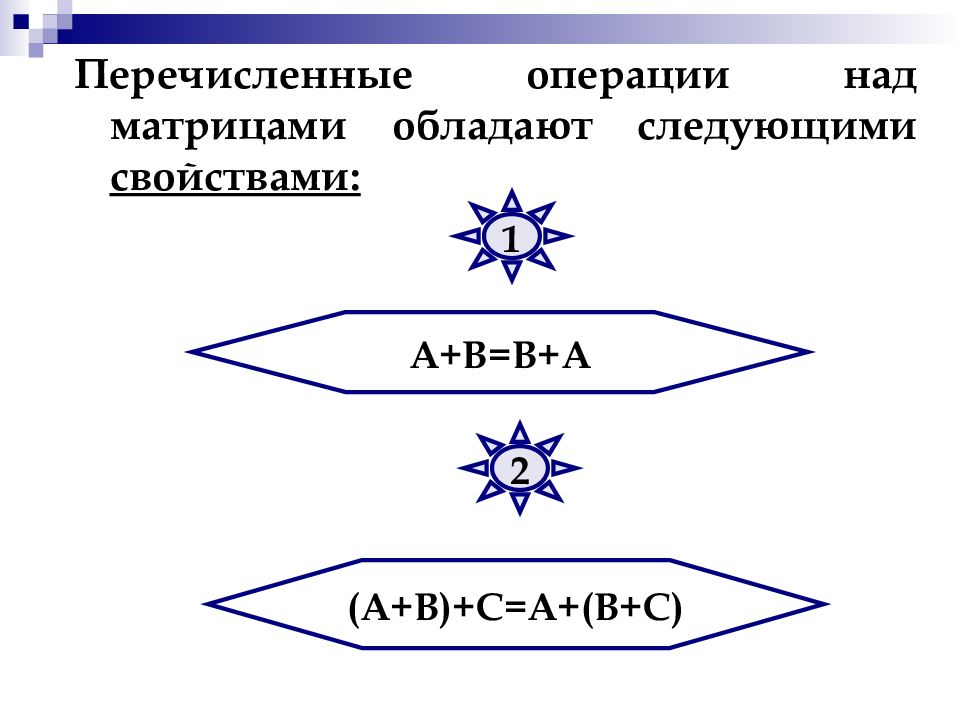
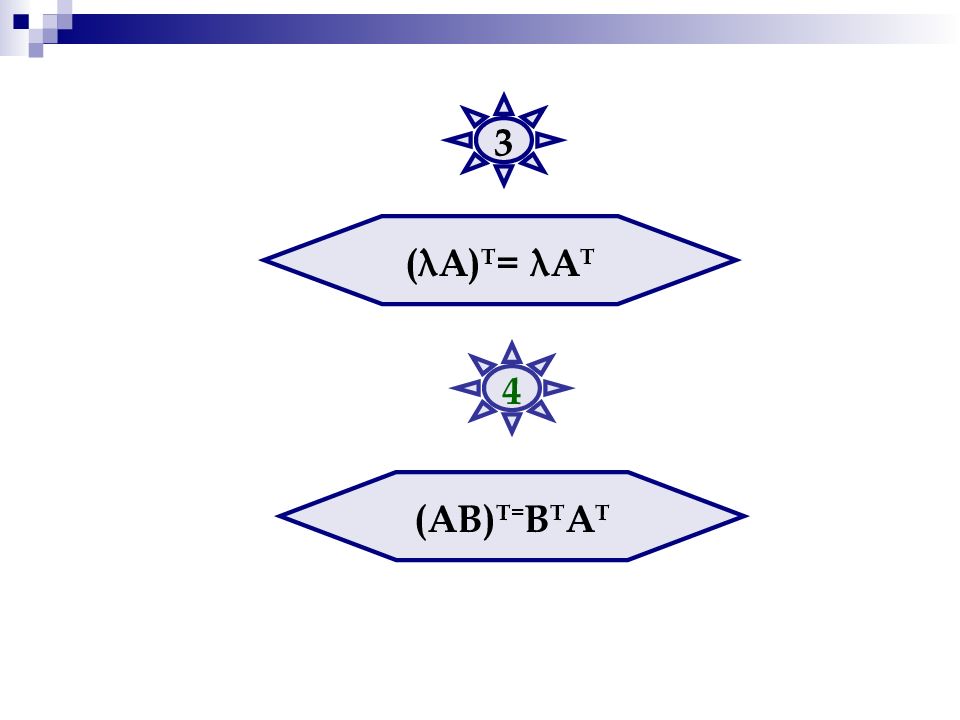
Перечисленные операции над матрицами обладают следующими свойствами: А+В=В+А (А+В)+С=А+(В+С) 1 2
Слайд 28
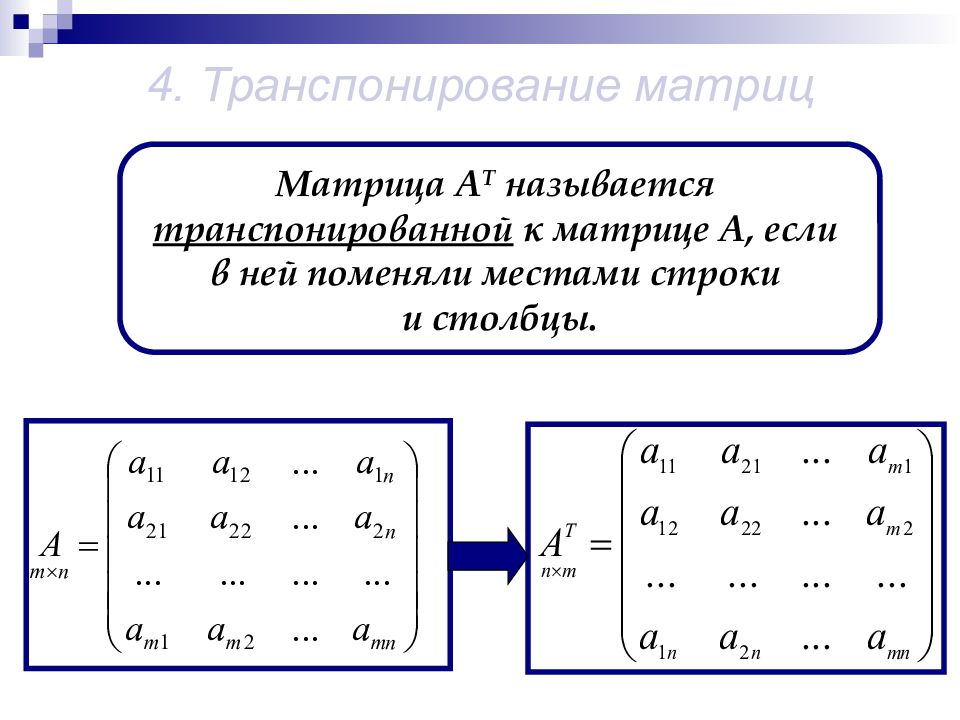
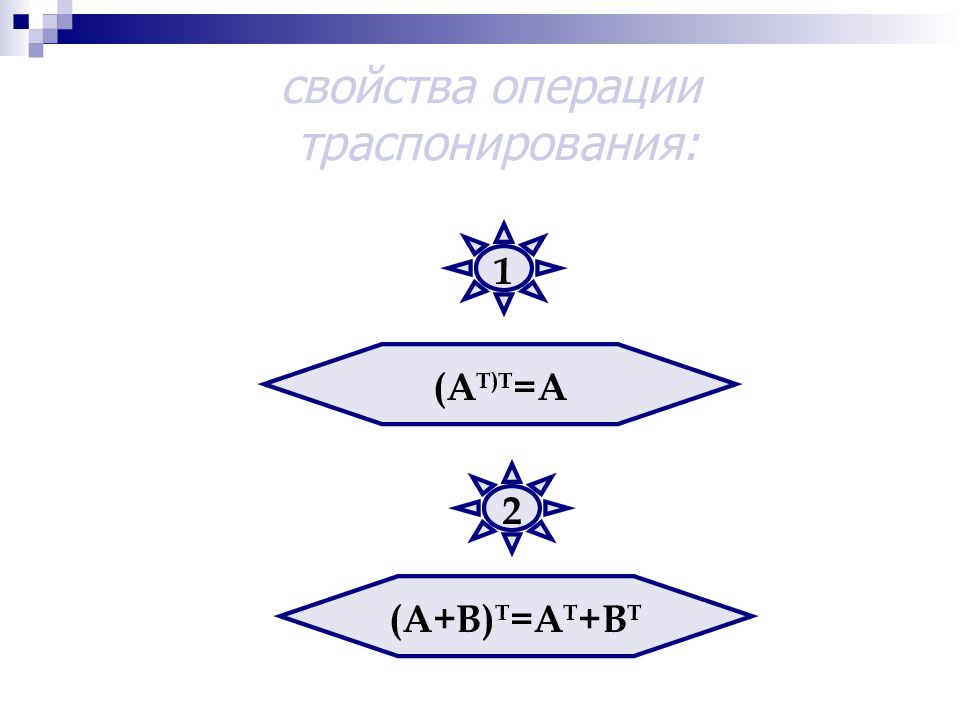
4. Транспонирование матриц Матрица А Т называется транспонированной к матрице А, если в ней поменяли местами строки и столбцы.
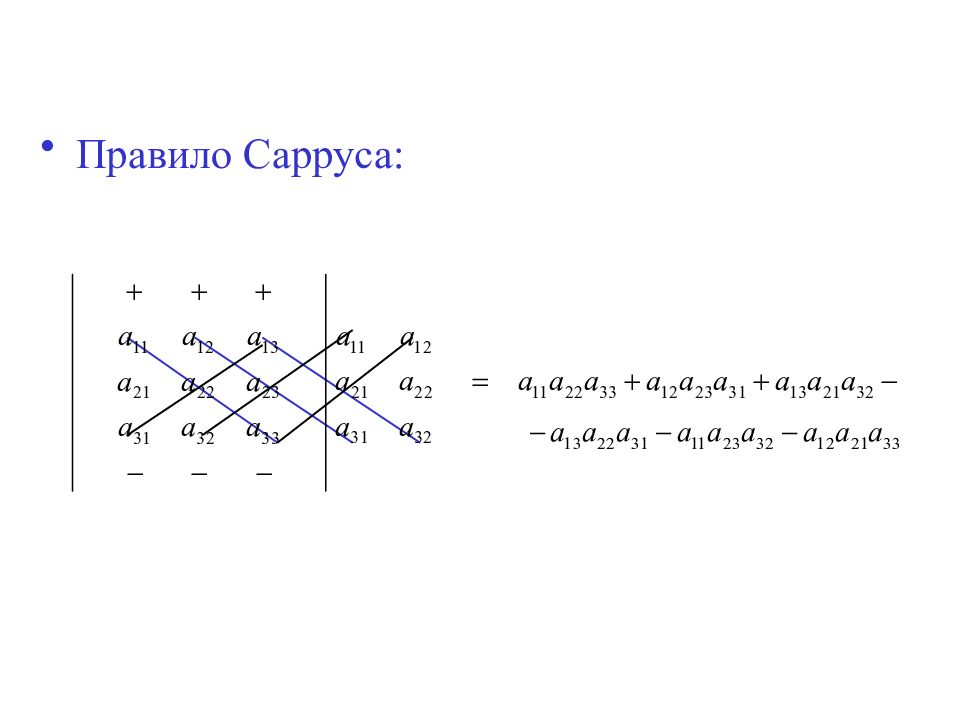
Слайд 33: Определители. Свойства определителей
Слайд 42: Свойства определителей
1. Определитель не изменится, если его транспонировать:
Слайд 43
2. При перестановке двух строк или столбцов определитель изменит свой знак на противоположный.
Слайд 44
3. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.
Слайд 47
5. Если все элементы двух строк (или столбцов) определителя пропорциональны, то определитель равен нулю.
Слайд 48
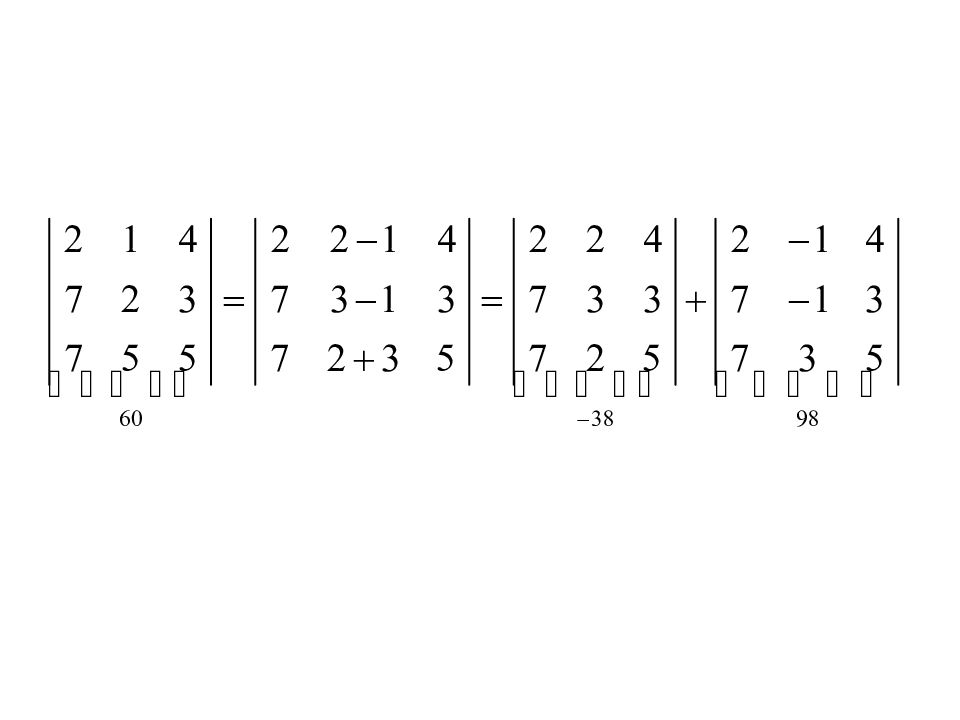
6. Если каждый элемент какого-либо ряда определителя представляет собой сумму двух слагаемых, то такой определитель равен сумме двух определителей, в первом из которых соответствующий ряд состоит из первых слагаемых, а во втором- из вторых слагаемых.
Слайд 51
7. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменится. × к
Слайд 53
8. Треугольный определитель равен произведению элементов главной диагонали.
× (-2) × (-5) = +
Слайд 55: Разложение определителя по элементам строки или столбца
Минором M ij элемента a ij det D называется такой новый определитель, который получается из данного вычеркиванием i -ой строки и j -го столбца содержащих данный элемент.
Слайд 58
Алгебраическим дополнением A ij элемента a ij det D называется минор M ij этого элемента, взятый со знаком т.е.
Слайд 60
Сумма произведений элементов любой строки (или столбца) определителя на их алгебраические дополнения равна этому определителю.
Слайд 62: Разложить данный определитель по элементам: 1) 3-ей строки; 2) 1-го столбца
Слайд 67: Основные методы вычисления определителя
1. разложение определителя по элементам строки или столбца; 2. метод эффективного понижения порядка; 3. приведение определителя к треугольному виду.
Слайд 68
Метод эффективного понижения порядка: Вычисление определителя n -го порядка сводится к вычислению одного определителя ( n-1 )-го порядка, сделав в каком-либо ряду все элементы, кроме одного, равными нулю.
Слайд 71: Вычислить определитель приведением его к треугольному виду
× (-3) × (-1)
Слайд 75: Определение. Матрица называется о б р а т н о й к квадратной матрице, если
Обратная матрица обозначается символом Примечание. Операция деления для матриц не определена. Вместо этого предусмотрена операция обращения (нахождения обратной) матрицы.
Слайд 76: Определение. Матрица, составленная из алгебраических дополнений для элементов исходной матрицы, называется с о ю з н о й м а т р и ц е й
Слайд 79: Алгоритм нахождения
1. Находим определитель матрицы А. Он должен быть отличен от нуля. 2. Находим алгебраические дополнения для каждого элемента матрицы А. 3. Составляем союзную матрицу и транспонируем ее. 4. Подставляем результаты п.1 и п.4 в формулу обратной матрицы.
Слайд 81
Р е ш е н и е. Действуем по алгоритму: 1. Находим определитель матрицы: Определитель отличен от нуля, следовательно, обратная матрица существует.
Слайд 86: 5. Проверка
Воспользуемся определением обратной матрицы и найдем произведение
Слайд 93: Элементарные преобразования матриц
перестановка строк (столбцов) местами; исключение из матрицы строк (столбцов), состоящих из нулей; умножение всех элементов какой-либо строки (столбца) матрицы на любое число, отличное от нуля; прибавление к одной строке (столбцу) другой, предварительно умноженной на любое число, отличное от нуля.
Последний слайд презентации: Матрицы и определители
Определение. Э к в и в а л е н т н ы м и называются матрицы, полученные одна из другой путем элементарных преобразований. Важным понятием для матриц является понятие РАНГА. Существует несколько определений этого понятия. Мы остановимся на одном из них, основанном на элементарных преобразованиях. Определение. Р а н г о м м а т р и ц ы называется число ненулевых строк в матрице, после приведения ее к ступенчатому виду (путем элементарных преобразований). Обозначение. Ранг матрицы будем обозначать или. Теорема. Ранг матрицы не меняется при элементарных преобразованиях.