7.12.
Устная работа Закончите определение: Пару значений (х;у), которая одно – временно является решением и первого и второго уравнений, называют … решением системы уравнений.
Устная работа Какая из следующих пар чисел является решением системы уравнений: а). (0;1) б). (-1;-1) в). (1;0) г). (1;1) а). (0;1) – является решением системы уравнений т.к. верно верно б). (-1;-1) – не является решением системы уравнений т.к. неверно верно в). (1;0) – не является решением системы уравнений т.к. верно неверно г). (1;1) – не является решением системы уравнений т.к. неверно неверно
Закончите определение: Устная работа Решить систему уравнений – это значит … найти все её решения или установить, что решений нет.
Устная работа Алгоритм графического метода при решении системы двух уравнений с двумя переменными х, у. Построить график первого уравнения. Построить график второго уравнения. Найти точки пересечения графиков. Координаты каждой точки пересечения являются решениями системы уравнений.
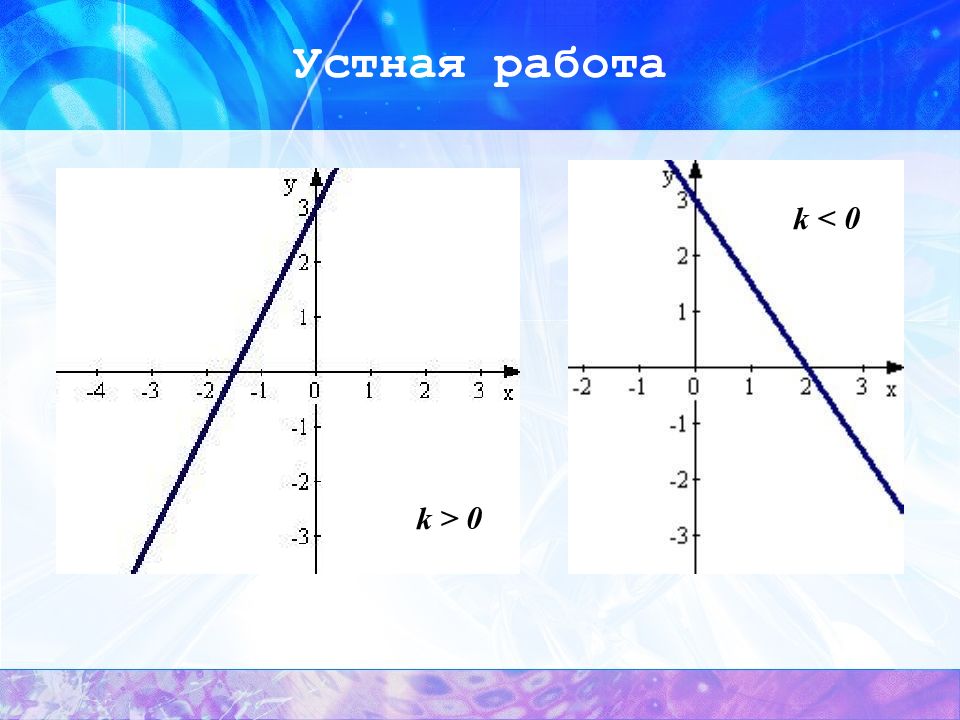
Устная работа Какая функция называется линейной функцией? Функция вида, где - числа, а - переменные, называется линейной функцией. Что является графиком линейной функции? Графиком линейной функции является прямая.
k > 0 k < 0 Устная работа
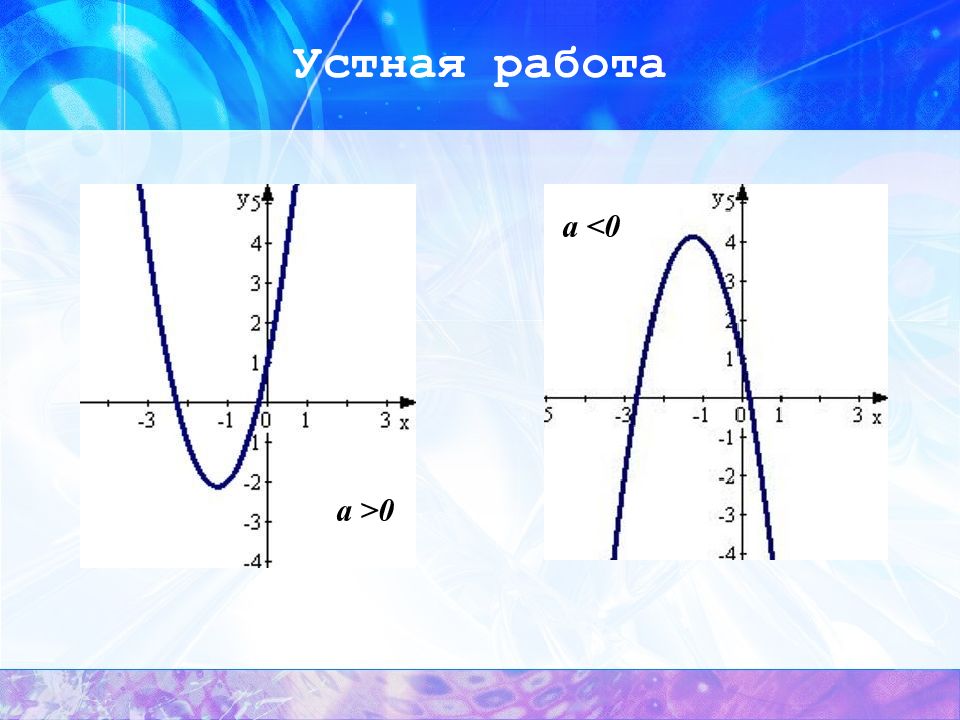
Устная работа Какая функция называется квадратичной функцией? Что является графиком квадратичной функции? Графиком квадратичной функции является парабола. Функция вида, где - числа, причём, а - переменные, называется квадратичной функцией.
a >0 a <0 Устная работа
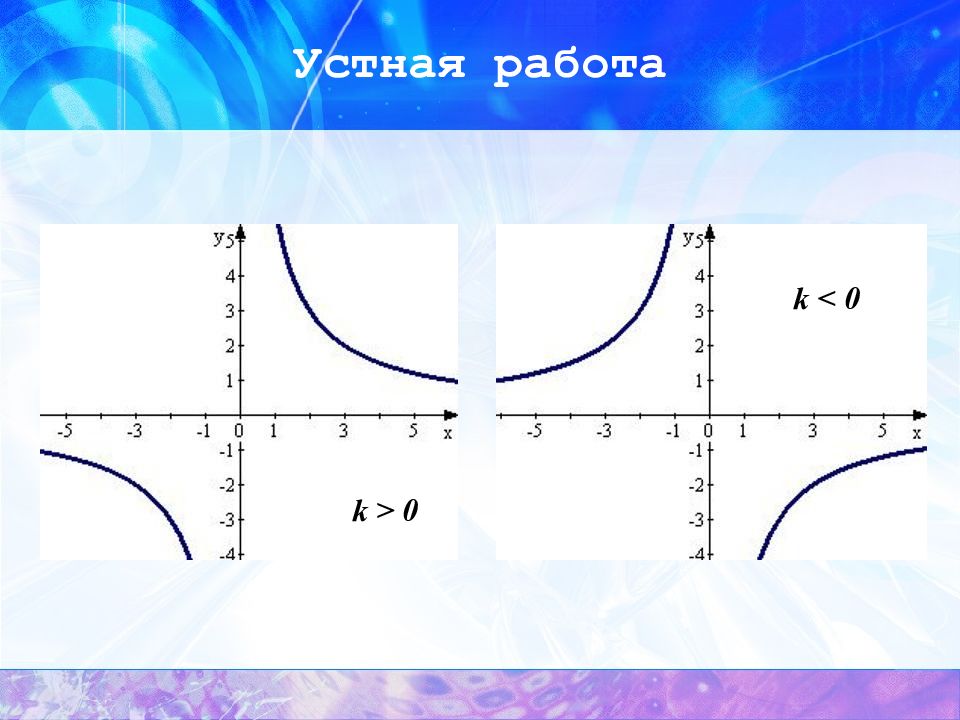
Устная работа Какая функция называется обратной пропорциональностью? Функция вида, где - число, а - переменные, называется функцией обратной пропорциональностью. Что является графиком обратной пропорциональности? Графиком обратной пропорциональности является гипербола.
k > 0 k < 0 Устная работа
Устная работа Графиком уравнения является окружность с центром в точке ( a;b) и радиусом R. Какая фигура является графиком уравнения ?
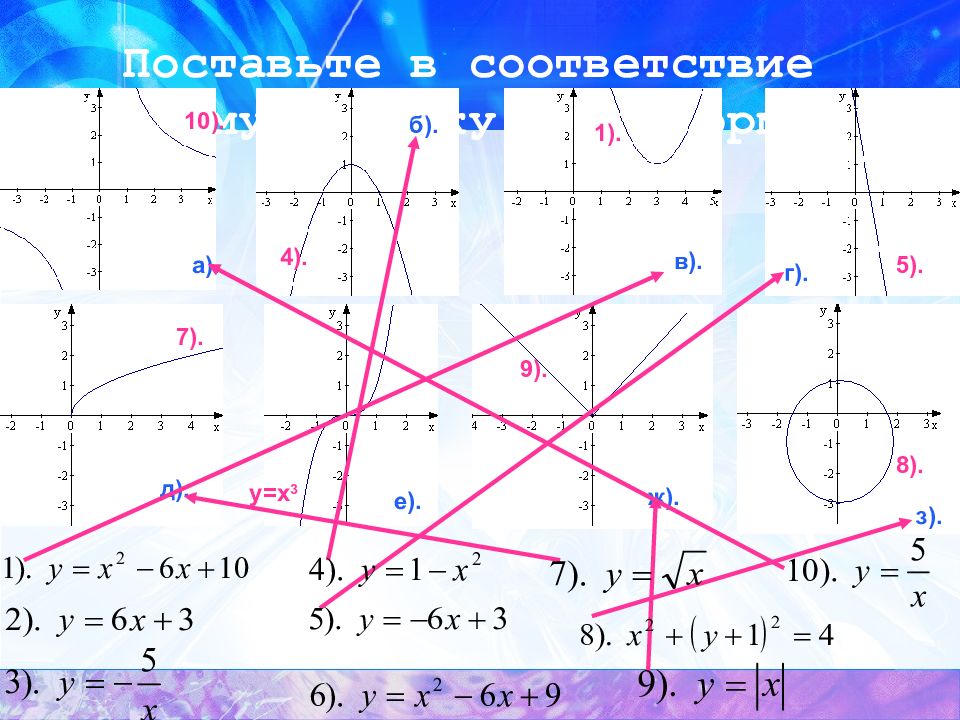
Поставьте в соответствие каждому графику свою формулу а). б). в). г). д). е). ж). з). 1). 4). 5). 7). 8). 9). 10). y=x 3
Методы решения систем уравнений 1). Графический метод 2). Метод подстановки 3). Метод алгебраического сложения 4). Метод введения новой переменной
1.Строим в одной системе координат графики функций. 2.Находим координаты точек пересечения графиков функций. 3. Записываем ответ.
Алгоритм метода подстановки при решении системы двух уравнений с двумя переменными х, у. 1). Выразить одну переменную через остальные компоненты одного из уравнений. 2). Подставить полученное выражение вместо выраженной переменной в другое уравнение системы. 3). Решить полученное уравнение от одной переменной. 4). Подставить поочерёдно каждый из найденных на третьем шаге корней уравнения в выражение, полученное на первом шаге. 5). Записать ответ в виде пар значений (х;у), которые были найдены соответственно на третьем и четвёртом шаге.
Решить систему уравнений методом подстановки или или Ответ: (-2;3); (-8;-3)
§ 13, № 450,452
449 (4) или 451(6) – на «3» 460 (2) - на «4» 462(3) – на «5»
На «4»: № 454(2,4),456(1,3) на «5» :№ 463 (2,4,6)
