Первый слайд презентации: Многогранники, вписанные в сферу
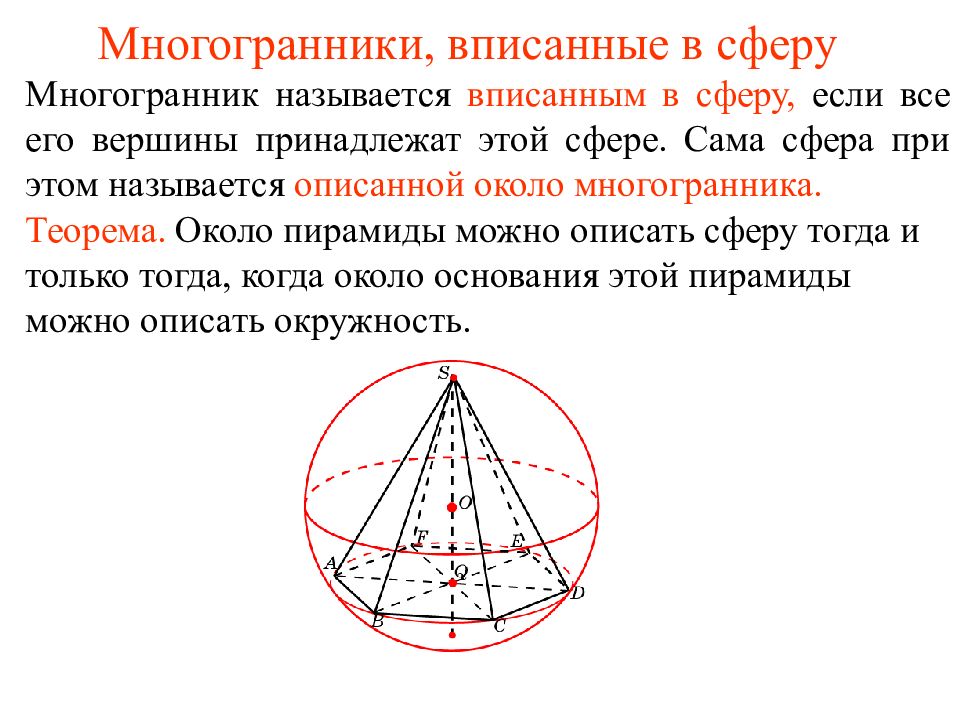
Многогранник называется вписанным в сферу, если все его вершины принадлежат этой сфере. Сама сфера при этом называется описанной около многогранника. Теорема. Около пирамиды можно описать сферу тогда и только тогда, когда около основания этой пирамиды можно описать окружность.
Слайд 2: Многогранники, вписанные в сферу
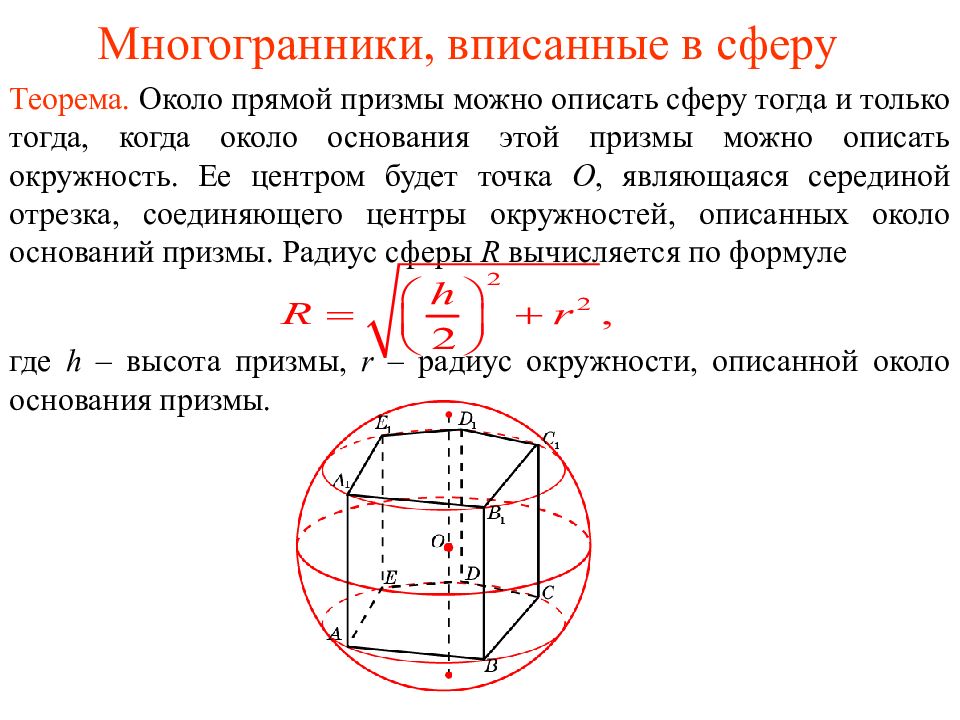
Теорема. Около прямой призмы можно описать сферу тогда и только тогда, когда около основания этой призмы можно описать окружность. Ее центром будет точка O, являющаяся серединой отрезка, соединяющего центры окружностей, описанных около оснований призмы. Радиус сферы R вычисляется по формуле где h – высота призмы, r – радиус окружности, описанной около основания призмы.
Слайд 3: Упражнение 1
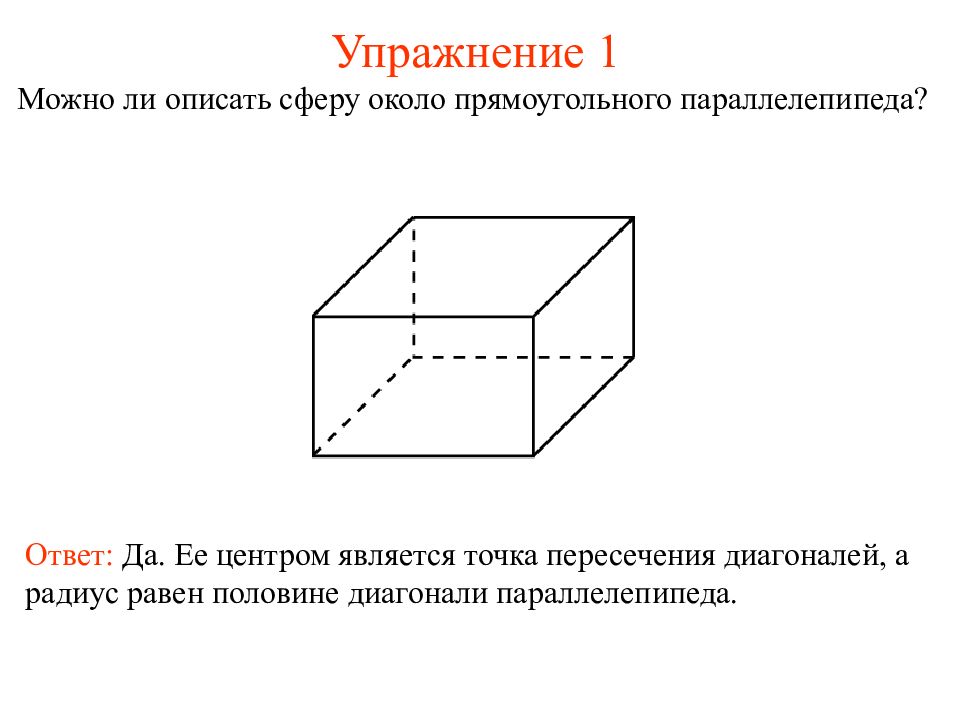
Можно ли описать сферу около прямоугольного параллелепипеда? Ответ: Да. Ее центром является точка пересечения диагоналей, а радиус равен половине диагонали параллелепипеда.
Слайд 4: Упражнение 2
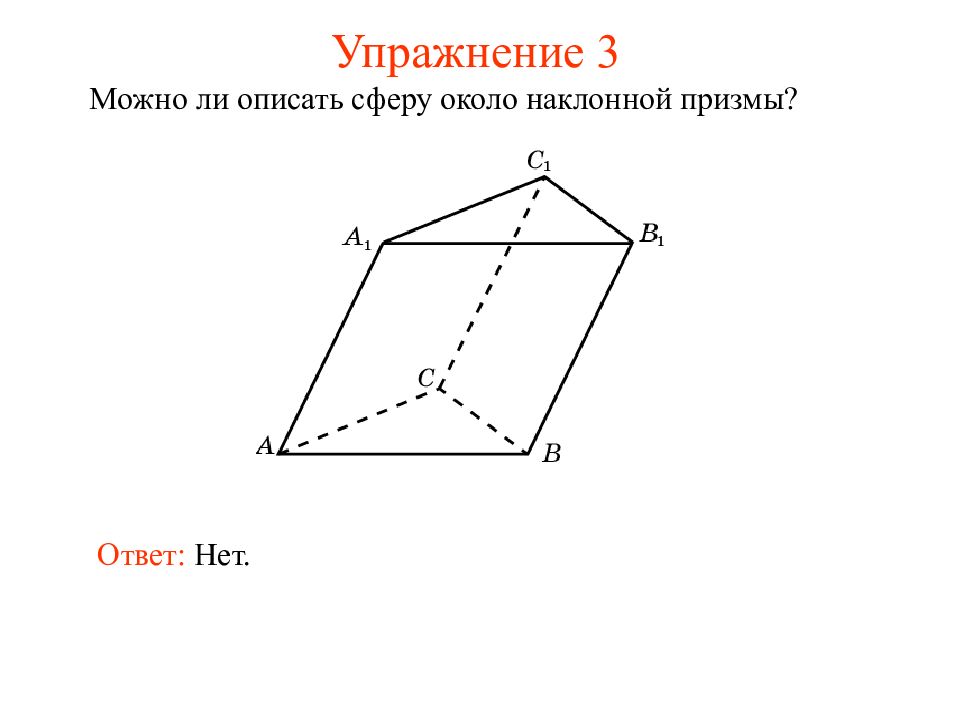
Можно ли описать сферу около наклонного параллелепипеда, все грани которого ромбы? Ответ: Нет.
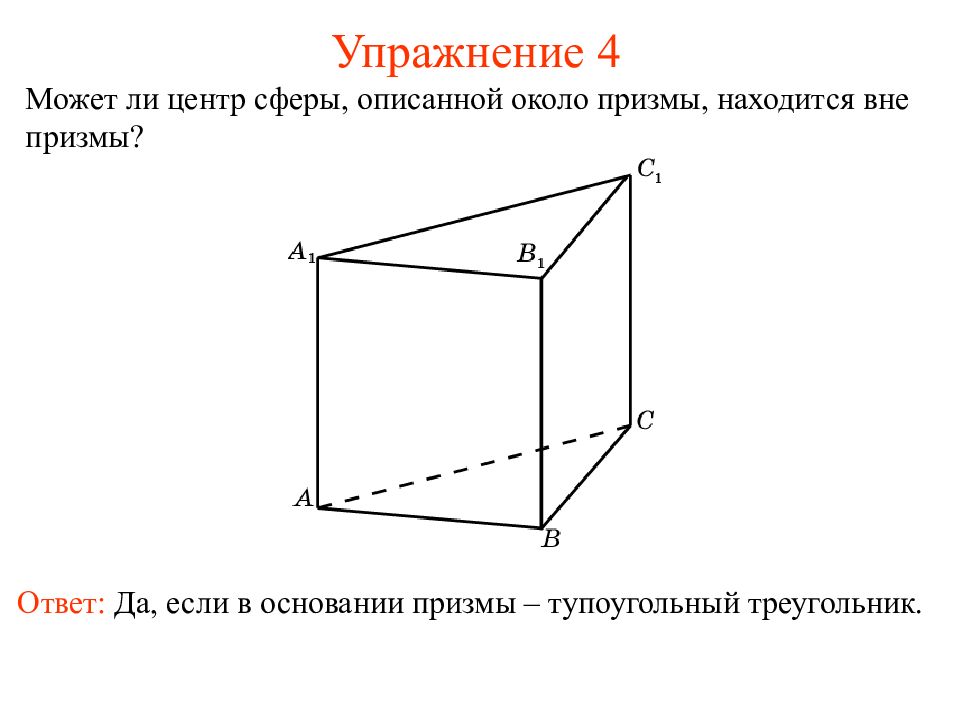
Слайд 6: Упражнение 4
Может ли центр сферы, описанной около призмы, находится вне призмы? Ответ: Да, если в основании призмы – тупоугольный треугольник.
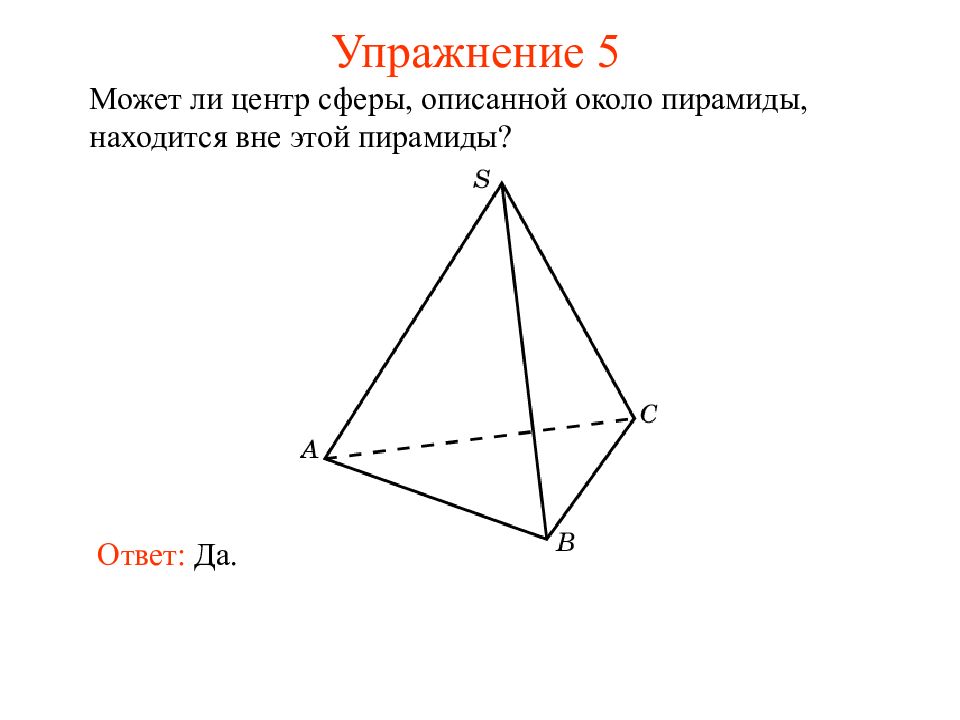
Слайд 7: Упражнение 5
Может ли центр сферы, описанной около пирамиды, находится вне этой пирамиды? Ответ: Да.
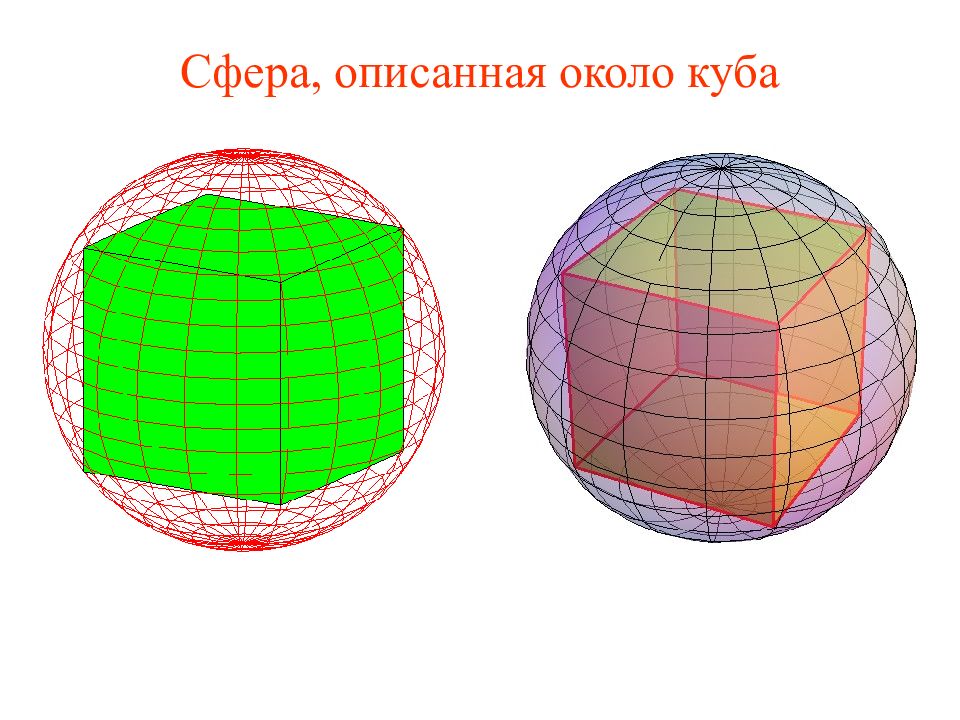
Слайд 8: Сфера, описанная около куба
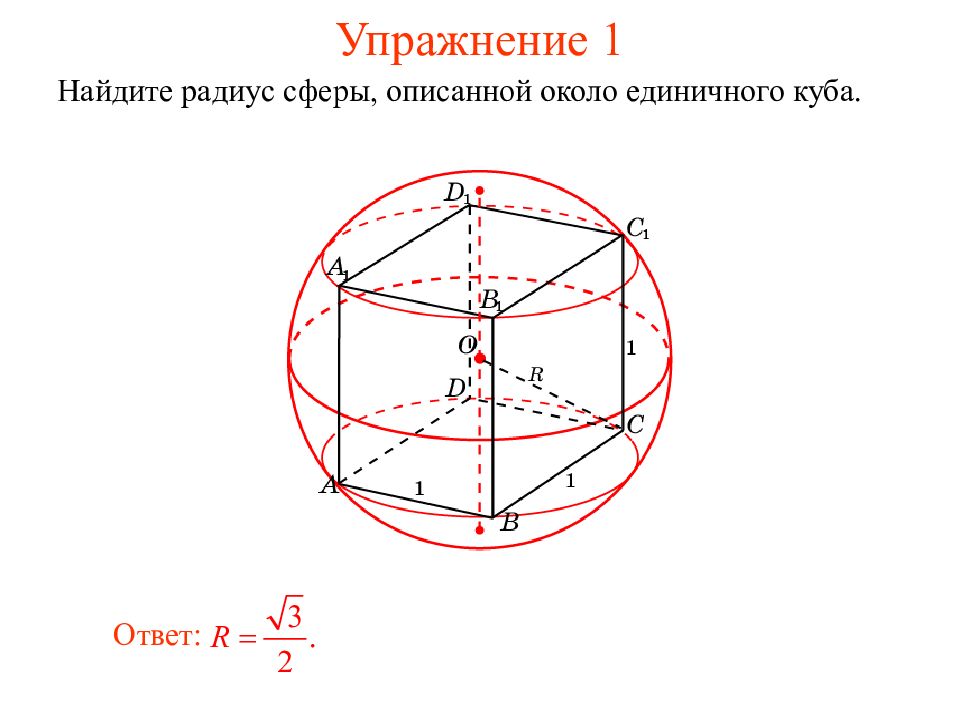
Слайд 9: Упражнение 1
Найдите радиус сферы, описанной около единичного куба. Ответ:
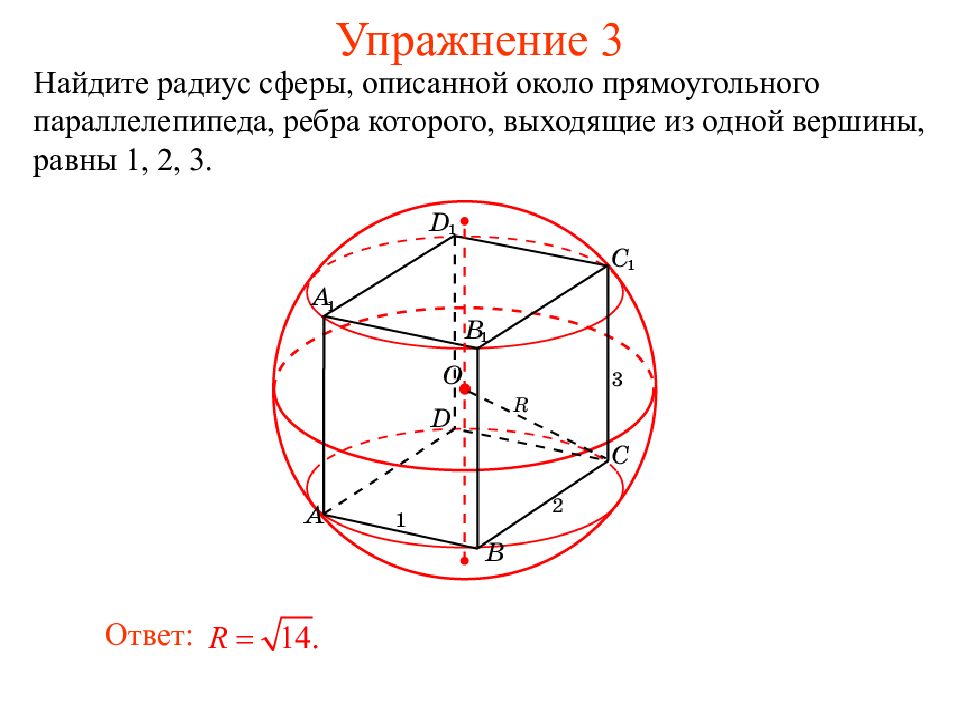
Слайд 11: Упражнение 3
Найдите радиус сферы, описанной около прямоугольного параллелепипеда, ребра которого, выходящие из одной вершины, равны 1, 2, 3. Ответ:
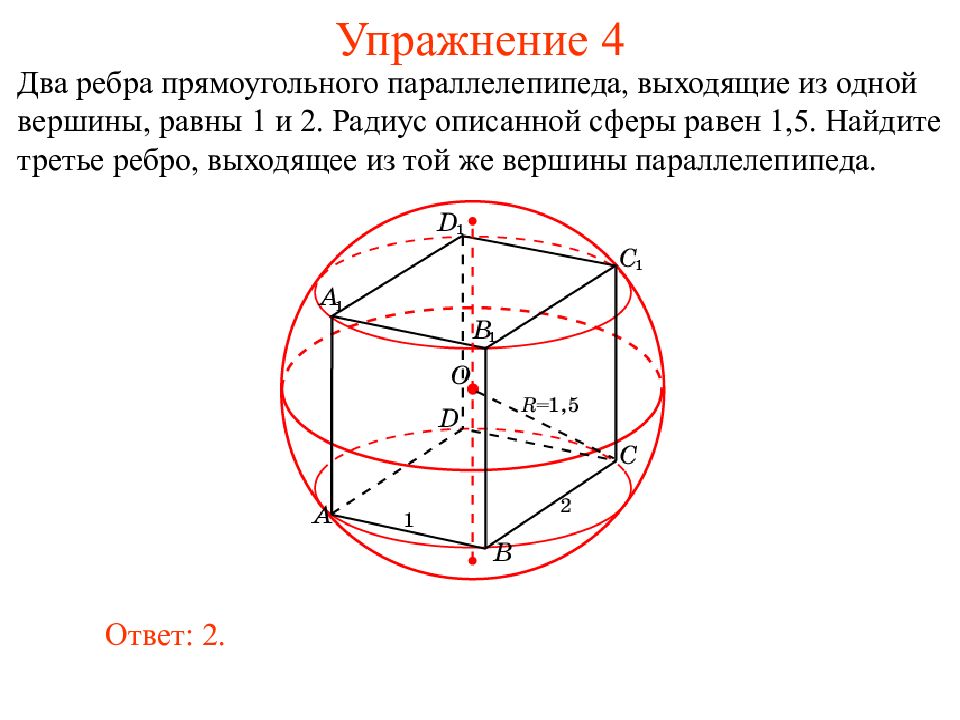
Слайд 12: Упражнение 4
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 2. Радиус описанной сферы равен 1,5. Найдите третье ребро, выходящее из той же вершины параллелепипеда. Ответ: 2.
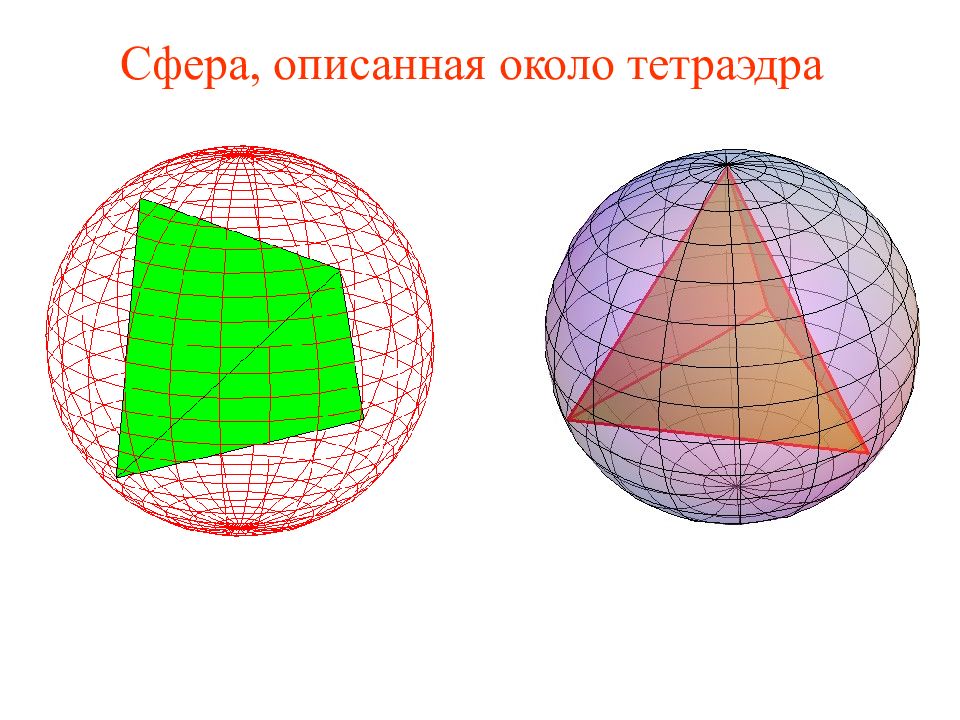
Слайд 13: Сфера, описанная около тетраэдра
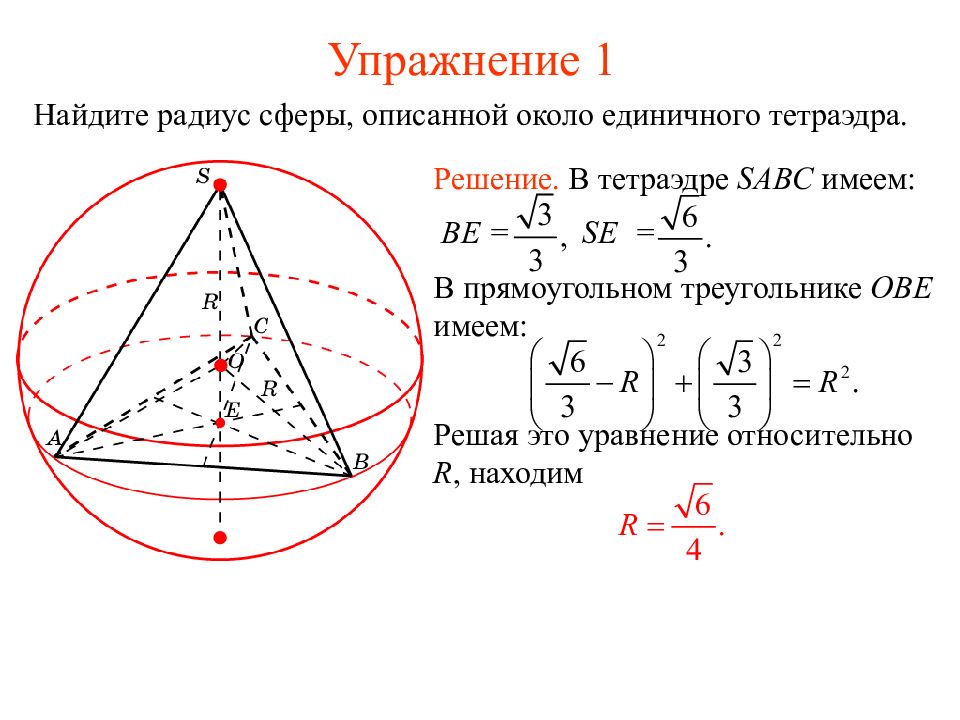
Слайд 14: Упражнение 1
Найдите радиус сферы, описанной около единичного тетраэдра. Решение. В тетраэдре SABC имеем: BE = SE = В прямоугольном треугольнике OBE имеем: Решая это уравнение относительно R, находим
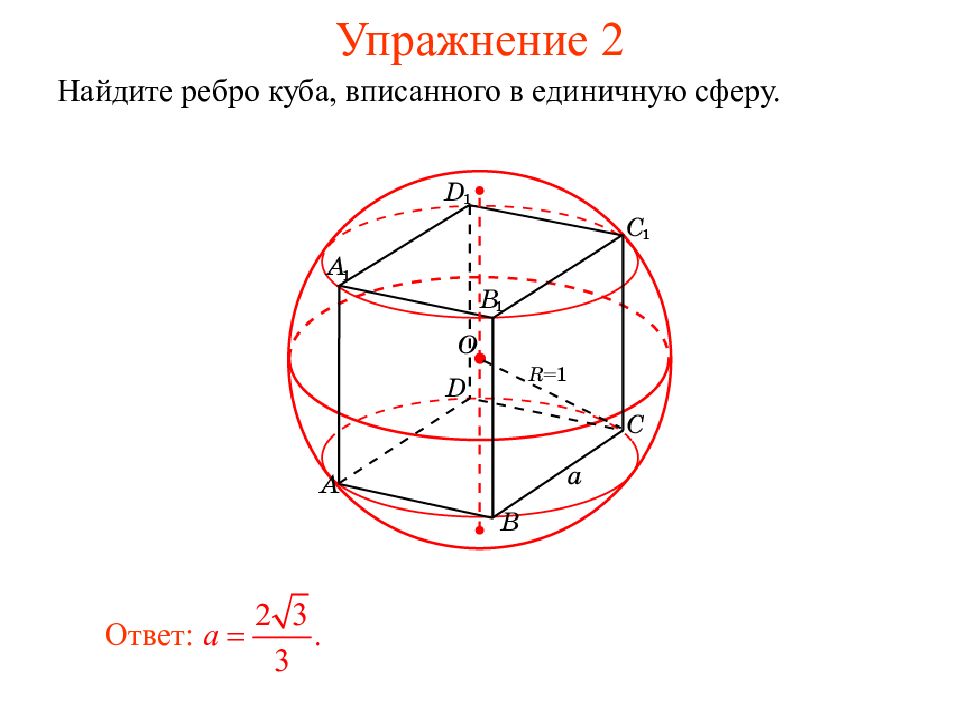
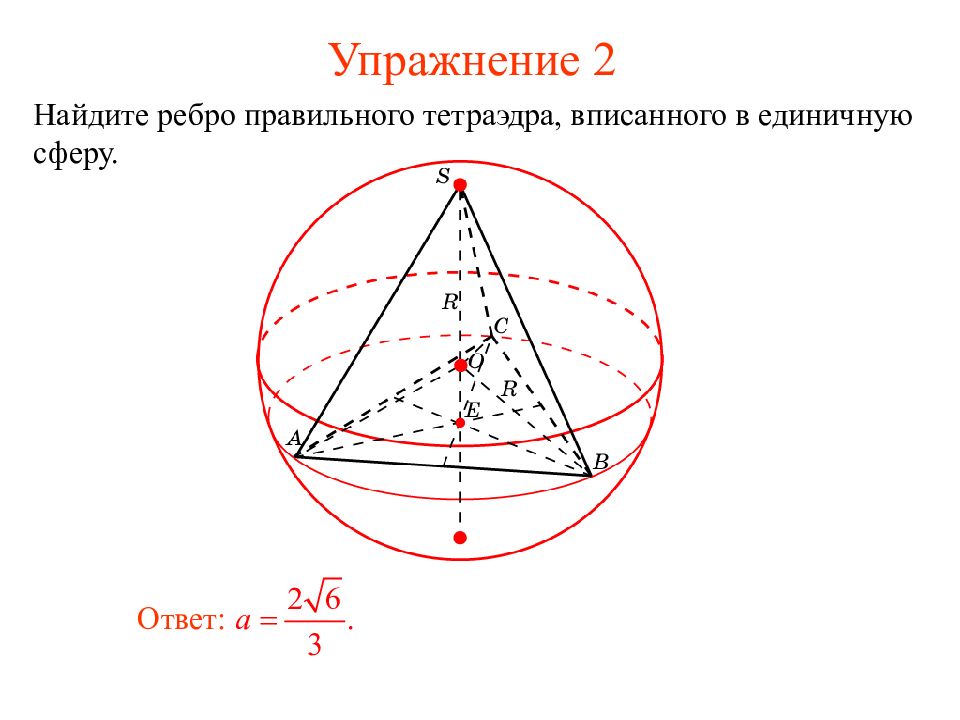
Слайд 15: Упражнение 2
Найдите ребро правильного тетраэдра, вписанного в единичную сферу. Ответ:
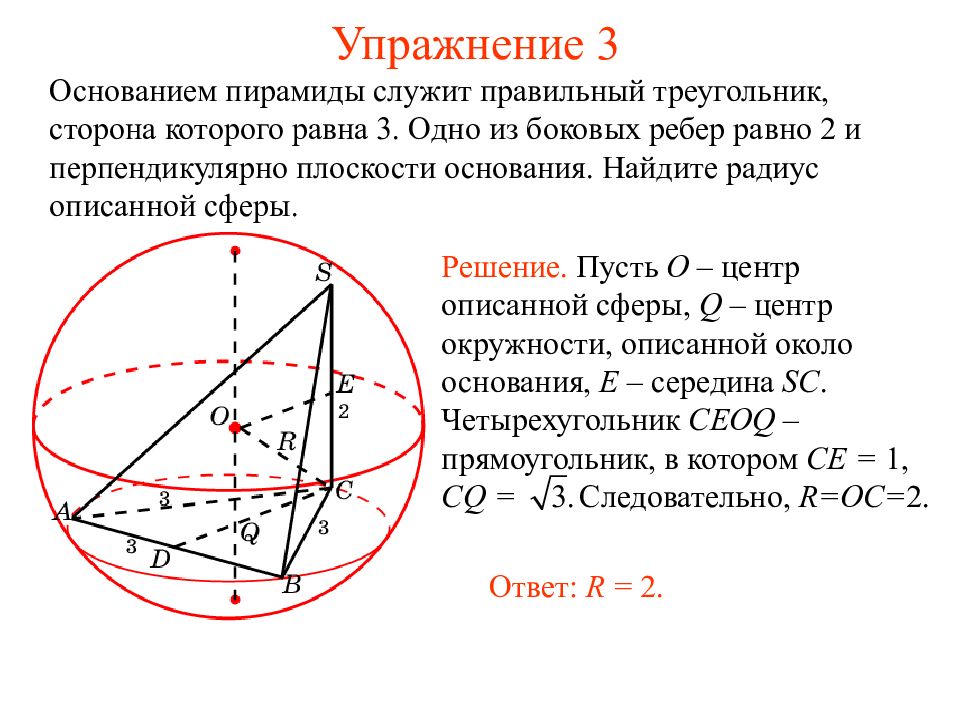
Слайд 16: Упражнение 3
Основанием пирамиды служит правильный треугольник, сторона которого равна 3. Одно из боковых ребер равно 2 и перпендикулярно плоскости основания. Найдите радиус описанной сферы. Решение. Пусть O – центр описанной сферы, Q – центр окружности, описанной около основания, E – середина SC. Четырехугольник CEOQ – прямоугольник, в котором CE = 1, CQ = Следовательно, R=OC= 2. Ответ: R = 2.
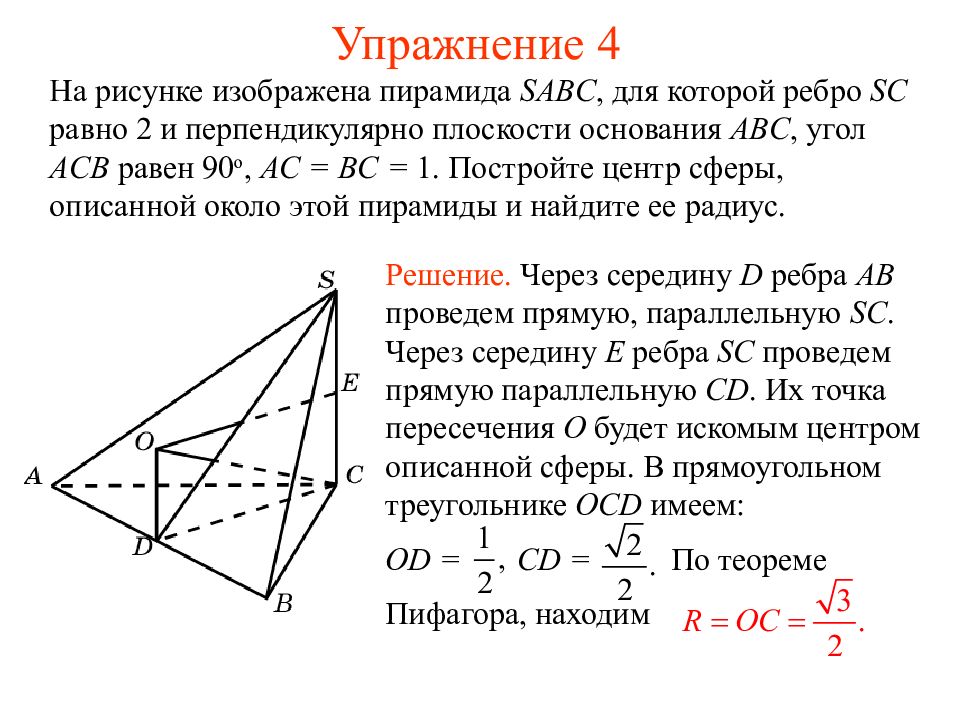
Слайд 17: Упражнение 4
На рисунке изображена пирамида SABC, для которой ребро SC равно 2 и перпендикулярно плоскости основания ABC, угол ACB равен 90 о, AC = BC = 1. Постройте центр сферы, описанной около этой пирамиды и найдите ее радиус. Решение. Через середину D ребра AB проведем прямую, параллельную SC. Через середину E ребра SC проведем прямую параллельную CD. Их точка пересечения O будет искомым центром описанной сферы. В прямоугольном треугольнике OCD имеем: OD = CD = По теореме Пифагора, находим
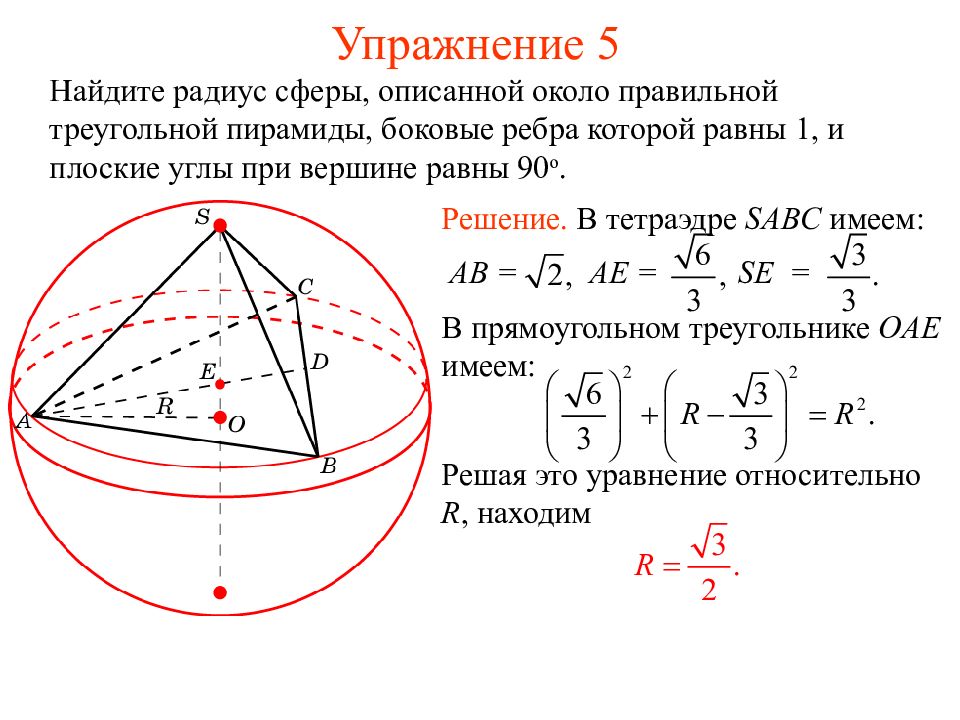
Слайд 18: Упражнение 5
Найдите радиус сферы, описанной около правильной треугольной пирамиды, боковые ребра которой равны 1, и плоские углы при вершине равны 90 о. Решение. В тетраэдре SABC имеем: AB = AE = SE = В прямоугольном треугольнике OAE имеем: Решая это уравнение относительно R, находим
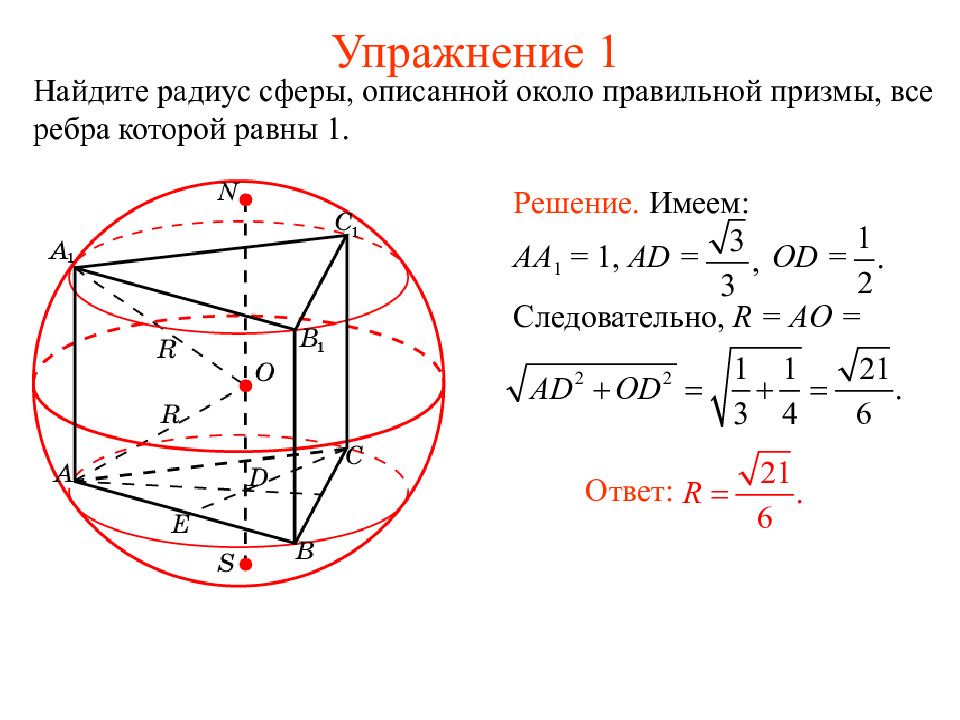
Слайд 20: Упражнение 1
Найдите радиус сферы, описанной около правильной призмы, все ребра которой равны 1. Ответ: Решение. Имеем: AA 1 = 1, AD = OD = Следовательно, R = AO =
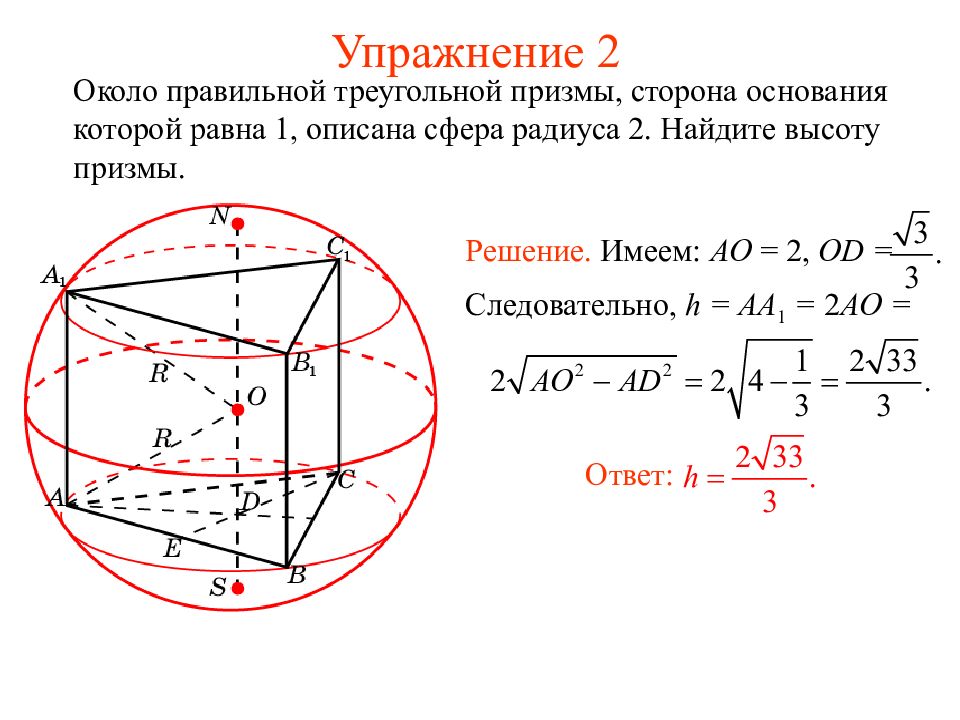
Слайд 21: Упражнение 2
Около правильной треугольной призмы, сторона основания которой равна 1, описана сфера радиуса 2. Найдите высоту призмы. Ответ: Решение. Имеем: AO = 2, OD = Следовательно, h = AA 1 = 2 AO =
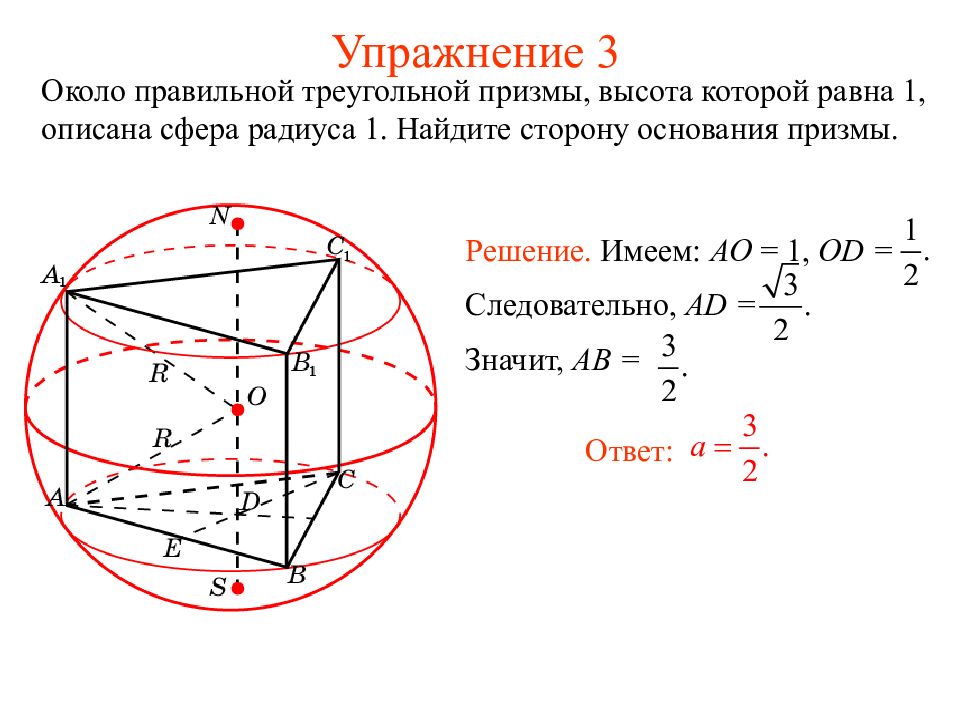
Слайд 22: Упражнение 3
Около правильной треугольной призмы, высота которой равна 1, описана сфера радиуса 1. Найдите сторону основания призмы. Ответ: Решение. Имеем: AO = 1, OD = Следовательно, AD = Значит, AB =
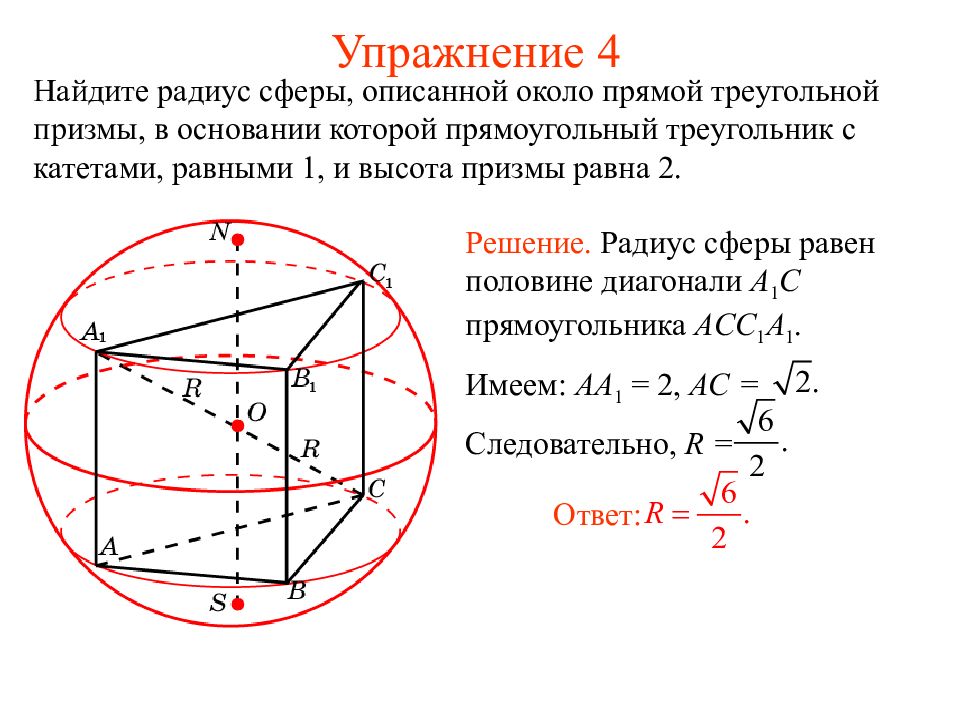
Слайд 23: Упражнение 4
Найдите радиус сферы, описанной около прямой треугольной призмы, в основании которой прямоугольный треугольник с катетами, равными 1, и высота призмы равна 2. Ответ: Решение. Радиус сферы равен половине диагонали A 1 C прямоугольника ACC 1 A 1. Имеем: AA 1 = 2, AC = Следовательно, R =
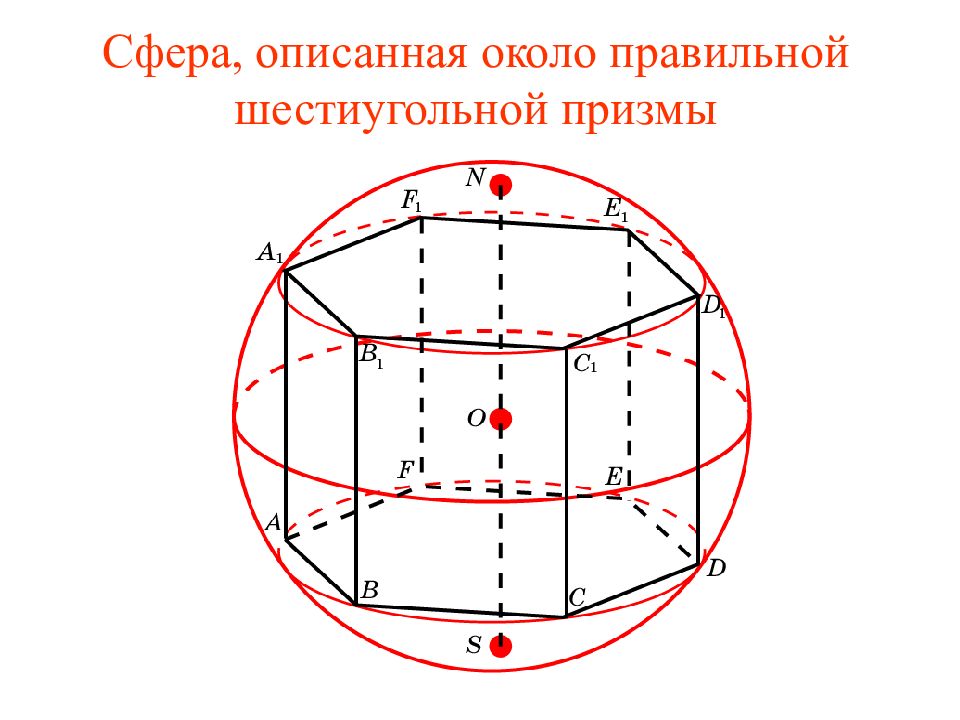
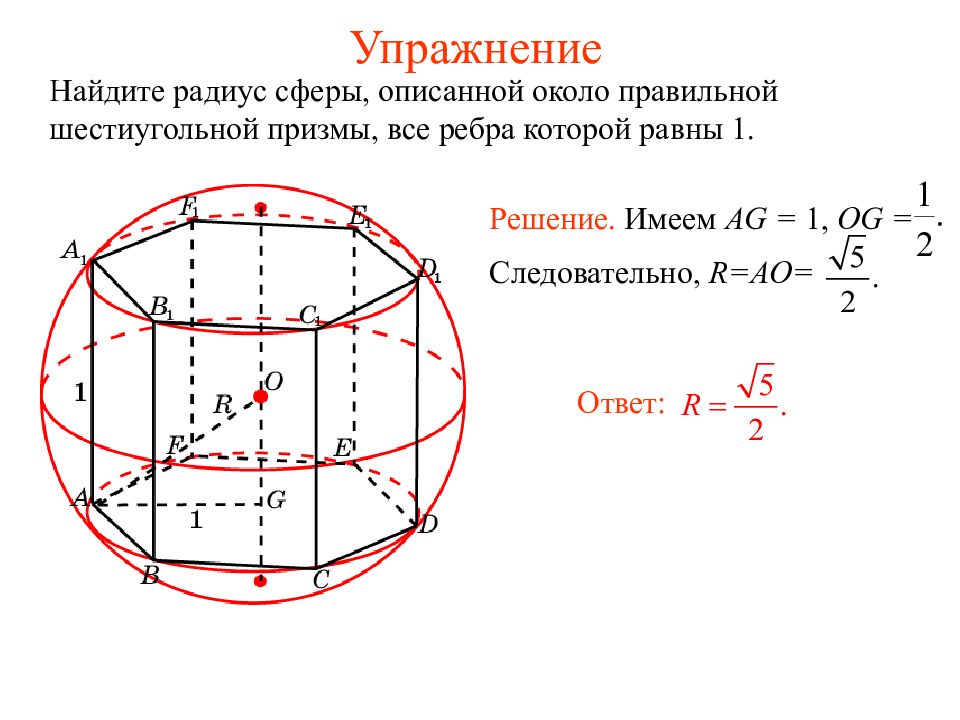
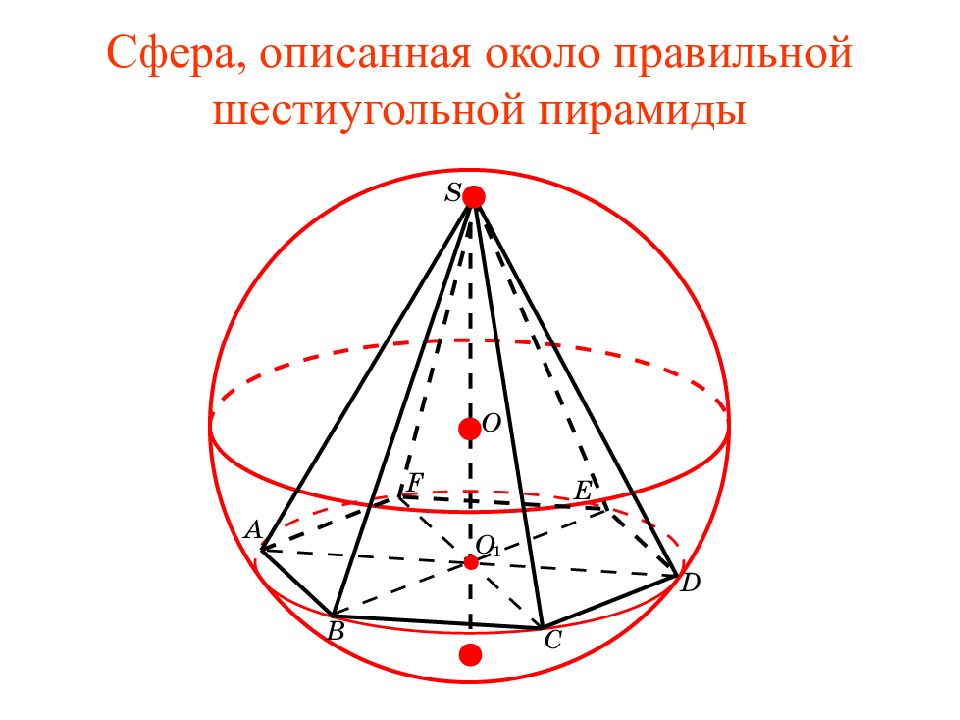
Слайд 25: Упражнение
Найдите радиус сферы, описанной около правильной шестиугольной призмы, все ребра которой равны 1. Ответ: Решение. Имеем AG = 1, OG = Следовательно, R=AO=
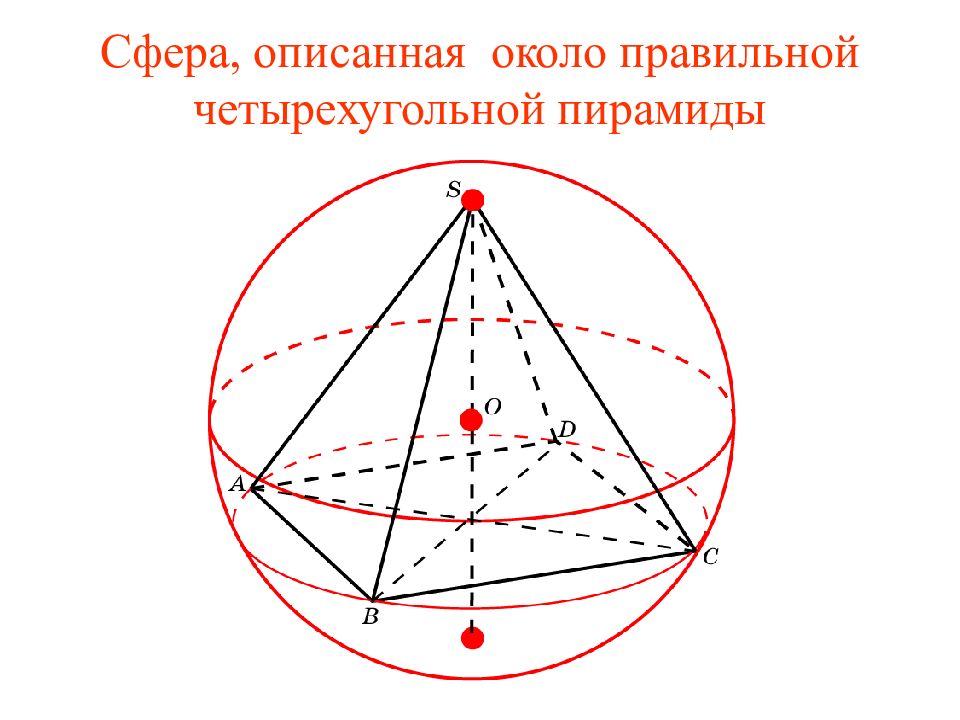
Слайд 27: Упражнение
Найдите радиус сферы, описанной около правильной четырехугольной пирамиды, все ребра которой равны 1. Ответ:
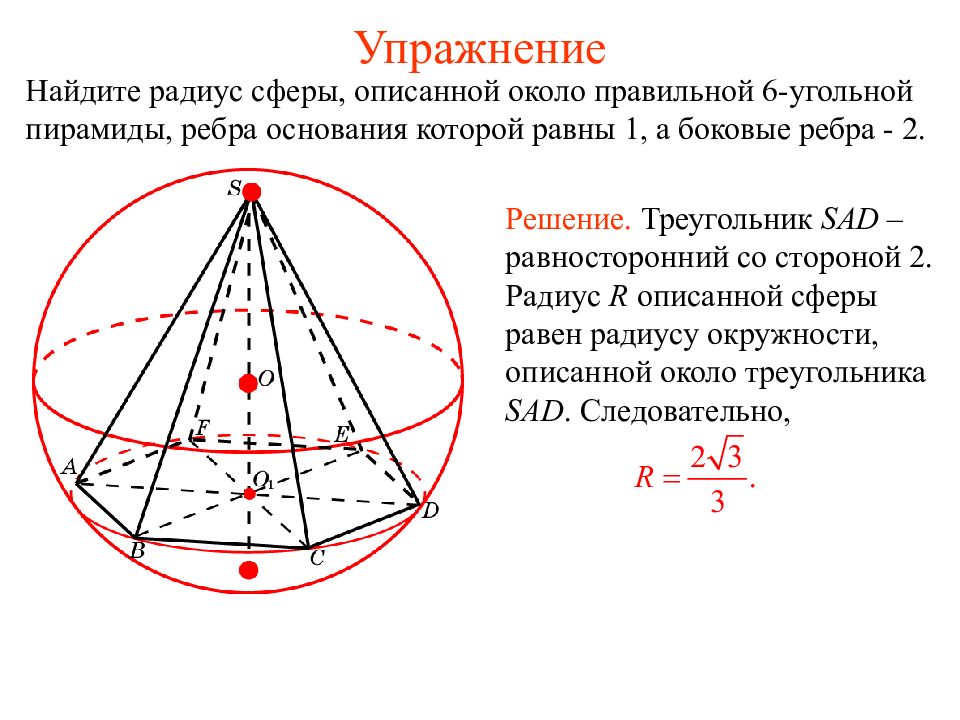
Слайд 29: Упражнение
Найдите радиус сферы, описанной около правильной 6-угольной пирамиды, ребра основания которой равны 1, а боковые ребра - 2. Решение. Треугольник SAD – равносторонний со стороной 2. Радиус R описанной сферы равен радиусу окружности, описанной около треугольника SAD. Следовательно,
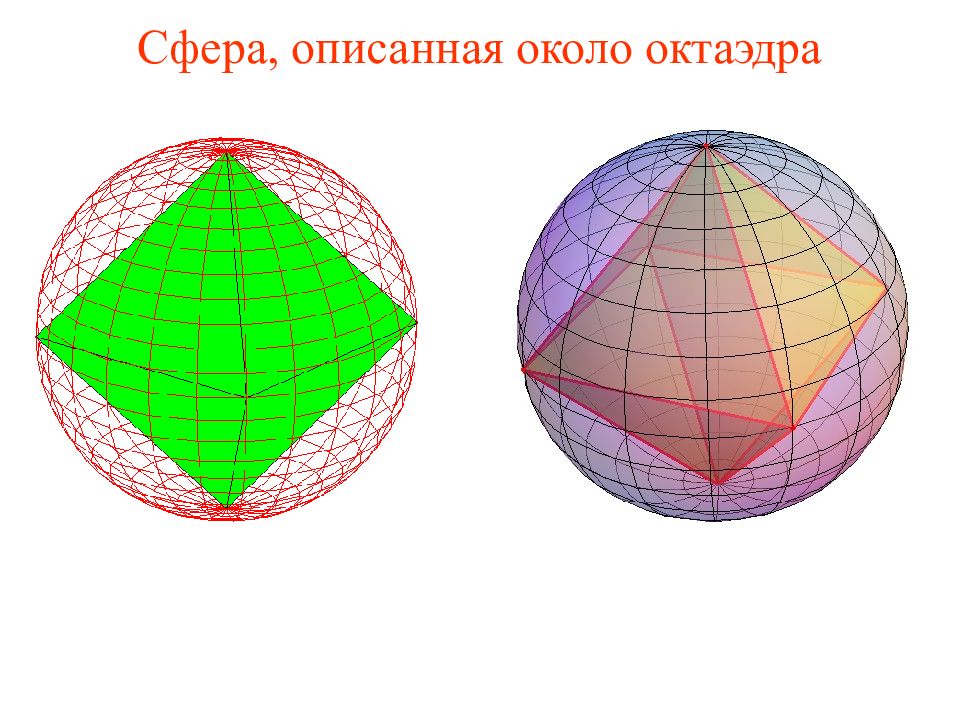
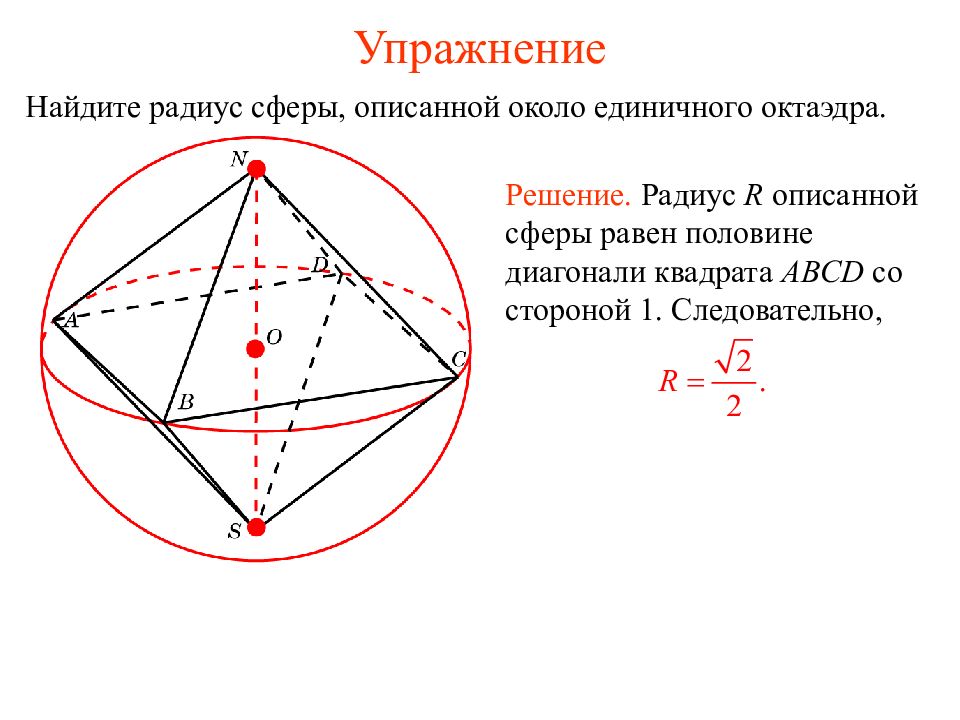
Слайд 31: Упражнение
Найдите радиус сферы, описанной около единичного октаэдра. Решение. Радиус R описанной сферы равен половине диагонали квадрата ABCD со стороной 1. Следовательно,
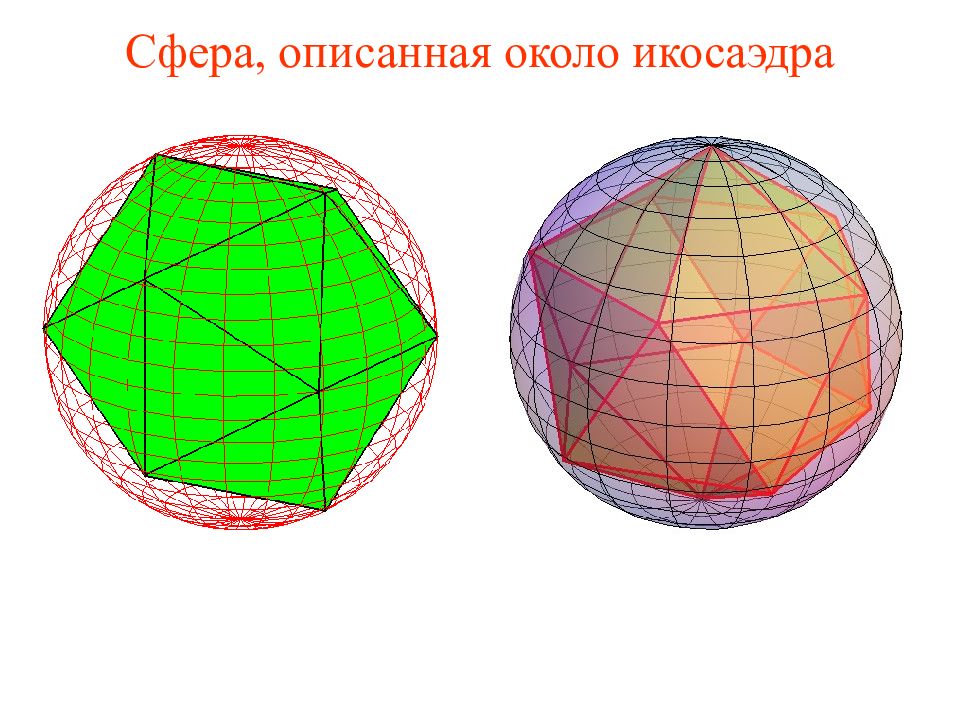
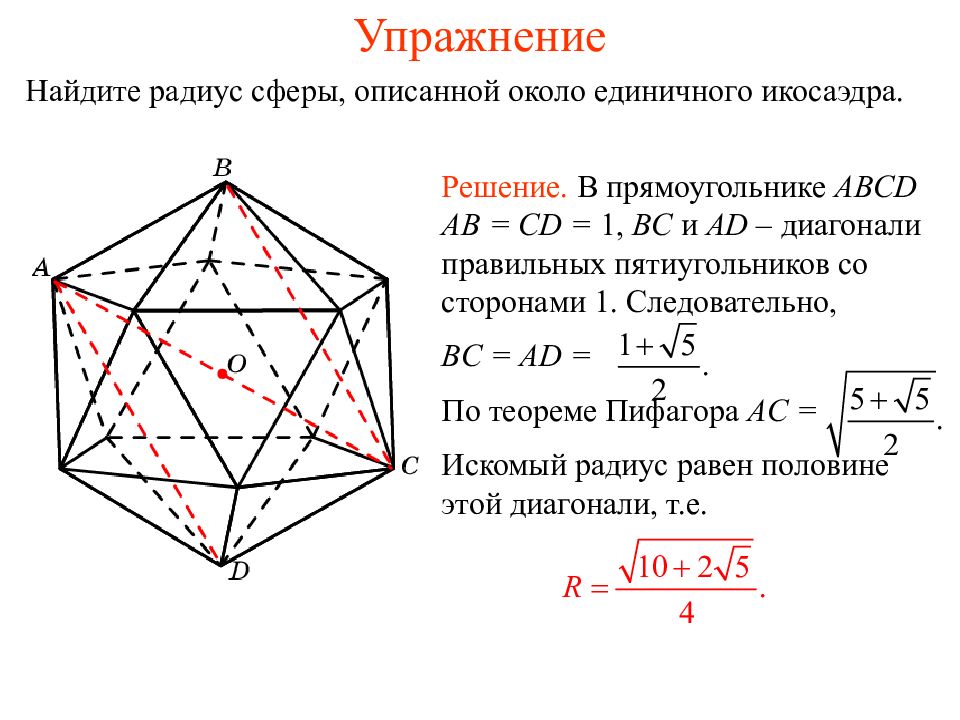
Слайд 33: Упражнение
Найдите радиус сферы, описанной около единичного икосаэдра. Решение. В прямоугольнике ABCD AB = CD = 1, BC и AD – диагонали правильных пятиугольников со сторонами 1. Следовательно, BC = AD = По теореме Пифагора AC = Искомый радиус равен половине этой диагонали, т.е.
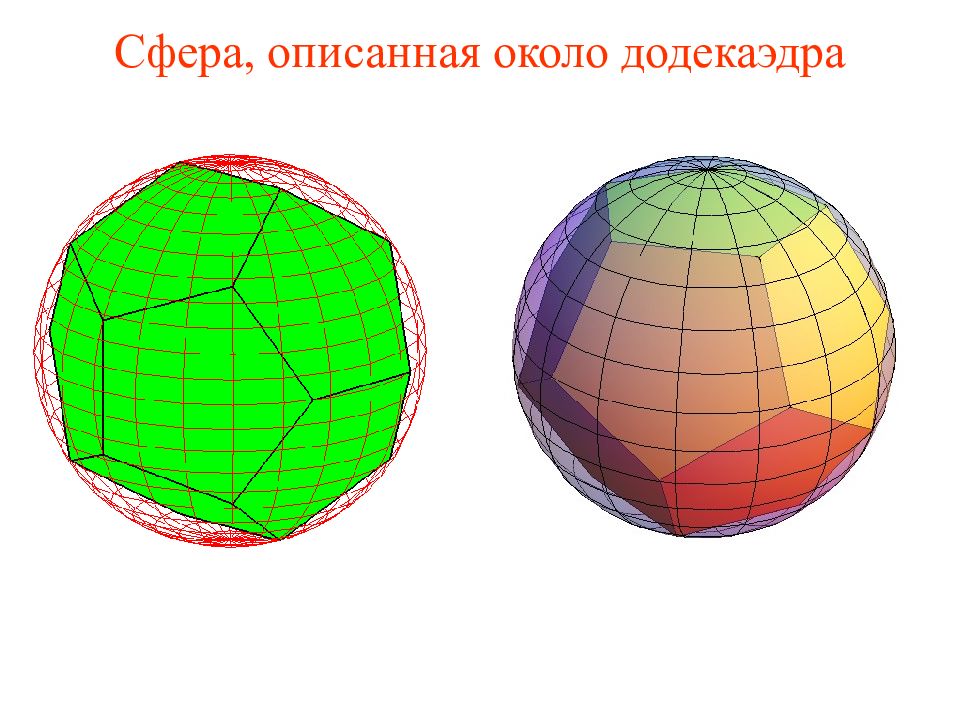
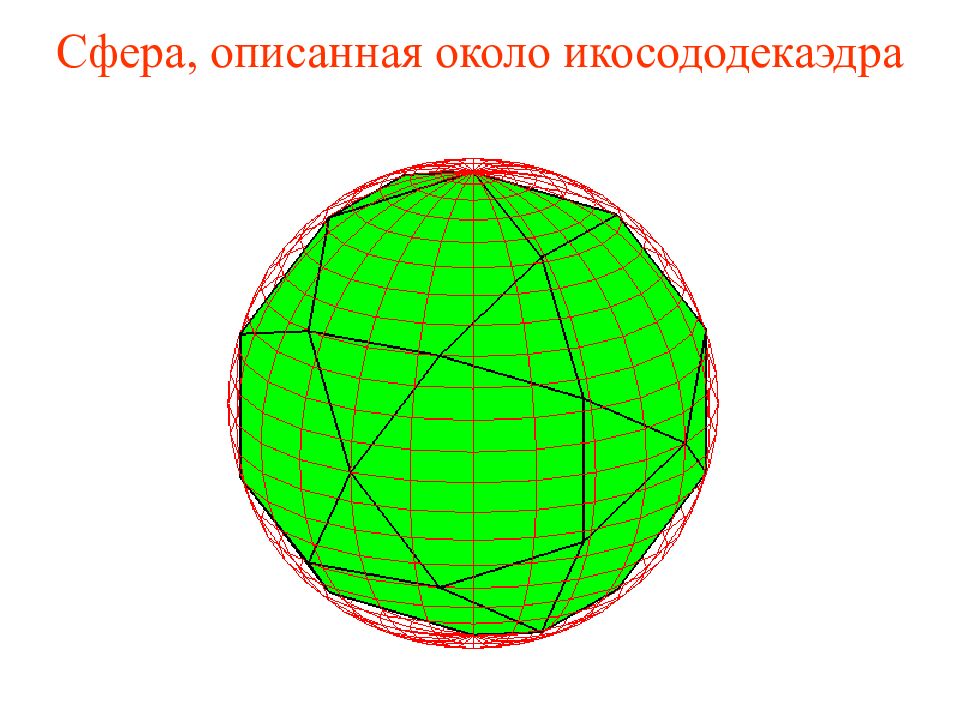
Слайд 35: Упражнение
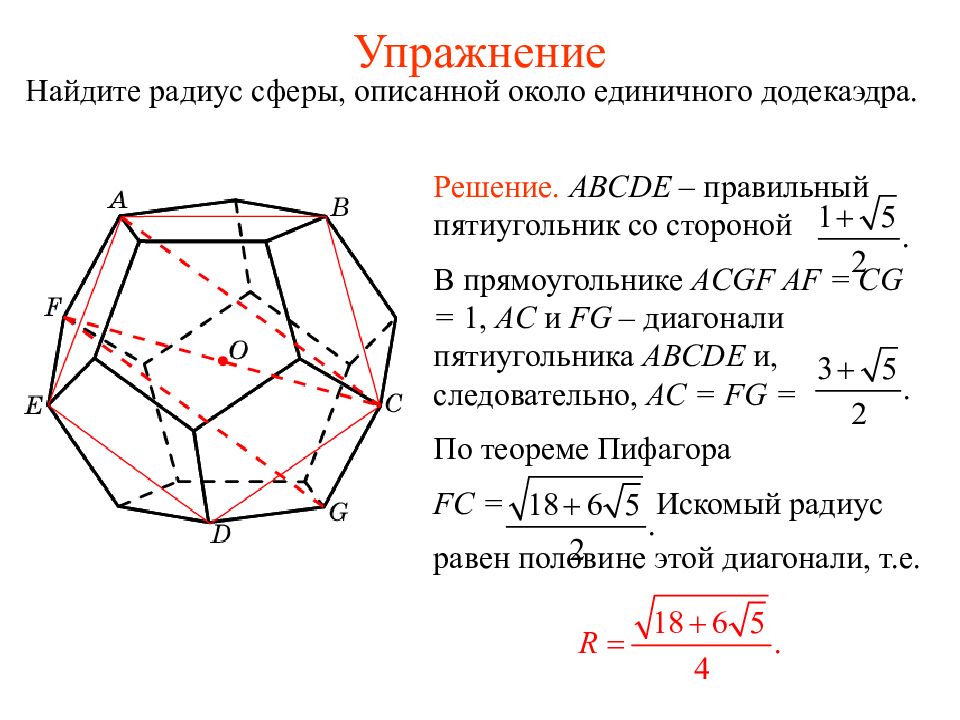
Найдите радиус сферы, описанной около единичного додекаэдра. Решение. ABCDE – правильный пятиугольник со стороной В прямоугольнике ACGF AF = CG = 1, AC и FG – диагонали пятиугольника ABCDE и, следовательно, AC = FG = По теореме Пифагора FC = Искомый радиус равен половине этой диагонали, т.е.
Слайд 37: Упражнение
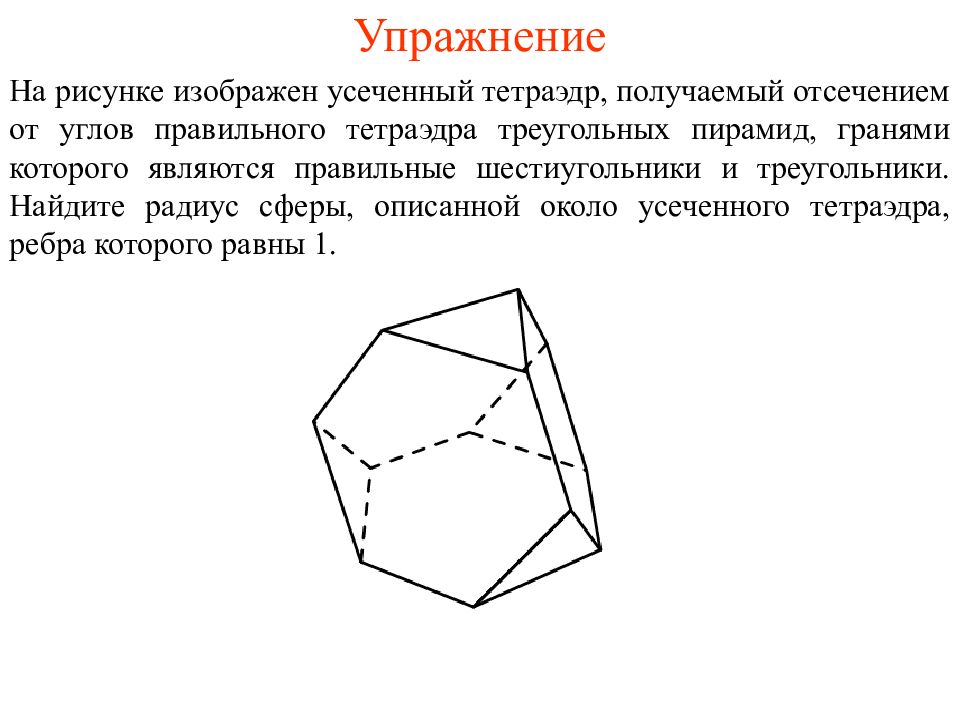
На рисунке изображен усеченный тетраэдр, получаемый отсечением от углов правильного тетраэдра треугольных пирамид, гранями которого являются правильные шестиугольники и треугольники. Найдите радиус сферы, описанной около усеченного тетраэдра, ребра которого равны 1.
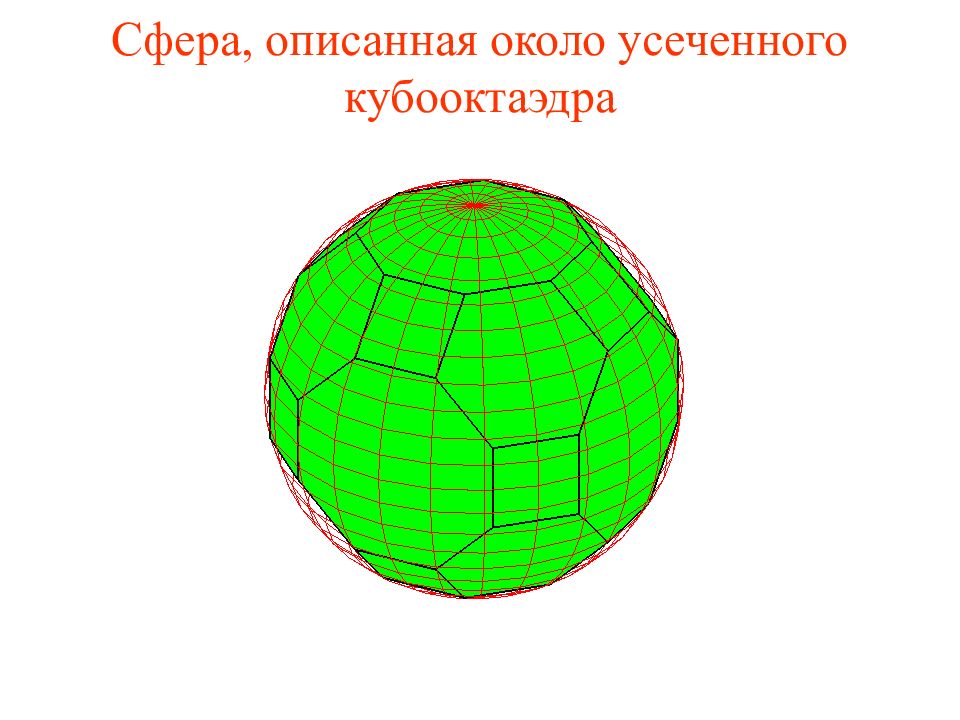
Слайд 39: Упражнение
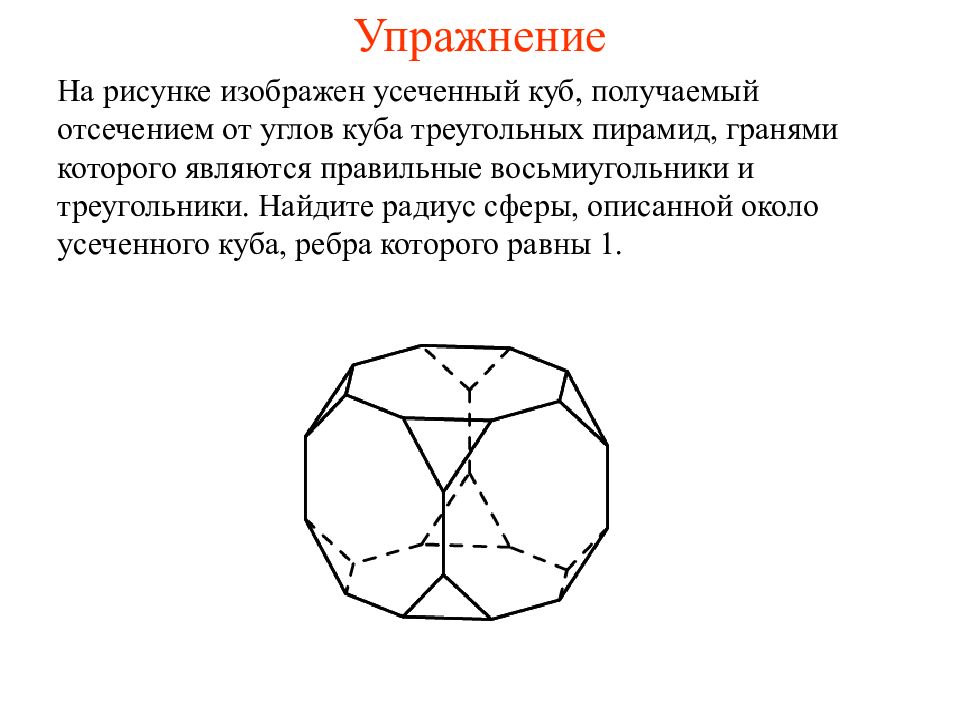
На рисунке изображен усеченный куб, получаемый отсечением от углов куба треугольных пирамид, гранями которого являются правильные восьмиугольники и треугольники. Найдите радиус сферы, описанной около усеченного куба, ребра которого равны 1.
Слайд 41: Упражнение
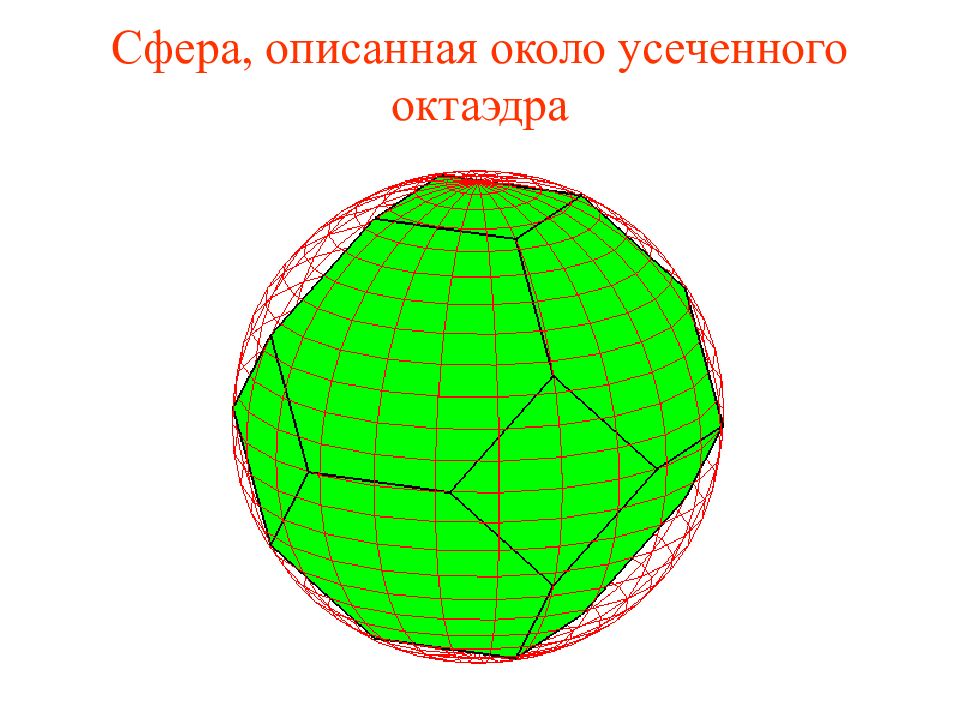
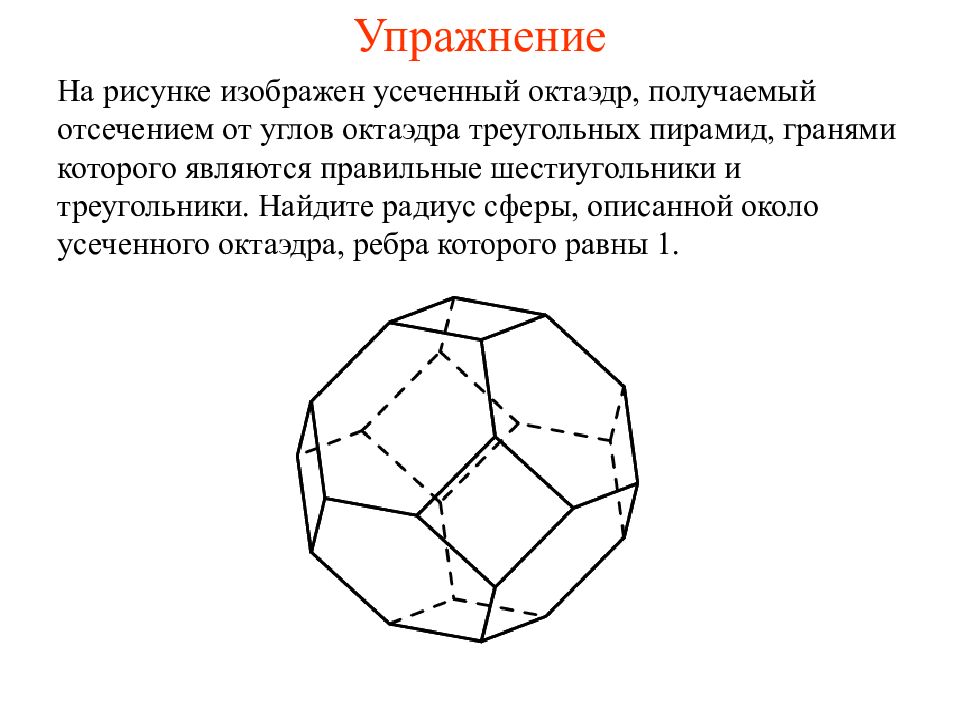
На рисунке изображен усеченный октаэдр, получаемый отсечением от углов октаэдра треугольных пирамид, гранями которого являются правильные шестиугольники и треугольники. Найдите радиус сферы, описанной около усеченного октаэдра, ребра которого равны 1.
Слайд 43: Упражнение
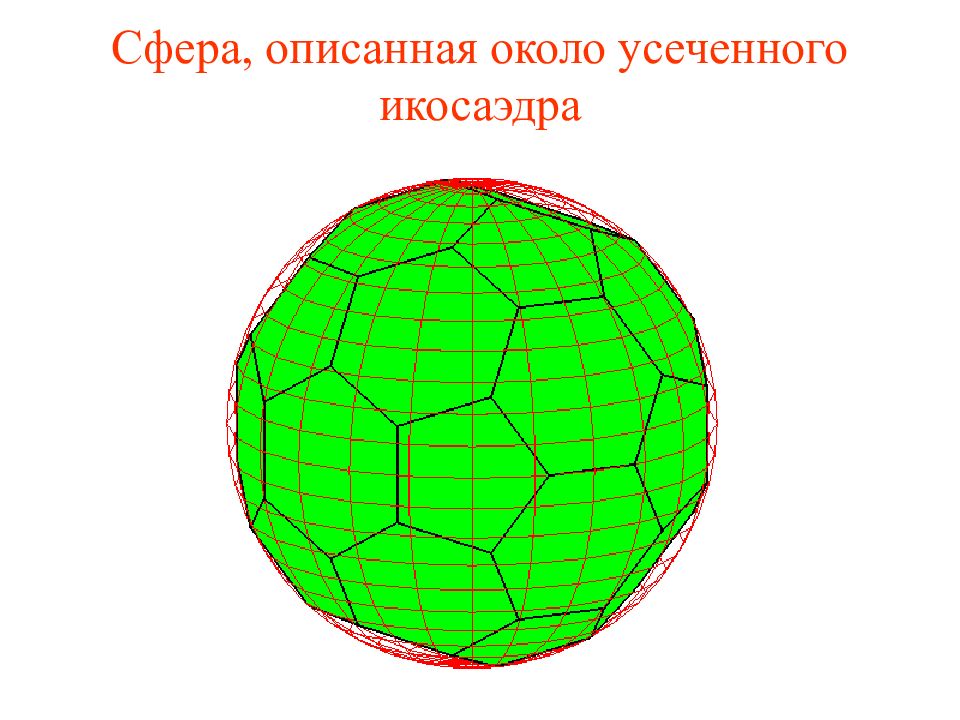
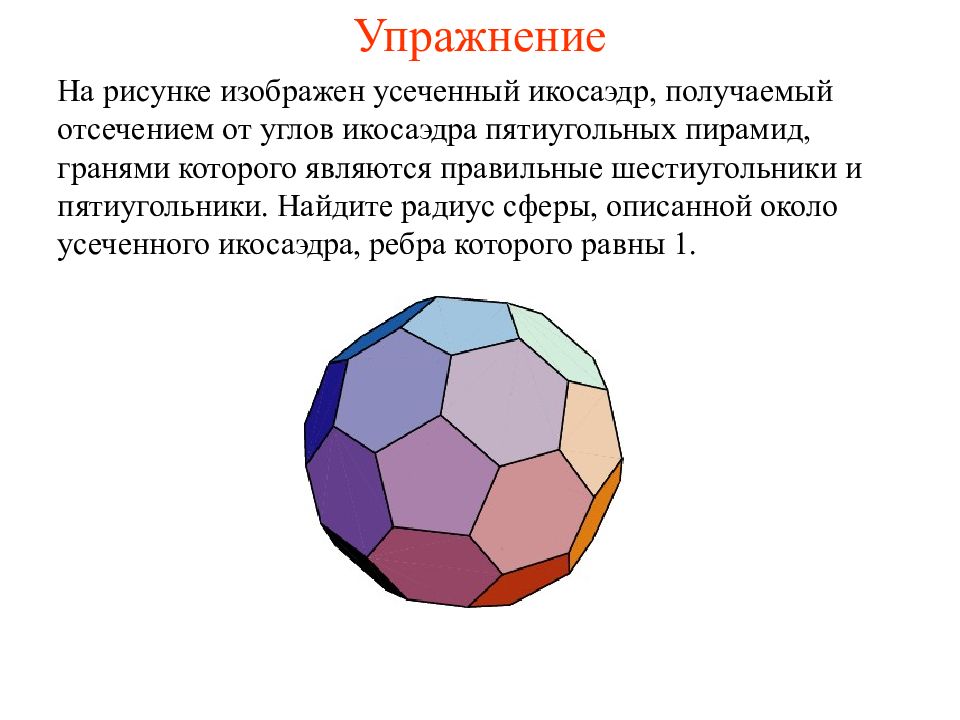
На рисунке изображен усеченный икосаэдр, получаемый отсечением от углов икосаэдра пятиугольных пирамид, гранями которого являются правильные шестиугольники и пятиугольники. Найдите радиус сферы, описанной около усеченного икосаэдра, ребра которого равны 1.
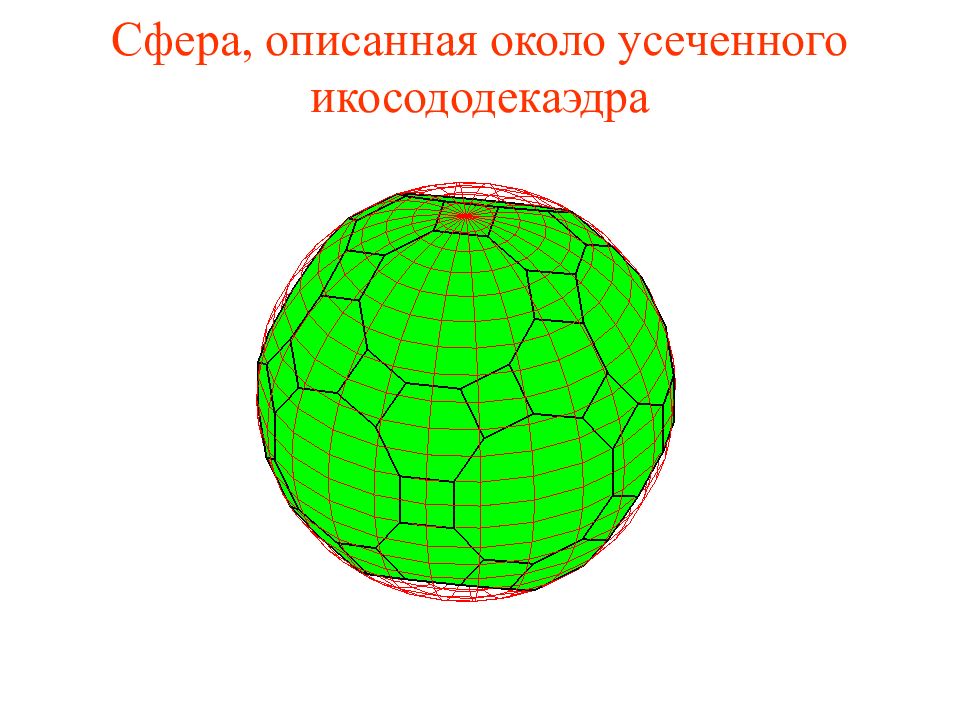
Слайд 45: Упражнение
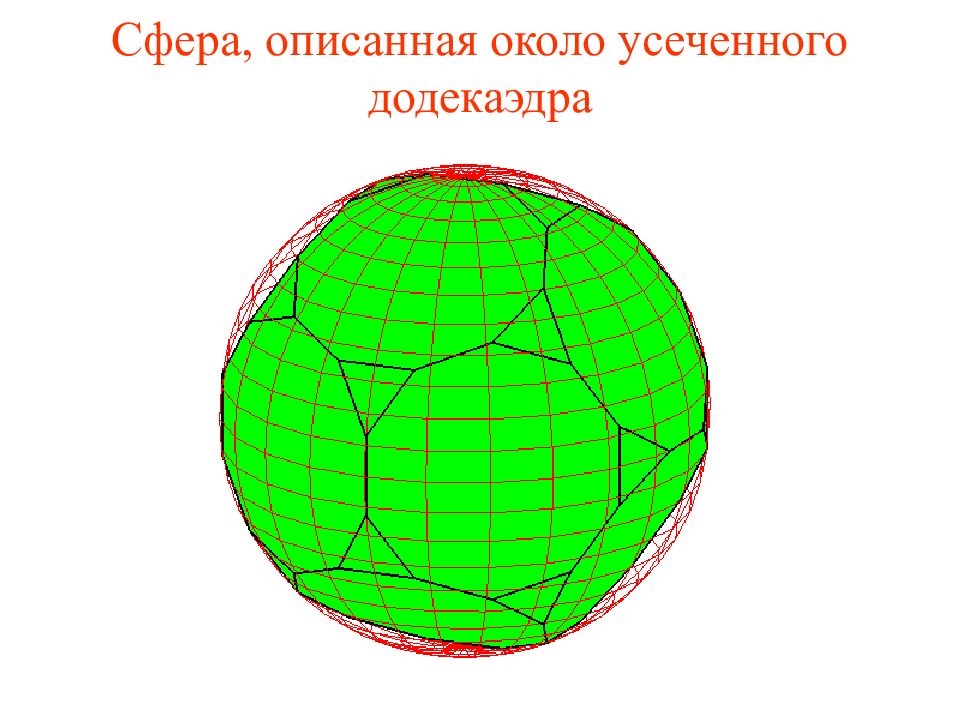
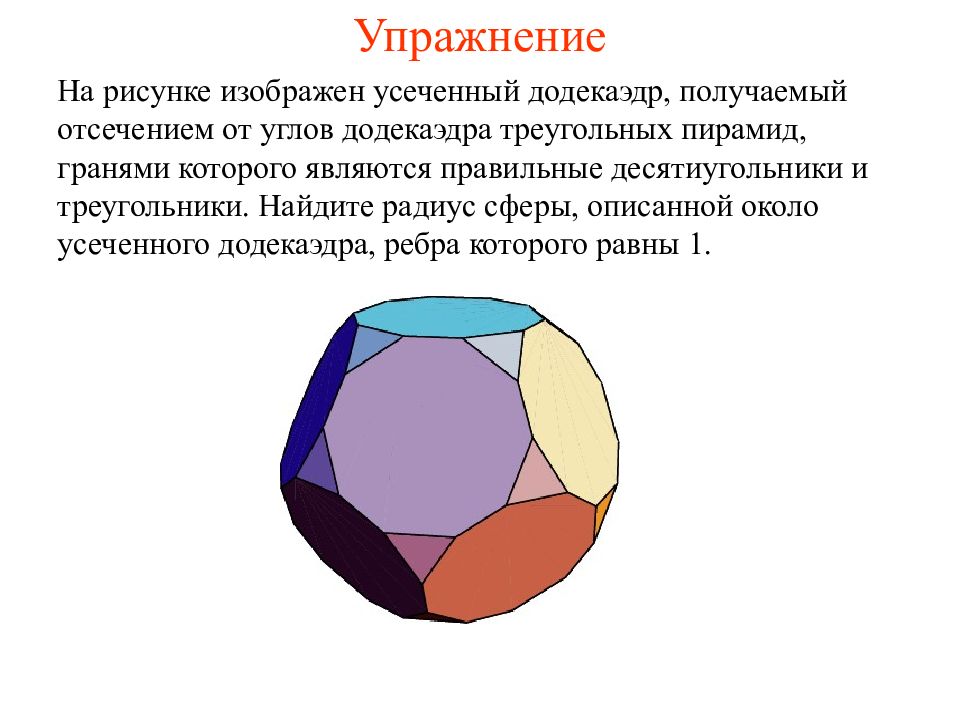
На рисунке изображен усеченный додекаэдр, получаемый отсечением от углов додекаэдра треугольных пирамид, гранями которого являются правильные десятиугольники и треугольники. Найдите радиус сферы, описанной около усеченного додекаэдра, ребра которого равны 1.
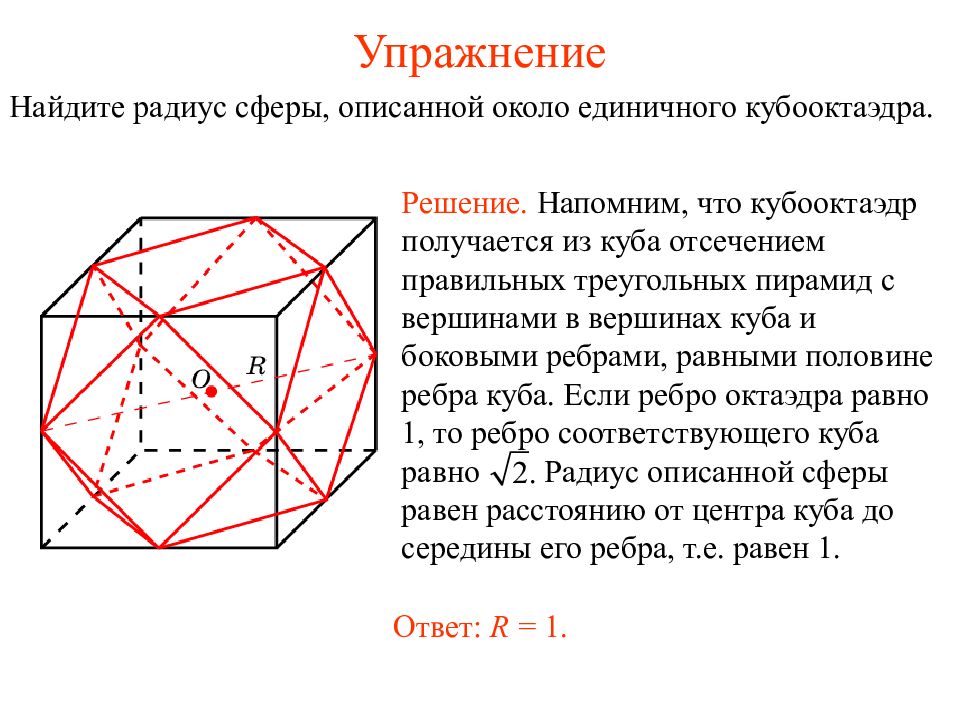
Слайд 47: Упражнение
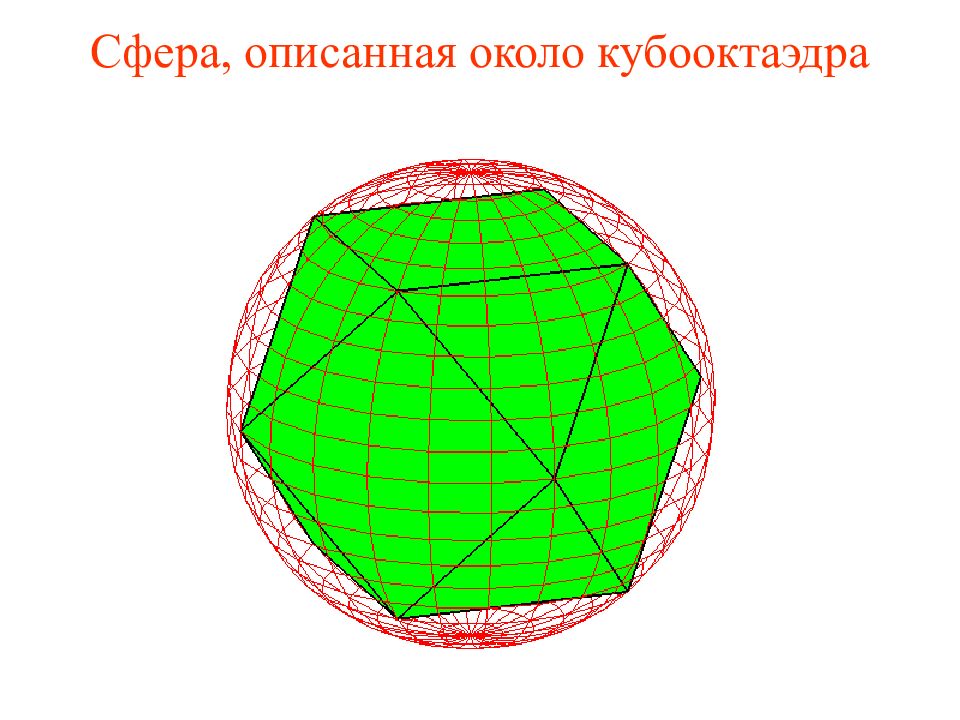
Найдите радиус сферы, описанной около единичного кубооктаэдра. Решение. Напомним, что кубооктаэдр получается из куба отсечением правильных треугольных пирамид с вершинами в вершинах куба и боковыми ребрами, равными половине ребра куба. Если ребро октаэдра равно 1, то ребро соответствующего куба равно Радиус описанной сферы равен расстоянию от центра куба до середины его ребра, т.е. равен 1. Ответ: R = 1.