Слайд 3: План занятия
Куб Прямоугольный параллелепипед Составные многогранники Призма
Слайд 4: Куб
Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.
Слайд 5: Куб
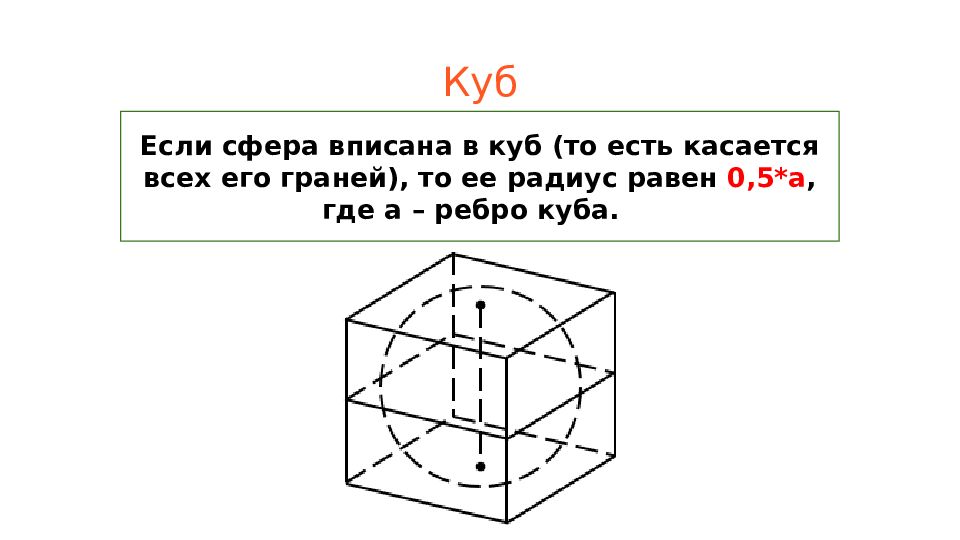
Если сфера вписана в куб (то есть касается всех его граней), то ее радиус равен 0,5*a, где a – ребро куба.
Слайд 6: Куб
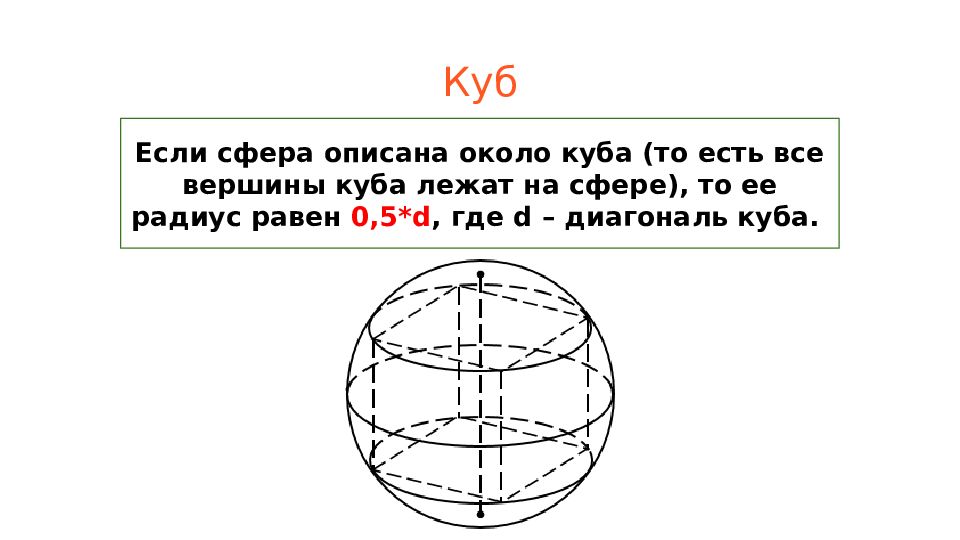
Если сфера описана около куба (то есть все вершины куба лежат на сфере), то ее радиус равен 0,5*d, где d – диагональ куба.
Слайд 7: Куб
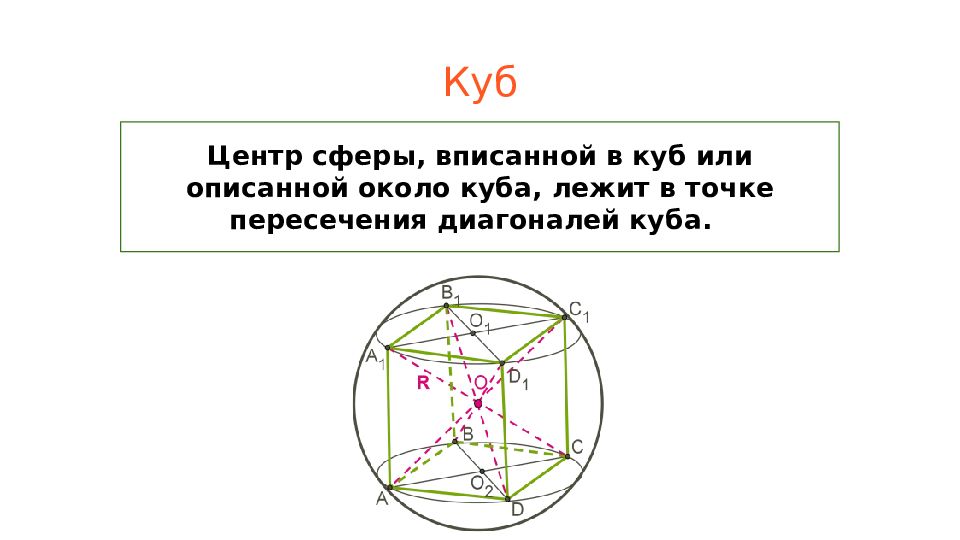
Центр сферы, вписанной в куб или описанной около куба, лежит в точке пересечения диагоналей куба.
Слайд 9
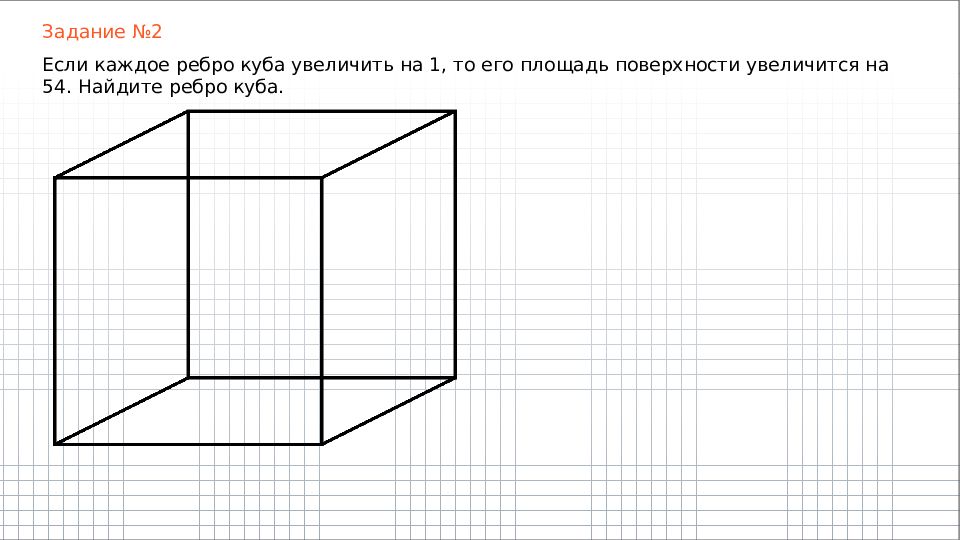
Задание №2 Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Слайд 11
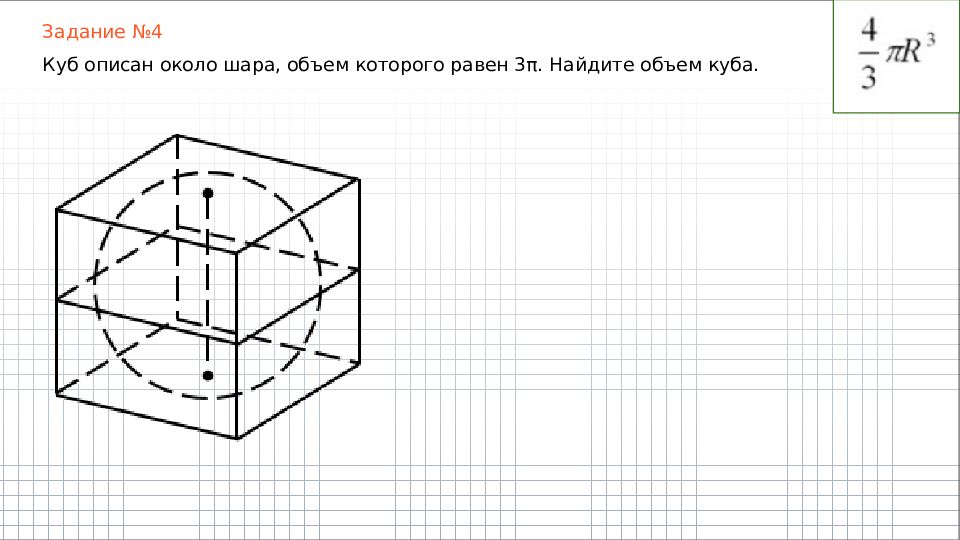
Задание №4 Куб описан около шара, объем которого равен 3π. Найдите объем куба.
Слайд 12: План занятия
Куб Прямоугольный параллелепипед Составные многогранники Призма
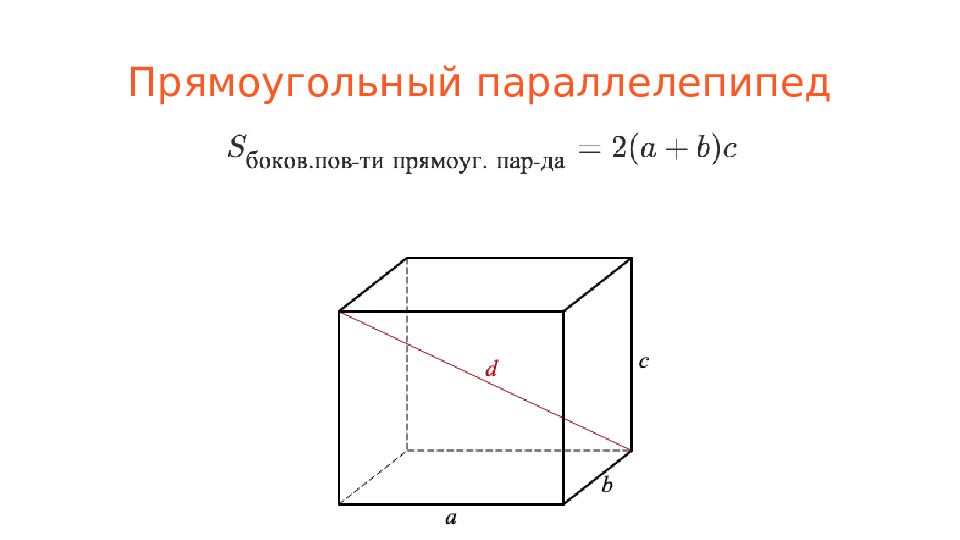
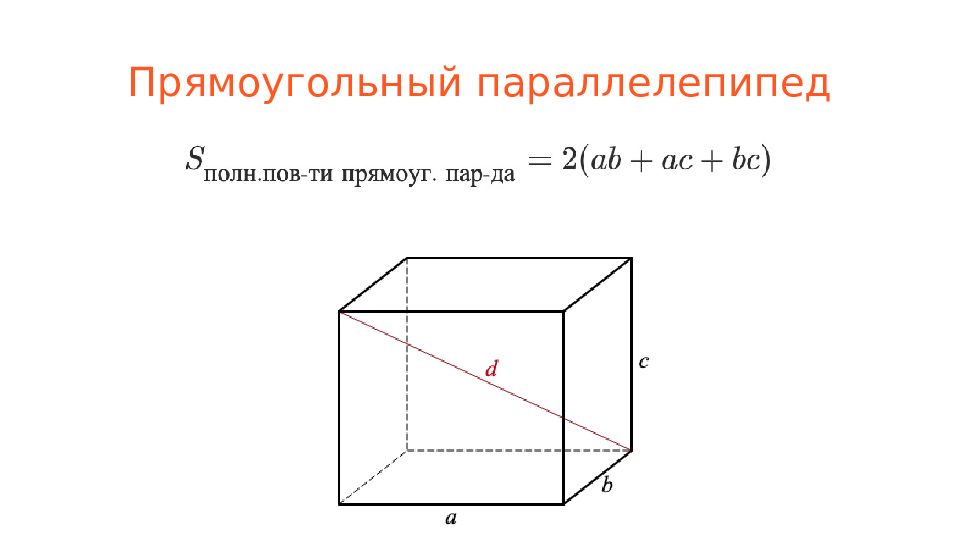
Слайд 13: Прямоугольный параллелепипед
Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Слайд 14: Прямоугольный параллелепипед
Слайд 16
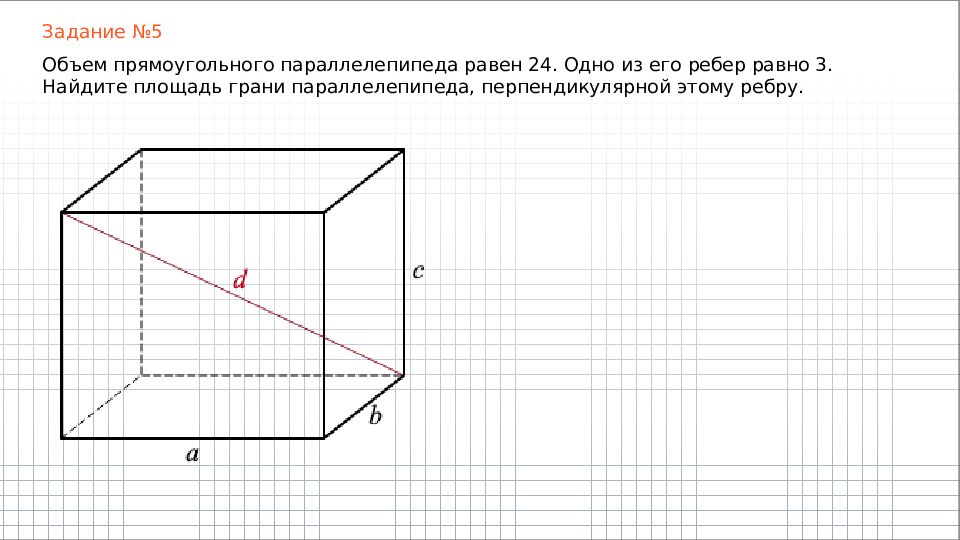
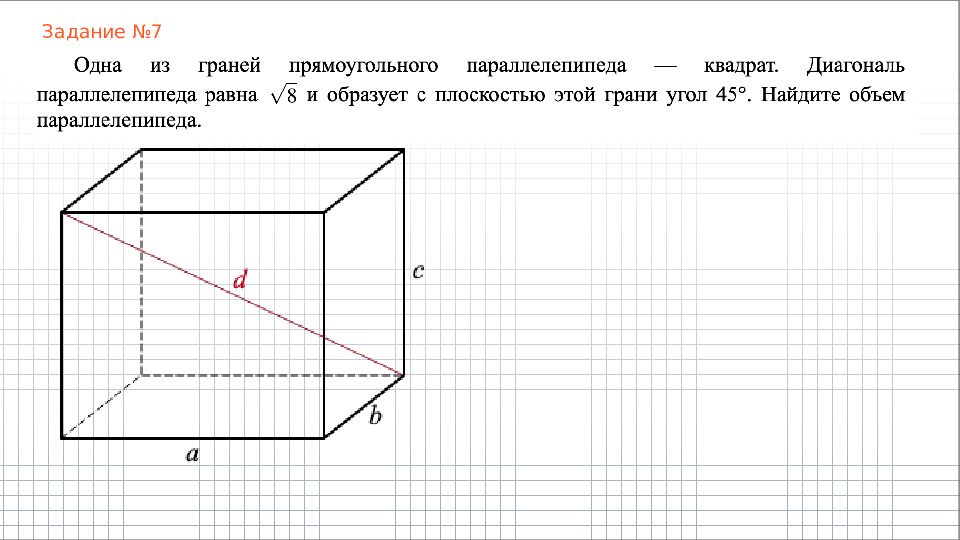
Задание №5 Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Слайд 17
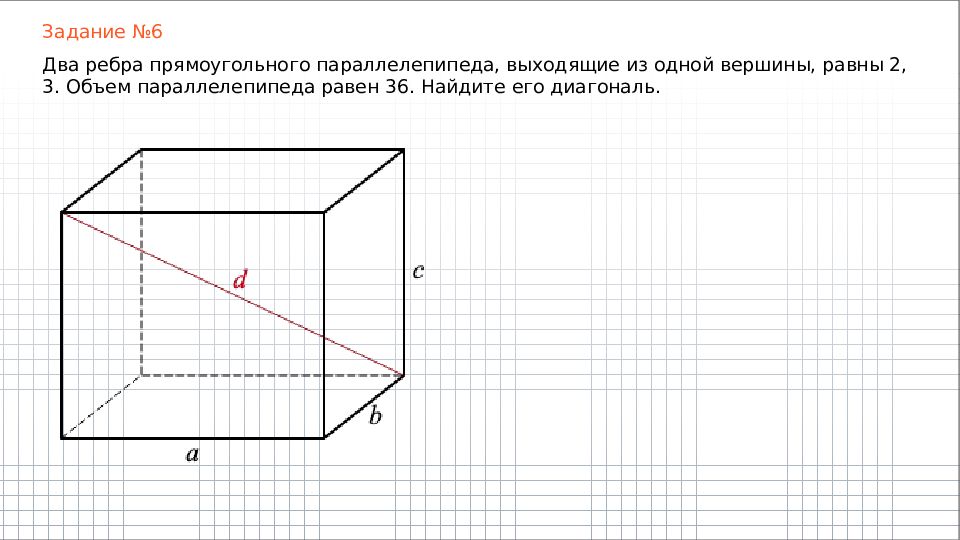
Задание №6 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Слайд 21
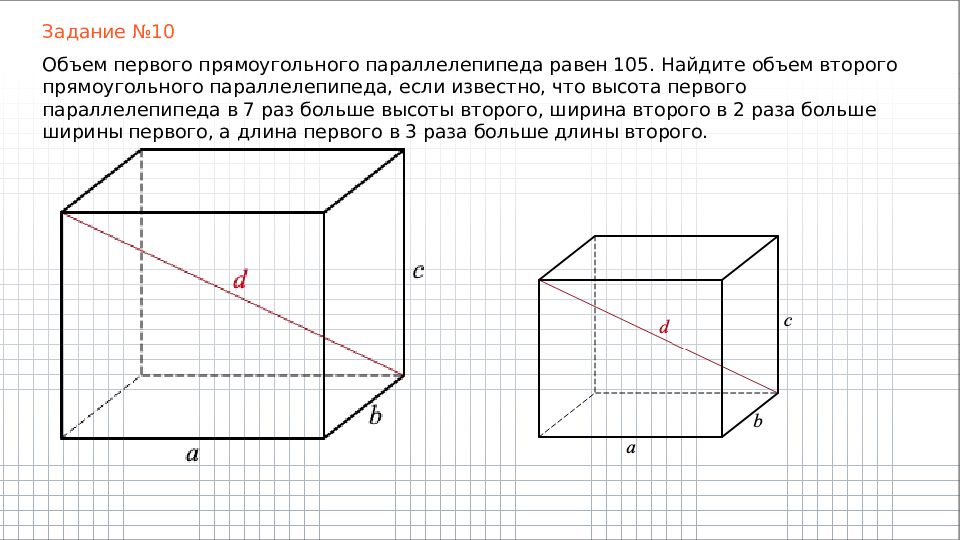
Задание №10 Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.
Слайд 22: План занятия
Куб Прямоугольный параллелепипед Составные многогранники Призма
Слайд 29: План занятия
Куб Прямоугольный параллелепипед Составные многогранники Призма
Слайд 30: Призма
В основании призмы лежат многоугольники. Боковые грани представляют собой параллелограммы. Высота призмы – перпендикуляр, опущенный из вершины одного основания к плоскости другого основания.
Слайд 31: Призма
Площадь боковой поверхности – сумма площадей ее боковых граней. Площадь полной поверхности – сумма площади боковой поверхности и площадей оснований.
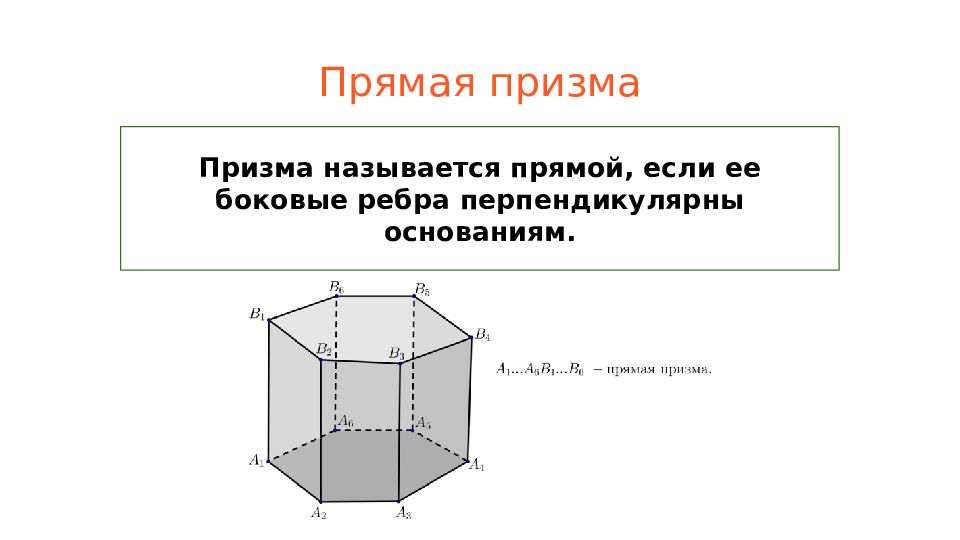
Слайд 32: Прямая п ризма
Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.
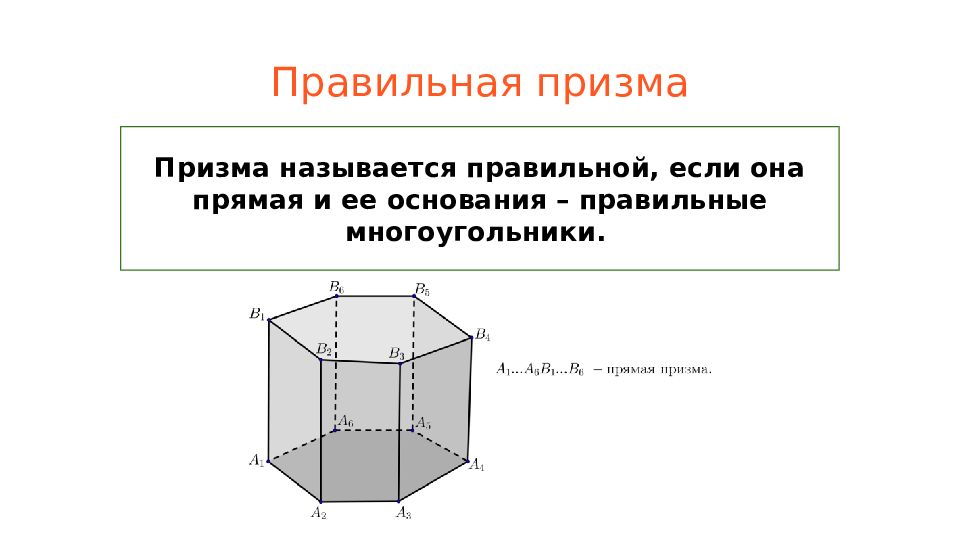
Слайд 33: Правильная призма
Призма называется правильной, если она прямая и ее основания – правильные многоугольники.
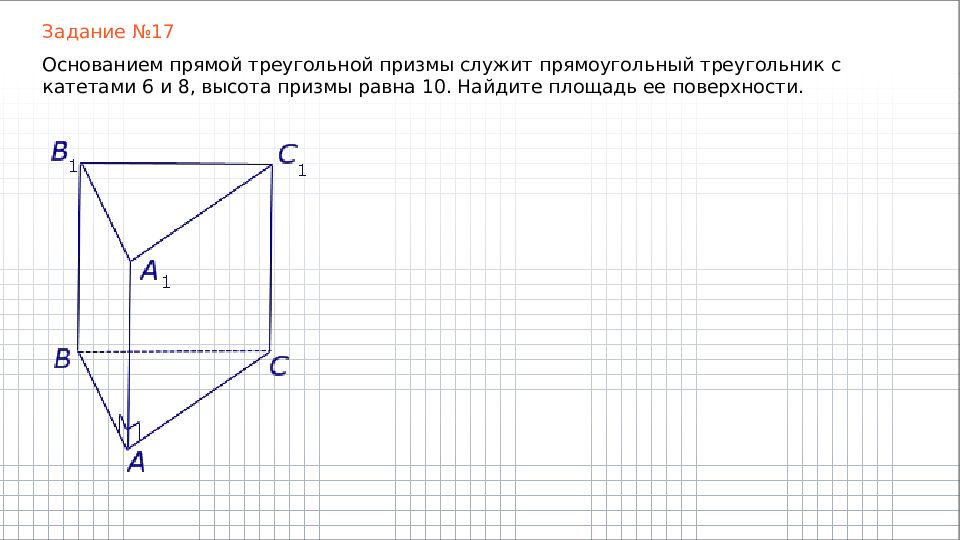
Слайд 34
Задание №17 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Слайд 35
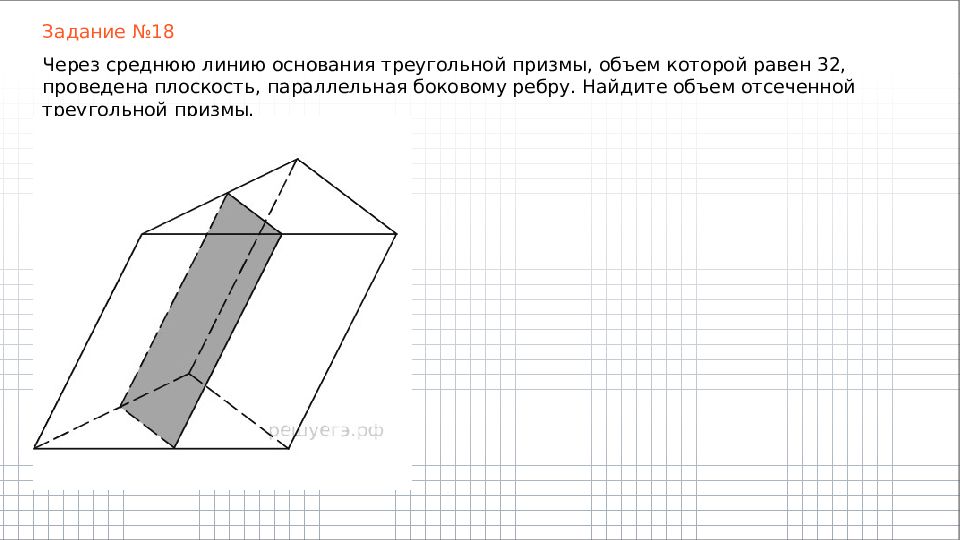
Задание №18 Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Слайд 39: План занятия
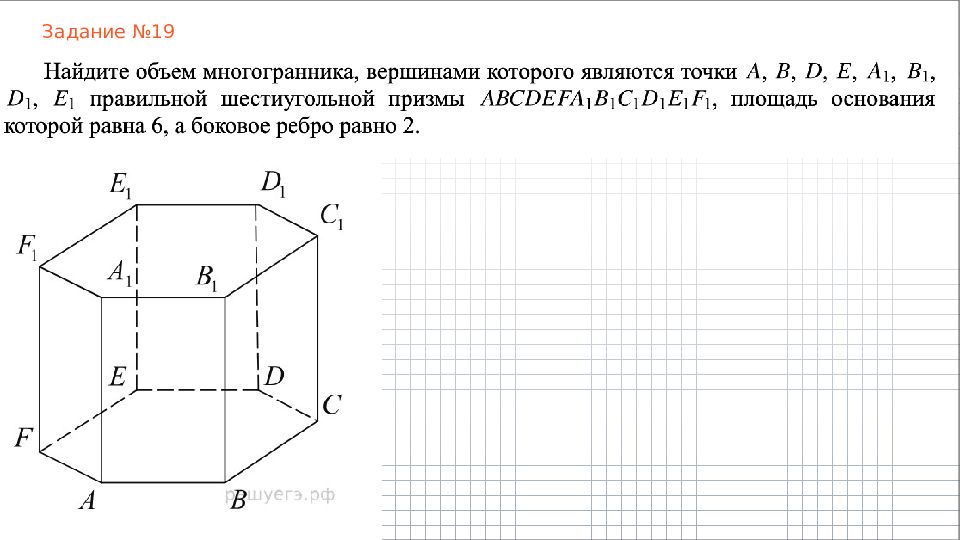
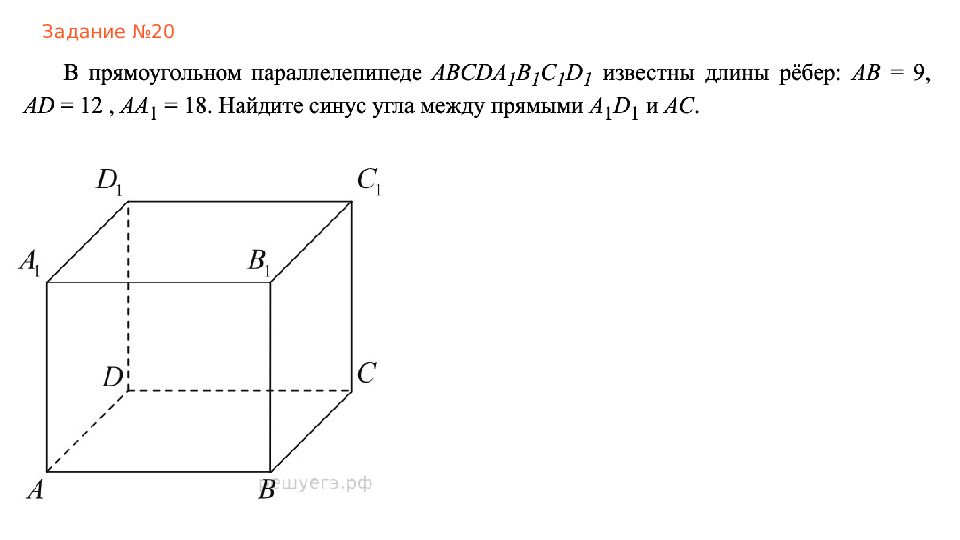
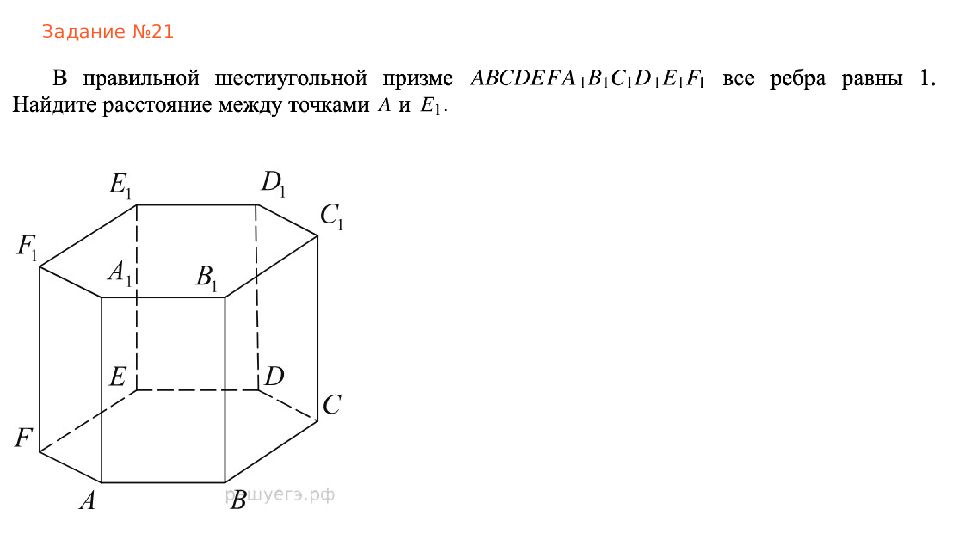
Куб Прямоугольный параллелепипед Составные многогранники Призма