Первый слайд презентации: ОБЪЕМ ШАРА
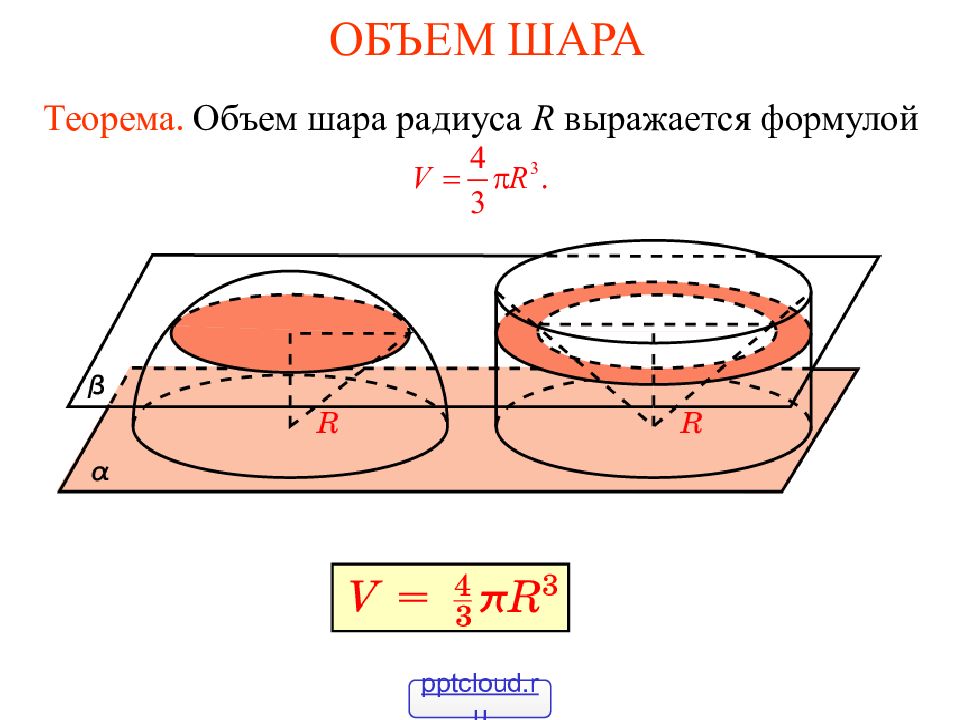
Теорема. Объем шара радиуса R выражается формулой pptcloud.ru
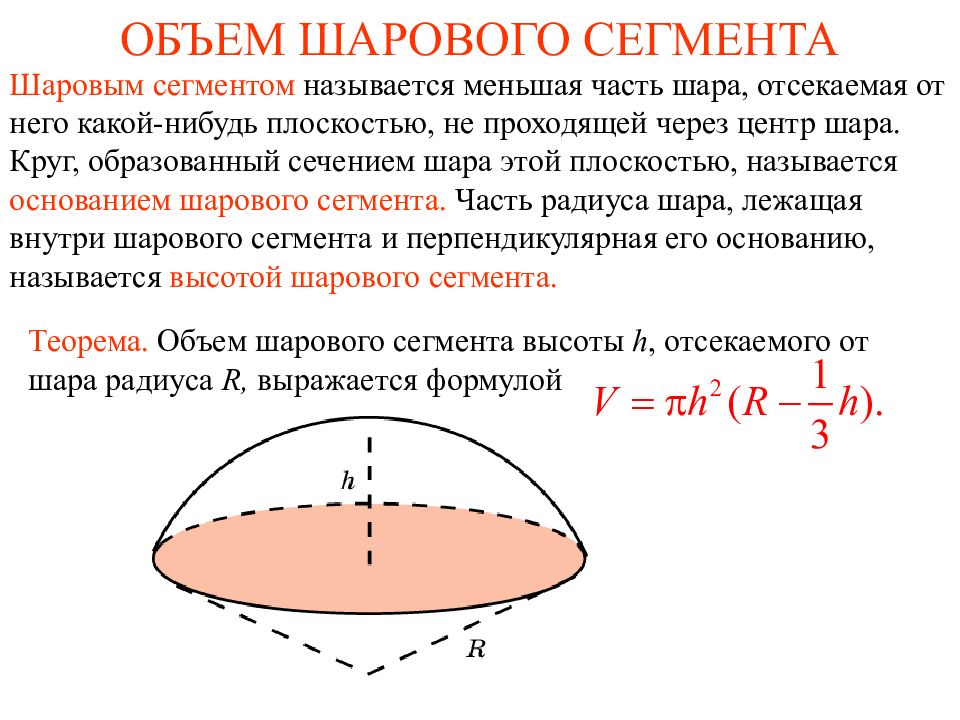
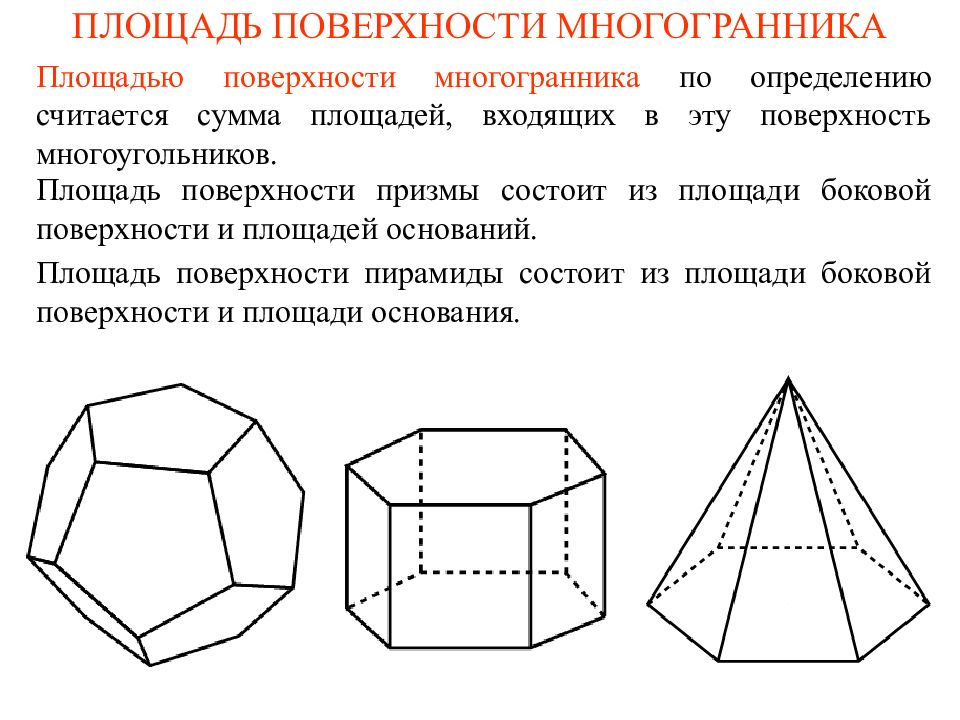
Слайд 2: ОБЪЕМ ШАРОВОГО СЕГМЕНТА
Шаровым сегментом называется меньшая часть шара, отсекаемая от него какой-нибудь плоскостью, не проходящей через центр шара. Круг, образованный сечением шара этой плоскостью, называется основанием шарового сегмента. Часть радиуса шара, лежащая внутри шарового сегмента и перпендикулярная его основанию, называется высотой шарового сегмента. Теорема. Объем шарового сегмента высоты h, отсекаемого от шара радиуса R, выражается формулой
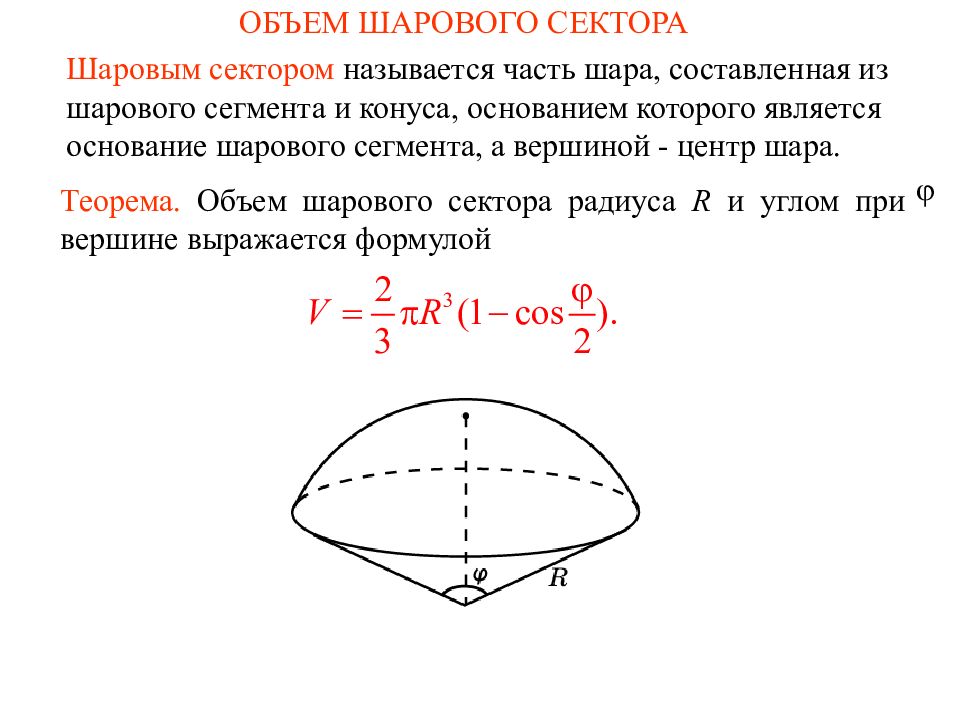
Слайд 3: ОБЪЕМ ШАРОВОГО СЕКТОРА
Теорема. Объем шарового сектора радиуса R и углом при вершине выражается формулой Шаровым сектором называется часть шара, составленная из шарового сегмента и конуса, основанием которого является основание шарового сегмента, а вершиной - центр шара.
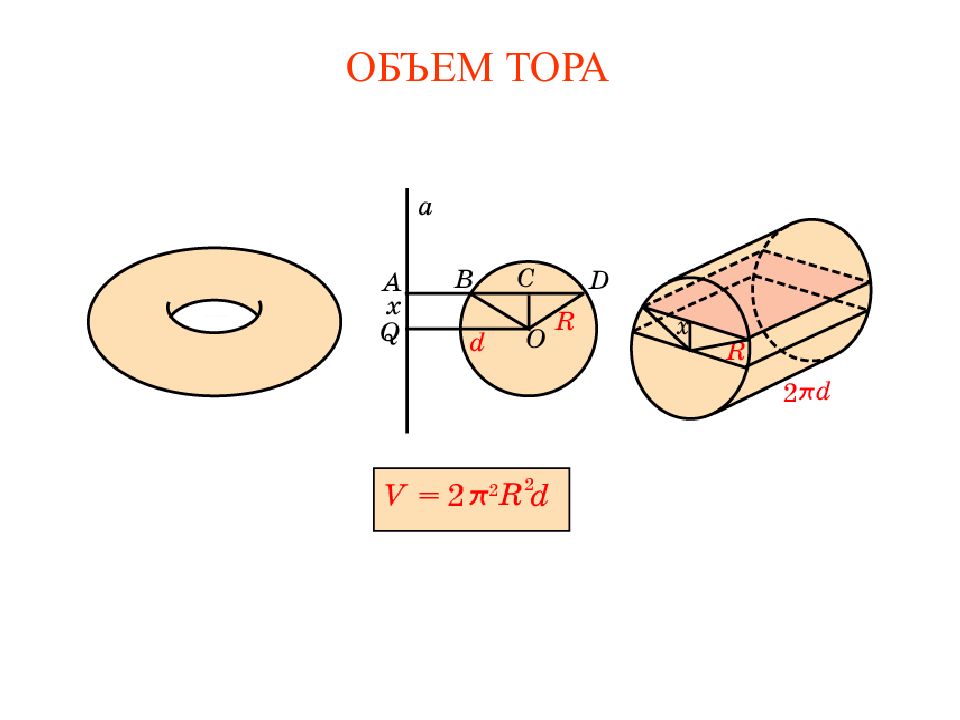
Слайд 5: ОБЪЕМ ТОРА
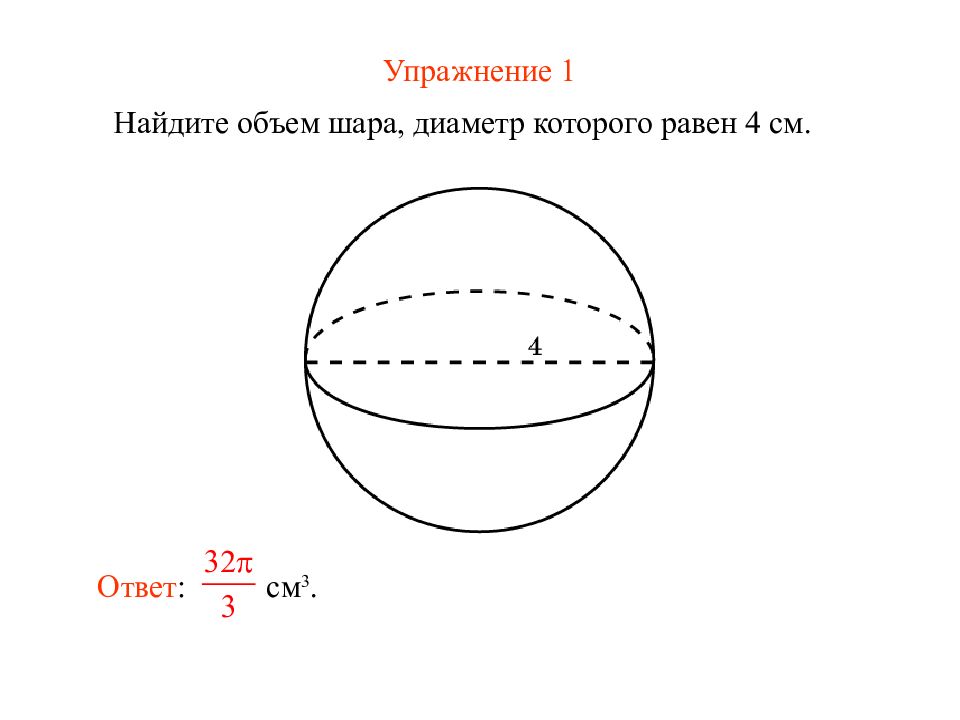
Слайд 6: Упражнение 1
Найдите объем шара, диаметр которого равен 4 см. Ответ : см 3.
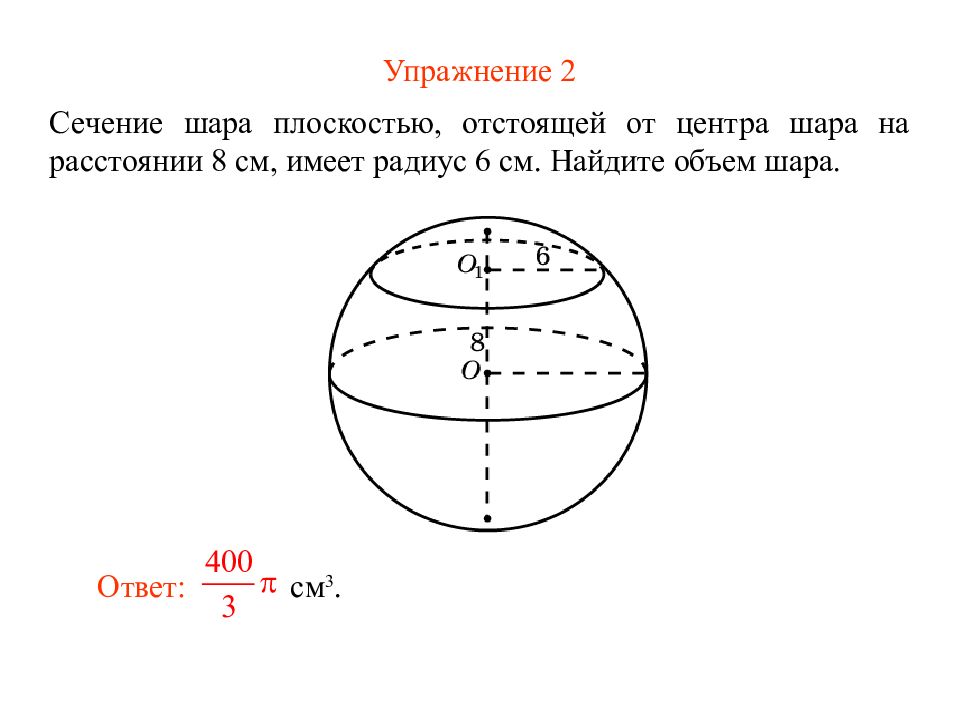
Слайд 7: Упражнение 2
Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите объем шара. Ответ: см 3.
Слайд 8: Упражнение 3
Во сколько раз увеличится объем шара, если его радиус увеличить: а) в 3 раза; б) в 4 раза? Ответ: а) В 27 раз; б) в 64 раза.
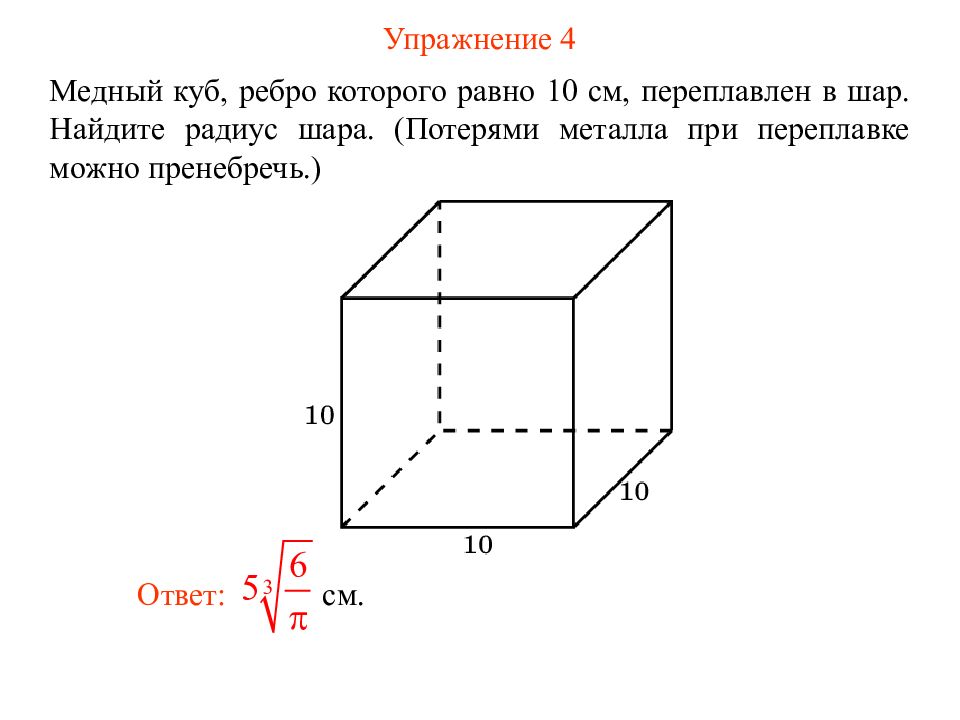
Слайд 9: Упражнение 4
Медный куб, ребро которого равно 10 см, переплавлен в шар. Найдите радиус шара. (Потерями металла при переплавке можно пренебречь.) Ответ: см.
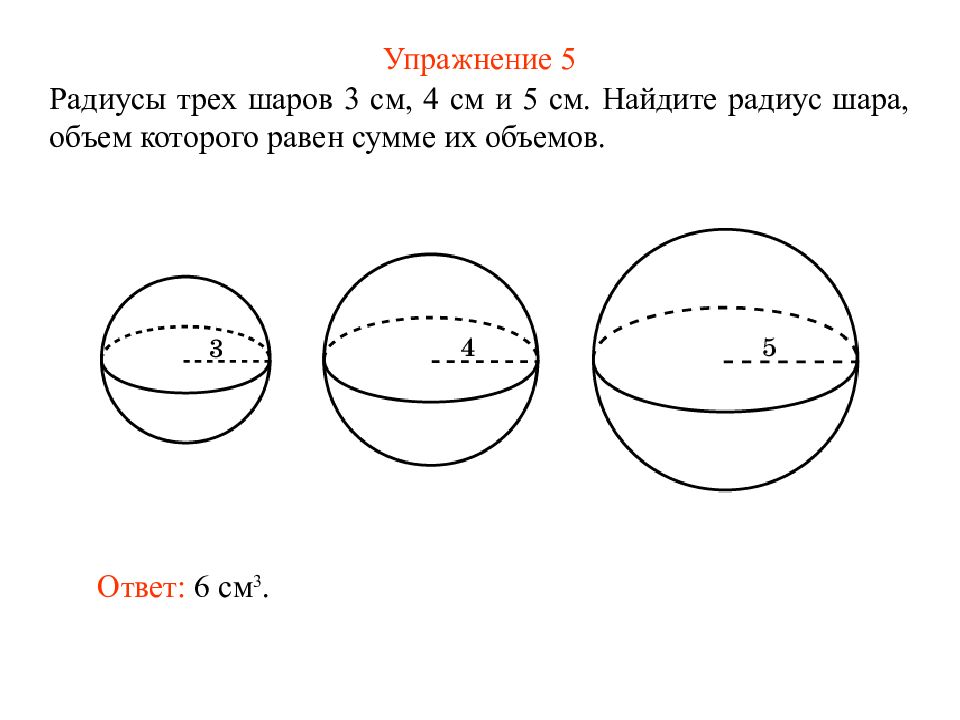
Слайд 10: Упражнение 5
Радиусы трех шаров 3 см, 4 см и 5 см. Найд ите радиус шара, объем которого равен сумме их объемов. Ответ: 6 см 3.
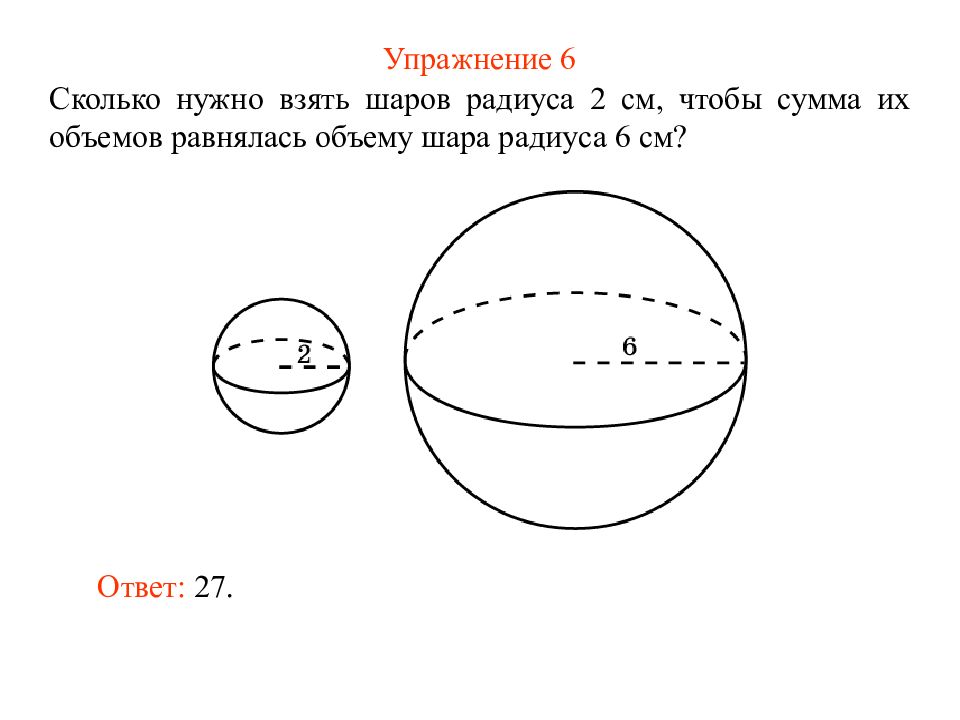
Слайд 11: Упражнение 6
Сколько нужно взять шаров радиуса 2 см, чтобы сумма их объемов равнялась объему шара радиуса 6 см? Ответ: 27.
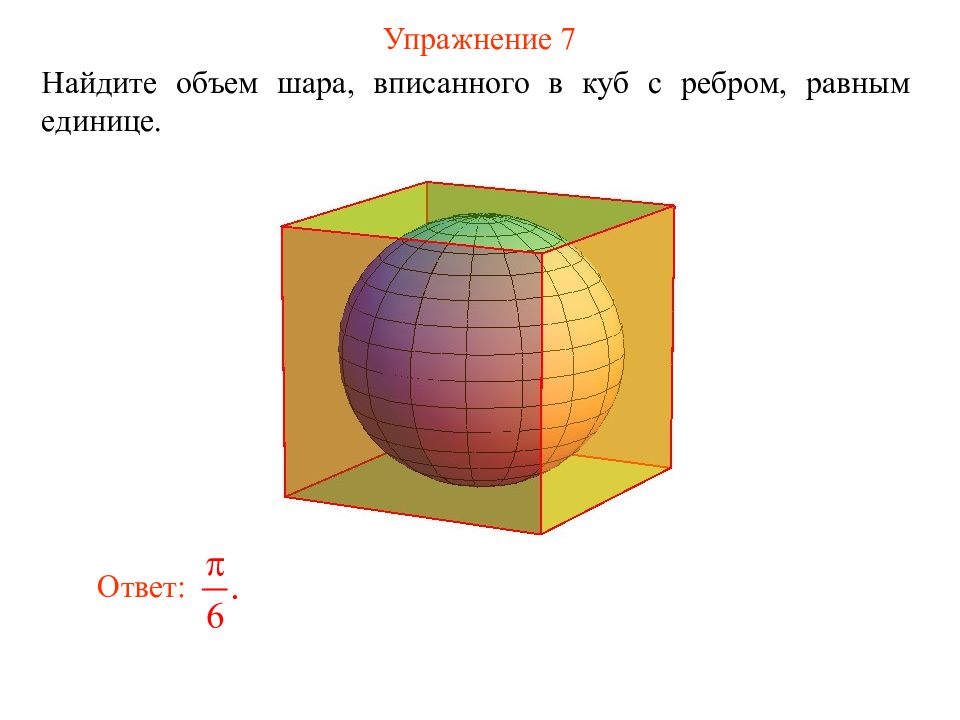
Слайд 12: Упражнение 7
Найдите объем шара, впи санного в куб с ребром, равным единице. Ответ:
Слайд 13: Упражнение 8
Найдите объем шара, описанного около куба с ребром, равным единице. Ответ:
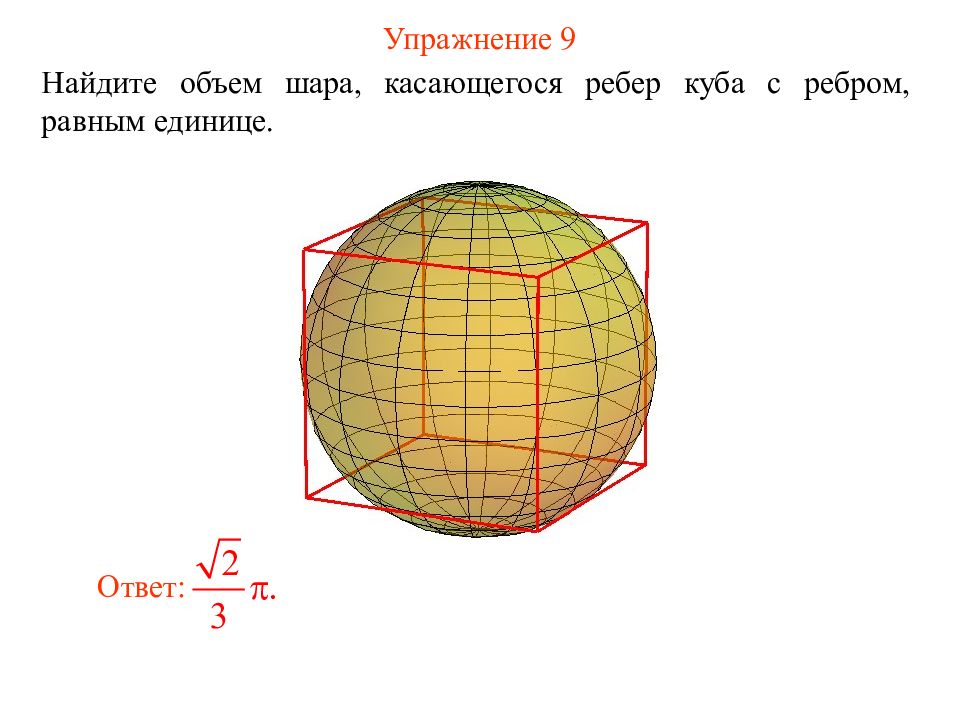
Слайд 14: Упражнение 9
Найдите объем шара, касающегося ребер куба с ребром, равным единице. Ответ:
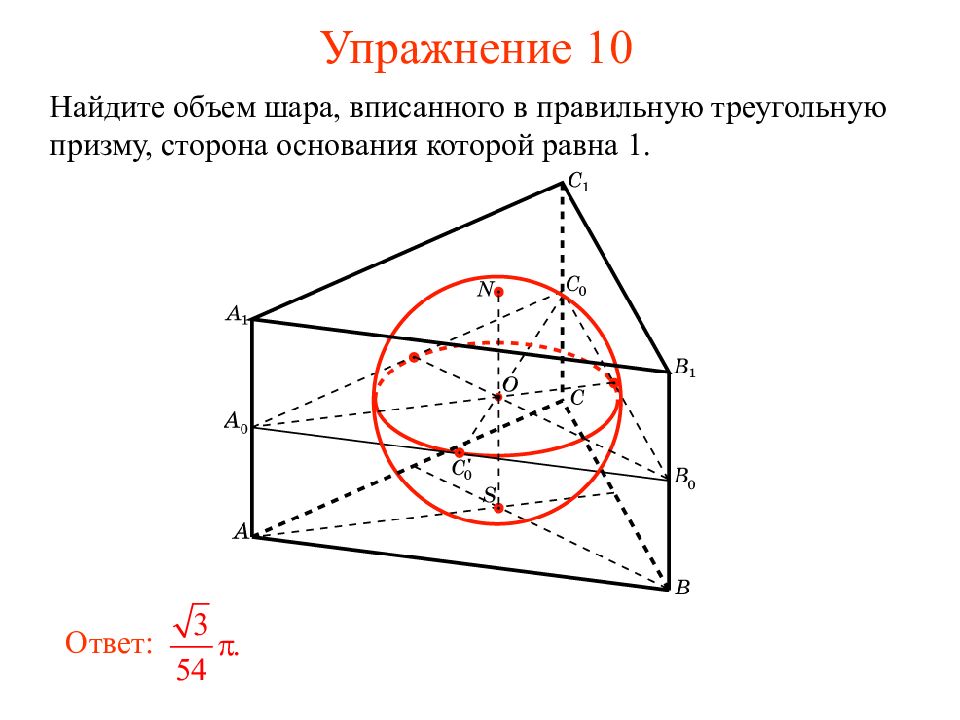
Слайд 15: Упражнение 10
Найдите объем шара, вписанного в правильную треугольную призму, сторона основания которой равна 1. Ответ:
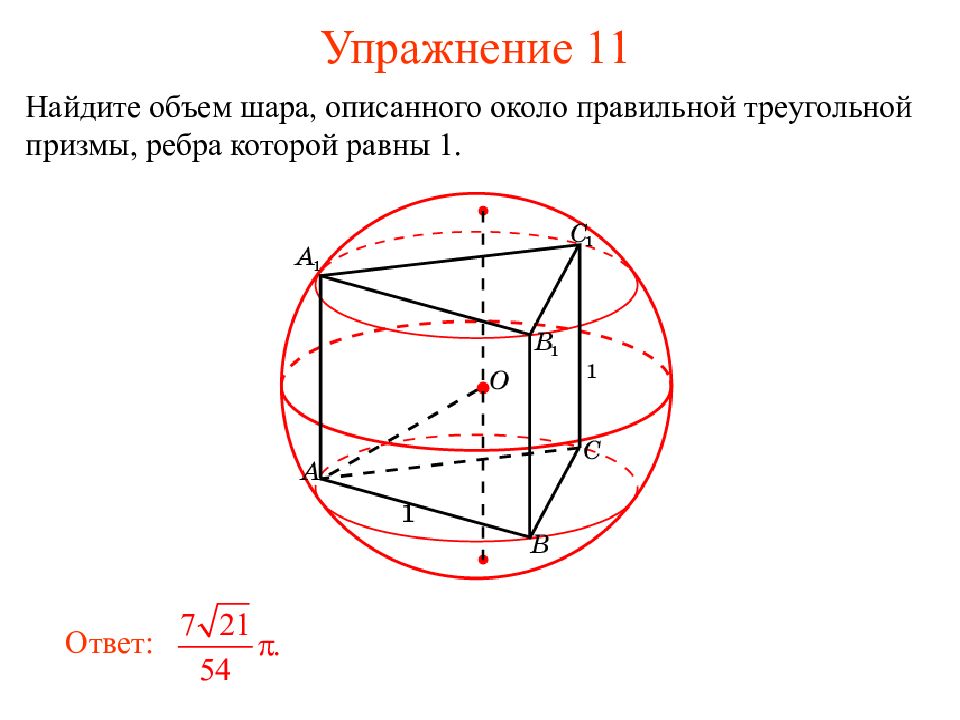
Слайд 16: Упражнение 11
Найдите объем шара, описанного около правильной треугольной призмы, ребра которой равны 1. Ответ:
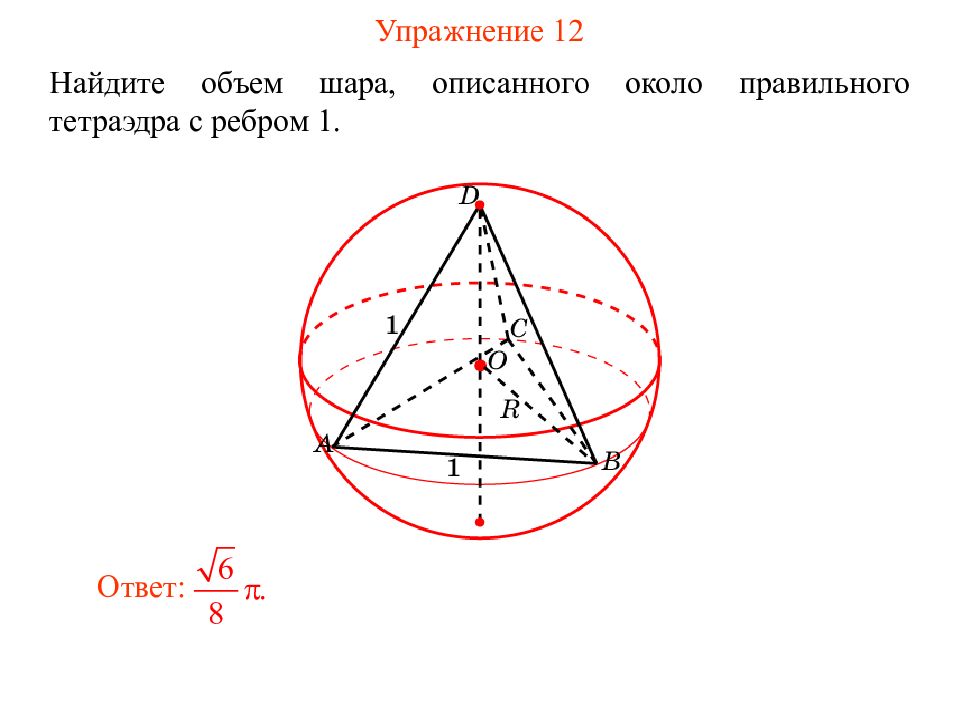
Слайд 17: Упражнение 12
Найдите объем шара, описанного около правильного тетраэдра с ребром 1. Ответ:
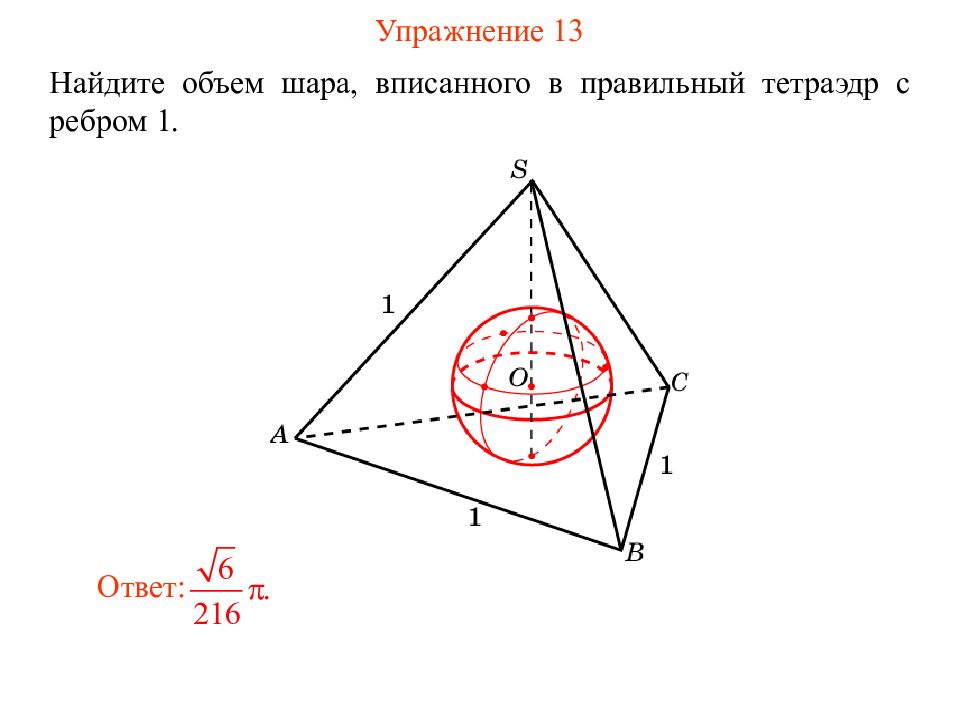
Слайд 18: Упражнение 13
Найдите объем шара, в писанного в правильн ый тетраэдр с ребром 1. Ответ:
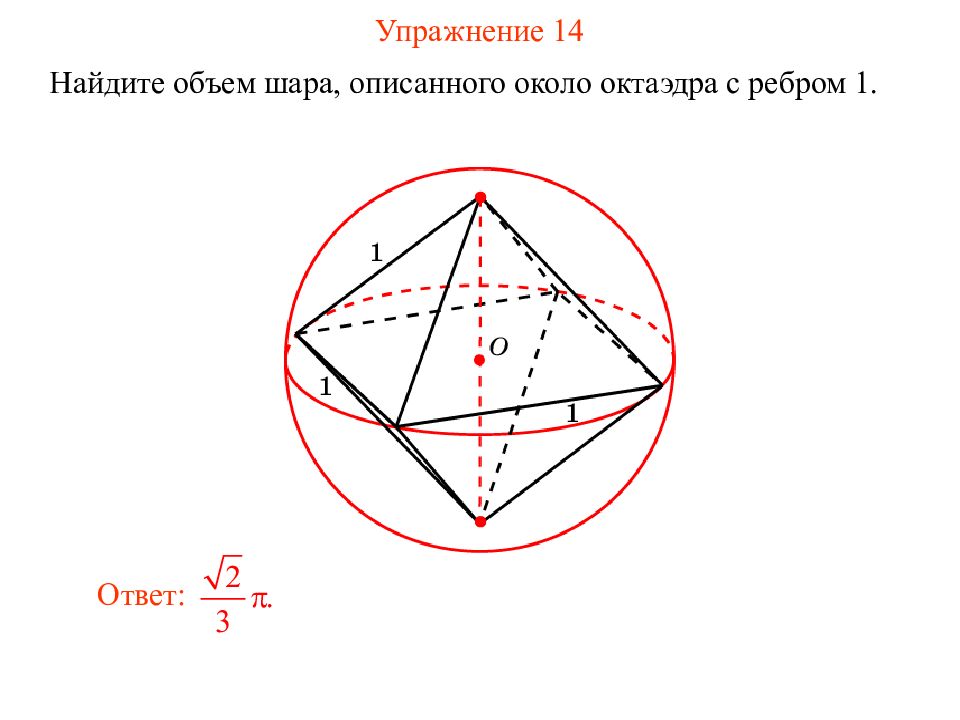
Слайд 19: Упражнение 14
Найдите объем шара, о писанного около октаэдр а с ребром 1. Ответ:
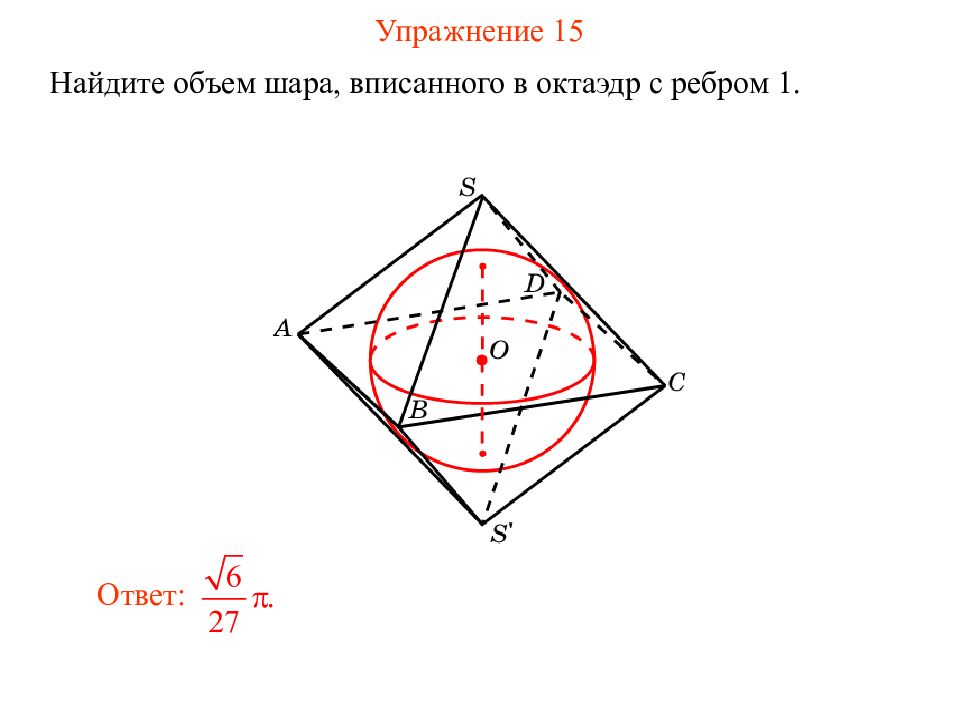
Слайд 20: Упражнение 15
Найдите объем шара, вписанного в октаэдр с ребром 1. Ответ:
Слайд 21: Упражнение 16
Найдите объем шара, вписанного в цилиндр, радиус основания которого равен 1. Ответ:
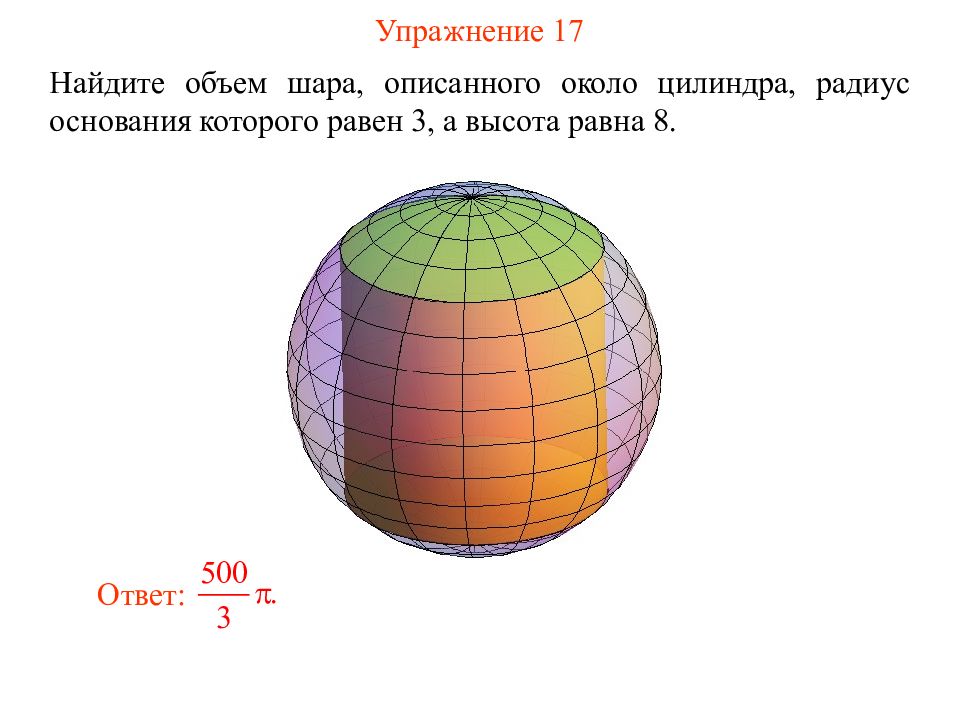
Слайд 22: Упражнение 17
Найдите объем шара, о писанного около цилиндра, радиус основания которого равен 3, а высота равна 8. Ответ:
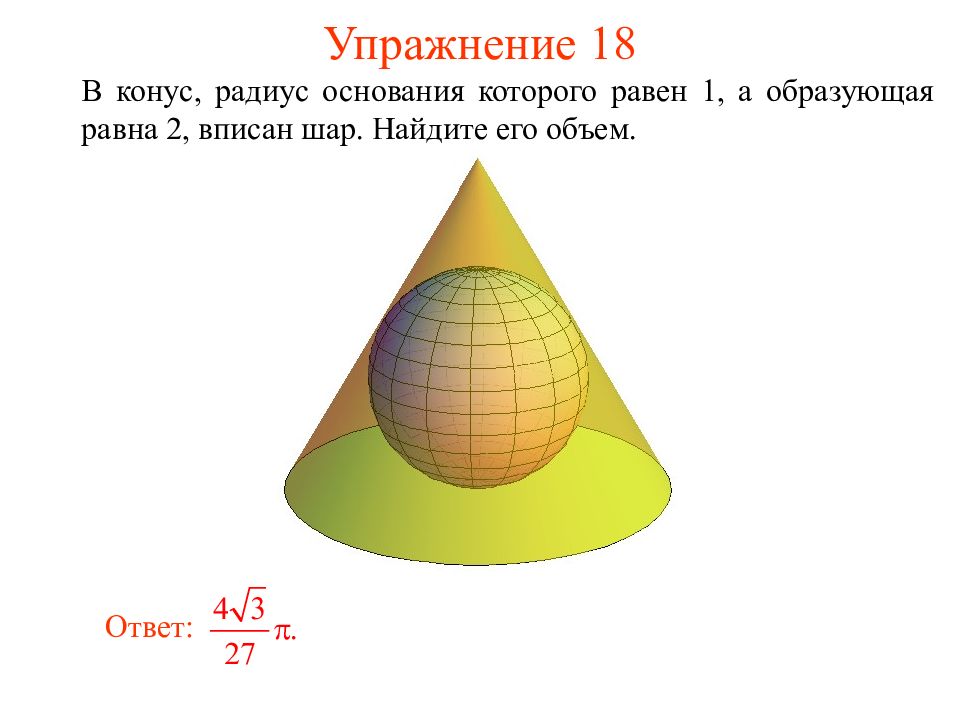
Слайд 23: Упражнение 18
В конус, радиус основания которого равен 1, а образующая равна 2, вписан шар. Найдите его объем. Ответ:
Слайд 24: Упражнение 19
Около конуса, радиус основания которого равен 1, а образующая равна 2, описан шар. Найдите его объем. Ответ:
Слайд 25: Упражнение 20
В усеченный конус, радиусы оснований которого равны 2 и 1, вписан шар. Найдите его объем. Ответ:
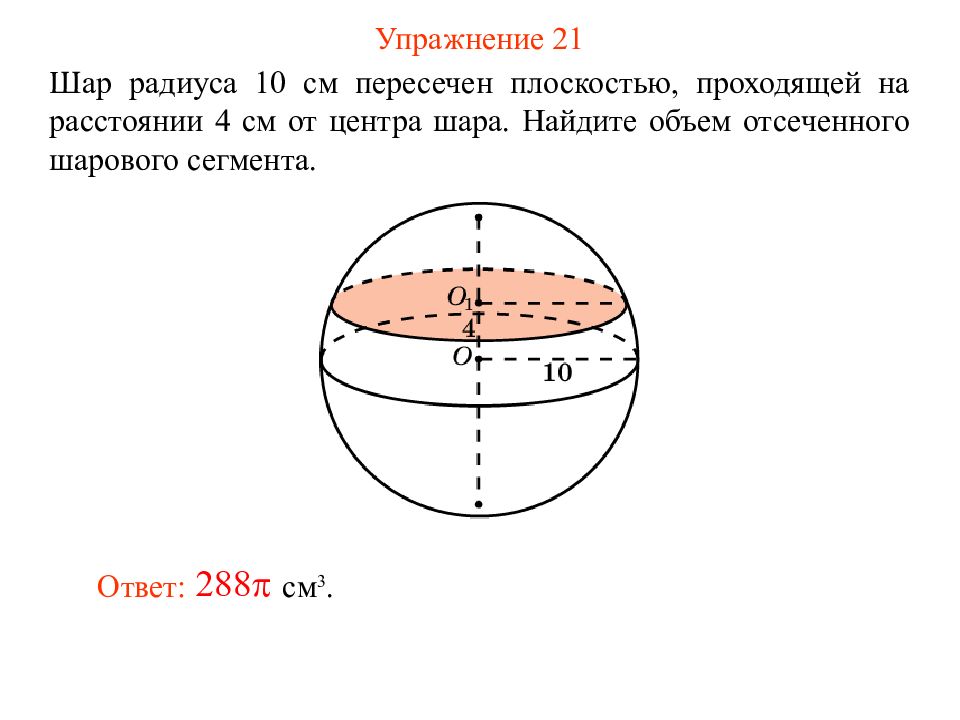
Слайд 26: Упражнение 21
Шар радиуса 10 см пересечен плоскостью, проходящей на расстоянии 4 см от центра шара. Найдите объем отсеченного шарового сегмента. Ответ: см 3.
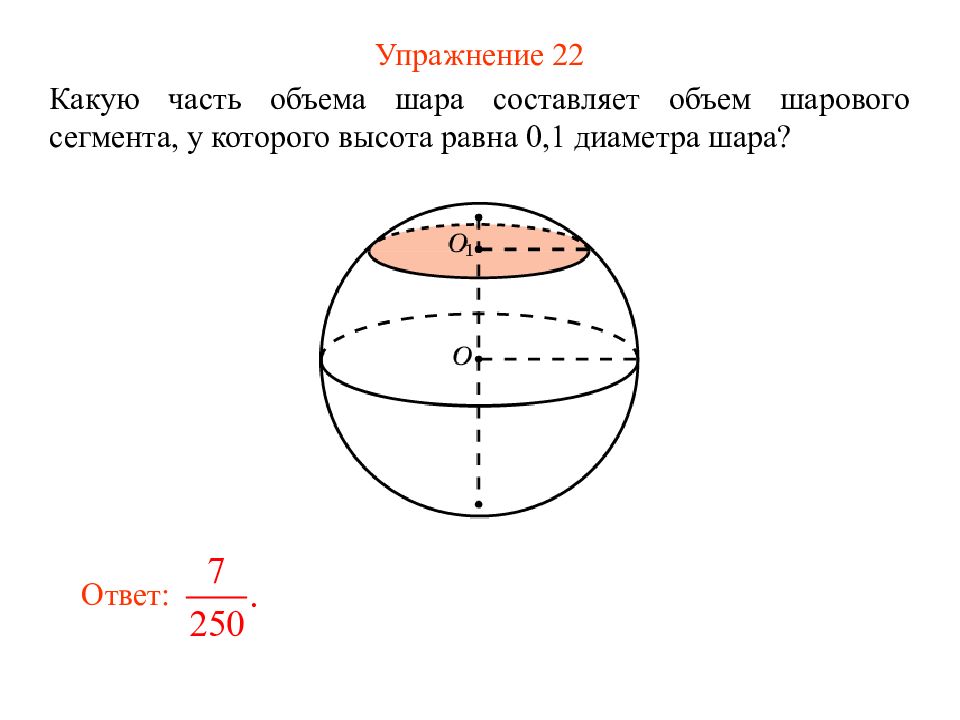
Слайд 27: Упражнение 22
Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара? Ответ:
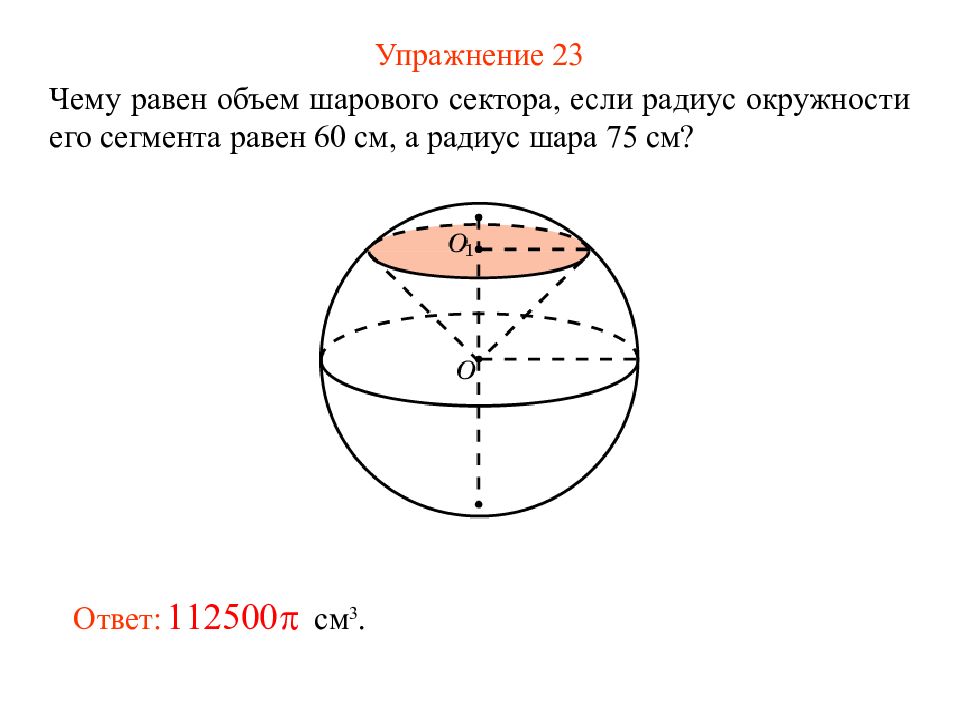
Слайд 28: Упражнение 23
Чему равен объем шарового сектора, если радиус окружности его сегмента равен 60 см, а радиус шара 75 см? Ответ: см 3.
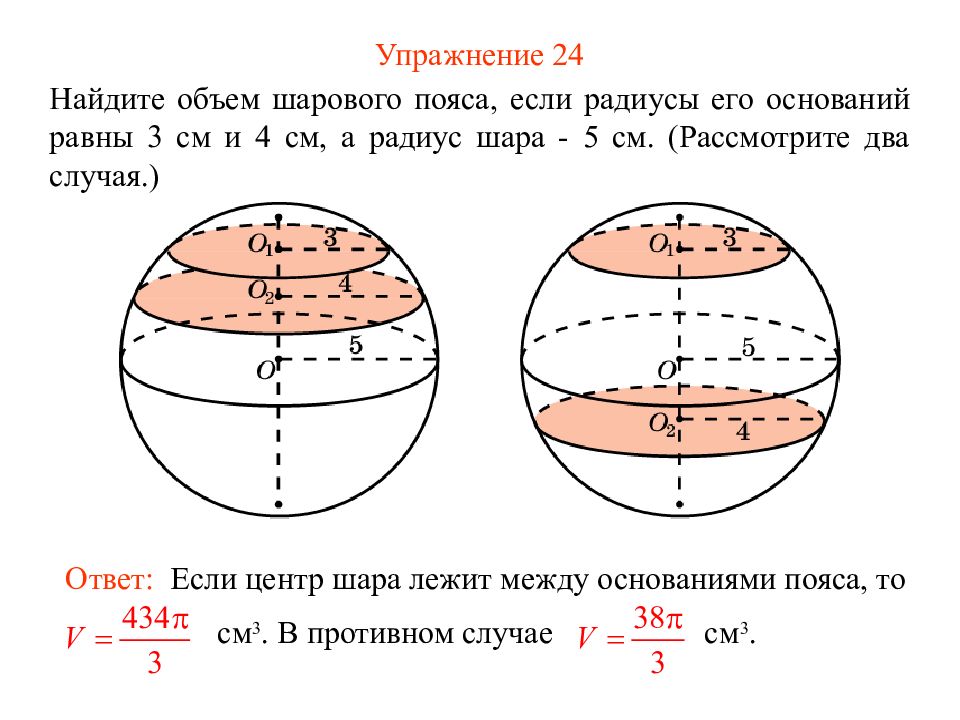
Слайд 29: Упражнение 24
Найдите объем шарового пояса, если радиусы его оснований равны 3 см и 4 см, а радиус шара - 5 см. (Рассмотрите два случая.) Ответ: Если центр шара лежит между основаниями пояса, то см 3. В противном случае см 3.
Последний слайд презентации: ОБЪЕМ ШАРА: Упражнение 25
Шар касается всех двенадцати ребер единичного куба. Найдите объем части шара, заключенной внутри этого куба. Решение: Часть шара, заключенная внутри куба, получается отсечением от шара радиуса шести шаровых сегментов высоты Объем каждого такого сегмента равен Объем части шара, содержащейся в кубе, равен Ответ: