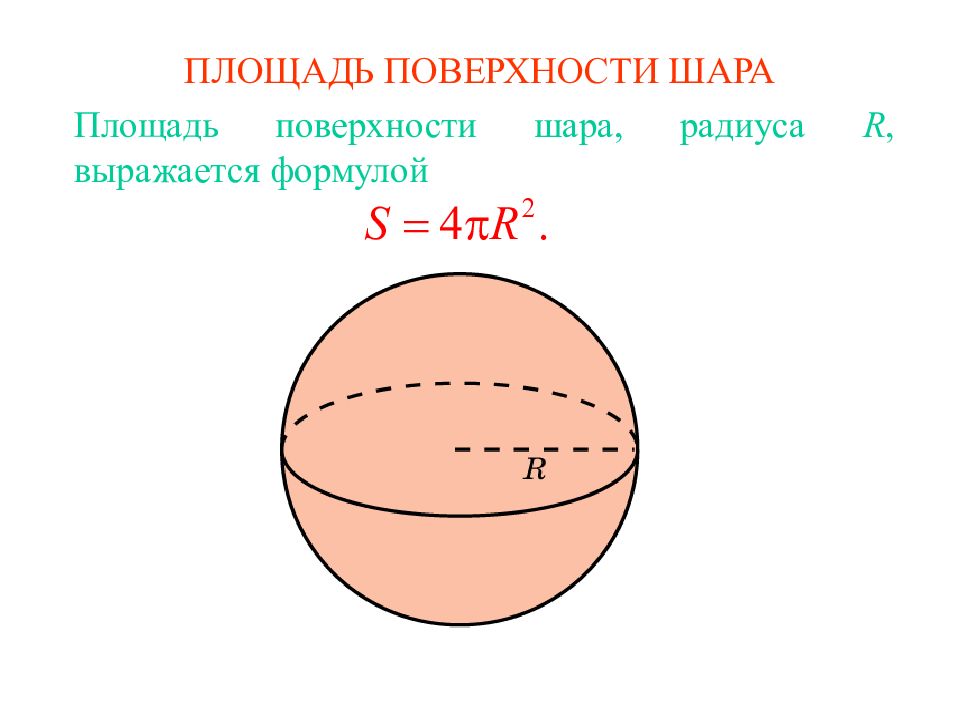
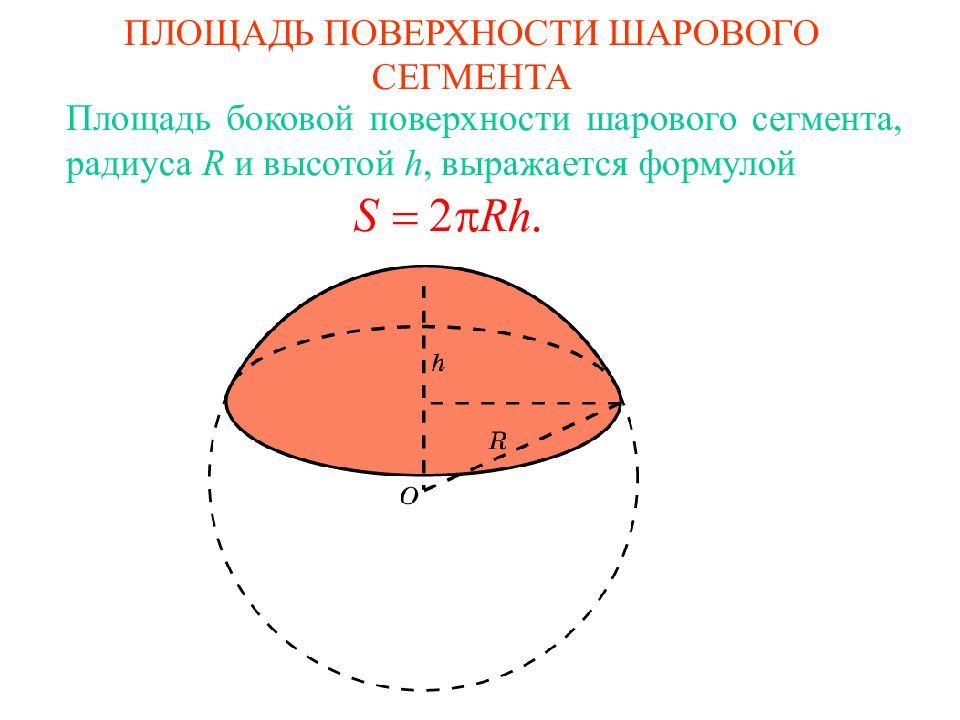
Первый слайд презентации: ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРА
Площадь поверхности шара, радиус а R, выражается формулой
Площадь боковой поверхности шарового сегмента, радиус а R и высотой h, выражается формулой
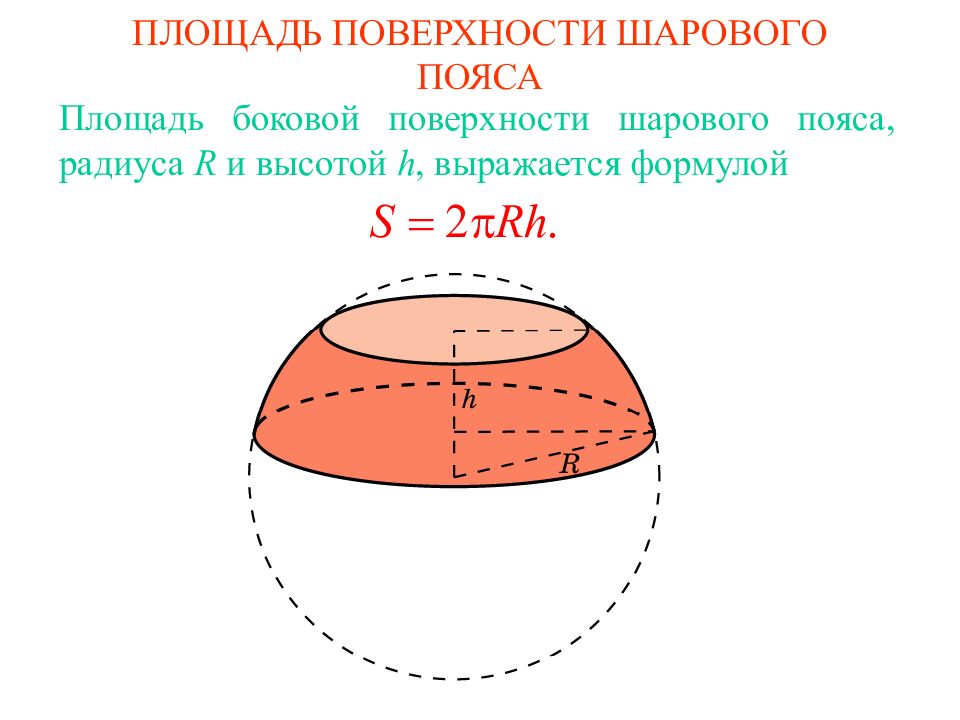
Слайд 3: ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРОВОГО ПОЯСА
Площадь боковой поверхности шарового пояса, радиус а R и высотой h, выражается формулой
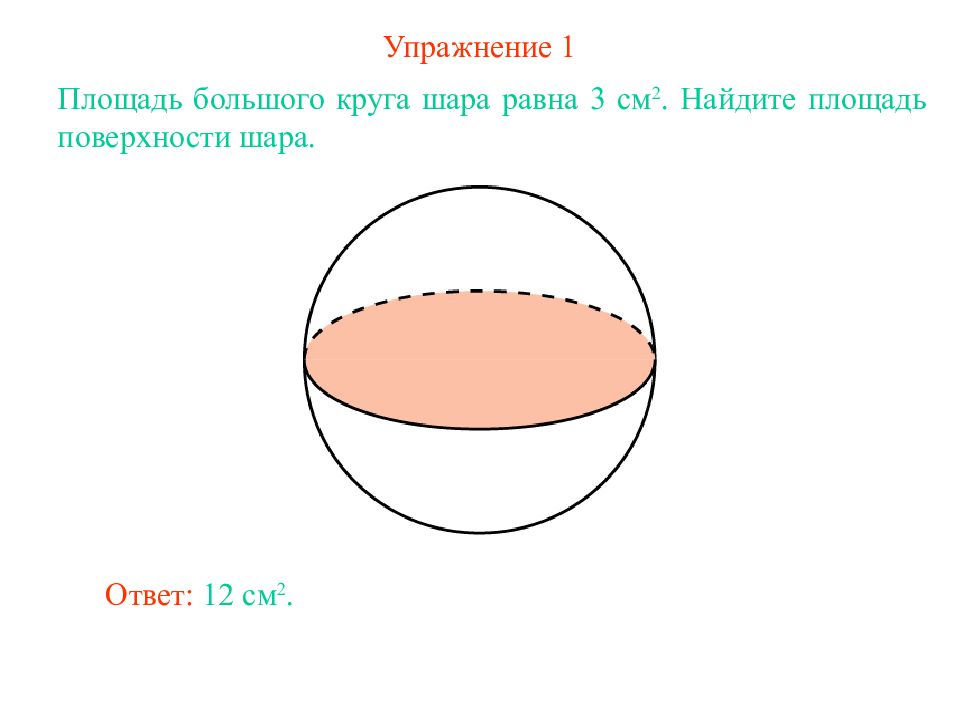
Слайд 4: Упражнение 1
Площадь большого круга шара равна 3 см 2. Найдите площадь поверхности шара. Ответ: 12 см 2.
Слайд 5: Упражнение 2
Как изменится площадь поверхности шара, если увеличить радиус шара в: а) 2 раза; б) 3 раза; в) n раз? Ответ: Увеличится в: а) 4 раза; б) 9 раз; в) n 2 раз.
Слайд 6: Упражнение 3
Площади поверхностей двух шаров относятся как 4 : 9. Найдите отношение их диаметров. Ответ: 2:3.
Слайд 7: Упражнение 4
Объём шара равен 288 дм 3. Найдите площадь его поверхности. Ответ: 144 дм 2.
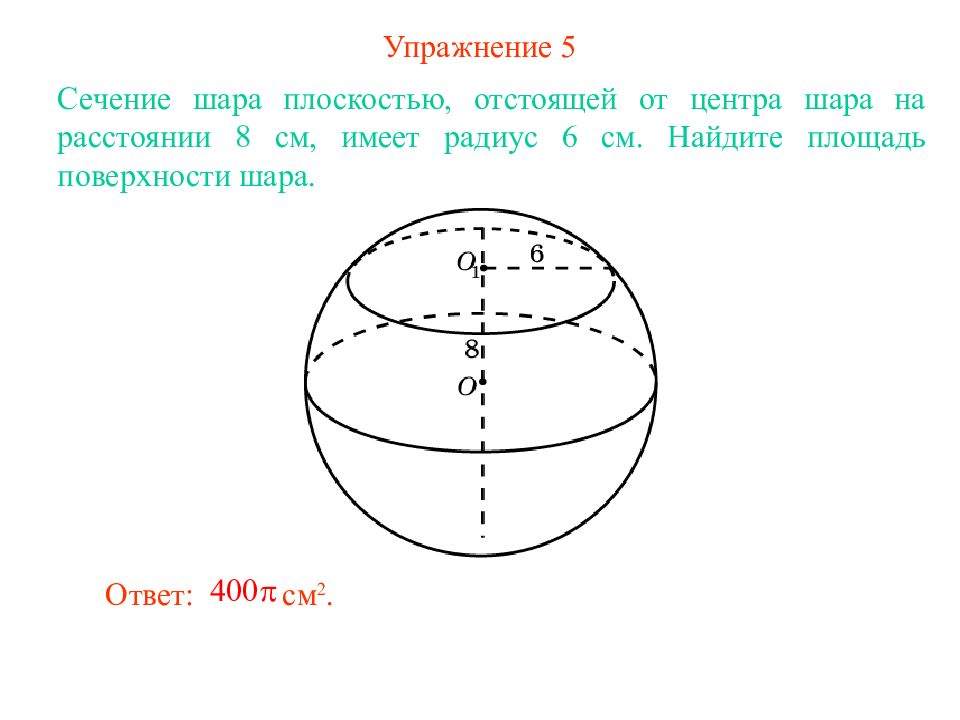
Слайд 8: Упражнение 5
Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите площадь поверхности шара. Ответ: см 2.
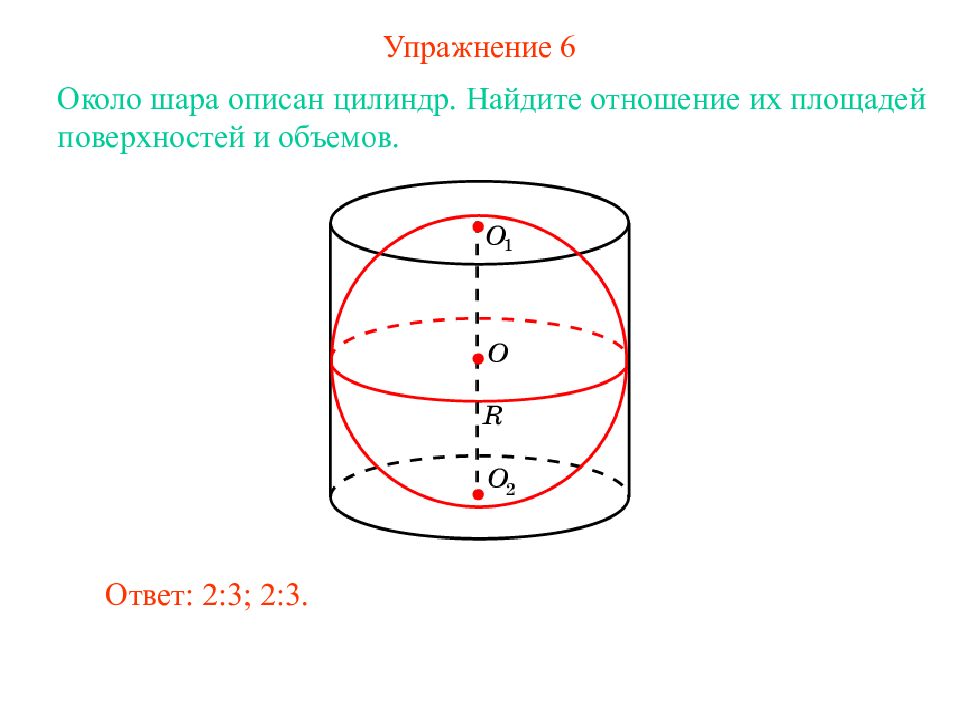
Слайд 9: Упражнение 6
Около шара описан цилиндр. Найдите отношение их площадей поверхностей и объемов. Ответ: 2:3; 2:3.
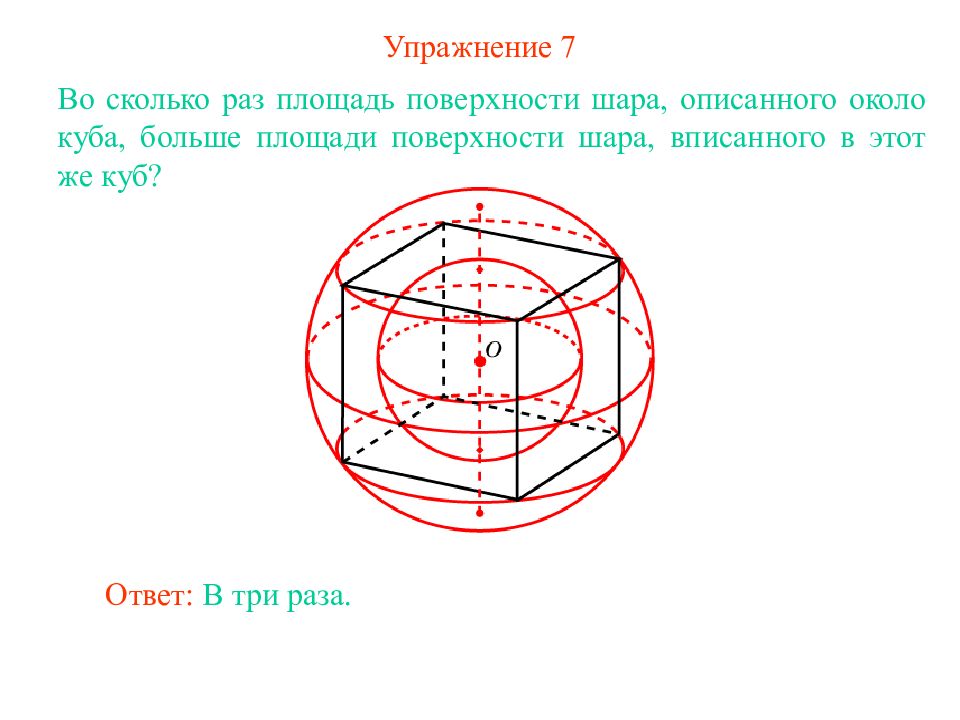
Слайд 10: Упражнение 7
Во сколько раз площадь поверхности шара, описанного около куба, больше площади поверхности шара, вписанного в этот же куб? Ответ: В три раза.
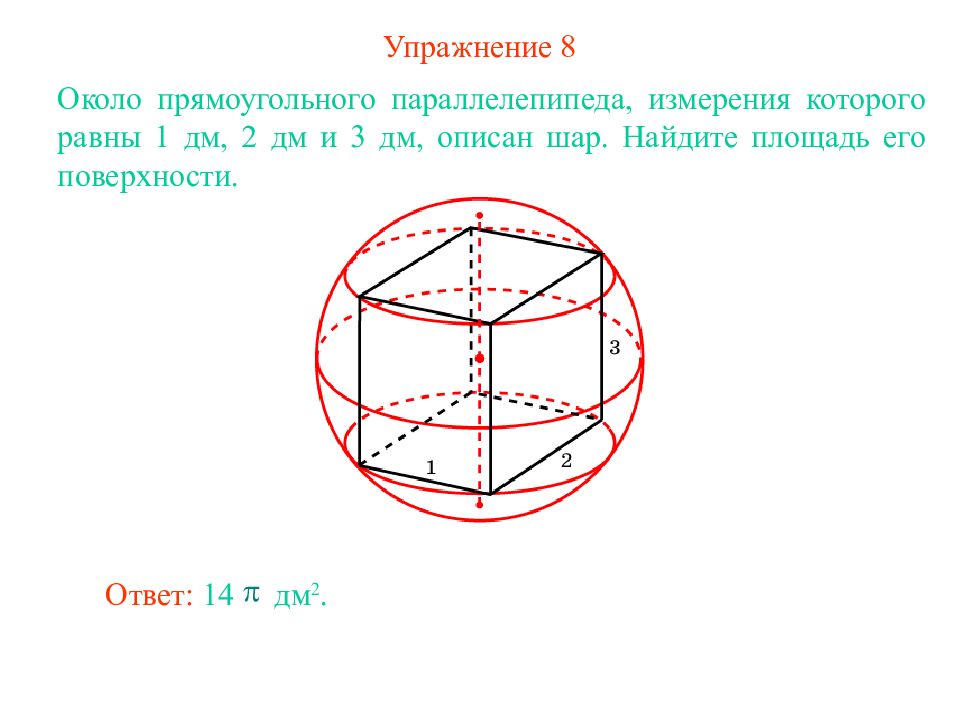
Слайд 11: Упражнение 8
Около прямоугольного параллелепипеда, измерения которого равны 1 дм, 2 дм и 3 дм, описан шар. Найдите площадь его поверхности. Ответ: 14 дм 2.
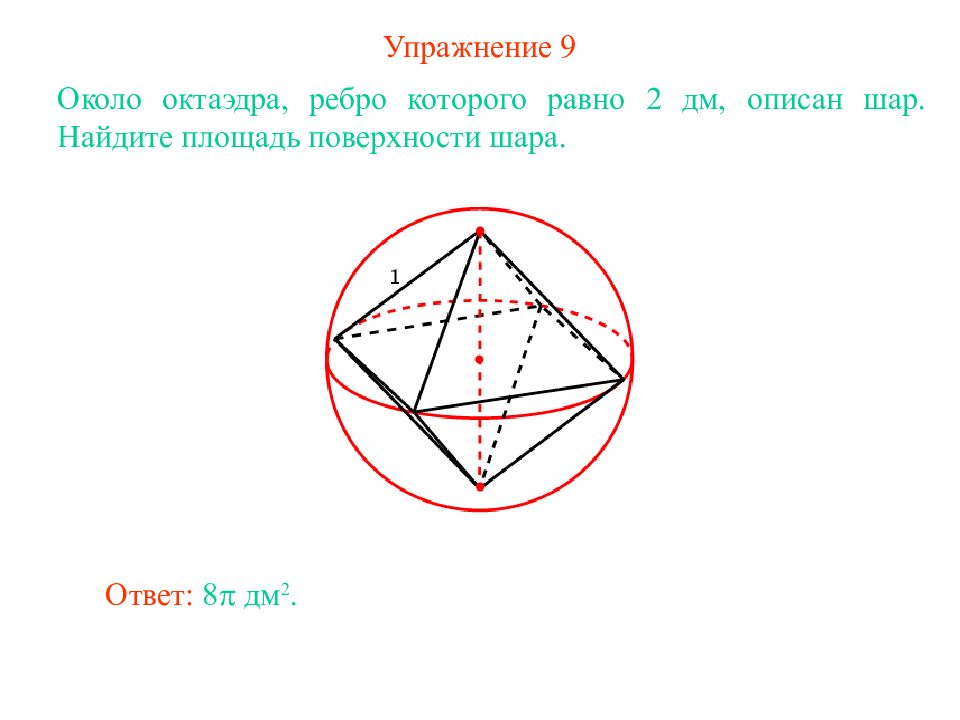
Слайд 12: Упражнение 9
Около октаэдра, ребро которого равно 2 дм, описан шар. Найдите площадь поверхности шара. Ответ: 8 дм 2.
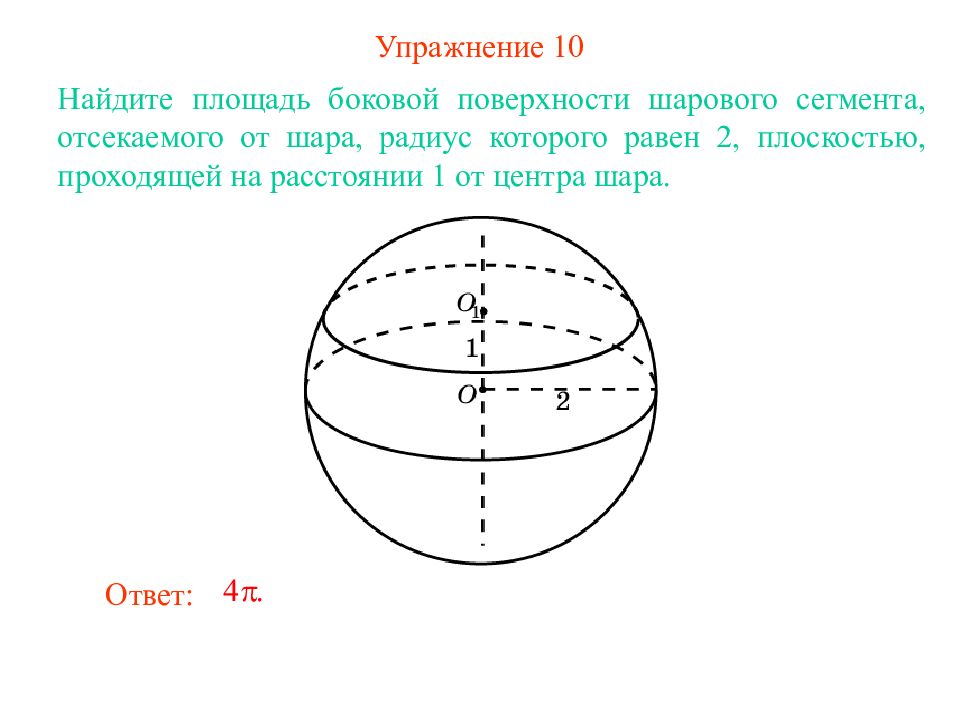
Слайд 13: Упражнение 1 0
Найдите площадь боковой поверхности шарового сегмента, отсекаемого от шара, радиус которого равен 2, плоскостью, проходящей на расстоянии 1 от центра шара. Ответ:
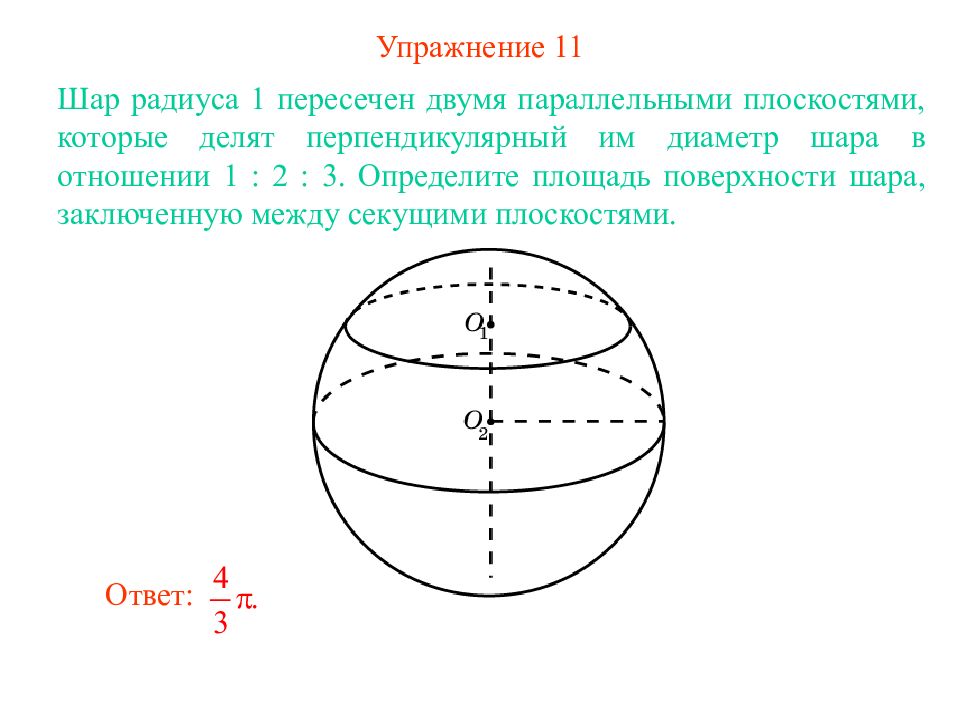
Слайд 14: Упражнение 1 1
Шар радиуса 1 пересечен двумя параллельными плоскостями, которые делят перпендикулярный им диаметр шара в отношении 1 : 2 : 3. Определите площадь поверхности шара, заключенную между секущими плоскостями. Ответ:
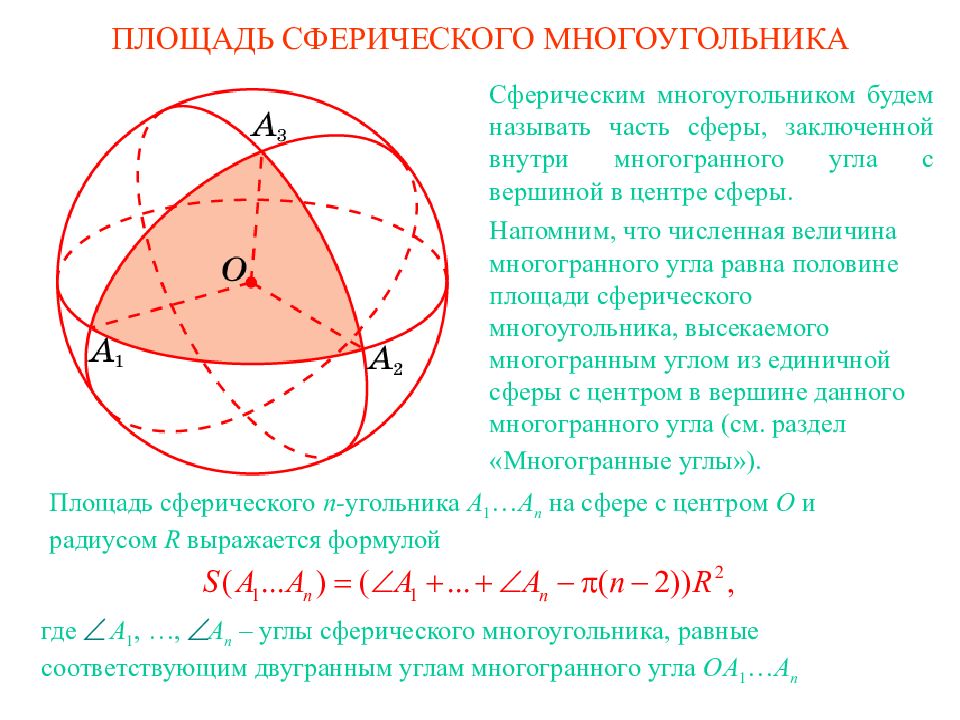
Слайд 15: ПЛОЩАДЬ СФЕРИЧЕСКОГО МНОГОУГОЛЬНИКА
Сферическим многоугольником будем называть часть сферы, заключенной внутри многогранного угла с вершиной в центре сферы. Напомним, что численная величина м ногогранн ого угл а равна половин е площади сферического многоугольника, высекаемого многогранным углом из единичной сферы с центром в вершине данного многогранного угла ( см. раздел «Многогранные углы»). где A 1, …, A n – углы сферического многоугольника, равные соответствующим двугранным углам многогранного угла OA 1 … A n Площадь сферического n- угольника A 1 … A n на сфере с центром O и радиусом R выражается формулой
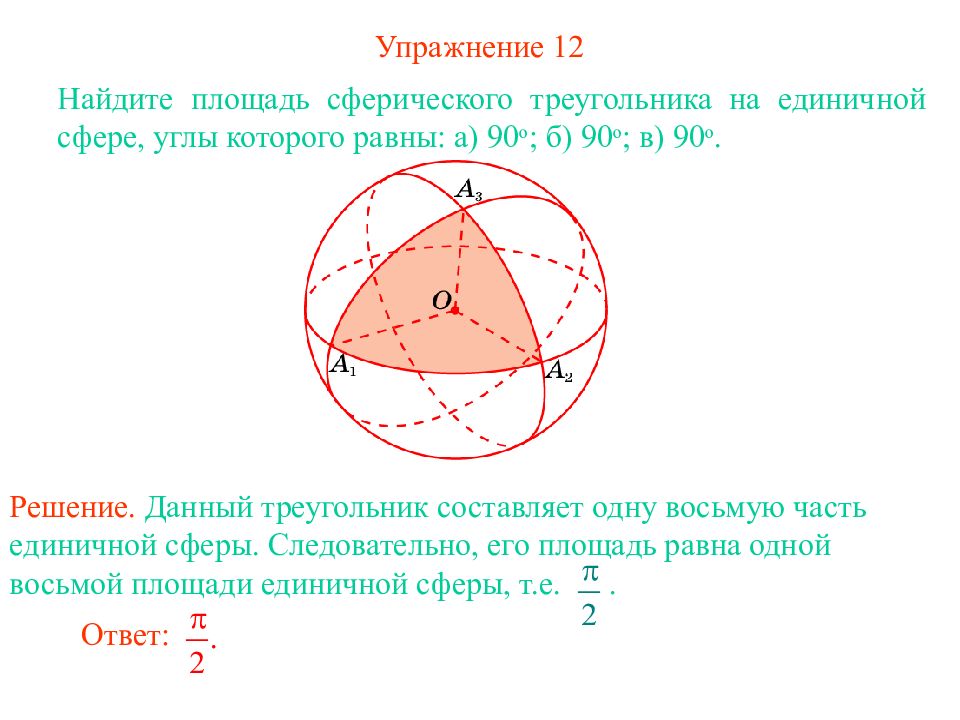
Слайд 16: Упражнение 1 2
Найдите площадь сферического треугольника на единичной сфере, углы которого равны: а) 90 о ; б) 90 о ; в) 90 о. Решение. Данный треугольник составляет одну восьмую часть единичной сферы. Следовательно, его площадь равна одной восьмой площади единичной сферы, т.е.. Ответ:
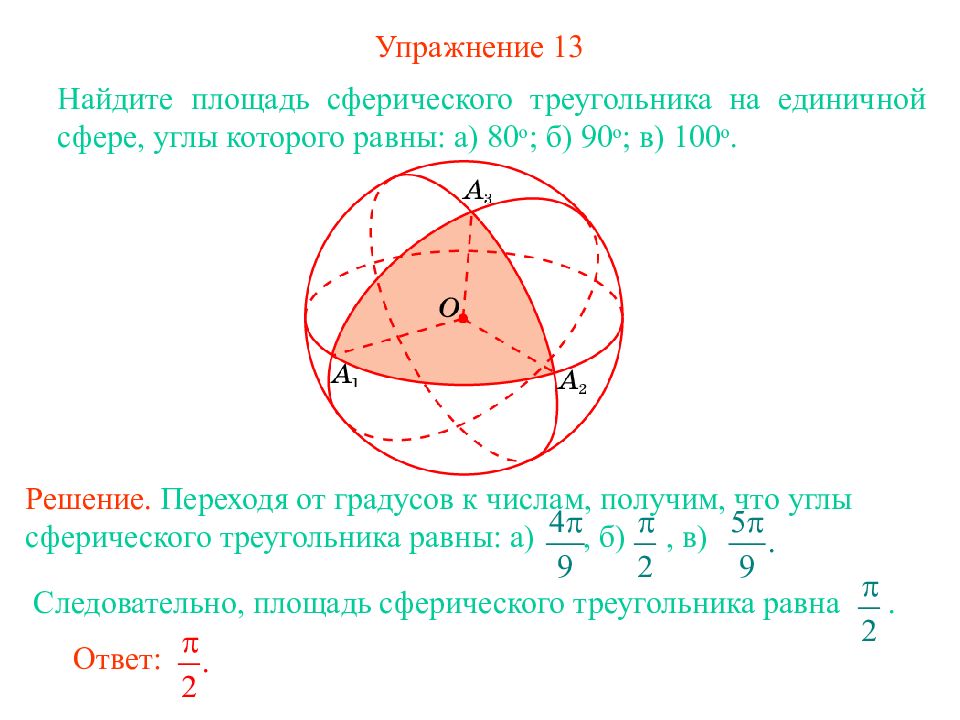
Слайд 17: Упражнение 1 3
Найдите площадь сферического треугольника на единичной сфере, углы которого равны: а) 80 о ; б) 90 о ; в) 100 о. Решение. Переходя от градусов к числам, получим, что углы сферического треугольника равны: а), б), в) Следовательно, площадь сферического треугольника равна. Ответ:
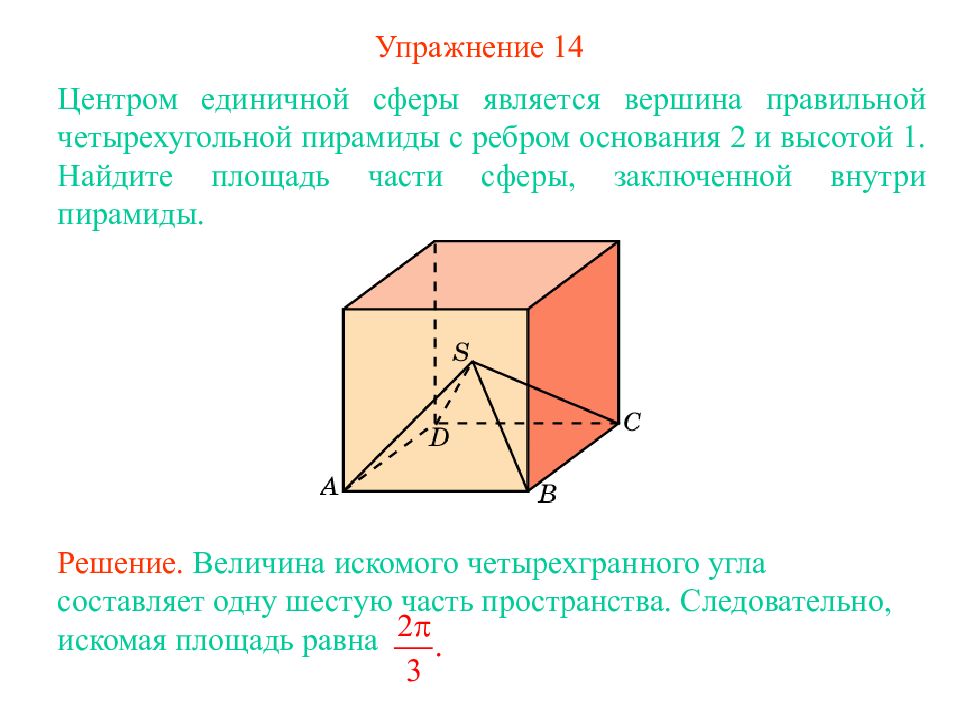
Слайд 18: Упражнение 1 4
Центром единичной сферы является вершина правильной четырехугольной пирамиды с ребром основания 2 и высотой 1. Найдите площадь части сферы, заключенной внутри пирамиды. Решение. Величина искомого четырехгранного угла составляет одну шестую часть пространства. Следовательно, искомая площадь равна
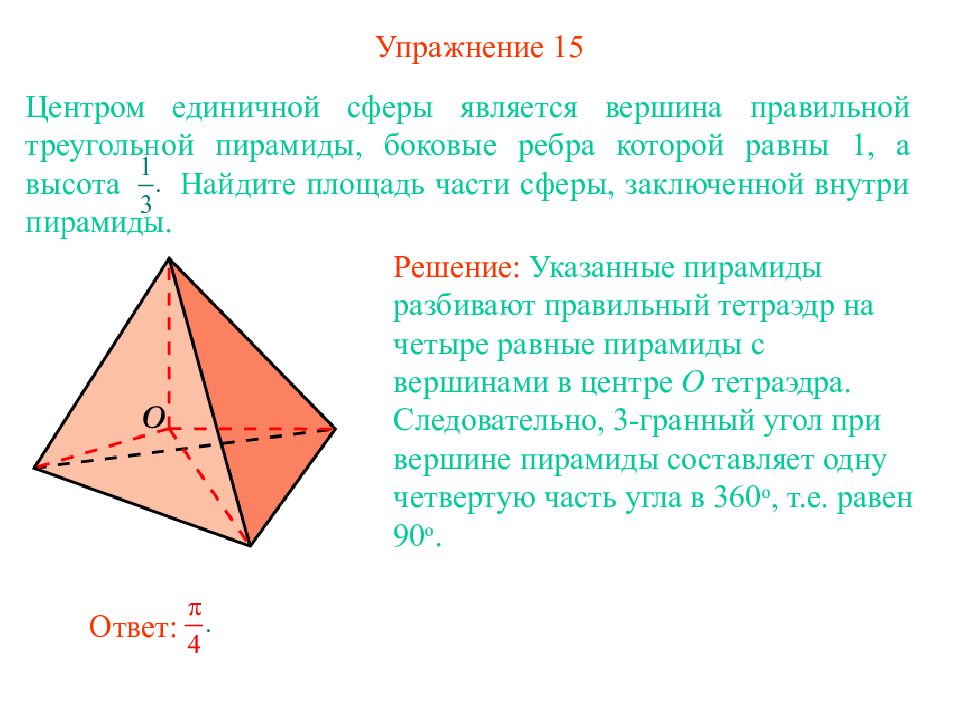
Слайд 19: Упражнение 15
Центром единичной сферы является вершина правильной тре угольной пирамид ы, боковые ребра которой равны 1, а высота Найдите площадь части сферы, заключенной внутри пирамиды. Решение: Указанные пирамиды разбивают правильный тетраэдр на четыре равные пирамиды с вершинами в центре O тетраэдра. Следовательно, 3-гранный угол при вершине пирамиды составляет одну четвертую часть угла в 360 о, т.е. равен 90 о. Ответ:
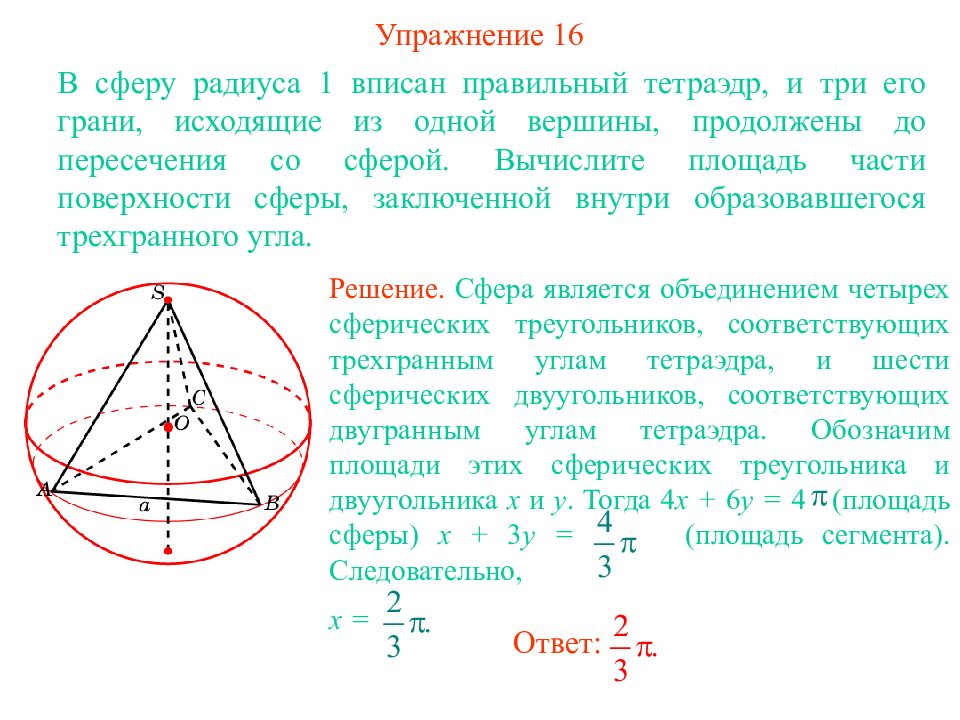
Последний слайд презентации: ПЛОЩАДЬ ПОВЕРХНОСТИ ШАРА: Упражнение 16
В сферу радиуса 1 вписан правильный тетраэдр, и три его грани, исходящие из одной вершины, продолжены до пересечения со сферой. Вычислите площадь части поверхности сферы, заключенной внутри образовавшегося трехгранного угла. Ответ: Решение. Сфера является объединением четырех сферических треугольников, соответствующих трехгранным углам тетраэдра, и шести сферических двуугольников, соответствующих двугранным углам тетраэдра. Обозначим площади этих сферических треугольника и двуугольника x и y. Тогда 4 x + 6 y = 4 (площадь сферы) x + 3 y = (площадь сегмента). Следовательно, x =