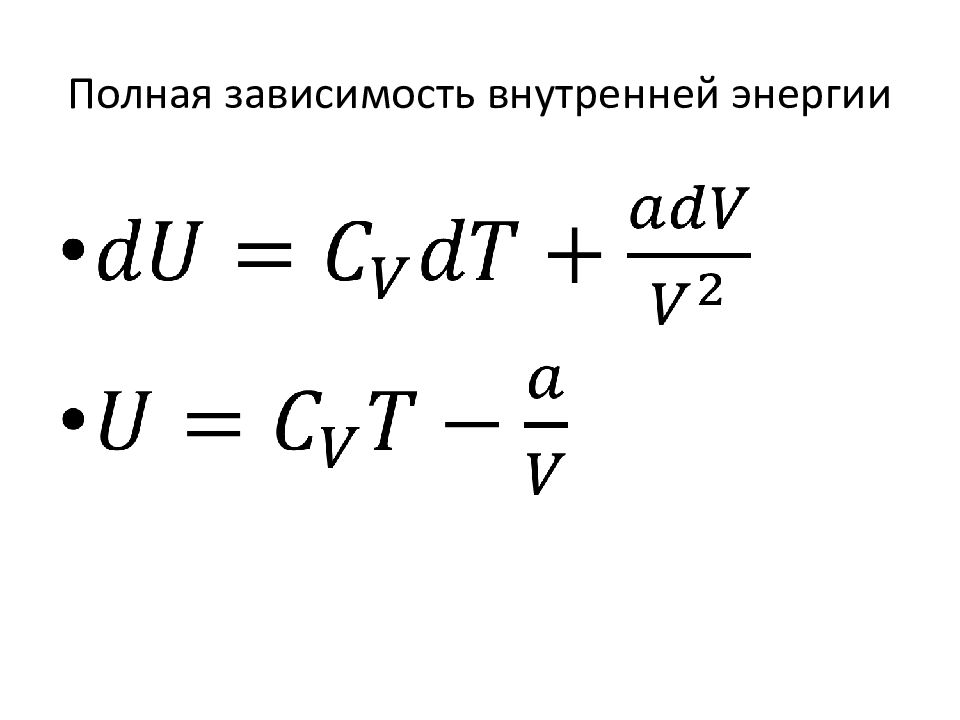Первый слайд презентации: Молекулярная физика
Лектор: Парахин А.С., к. ф.-м. наук, доцент.
Слайд 2: 5. Реальные газы
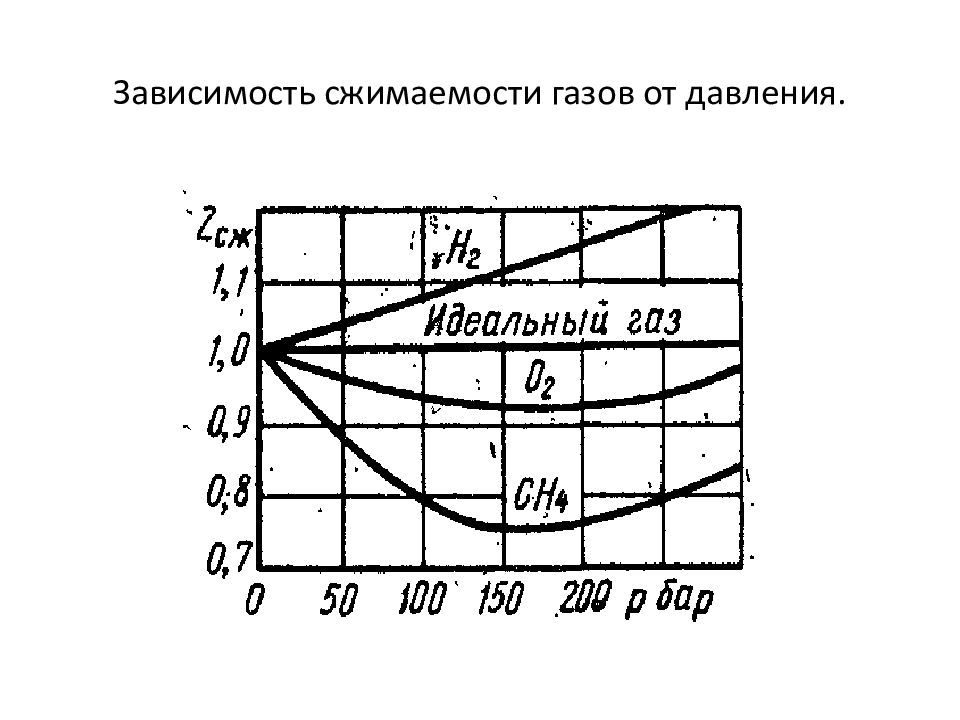
5. 1. Отступление от идеальности. Идеальные газы подчиняются уравнению Менделеева-Клапейрона: Голландский учёный ван Марум (1750-1837) в конце 18 века получил сжиженный газ. - сжимаемость газов.
Слайд 4: 5.2.Уравнение Ван-дер-Ваальса
Уравнение Менделеева-Клапейрона удовлетворительно описывает разряжённые газы. Это значит, новое уравнение должно для малых плотностей газов переходить в уравнение Менделеева-Клапейрона. Уравнение Менделеева-Клапейрона должно быть просто модифицировано.
Слайд 8: Уравнение Ван-дер-Ваальса
Параметры и называются константами Ван-дер-Ваальса. Для разных газов они разные и табулированы для одного моля.
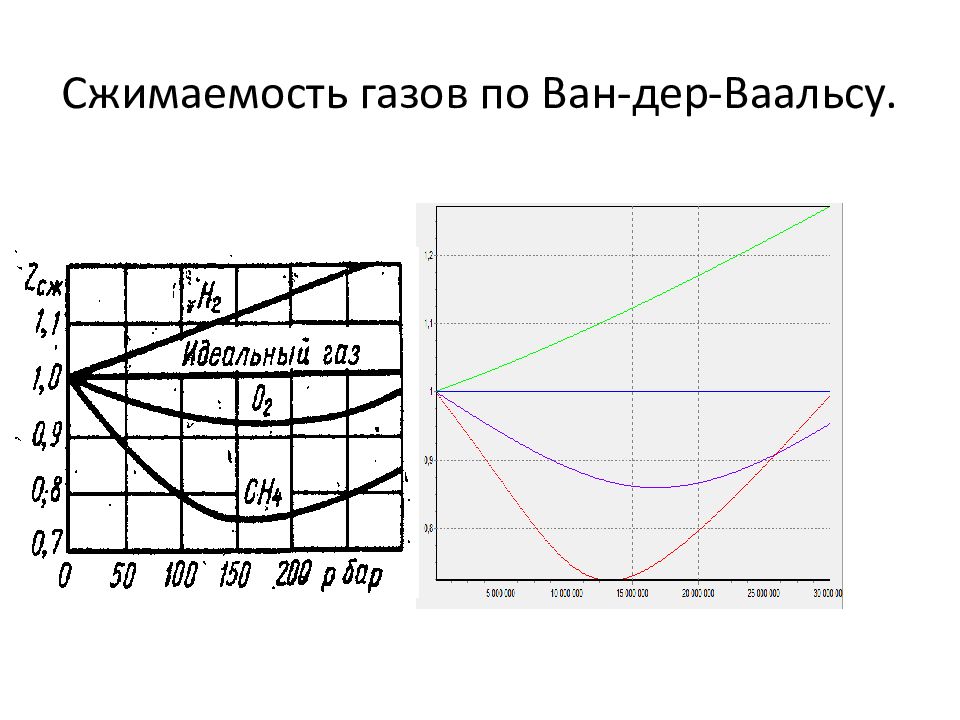
Слайд 10: Коэффициент сжимаемости
и разделим на : Откуда найдём коэффициент сжимаемости:
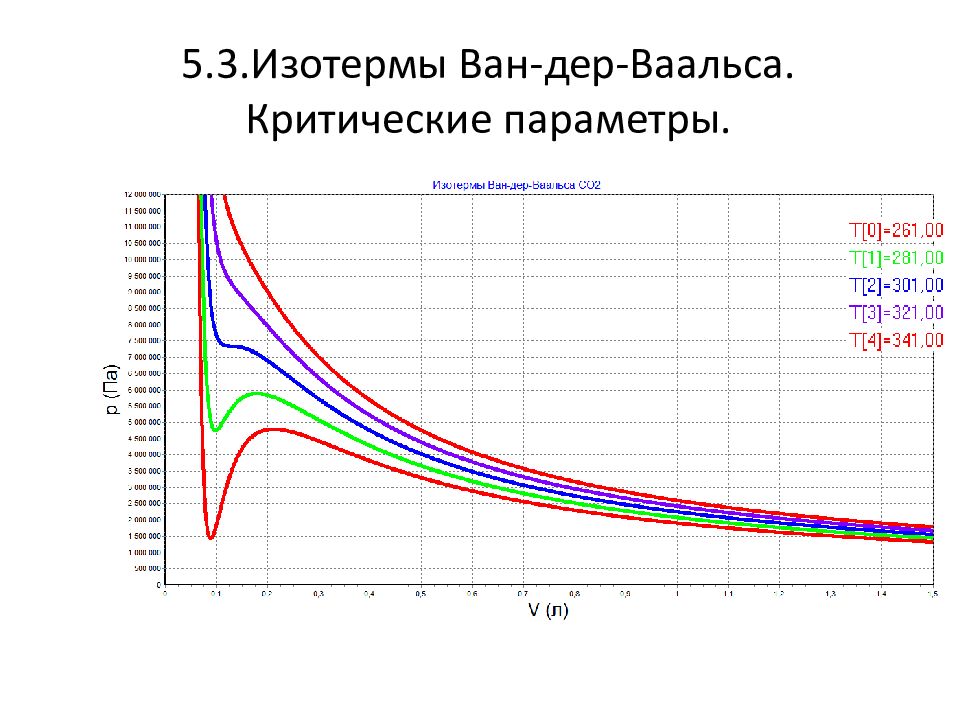
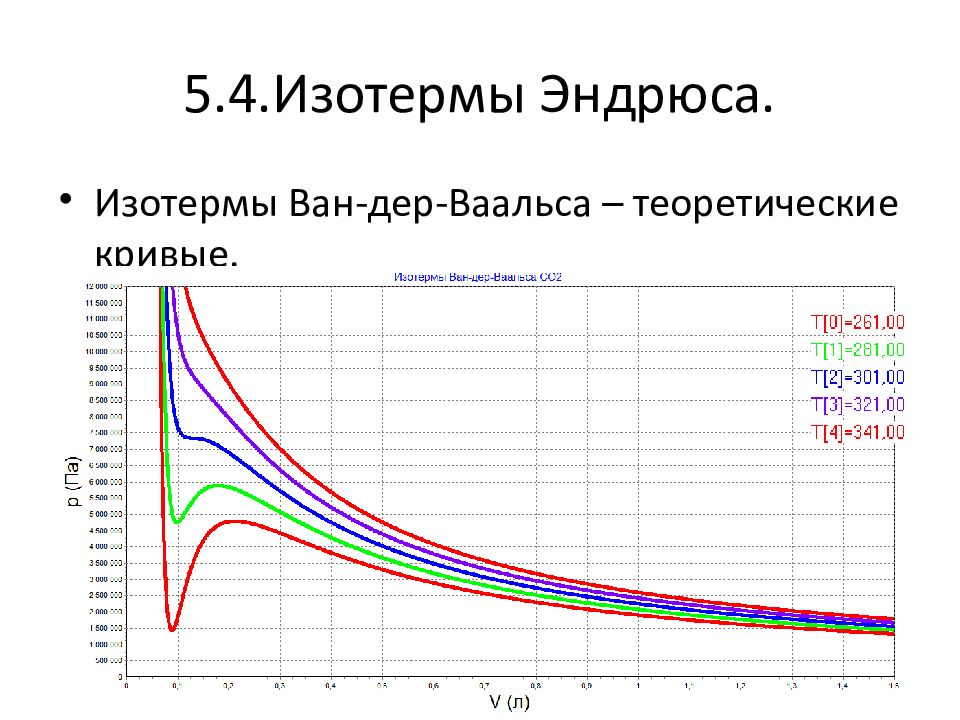
Слайд 13: Изотермы Вар-дер- Ваальса
Progr D : Progr E : Progr F : Progr G : Progr H:
Слайд 15: Преобразование системы
Разнесём слагаемые в этих уравнениях по разные стороны от равенства:
Слайд 16: Критический объём
и поделим первое на второе: Откуда находим критический объём:
Слайд 17: Критическая температура
Из первого уравнения найдём критическую температуру:
Слайд 18: Критическое давление
Наконец, найдём критическое давление из самого уравнения Ван-дер-Ваальса:
Слайд 19: Безразмерные параметры
С помощью критически параметров можно уравнение Ван-дер-Ваальса записать в безразмерном виде. Обозначим:
Слайд 20: Размерные параметры
и выразим через них размерные термодинамические параметры:
Слайд 21: Уравнение Ван-дер-Ваальса с безразмерными параметрами
Подставим их в уравнение Ван-дер-Ваальса:
Слайд 22: Безразмерное уравнение Ван-дер-Ваальса
Подставим сюда выражения критических параметров Сократив выражение, получим: Для соответственных состояний
Слайд 24: Эксперименты Марума
Экспериментальные изотермы выглядят иначе. Марум обнаружил возможность сжижения газов. При 7 Атм. Давление преставало изменяться.
Слайд 25: Исследование Эндрюса
А нглийский химик Томас Эндрюс (1813 – 1885 ) исследовал углекислый газ. Заметил появление капелек жидкости, которые постепенно разрастались и заполнили весь объём под поршнем.
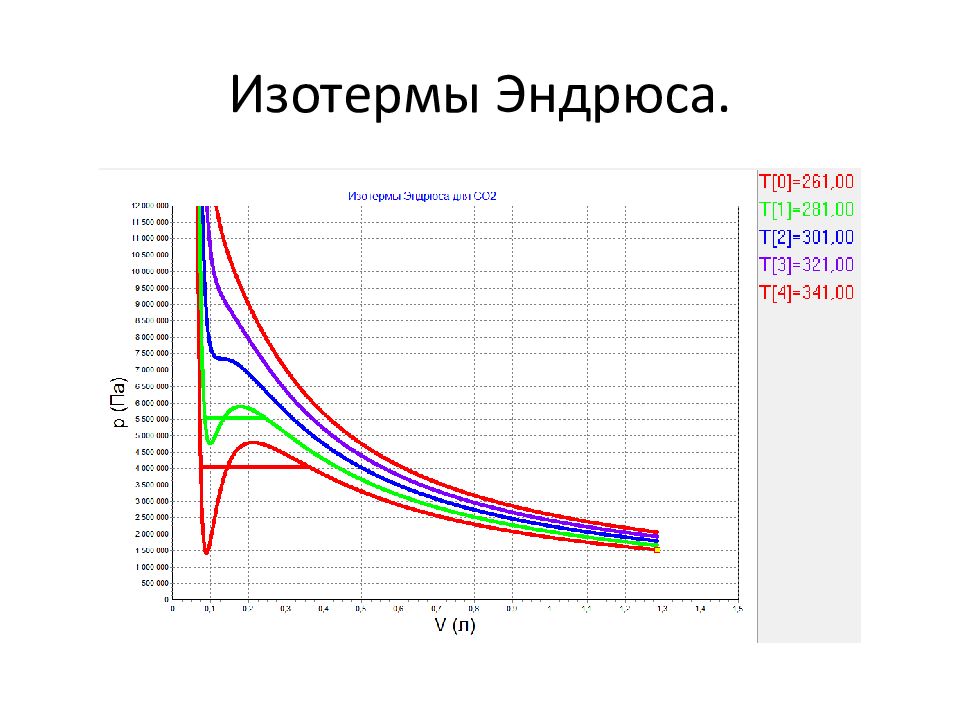
Слайд 27: Исследование изотерм Эндрюса
Progr D : Progr E : Progr F : Progr G : Progr H:
Слайд 28: Правило Максвелла
Внутренняя энергия есть функция состояния и на замкнутом контуре её изменение равно нулю.
Слайд 29: Условие сжижения газов
Чтоб сжидить газ его нужно охладить до температуры ниже критической. Этим объясняется неудача многих экспериментаторов, старавшихся превратить в жидкость такие газы, как кислород, азот и т.п.
Слайд 30: Правило рычага. Обозначения
обозначим объём в точке синей, это объём всей жидкости в точке красной,это объём всего газа объём в данной точке участка просто, он равен сумме объёмов газа и жидкости
Слайд 32: Плотности жидкости и газа
в крайних точках. В промежуточных точках можно записать равенство:
Слайд 33: Правило рычага
Поскольку полная масс равна сумме масс газа и жидкости, то можно записать равенство: Из него находим отношение масс:
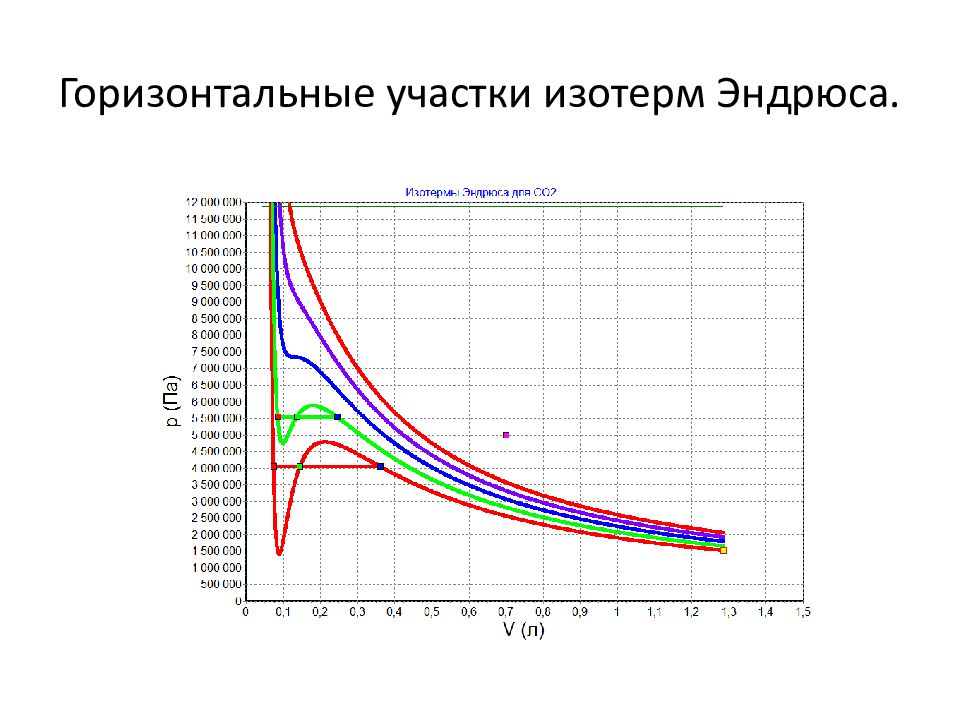
Слайд 34: Отрезки на горизонтальном участке
Но пропорционально отрезку от точки на горизонтальном участке до красной точки, примыкающему к жидкости, а величина пропорциональна отрезку от точки до синей точки. Этот отрезок примыкает к газу.
Слайд 35: Формулировка правила рычага
Таким образом, массы фаз, жидкой и газообразной, обратно пропорциональны величинам отрезков от текущей точки на горизонтальной части изотерм Эндрюса до концов горизонтального отрезка. Это утверждение и носит название правило рычага, т.к. оно совпадает с условием равновесия рычага, на концах которого подвешены грузы.
Слайд 36: 5.5. Внутренняя энергия газа Ван-дер-Ваальса
Силы взаимодействия молекул реального газа создают дополнительное давление:
Слайд 37: Зависимость внутренней энергии от температуры
Зависимость внутренней энергии от температуры при постоянном объёме определяется теплоёмкостью при постоянном объёме:
Слайд 40: 5.6.Эффект Джоуля-Томсона
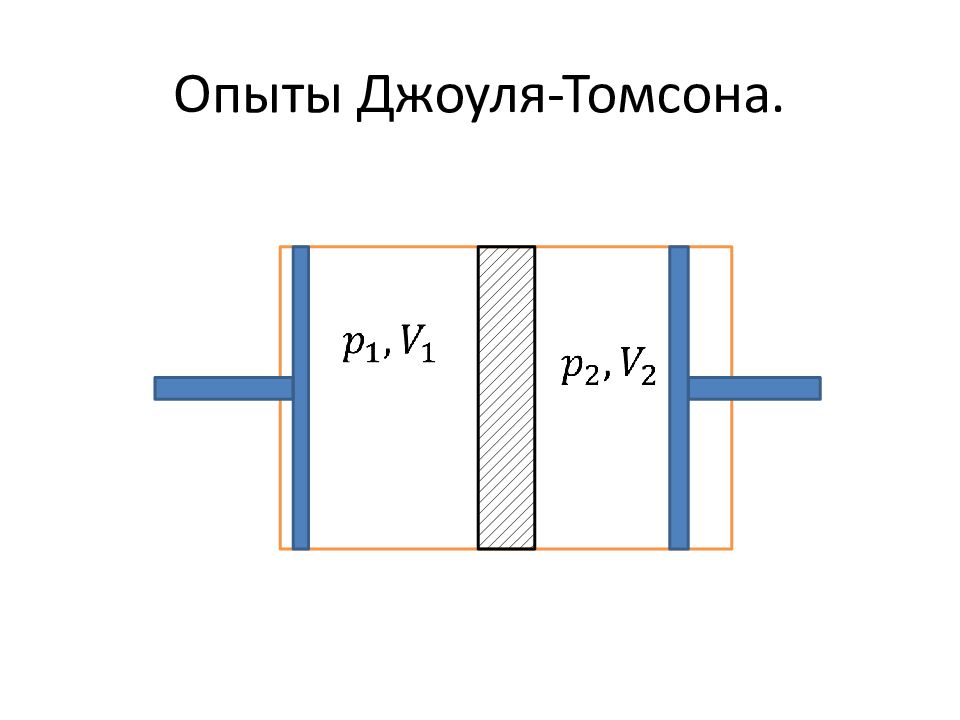
Работы по сжижению газов. Опыты Джоуля и Томсона по дросселированию. Определение. Дросселированием называется процесс пропускания газа через какое-либо препятствие.
Слайд 42: Определение эффекта Джоуля-Томсона
Эффектом Джоуля-Томсона называется явление изменения температуры газа при дросселировании.
Слайд 43: Работа газа и над газом
Работа в левой части совершается над газом Газ в правой половине газ совершает работу: Результирующая работа:
Слайд 44: Изменение внутренней энергии
Поскольку процесс адиабатический, то согласно первому началу:
Слайд 45: Энтальпия
Величина Называется энтальпией или тепловой функцией. Процесс Джоуля –Томсона – изоэнтальпический процесс
Слайд 46: Дифференциал энтальпии
Найдём полный дифференциал энтальпии и приравняем к нулю, поскольку она неизменна:
Слайд 47: Производная температуры по давлению
Откуда и находим производную температуры по давлению:
Слайд 48: Теплоёмкость при постоянном давлении
Преобразуем это выражение. Найдём знаменатель:
Слайд 49: Естественные параметры
Определение. Естественными параметрами некоторой термодинамической функции состояния называются параметры, через дифференциалы которых выражается дифференциал этой функции, исходя из первого начала термодинамики.
Слайд 50: Для внутренней энергии
Так из первого начала следует: Согласно определению энтропии:
Слайд 51: Дифференциал внутренней энергии
Так что: - Объединённое начало. Выразим отсюда дифференциал внутренней энергии: Отсюда видно, что естественными параметрами для внутренней энергии являются энтропия и объём.
Слайд 52: Преобразование первого начала термодинамики
Добавим выражения От этого равенство не нарушится: Но теперь можно свернуть второе и четвёртое вместе и перенести влево:
Слайд 53: Дифференциал энтальпии в естественных параметрах
Отсюда следует, что естественные параметры энтальпии: энтропия и давление.
Слайд 54: Производная энтальпии по давлению
Разделим это на, считая температуру постоянной
Слайд 55: Формула эффекта Джоуля-Томсона
Тогда эффект Джоуля-Томсона будет вычисляться по формуле:
Слайд 56: Термодинамический потенциал Гиббса
Термодинамический потенциал Гиббса: Естественные параметры потенциала Гиббса – давление и температура.
Слайд 57: Математическая формула дифференциала потенциала Гиббса
С другой стороны:
Слайд 58: Выражения для давления и энтропии
Сравнивая эти два выражения, находим: Для любой функции состояния смешанные производные равны:
Слайд 60: Анализ формулы
Знаменатель положителен. Знак эффекта зависит от числителя: 1. – эффект положителен. 2. – эффект отрицателен. 3. – эффект отсутствует.
Слайд 61: 5.7.Идеальный и реальный газы
Идеальный газ. Подставим в формулу эффекта: Таким образом, для идеального газа эффект Джоуля-Томсона равен нулю. Это значит, что идеальный газ, проходя через пробку, не нагревается и не охлаждается.