Первый слайд презентации: Молекулярная физика
Лектор: Парахин А.С., к. ф.-м. наук, доцент.
Определение. Адиабатическим процессом называется процесс, при котором теплообмена не происходит. Из первого начала термодинамики для адиабатического процесса находим .
Слайд 3: Вывод уравнения адиабаты
Т.к. для идеального газа, а , то из первого начала следует .
Слайд 4: Приведение подобных слагаемых
Приведём подобные члены , Приведя к общему знаменателю в скобках, сократив на и учтя равенство Майера, найдём .
Слайд 5: Диф. уравнение адиабаты
Получили дифференциальное уравнение, которое можно решить разделением переменных . Величину. называется показателем адиабаты.
Слайд 6: Интегрирование уравнения
Используя этот параметр, диф. уравнение адиабаты можно записать так . Проинтегрируем правую и левую часть . или .
Слайд 7: Уравнение адиабаты
И, наконец, . Это уравнение и носит название уравнения адиабаты. График его представляет собой график степенной функции с показателем меньше нуля, а по модулю больше единицы. Progr D: Progr E: Progr F: Progr G: Progr H:
Слайд 9: Расчёт работы в адиабатическом процессе
Найдём работу идеального газа при адиабатическом процессе. Согласно первому началу для адиабат. п роцесса; . Или для конечных изменений параметров . Progr D: Progr E: Progr F: Progr G: Progr H:
Слайд 10: 2.6. Второе начало термодинамики
На основе первого начала термодинамики можно решить много термодинамических задач. Однако, не все явления термодинамики описываются этим законом. Этот закон не устанавливает направленность процессов. Progr D: Progr E: Progr F: Progr G: Progr H : Progr D: Progr E: Progr F: Progr G: Progr H:
Слайд 11: Необратимость потоков тепла
Как мы видели выше, тепловые процессы сами по себе протекают всегда в направлении, когда тепло перетекает от более горячего тела к более холодному. В этом и состоит одна из формулировок второго начала термодинамики. Иначе говоря, не возможны процессы, при которых тепло самопроизвольно перетекало бы от холодного тела к горячему.
Слайд 12: Замечание
В этой формулировке существенным является уточнение «самопроизвольно». Перекачка тепла от холодного тела к горячему возможна (это подтверждает работа холодильников), но для этого необходимо затратить дополнительную энергию, т.е. произвести работу над системой.
Слайд 13: Приведённая теплота
Выразим количественно этот закон. Для этого предположим, что тела с разными температурами приведены в тепловой контакт. Температуру первого тела обозначим, температуру второго тела. Пусть одно тело передало другому теплоту величиной. Определение. Величина, равная отношению переданной теплоты к температуре, называется приведённой теплотой.
Слайд 14: Равновесные и неравновесные процессы
Определение. Процессы, протекающие при конечных разностях термодинамических параметров, называются неравновесными. Это название обусловлено тем, в течение этих процессов система не успевает прийти к равновесию. Определение. Процессы, протекающие при бесконечно малых разностях термодинамических параметров, называются равновесными.
Слайд 15: Характеристика равновесных процессов
Они характерны тем, что каждое промежуточное состояние системы в этих процессах можно считать равновесным. Такие процессы, очевидно должны быть достаточно медленными, чтобы успевали пройти тепловые процессы выравнивания термодинамических параметров.
Слайд 16: Понятие энтропии
Определение. Энтропией называется величина, изменение которой в равновесном процессе равно приведённой теплоте. Обозначается энтропия. . Измеряется энтропия в единицах теплоты, делённых на единицу температуры, т.е.. Единицы измерения энтропии совпадают с единицами измерения теплоёмкости.
Слайд 17: Перетекание энтропии
В процессе передачи тепла от горячего тела к холодному горячее тело теряет энтропию , а холодное тело наоборот приобретает
Слайд 18: Энтропия при равновесных процессах
Если процесс передачи тепла происходит при бесконечно малой разности температур между телами, то температуры тел можно считать одинаковыми, и тогда энтропия, отданная первым телом, будет равна энтропии, принятой вторым телом. А общее изменение энтропии равно нулю. Таким образом, для равновесных, обратимых процессов .
Слайд 19: Передача тепла при конечной разности температур
Будем теперь считать, что процесс передачи тепла происходит при конечных разностях температур, но столь медленно, что каждое из тел остаётся однородным по температуре. Тогда этот процесс снова можно считать равновесным. Кроме того количество тепла столь мало, что температура тел существенно не меняется.
Слайд 20: Второе начало термодинамики
Поскольку, первое тело теряет меньше энтропии, чем приобретает второе. В результате общее изменение температур обоих тело строго положительно. Объединяя эти два случая вместе, можно записать . Это и есть математическое выражение второго начала термодинамики.
Слайд 21: Вторая формулировка второго начала
Существует ряд других формулировок второго начала. Невозможно создать машину, единственным результатом действия которой было бы отнятие теплоты от некоторого тела и полностью превращение её в работу. В этом случае коэффициент полезного действия был бы равен 100 %.
Слайд 22: Третья формулировка второго начала
Отсюда вытекает ещё одна формулировка. Не возможен вечный двигатель второго рода, т.е. двигатель, кпд которого равен единице. Можно показать, что все формулировки второго начала термодинамики эквивалентны.
Слайд 23: 2.7. Круговые процессы. Цикл Карно
Определение. Процессы, при которых термодинамические параметры в начале и конце процесса совпадают, называются круговыми процессами или термодинамическими циклами. Одним из самых важных в термодинамике циклов является цикл Карно. Он состоит из двух адиабат и двух изотерм.
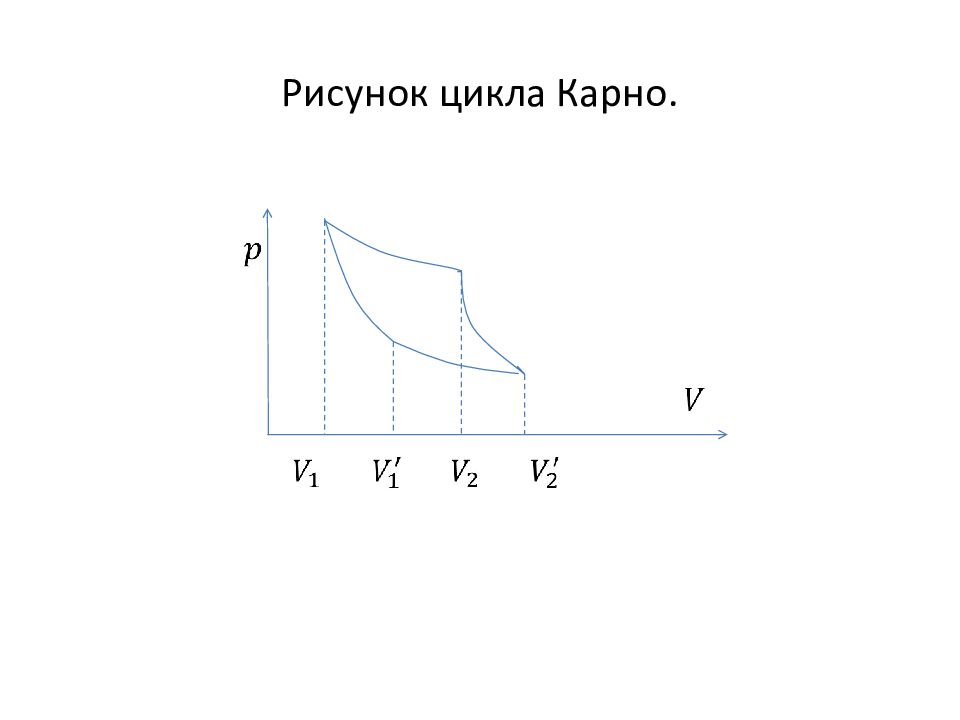
Слайд 24: Цикл Карно
Сначала система расширяется изотермически при температуре, принимая от нагревателя тепло и совершая некоторую работу. Затем система расширяется адиабатически, не принимая ни какого тепла, но совершая некоторую работу за счёт внутренней энергии. Затем система сжимается изотермически при температуре, отдавая холодильнику некоторое количество теплоты. И, наконец, в последнем процессе система адиабатически сжимается, не отдавая и не принимая тепла.
Слайд 26: Количество теплоты на первой изотерме цикла
Найдём изменение энтропии в таком цикле для идеального газа. На первом участке внутренняя энергия не изменяется, поэтому согласно первому началу термодинамики теплота, принятая системой будет равна работе, которую она совершила. . Здесь объём идеального газа в начале первого изотермического процесса, объём газа в конце первого изотермического процесса.
Слайд 27: Теплота на втором изотермическом участке цикла
Аналогично можно найти теплоту на втором изотермическом процессе
Слайд 29: Соотношения для объёмов
Объёмы и связаны между собой адиабатическим процессом, для которого можно записать уравнение Подобное соотношение можно записать и для объёмов и Разделим эти равенства друг на друга, получим или.
Слайд 32: 2.8. Функции состояния
Изменение энтропии в замкнутом цикле. Тогда из предыдущих формул находим, что или . Здесь учтено, что теплота, отданная системой отрицательна. Таким образом, полное изменение энтропии за цикл равно нулю.
Слайд 33: Функции состояния
Определение. Параметры термодинамической системы, изменение которых за полный цикл равно нулю, называются функциями состояния системы. С математической точки зрения это означает, что их элементарное изменение представляет собой полный дифференциал. Согласно определению и последнему равенству энтропия есть функция состояния системы.
Слайд 34: Первое начало с использованием энтропии
Из первого начала термодинамики . Разделим это равенство на температуру .
Слайд 35: Дифференциал энтропии
Согласно определению , поэтому для энтропии получим .
Слайд 36: Приведём подобные
Или, приведя подобные . Согласно правилам дифференцирования функций нескольких переменных , .
Слайд 37: Связь энтропии с давлением и теплоёмкостью
Но, Поэтому. Для идеального газа , так что для энтропии идеального газа справедливо выражение:
Слайд 38: Соотношения между термодинамическими параметрами
Таким образом, только из того факта, что некоторая величина есть функция состояния, можно находить соотношения между термодинамическими параметрами.