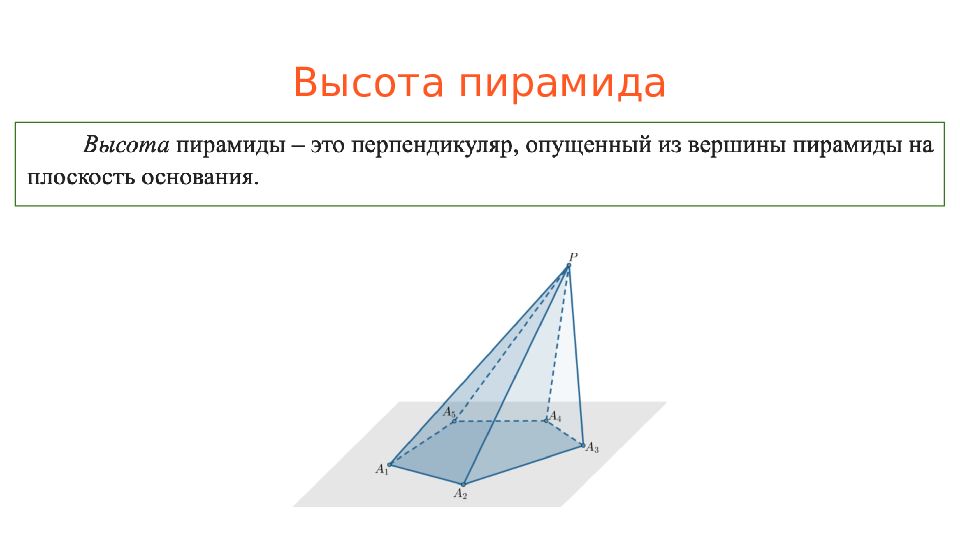
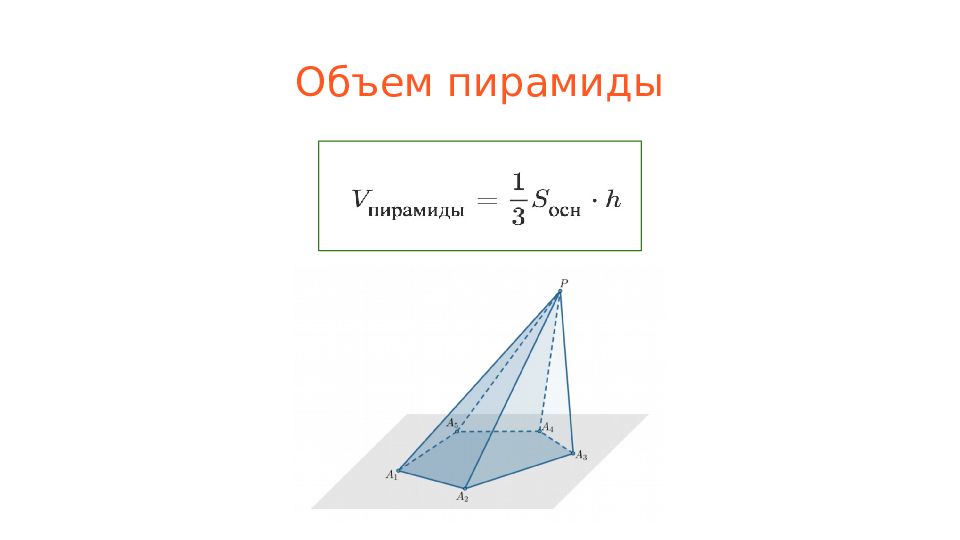
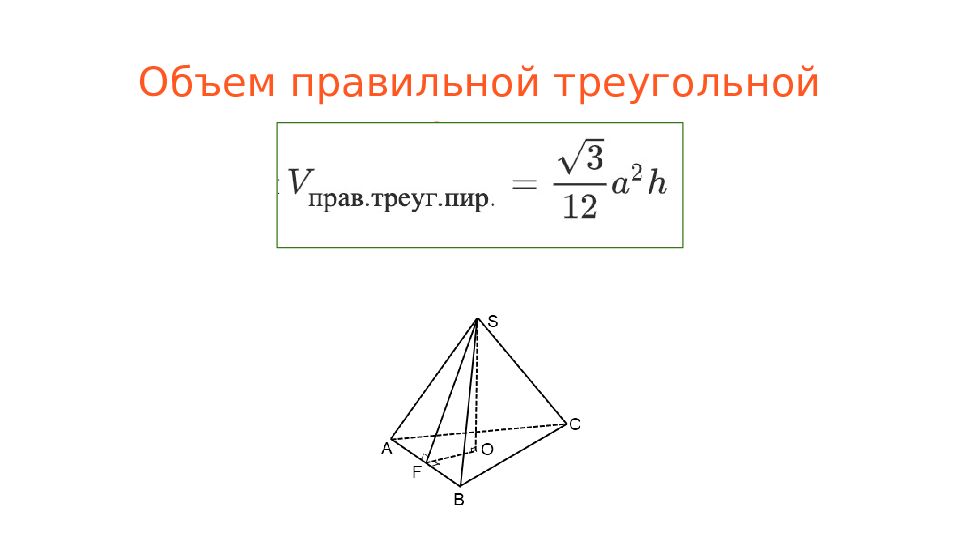
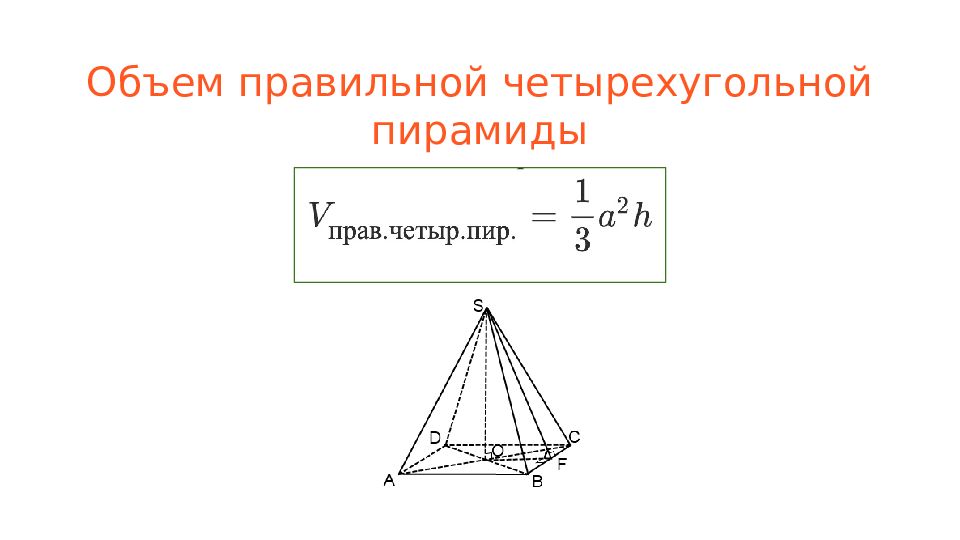
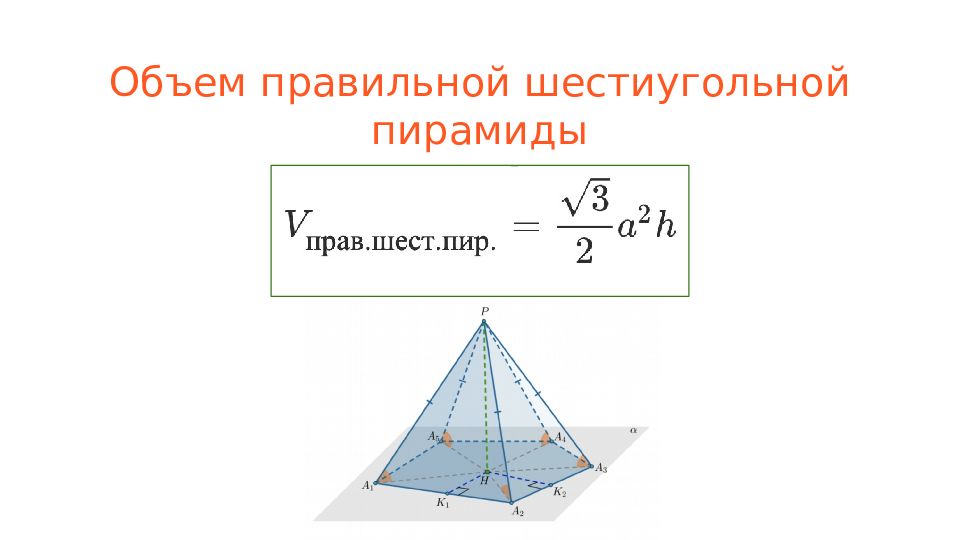
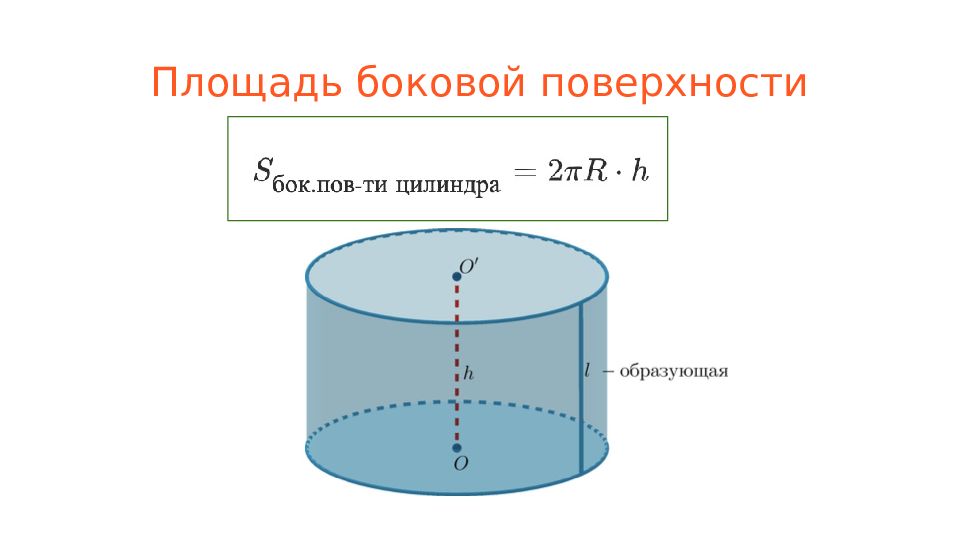
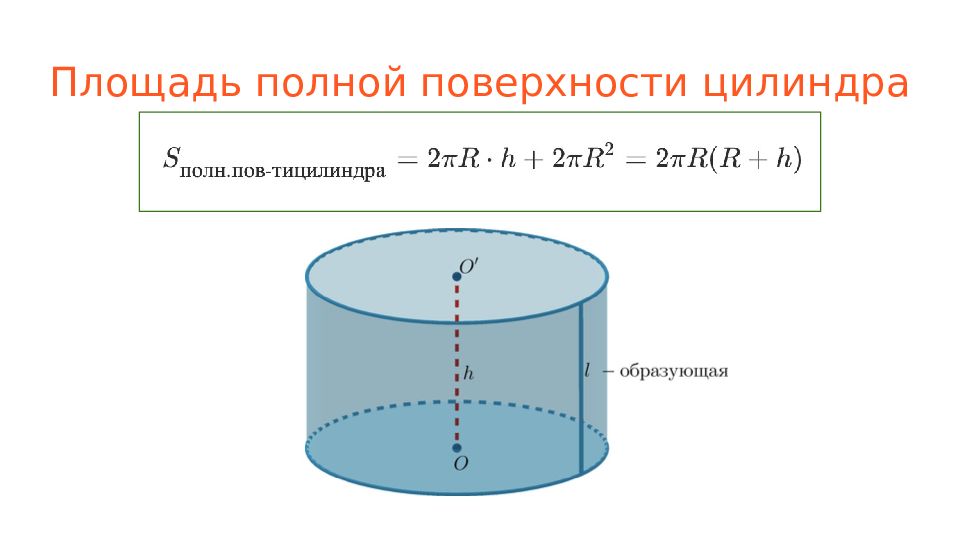
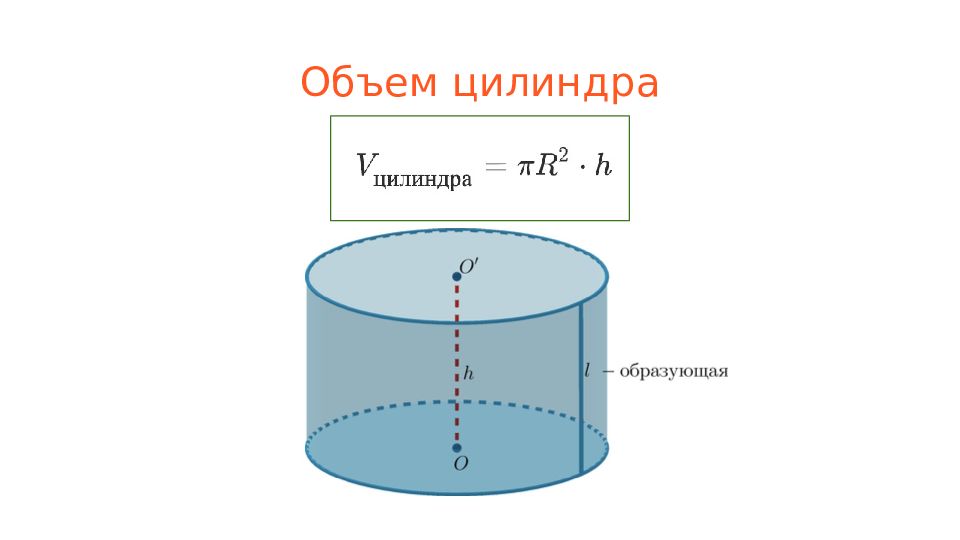
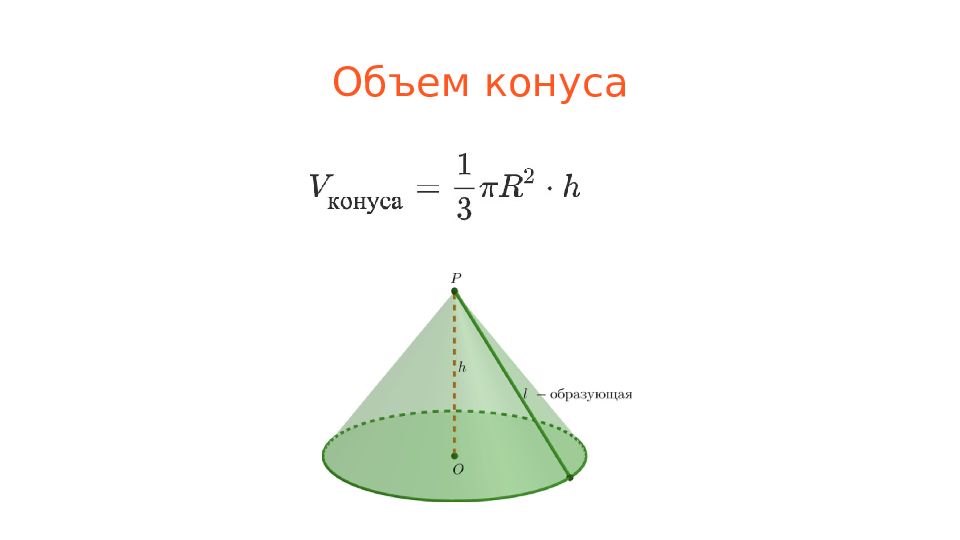
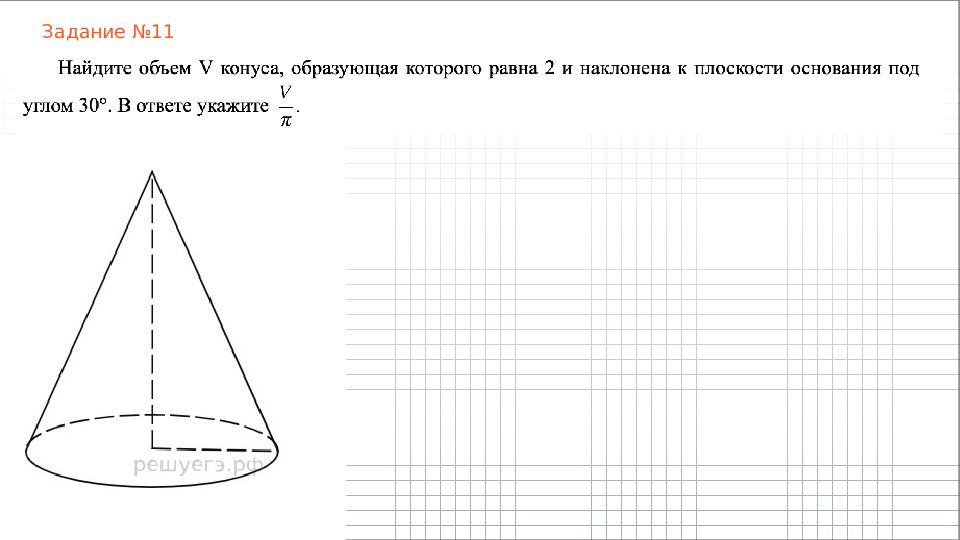
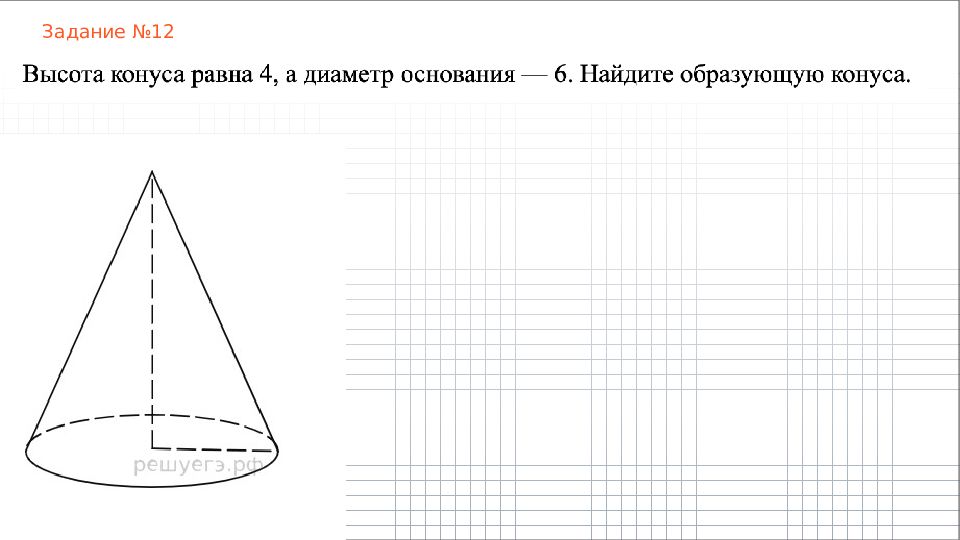
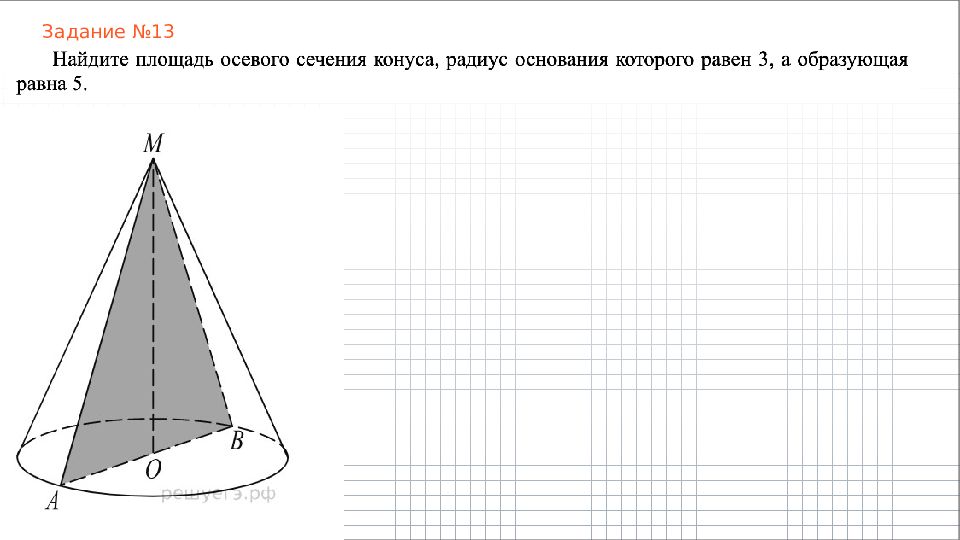
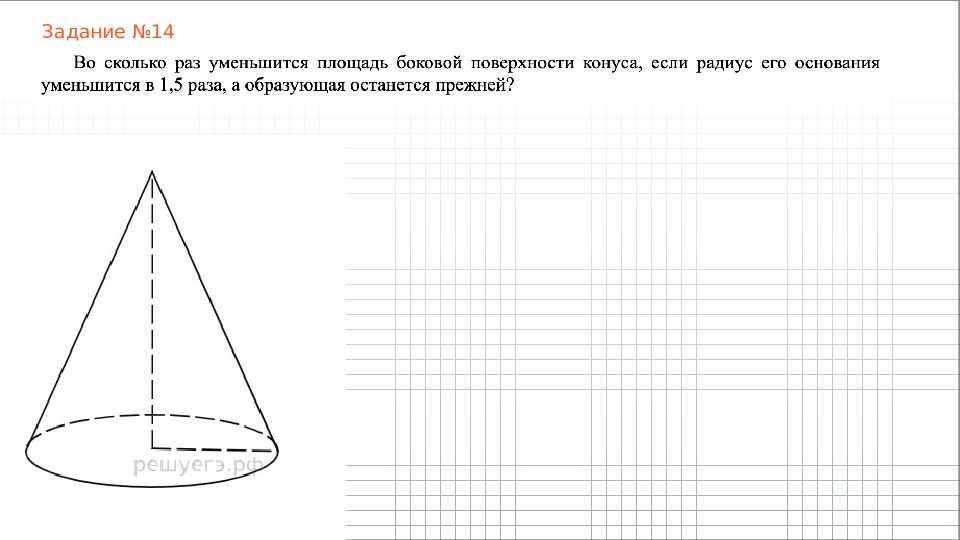
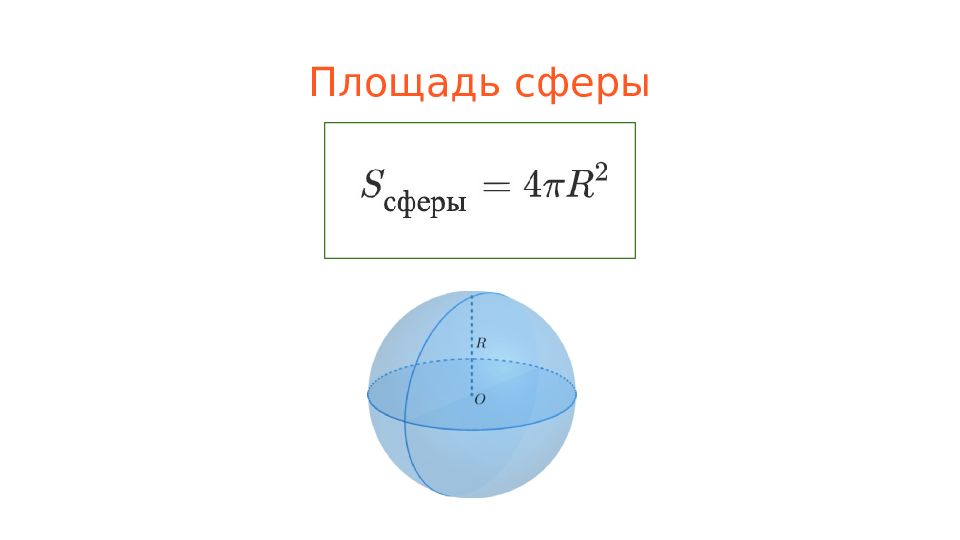
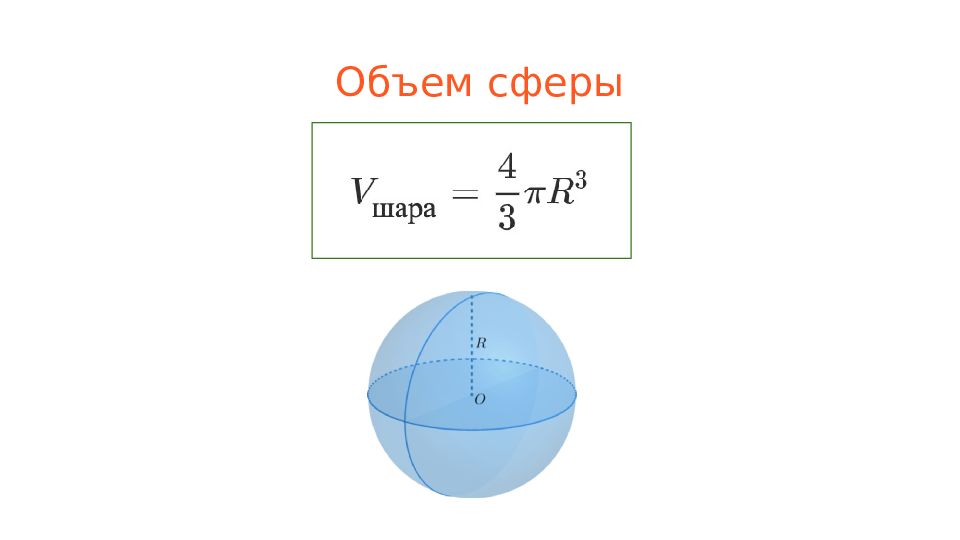
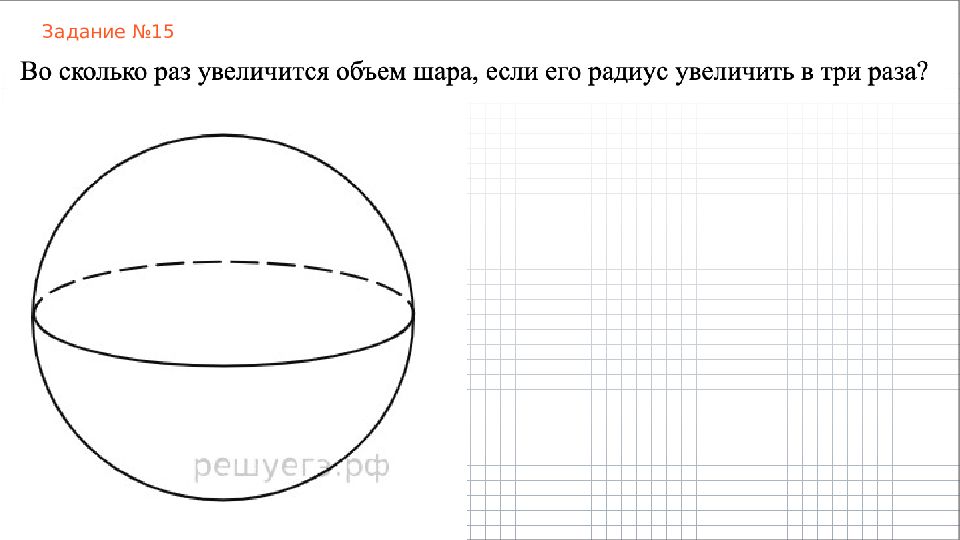
Слайд 4: Пирамида
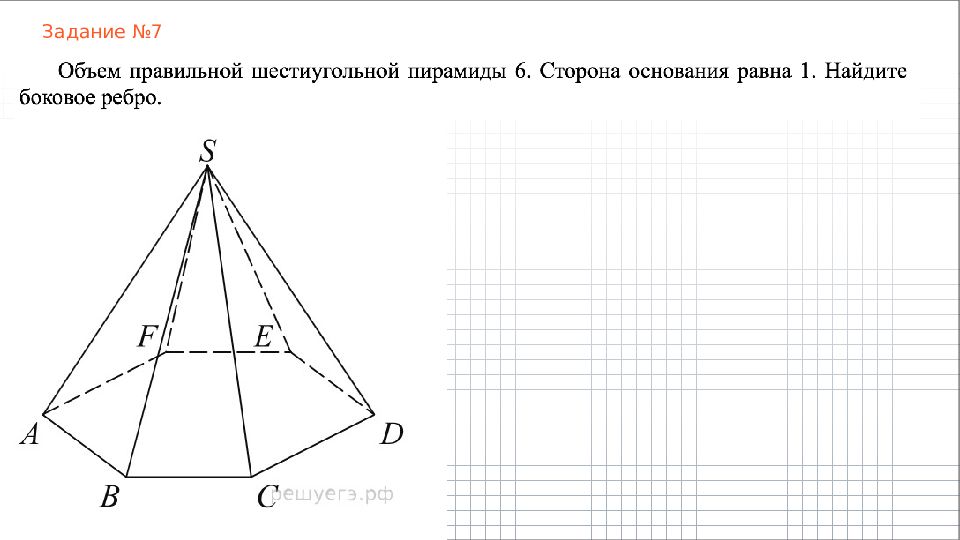
Слайд 7: Правильная п ирамида
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий: (a) боковые ребра пирамиды равны; (b) высота пирамиды проходит через центр описанной около основания окружности;
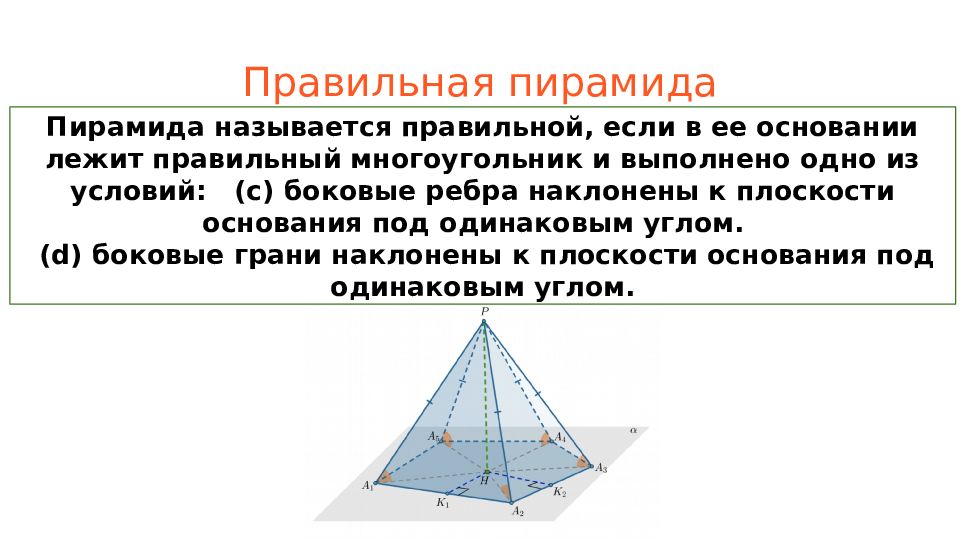
Слайд 8: Правильная пирамида
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий: (c) боковые ребра наклонены к плоскости основания под одинаковым углом. (d) боковые грани наклонены к плоскости основания под одинаковым углом.
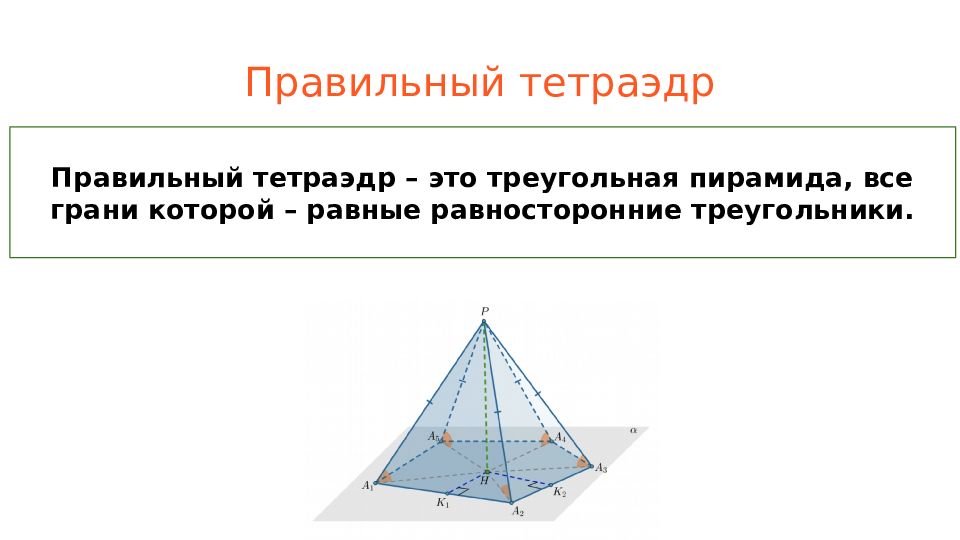
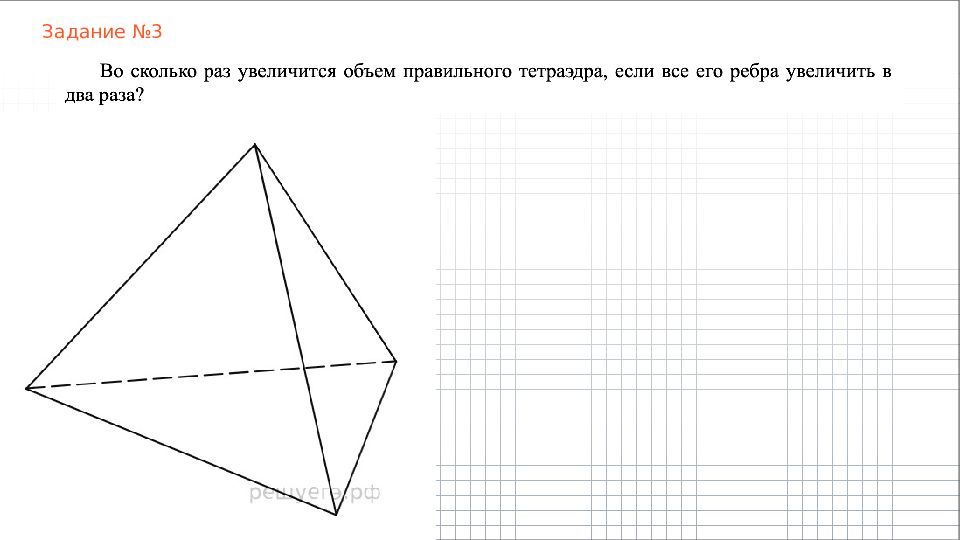
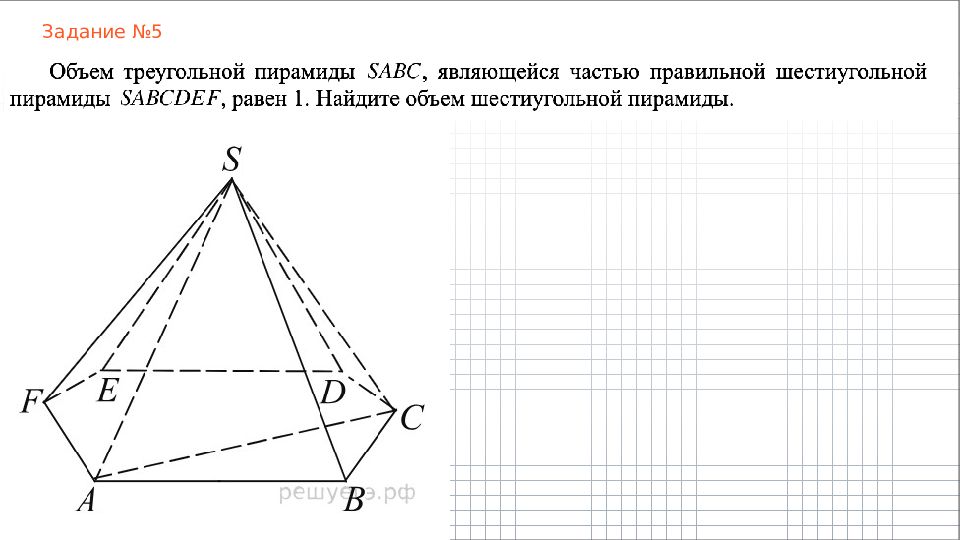
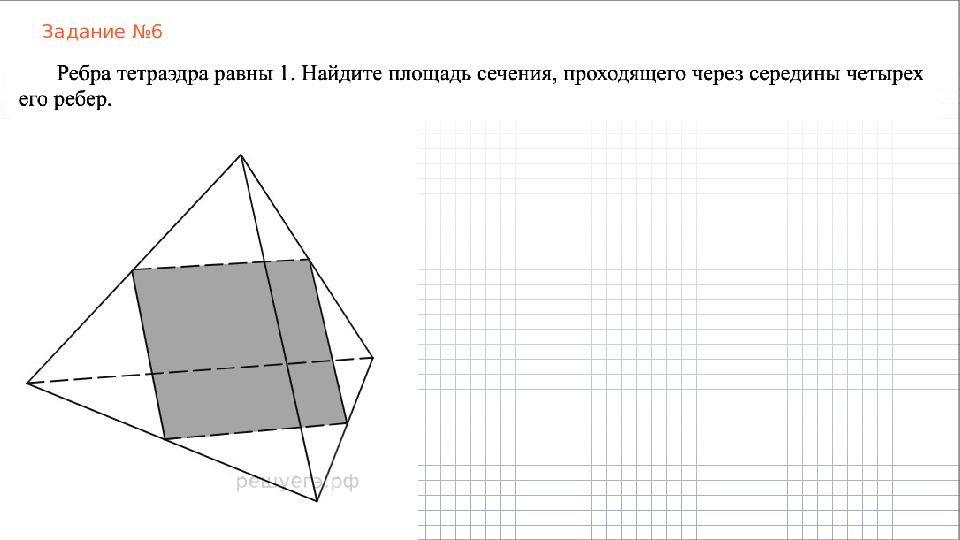
Слайд 9: Правильный тетраэдр
Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние тр е угольники.
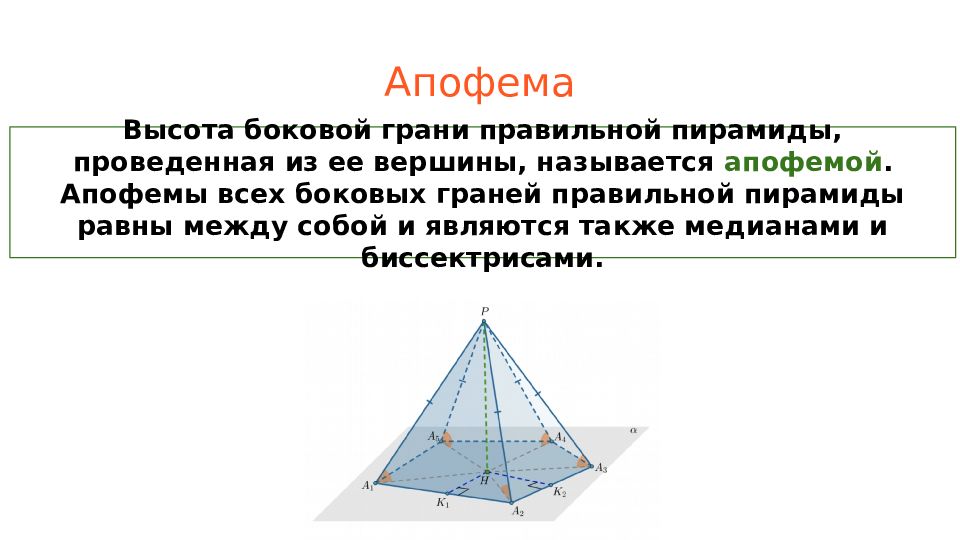
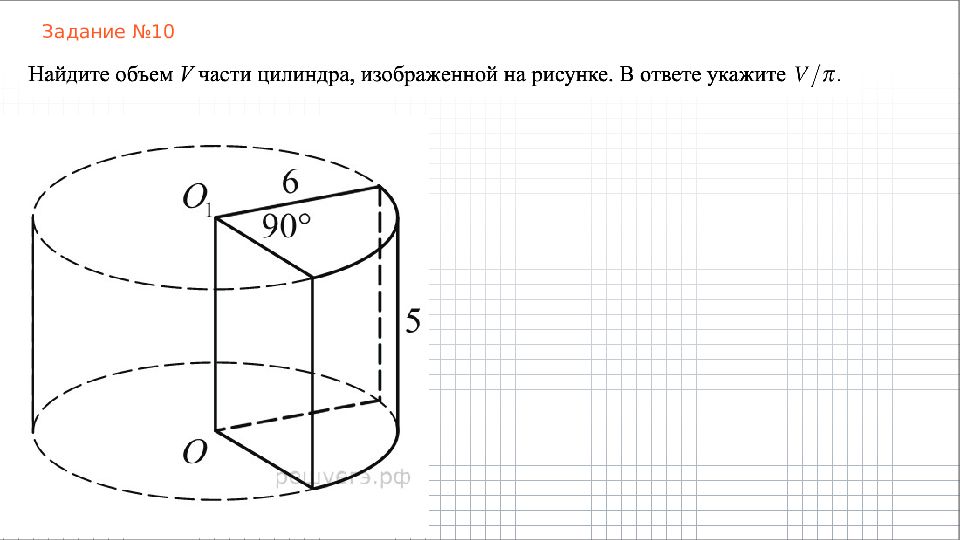
Слайд 10: Апофема
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.
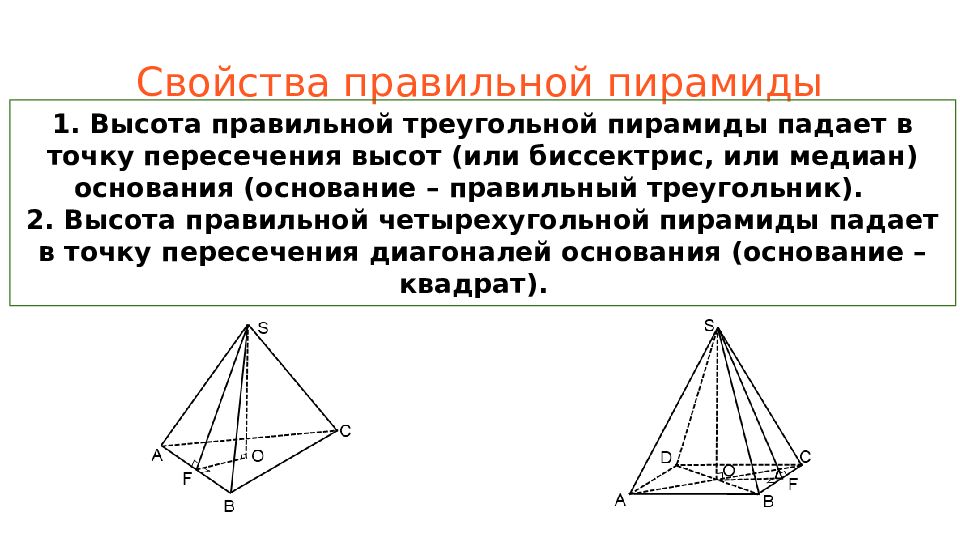
Слайд 11: Свойства правильной п ирамиды
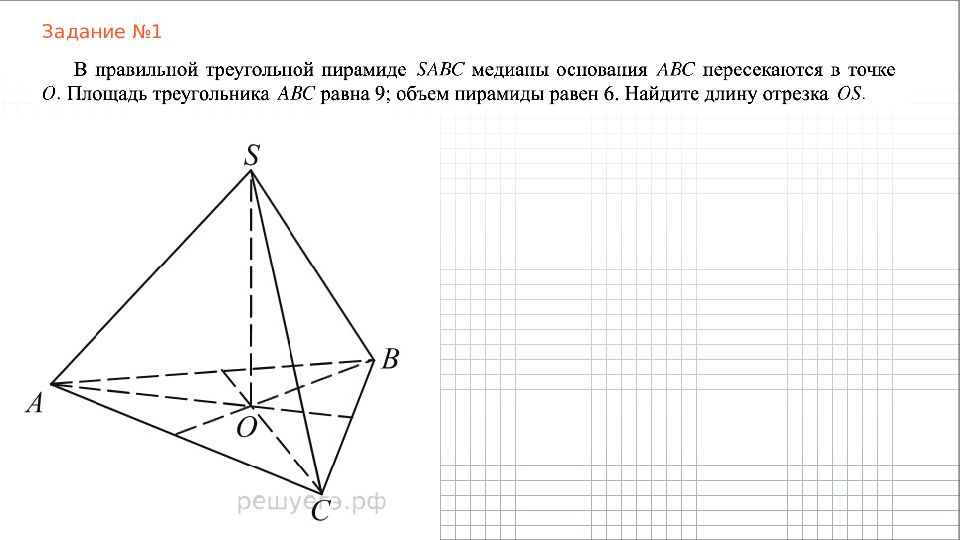
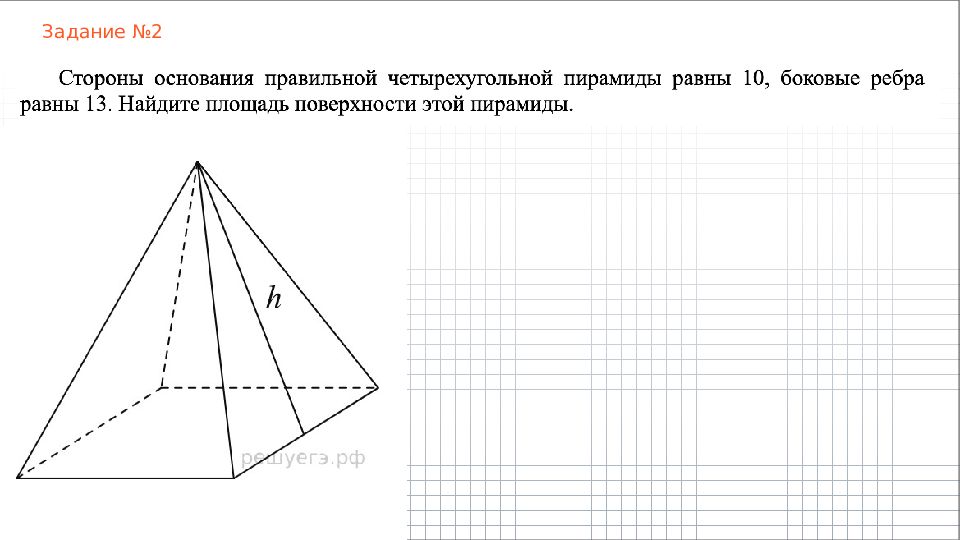
1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник). 2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).
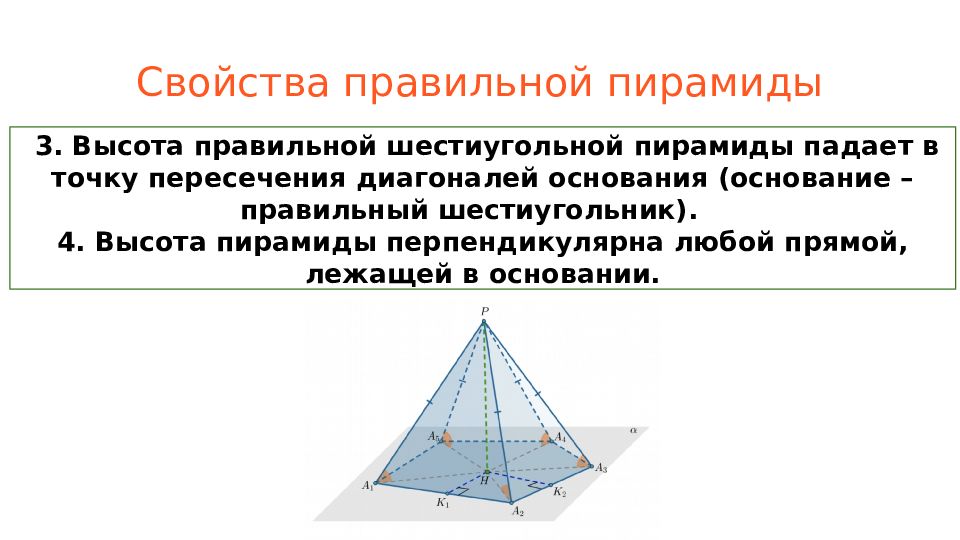
Слайд 12: Свойства правильной пирамиды
3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник). 4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.
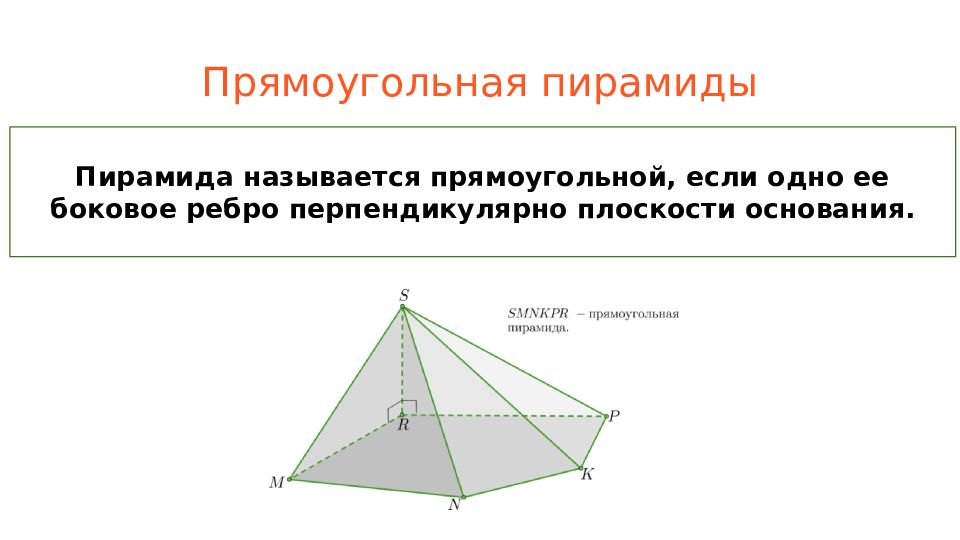
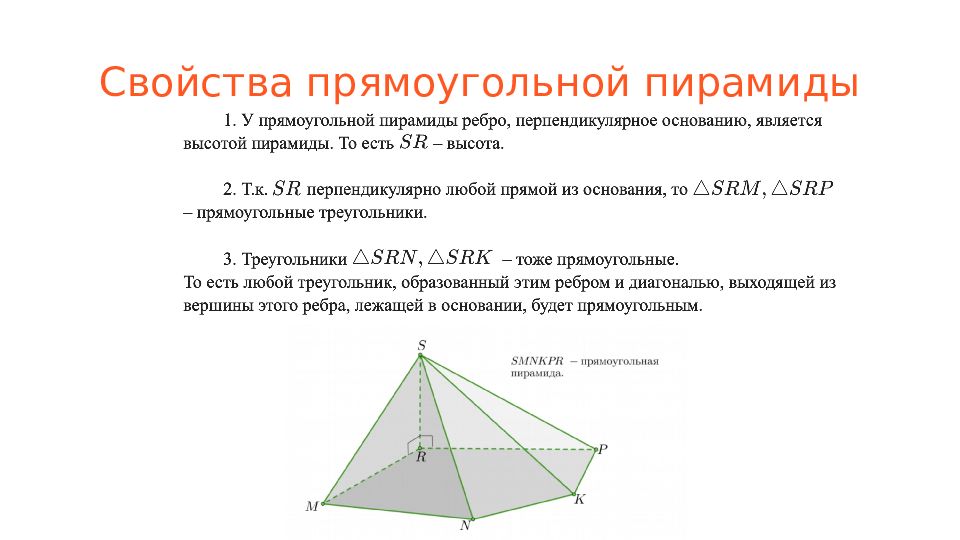
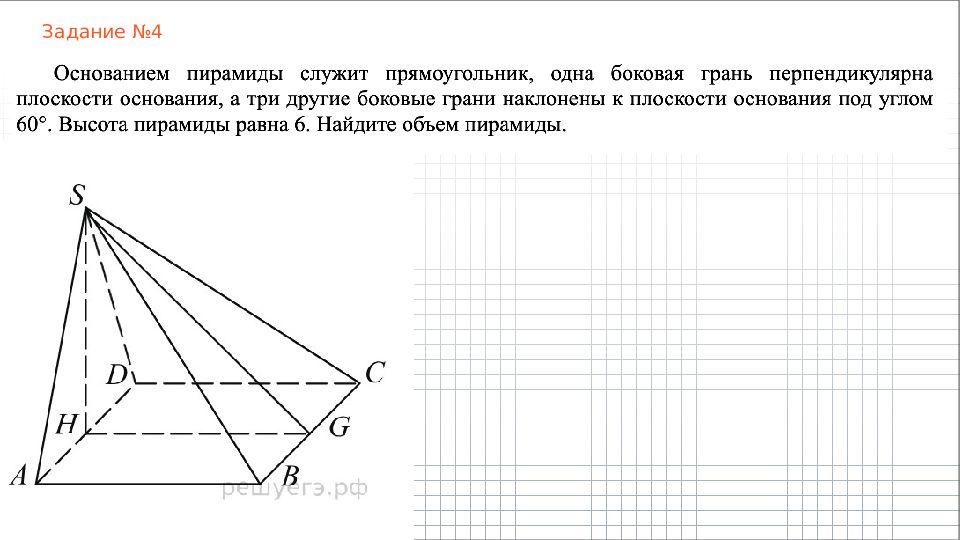
Слайд 13: Прямоугольная пирамиды
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.