Вариант 1 Вариант 2 Использован шаблон создания тестов в PowerPoint
в ) цилиндрической б) концентрической а) конической г) сферической 2 Цилиндром называется тело, ограниченное поверхностью :
а) апофема б) высота в) образующая г) радиус 2. Назовите элемент, не принадлежащий цилиндру. 3
3. Осевым сечением цилиндра является : 4 в) прямоугольник б) круг а) треугольник г) трапеция
а) 2П RL б) П R²H г) П RL в) П R Н 4. Боковая поверхность цилиндра определяется по формуле, где L -образующая, R - радиус, Н-высота : 5
г) П RL²+ П R Н в) 2П R ²+2П RL² б) 2П L ( L+H) 5. Полная поверхность цилиндра определяется по формуле, где R -радиус основания, L - образующая, Н- высота : 6 а) 2П R ( R+H )
6. Конус может быть получен вращением : 7 в) прямоугольного треугольника вокруг одного из его катетов б) равностороннего треугольника вокруг медианы а) прямоугольника вокруг одной из его сторон г) равнобедренного треугольника
7. Назовите элемент не принадлежащий конусу : 8 г) медиана б) ось в) высота а) образующая
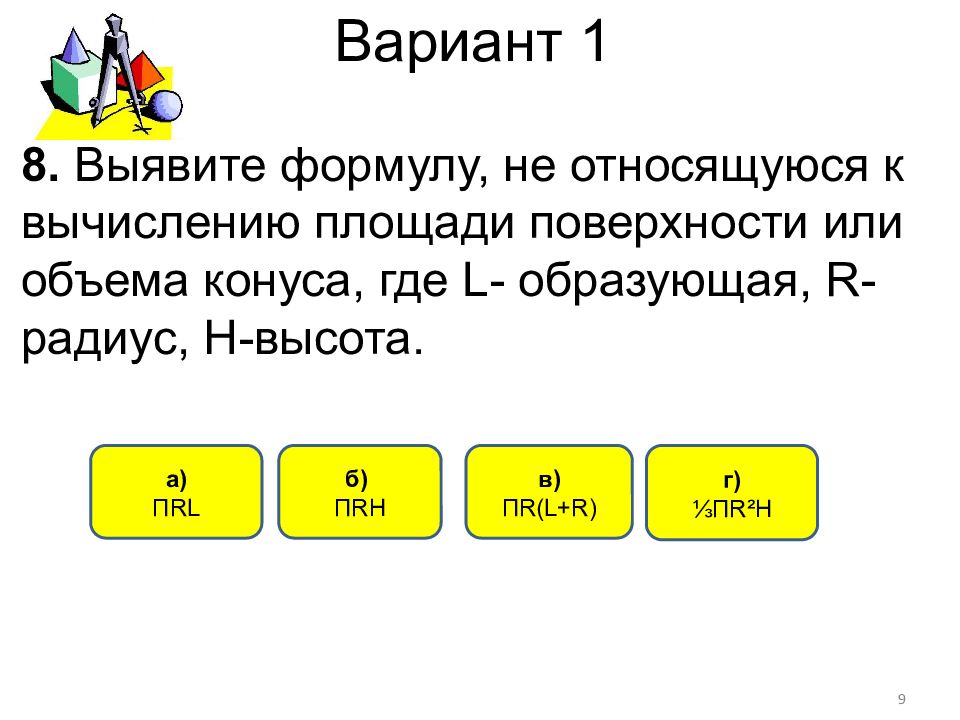
б) П R Н г) ⅓П R² Н а) П RL 8. Выявите формулу, не относящуюся к вычислению площади поверхности или объема конуса, где L - образующая, R - радиус, Н-высота. 9 в) П R(L+R)
г) Часть конической поверхности а) Часть цилиндрической поверхности 9. Боковой поверхностью усеченного конуса является : 10 в) Часть поверхности шара б) Часть сферической поверхности
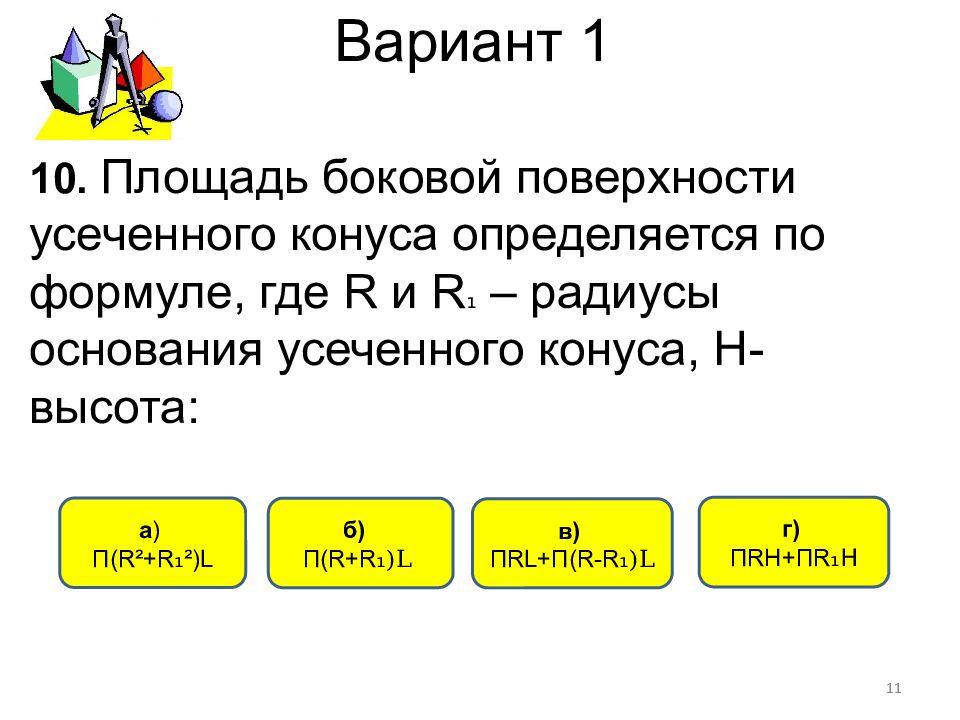
б) П( R+R ₁)L a ) П( R²+R ₁ ²)L в) П RL+ П (R-R ₁)L г) П RH+ П R ₁ Н 10. Площадь боковой поверхности усеченного конуса определяется по формуле, где R и R ₁ – радиусы основания усеченного конуса, Н- высота : 11
11. Апофема – это ….. 12 в) высота боковой грани пирамиды б) высота конуса а) образующая цилиндра г) высота усеченного конуса
б) 17 см г) 6 см а) 14 см 12. Если высота конуса 15см, а радиус основания 8см, образующая конуса равна : 13 в) 13 см
г) 4 / 3 R шара в) 1 / 3 R шара а) √ R шара 13. Шар и цилиндр имеют равные объемы, а диаметр шара равен диаметру основания цилиндра. Если выразить высоту цилиндра через радиус шара, то она будет равна : 14 б) R шара
г ) шара б) усеченного конуса в) цилиндра а) конуса 15 Сфера является поверхностью :
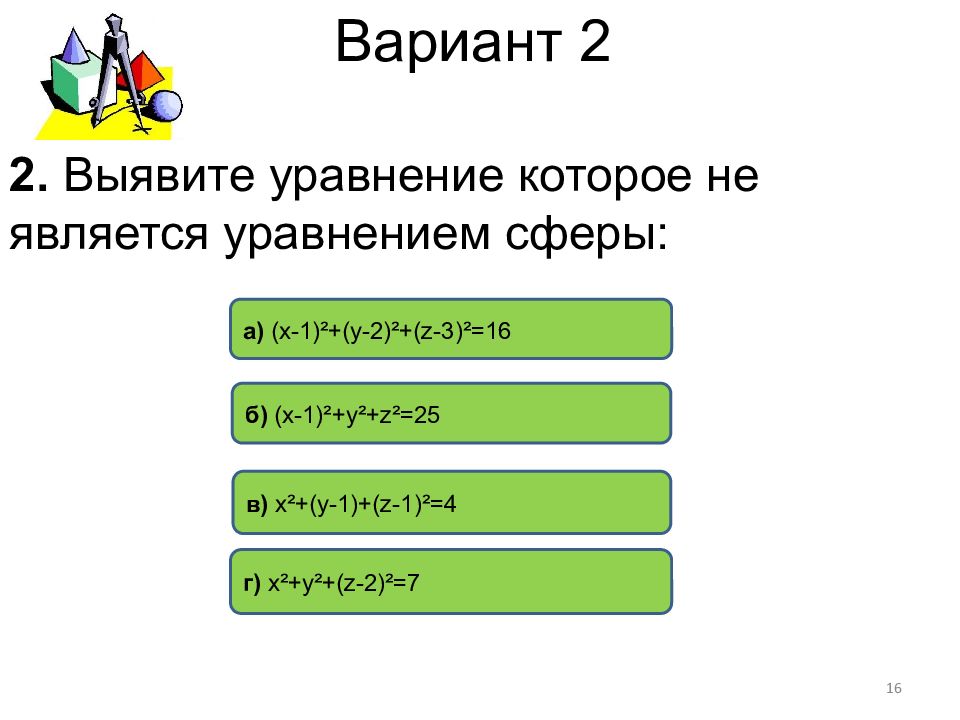
в) х²+(у-1)+( z -1)²=4 а) (х-1)²+(у-2)²+( z- 3)²=16 б) (х-1)²+у²+ z ²=25 г) х²+у²+( z -2)²=7 2. Выявите уравнение которое не является уравнением сферы : 16
3. Сфера и плоскость не могут иметь : 17 в ) две общие точки б) ни одной общей точки г) много общих точек а) одну общую точку
4. Площадь поверхности сферы определяется по формуле, где R- радиус сферы : 18 г) 4П R ² a ) 2П R² в) 4П² R² б) 4П R³
5. Какой не может быть призма ? 19 г) усеченной б) наклонной в) правильной а) прямой
6. Какая формула используется для вычисления как объема призмы, так и цилиндра, где R -радиус основания, Н-высота ? 20 в) S осн ∙ Н г) ⅓Н( S + S ₁+√ SS₁ а) ⅓ S осн ∙Н б) П R² Н
7. Прямоугольный параллелепипед- это… 21 б) призма г) тетраэдр в) октаэдр а) пирамида
8. Назовите, какая фигура не является правильным многогранником : 22 г) параллелепипед б) додекаэдр в) октаэдр а) куб
9. Объем пирамиды определяется по формуле, где S осн - площадь основания, Н- высота, R - радиус 23 а) ⅓∙S осн ∙ Н г) ⅔П R ²Н в) S осн ∙Н б) ⅓П R² Н
10. Объем конуса определяется по формуле, где S осн - площадь основания, Н- высота, R - радиус : 24 а) ⅓∙ П R ²∙ Н г) 4 / 3П R ³ в) S осн ∙Н б) П R² Н
г) 4П R ² a ) 4 / 3П R ³ в) ⅔∙П R ²Н б) ПН²( R -⅓∙Н) 11. Определите формулу, не имеющую отношения к определению объема шара и его частей (сегмент, слой, сектор), где R- радиус, Н- высота : 25
в) 169√3 см³ г) 24√6 см³ а) 156 см³ 12. Объем правильной треугольной пирамиды, высота которой равна 12см, а сторона основания 13см, равняется : 26 б) 207 см³
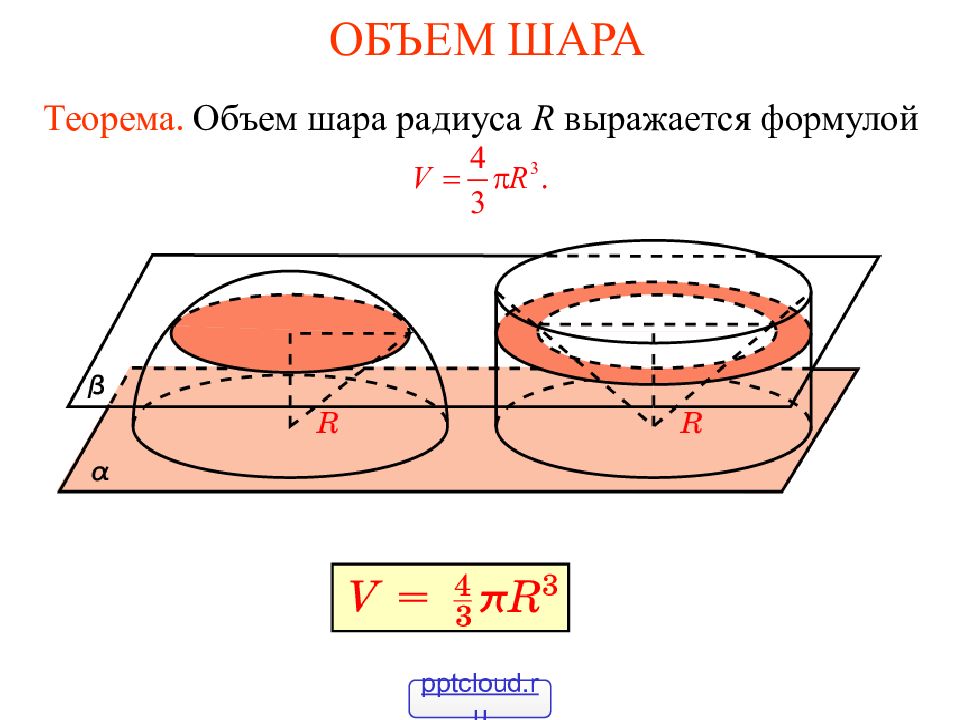
г) 4 / 3 R шара в) 1 / 3 R шара а) √ R шара 13. Шар и цилиндр имеют равные объемы, а диаметр шара равен диаметру основания цилиндра. Если выразить высоту цилиндра через радиус шара, то она будет равна : 27 б) R шара
