Первый слайд презентации
Пересечение поверхностей. Способ вспомогательных секущих плоскостей
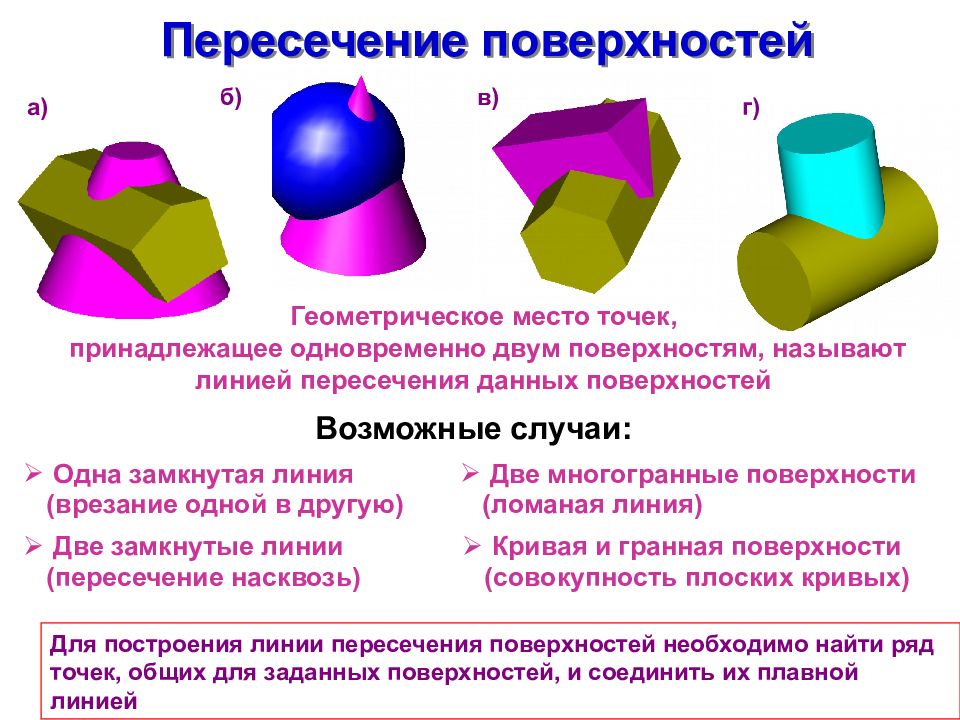
Слайд 2: Пересечение поверхностей
Для построения линии пересечения поверхностей необходимо найти ряд точек, общих для заданных поверхностей, и соединить их плавной линией Геометрическое место точек, принадлежащее одновременно двум поверхностям, называют линией пересечения данных поверхностей а) б) в) г) Возможные случаи: Две замкнутые линии (пересечение насквозь) Одна замкнутая линия (врезание одной в другую) Кривая и гранная поверхности (совокупность плоских кривых) Две многогранные поверхности (ломаная линия)
Слайд 3: Анализ заданных поверхностей
Линия пересечения 2-х поверхностей в общем случае представляет собой пространственную кривую Если заданы поверхности второго порядка, то при их пересечении получается пространственная кривая четвертого порядка 3. Часть искомой линии пересечения получается видимой в пересечении видимых частей поверхностей
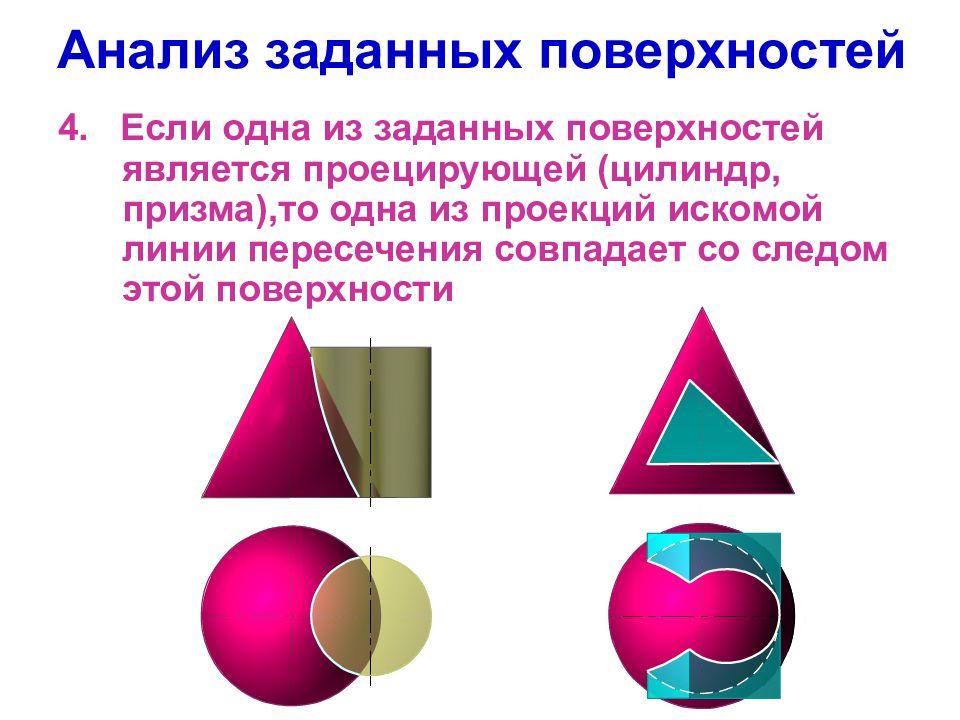
Слайд 4: Анализ заданных поверхностей
4. Если одна из заданных поверхностей является проецирующей (цилиндр, призма),то одна из проекций искомой линии пересечения совпадает со следом этой поверхности
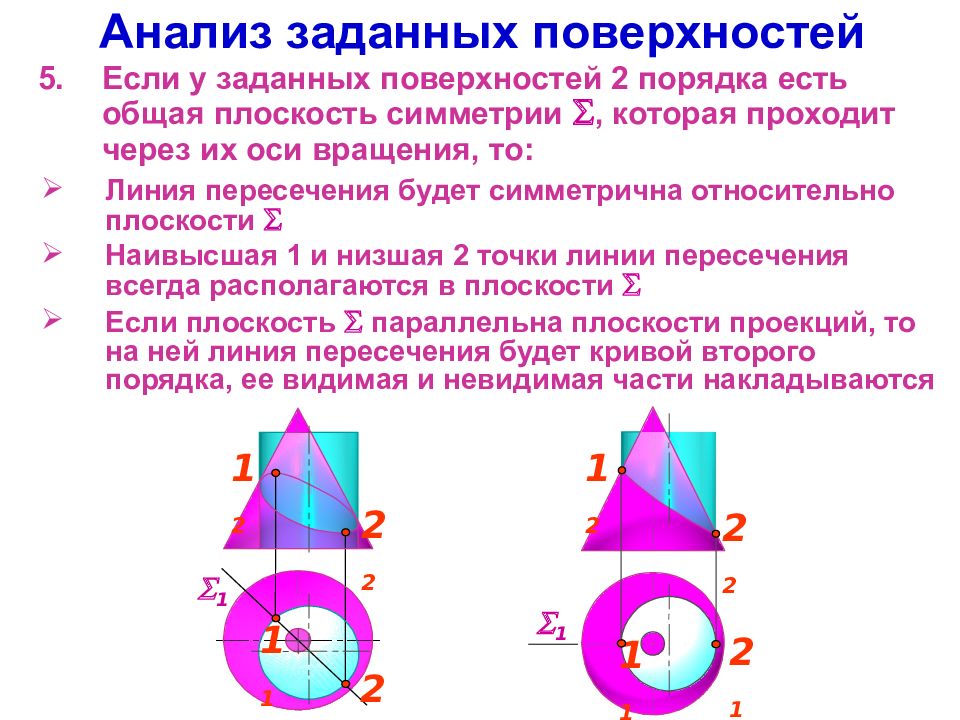
Слайд 5: Анализ заданных поверхностей
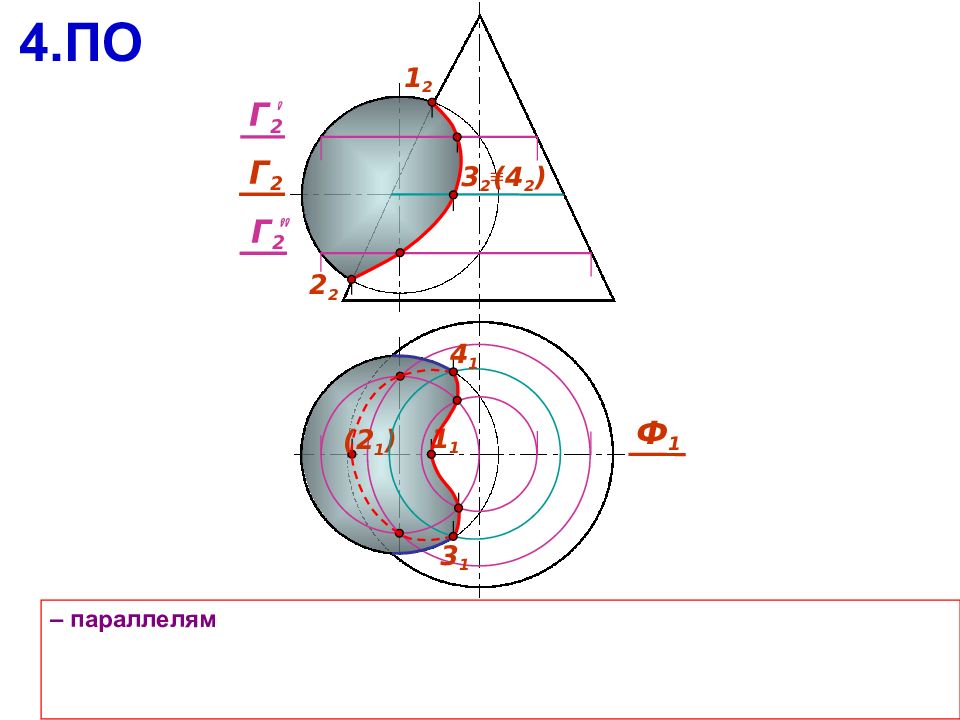
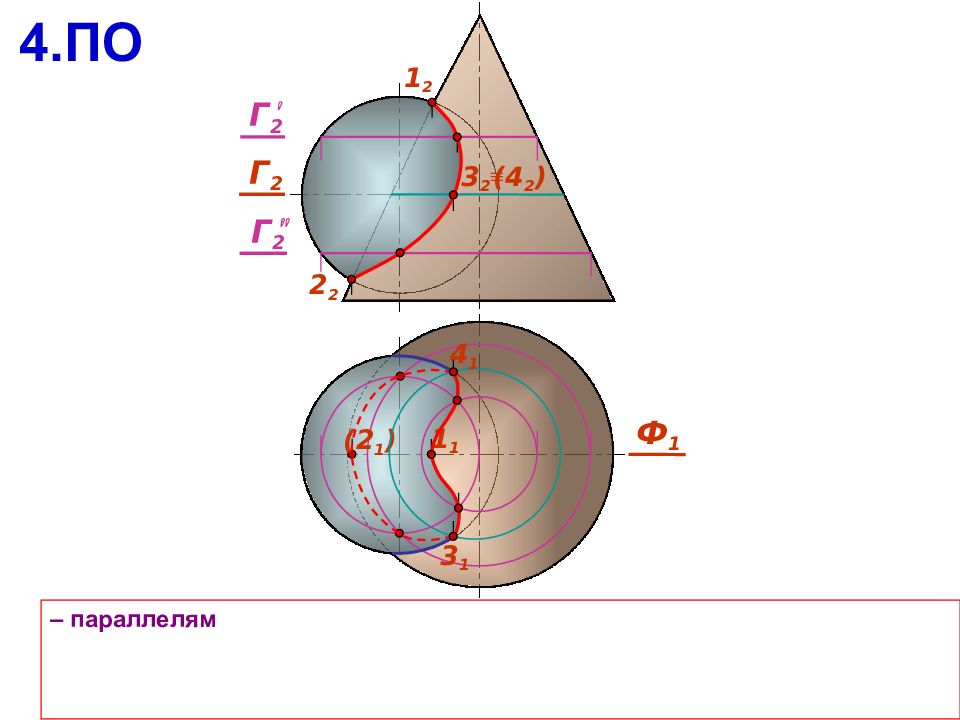
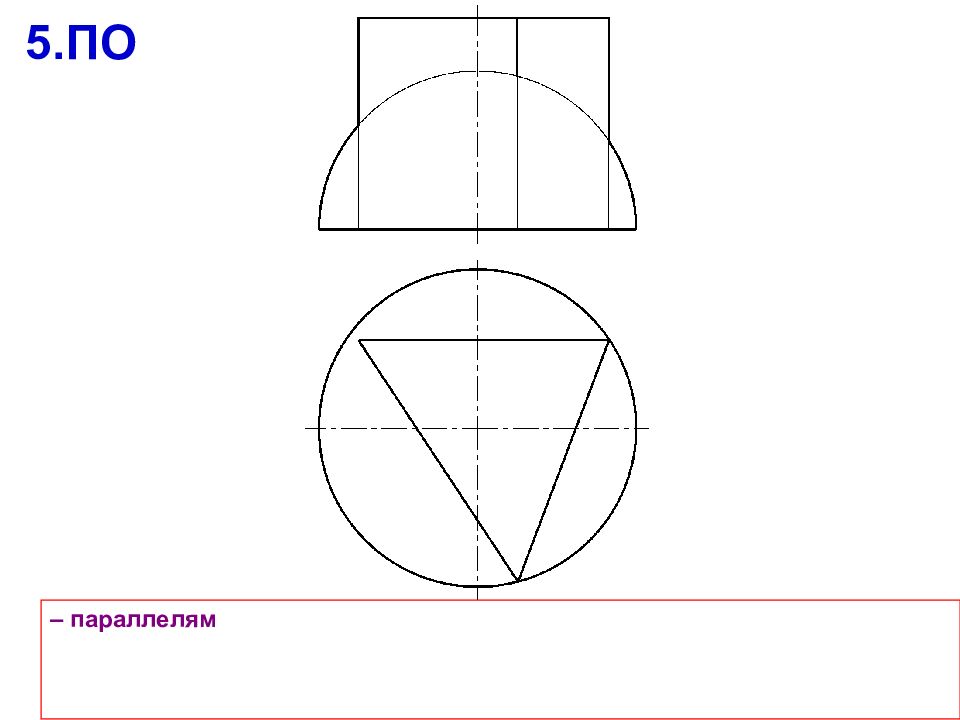
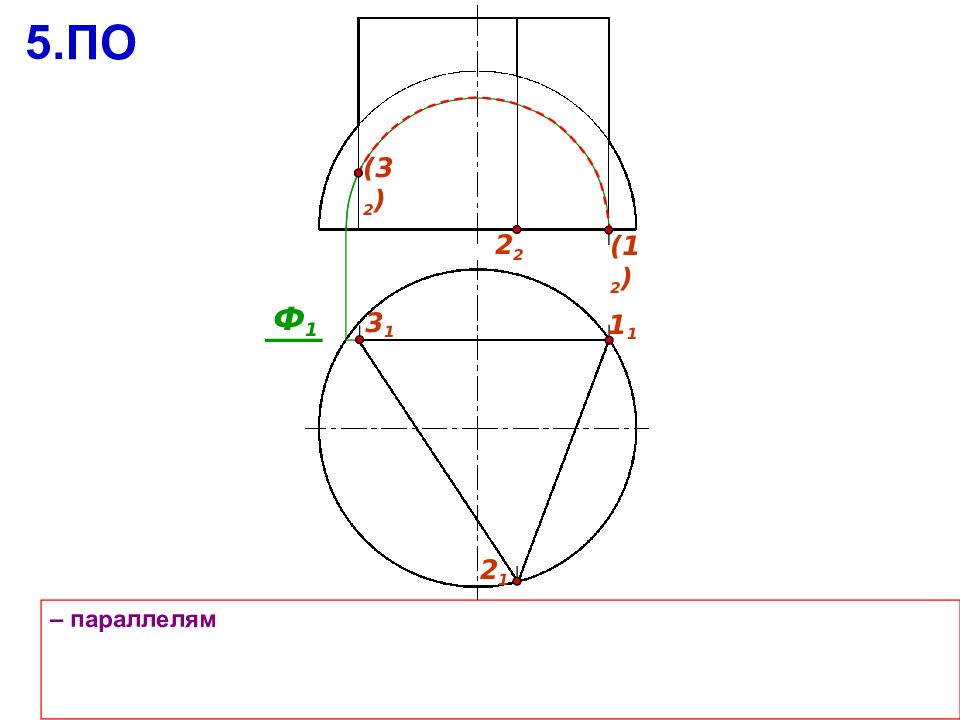
Если у заданных поверхностей 2 порядка есть общая плоскость симметрии , которая проходит через их оси вращения, то: Линия пересечения будет симметрична относительно плоскости Наивысшая 1 и низшая 2 точки линии пересечения всегда располагаются в плоскости Если плоскость параллельна плоскости проекций, то на ней линия пересечения будет кривой второго порядка, ее видимая и невидимая части накладываются 1 1 1 1 2 1 1 2 2 2 2 2 1 2 2 1 1 1
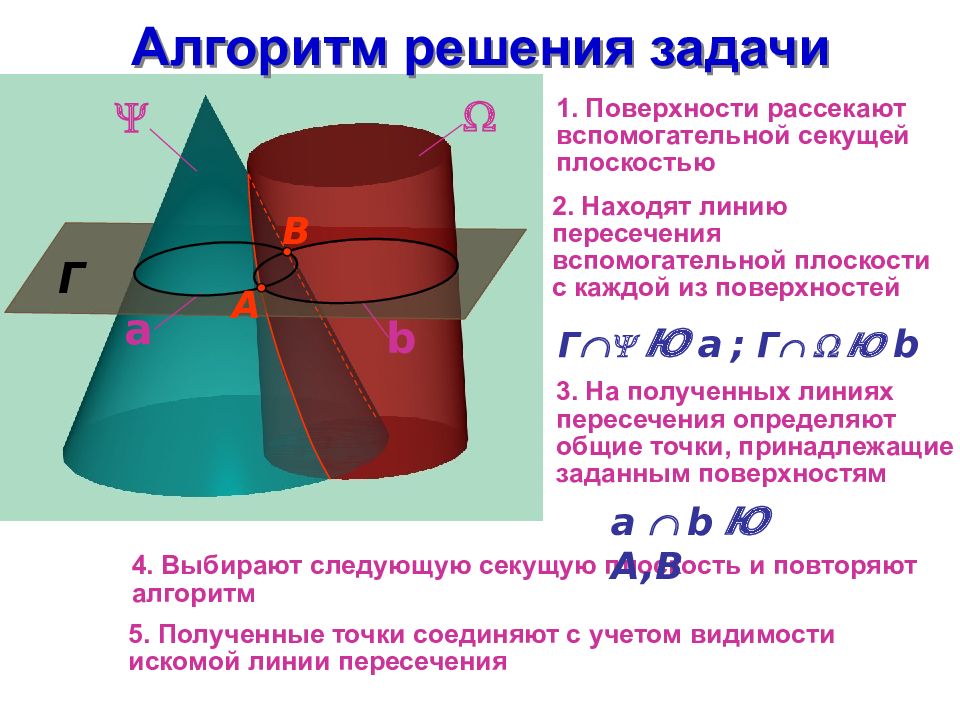
Слайд 6: Алгоритм решения задачи
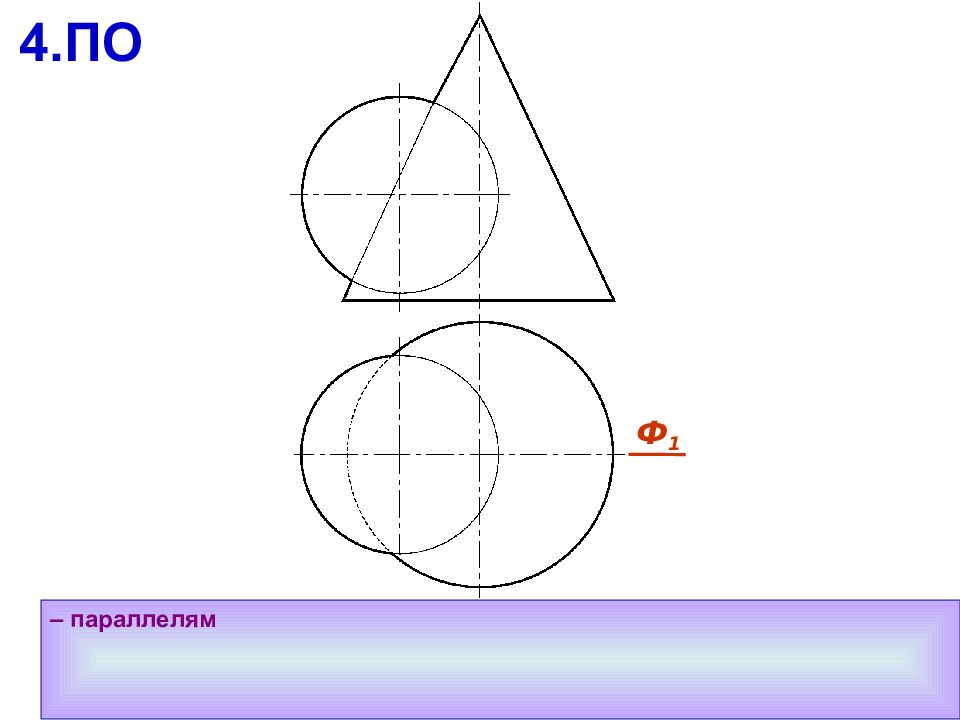
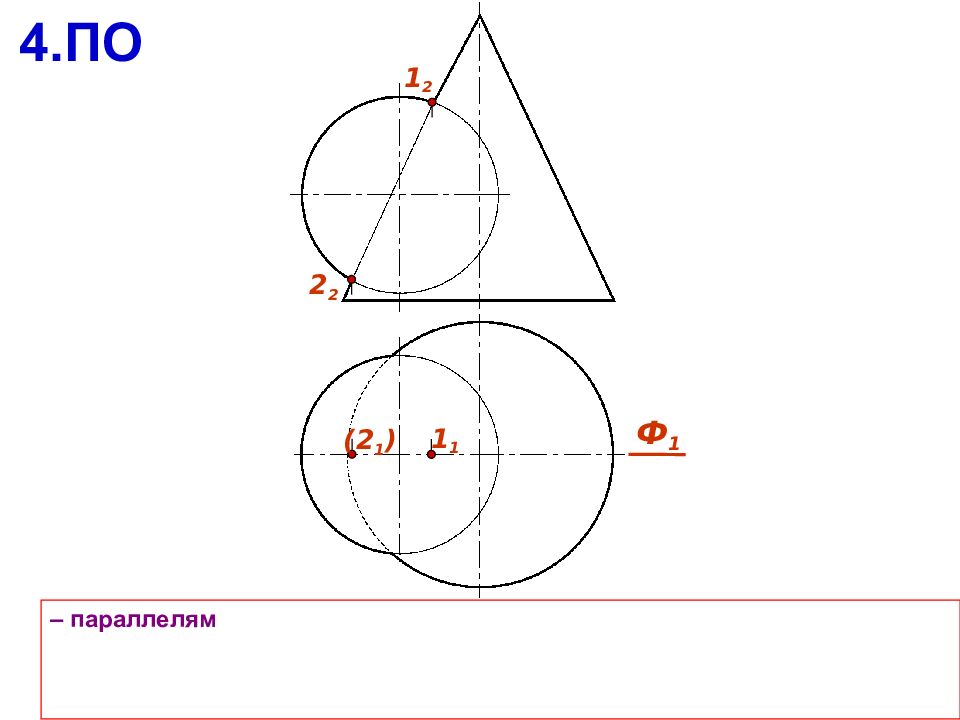
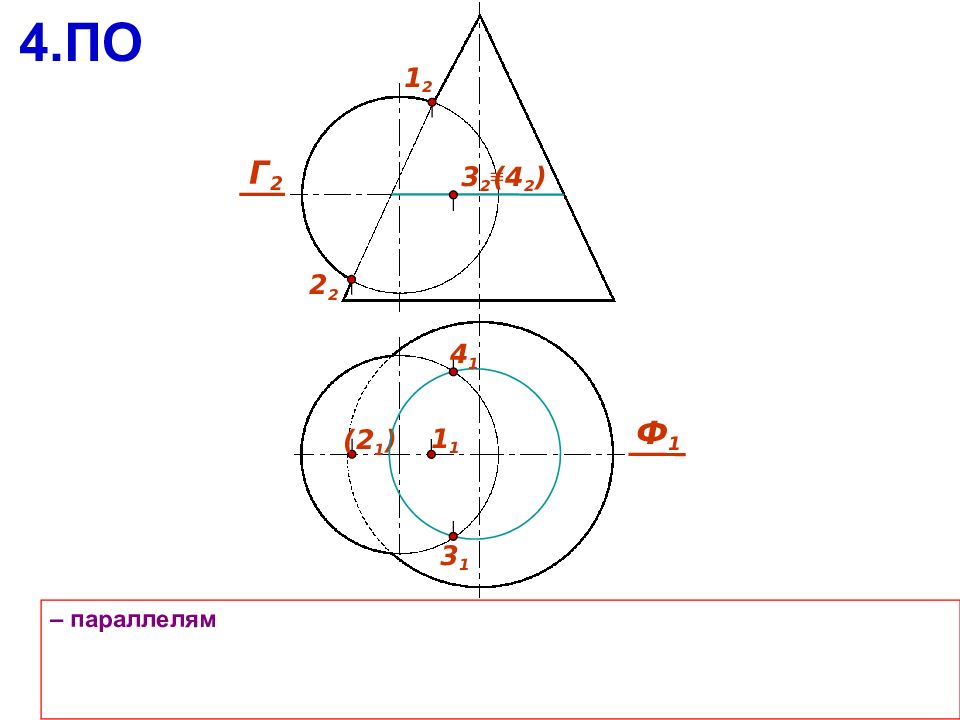
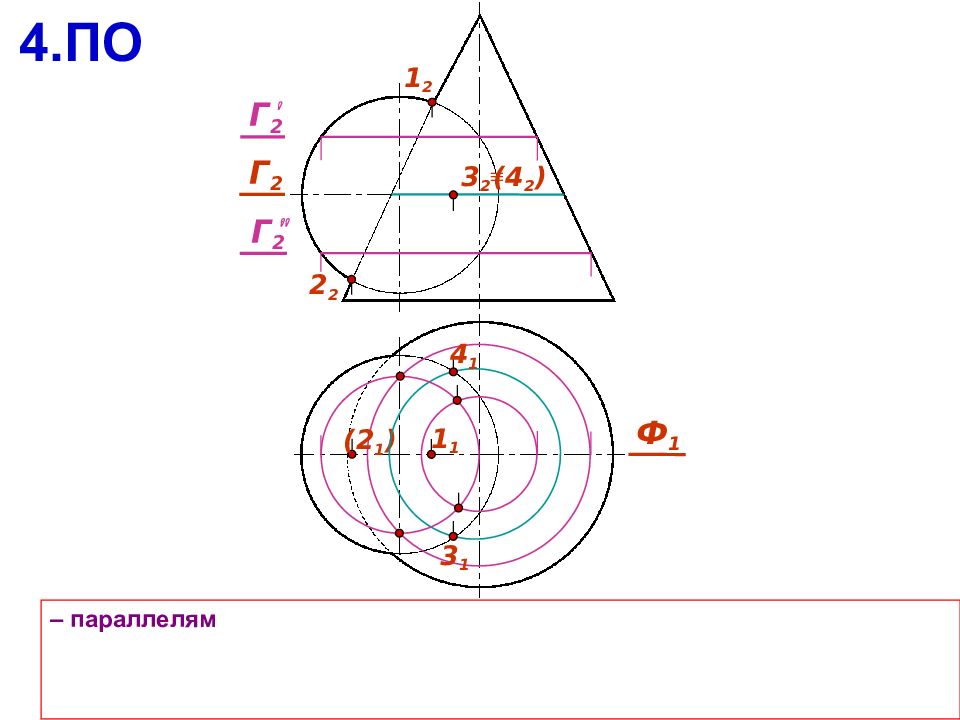
a b Алгоритм решения задачи Г 1. Поверхности рассекают вспомогательной секущей плоскостью 2. Находят линию пересечения вспомогательной плоскости с каждой из поверхностей 3. На полученных линиях пересечения определяют общие точки, принадлежащие заданным поверхностям 4. Выбирают следующую секущую плоскость и повторяют алгоритм 5. Полученные точки соединяют с учетом видимости искомой линии пересечения А B Г Ю b Г Ю а ; a b Ю A,B
Слайд 7: Методические указания
Вспомогательные плоскости следует выбирать так, чтобы в сечении получались простые линии Сначала определяют опорные точки: экстремальные точки; точки перемены видимости, лежащие на очерках поверхностей; особые точки кривых пересечения (концы осей эллипса, вершины гиперболы или параболы, вершины ломанной) Уточняют линию пересечения с помощью промежуточных точек
Слайд 11
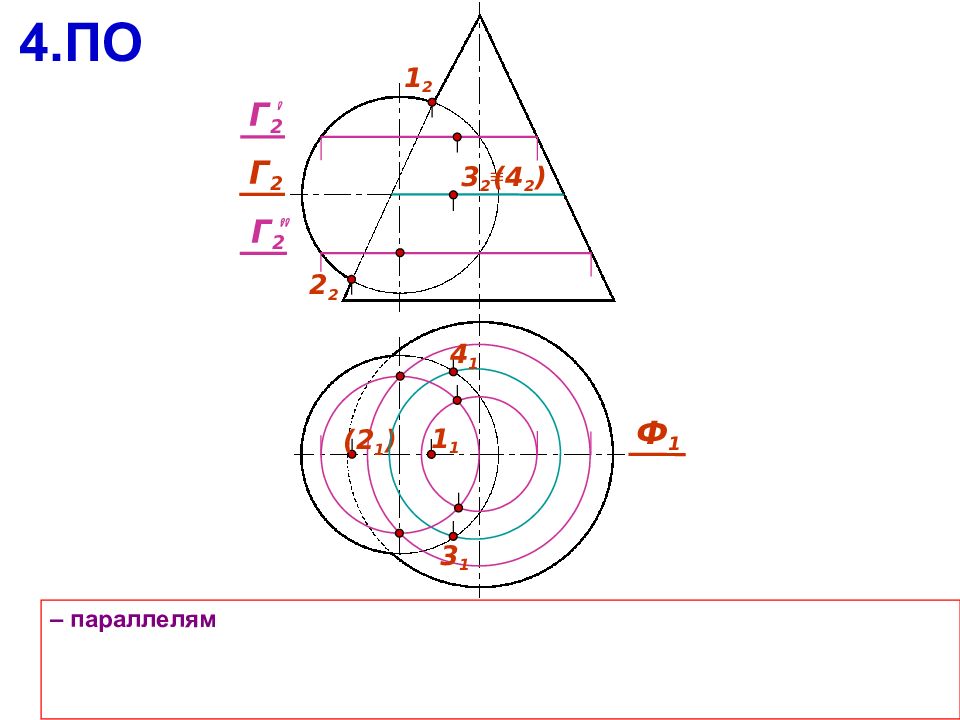
– параллелям 4.ПО 1 2 2 2 Ф 1 ( 2 1 ) 1 1 Г 2 3 1 4 1 ( 4 2 ) 3 2 Г 2 Г 2
Слайд 12
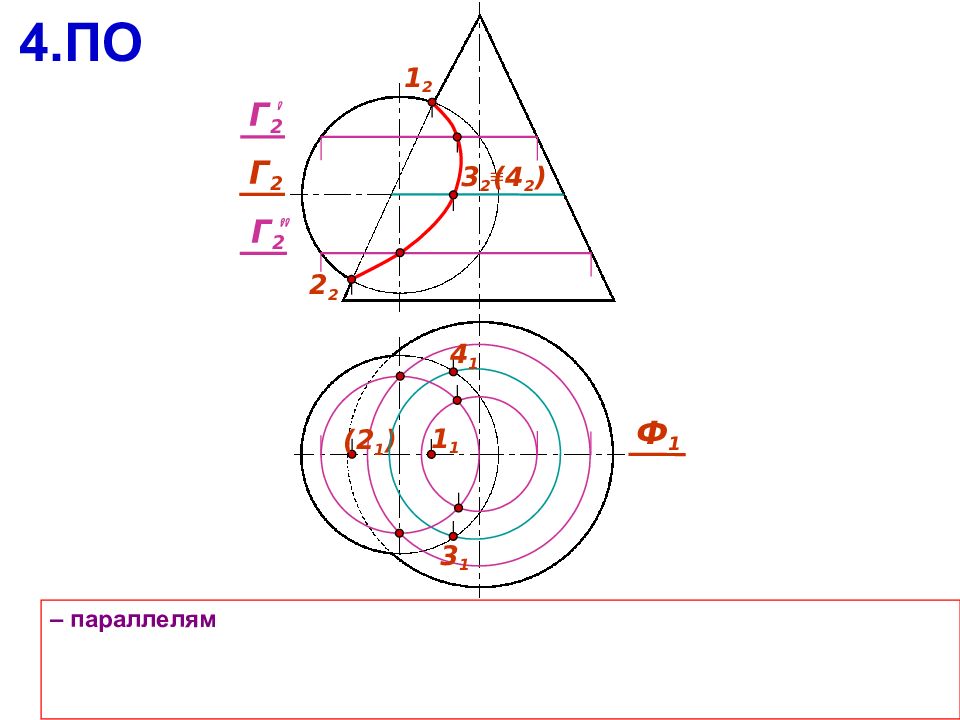
– параллелям 4.ПО 1 2 2 2 Ф 1 ( 2 1 ) 1 1 Г 2 3 1 4 1 ( 4 2 ) 3 2 Г 2 Г 2
Слайд 13
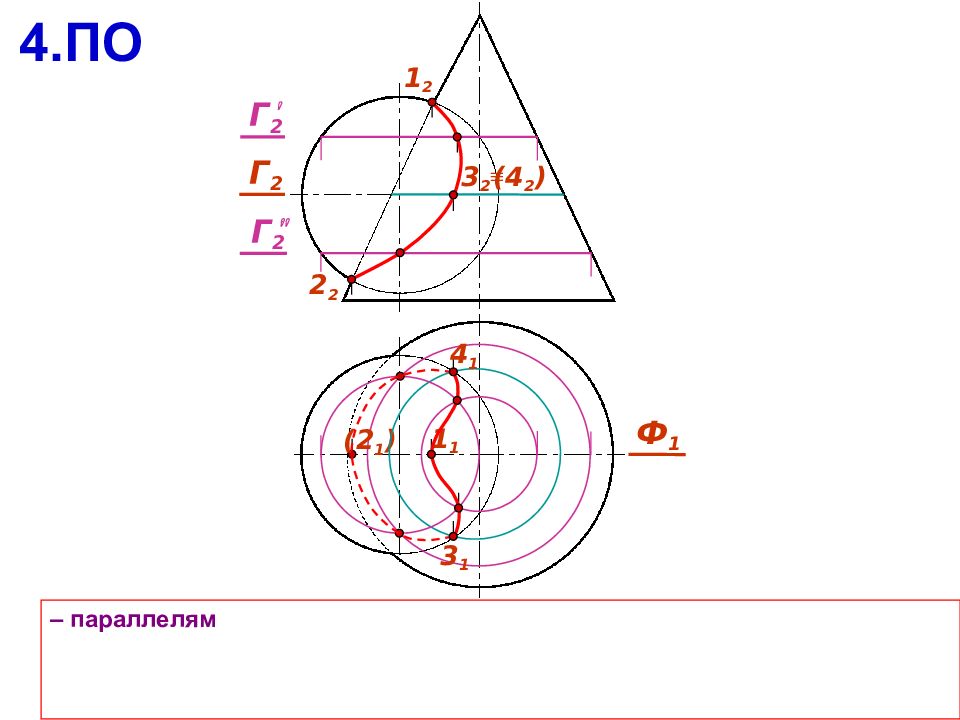
– параллелям 4.ПО 1 2 2 2 Ф 1 ( 2 1 ) 1 1 Г 2 3 1 4 1 ( 4 2 ) 3 2 Г 2 Г 2
Слайд 14
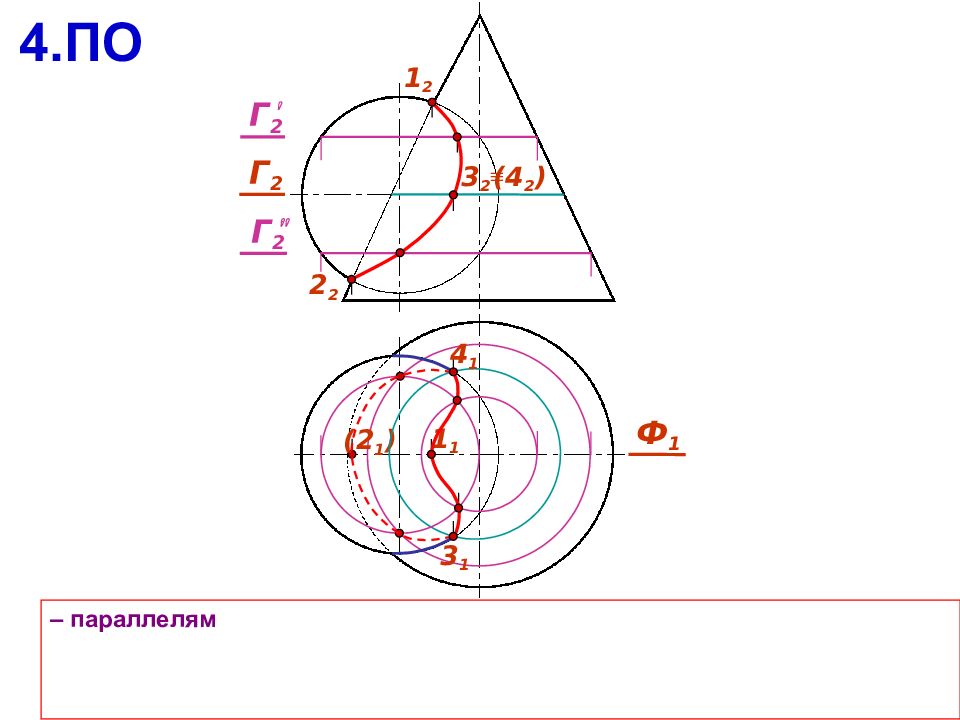
– параллелям 4.ПО 1 2 2 2 Ф 1 ( 2 1 ) 1 1 Г 2 3 1 4 1 ( 4 2 ) 3 2 Г 2 Г 2
Слайд 15
– параллелям 4.ПО 1 2 2 2 Ф 1 ( 2 1 ) 1 1 Г 2 3 1 4 1 ( 4 2 ) 3 2 Г 2 Г 2
Слайд 16
– параллелям 4.ПО 1 2 2 2 Ф 1 ( 2 1 ) 1 1 Г 2 3 1 4 1 ( 4 2 ) 3 2 Г 2 Г 2
Слайд 17
– параллелям 4.ПО 1 2 2 2 Ф 1 ( 2 1 ) 1 1 Г 2 3 1 4 1 ( 4 2 ) 3 2 Г 2 Г 2
Слайд 20
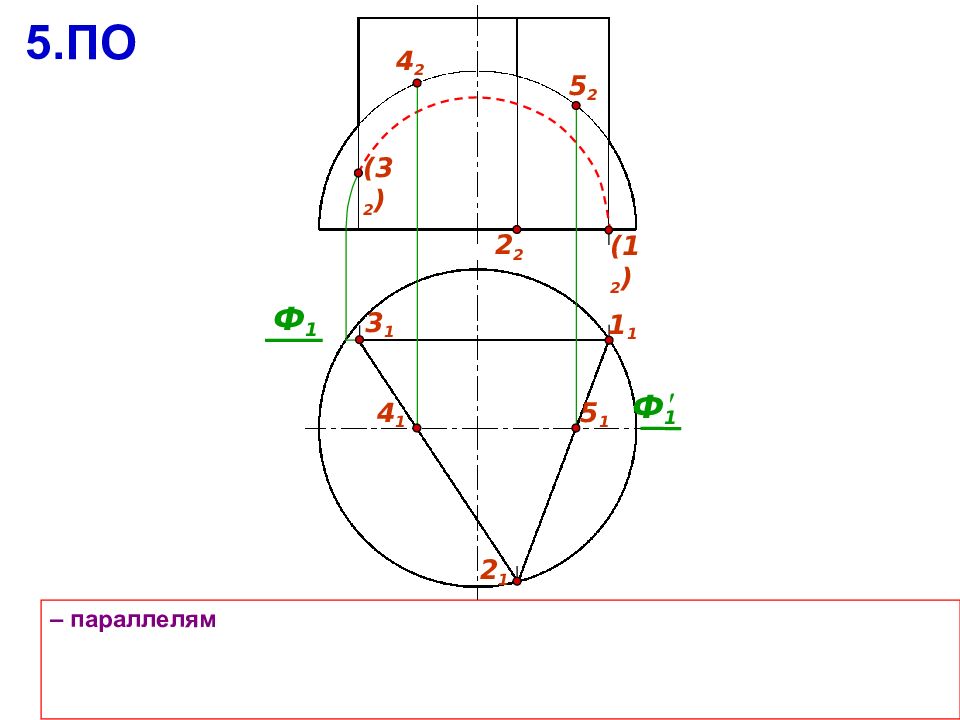
3 1 1 1 – параллелям 2 1 ( 1 2 ) ( 3 2 ) 4 2 5 2 2 2 5.ПО Ф 1 Ф 1 4 1 5 1
Слайд 21
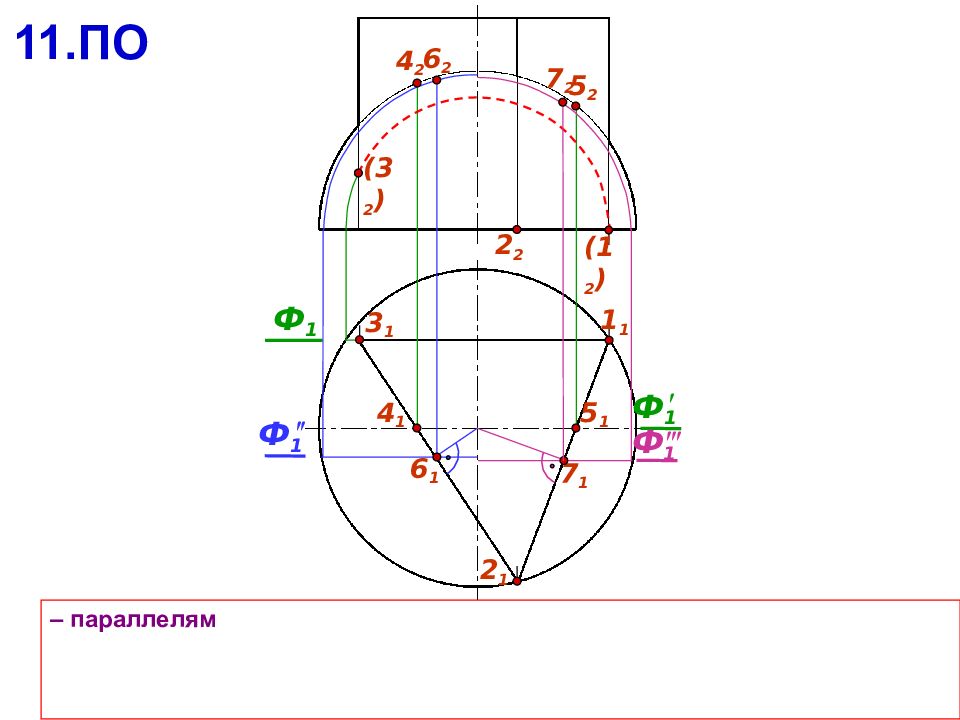
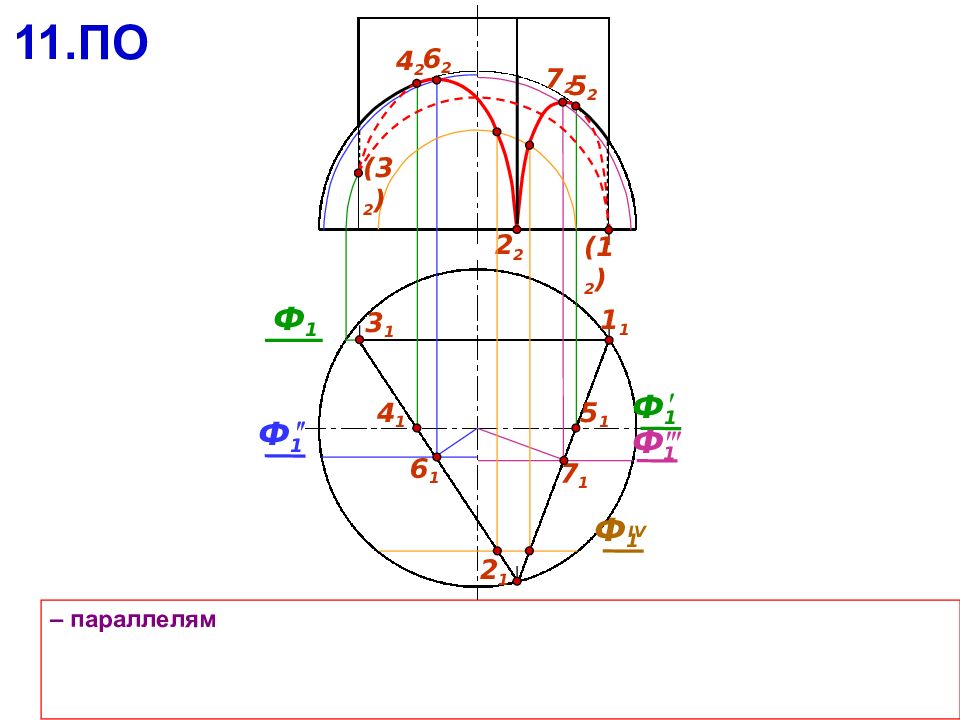
3 1 1 1 – параллелям 2 1 Ф 1 ( 1 2 ) ( 3 2 ) Ф 1 4 2 5 2 4 1 5 1 Ф 1 6 2 2 2 11.ПО Ф 1 7 1 6 1 7 2
Слайд 22
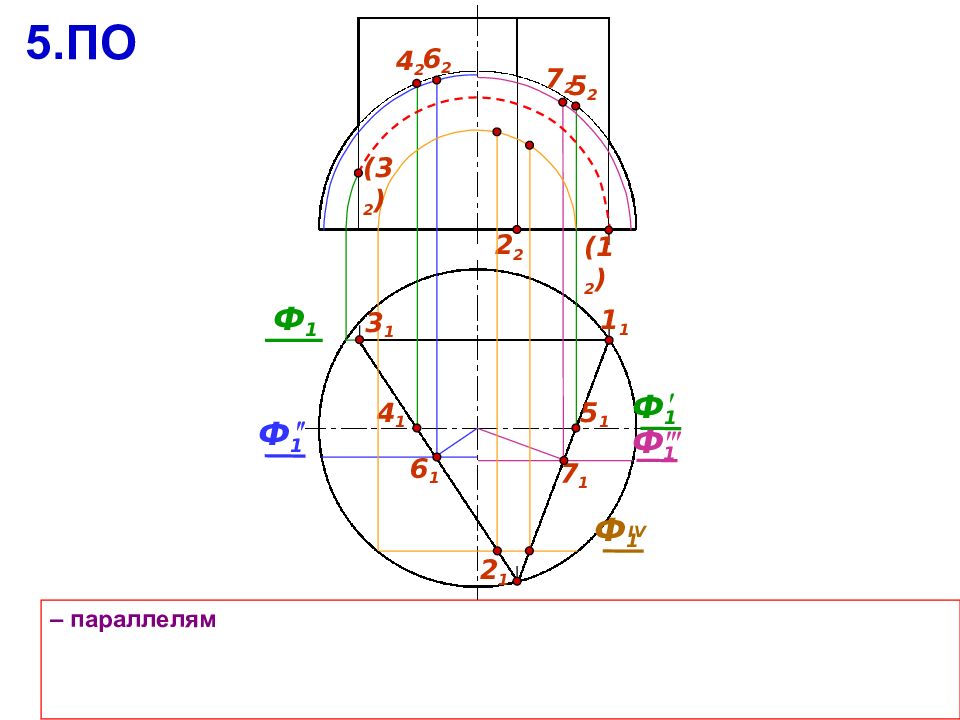
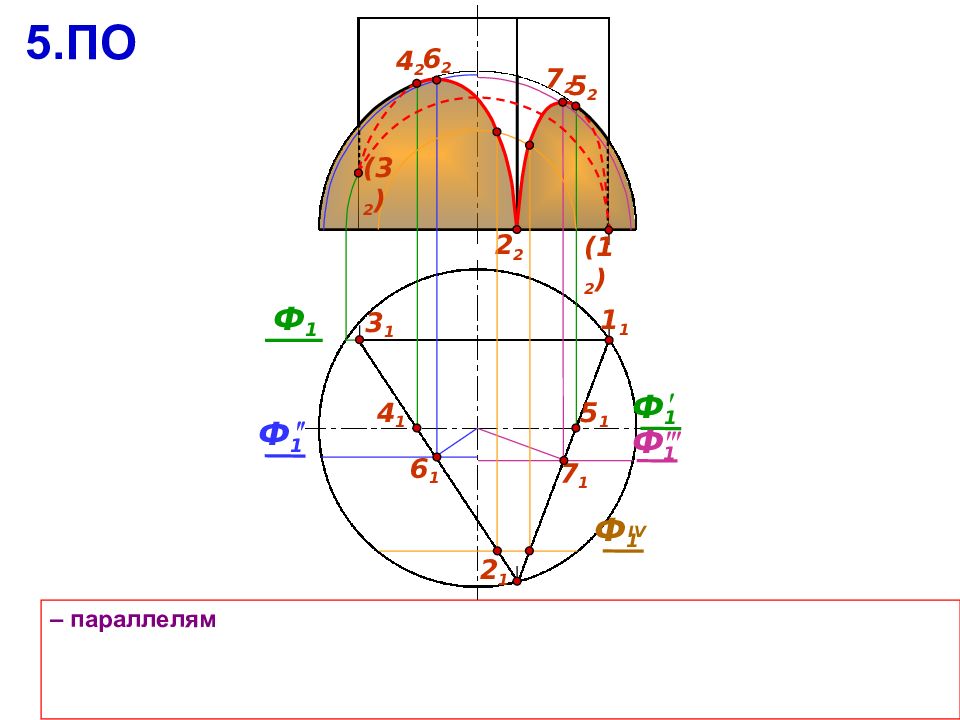
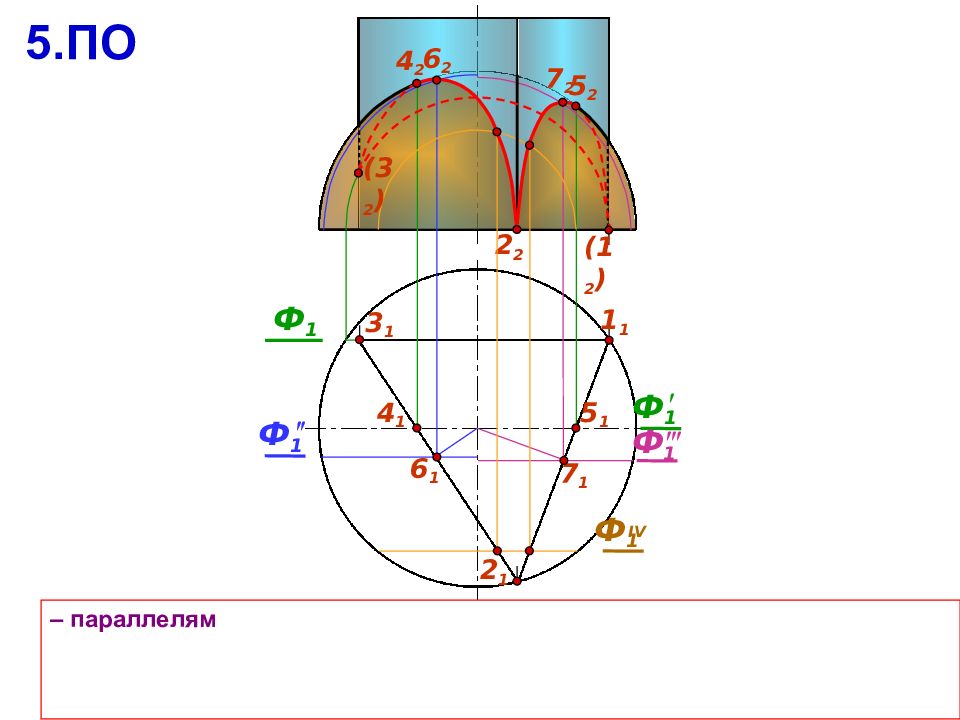
2 2 – параллелям 2 1 Ф 1 4 2 5 2 4 1 7 1 6 1 5 1 Ф 1 6 2 ( 3 2 ) 5.ПО Ф 1 Ф 1 IV 7 2 3 1 Ф 1 1 1 ( 1 2 )
Слайд 23
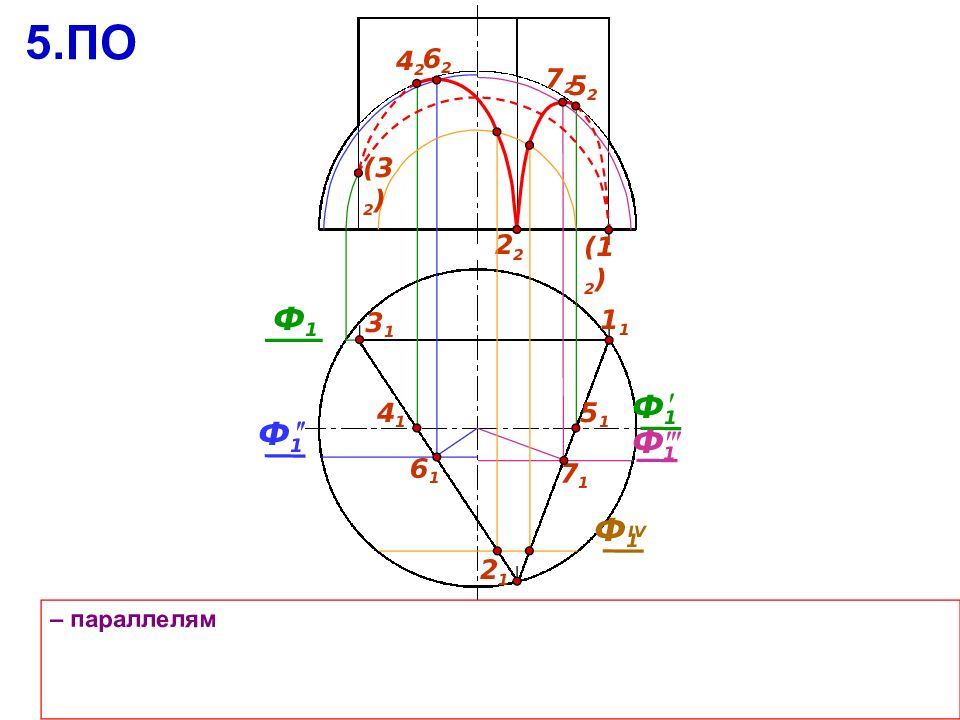
2 2 3 1 – параллелям 2 1 Ф 1 Ф 1 4 2 5 2 4 1 7 1 6 1 5 1 Ф 1 6 2 ( 3 2 ) 5.ПО Ф 1 Ф 1 IV 7 2 1 1 ( 1 2 )
Слайд 24
2 2 3 1 – параллелям 2 1 Ф 1 Ф 1 4 2 5 2 4 1 7 1 6 1 Ф 1 IV 5 1 Ф 1 6 2 ( 3 2 ) 11.ПО Ф 1 7 2 1 1 ( 1 2 )
Слайд 25
2 2 3 1 – параллелям 2 1 Ф 1 Ф 1 4 2 5 2 4 1 7 1 6 1 Ф 1 IV 5 1 Ф 1 6 2 ( 3 2 ) 5.ПО Ф 1 7 2 1 1 ( 1 2 )