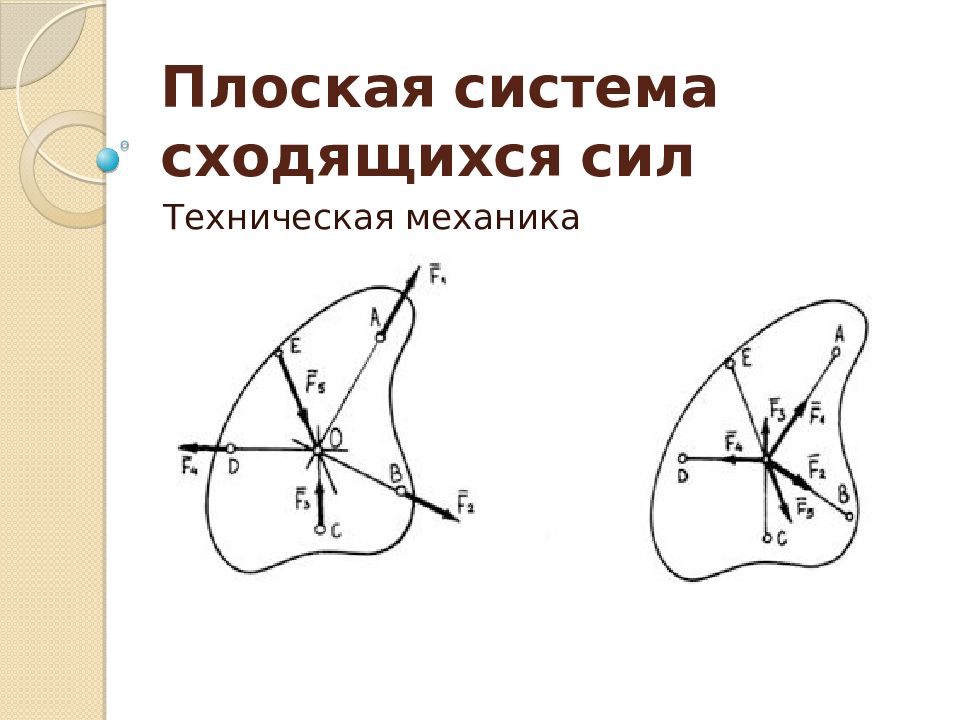
Слайд 2: Плоская система сил
Линии действия всех сил лежат в одной плоскости Пространственная система сил если линии действия всех сил не лежат в одной плоскости
Слайд 3: Сходящаяся система сил
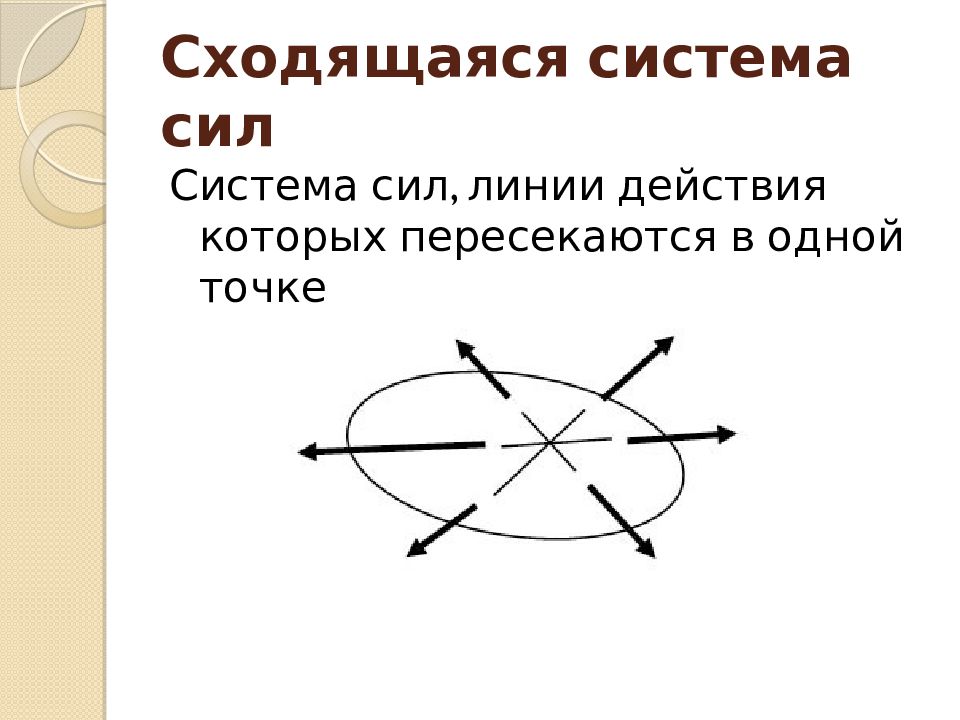
Система сил, линии действия которых пересекаются в одной точке
Слайд 4
Система сходящихся сил эквивалентна одной силе – равнодействующей, которая равна векторной сумме сил приложена в точке пересечения линий их действия
Слайд 5: Методы определения равнодействующей
Слайд 6: Метод параллелограммов сил
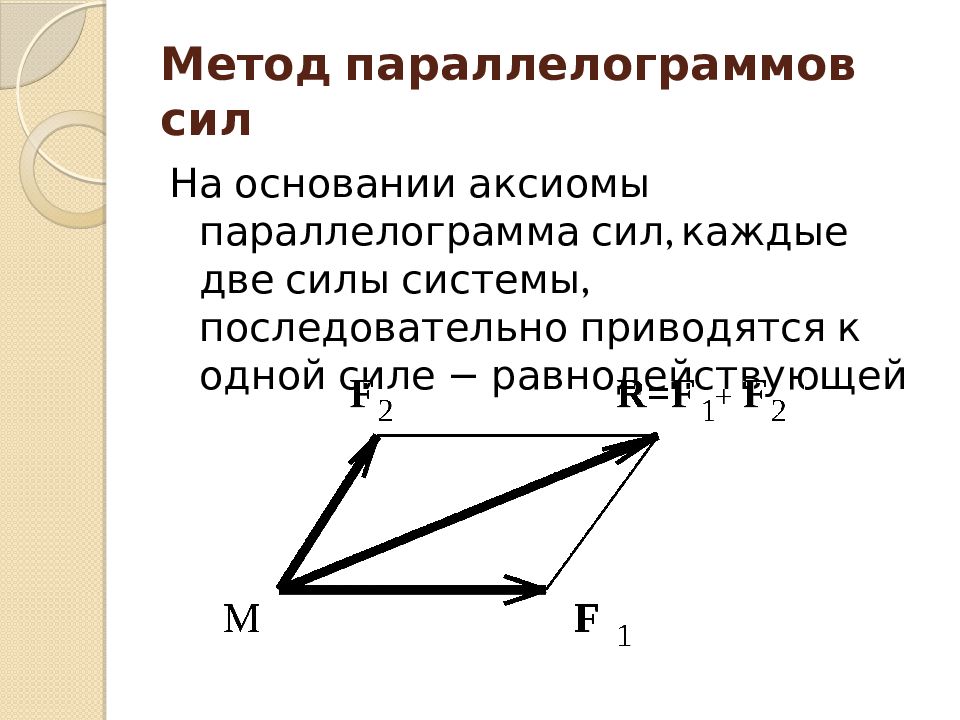
На основании аксиомы параллелограмма сил, каждые две силы системы, последовательно приводятся к одной силе − равнодействующей
Слайд 7: Векторный силовой многоугольник
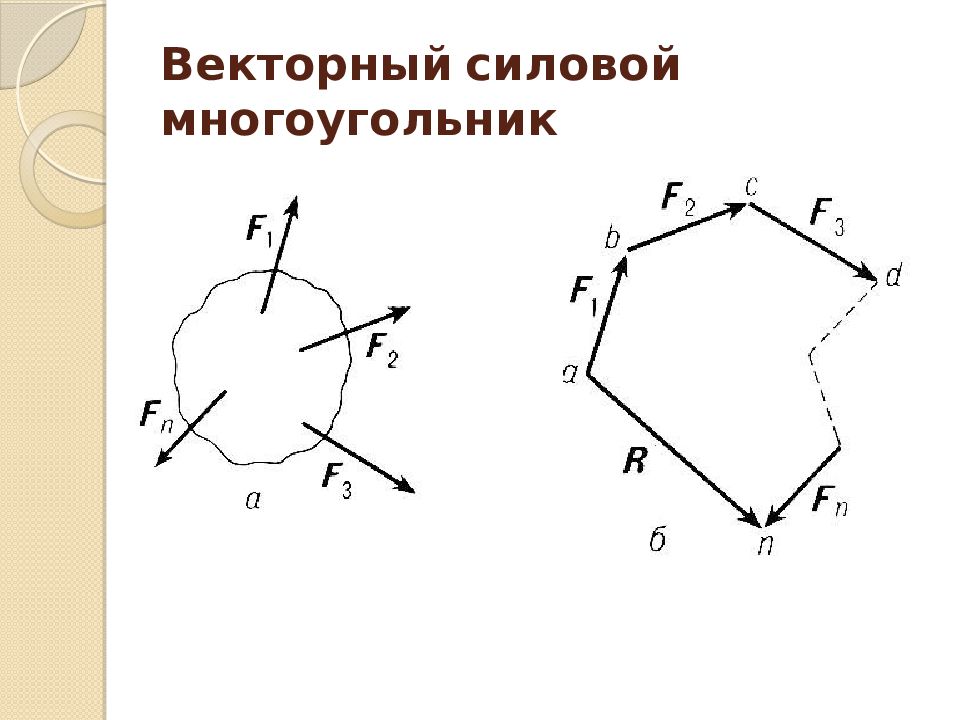
Поочерёдно откладываем каждый вектор силы от конечной точки предыдущего вектора Получаем многоугольник: стороны векторы сил системы, замыкающая сторона − вектор равнодействующей системы сходящихся сил
Слайд 9: Условия равновесия системы сходящихся сил
Геометрическое условие для равновесия системы сходящихся сил необходимо и достаточно, чтобы векторный силовой многоугольник, построенный на этих силах, был замкнутым
Слайд 10: Условия равновесия системы сходящихся сил
Аналитические условия Для равновесия системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на координатные оси равнялись нулю
Слайд 12: Геометрический способ
Удобен, если в системе три силы Тела считаются абсолютно твёрдым
Слайд 13: Алгоритм
1. Определить возможное направление реакций связей 2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе 3. Измерить полученные векторы сил, определить их величину, учитывая масштаб 4. Для уточнения определить величины векторов с помощью геометрических зависимостей
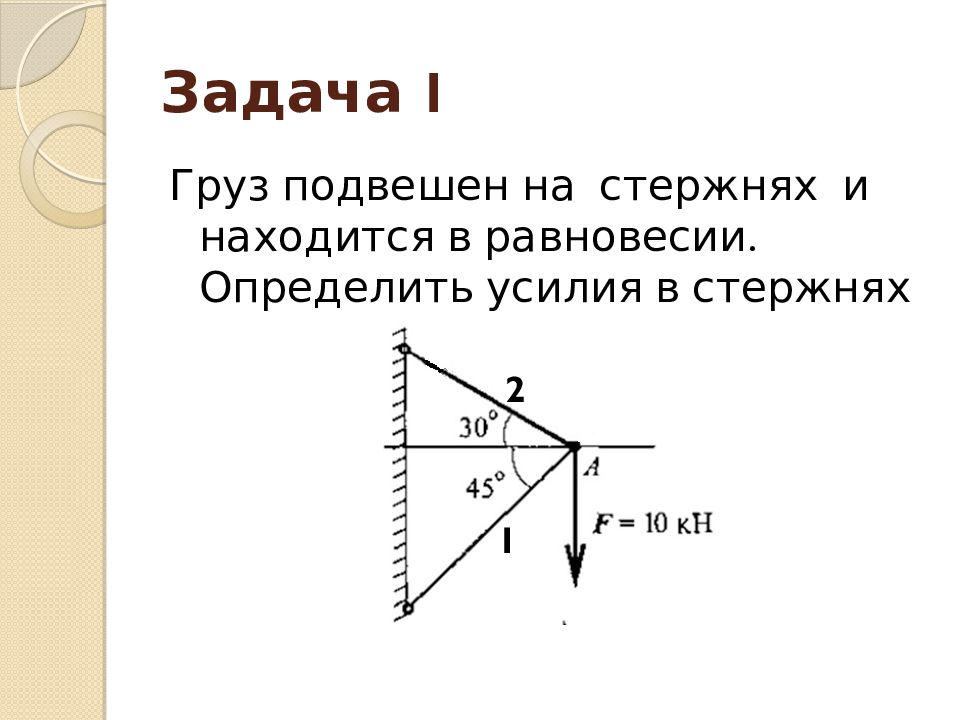
Слайд 14: Задача 1
Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях 1 2
Слайд 15: Решение
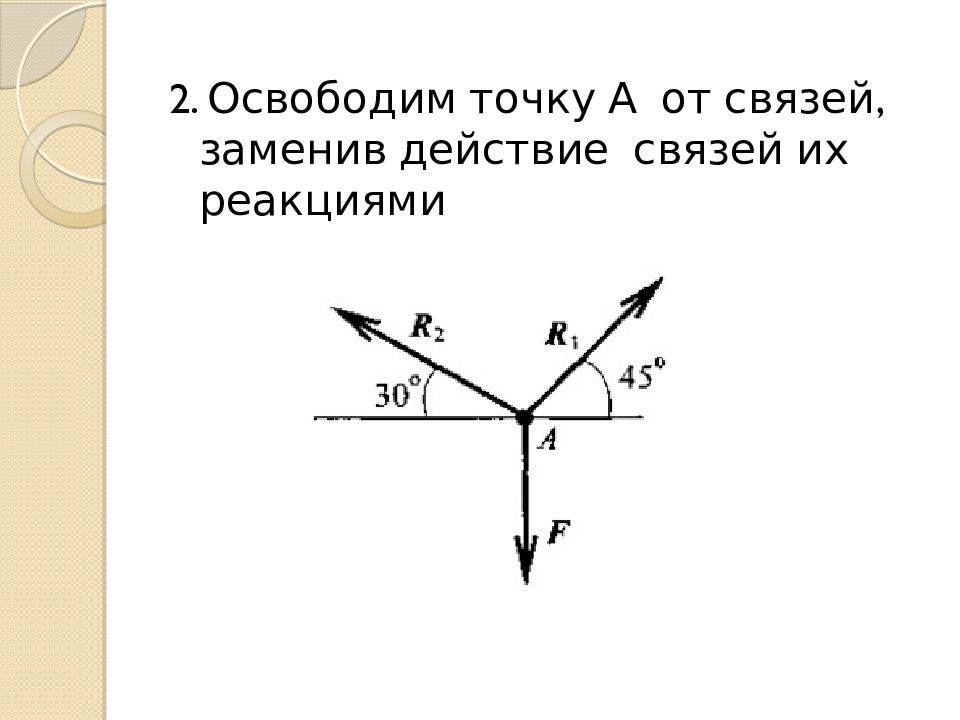
1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз 5 аксиома статики Определяем возможные направления реакций связей «жёсткие стержни» Усилия направлены вдоль стержней
Слайд 17
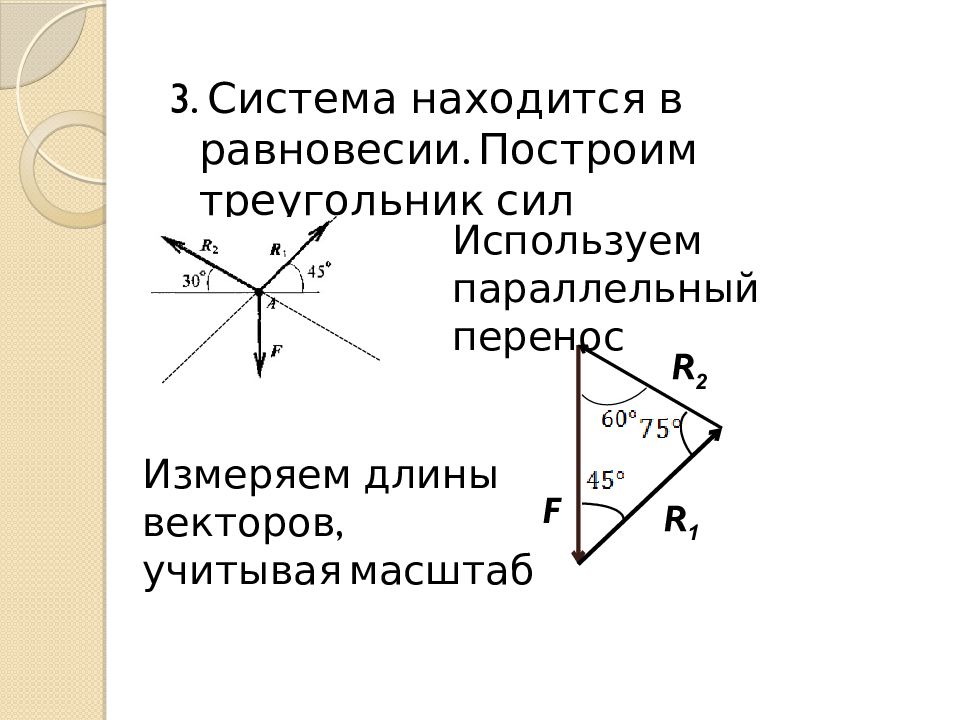
3. Система находится в равновесии. Построим треугольник сил F R 1 R 2 Используем параллельный перенос Измеряем длины векторов, учитывая масштаб
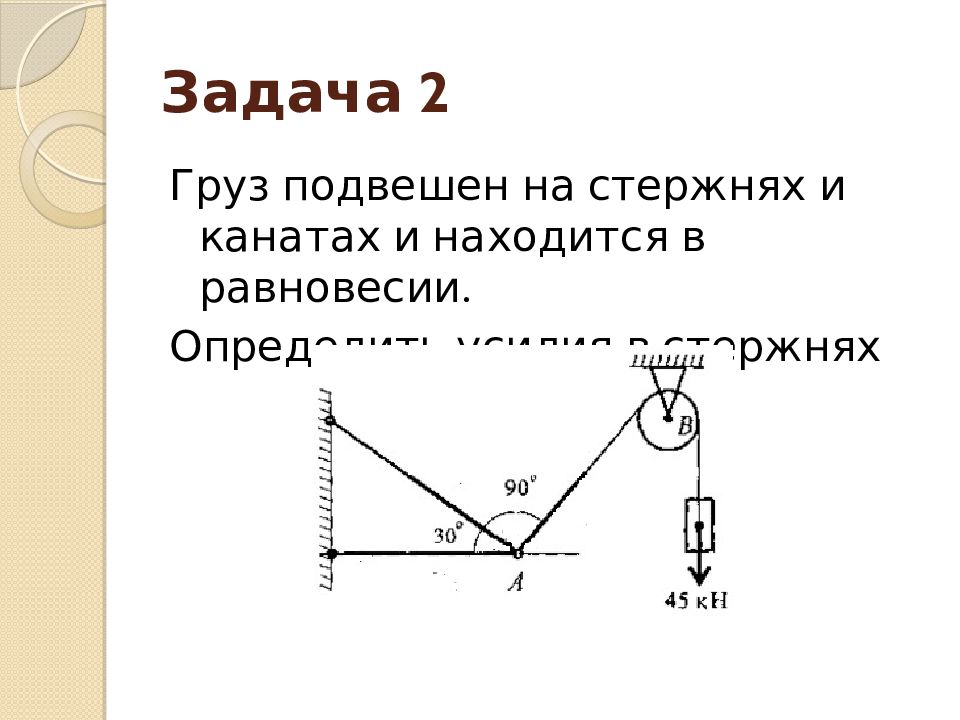
Слайд 19: Задача 2
Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях
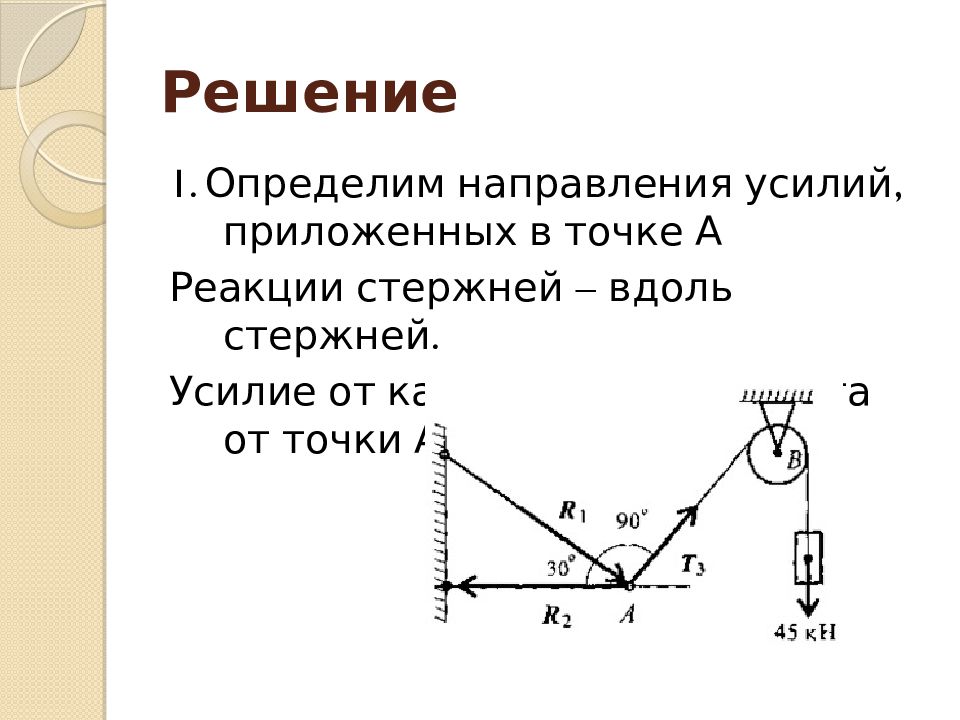
Слайд 20: Решение
1. Определим направления усилий, приложенных в точке А Реакции стержней вдоль стержней. Усилие от каната вдоль каната от точки А к точке В
Слайд 21
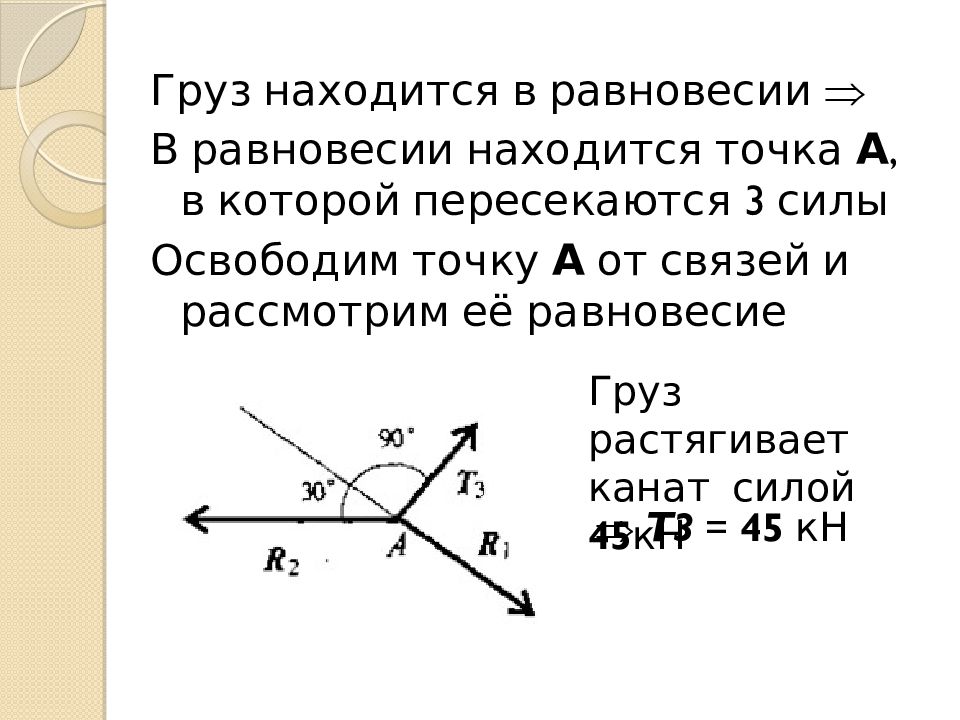
Груз находится в равновесии В равновесии находится точка А, в которой пересекаются 3 силы Освободим точку А от связей и рассмотрим её равновесие Груз растягивает канат силой 45 кН Т3 = 45 кН
Слайд 22
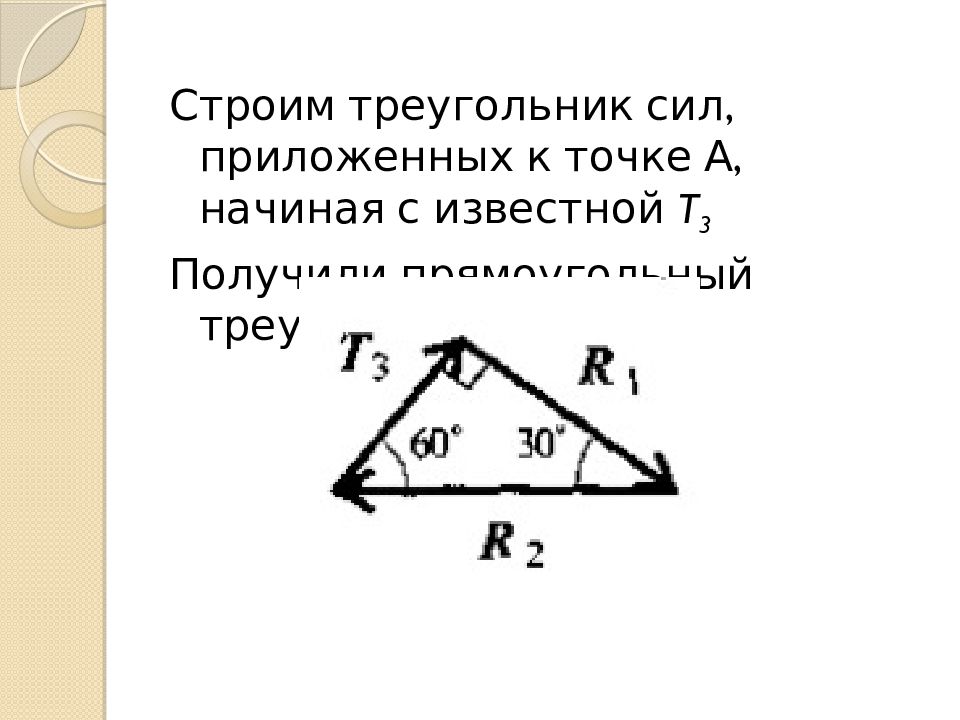
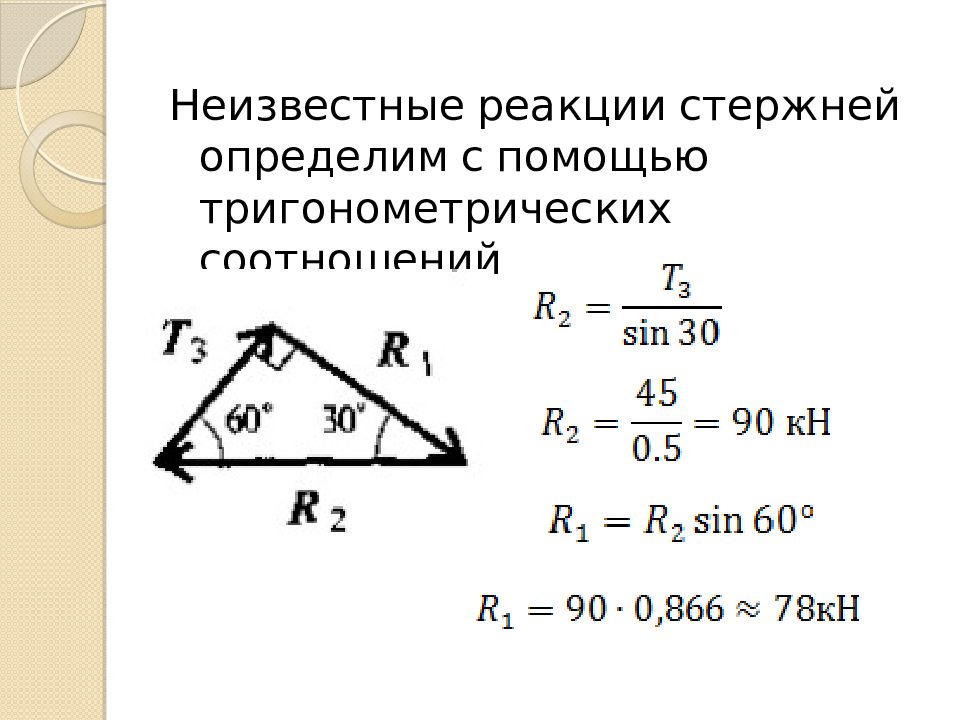
Строим треугольник сил, приложенных к точке А, начиная с известной T 3 Получили прямоугольный треугольник
Слайд 23
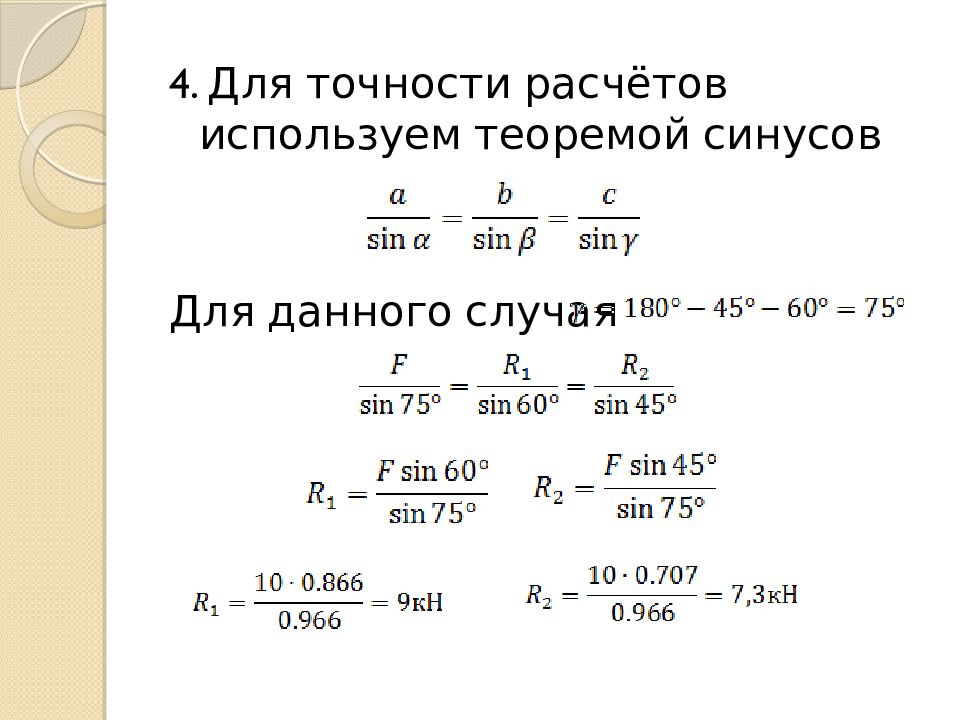
Неизвестные реакции стержней определим с помощью тригонометрических соотношений
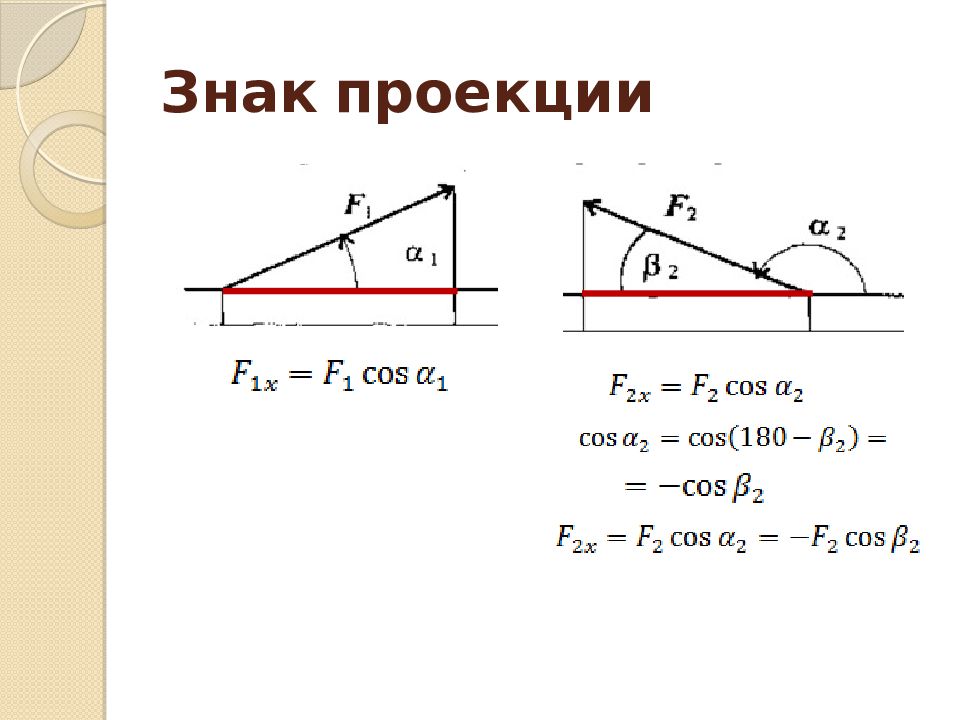
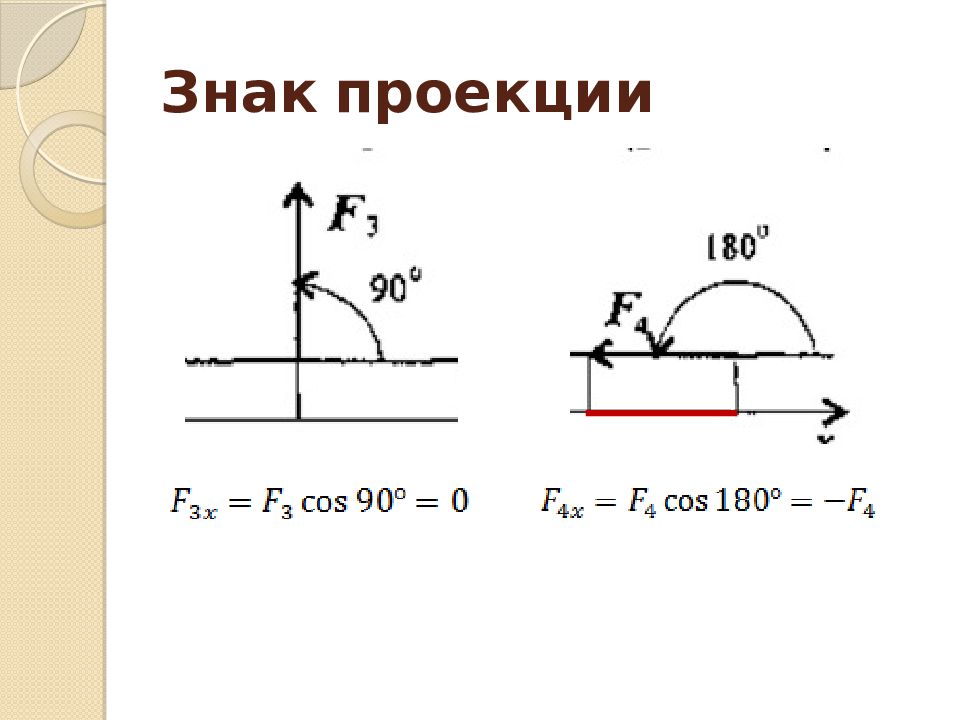
Слайд 24: Проекция силы на ось
Определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора
Слайд 31
Модуль равнодействующей найдём по теореме Пифагора Направление равнодействующей по величинам и знакам косинусов углов
Слайд 33: Условие равновесия в аналитической форме
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось системы
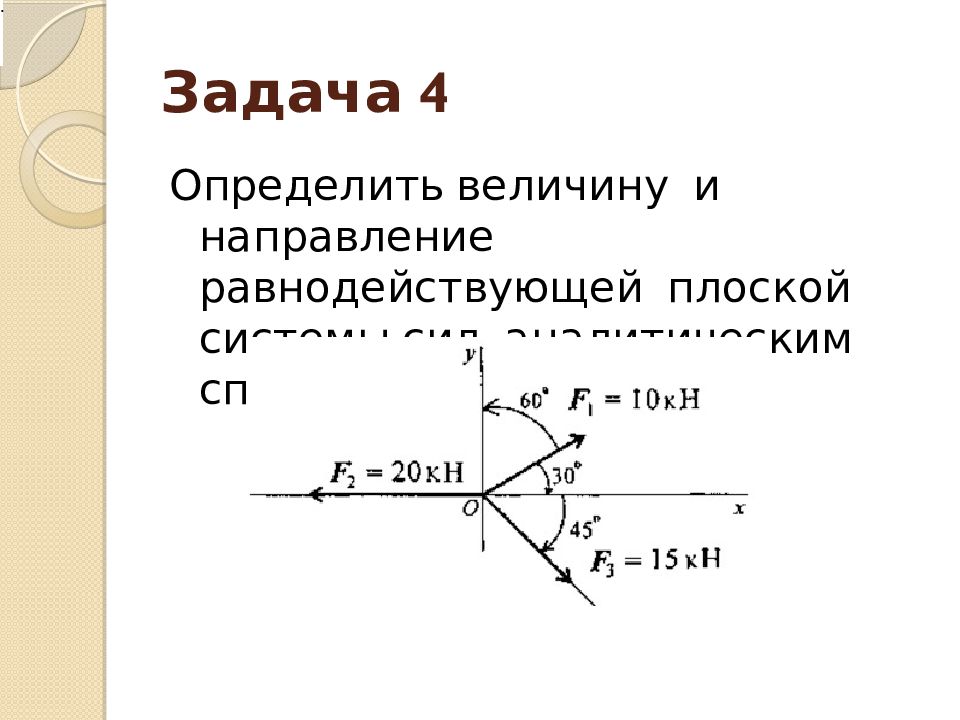
Слайд 36: Задача 4
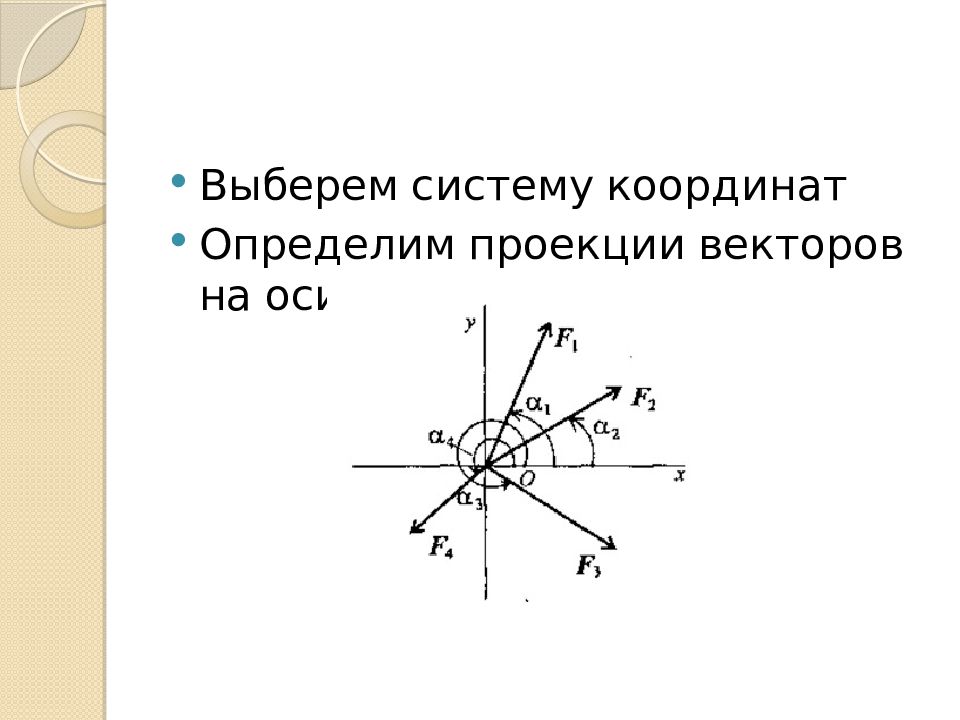
Определить величину и направление равнодействующей плоской системы сил аналитическим способом
Слайд 37: Решение
Проекции сил системы на ось Х Проекция равнодействующей на ось Х направлена влево
Слайд 38
Проекции сил системы на ось Y Проекция равнодействующей на ось Y направлена вниз
Слайд 39
Определяем модуль равнодействующей Определяем значение углов равнодействующей с осями
Последний слайд презентации: Плоская система сходящихся сил: Задача 5
Система трёх сил находится в равновесии. Известны проекции двух сил на взаимно перпендикулярные оси OX и OY F 1x = 10 кН F 2 x = 5 кН F 1y = - 2 кН F 2 y = 6 кН Определить, чему равна и как направлена третья сила системы.