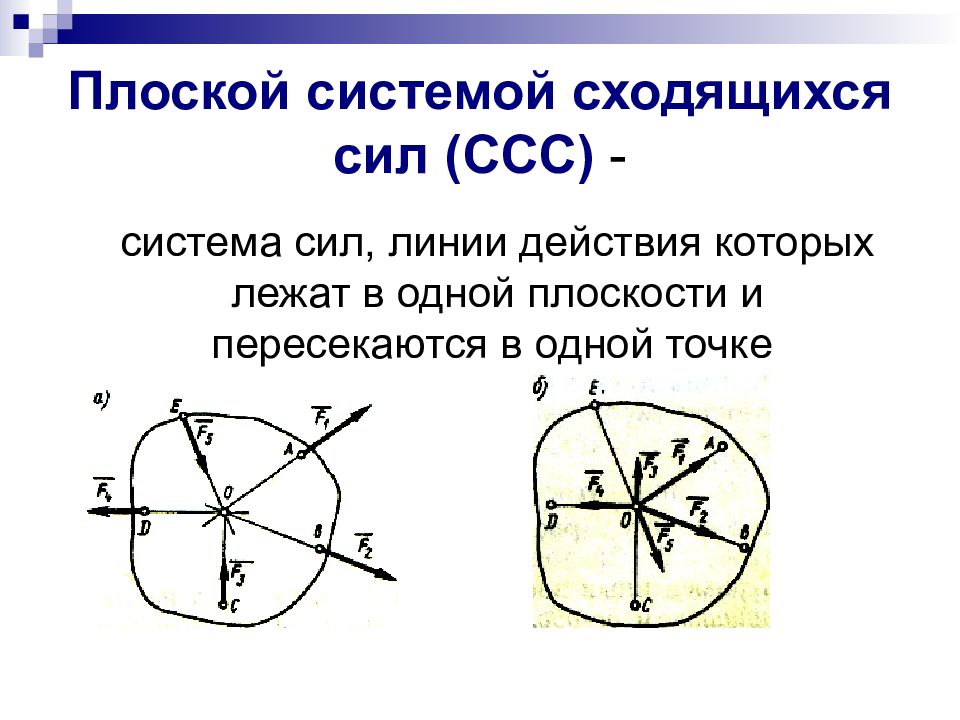
Слайд 2: Плоской системой сходящихся сил (ССС) -
система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке
Слайд 4
Существует три способа определения равнодействующей силы плоской системы сходящихся сил: - графический, - геометрический, - аналитический.
Равнодействующая определяется из чертежа силового многоугольника, выполненного в масштабе
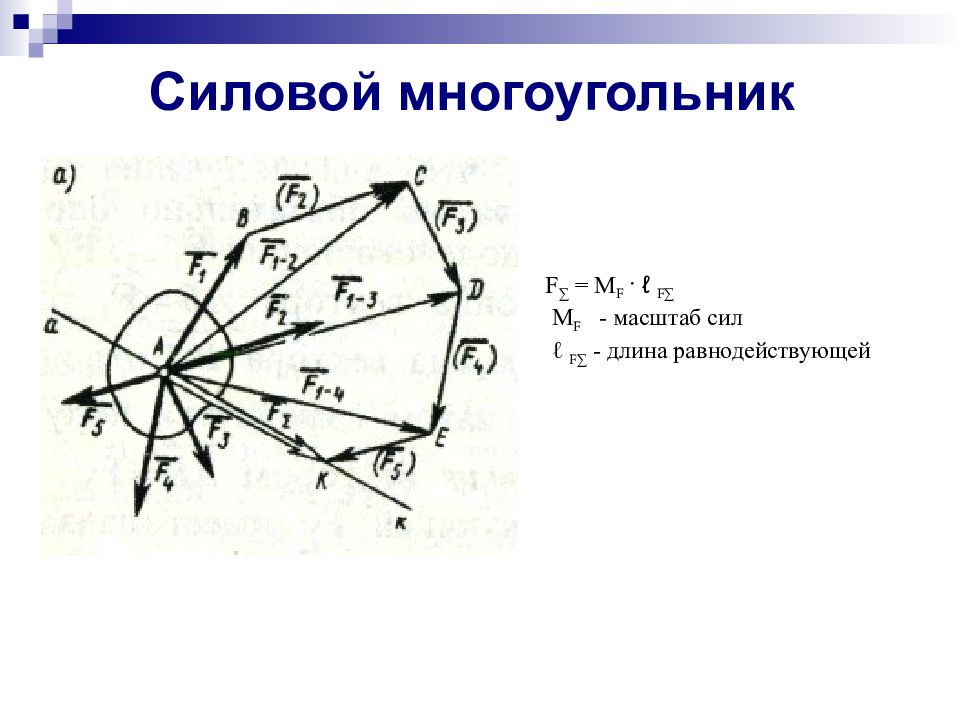
Слайд 6: Силовой многоугольник
F ∑ = M F · ℓ F ∑ M F - масштаб сил ℓ F ∑ - длина равнодействующей
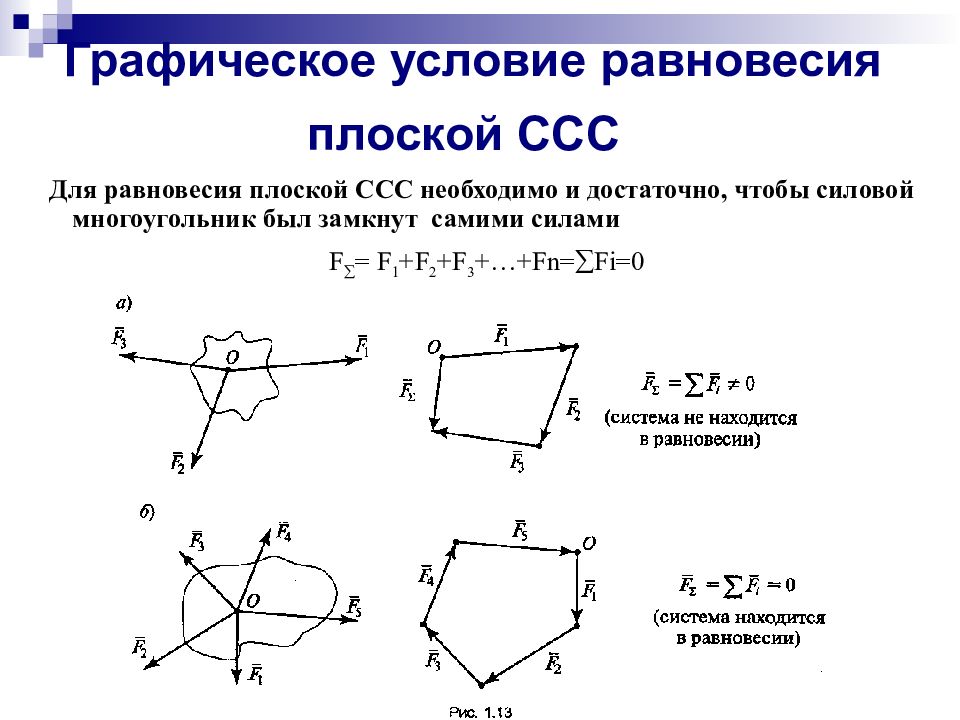
Слайд 7: Графическое условие равновесия плоской ССС
Для равновесия плоской ССС необходимо и достаточно, чтобы силовой многоугольник был замкнут самими силами F = F 1 + F 2 + F 3 +…+ Fn = Fi =0
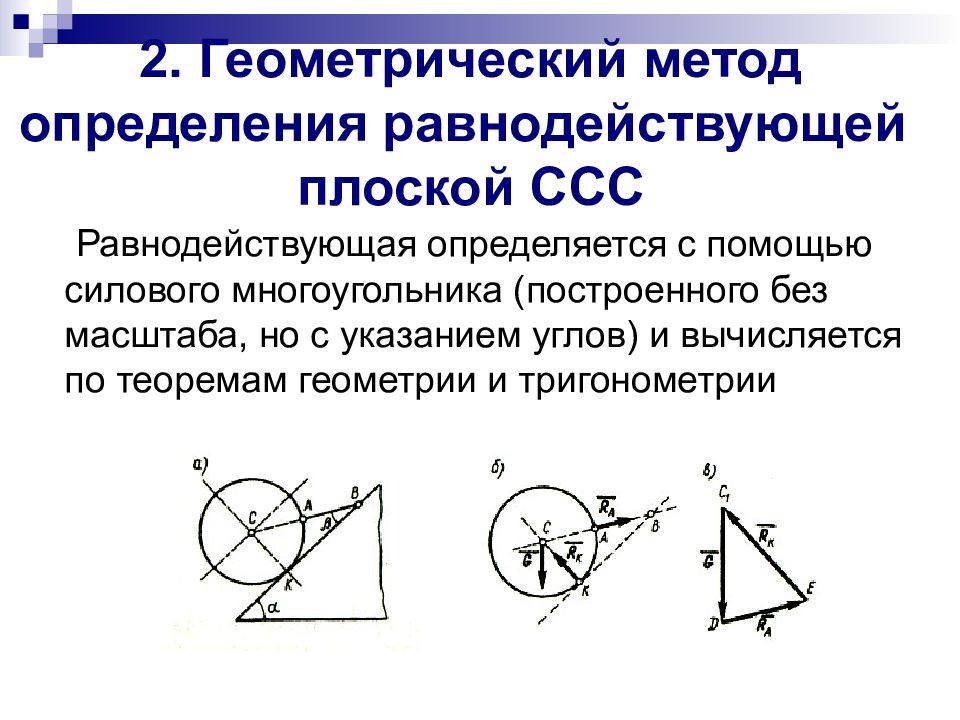
Слайд 8: 2. Геометрический метод определения равнодействующей плоской ССС
Равнодействующая определяется с помощью силового многоугольника (построенного без масштаба, но с указанием углов) и вычисляется по теоремам геометрии и тригонометрии
Слайд 9: 3.Аналитический метод определения равнодействующей плоской ССС (метод проекций)
Все силы проецируются на оси координат х и у, находится алгебраическая сумма проекций всех сил на каждую ось и по теореме Пифагора вычисляется модуль равнодействующей.
Слайд 10: Проекция силы на ось координат-
отрезок оси, отсекаемый перпендикулярами, опущенными из начала и конца вектора
Слайд 11: Правило знаков:
Если направление проекции силы и оси совпадают, то эта проекция считается положительной, а если не совпадают - отрицательной.
Слайд 12: Проекция силы
Если вектор силы параллелен оси, то он проецируется на эту ось в натуральную величину: F оси Х, то Fx = F Если вектор силы перпендикулярен оси, то его проекция на ось равна 0: F оси Х, то Fx =0 = 0
Слайд 13: Проекция силы на любую ось
равна произведению модуля этой силы на косинус угла между направлением силы и ее проекцией ( между ними)
Слайд 14: Модуль и направление равнодействующей силы :
- модуль F Ʃ F Ʃ = F 2 x + F 2 y - направление F Ʃ cos = cos ( F ; X )= F x / F Ʃ tg = F x / Fy
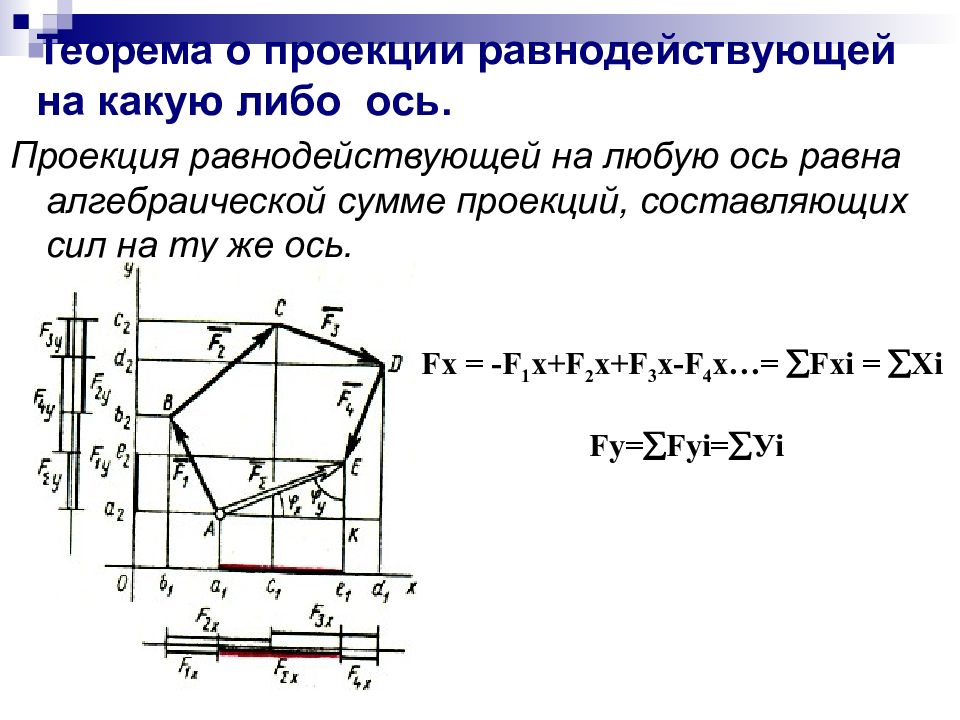
Слайд 15: Теорема о проекции равнодействующей на какую либо ось
Проекция равнодействующей на любую ось равна алгебраической сумме проекций, составляющих сил на ту же ось. Fx = - F 1 x+F 2 x+F 3 x - F 4 x…= F xi = X i Fy= F yi= У i
Последний слайд презентации: Тема 1.2 ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ: Аналитическое условие равновесия плоской ССС
Для равновесия плоской ССС необходимо и достаточно, чтобы равнодействующая системы, а значит и её проекции на оси координат х и у были равны 0. 1) Fix = Х = 0 Если F Ʃ =0, то 2) Fiy = У = 0