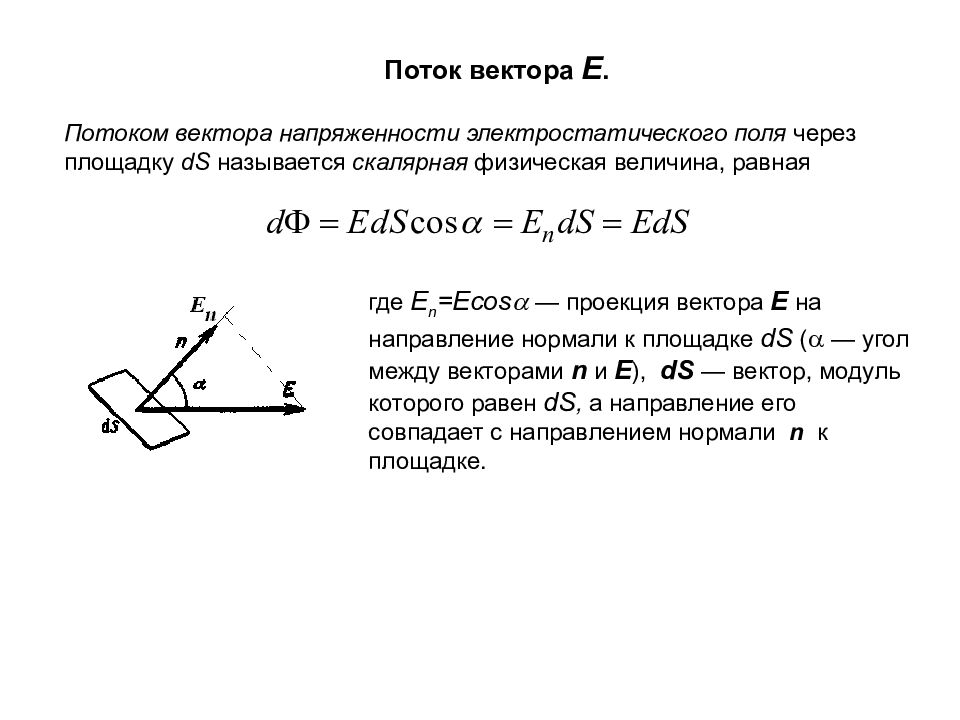
Поток вектора E. Потоком вектора напряженности электростатического поля через площадку dS называется скалярная физическая величина, равная где E n =Ecos — проекция вектора E на направление нормали к площадке dS ( — угол между векторами n и E ), dS — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке.
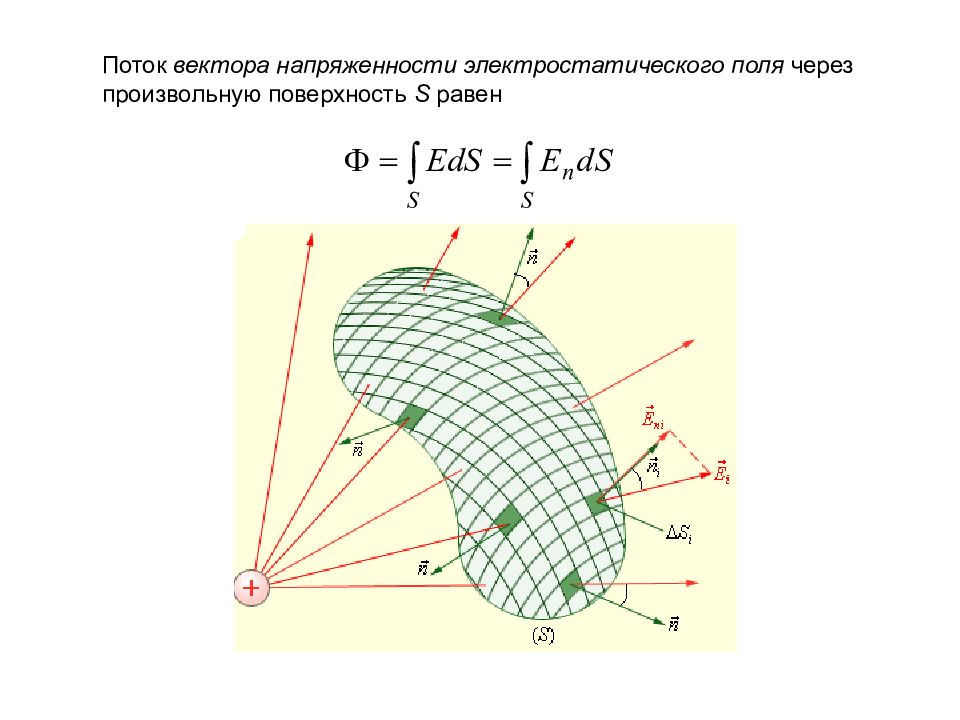
Поток вектора напряженности электростатического поля через произвольную поверхность S равен
Теорема Гаусса ( в интегральной форме): поток вектора E сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на 0. Продемонстрируем это на примере точечного заряда. Окружим его замкнутой сферической поверхностью. Поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд q, находящийся в ее центре, равен
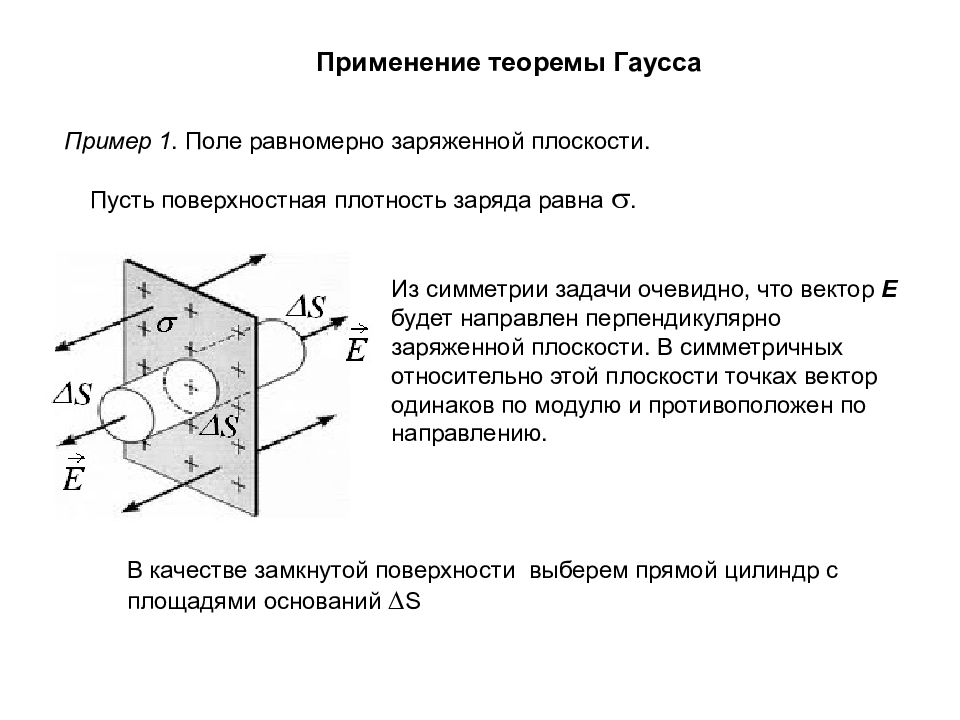
Применение теоремы Гаусса Пример 1. Поле равномерно заряженной плоскости. Пусть поверхностная плотность заряда равна . Из симметрии задачи очевидно, что вектор E будет направлен перпендикулярно заряженной плоскости. В симметричных относительно этой плоскости точках вектор одинаков по модулю и противоположен по направлению. В качестве замкнутой поверхности выберем прямой цилиндр с площадями оснований S
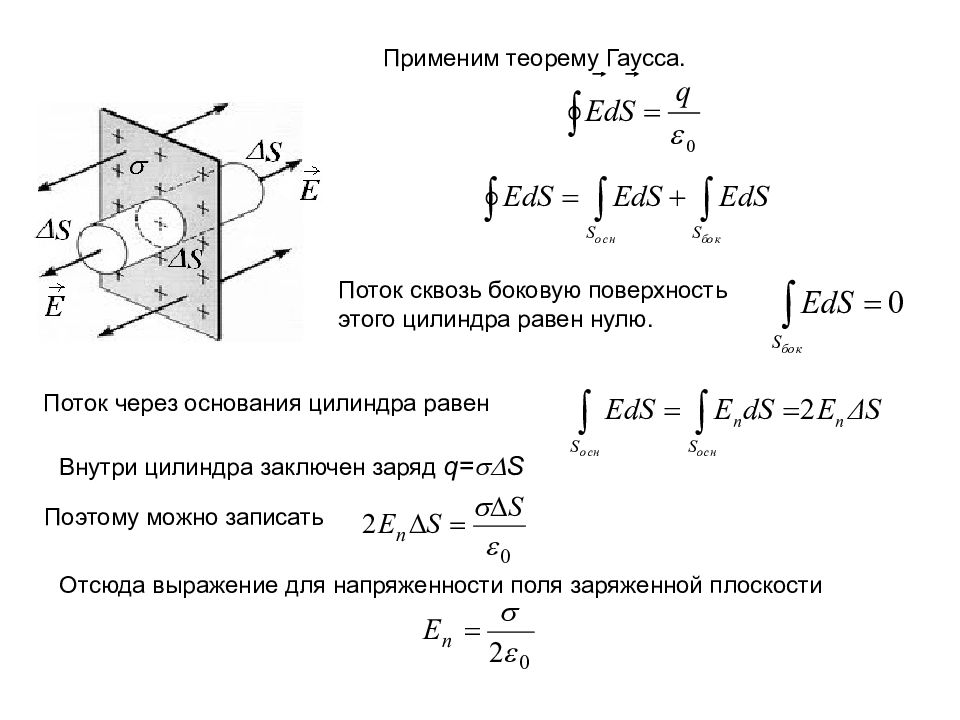
Поток сквозь боковую поверхность этого цилиндра равен нулю. Поток через основания цилиндра равен Применим теорему Гаусса. Внутри цилиндра заключен заряд q= S Поэтому можно записать Отсюда выражение для напряженности поля заряженной плоскости
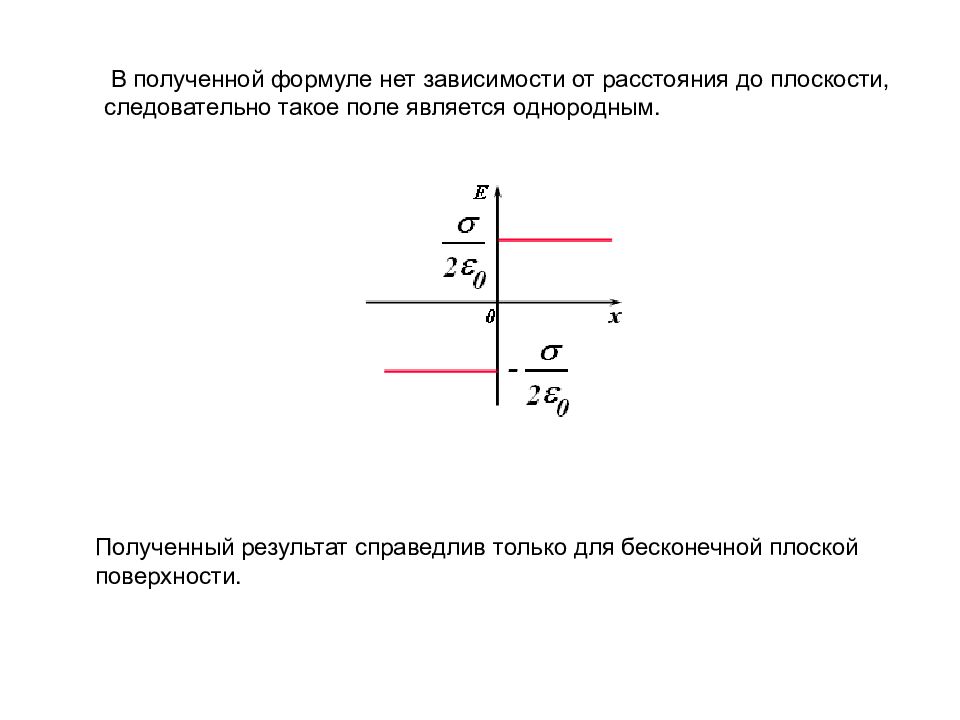
В полученной формуле нет зависимости от расстояния до плоскости, следовательно такое поле является однородным. Полученный результат справедлив только для бесконечной плоской поверхности.
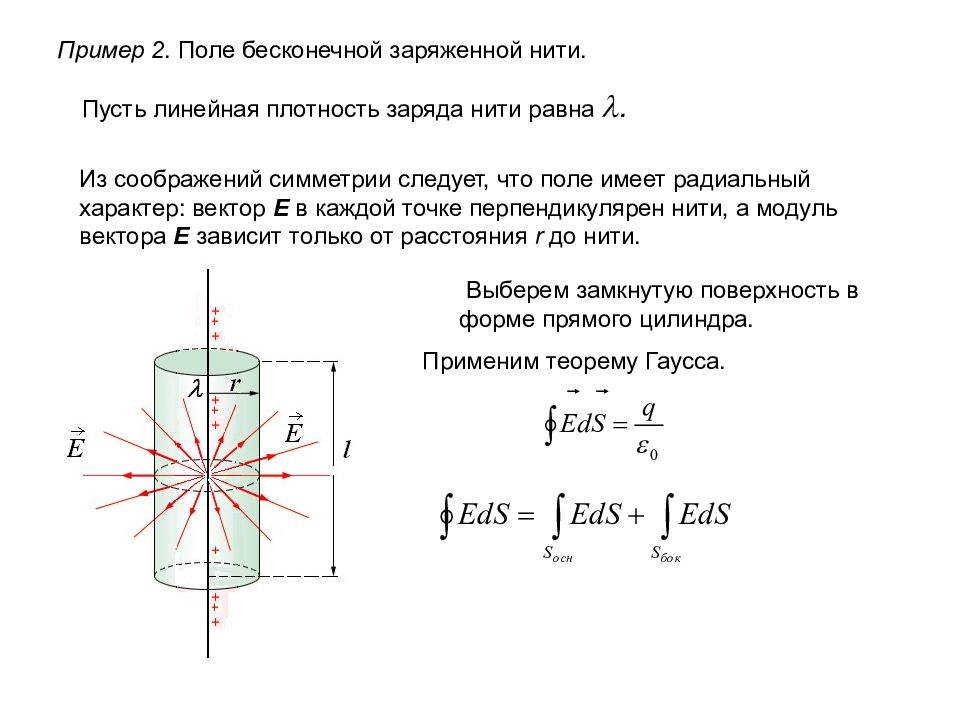
Пример 2. Поле бесконечной заряженной нити. Пусть линейная плотность заряда нити равна . Из соображений симметрии следует, что поле имеет радиальный характер: вектор E в каждой точке перпендикулярен нити, а модуль вектора E зависит только от расстояния r до нити. Выберем замкнутую поверхность в форме прямого цилиндра. Применим теорему Гаусса.
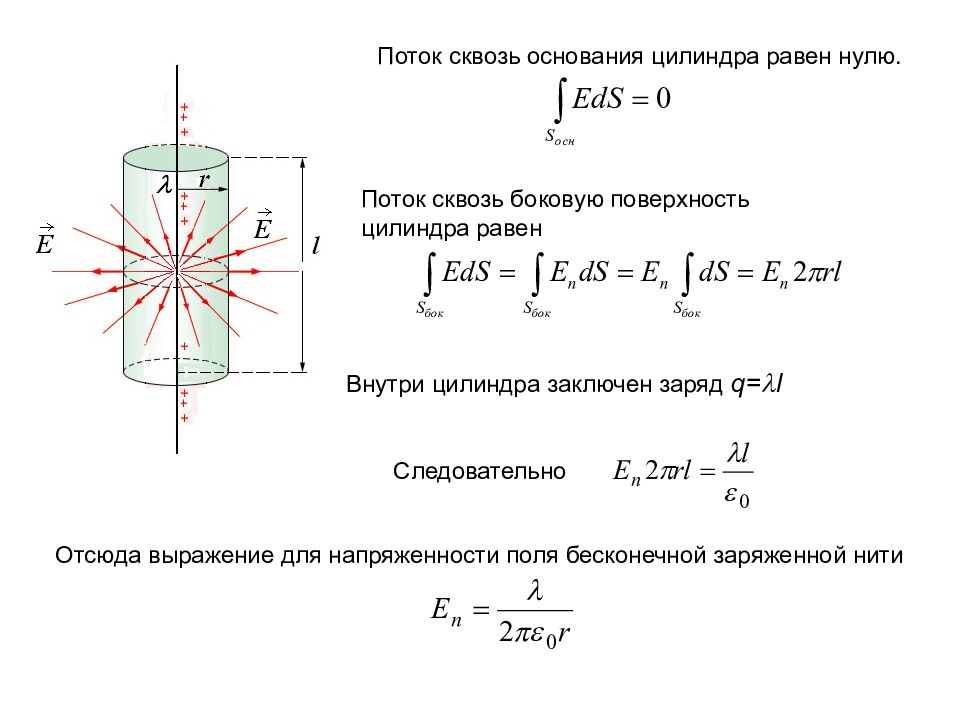
Поток сквозь основания цилиндра равен нулю. Поток сквозь боковую поверхность цилиндра равен Внутри цилиндра заключен заряд q= l Следовательно Отсюда выражение для напряженности поля бесконечной заряженной нити
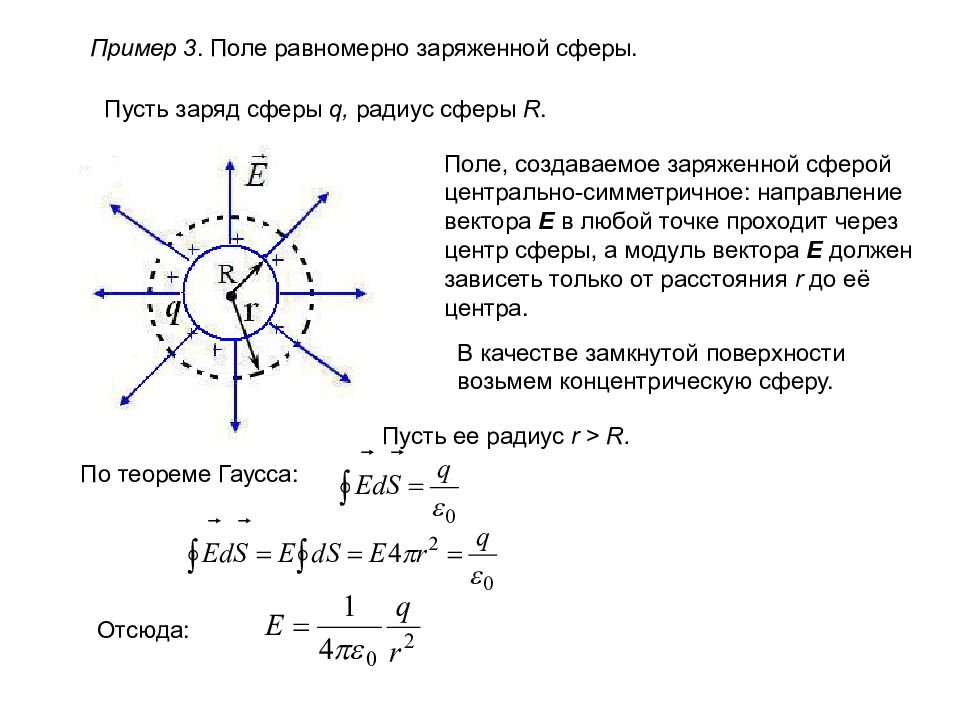
Пример 3. Поле равномерно заряженной сферы. Пусть заряд сферы q, радиус сферы R. Поле, создаваемое заряженной сферой центрально-симметричное: направление вектора E в любой точке проходит через центр сферы, а модуль вектора E должен зависеть только от расстояния r до e ё центра. В качестве замкнутой поверхности возьмем концентрическую сферу. Пусть ее радиус r > R. По теореме Гаусса: Отсюда:
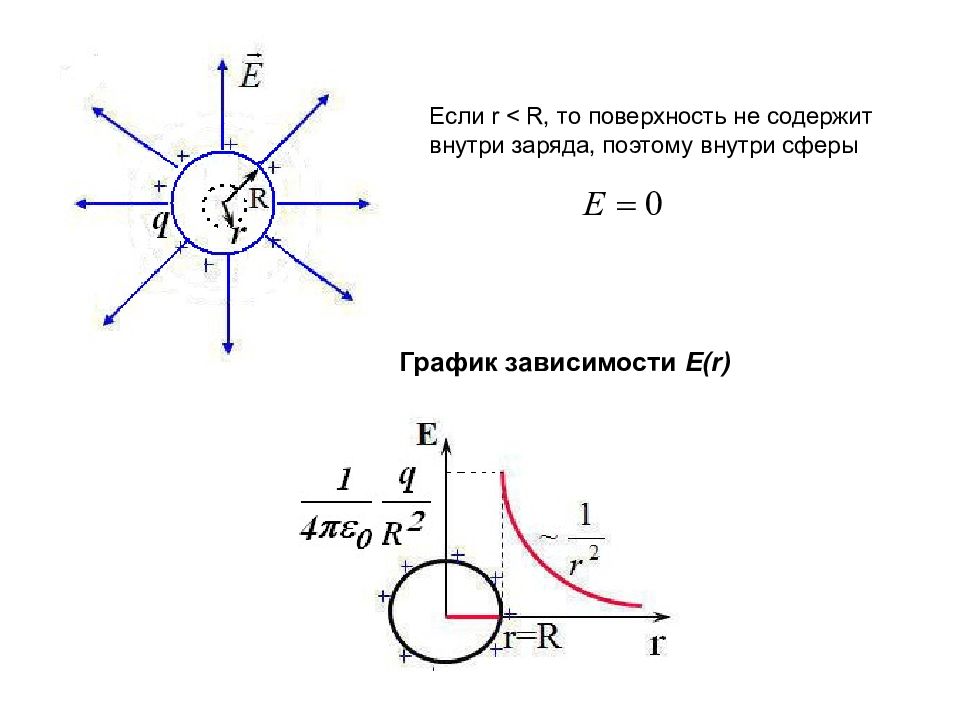
Если r < R, то поверхность не содержит внутри заряда, поэтому внутри сферы График зависимости E(r)
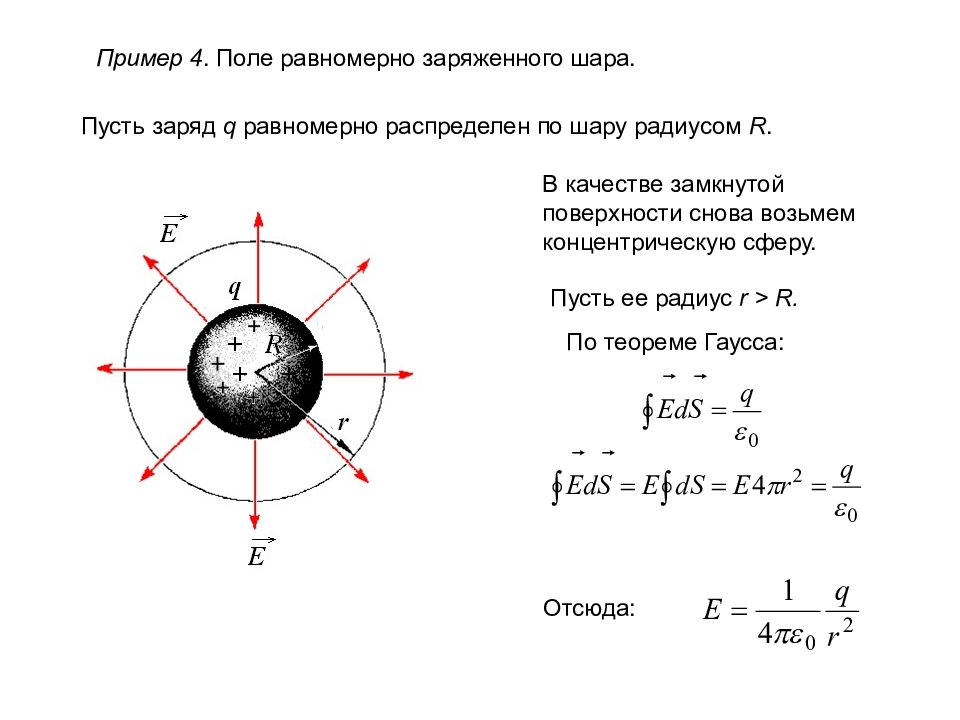
Пример 4. Поле равномерно заряженного шара. Пусть заряд q равномерно распределен по шару радиусом R. В качестве замкнутой поверхности снова возьмем концентрическую сферу. Пусть ее радиус r > R. По теореме Гаусса: Отсюда:
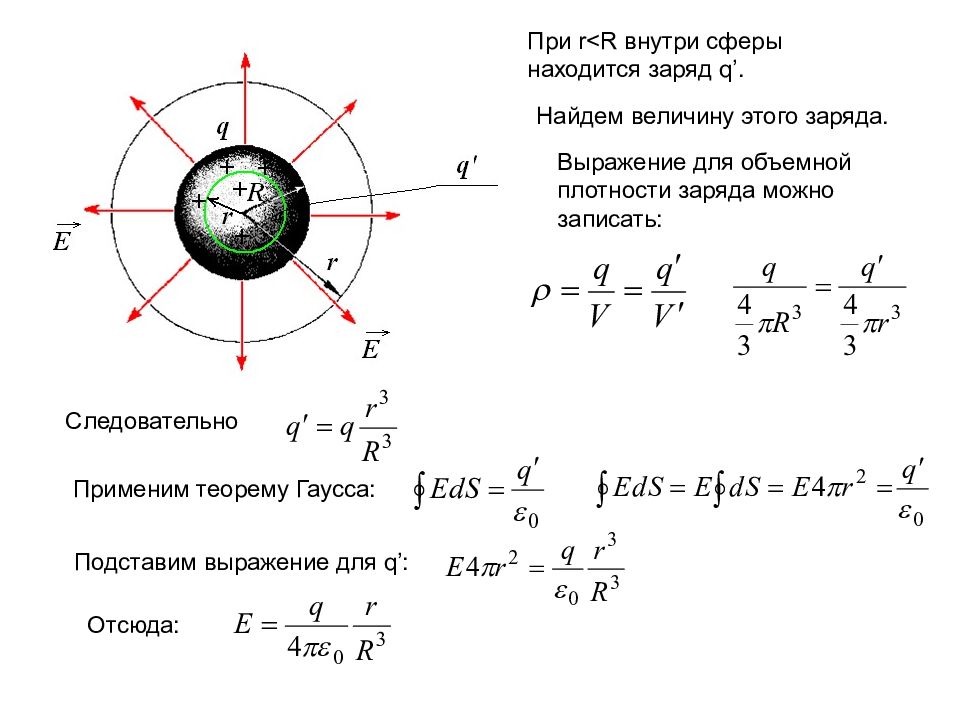
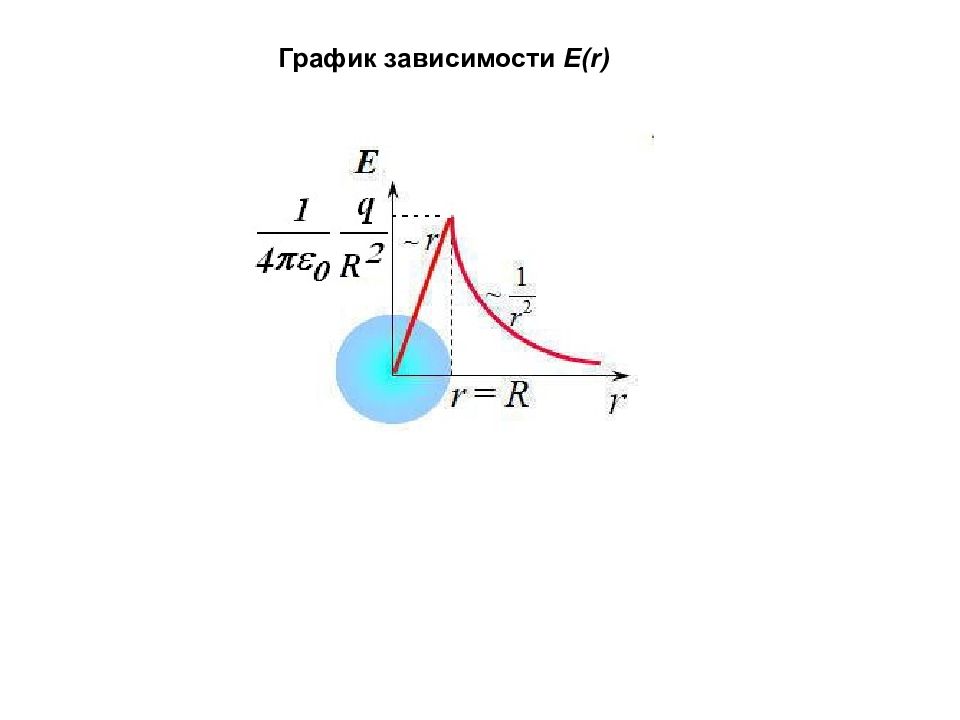
При r<R внутри сферы находится заряд q’. Найдем величину этого заряда. Выражение для объемной плотности заряда можно записать: Следовательно Применим теорему Гаусса: Подставим выражение для q’ : Отсюда:
График зависимости E(r)
Общие выводы. Полученные в этих примерах результаты можно было бы найти с использованием принципа суперпозиции,но использование теоремы Гаусса позволяет решать эти задачи более простым путем. Применение теоремы Гаусса для расчета полей эффективно лишь в тех случаях, где поле обладает специальной симметрией (плоской, цилиндрической или сферической).
Дифференциальная форма теоремы Гаусса. Пусть поверхность S охватывает заряженную область объемом V, с объемной плотностью заряда (x,y,z ). Суммарный заряд области можно представить как - среднее значение объемной плотности заряда. Запишем теорему Гаусса Устремим объем области к нулю V 0, тогда ( x,y,z ). Обозначим предел левой части выражения, как div E – называется дивергенцией вектора E
С учетом этого, получим Эта формула выражает теорему Гаусса в дифференциальной форме.
Дивергенция вектора. Дивергенция представляет собой скалярную функцию координат. Если компоненты вектора E заданы как E x (x,y,z), E у (x,y,z), E z (x,y,z), то дивергенцию можно найти по формуле: Определим векторный дифференциальный оператор набла . В декартовых координатах Тогда
