Первый слайд презентации
Практикум №6 по решению планиметрических задач ( базового уровня)
Слайд 3: Содержание
Задача №1 Задача №2 Задача №3 Задача №4 Задача №5 Задача №6 Задача №7 Задача №8 Задача №9 Задача №10 Задача №11 Задача №12 Задача №13 Задача №14 Задача №15 Задача №16 Задача №17 Задача №18 Задача №19 Задача №20 Задача №21 Задача №22 Задача №23 Задача №24 Задача №25 Задача №26 Задача №27 Задачи для самостоятельного решения
Слайд 4: Задача №1
Найдите площадь прямоугольника, вершины которого имеют координаты (1;1), (10;1), (10;7), (1;7).
Слайд 5: Задача №2
Найдите площадь квадрата, если его диагональ равна 1. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.
Слайд 6: Задача №3
Найдите диагональ квадрата, если его площадь равна 2. Площадь квадрата равна половине произведения его диагоналей. Поэтому произведение диагоналей равно 4, а каждая из них равна 2.
Слайд 7: Задача №4
Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9. Поэтому сторона квадрата, площадь которого равна 36, равна 6.
Слайд 8: Задача №5
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой. Пусть одна из сторон прямоугольника равна a, тогда вторая равна a+3. P = 2 a + 2( a + 3) = 18; 2а+2а +6=18; 4а=12; а=3 S = 3 · 6 = 18.
Слайд 9: Задача №6
Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2 a. Периметр будет соответственно равен P = 2 a + 2; 2 a = 18, тогда одна из сторон равна 3, а другая 6. Поэтому S = 3 · 6 = 18.
Слайд 10: Задача №7
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2 a. Площадь прямоугольника будет равна S = 2 a 2 = 18, тогда одна из сторон равна 3, а другая 6. Поэтому P = 2 · 3 + 2 · 6 = 18.
Слайд 11: Задача №8
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника. Пусть одна из сторон прямоугольника равна a, вторая равна b. Площадь и периметр прямоугольника будут соответственно равны S = a · b = 98, P = 2 · a + 2 · b = 42. Решая систему из этих уравнений, получаем, что a 1 = 7, a 2 = 14, b 1 = 14, b 2 = 7. Значит большая сторона равна 14.
Слайд 12: Задача №9
Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника. Диагональ разбивает прямоугольник на два прямоугольных треугольника, в которых она является гипотенузой. Пусть длина диагонали равна с, тогда по теореме Пифагора
Слайд 13: Задача №10
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника. Пусть одна из сторон прямоугольника равна 4 a, тогда диагональ равна 5 a. Диагональ образует в прямоугольнике два прямоугольных треугольника. По теореме Пифагора 16 a 2 + 36 = 25 a 2, тогда 9 a 2 = 36, откуда a = 2. Значит S = 8 · 6 = 48.
Слайд 14: Задача №11
Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов. Площадь квадрата равна половине квадрата его диагонали. Поэтому площадь первого квадрата равна 50, а площадь второго квадрата равна 18. Разность найденных площадей равна 32, значит, квадрат искомой диагонали равен 64, а сама она равна 8.
Слайд 15: Задача №12
Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность? Пусть радиус окружности равен R. Тогда сторона описанного вокруг нее квадрата равна 2 R, а его площадь, равная квадрату стороны, равна 4 R ². Диагональ вписанного квадрата также равна 2 R, поэтому его площадь, равная половине произведения диагоналей, равна 2 R ². Значит, отношение площади описанного квадрата к площади вписанного равно 2.
Слайд 16: Задача №13
Две стороны прямоугольника АВС D равны 6 и 8. Найдите длину вектора АС. Вектор АС образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора
Слайд 17: Задача № 14
Две стороны прямоугольника АВС D равны 6 и 8. Найдите сумму векторов АВ и А D. Сумма векторов АВ и А D равна вектору АС. Вектор АС образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора
Слайд 18: Задача №15
Две стороны прямоугольника АВС D равны 6 и 8. Найдите разность векторов Разность векторов АВ и А D равна вектору D В. Вектор D В образует в прямоугольнике два прямоугольных треугольника. Поэтому
Слайд 19: Задача №16
Две стороны прямоугольника АВС D равны 6 и 8. Найдите скалярное произведение векторов АВ и А D. Скалярное произведение двух векторов равно произведению их длин на косинус угла между ними. Так как косинус прямого угла равен нулю, то и скалярное произведение тоже равно нулю.
Слайд 20: Задача №17
Две стороны прямоугольника АВС D равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину суммы векторов АО и ВО. Сумма векторов АО и ВО равна вектору А D. Значит его длина равна 6.
Слайд 21: Задача №18
Две стороны прямоугольника АВС D равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО. Разность векторов АО и ВО равна вектору АВ. Значит длина вектора равна 8 .
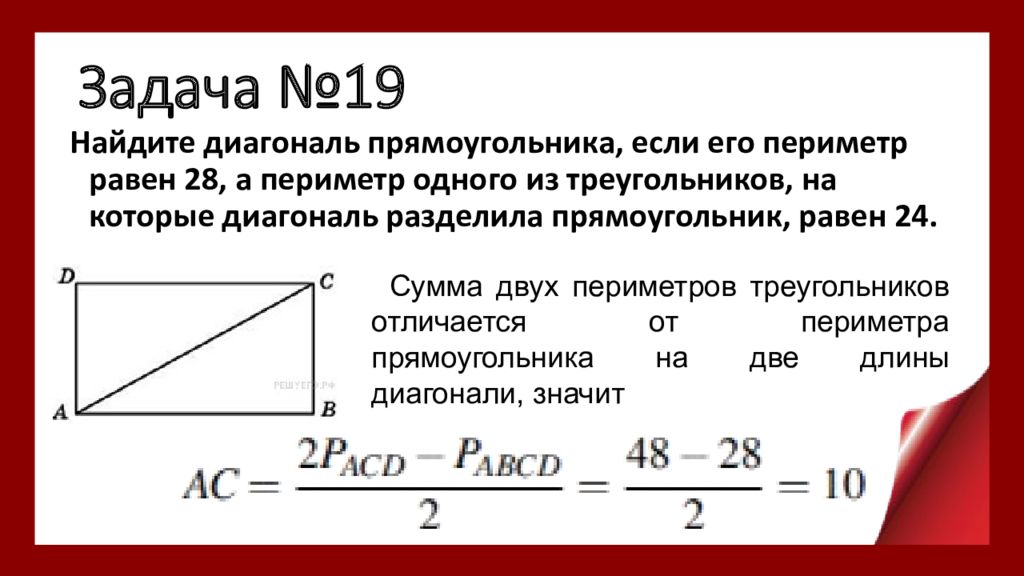
Слайд 22: Задача №19
Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 24. Сумма двух периметров треугольников отличается от периметра прямоугольника на две длины диагонали, значит
Слайд 23: Задача №20
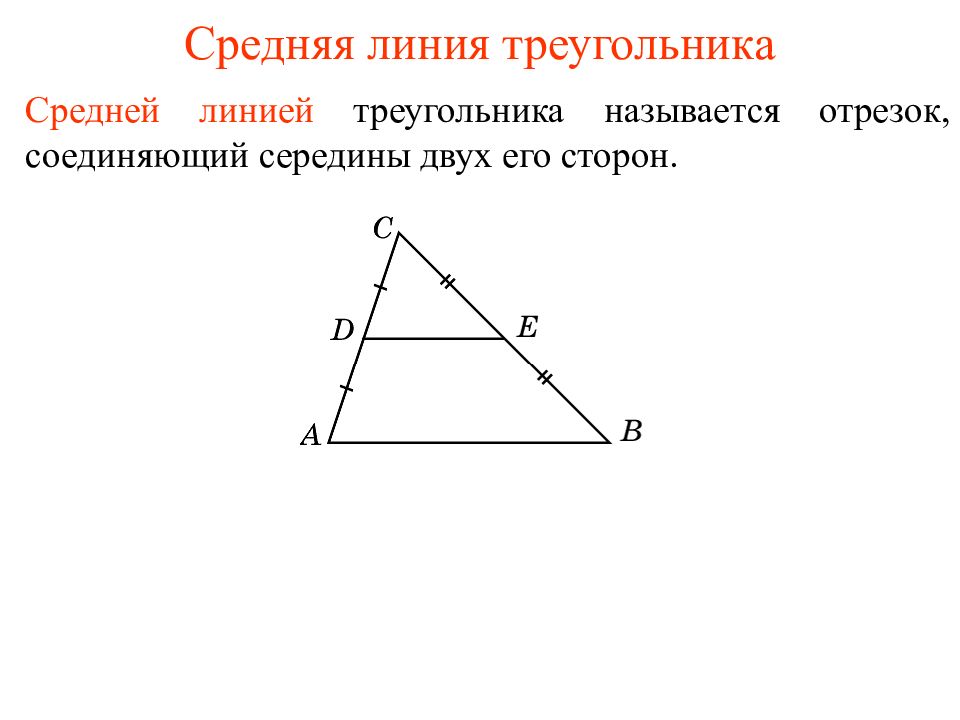
Середины сторон прямоугольника, диагональ которого равна 5, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника. Четырехугольник EHGF ромб, значит, его периметр равен 4 · EF. Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Значит стороны искомого четырехугольника равны половинам диагоналей. Значит, имеем:
Слайд 24: Задача №21
В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника. =>
Слайд 25: Задача №22
Найдите периметр четырехугольника АВС D, если стороны квадратных клеток равны √10. по теореме Пифагора найдем сторону четырехугольника:
Слайд 26: Задача №23
Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом 60 °. Найдите диагонали прямоугольника. значит, треугольник D ОА – равносторонний.
Слайд 27: Задача №24
Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, который образует диагональ со сторонами прямоугольника? Ответ выразите в градусах. Диагональ прямоугольника является гипотенузой прямоугольного треугольника. Так как она вдвое больше одной из сторон прямоугольника, являющейся катетом того же треугольника, то угол, лежащий против этой стороны, равен 30 °. Больший угол будет равен 90 ° - 30 ° = 60 °
Слайд 28: Задача №25
В прямоугольнике диагональ делит угол в отношении 1 : 2, меньшая его сторона равна 6. Найдите диагональ данного прямоугольника. Т.к. диагональ делит угол в отношении 1 : 2, значит, углы равны 30 ° и 60 °. Диагональ тогда равна удвоенной длине катета, лежащего против угла в 30 °, то есть 12.
Слайд 30: Задача №27
В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 7. Найдите периметр этого квадрата. В квадрате расстояние от точки пересечения диагоналей до стороны равно половине стороны. Поэтому сторона квадрата равна 14, а тогда его периметр 56.
Слайд 32: Задача №1 Решите самостоятельно
Найдите площадь прямоугольника, вершины которого имеют координаты (1;2), (10;2), (10;7), (1;7). Ответ: 2) Найдите площадь прямоугольника, вершины которого имеют координаты (2;2), (10;2), (10;9), (2;9). Ответ: 3) Найдите площадь прямоугольника, вершины которого имеют координаты (4;1), (10;1), (10;8), (4;8). Ответ:
Слайд 33: Задача №2 Решите самостоятельно
1) Найдите площадь квадрата, если его диагональ равна 38. Ответ: 722 2) Найдите площадь квадрата, если его диагональ равна 30. Ответ: 3) Найдите площадь квадрата, если его диагональ равна 16. Ответ:
Слайд 34: Задача №5 Решите самостоятельно
Найдите площадь прямоугольника, если его периметр равен 80, и одна сторона на 6 больше другой. Ответ: 2) Найдите площадь прямоугольника, если его периметр равен 12, и одна сторона на 2 больше другой. Ответ: 3) Найдите площадь прямоугольника, если его периметр равен 88, и одна сторона на 6 больше другой. Ответ:
Слайд 35: Задача №6 Решить самостоятельно
Найдите площадь прямоугольника, если его периметр равен 140, а отношение соседних сторон равно 4:31. Ответ:496 2) Найдите площадь прямоугольника, если его периметр равен 126, а отношение соседних сторон равно 2:19. 3) Найдите площадь прямоугольника, если его периметр равен 64, а отношение соседних сторон равно 3:13.
Слайд 36: Задача №7 Решить самостоятельно
Найдите периметр прямоугольника, если его площадь равна 176, а отношение соседних сторон равно 4:11. Ответ:60 2) Найдите периметр прямоугольника, если его площадь равна 272, а отношение соседних сторон равно 4:17. 3) Найдите периметр прямоугольника, если его площадь равна 432, а отношение соседних сторон равно 4:27.
Слайд 37: Задача №8 Решить самостоятельно
Периметр прямоугольника равен 42, а площадь 108. Найдите большую сторону прямоугольника. Ответ: 2) Периметр прямоугольника равен 90, а площадь 234. Найдите большую сторону прямоугольника. Ответ: 3) Периметр прямоугольника равен 30, а площадь 36. Найдите большую сторону прямоугольника. Ответ:
Слайд 38: Задача №10 Решить самостоятельно
Сторона прямоугольника относится к его диагонали, как 12:13, а другая сторона равна 35. Найдите площадь прямоугольника. Ответ: 2) Сторона прямоугольника относится к его диагонали, как 21:29, а другая сторона равна 80. Найдите площадь прямоугольника. Ответ: 3) Сторона прямоугольника относится к его диагонали, как 15:17, а другая сторона равна 48. Найдите площадь прямоугольника. Ответ:
Слайд 39: Задача №11 Решить самостоятельно
1) Даны два квадрата, диагонали которых равны 196 и 261. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов. 2) Даны два квадрата, диагонали которых равны 72 и 75. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов. 3) Даны два квадрата, диагонали которых равны 192 и 200. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
Слайд 40: Задача №19 Решить самостоятельно
1) Найдите диагональ прямоугольника, если его периметр равен 42, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 37. 2) Найдите диагональ прямоугольника, если его периметр равен 100, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 87.
Слайд 41: Задача №20 Решить самостоятельно
Середины сторон прямоугольника, диагональ которого равна 24, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника. Ответ: 48 Середины сторон прямоугольника, диагональ которого равна 46, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Слайд 42: Задача №21 Решить самостоятельно
В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 2 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 52. Найдите меньшую сторону прямоугольника. В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 3 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 124. Найдите меньшую сторону прямоугольника.
Слайд 43: Задача №22 Решить самостоятельно
1) Найдите периметр четырехугольника АВС D, если стороны квадратных клеток равны √5. Ответ: 30.
Слайд 44: Задача №23 Решить самостоятельно
Меньшая сторона прямоугольника равна 59, диагонали пересекаются под углом 60 °. Найдите диагонали прямоугольника. 2) Меньшая сторона прямоугольника равна 1, диагонали пересекаются под углом 60 °. Найдите диагонали прямоугольника. 3) Меньшая сторона прямоугольника равна18, диагонали пересекаются под углом 60 °. Найдите диагонали прямоугольника.
Слайд 45: Задача №25 Решить самостоятельно
1) В прямоугольнике диагональ делит угол в отношении 1 : 2, меньшая его сторона равна 57. Найдите диагональ данного прямоугольника. 2) В прямоугольнике диагональ делит угол в отношении 1 : 2, меньшая его сторона равна 39. Найдите диагональ данного прямоугольника. 3) В прямоугольнике диагональ делит угол в отношении 1 : 2, меньшая его сторона равна 23. Найдите диагональ данного прямоугольника.
Слайд 46: Задача №26 Решите самостоятельно
Найдите сторону квадрата, диагональ которого равна 5 √2. Ответ: 5 Найдите сторону квадрата, диагональ которого равна 14 √2. Найдите сторону квадрата, диагональ которого равна 9 √2.
Последний слайд презентации: Практикум №6 по решению планиметрических задач ( базового уровня): Интернет ресурсы
https://img-fotki.yandex.ru/get/15509/83186431.80f/0_a284a_ce0b20bd_S Шаблон подготовила учитель русского языка и литературы Тихонова Надежда Андреевна http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа: http://mathb.reshuege.ru Автор и источник заимствования неизвестен