Первый слайд презентации: Прямоугольник
Четырехугольник, у которого все углы прямые, называется прямоугольником. Ясно, что прямоугольник является частным случаем параллелограмма, следовательно, он обладает всеми свойствами параллелограмма. В частности, в прямоугольнике противоположные стороны попарно равны и диагонали в точке пересечения делятся пополам.
Слайд 2: Упражнение 1
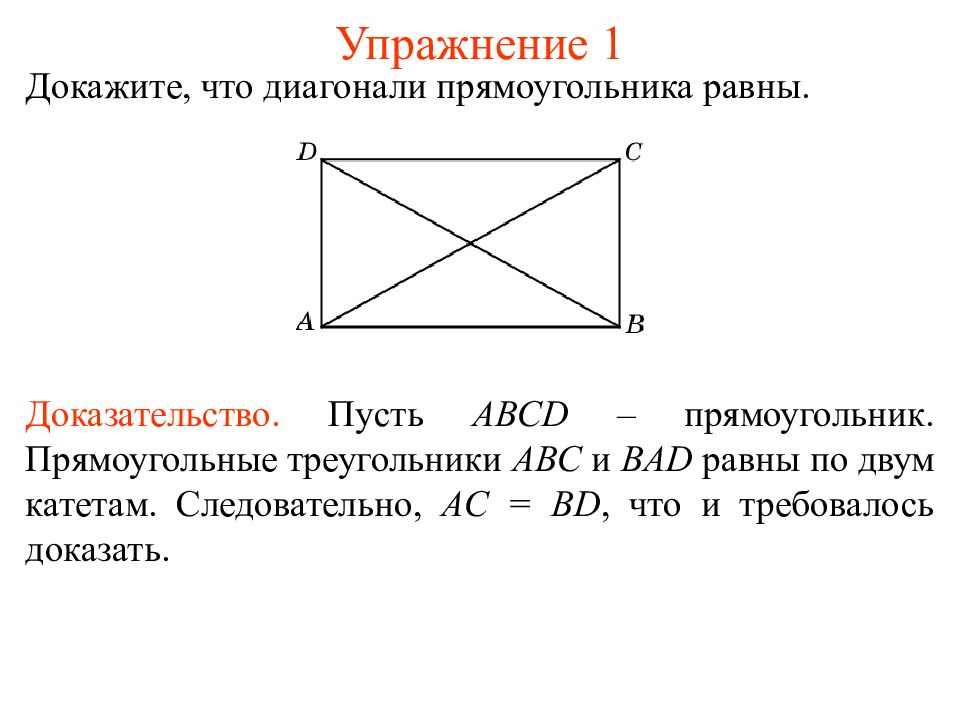
Докажите, что диагонали прямоугольника равны. Доказательство. Пусть ABCD – прямоугольник. Прямоугольные треугольники ABC и BAD равны по двум катетам. Следовательно, AC = BD, что и требовалось доказать.
Слайд 3: Признак прямоугольника
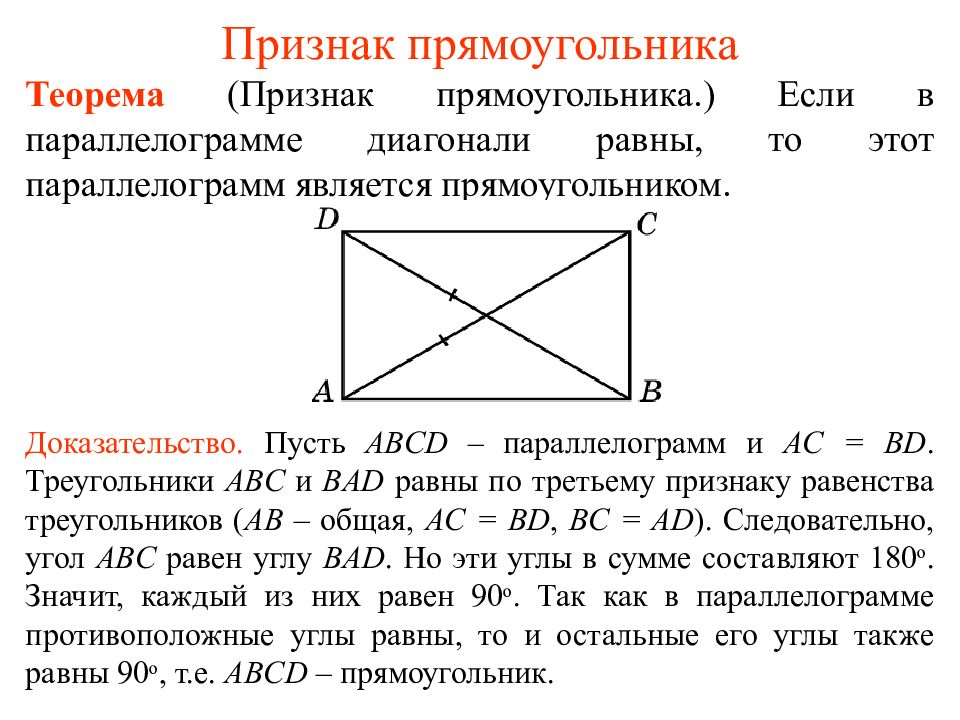
Теорема (Признак прямоугольника.) Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником. Доказательство. Пусть ABCD – параллелограмм и AC = BD. Т реугольники ABC и BAD равны по третьему признаку равенства треугольников ( AB – общая, AC = BD, BC = AD ). Следовательно, угол ABC равен углу BAD. Но эти углы в сумме составляют 180 о. Значит, каждый из них равен 90 о. Так как в параллелограмме противоположные углы равны, то и остальные его углы также равны 90 о, т.е. ABCD – прямоугольник.
Слайд 4: Ромб
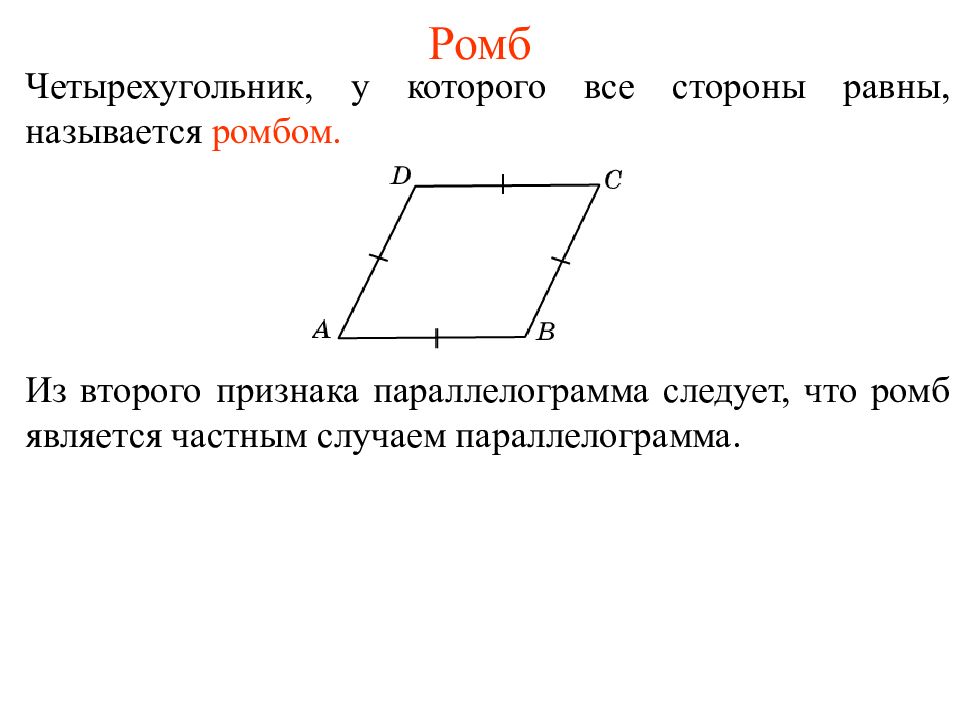
Четырехугольник, у которого все стороны равны, называется ромбом. Из второго признака параллелограмма следует, что ромб является частным случаем параллелограмма.
Слайд 5: Упражнение 2
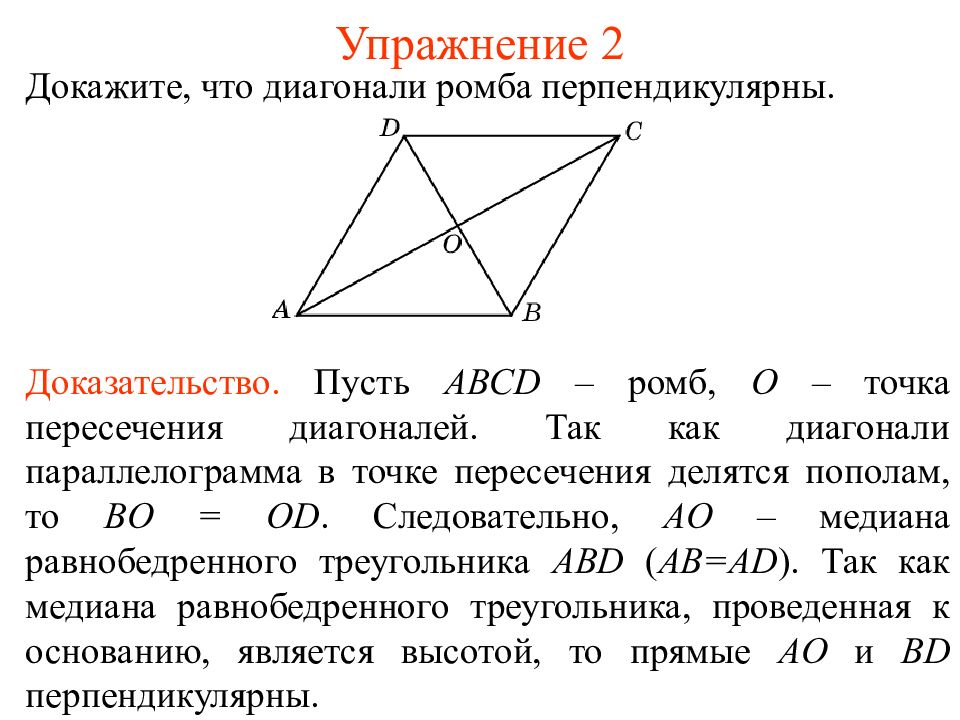
Докажите, что диагонали ромба перпендикулярны. Доказательство. Пусть ABCD – ромб, O – точка пересечения диагоналей. Так как диагонали параллелограмма в точке пересечения делятся пополам, то BO = OD. Следовательно, AO – медиана равнобедренного треугольника ABD ( AB=AD ). Так как медиана равнобедренного треугольника, проведенная к основанию, является высотой, то прямые AO и BD перпендикулярны.
Слайд 6: Признак ромба
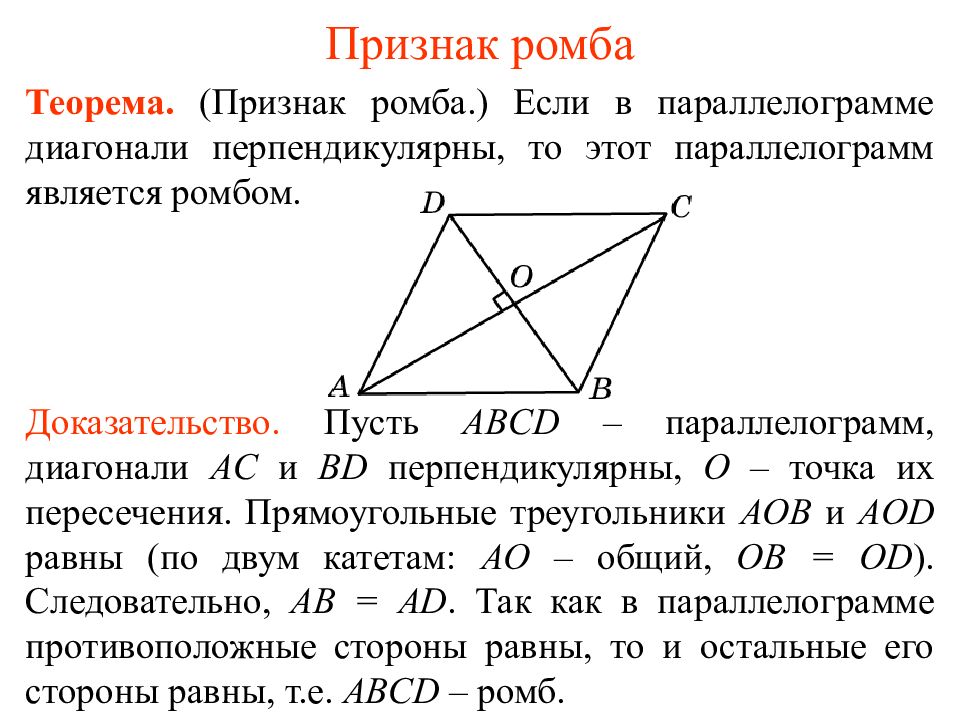
Теорема. (Признак ромба.) Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом. Доказательство. Пусть ABCD – параллелограмм, диагонали AC и BD перпендикулярны, O – точка их пересечения. П рямоугольные треугольники AOB и AOD равны (по двум катетам: AO – общий, OB = OD ). Следовательно, AB = AD. Так как в параллелограмме противоположные стороны равны, то и остальные его стороны равны, т.е. ABCD – ромб.
Слайд 7: Квадрат
Прямоугольник, у которого все стороны равны, называется квадратом. Можно также сказать, что квадратом является ромб, у которого все углы прямые.
Слайд 8: Упражнение 3
Три угла четырехугольника равны 90 о. Является ли этот четырехугольник прямоугольником ? Ответ: Да.
Слайд 9: Упражнение 4
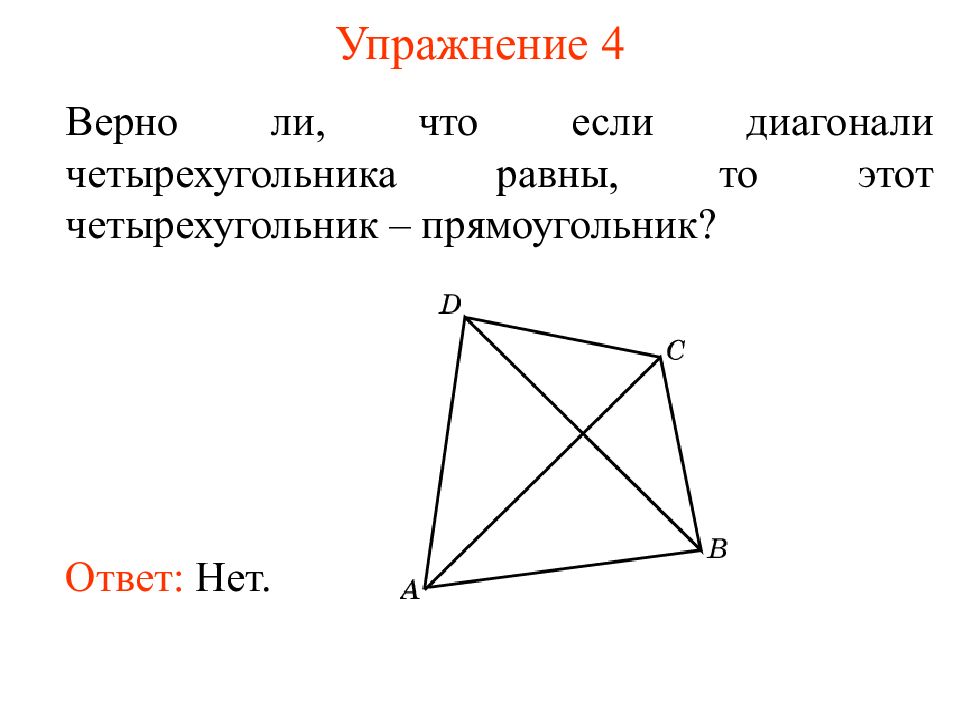
Верно ли, что если диагонали четырехугольник а равны, то этот четырехугольник – прямоугольник ? Ответ: Нет.
Слайд 10: Упражнение 5
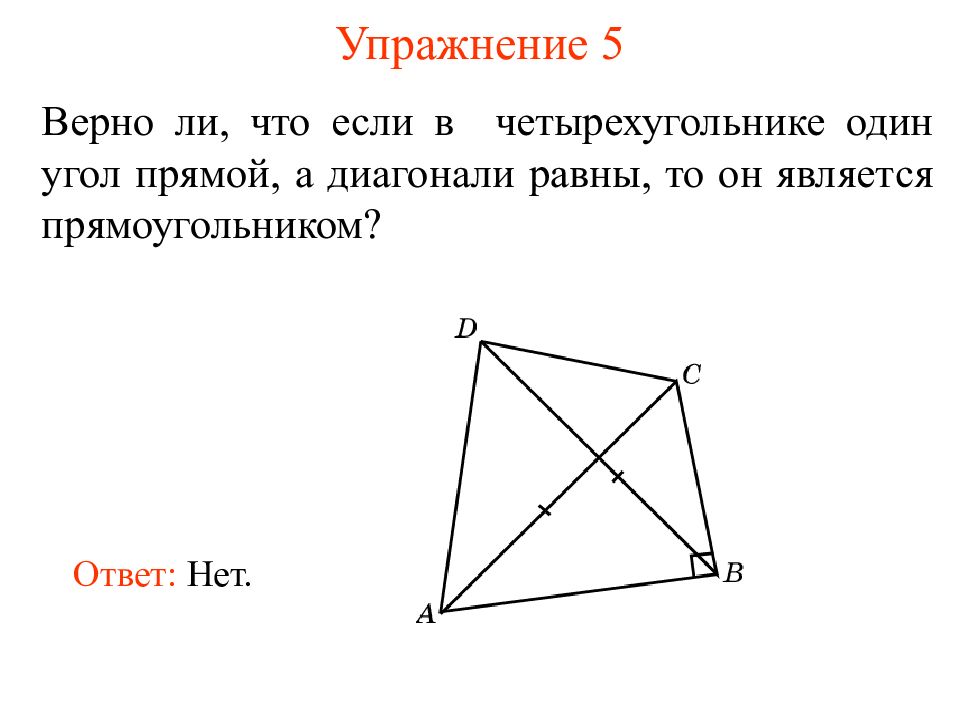
Верно ли, что если в четырехугольнике один угол прямой, а диагонали равны, то он является прямоугольником? Ответ: Нет.
Слайд 11: Упражнение 6
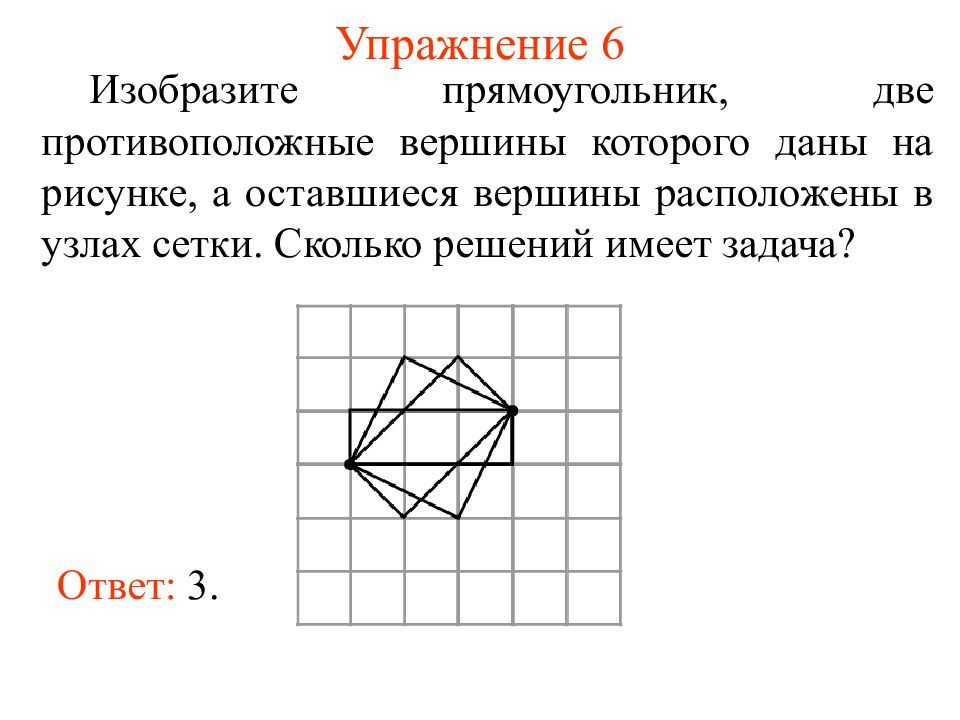
Изобразите прямоугольник, две противоположные вершины которого даны на рисунке, а оставшиеся вершины расположены в узлах сетки. Сколько решений имеет задача? Ответ: 3.
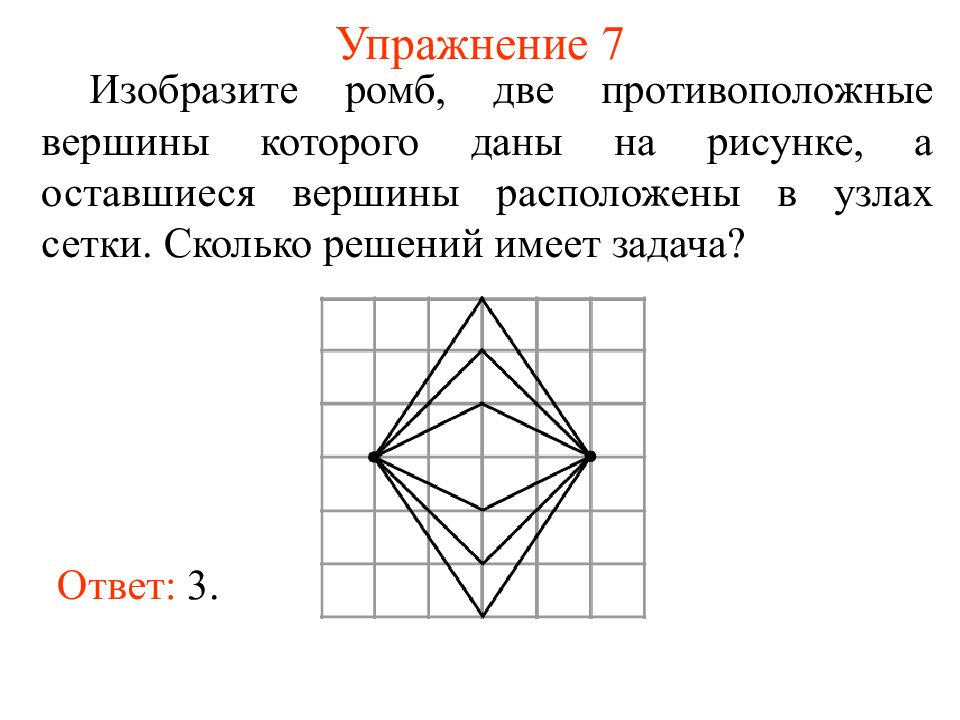
Слайд 12: Упражнение 7
Изобразите ромб, две противоположные вершины которого даны на рисунке, а оставшиеся вершины расположены в узлах сетки. Сколько решений имеет задача? Ответ: 3.
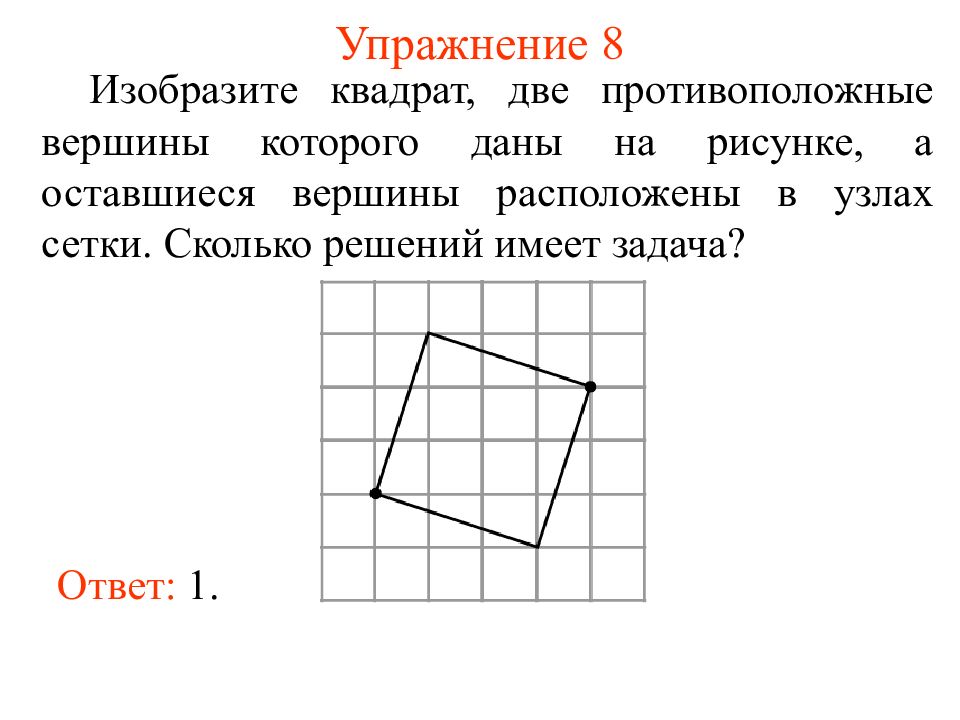
Слайд 13: Упражнение 8
Изобразите квадрат, две противоположные вершины которого даны на рисунке, а оставшиеся вершины расположены в узлах сетки. Сколько решений имеет задача? Ответ: 1.
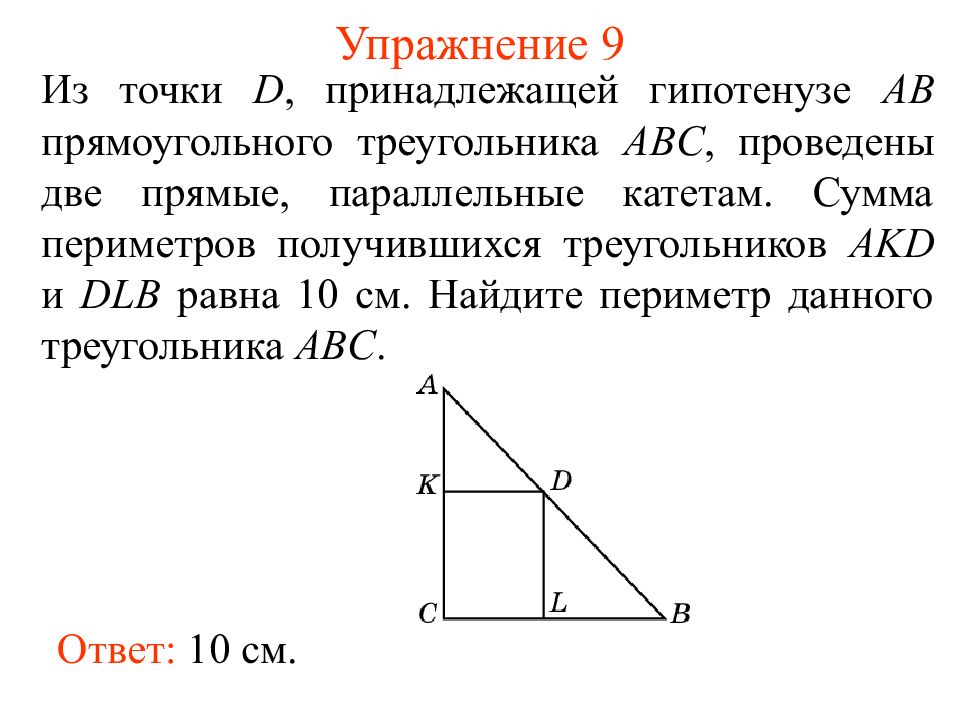
Слайд 14: Упражнение 9
Из точки D, принадлежащей гипотенузе AB прямоугольного треугольника ABC, проведены две прямые, параллельные катетам. Сумма периметров получившихся треугольников AKD и DLB равна 10 см. Найдите периметр данного треугольника ABC. Ответ: 10 см.
Слайд 15: Упражнение 10
Два равных прямоугольных треугольника приложили один к другому таким образом, что их гипотенузы совпали, а неравные острые углы приложились один к другому. Какой при этом получился четырехугольник? Ответ: Прямоугольник.
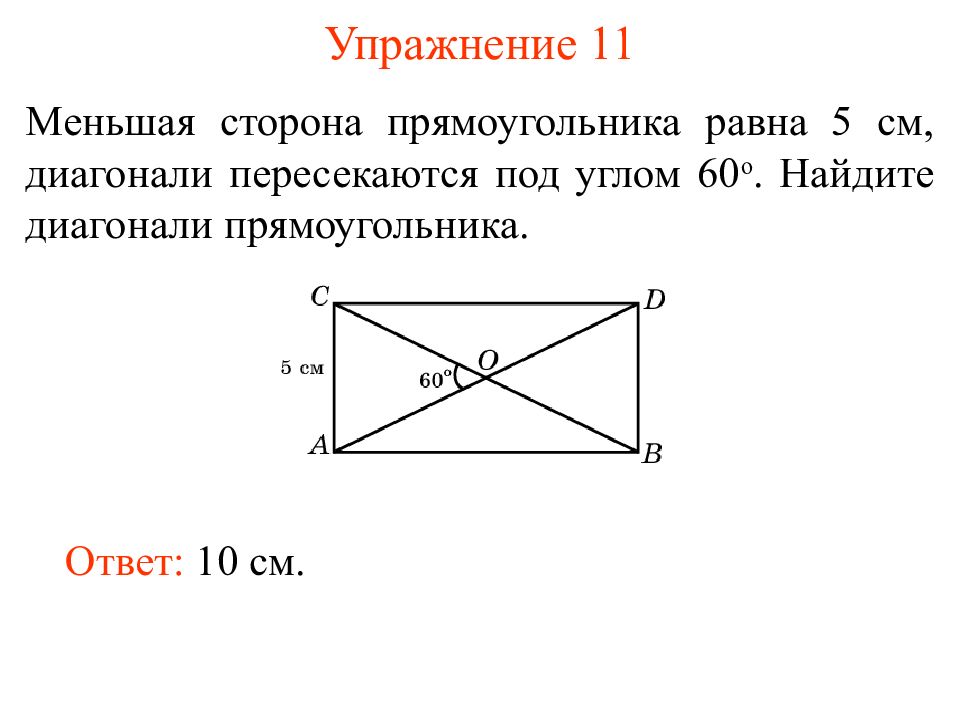
Слайд 16: Упражнение 11
Меньшая сторона прямоугольника равна 5 см, диагонали пересекаются под углом 60 о. Найдите диагонали прямоугольника. Ответ: 10 см.
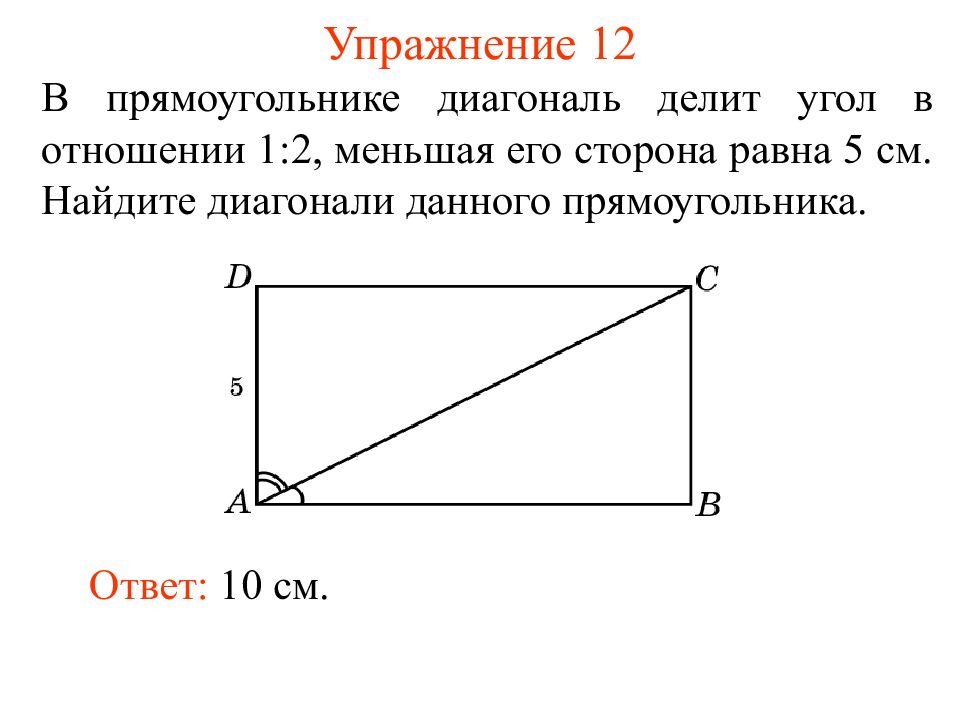
Слайд 17: Упражнение 12
В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 5 см. Найдите диагонали данного прямоугольника. Ответ: 10 см.
Слайд 18: Упражнение 13
Диагональ прямоугольника вдвое больше одной из его сторон. Какие углы образуют диагонали со сторонами прямоугольника? Ответ: 30 о и 60 о.
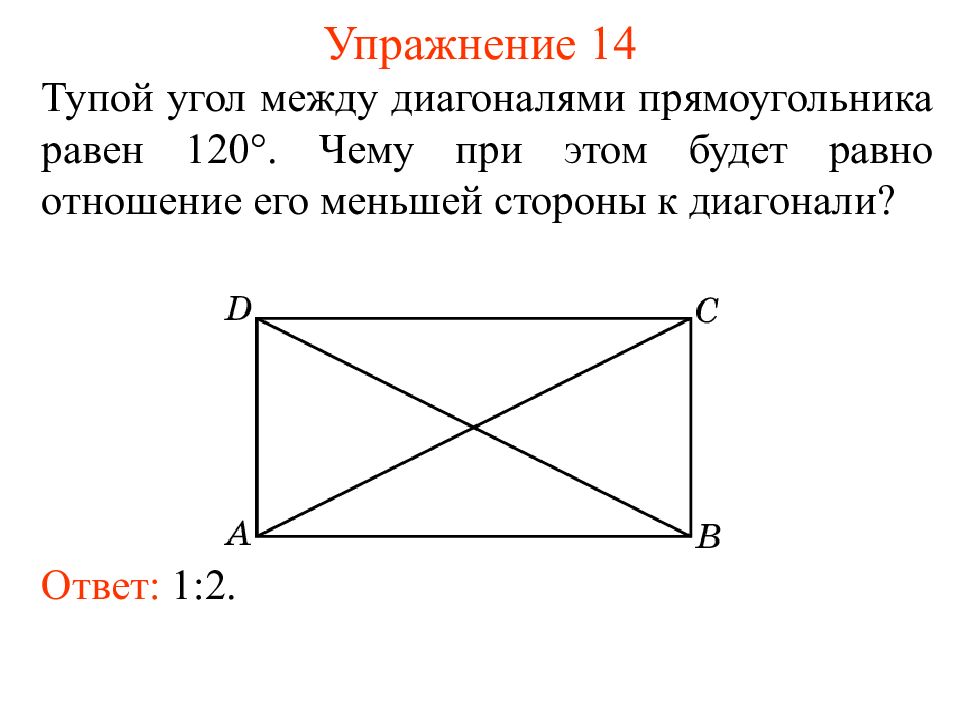
Слайд 19: Упражнение 14
Тупой угол между диагоналями прямоугольника равен 120 . Чему при этом будет равно отношение его меньшей стороны к диагонали? Ответ: 1:2.
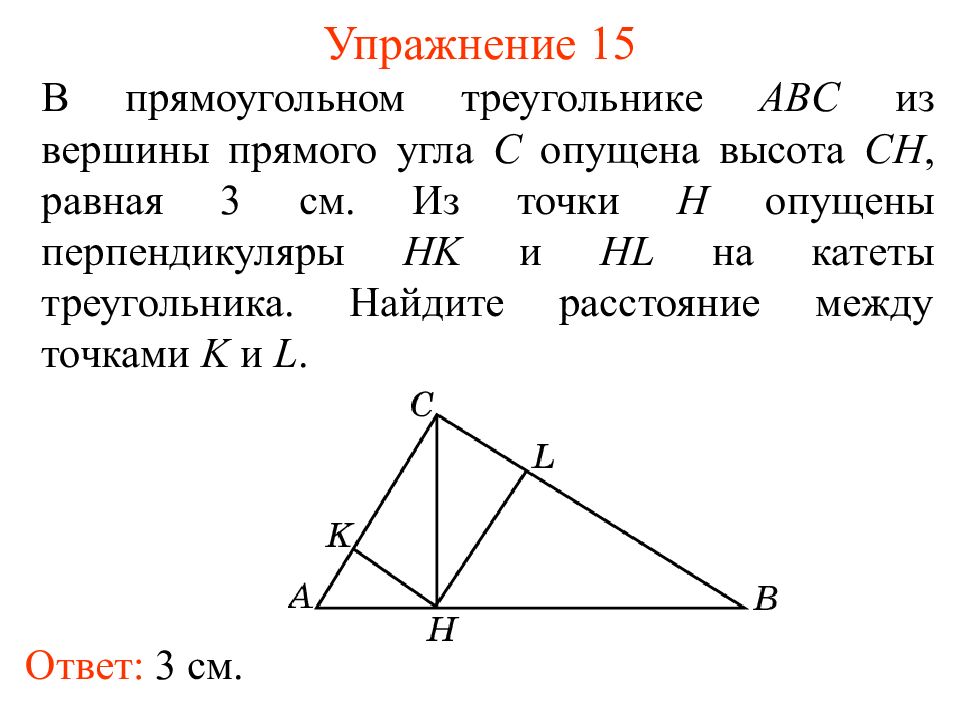
Слайд 20: Упражнение 15
В прямоугольном треугольнике ABC из вершины прямого угла C опущена высота CH, равная 3 см. Из точки H опущены перпендикуляры HK и HL на катеты треугольника. Найдите расстояние между точками K и L. Ответ: 3 см.
Слайд 21: Упражнение 16
Найдите диагонали прямоугольника, если его периметр равен 34 см, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 30 см. Ответ: 13 см.
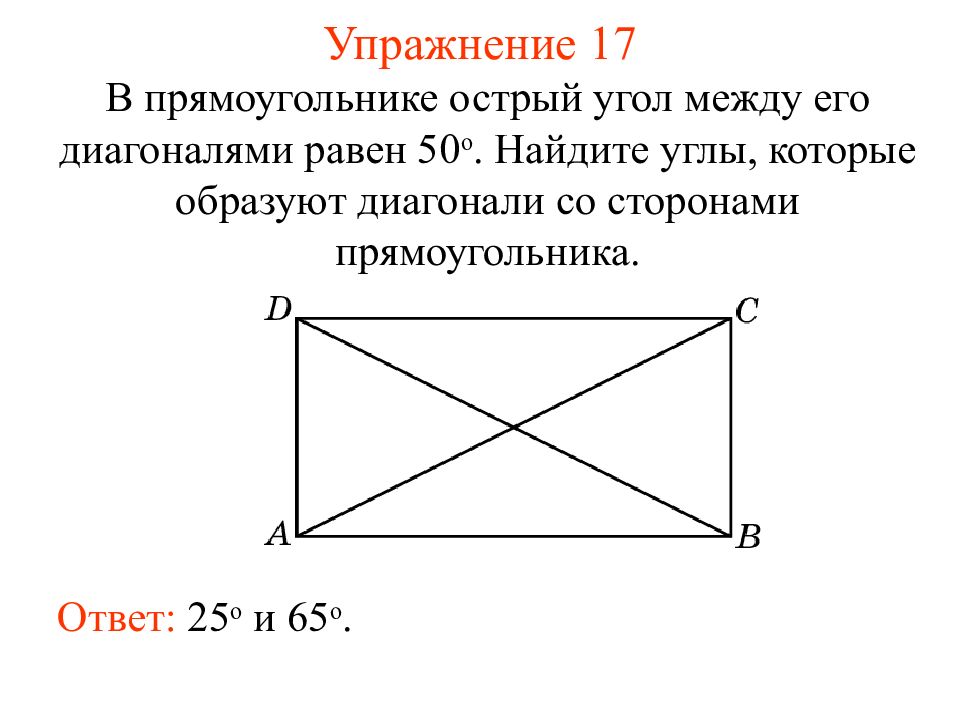
Слайд 22: Упражнение 17
В прямоугольнике острый угол между его диагоналями равен 50 о. Найдите углы, которые образуют диагонали со сторонами прямоугольника. Ответ: 25 о и 65 о.
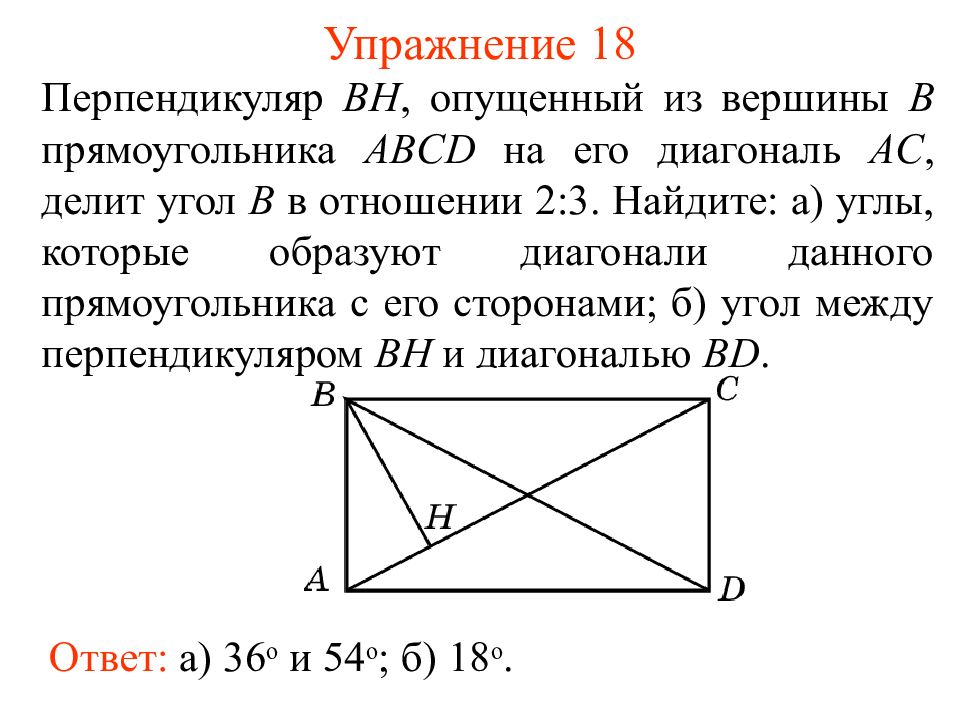
Слайд 23: Упражнение 18
Перпендикуляр BH, опущенный из вершины B прямоугольника ABCD на его диагональ AC, делит угол B в отношении 2:3. Найдите: а) углы, которые образуют диагонали данного прямоугольника с его сторонами; б) угол между перпендикуляром BH и диагональю BD. Ответ: а) 36 о и 54 о ; б) 18 о.
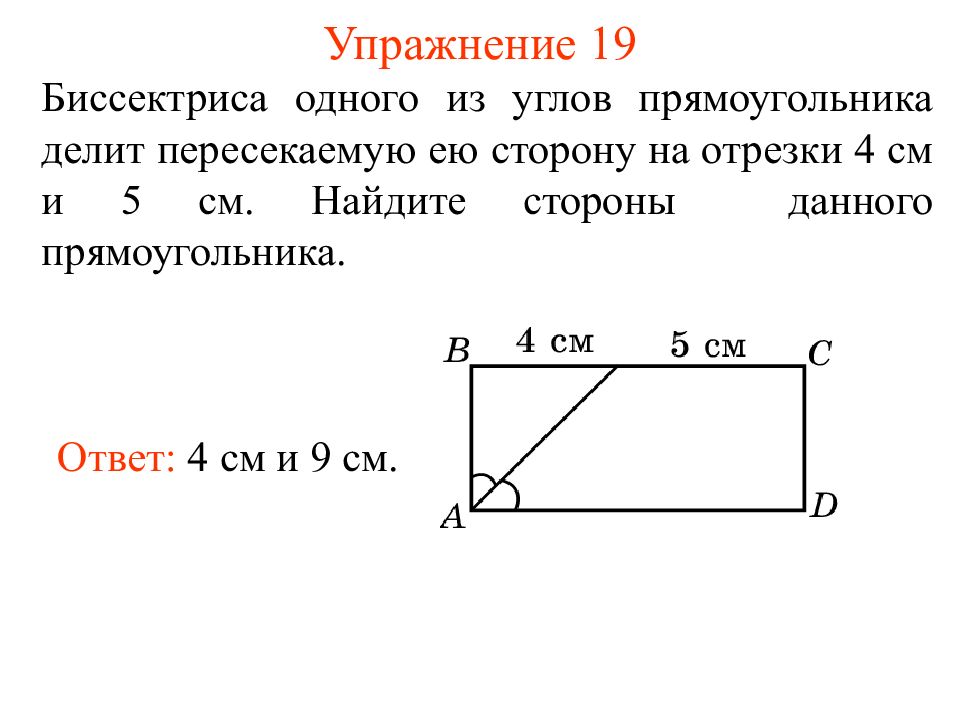
Слайд 24: Упражнение 19
Биссектриса одного из углов прямоугольника делит пересекаемую ею сторону на отрезки 4 см и 5 см. Найдите стороны данного прямоугольника. Ответ: 4 см и 9 см.
Слайд 25: Упражнение 20
Чему равна меньшая диагональ ромба со стороной а и острым углом в 60 о ? Ответ: a.
Слайд 26: Упражнение 21
В ромбе одна из диагоналей равна его стороне. Найдите углы ромба. Ответ: 60 o, 120 o, 60 o, 120 o.
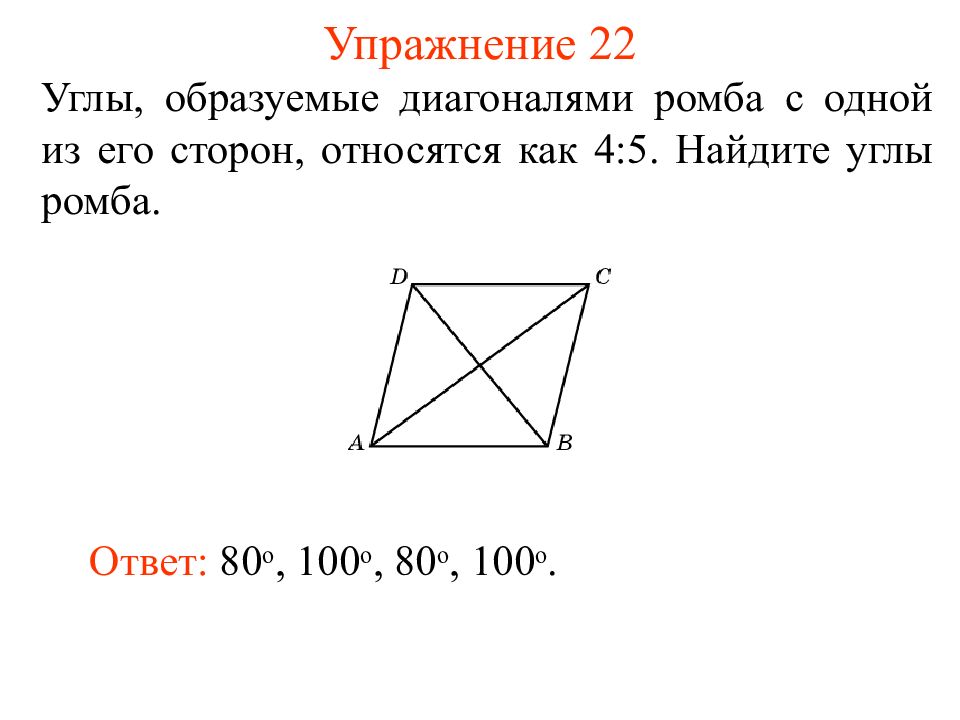
Слайд 27: Упражнение 22
Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 4:5. Найдите углы ромба. Ответ: 8 0 o, 1 0 0 o, 8 0 o, 1 0 0 o.
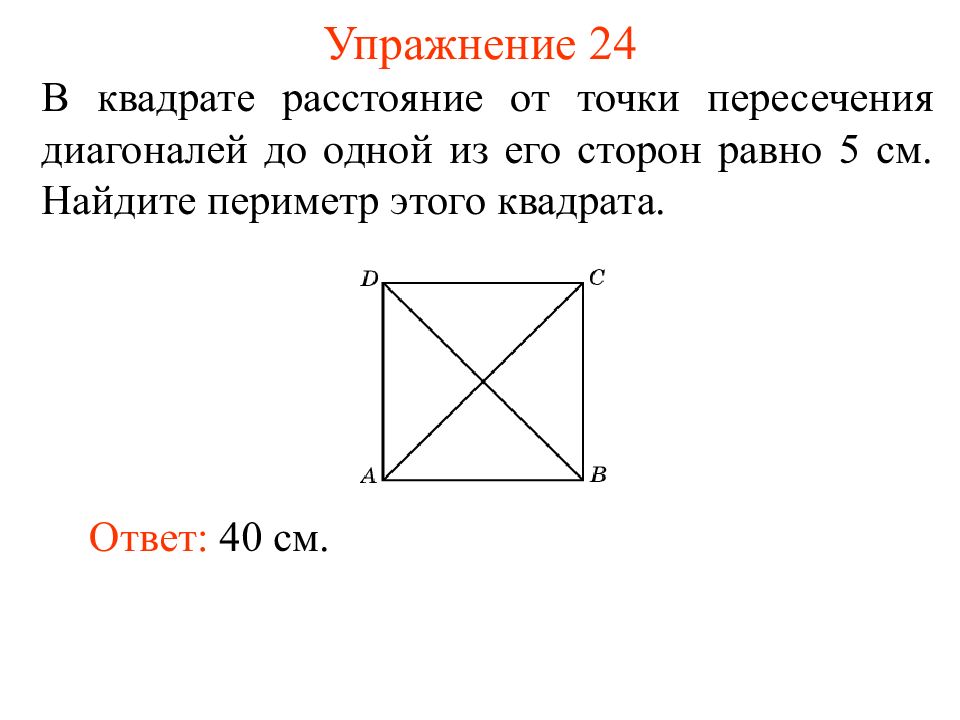
Слайд 28: Упражнение 23
Чему равен угол между: а) диагоналями квадрата: б) диагональю и стороной квадрата? Ответ: а) 9 0 o ; б) 45 o.