Первый слайд презентации: Решение задач с помощью уравнений урок математики в 5 классе
Автор : Овчинникова Наталья Александровна, учитель математики высшей категории МБУ лицея №6 г. Тольятти Урок математики
Урок математики
Слайд 3: Цели урока :
Знать алгоритм решения уравнений. Уметь решать задачи с помощью уравнений, выделяя три этапа математического моделирования. Развивать умение анализировать, логическое мышление, грамотную математическую речь. Формировать у учащихся положительную мотивацию учения, аккуратность математических записей, умение работать в коллективе. Урок математики
Слайд 4
Разминка: а) Ученик решал уравнение 16 : 2х = 4 так: 16: 2х=4 2х = 16: 4 2х = 4 х = 4: 2 х = 2 Найди ошибку в решении. б) Два ученика решали уравнение 2(х+1)=18 так : 2(х+1)=18 2(х+1)=18 2х+1=18 2х+2=18 2х=18-1 2х=18-2 2х=17 2х=16 х=17: 2 х=16: 2 х=8,5 х=8 Найди верное решение. Объясни свой выбор. Сделай проверку. Урок математики
Слайд 5: Этапы математического моделирования
4 Составление математической модели 1 2 3 Решение математической модели Ответ на вопрос задачи Урок математики 1 2 3
Задача №1 Урок математики
Слайд 7: Решение:
Пусть младшему сыну было х лет, тогда среднему сыну – ( х + 9 ) лет, а старшему – ( 2х ) лет, по условию задачи вместе им 85 лет, составим уравнение: 2х + х + 9 + х = 85 4х + 9 = 85 4х = 85 – 9 4х = 76 х = 76 : 4 х = 19 19 лет – младшему сыну 1) 2· 19 = 38 ( лет) – старшему сыну 2) 19 + 9 = 28 ( лет) – среднему сыну Ответ: 38 лет, 28 лет, 19 лет Урок математики Составление математической модели Решение математической модели Ответ на вопрос задачи
Слайд 8
Задача №2 «И пошли братья счастья пытать, стрелы метать». Стрела старшего брата летела на 25 мин дольше, чем стрела среднего, а стрела младшего летела на 15 мин дольше, чем стрела старшего брата. Сколько минут летела каждая стрела, если общее время полета стрел 125 мин? Урок математики
Слайд 9: Решение:
Пусть стрела среднего сына летела х мин, тогда стрела старшего летела ( х + 25 ) мин, а стрела младшего - (х + 25 + 15) мин, по условию задачи общее время - 125 мин, составим уравнение: х + 25 + х + х + 25 + 15 = 125 3х + 65 = 125 3х = 125 – 65 3х = 60 х = 60 : 3 х = 20 20 мин – летела стрела среднего 1) 20 + 25 = 45 (мин) – летела стрела старшего 2) 45 + 15 = 60 (мин) – летела стрела младшего Ответ: 45 мин, 20 мин, 60 мин. Урок математики
Слайд 10
Задача №3 Три снохи царя соткали ковры общей площадью 63 м 2. Купеческая дочь соткала ковер в 2 раза больше, чем боярская, а Василиса Премудрая в 2 раза больше купеческой. Сколько квадратных метров ковров соткала каждая девушка? Урок математики
Слайд 11: Решение:
Пусть боярыня соткала ковер площадью х м², Тогда ковер купчихи имел площадь (2 х) м², а ковер Василисы был ( 2· 2х ) м², по условию задачи общая площадь ковров - 63 м², составим уравнение: х + 2х + 4х = 63 7х = 63 х = 63 : 7 х = 9 9 м² – площадь ковра боярыни 1) 9 · 2 = 18 (м² ) – площадь ковра купчихи 2) 4 · 9 = 36 (м² ) – площадь ковра Василисы Ответ: 9 м², 18 м², 36 м². Урок математики
Слайд 12: На пиру было выпито 88 л напитков. Трехлитровых чарок медовухи выпито столько же, сколько пятилитровых ковшей кваса. Сколько чарок медовухи было выпито?
Задача №4 Урок математики
Слайд 13: Решение:
Пусть чарок и ковшей было по х штук, составим уравнение: 3 х + 5х = 88 8х = 88 х = 88 : 8 х = 11 11 штук – чарок или ковшей Ответ : 11 чарок Количество ёмкостей (штук) Объём одной ёмкости (л) Общий объём (л) Чарки х 3 (3х) Ковши х 5 (5х) 88 л Урок математики
Слайд 14: Чтобы испечь хлеб для царя Василиса Премудрая взяла 10 частей воды, 5 частей муки и 2 части масла (по массе). Сколько граммов каждого вещества надо взять, чтобы приготовить каравай хлеба весом 3 кг 400г?
Задача №5 Урок математики
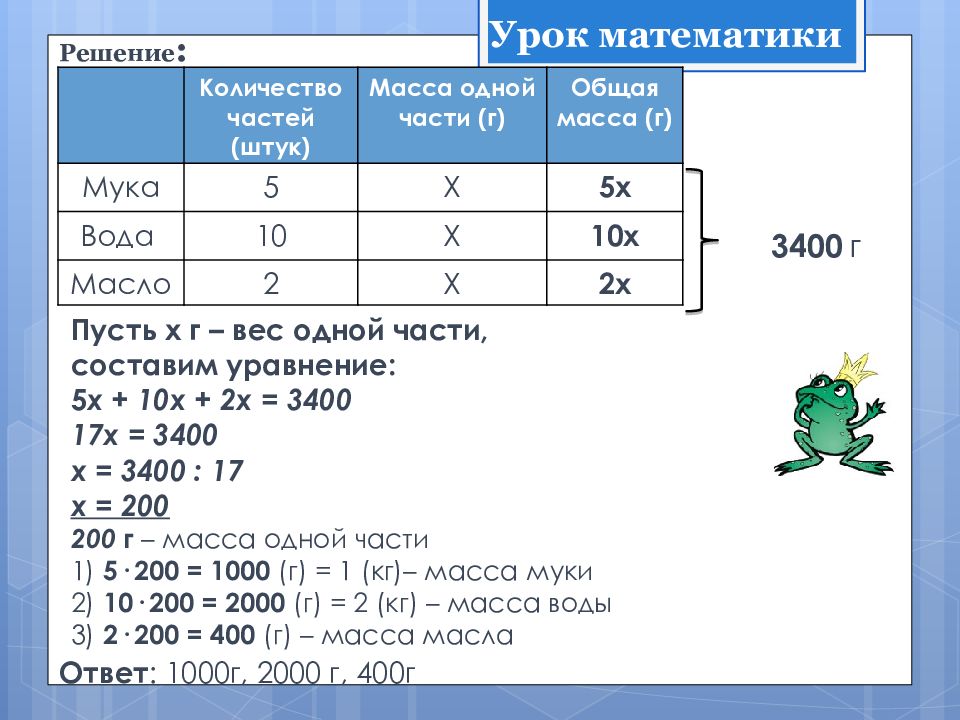
Слайд 15: Решение :
Пусть х г – вес одной части, составим уравнение: 5 х + 10х + 2х = 3400 17х = 3400 х = 3400 : 17 х = 200 200 г – масса одной части 1) 5· 200 = 1000 (г) = 1 (кг)– масса муки 2) 10· 200 = 2000 (г) = 2 (кг) – масса воды 3) 2· 200 = 400 (г) – масса масла Ответ : 1000г, 2000 г, 400г Количество частей (штук) Масса одной части (г) Общая масса (г) Мука 5 Х 5х Вода 10 Х 10х Масло 2 Х 2х 3400 г Урок математики
Слайд 16
Задача №6 Кощей старше царя на 1037 лет, а царь моложе Кощея в 18 раз. Сколько лет царю и сколько лет Кощею? Урок математики
Слайд 17: Решение:
Пусть Царю было х лет, тогда Кощею было (18 х) лет, разница в возрасте составляет (18х – х ) лет, по условию задачи – это 1037 лет, составим уравнение: 18х – х = 1037 17х = 1037 х = 1037 : 17 х = 61 61 год – возраст Царя 1) 1037 – 61 = 976 (лет ) – возраст Кощея Ответ: 61 год, 976 лет. Урок математики
Слайд 18: Итоги урока
Что узнали нового? Чему научились? Что еще хотели бы узнать? Спасибо за урок! Урок математики
Последний слайд презентации: Решение задач с помощью уравнений урок математики в 5 классе: Список используемых источников
Дорофеев Г. В., Петерсон Л. Г. Математика. 5 класс. – М.: Издательство «Ювента», 2011. Картинки из сказки «Царевна - лягушка» https://www.google.ru/search?q= картинки+из+сказки+царевна+лягушка& newwindow=1&espv=2&biw=1366&bih=635&site=webhp&tbm=isch&tbo=u&source=univ&sa=X&ved=0CBsQsARqFQo Урок математики