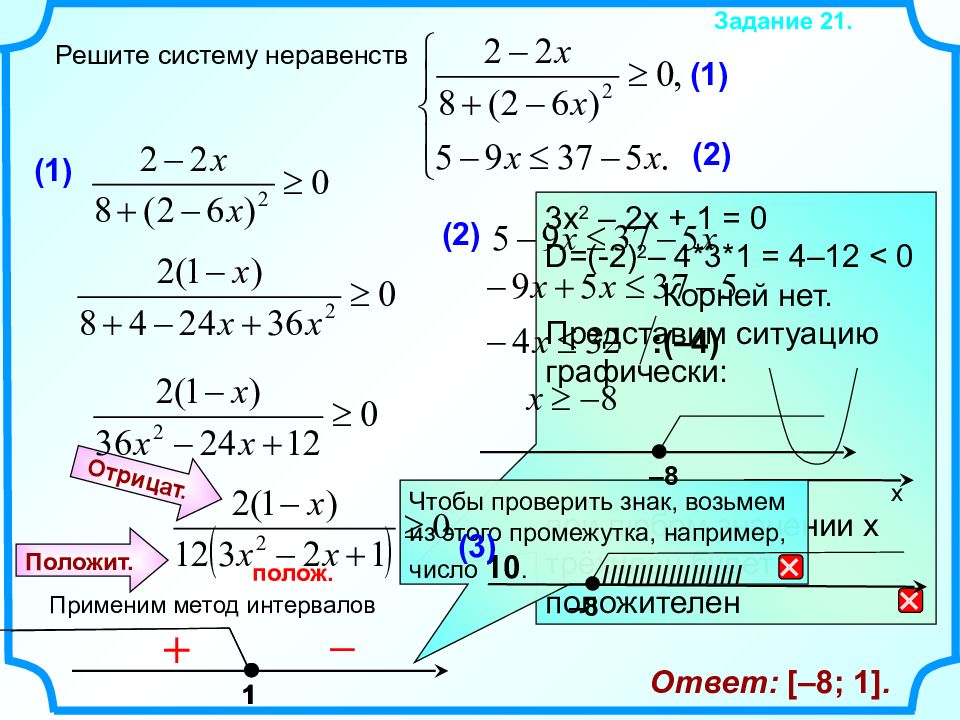
Решите систему неравенств Задание 2 1. (1) (2) (1) 3 x 2 – 2x + 1 = 0 D = (-2) 2 – 4*3*1 = 4–12 < 0 Корней нет. Представим ситуацию графически: при любом значении x трёхчлен будет положителен x полож. Применим метод интервалов 1 – + Чтобы проверить знак, возьмем из этого промежутка, например, число 10. Положит. Отрицат. (2) :(–4) –8 –8 (3) 1 IIIIIIIIIIIIIIIIIII Ответ: [–8; 1].
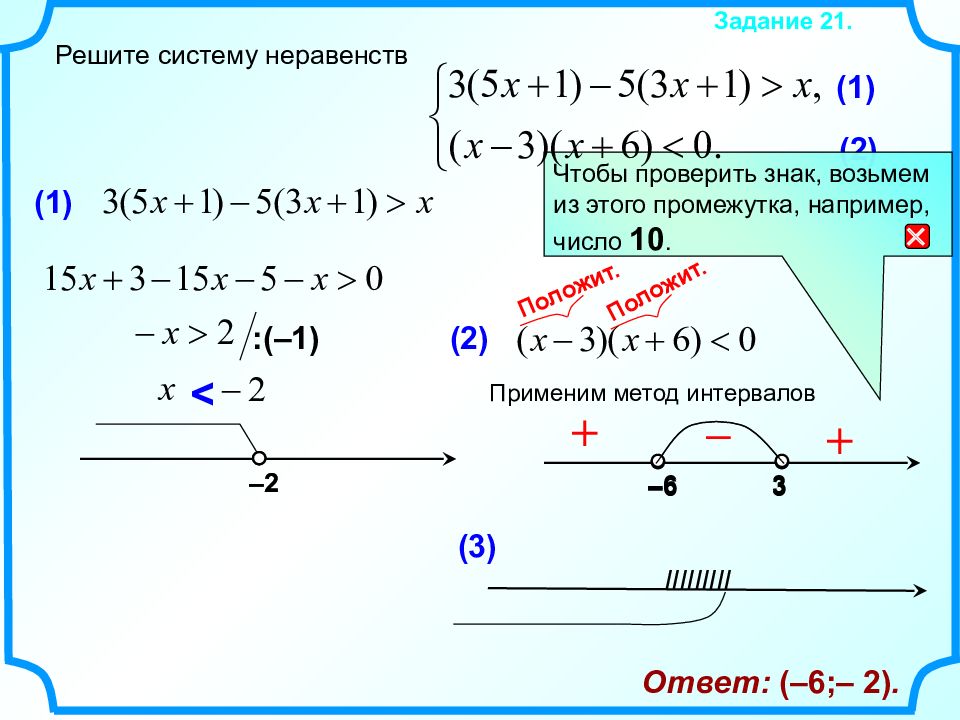
3 –6 3 –6 Решите систему неравенств Задание 2 1. (1) (2) Применим метод интервалов + – (1) :(–1) –2 (3) IIIIIIIII Ответ: (–6;– 2). Чтобы проверить знак, возьмем из этого промежутка, например, число 10. + Положит. Положит. –2 < (2)
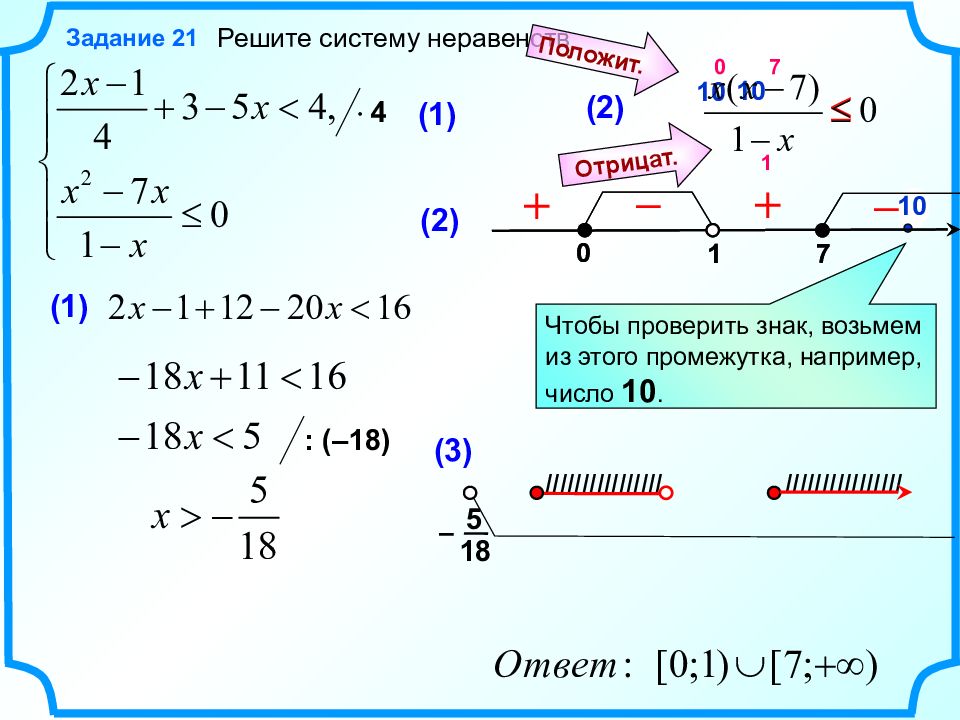
Решите систему неравенств Задание 2 1 (1) (2) 4 (1) : (– 18 ) (2) 1 0 7 Чтобы проверить знак, возьмем из этого промежутка, например, число 10. Отрицат. Положит. 7 0 1 10 10 10 – + – + £ (3) 1 0 7 5 18 – IIIIIIIIIIIIIIII IIIIIIIIIIIIIIII
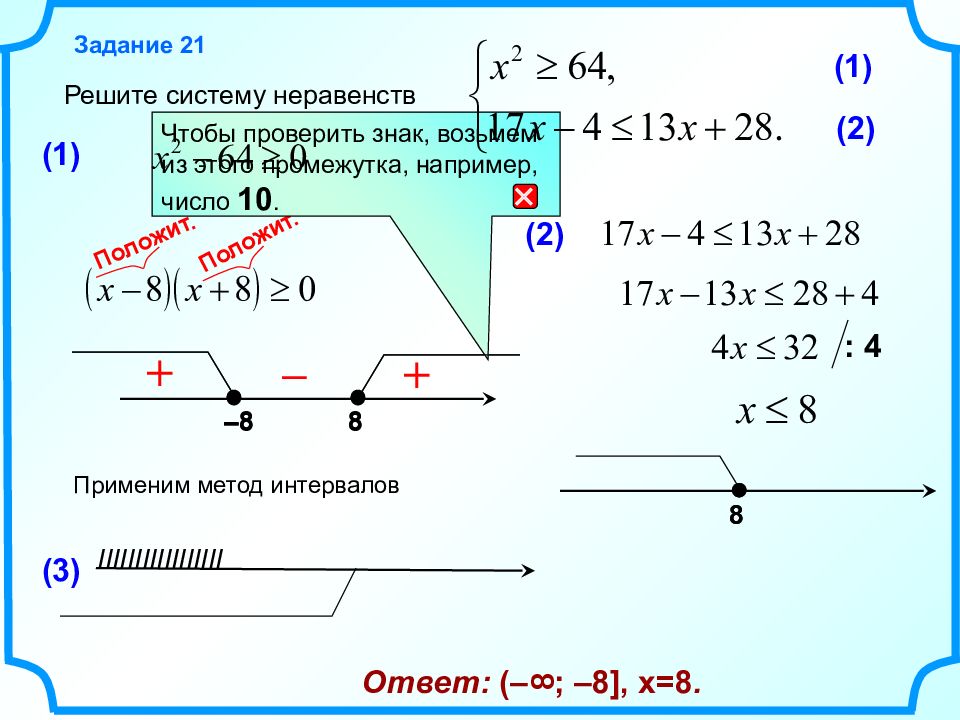
8 – 8 Решите систему неравенств Задание 2 1 (1) (2) Применим метод интервалов + – ( 2 ) : 4 8 (3) IIIIIIIIIIIIIIIII + Положит. Положит. 8 ( 1 ) Чтобы проверить знак, возьмем из этого промежутка, например, число 10. 8 – 8 Ответ: (– ; –8], x=8. 8
Найдите область определения выражения Задание 2 1 (1) (2) (1) < ! (2) x 2 – 5x – 14 = 0 х 1 = 7 х 2 = – 2 х 1 +х 2 = 5 х 1 х 2 = –14 Это приведённое квадратное уравнение (старший коэффициент равен 1). Найдем корни по теореме Виета. 1 7 –2 + – 2,5 (3) IIIIIIIII Ответ: (– 2 ; 2,5 ]. + 2,5 7 –2 Разложим квадратный трехчлен по формуле a ( x–x 1 )( x–x 2 )
4 –3 Найдите область определения выражения Задание 2 1 (1) (2) (1) (2) x 2 – x – 1 2 = 0 х 1 =4 х 2 = – 3 х 1 +х 2 = 1 х 1 х 2 = –1 2 Это приведённое квадратное уравнение (старший коэффициент равен 1). Найдем корни по теореме Виета. 1 4 –3 + – (3) Ответ: (– 3 ; 3), (3; 4 ]. + Разложим квадратный трехчлен по формуле a ( x–x 1 )( x–x 2 ) 3 I IIIIIIIIIIIII III I I
–2 1 3 Найдите область определения выражения Задание 2 1. (1) (2) (1) (2) + – (3) + 0 I IIIIIIIIIIIII III I I Разложим квадратный трехчлен по формуле a ( x–x 1 )( x–x 2 ) 3х 2 +5х–2 = 0 D = b 2 – 4ac x = –b – + 2a D D =5 2 – 4 3 (– 2 )= 25 + 24 =49= 7 2 х = = – 5 7 – + 2 3 x 2 = – = –2 12 6 x 1 = = 1 3 2 6 –2 1 3 Ответ: [–2; 0 ), ( 0 ; ]. 1 3
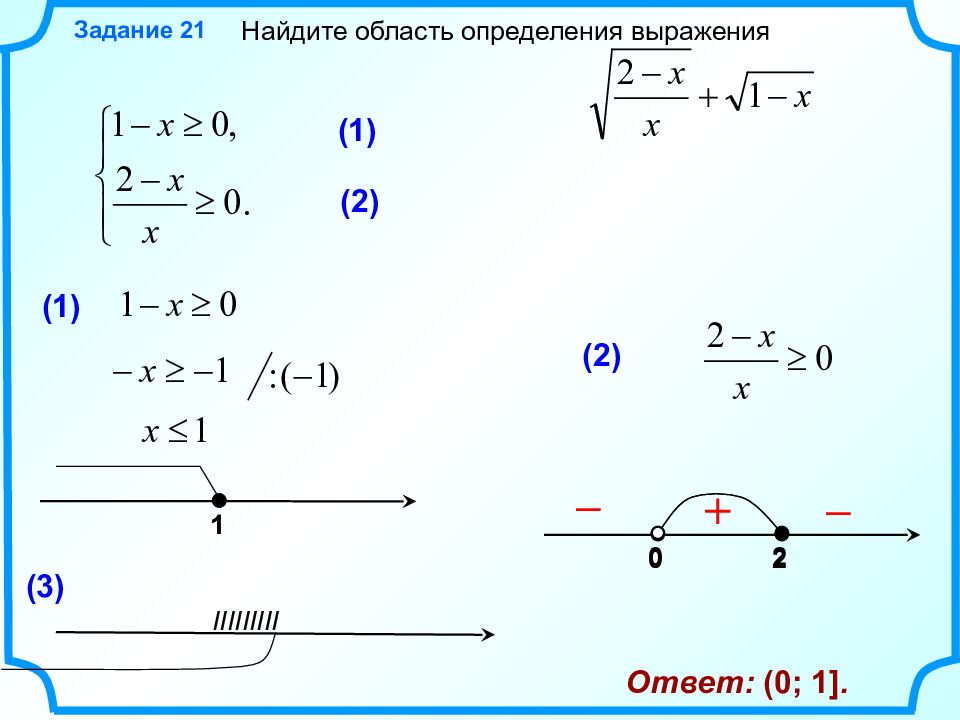
2 0 1 Найдите область определения выражения Задание 2 1 (1) (2) (1) (2) 2 0 – + 1 (3) IIIIIIIII Ответ: (0; 1]. –
x+2 x 2 > 0 : (–3) Решите систему неравенств Задание 2 1 (1) (2) (1) x (2) 8 – 1 + – + Чтобы проверить знак, возьмем из этого промежутка, например, число 10. Положит. Положит. 2 0 < 2 Ответ: [ – 1 ; 0), ( 0 ; 2 ). IIIIIIII IIIIIIIIIIIIII x 2 – 7x – 8 =0. Это приведённое квадратное уравнение (старший коэффициент равен 1). Найдем корни по теореме Виета. –2 Используем формулу для разложения квадратного трехчлена на множители ax 2 +bx+c=a(x- x 1 )(x- x 2 ) 1
: (–3) Решите систему неравенств Задание 2 1. (1) (2) (1) x 2 (2) 7 – 1 + – + Чтобы проверить знак, возьмем из этого промежутка, например, число 10. Положит. Положит. 1 0 < 2 Ответ: (–1; 0), ( 0 ; 1 ). IIIIIIIIIIII IIIIIIIIIII x 2 –1 x 2 2 > 0 x 2 – 6x – 7 = 0 Это приведённое квадратное уравнение (старший коэффициент равен 1). Найдем корни по теореме Виета. Используем формулу для разложения квадратного трехчлена на множители ax 2 +bx+c=a(x- x 1 )(x- x 2 ) 1
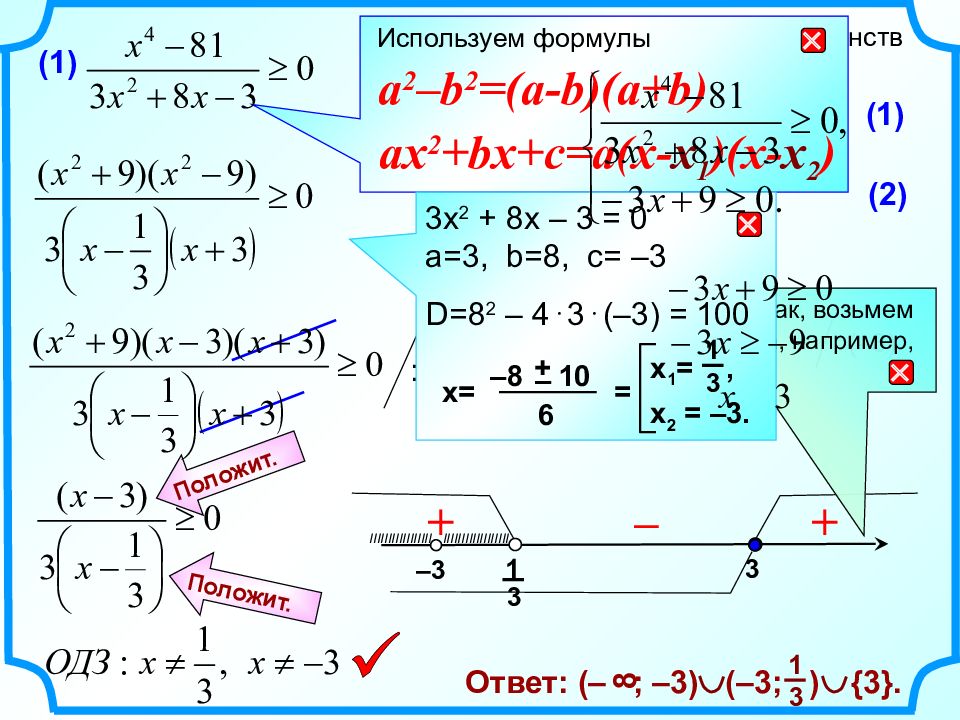
3 3 1 : (–3) Решите систему неравенств Задание 2 1. (1) (2) (1) (2) + – + Положит. Положит. IIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIII – 3 > Ответ: (– ; –3) (–3; ) 1 3 8 { 3 }. : (x 2 +9) > 0 Используем формулы ax 2 +bx+c=a(x- x 1 )(x- x 2 ) a 2 – b 2 =(a-b)(a+b) Чтобы проверить знак, возьмем из этого промежутка, например, число 10. 3x 2 + 8x – 3 = 0 a=3, b=8, c= –3 D=8 2 – 4 3 (–3) = 100 x= = –8 10 – + 6 x 2 = –3. x 1 =, 1 3
