Первый слайд презентации
Урок алгебры 10 класс Решение тригонометрических уравнений «Каждая решенная мною задача становится образом, который служит впоследствии для решения других задач» Р.Декарт
Слайд 2: Изложение нового материала
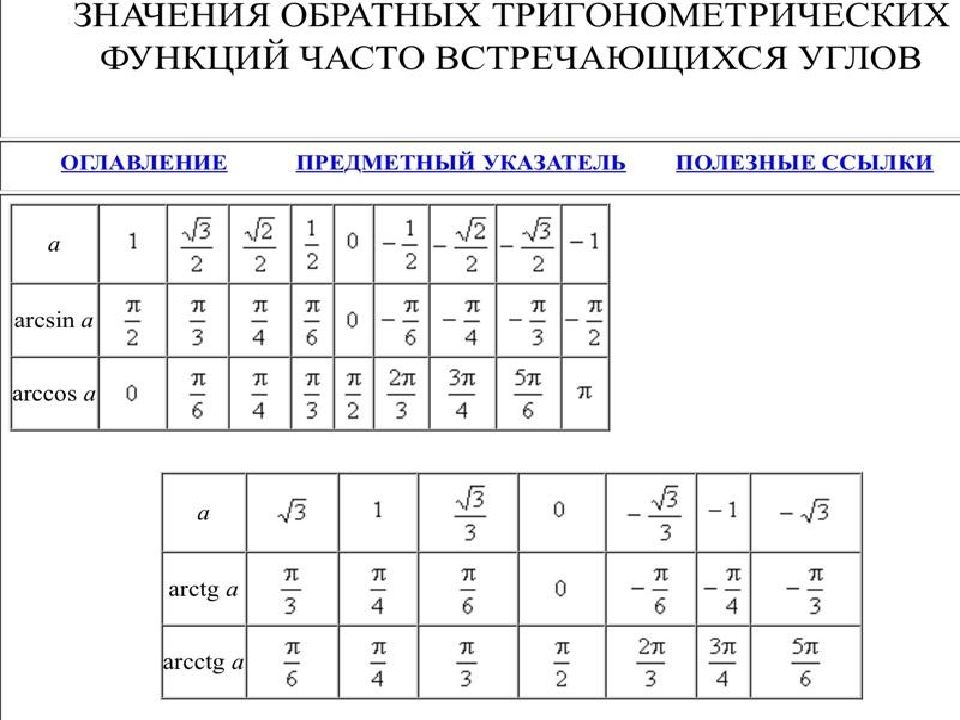
Слайд 3
Что называется arcsin a ? Что называется arccos a ? Арксинус числа a∈[−1, 1] – это угол −90°≤α≤90° (−π/2≤α≤π/2), синус которого равен a. Арккосинус числа a ∈[−1, 1] – это угол 0°≤α≤180° (0≤α≤π), косинус которого равен a.
1) arccos =, так как cos = 2) arcsin =, так как = 3) arccos (- ) =, так как arccos (- ) = π - arccos = π - = 4) arcsin (- ) = -, так как arcsin (- )= - arcsin = - 3) и 4) примеры делаются всегда по формулам :
Уравнения вида sinx =a, cosx =a, tgx =a, ctgx =a называются простейшими тригонометрическими уравнениями
Если уравнение не имеет решения. Если Если уравнение не имеет решения. Если
Слайд 10: Обрати внимание на эти формулу: Если в правой части уравнения стоит отрицательное число, то нужно применять эти формулы
Слайд 11
Формула для решений уравнения sin x = - a Так как arcsin (- a) = - arcsin a , то получаем формулу: x = (-1) k+1 ∙ arcsin a + π k, к є Z Пример Решить уравнение: Ответ
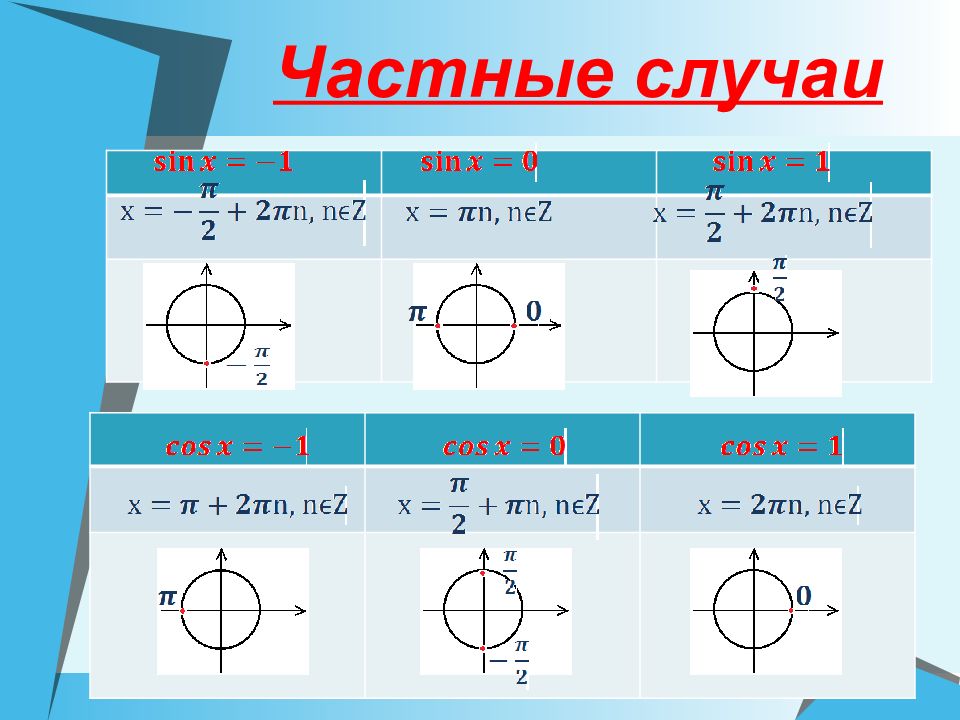
Слайд 13: Теперь рассмотрим частные случаи решения тригонометрических уравнений. Их нужно применять, когда значения функций равны 1,-1 и 0
Слайд 15
Уравнения, приводимые к алгебраическим С помощью замены переменной можно привести тригонометрическое уравнение к алгебраическому. Рассмотрим несколько типов уравнений: Тип уравнения Замена Алгебраическое уравнение
Слайд 16
Уравнения, приводимые к алгебраическим С помощью замены переменной можно привести тригонометрическое уравнение к алгебраическому. Рассмотрим несколько типов уравнений: Тип уравнения Замена Алгебраическое уравнение
Слайд 17: Запомни! Это основные формулы, по которым нужно решать тригонометрические уравнения
Слайд 24: Решите уравнение: 7)
Замена: По т,обр. Виета:, Решите уравнение: 7) Решений нет, т.к. |-5| >1
Последний слайд презентации: Урок алгебры 10 класс Решение тригонометрических уравнений «Каждая решенная: Домашнее задание:
I. Выписать в тетрадь основные определения и формулы по новой теме, а также разобранные уравнения II. Решить уравнения( решение расписать подробно, по образцу классных задач) 1) 2) = 3) 4) = 0 5) = - 6) 5 ) 2 sin 2 x – 5 sin x – 7 = 0 6) 3 cos 2 x – 5 cos x – 8 = 0