Решение простейших тригонометрических неравенств
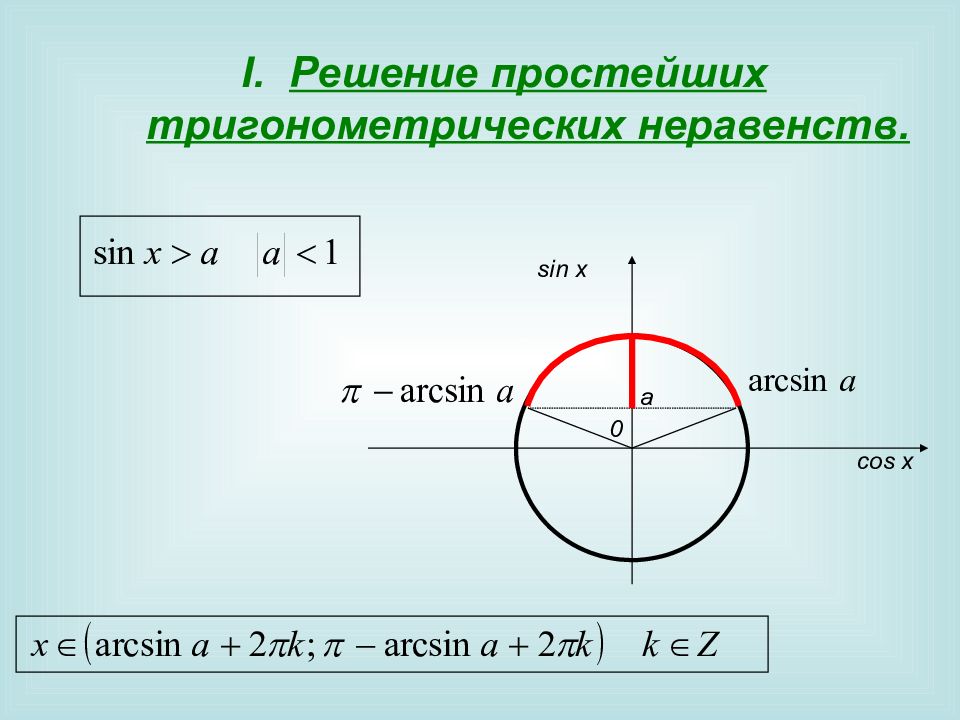
Решение простейших тригонометрических неравенств. Тригонометрическими неравенствами называются неравенства, содержащие переменную в аргументе тригонометрической функции.
Решение простейших тригонометрических неравенств. 0 sin x cos x a
Решение простейших тригонометрических неравенств. 0 sin x cos x a
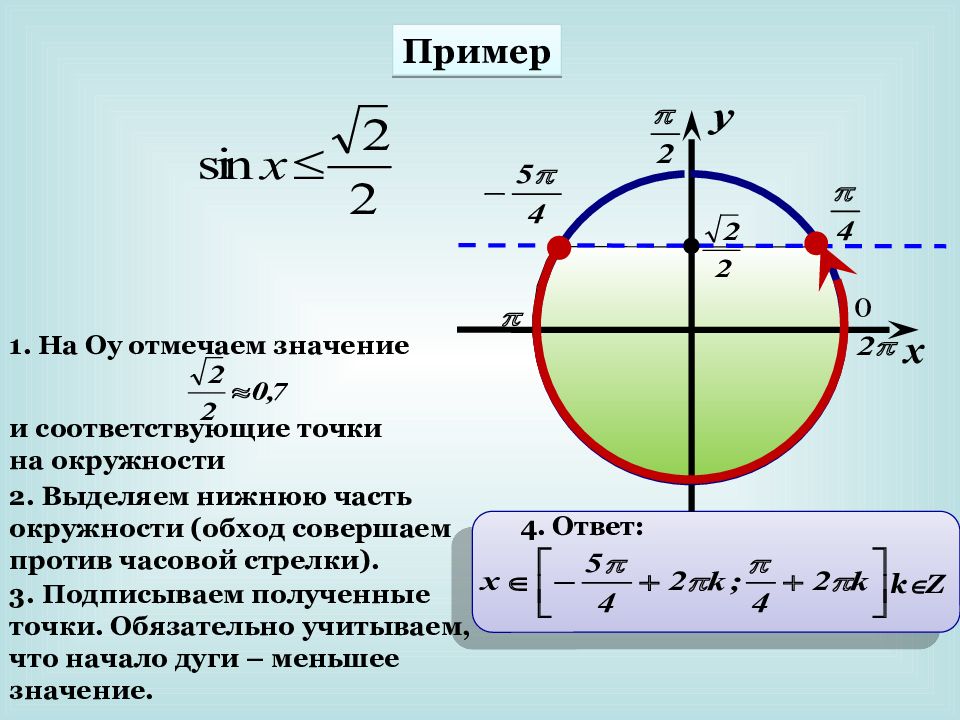
1. На Оу отмечаем значение и соответствующие точки на окружности 2. Выделяем нижнюю часть окружности (обход совершаем против часовой стрелки). 3. Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение. 4. Ответ: k Z Пример
Решение простейших тригонометрических неравенств. 0 sin x cos x a
Решение простейших тригонометрических неравенств. 0 sin x cos x a
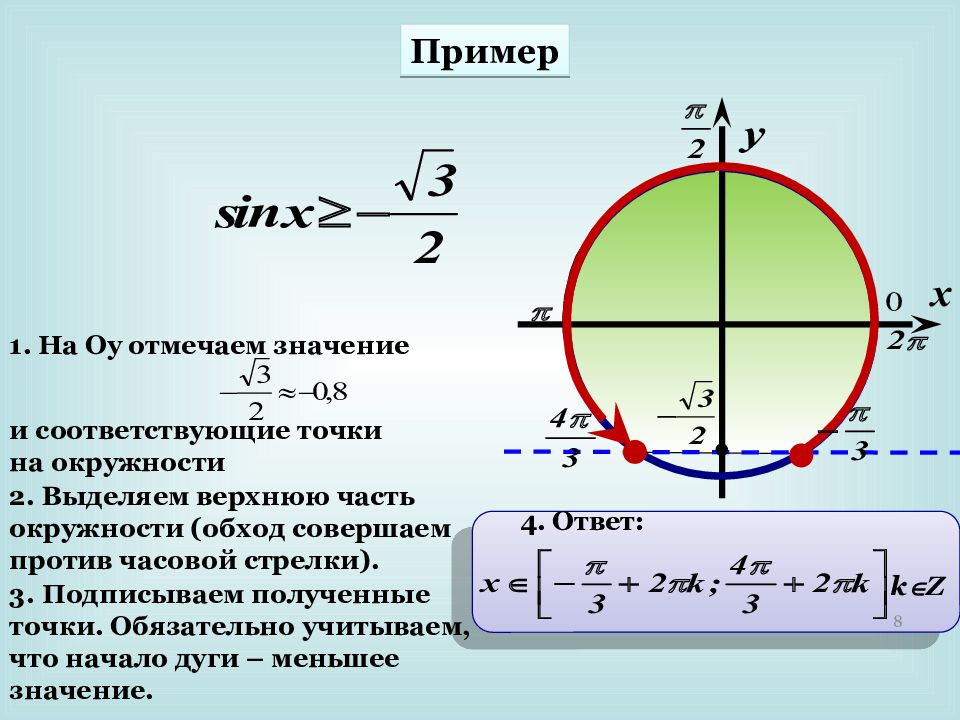
Пример 8 1. На Оу отмечаем значение и соответствующие точки на окружности 2. Выделяем верхнюю часть окружности (обход совершаем против часовой стрелки). 3. Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение. 4. Ответ: k Z
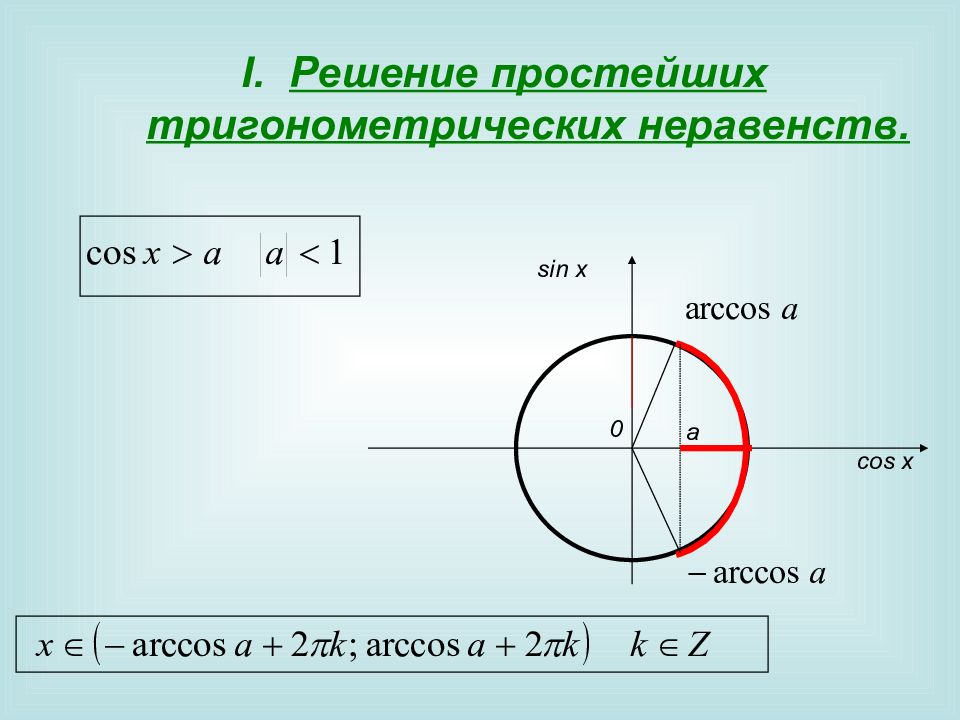
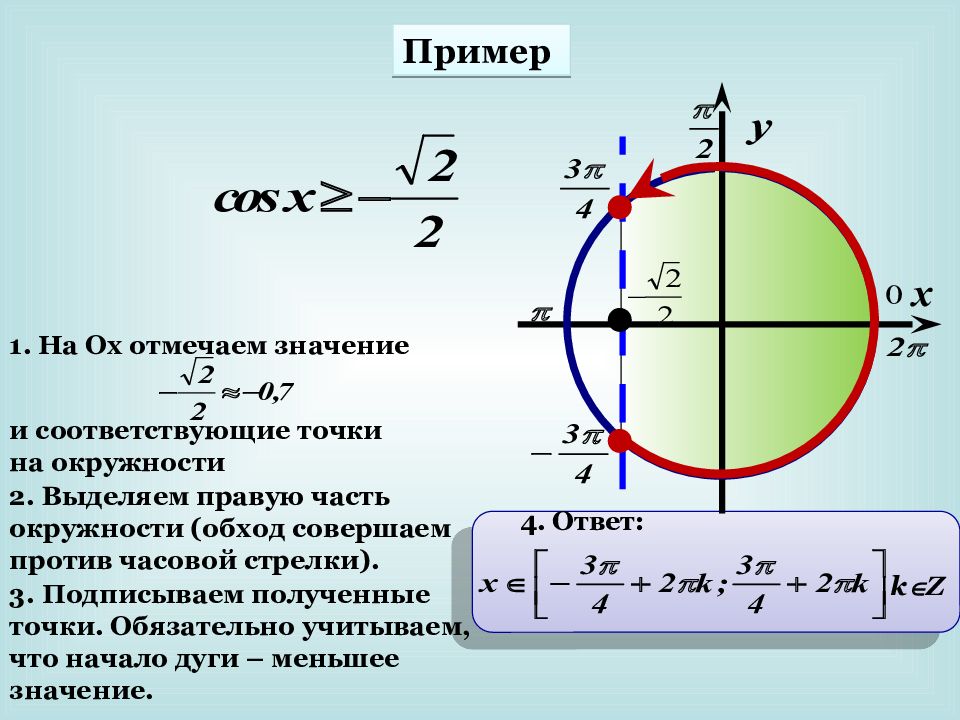
Пример 1. На Ох отмечаем значение и соответствующие точки на окружности 2. Выделяем правую часть окружности (обход совершаем против часовой стрелки). 3. Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение. 4. Ответ: k Z
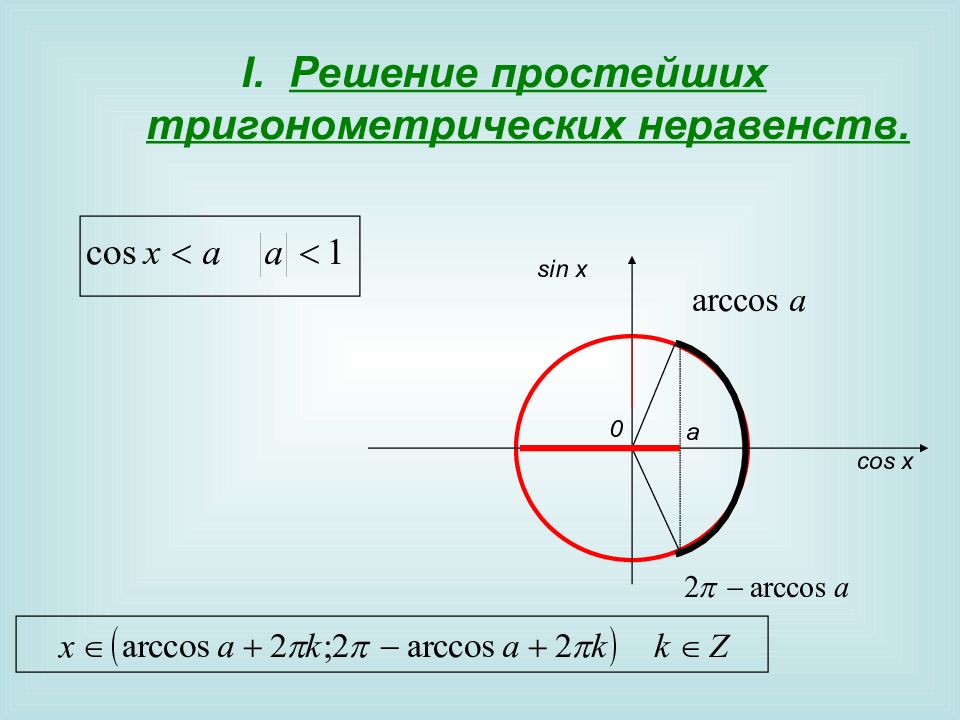
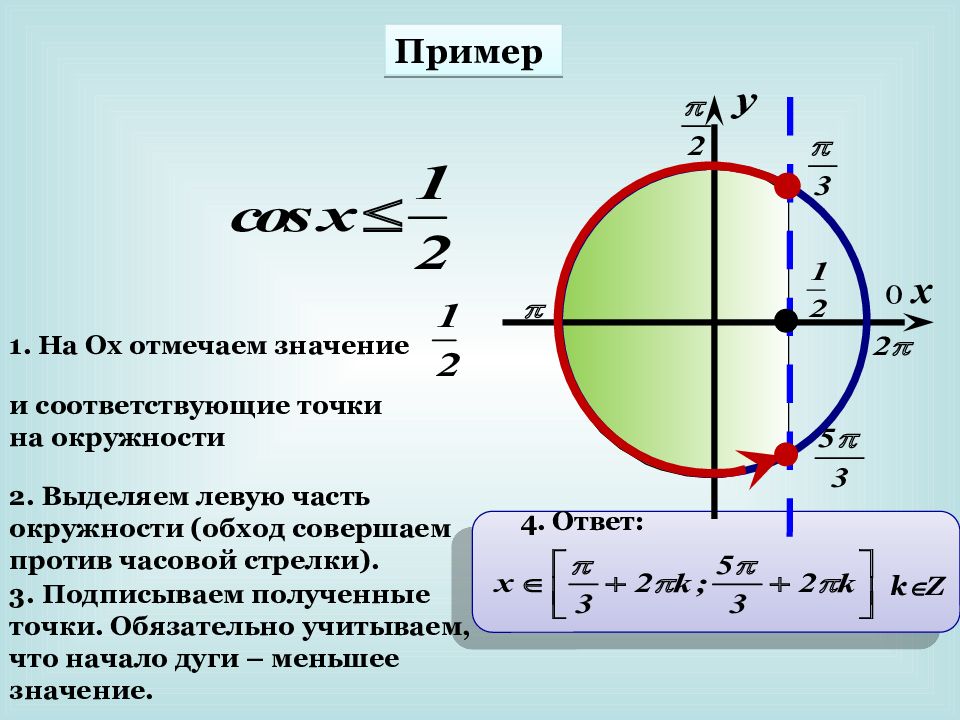
Пример k Z 1. На Ох отмечаем значение и соответствующие точки на окружности 2. Выделяем левую часть окружности (обход совершаем против часовой стрелки). 3. Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение. 4. Ответ:
Решение простейших тригонометрических неравенств. 0 sin x cos x a tg x
Решение простейших тригонометрических неравенств. 0 sin x cos x a tg x
k Z 5. Ответ: 1. На линии тангенсов отмечаем значение 2. Выделяем нижнюю часть линии тангенсов, поскольку решаем неравенство со знаком ≤ 3. Выделяем соответствующую часть окружности (обход совершаем против часовой стрелки). 4. Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение. Пример
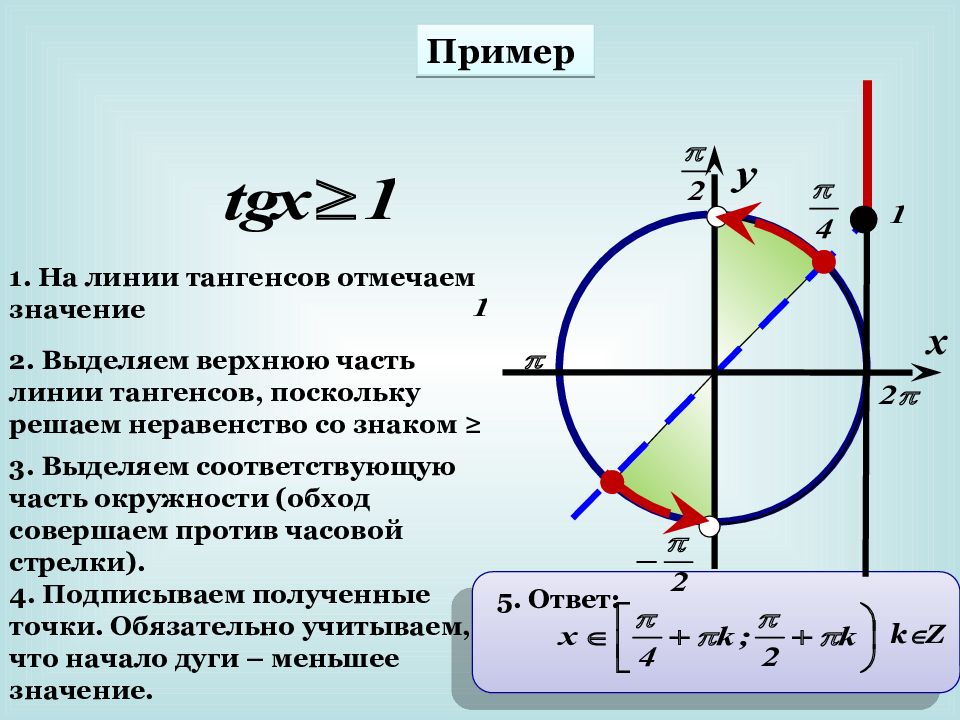
Пример k Z 5. Ответ: 1. На линии тангенсов отмечаем значение 2. Выделяем верхнюю часть линии тангенсов, поскольку решаем неравенство со знаком ≥ 3. Выделяем соответствующую часть окружности (обход совершаем против часовой стрелки). 4. Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
Решение простейших тригонометрических неравенств. 0 sin x cos x a с tg x
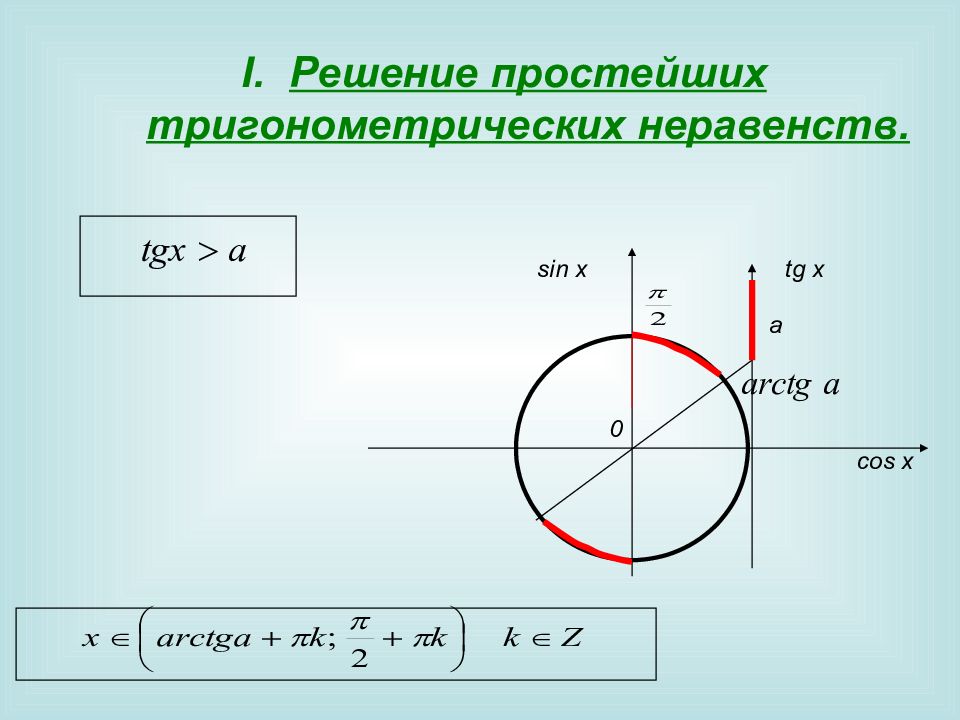
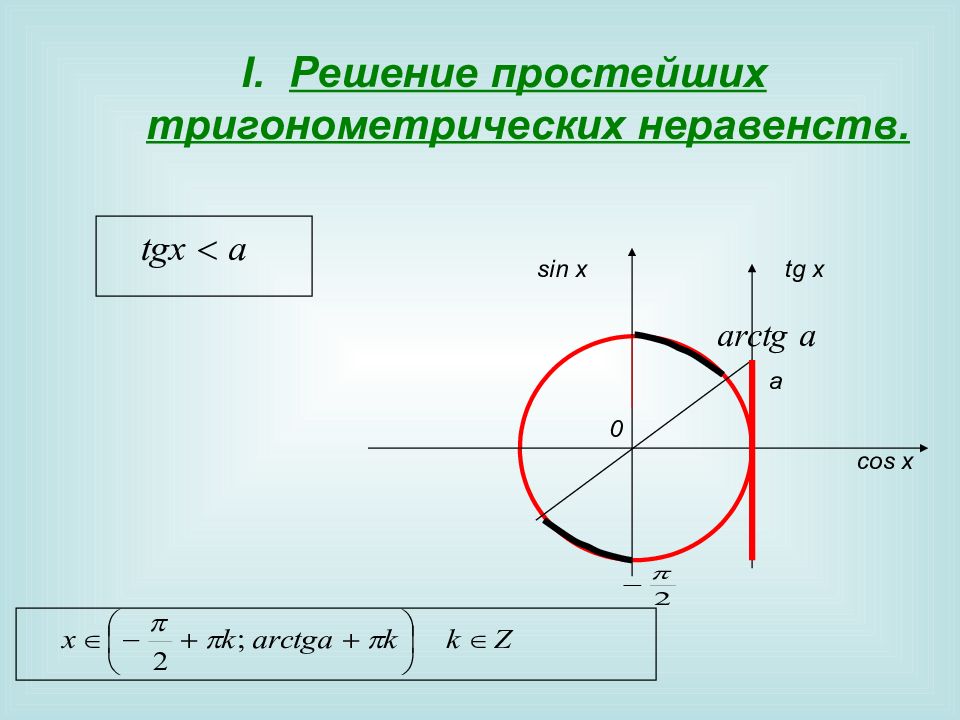
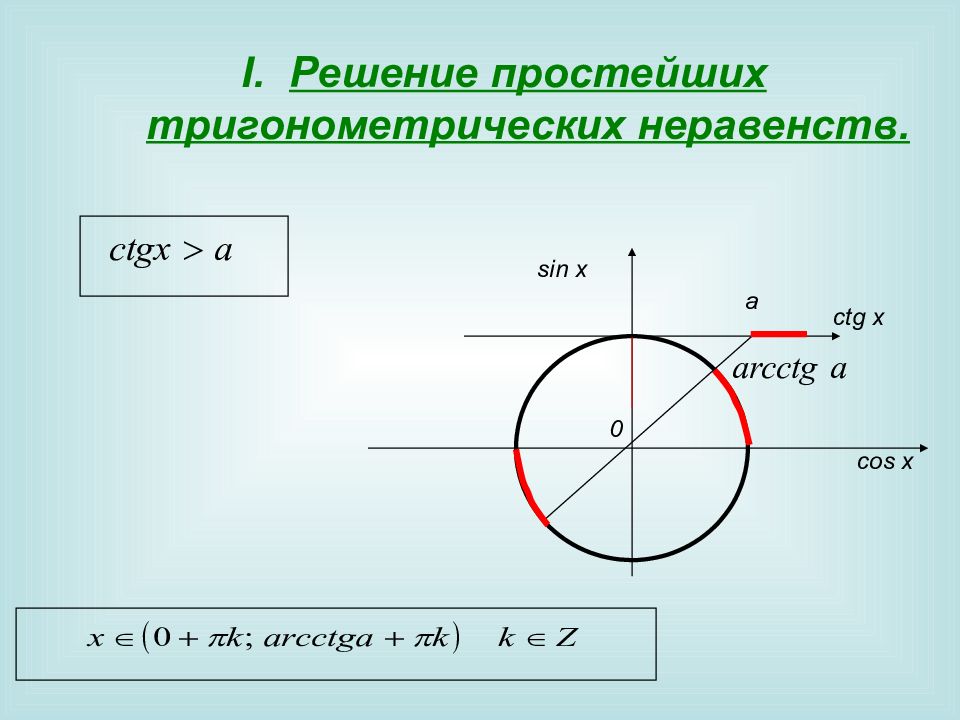
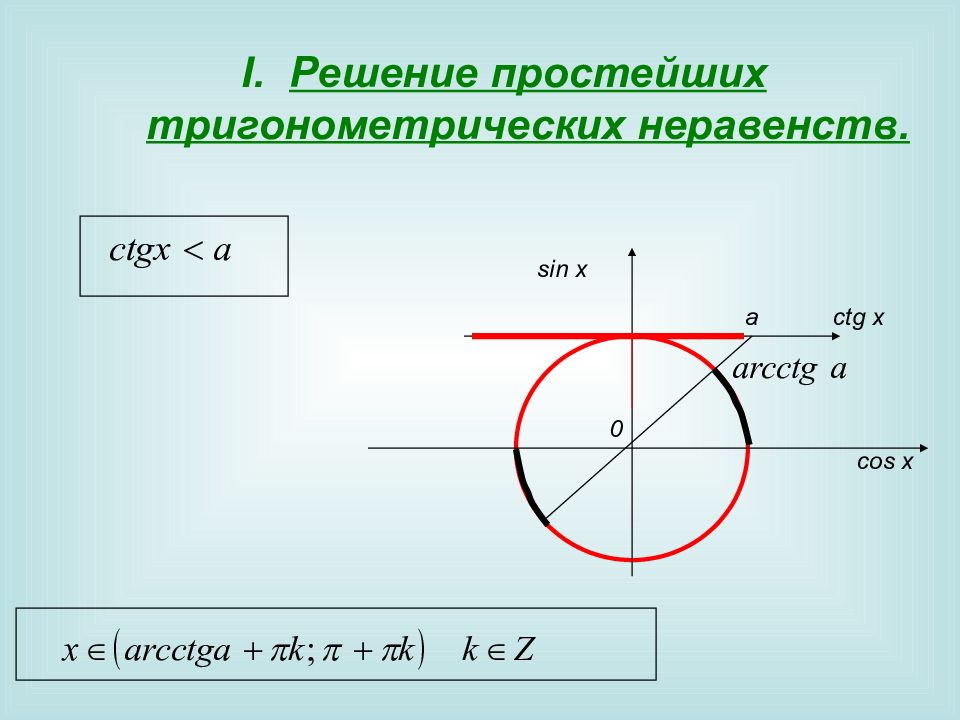
Решение простейших тригонометрических неравенств. 0 sin x cos x a с tg x
