Слайд 2
2 2 Чертеж – международный язык общения техников. Начертательная геометрия – грамматика этого языка (чертежа). Начертательная геометрия изучает методы построения изображений пространственных объектов на плоскости, а также способы преобразования полученных изображений для упрощения решения различных инженерных задач.
Слайд 4
4 Точка – абстрактное математическое понятие. Нульмерный объект (не имеет измерений). Линия – непрерывное одномерное множество точек ( цепочка точек). Непрерывная последо-вательность положений точки, перемещаю- щейся в пространстве по определенному закону (траектории). Измерение : только длина. Толщины нет. Поверхность – непрерывное двумерное мно-жество точек. Непрерывная последователь- ность положений линии, перемещающейся в пространстве по определенному закону. Измерения : длина, ширина, площадь. Толщины и объема нет.
Слайд 5: Изображение геометрических объектов
Слайд 6
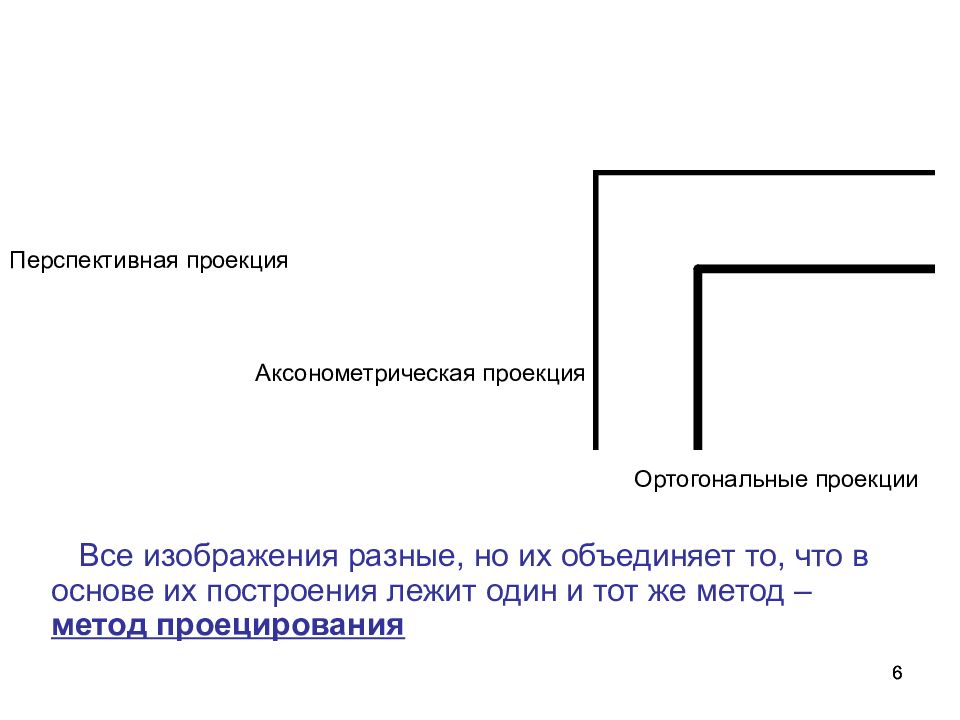
6 6 Все изображения разные, но их объединяет то, что в основе их построения лежит один и тот же метод – метод проецирования Перспективная проекция Аксонометрическая проекция Ортогональные проекции
Слайд 8
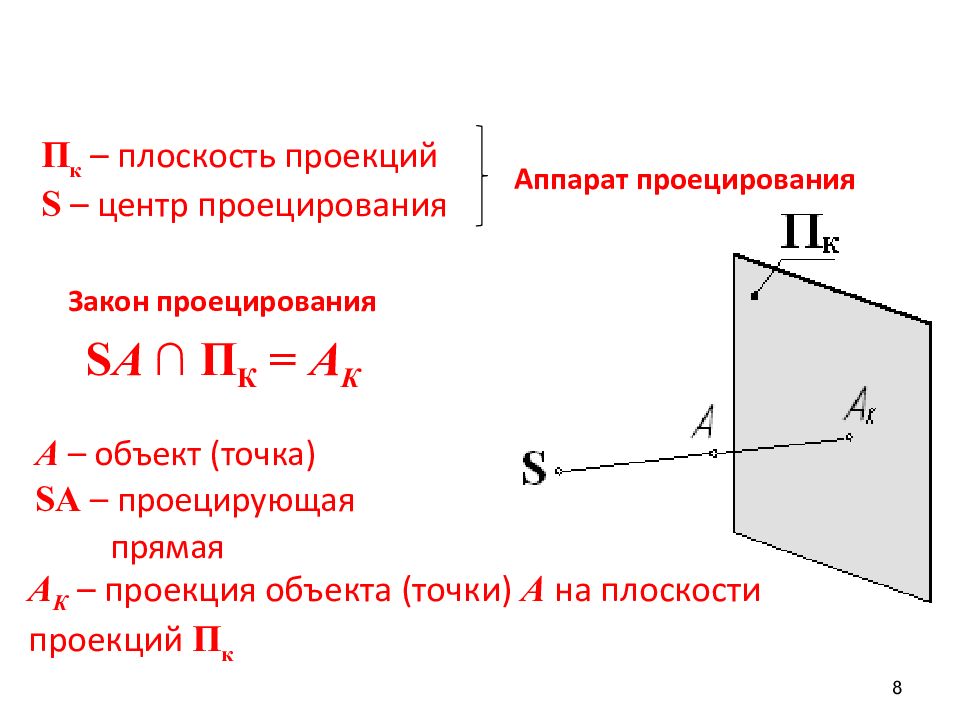
8 А – объект (точка) SA – проецирующая прямая S A ∩ П К = А К А К – проекция объекта (точки) А на плоскости проекций П к П к – плоскость проекций S – центр проецирования Аппарат проецирования Закон проецирования
Слайд 9
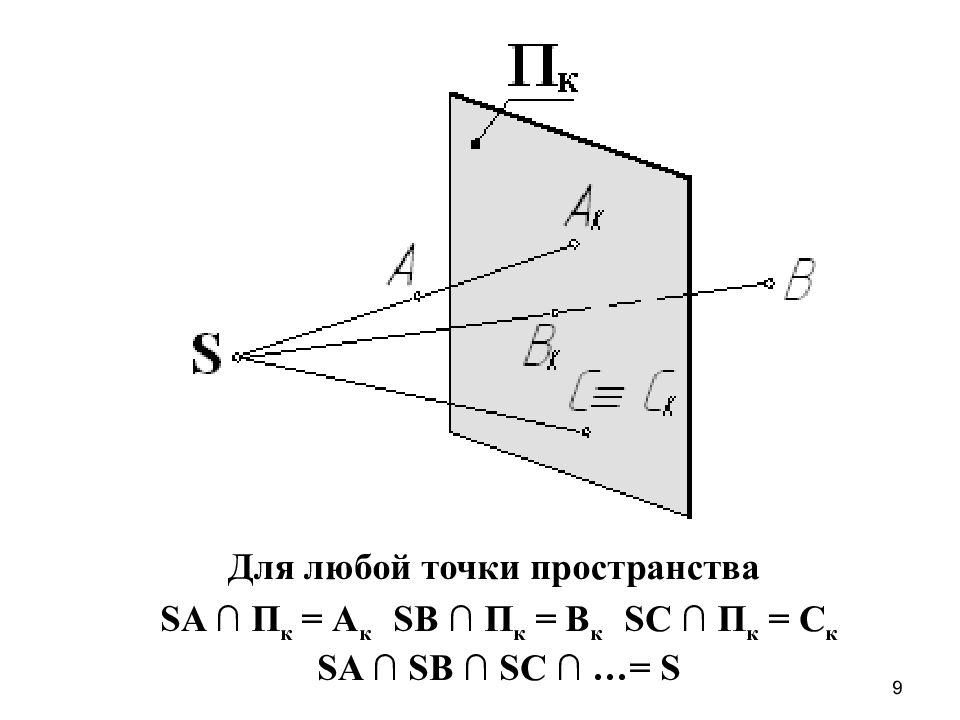
9 Для любой точки пространства SA ∩ П к = A к S В ∩ П к = B к S С ∩ П к = C к SA ∩ S В ∩ S С ∩ …= S
Слайд 11: Центральное проецирование
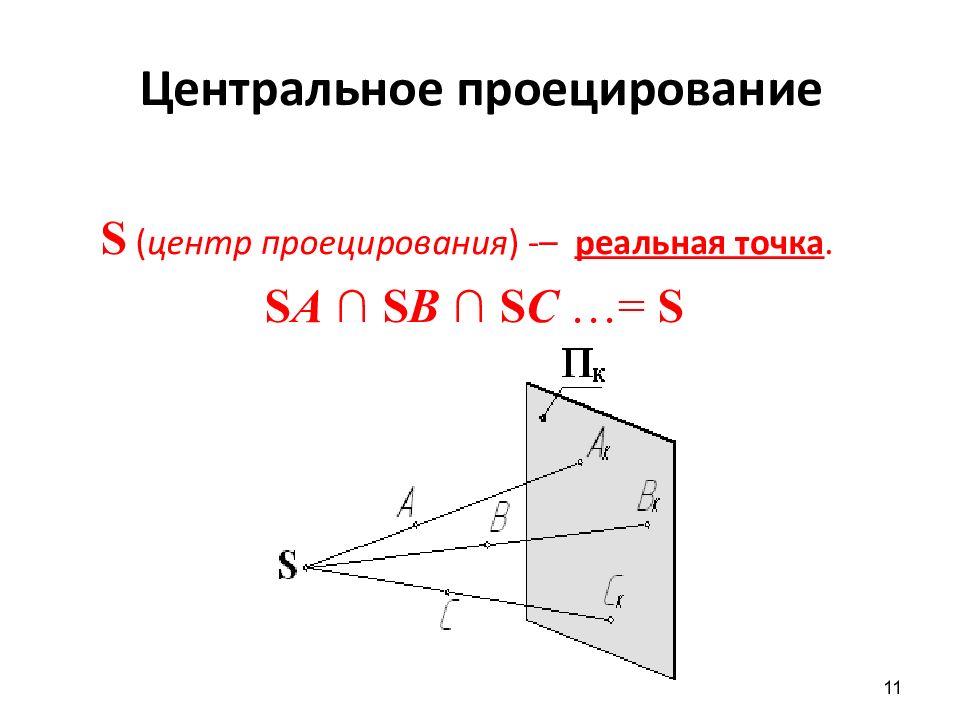
11 Центральное проецирование S ( ц ентр проецирования ) -– реальная точка. S A ∩ S B ∩ S C …= S
Слайд 12: Параллельное проецирование
12 Параллельное проецирование S ( центр проецирования ) – несобственная точка S S S A ∩ S B ∩ S C …= S следовательно S A S B S C … s s – направление проецирования; S s
Слайд 13: Виды параллельного проецирования
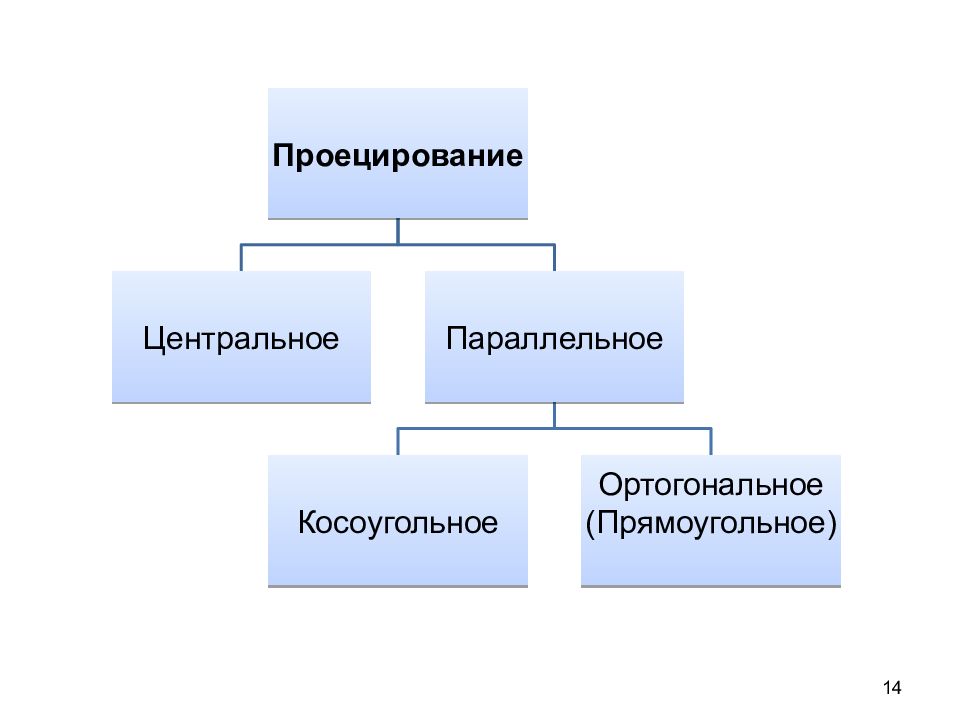
13 Виды параллельного проецирования ( s ^ П к )= φ φ =90 º ( s П к ) проецирование прямоугольное (ортогональное) φ =90 º ( s П к ) проецирование косоугольное
Слайд 15: Свойства ортогонального проецирования
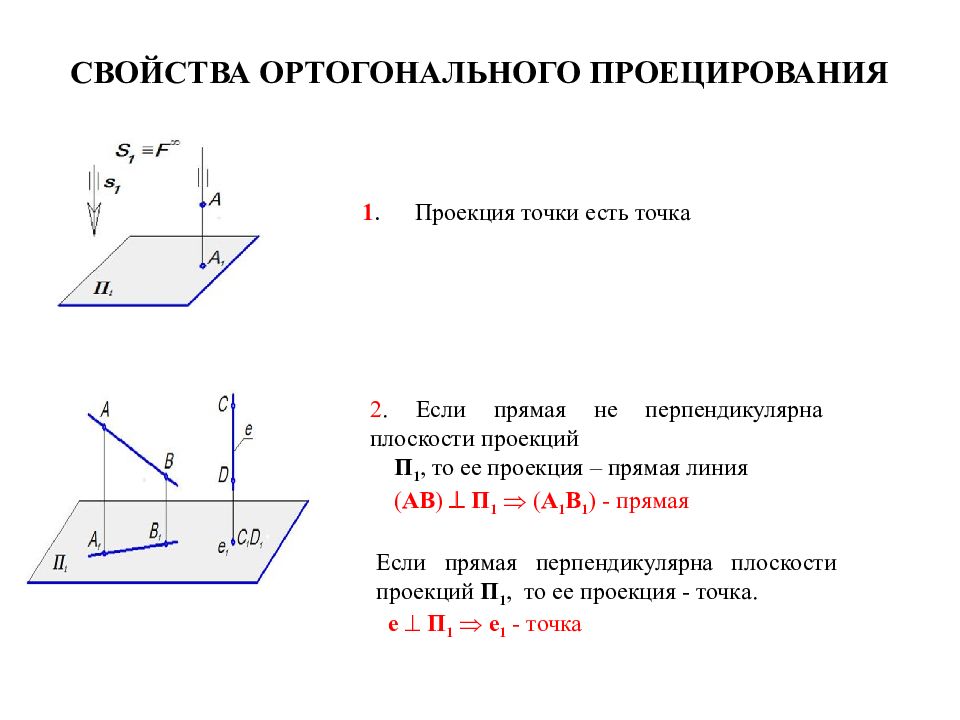
1. Проекция точки есть точка 2. Если прямая не перпендикулярна плоскости проекций П 1, то ее проекция – прямая линия ( AB ) П 1 ( A 1 B 1 ) - прямая Если прямая перпендикулярна плоскости проекций П 1, то ее проекция - точка. e П 1 e 1 - точка
Слайд 16
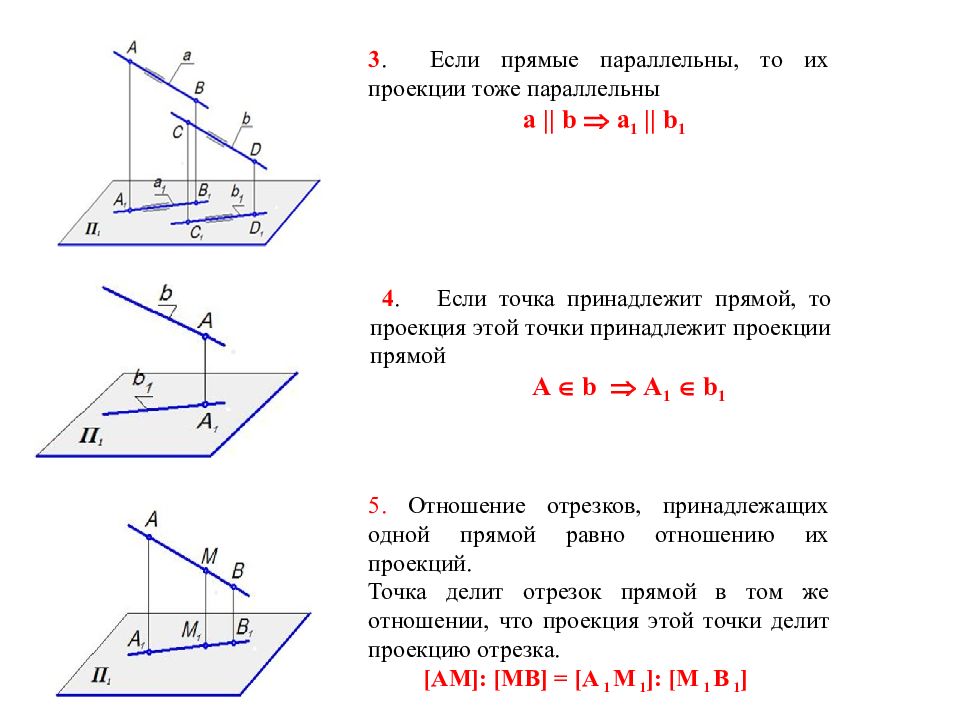
3. Если прямые параллельны, то их проекции тоже параллельны a || b a 1 || b 1 4. Если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой A b A 1 b 1 5. Отношение отрезков, принадлежащих одной прямой равно отношению их проекций. Точка делит отрезок прямой в том же отношении, что проекция этой точки делит проекцию отрезка. [ AM ]: [ MB ] = [ A 1 M 1 ]: [ M 1 B 1 ]
Слайд 17
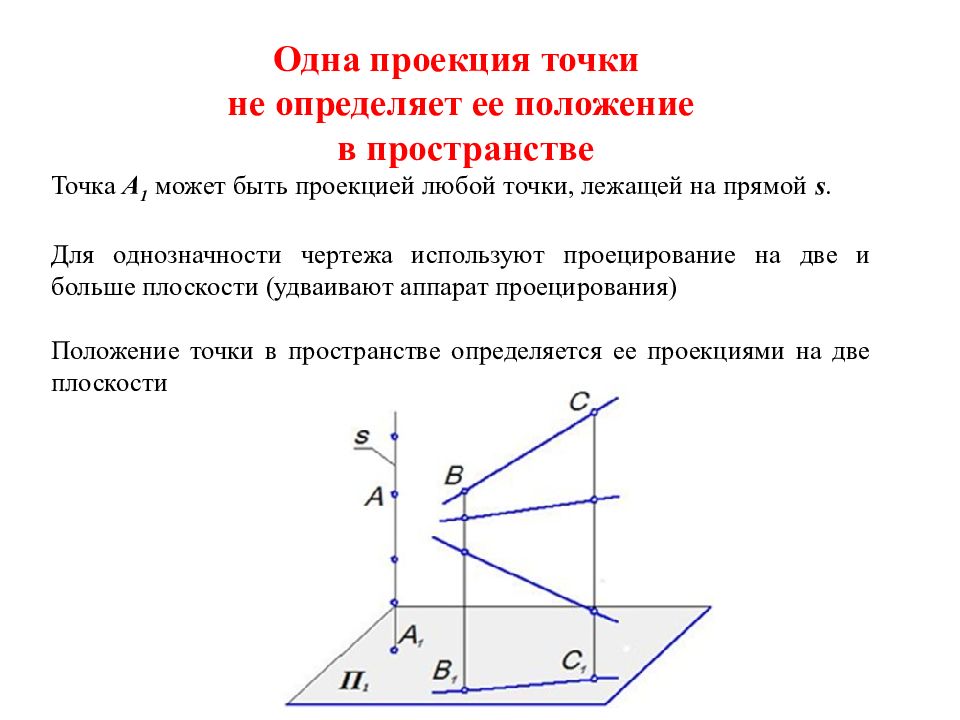
Одна проекция точки не определяет ее положение в пространстве Точка A 1 может быть проекцией любой точки, лежащей на прямой s. Для однозначности чертежа используют проецирование на две и больше плоскости (удваивают аппарат проецирования) Положение точки в пространстве определяется ее проекциями на две плоскости
Слайд 19
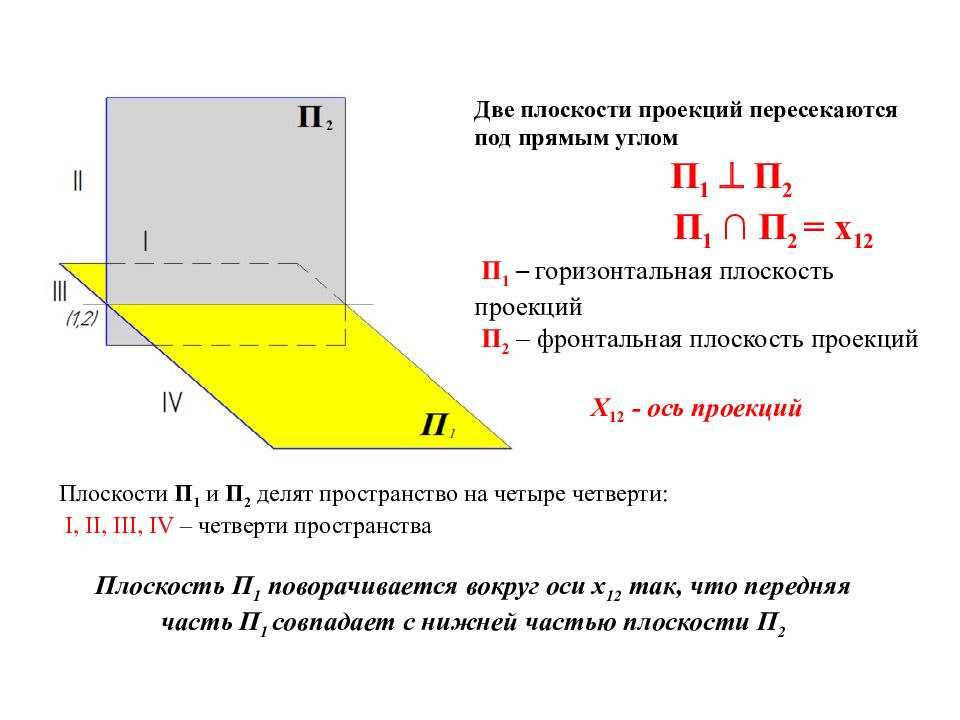
Две плоскости проекций пересекаются под прямым углом П 1 П 2 П 1 ∩ П 2 = x 12 П 1 – горизонтальная плоскость проекций П 2 – фронтальная плоскость проекций X 12 - ось проекций Плоскости П 1 и П 2 делят пространство на четыре четверти: I, II, III, IV – четверти пространства Плоскость П 1 поворачивается вокруг оси x 12 так, что передняя часть П 1 совпадает с нижней частью плоскости П 2
Слайд 20
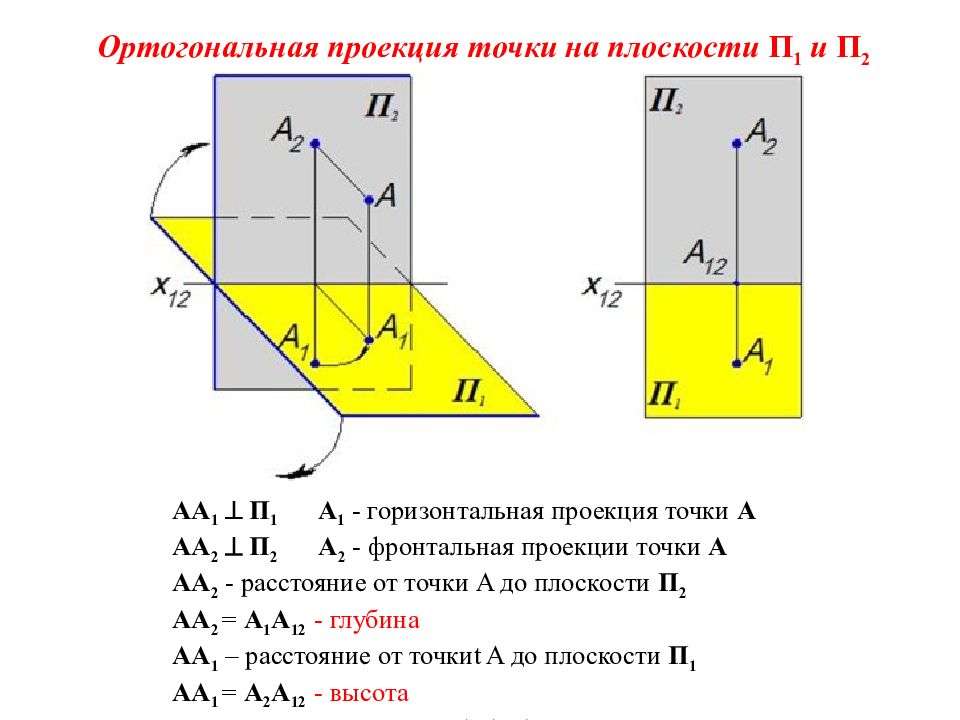
Ортогональная проекция точки на плоскости П 1 и П 2 AA 1 П 1 A 1 - горизонтальная проекция точки A AA 2 П 2 A 2 - фронтальная проекции точки A AA 2 - расстояние от точки A до плоскости П 2 AA 2 = A 1 A 12 - глубина AA 1 – расстояние от точки t A до плоскости П 1 AA 1 = A 2 A 12 - высота А 1 А 2 х 12
Слайд 21
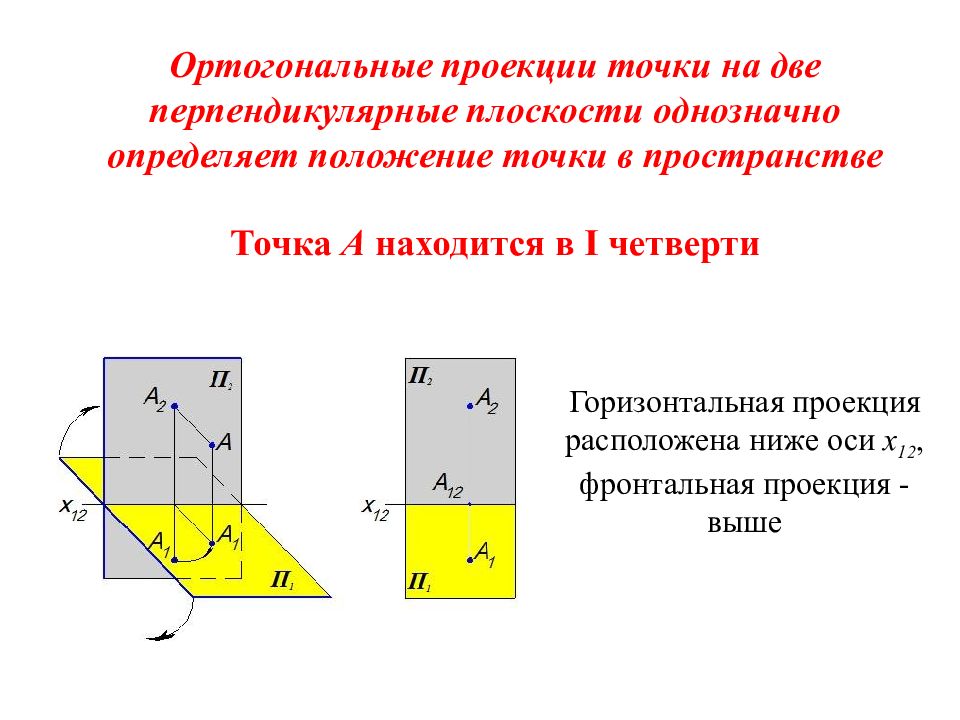
Ортогональные проекции точки на две перпендикулярные плоскости однозначно определяет положение точки в пространстве Точка A находится в I четверти Горизонтальная проекция расположена ниже оси x 12, фронтальная проекция - выше
Слайд 22
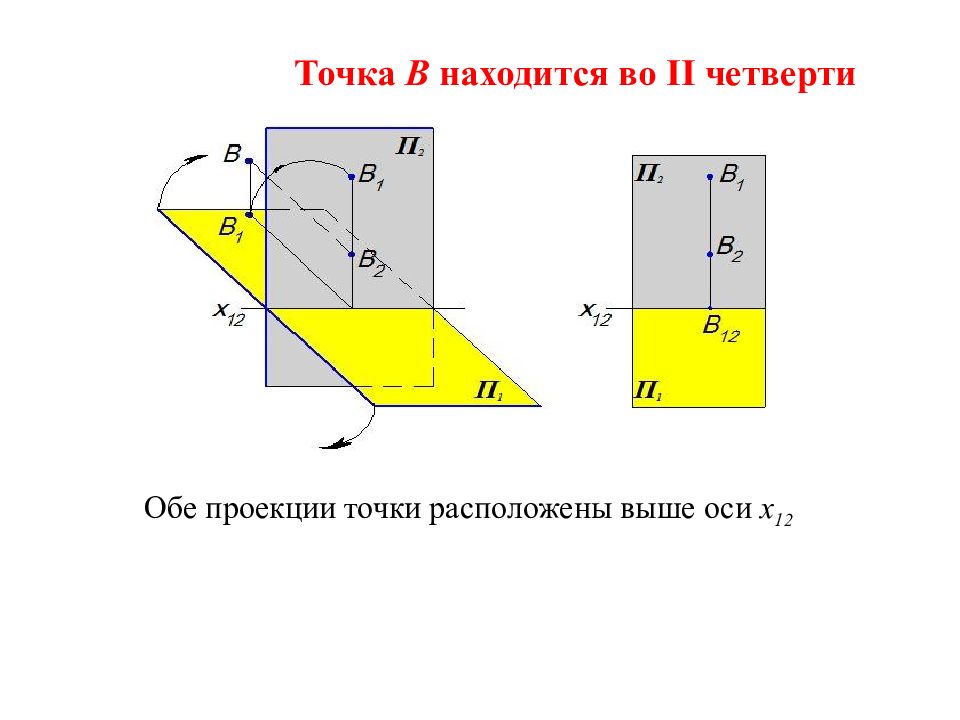
Точка B находится во II четверти Обе проекции точки расположены выше оси x 12
Слайд 23
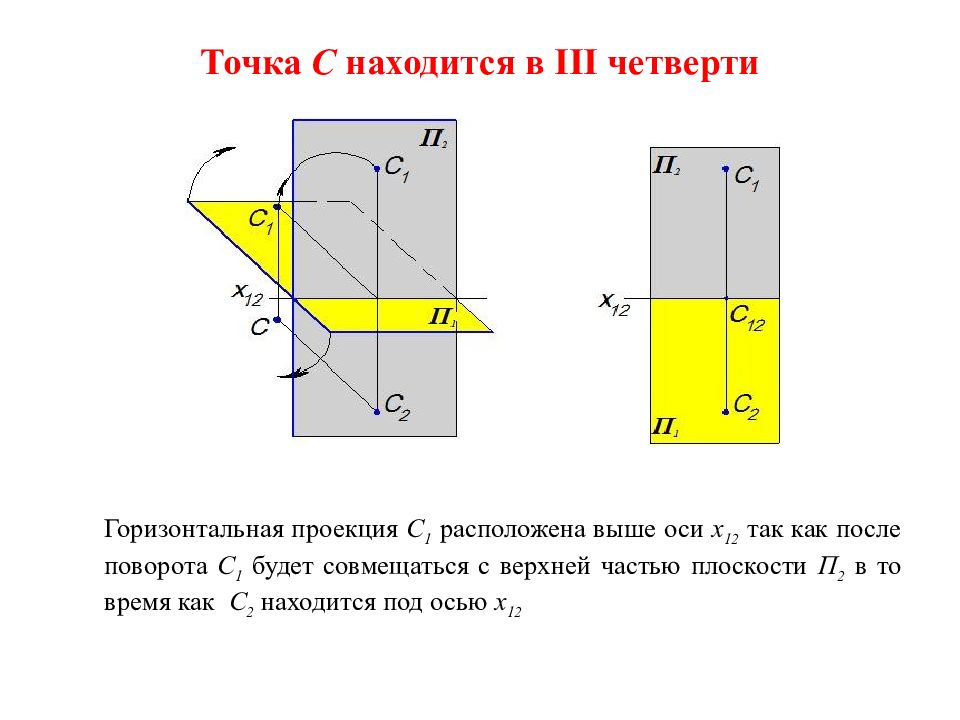
Точка C находится в III четверти Горизонтальная проекция C 1 расположена выше оси x 12 так как после поворота C 1 будет совмещаться с верхней частью плоскости П 2 в то время как C 2 находится под осью x 12
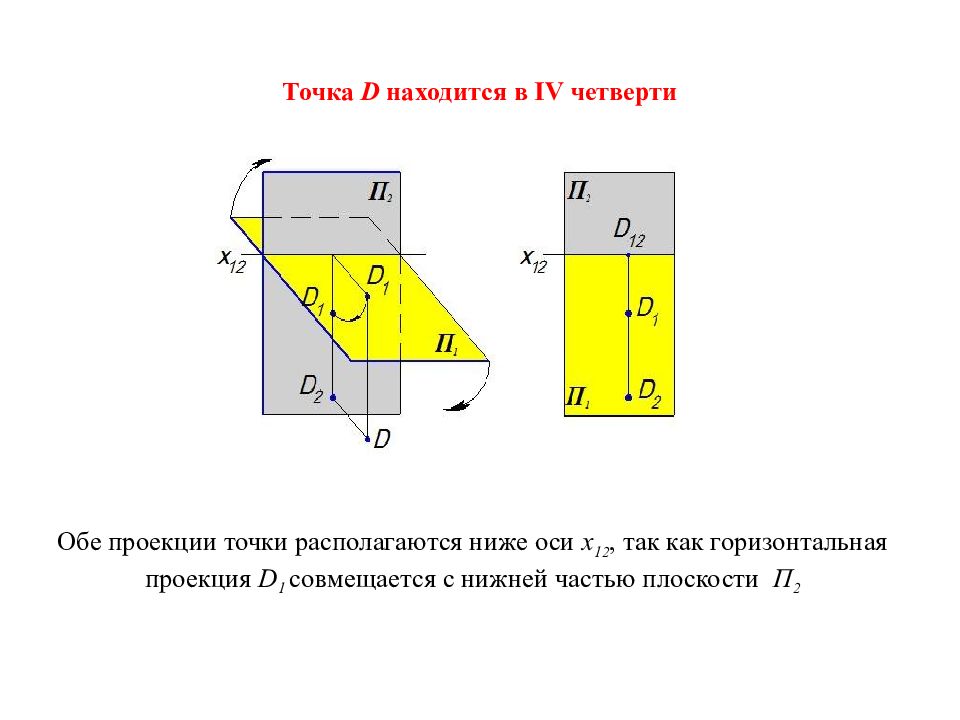
Слайд 24: Точка D находится в IV четверти
Обе проекции точки располагаются ниже оси x 12, так как горизонтальная проекция D 1 совмещается с нижней частью плоскости П 2
Слайд 25
25 Проекции всех точек A, B, C, D представлены на чертеже Горизонтальные и фронтальные проекции точек A и C, расположенных в нечетных четвертях пространства ( 1 and 3 ), находятся по обе стороны оси x 12, в то время как проекции точек B и D, находящихся в четных четвертях пространства (2 and 4), расположены по одну сторону от оси x 12
Слайд 26
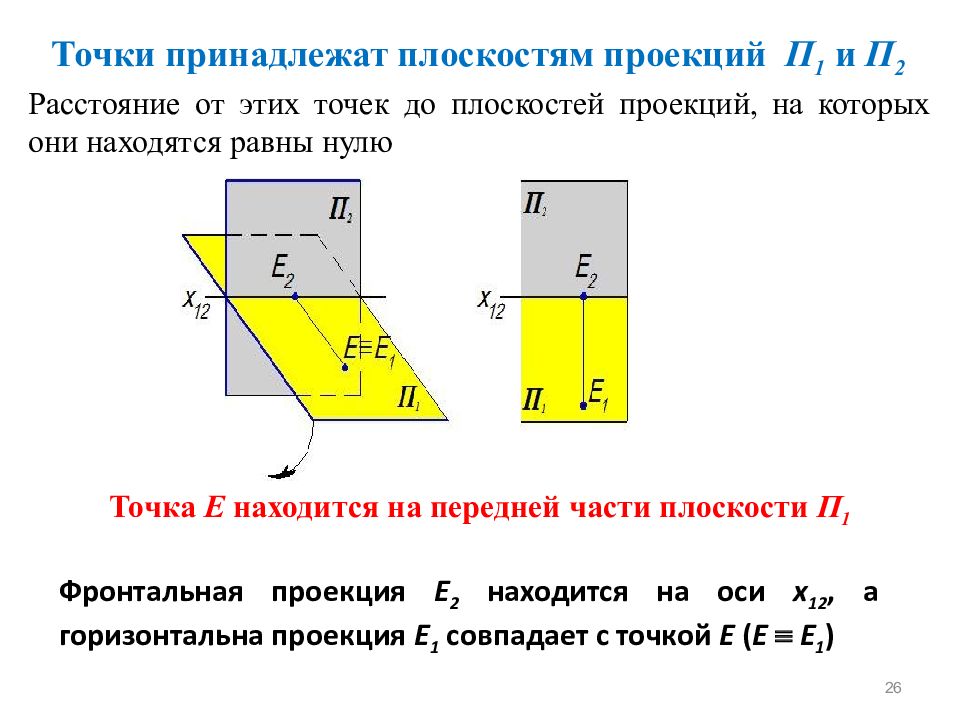
26 Точки принадлежат плоскостям проекций П 1 и П 2 Расстояние от этих точек до плоскостей проекций, на которых они находятся равны нулю Точка E находится на передней части плоскости П 1 Фронтальная проекция E 2 находится на оси x 12, а горизонтальна проекция E 1 совпадает с точкой E ( E E 1 )
Слайд 27
27 Точка K лежит на задней части плоскости П 1. Точка L – на верхней части плоскости П 2. Точка M находится на нижней части плоскости П 2. Одна проекция каждой точки K, L, M совпадает с самой точкой, а вторая лежит на оси x 12. Точка N расположена на оси x 12, обе ее проекции N 1 и N 2 совпадают с самой точкой N.
Слайд 28: Прямая линия
28 Прямая линия Линия рассматривается как траектория постоянно движущейся в пространстве точки. Линии могут быть прямыми, ломаными и кривыми
Слайд 29
29 Проекции прямой линии l ( A, B ) A l B l Проекция прямой линии в общем случае может быть определена, если заданы проекции двух ее точек
Слайд 30
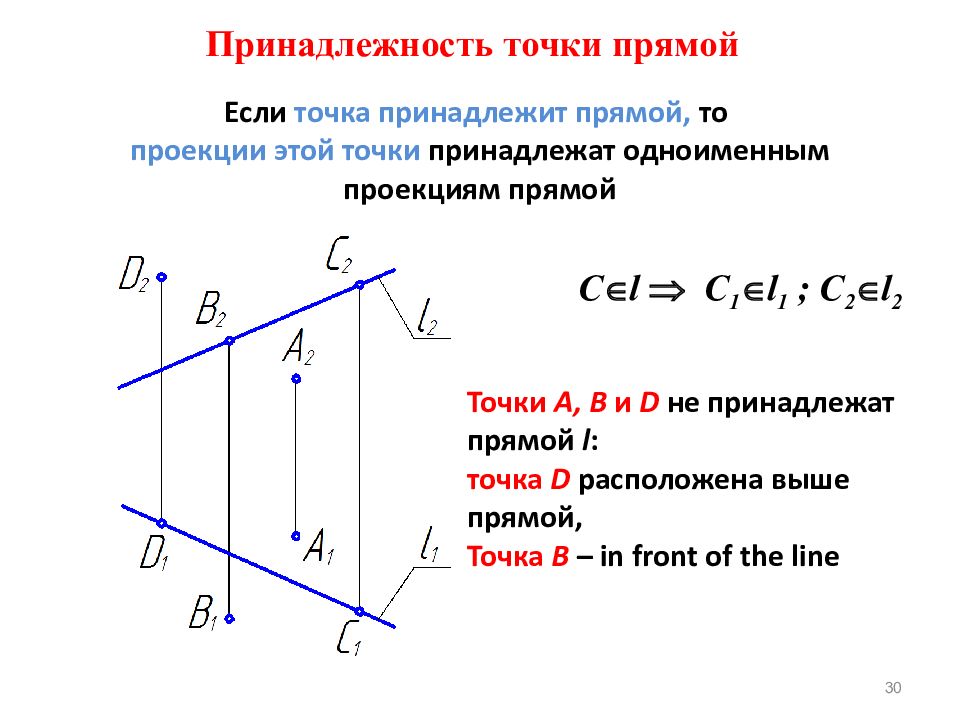
30 Принадлежность точки прямой Если точка принадлежит прямой, то проекции этой точки принадлежат одноименным проекциям прямой C l C 1 l 1 ; C 2 l 2 Точки A, B и D не принадлежат прямой l : точка D расположена выше прямой, Точка B – in front of the line
Слайд 31: Положение прямой относительно плоскости проекций
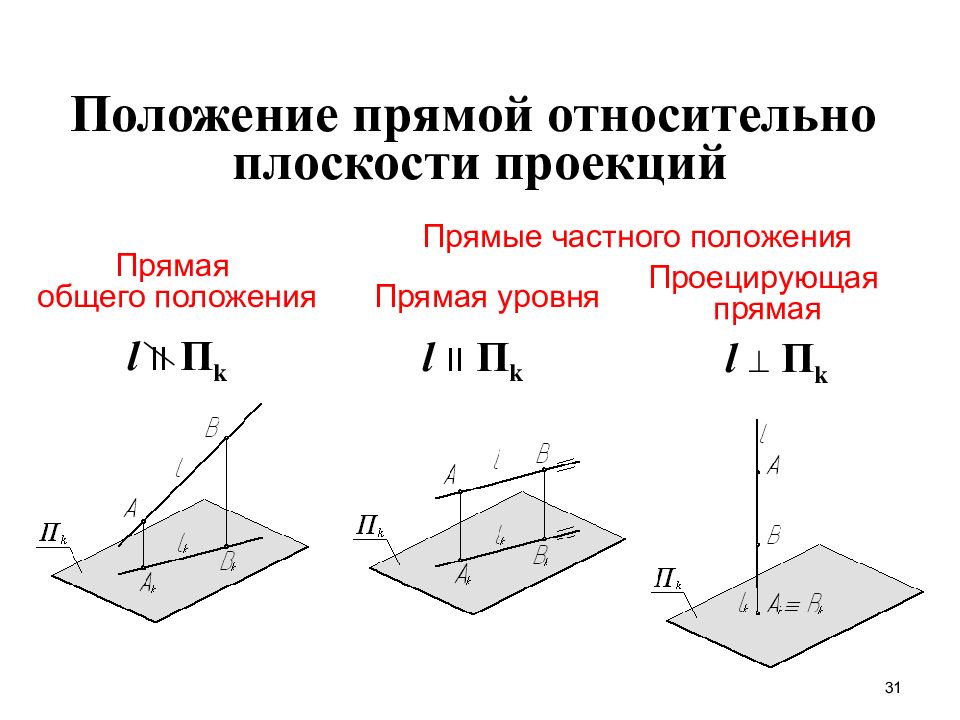
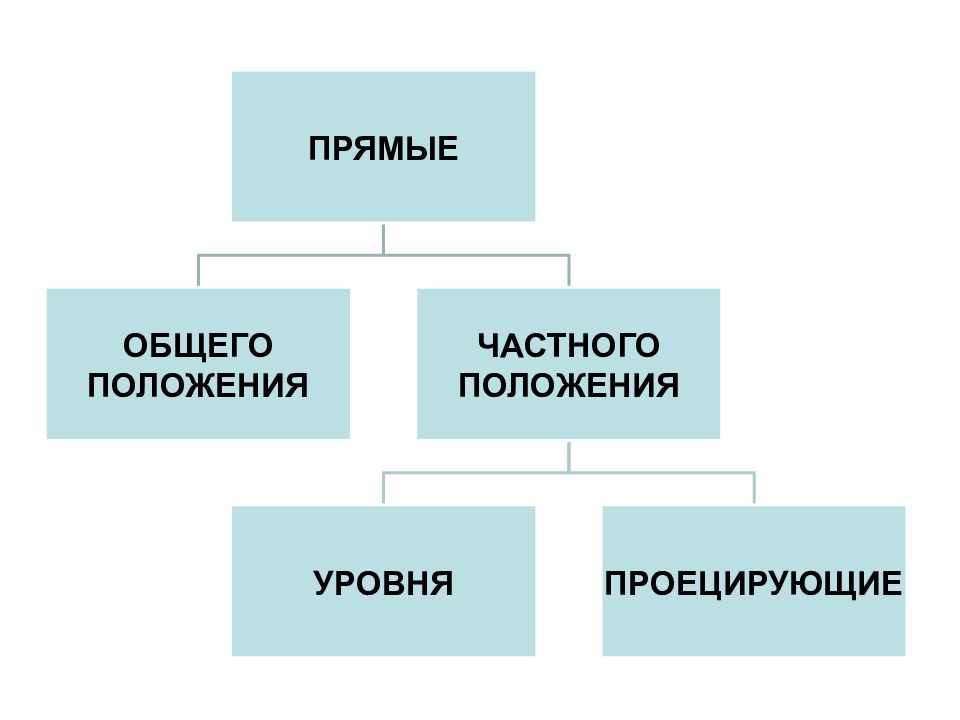
31 Положение прямой относительно плоскости проекций Прямая общего положения Прямые частного положения l II П k l II П k l П k Прямая уровня Проецирующая прямая
Слайд 33
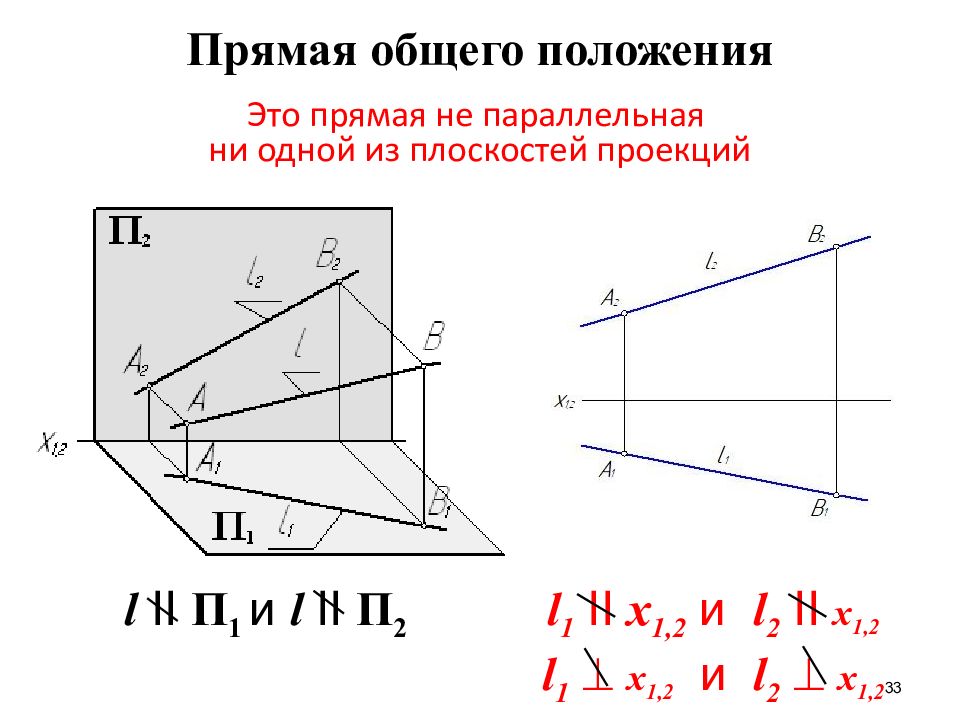
33 l II П 1 и l II П 2 l 1 II x 1,2 и l 2 II x 1,2 l 1 x 1,2 и l 2 x 1,2 Прямая общего положения Это прямая не параллельная ни одной из плоскостей проекций
Слайд 34: Прямые уровня
34 Прямые уровня Это прямые параллельные какой-либо одной плоскости проекций l II П к
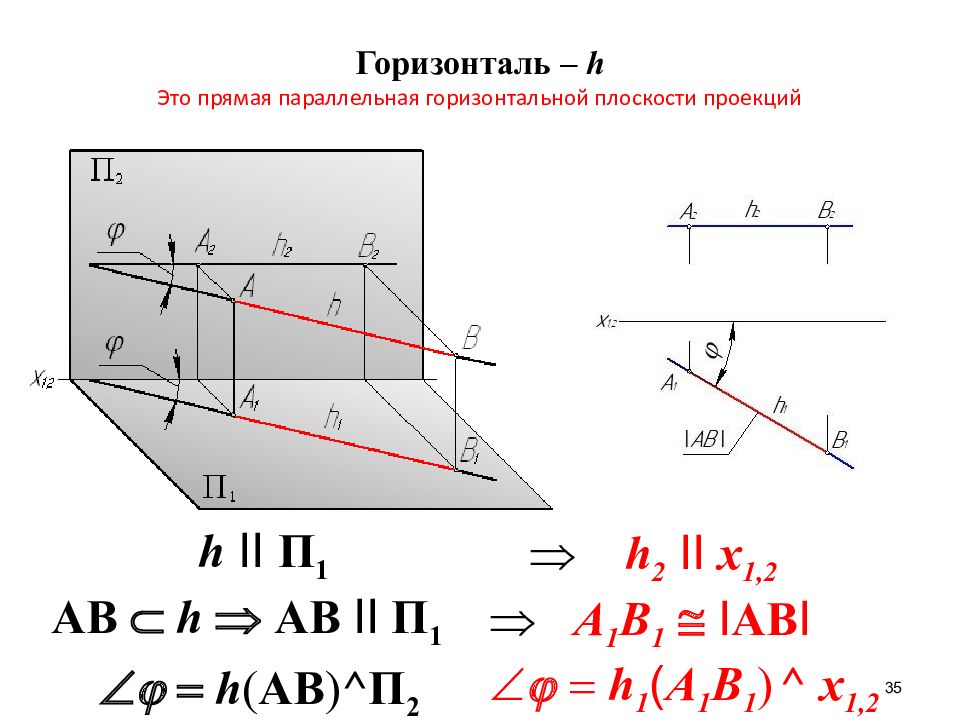
Слайд 35: Горизонталь – h Это прямая параллельная горизонтальной плоскости проекций
35 Горизонталь – h Это прямая параллельная горизонтальной плоскости проекций h II П 1 AB h AB II П 1 h ( AB ) ^ П 2 h 2 II x 1,2 А 1 В 1 I AB I h 1 ( А 1 В 1 ) ^ x 1,2
Слайд 36: Фронталь – f Это прямая параллельная фронтальной плоскости проекций
36 Фронталь – f Это прямая параллельная фронтальной плоскости проекций f II П 2 AB f AB II П 2 f ( AB ) ^ П 1 f 1 II x 1,2 А 2 В 2 I AB I f 2 ( А 2 В 2 ) ^ x 1,2
Слайд 37: Характерная особенность эпюра горизонтали и фронтали – одна из проекций параллельна оси х 1,2
37 Характерная особенность эпюра горизонтали и фронтали – одна из проекций параллельна оси х 1,2
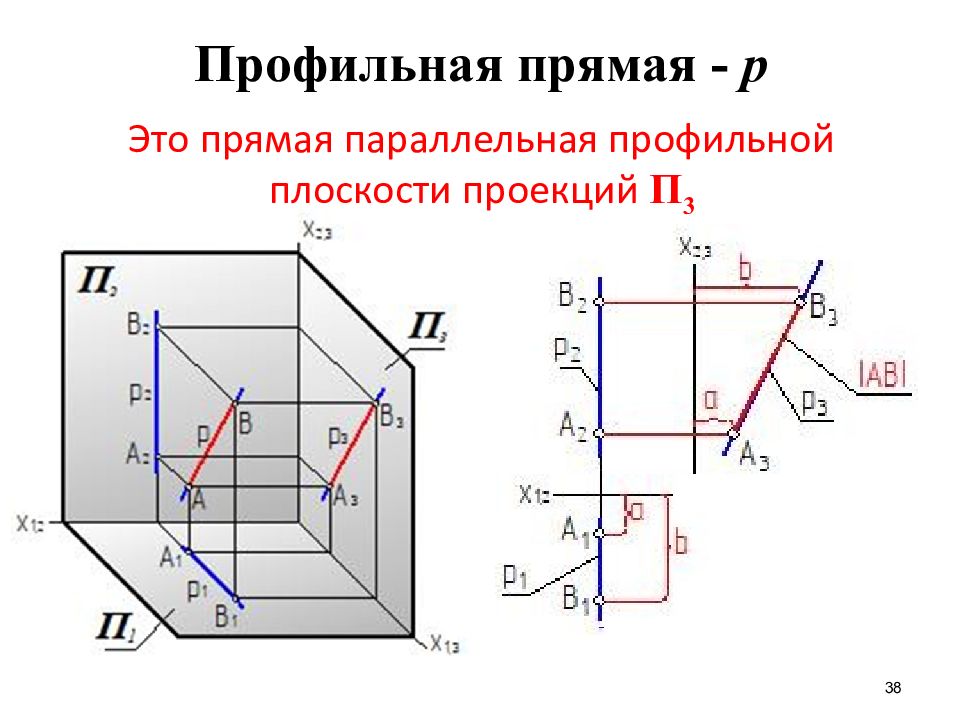
Слайд 38: Профильная прямая - p
38 Профильная прямая - p Это прямая параллельная профильной плоскости проекций П 3
Слайд 39: Проецирующие прямые
39 Проецирующие прямые Это прямые перпендикулярные какой-либо одной плоскости проекций l П к
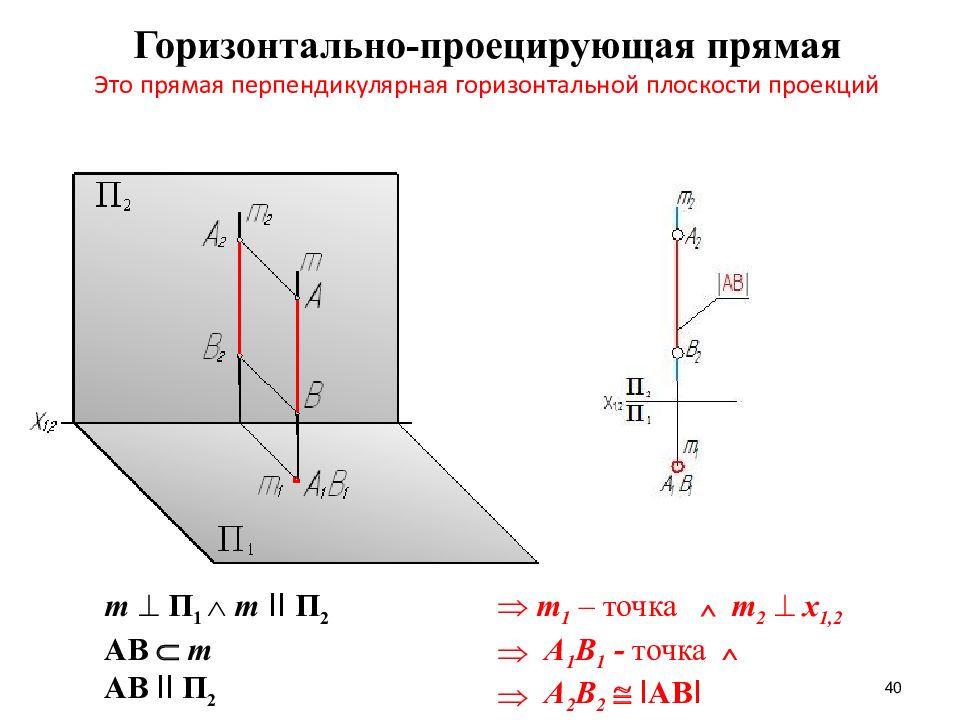
Слайд 40: Горизонтально-проецирующая прямая Это прямая перпендикулярная горизонтальной плоскости проекций
40 Горизонтально-проецирующая прямая Это прямая перпендикулярная горизонтальной плоскости проекций m П 1 m II П 2 AB m AB II П 2 m 1 – точка m 2 x 1,2 А 1 В 1 - точка А 2 В 2 I AB I
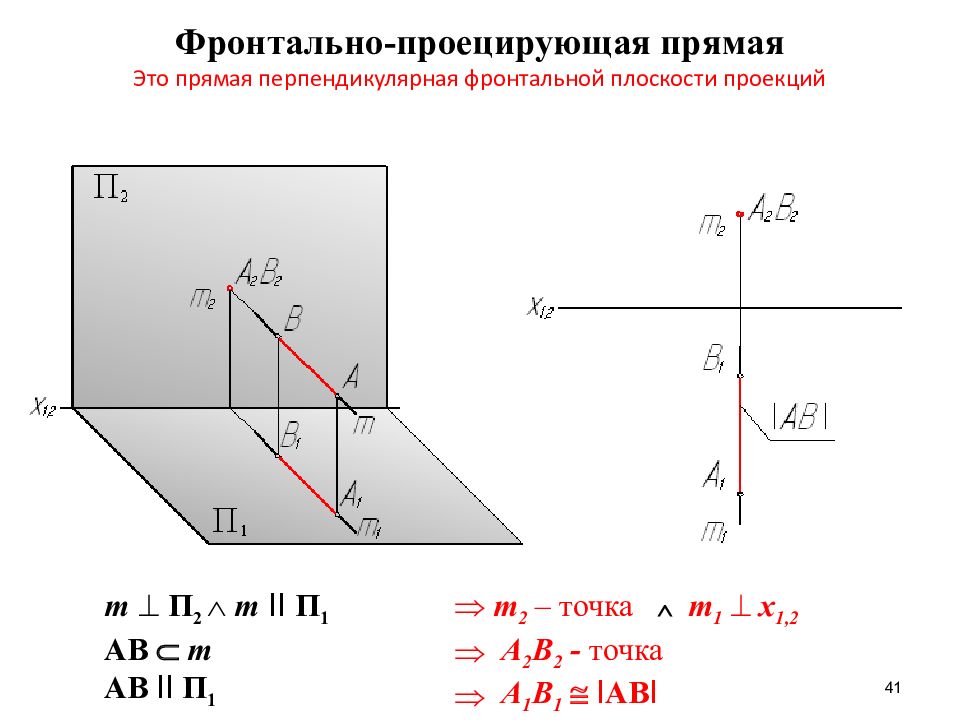
Слайд 41: Фронтально-проецирующая прямая Это прямая перпендикулярная фронтальной плоскости проекций
41 Фронтально-проецирующая прямая Это прямая перпендикулярная фронтальной плоскости проекций m П 2 m II П 1 AB m AB II П 1 m 2 – точка m 1 x 1,2 А 2 В 2 - точка А 1 В 1 I AB I
Слайд 42: Характерная особенность эпюра проецирующей прямой – одна из проекций прямой точка
42 Характерная особенность эпюра проецирующей прямой – одна из проекций прямой точка
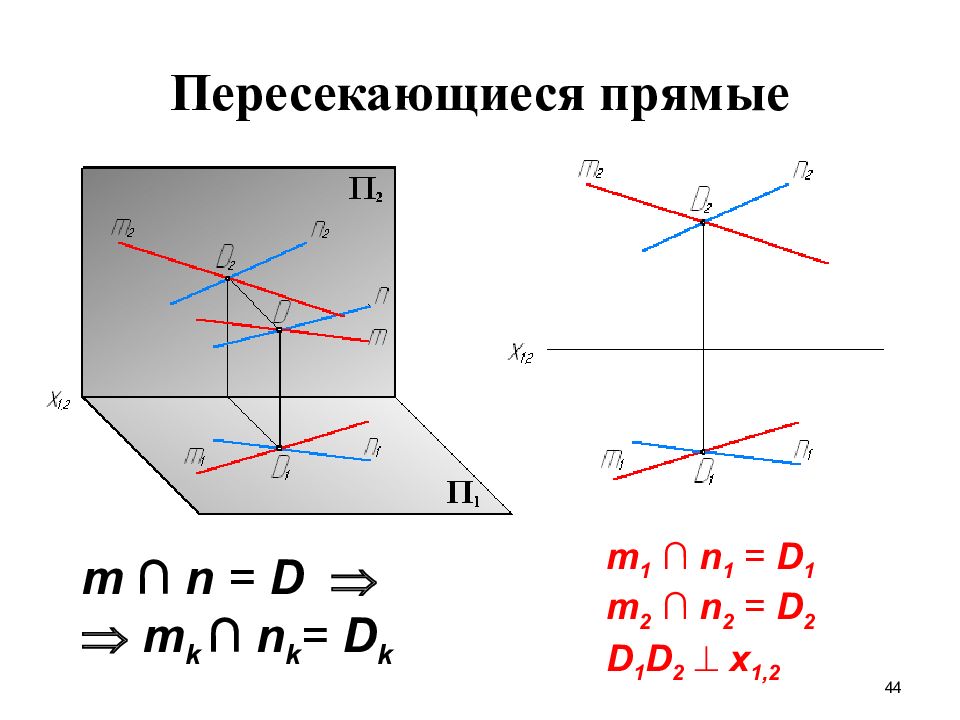
Слайд 44: Пересекающиеся прямые
44 Пересекающиеся прямые m ∩ n = D m k ∩ n k = D k m 1 ∩ n 1 = D 1 m 2 ∩ n 2 = D 2 D 1 D 2 x 1,2
Слайд 45: Параллельные прямые
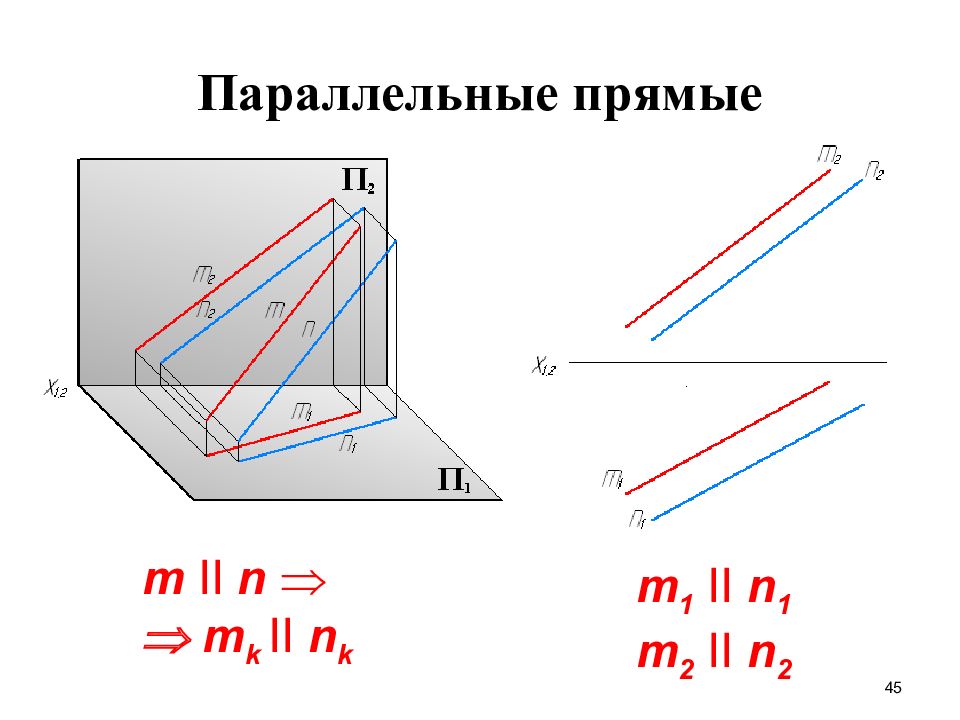
45 Параллельные прямые m II n m k II n k m 1 II n 1 m 2 II n 2
Слайд 46: Скрещивающиеся прямые
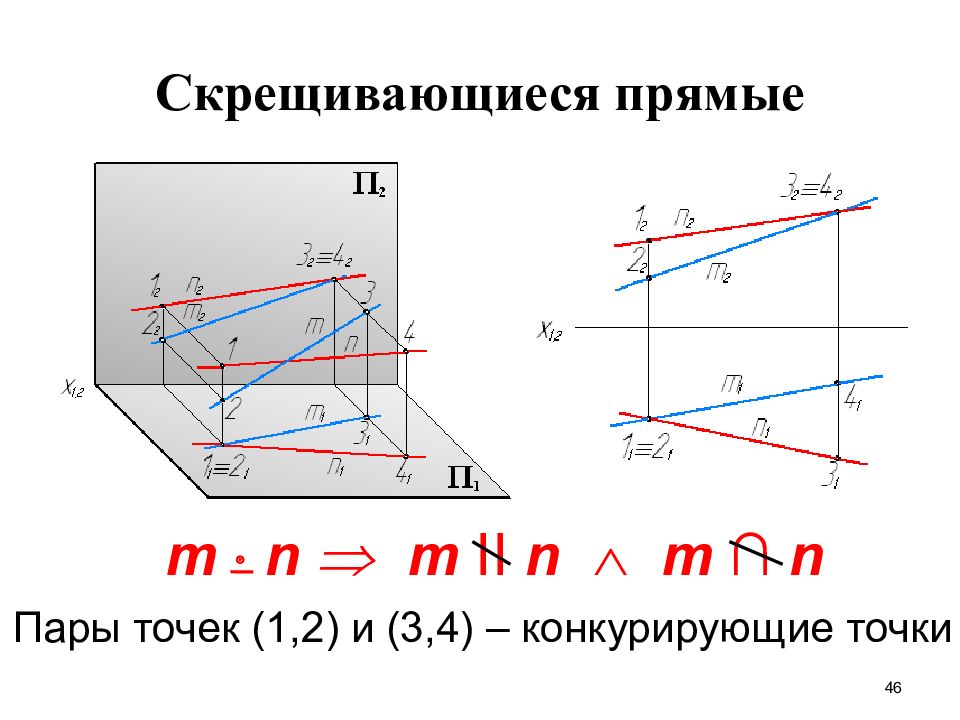
46 Скрещивающиеся прямые m n m II n m ∩ n Пары точек ( 1,2 ) и ( 3,4 ) – конкурирующие точки
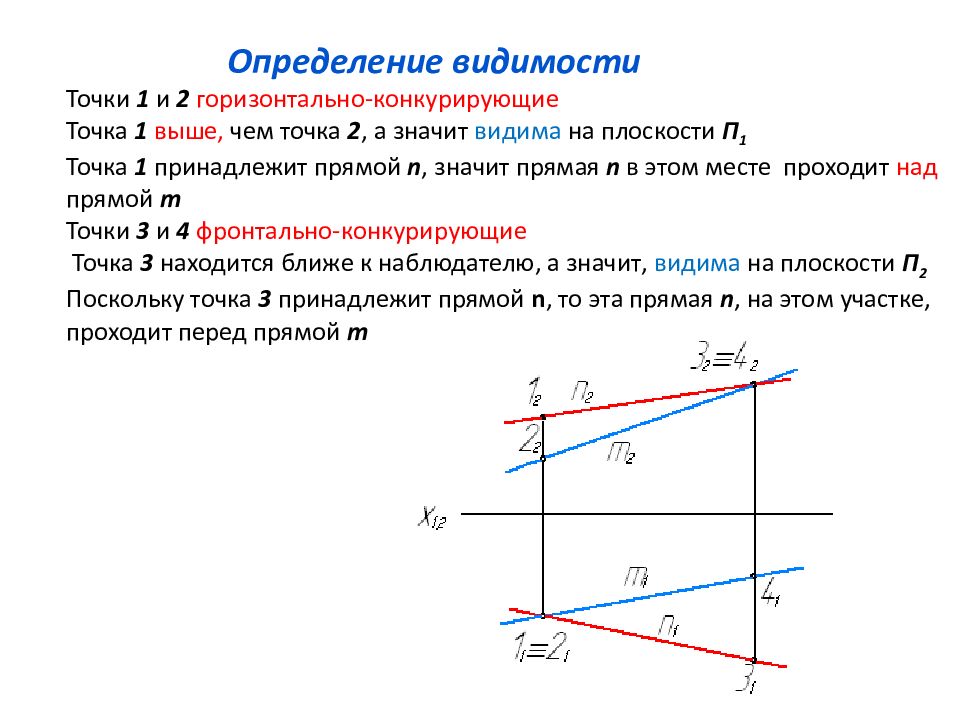
Слайд 47: Определение видимости Точки 1 и 2 горизонтально-конкурирующие Точка 1 выше, чем точка 2, а значит видима на плоскости П 1 Точка 1 принадлежит прямой n, значит прямая n в этом месте проходит над прямой m Точки 3 и 4 фронтально-конкурирующие Точка 3 находится ближе к наблюдателю, а значит, видима на плоскости П 2 Поскольку точка 3 принадлежит прямой n, то эта прямая n, на этом участке, проходит перед прямой m
Слайд 51: Способы задания плоскости
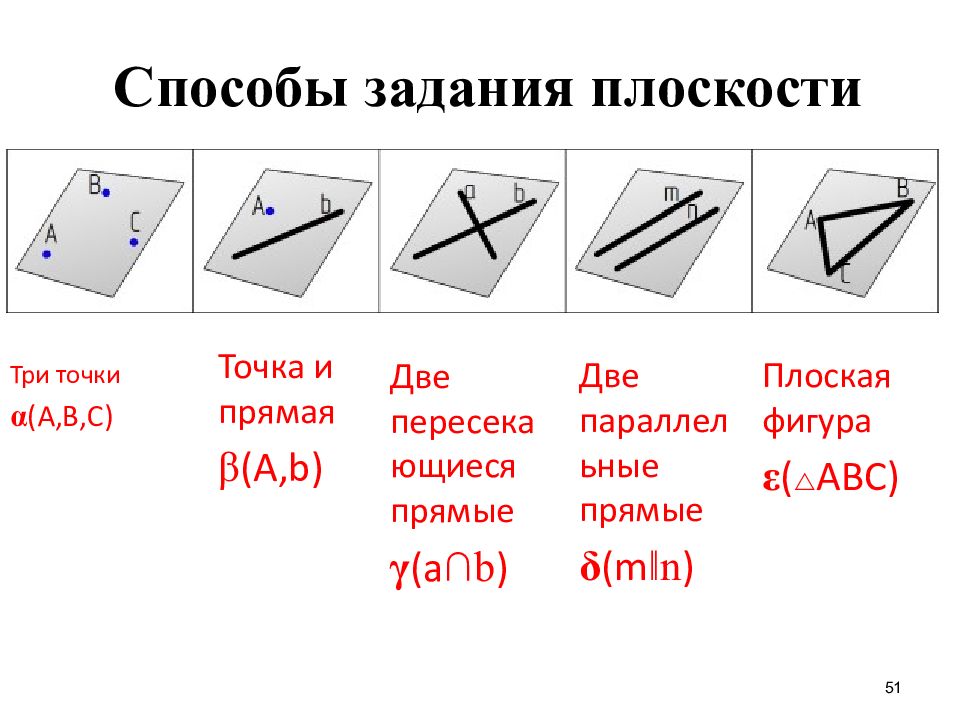
Три точки α (А,В,С) 51 Способы задания плоскости Две параллельные прямые δ ( m ‖n ) Точка и прямая β (А, b ) Плоская фигура ε ( АВС) Две пересекающиеся прямые γ ( a ∩b )
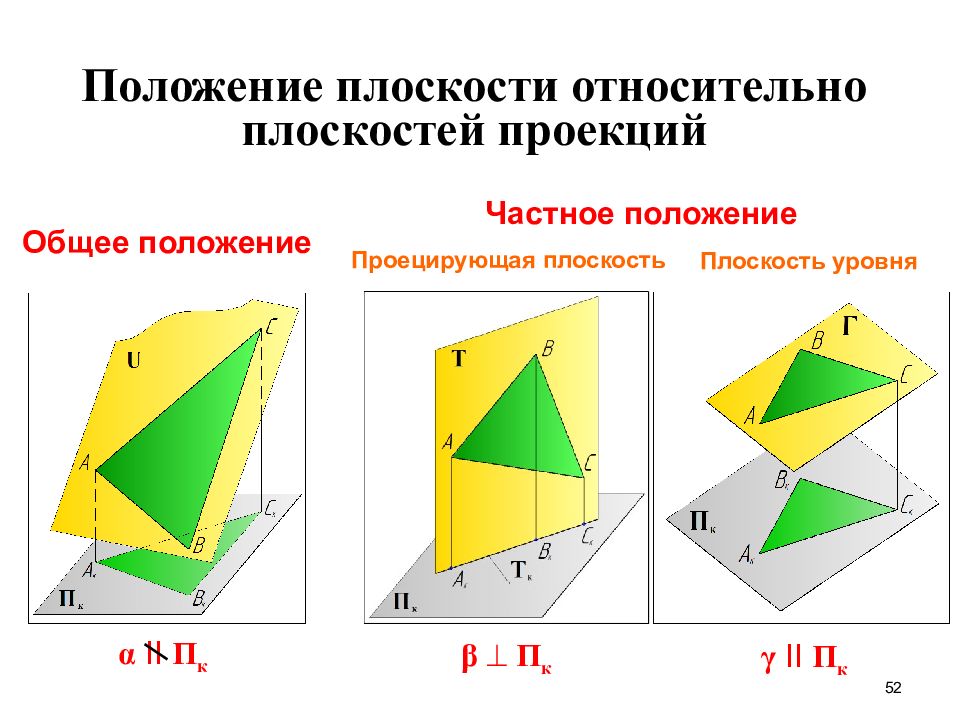
Слайд 52: Положение плоскости относительно плоскостей проекций
52 α II П к Общее положение Частное положение β П к γ II П к Проецирующая плоскость Плоскость уровня Положение плоскости относительно плоскостей проекций
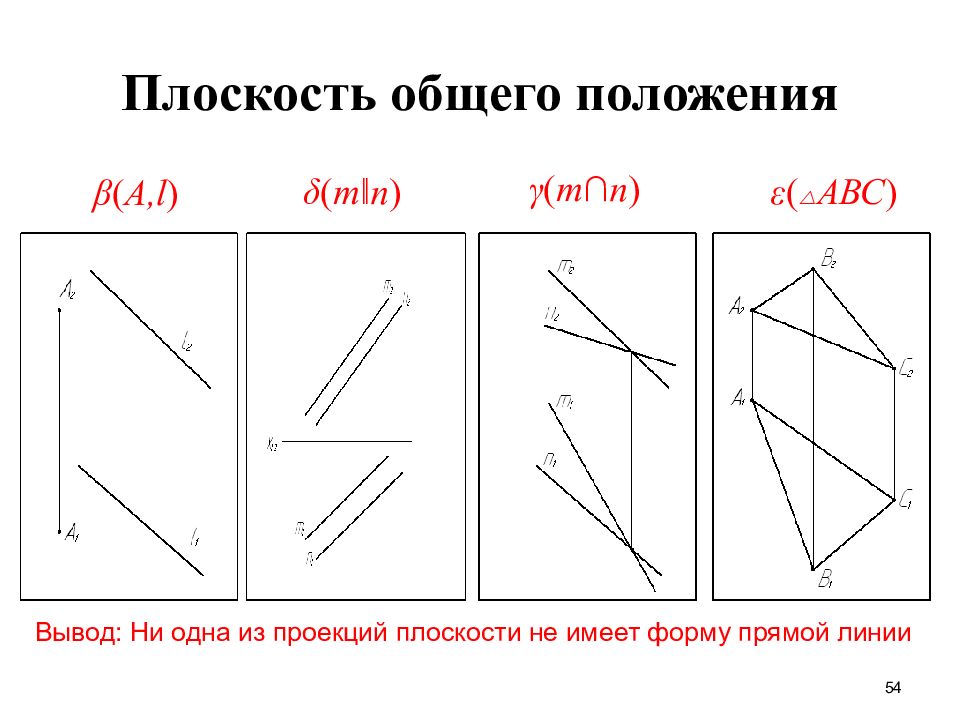
Слайд 54: Плоскость общего положения
54 Плоскость общего положения Вывод: Ни одна из проекций плоскости не имеет форму прямой линии β ( А, l ) γ ( m ∩ n ) δ ( m ‖ n ) ε ( АВС )
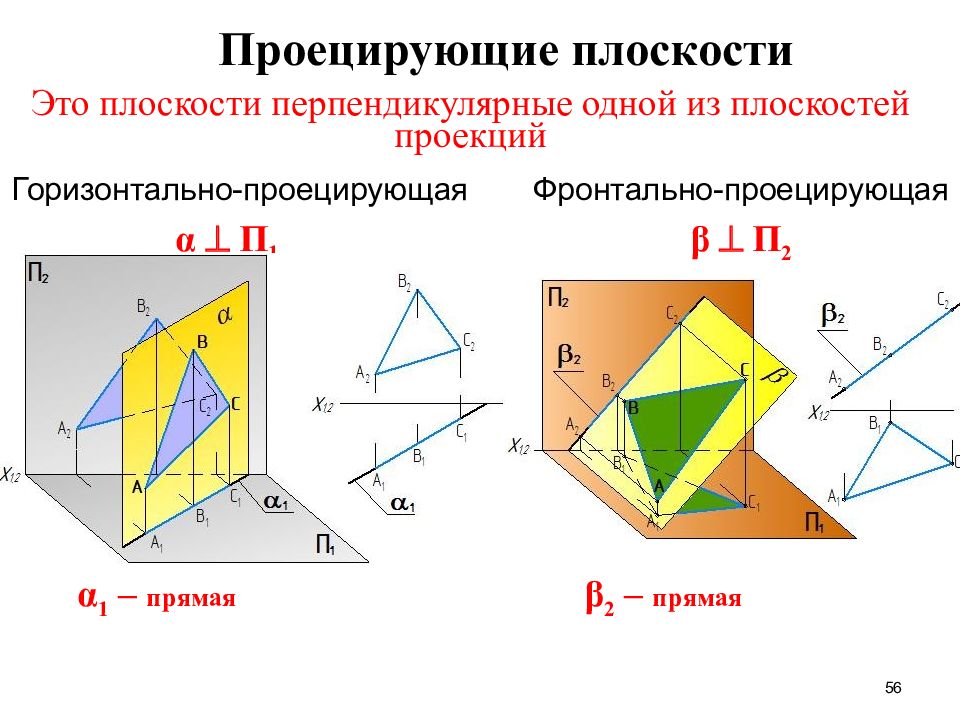
Слайд 56: Это плоскости перпендикулярные одной из плоскостей проекций
56 Это плоскости перпендикулярные одной из плоскостей проекций Горизонтально-проецирующая Фронтально-проецирующая α 1 – прямая β 2 – прямая Проецирующие плоскости α П 1 β П 2
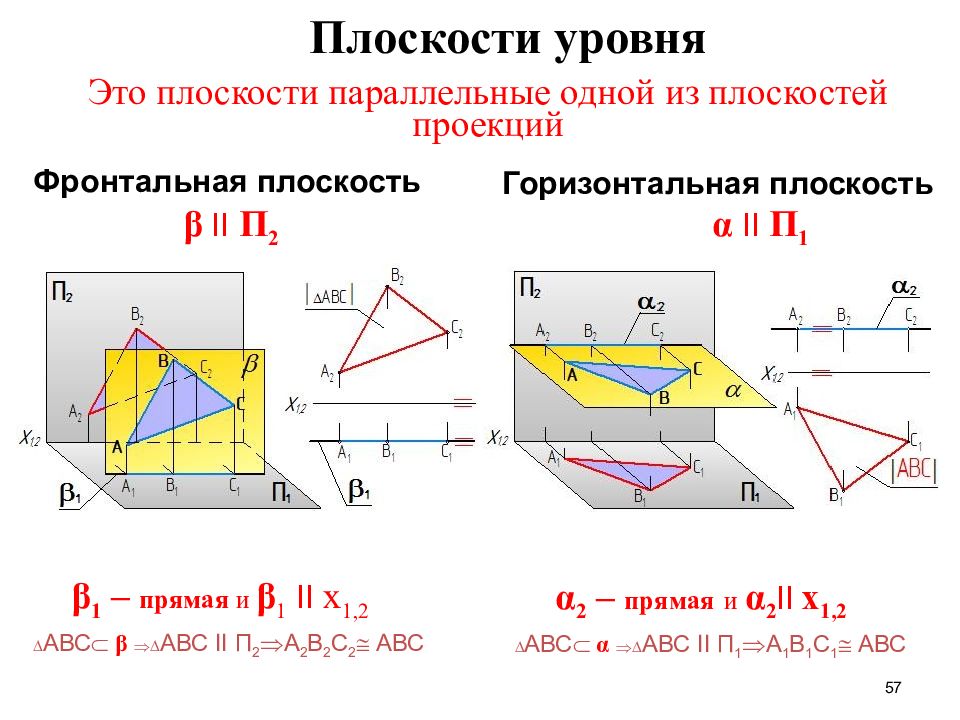
Слайд 57: Это плоскости параллельные одной из плоскостей проекций
57 Это плоскости параллельные одной из плоскостей проекций Горизонтальная плоскость Фронтальная плоскость Плоскости уровня β II П 2 α II П 1 α 2 – прямая и α 2 II x 1,2 β 1 – прямая и β 1 II x 1,2 АВС α АВС II П 1 А 1 В 1 С 1 АВС АВС β АВС II П 2 А 2 В 2 С 2 АВС
Слайд 59
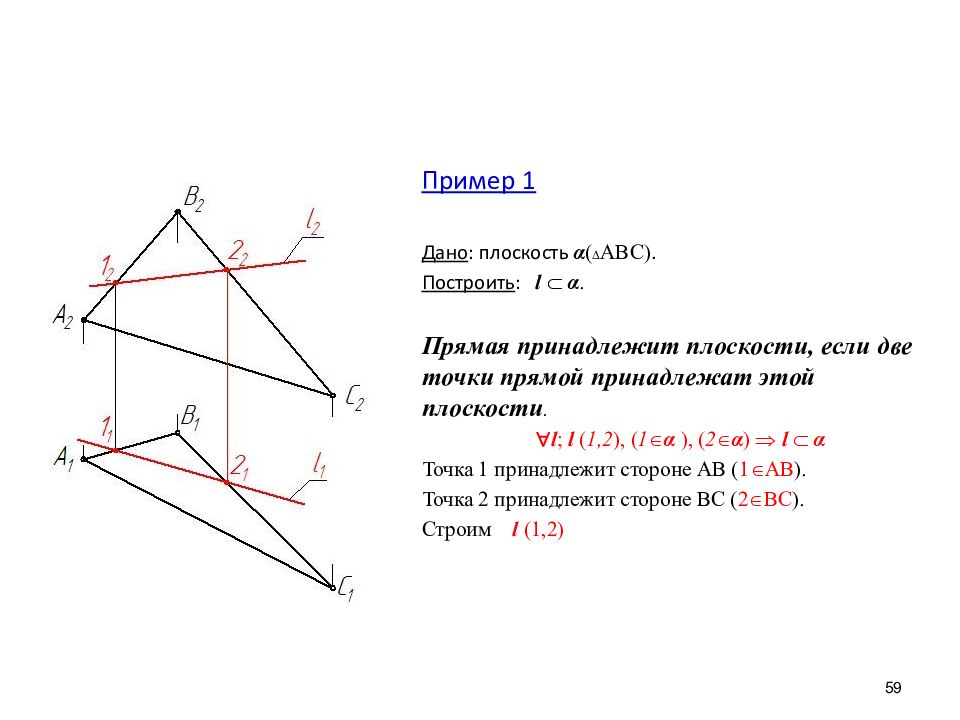
59 Пример 1 Дано : плоскость α АВС . Построить : l α. Прямая принадлежит плоскости, если две точки прямой принадлежат этой плоскости. l ; l ( 1,2 ), ( 1 α ), ( 2 α ) l α Точка 1 принадлежит стороне АВ ( 1 АВ ). Точка 2 принадлежит стороне ВС ( 2 ВС ). Строим l (1,2 )
Слайд 60
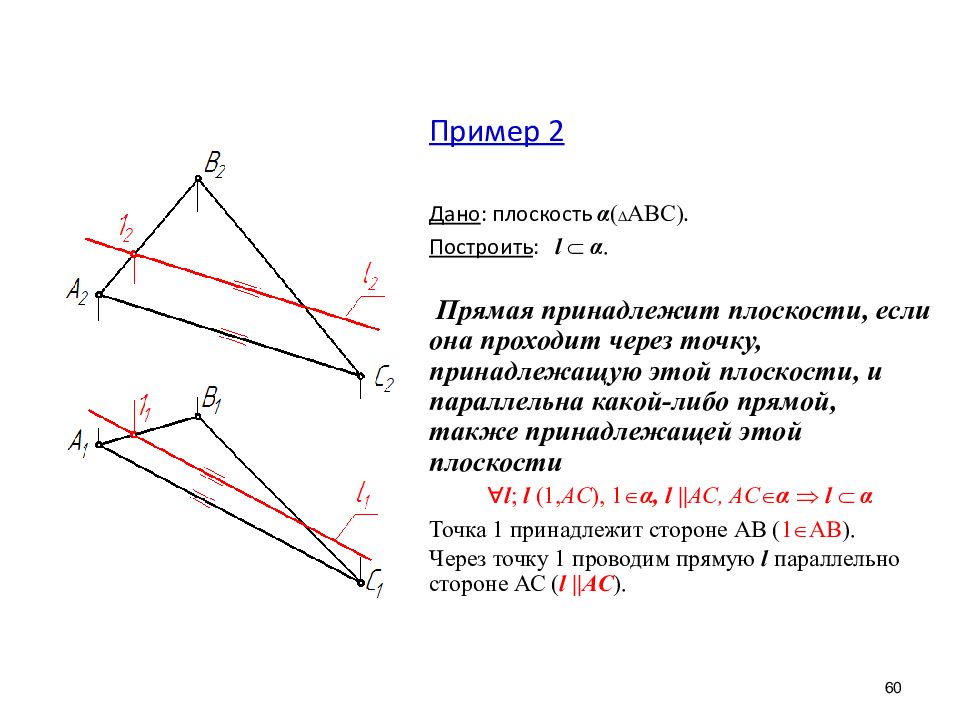
60 Пример 2 Дано : плоскость α АВС . Построить : l α. Прямая принадлежит плоскости, если она проходит через точку, принадлежащую этой плоскости, и параллельна какой-либо прямой, также принадлежащей этой плоскости l ; l (1, AC ), 1 α, l || AC, AC α l α Точка 1 принадлежит стороне АВ ( 1 АВ ). Через точку 1 проводим прямую l параллельно стороне АС ( l ||AC ).
Слайд 62: Горизонталь плоскости
62 Горизонталь плоскости Дано : Плоскость α АВС Построить : h α h 1 h 2 x 1,2 Задаем h ( А,1 ); 1 ВС Строим h 1 ( А 1, 1 1 ) Это прямая, принадлежащая плоскости, и параллельная горизонтальной плоскости проекций
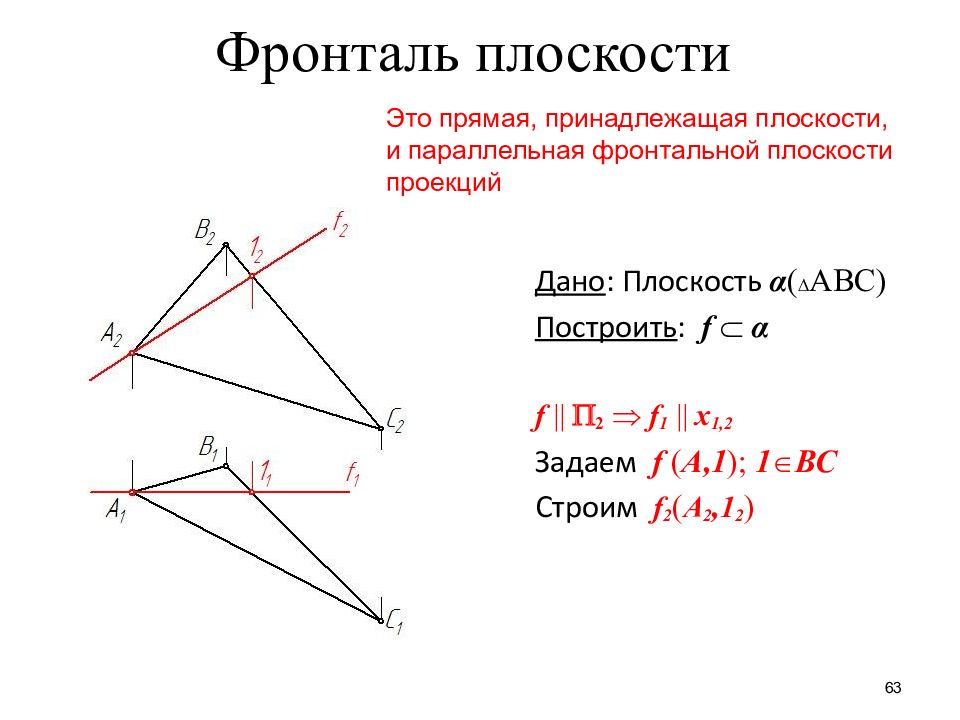
Слайд 63: Фронталь плоскости
63 Фронталь плоскости Дано : Плоскость α АВС Построить : f α f 2 f 1 x 1,2 Задаем f ( А,1 ); 1 ВС Строим f 2 ( А 2, 1 2 ) Это прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций
Слайд 65
65 Точка принадлежит плоскости, если она принадлежит прямой, принадлежащей этой плоскости А α А l, l α
Слайд 66
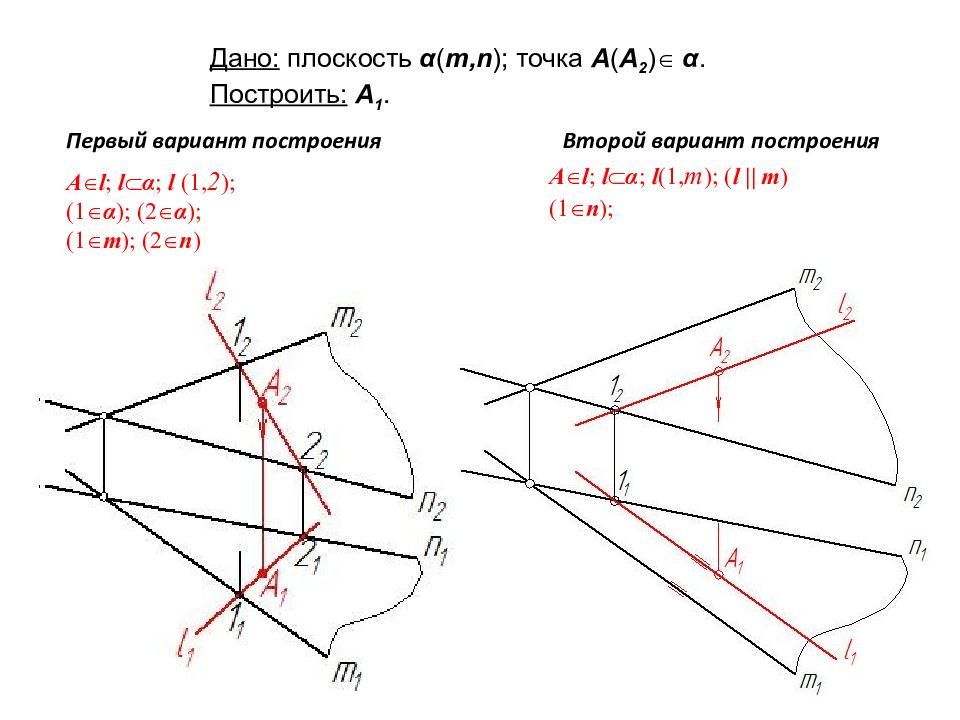
66 А l ; l α ; l (1, 2 ) ; ( 1 α ); (2 α ); ( 1 m ); (2 n ) А l ; l α ; l (1, m ) ; ( l || m ) ( 1 n ); Дано: плоскость α ( m,n ) ; точка А ( А 2 ) α. Построить: А 1. Первый вариант построения Второй вариант построения
Слайд 67
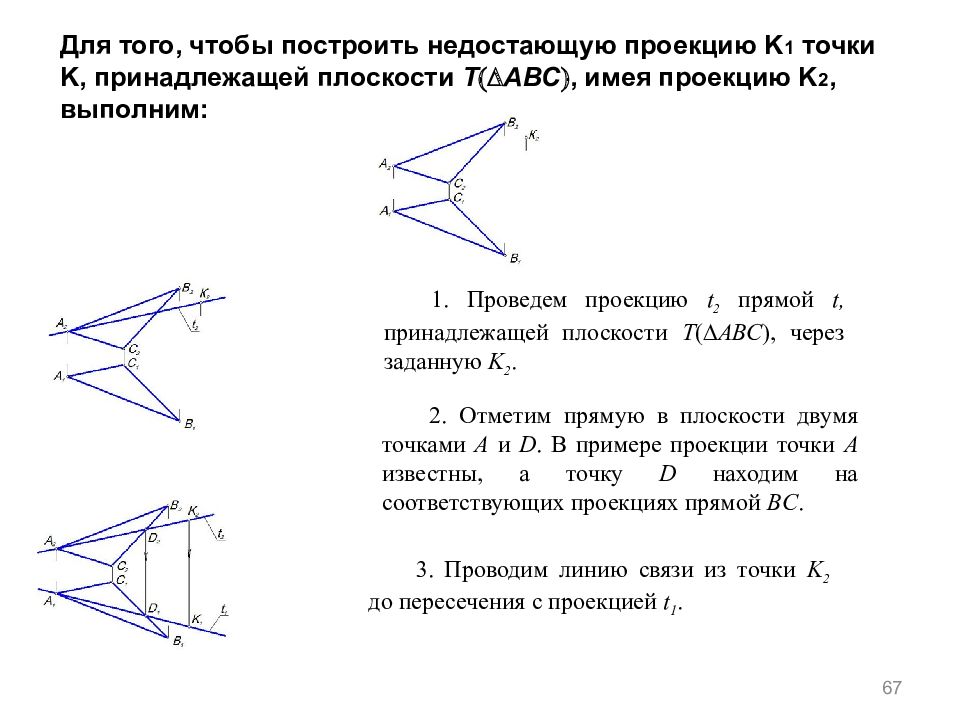
67 Для того, чтобы построить недостающую проекцию K 1 точки K, принадлежащей плоскости Т АВС , имея проекцию K 2, выполним : 1. Проведем проекцию t 2 прямой t, принадлежащей плоскости Т АВС , через заданную K 2. 2. Отметим прямую в плоскости двумя точками A и D. В примере проекции точки A известны, а точку D находим на соответствующих проекциях прямой BC. 3. Проводим линию связи из точки K 2 до пересечения с проекцией t 1.
Слайд 68: Взаимное положение двух плоскостей
68 Взаимное положение двух плоскостей
Слайд 70
70 Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Т ( a ∩ b ) ; P ( c ∩ d ) ; a II c ; b II d ; T II P
Слайд 72
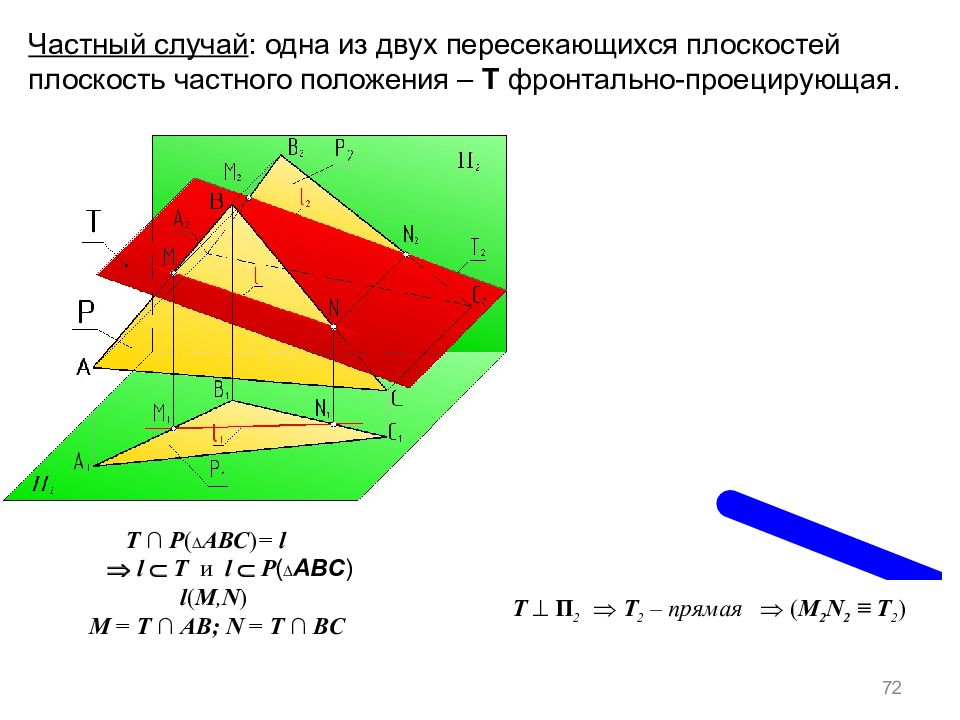
72 Т ∩ P ( ∆ АВС ) = l l Т и l P ( ∆ АВС ) l ( M, N ) M = Т ∩ AB ; N = Т ∩ BC Т П 2 Т 2 – прямая ( M 2 N 2 ≡ Т 2 ) Частный случай : одна из двух пересекающихся плоскостей плоскость частного положения – Т фронтально-проецирующая.
Слайд 73
Линией пересечения плоскостей является прямая, которая должна быть задана двумя точками. Любая из этих двух точек может быть получена: пересечением двух прямых (в каждой из двух заданных плоскостей выбирается по одной прямой и находится точка их пересечения); пересечением прямой с плоскостью (в одной из двух заданных плоскостей выбирается прямая и определяется точка ее пересечения с другой плоскостью); пересечением трех плоскостей (вводится дополнительная третья плоскость, и строится точка пересечения двух заданных плоскостей и дополнительной).
Слайд 74
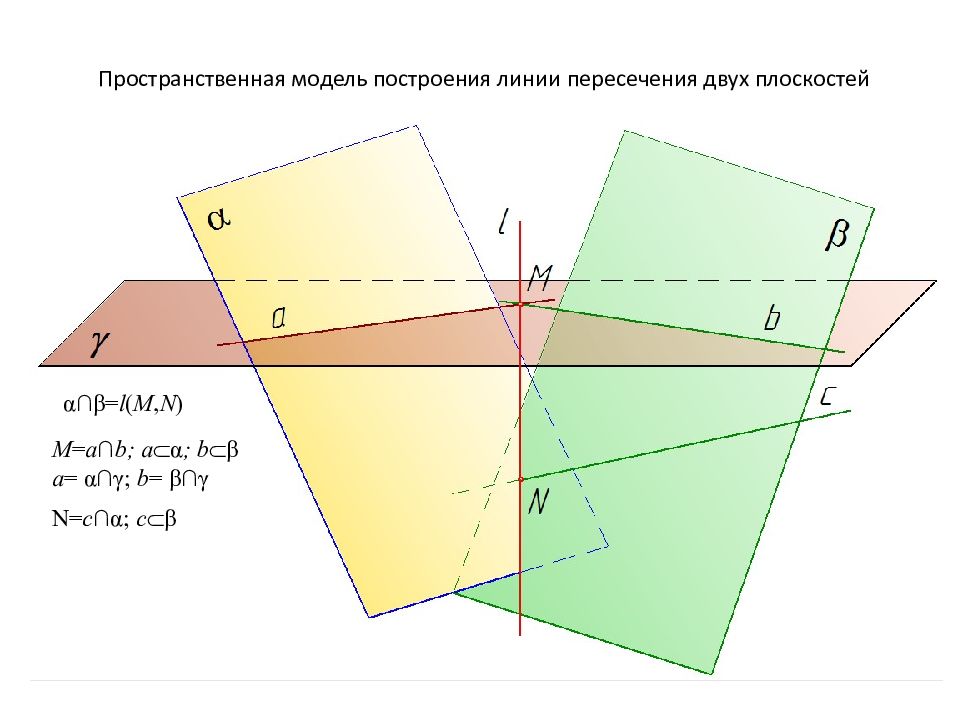
Пространственная модель построения линии пересечения двух плоскостей α∩β = l ( M, N ) M = a ∩ b ; a α ; b β a = α∩γ ; b = β∩γ N= c ∩ α ; c β
Слайд 75
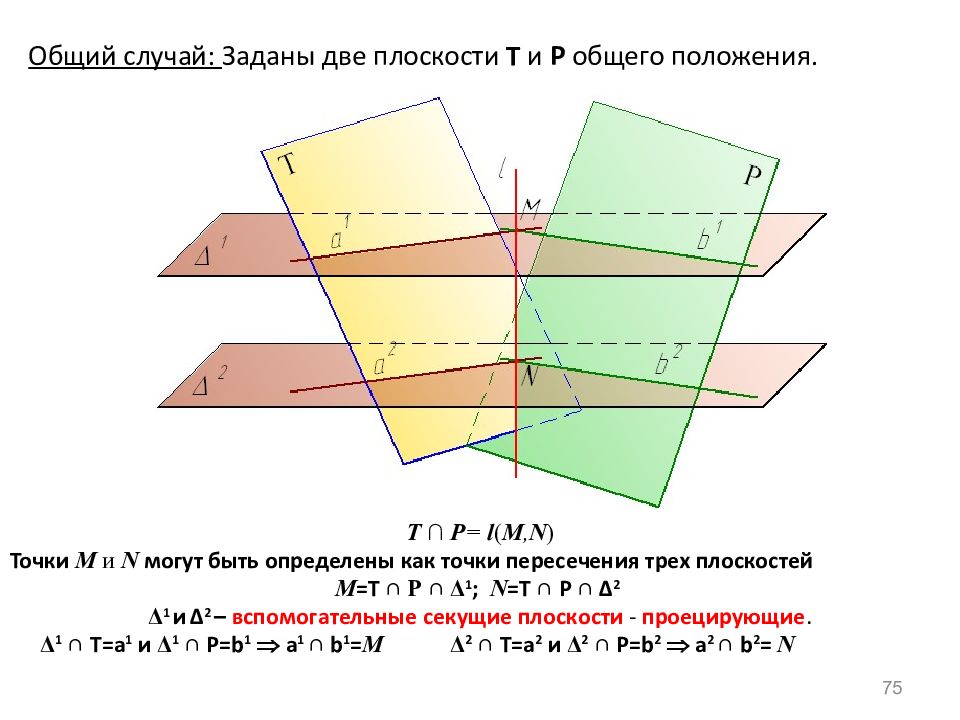
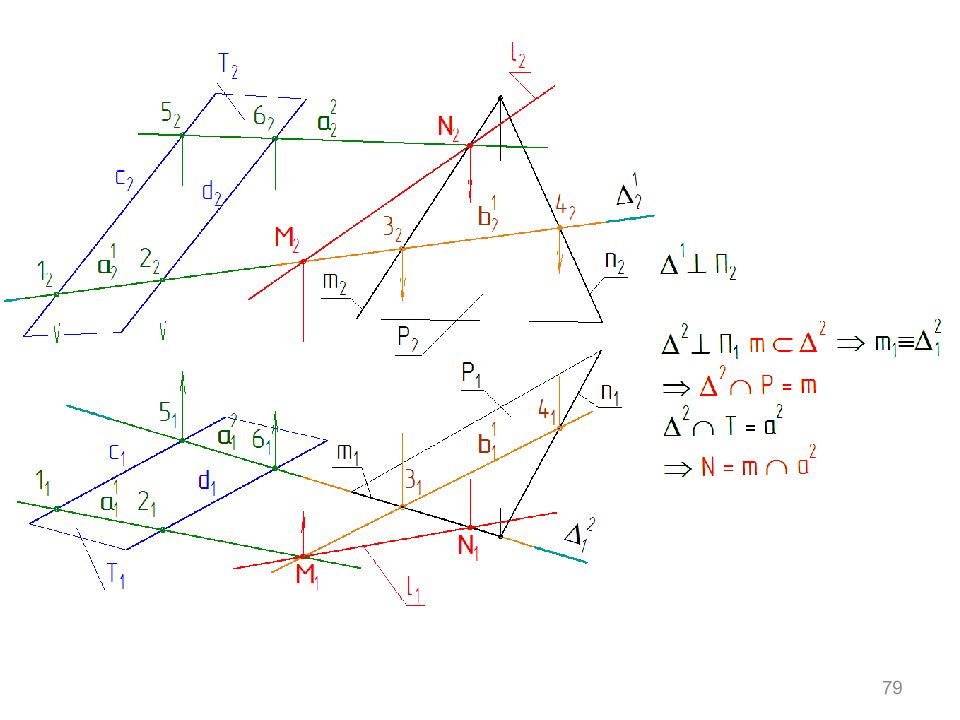
75 Т ∩ P = l ( M, N ) Точки M и N могут быть определены как точки пересечения трех плоскостей М =Т ∩ Р ∩ Δ 1 ; N =Т ∩ Р ∩ Δ 2 Δ 1 и Δ 2 – вспомогательные секущие плоскости - проецирующие. Δ 1 ∩ Т= a 1 и Δ 1 ∩ Р= b 1 a 1 ∩ b 1 = М Δ 2 ∩ Т= a 2 и Δ 2 ∩ Р= b 2 a 2 ∩ b 2 = N Общий случай: Заданы две плоскости Т и Р общего положения.
Слайд 77: Построение точки, принадлежащей линии пересечения двух плоскостей, введением дополнительной секущей плоскости
γ – дополнительная секущая плоскость (проецирующая)
Слайд 78: Построение точки, принадлежащей линии пересечения двух плоскостей, как точки пересечения прямой, принадлежащей одной из заданных плоскостей, с другой заданной плоскостью
Слайд 80: Взаимное положение прямой и плоскости
80 Взаимное положение прямой и плоскости
Слайд 81
81 Прямая по отношению к плоскости может занимать следующие положения: Принадлежать Быть параллельной Пересекать Быть перпендикулярна
Слайд 82
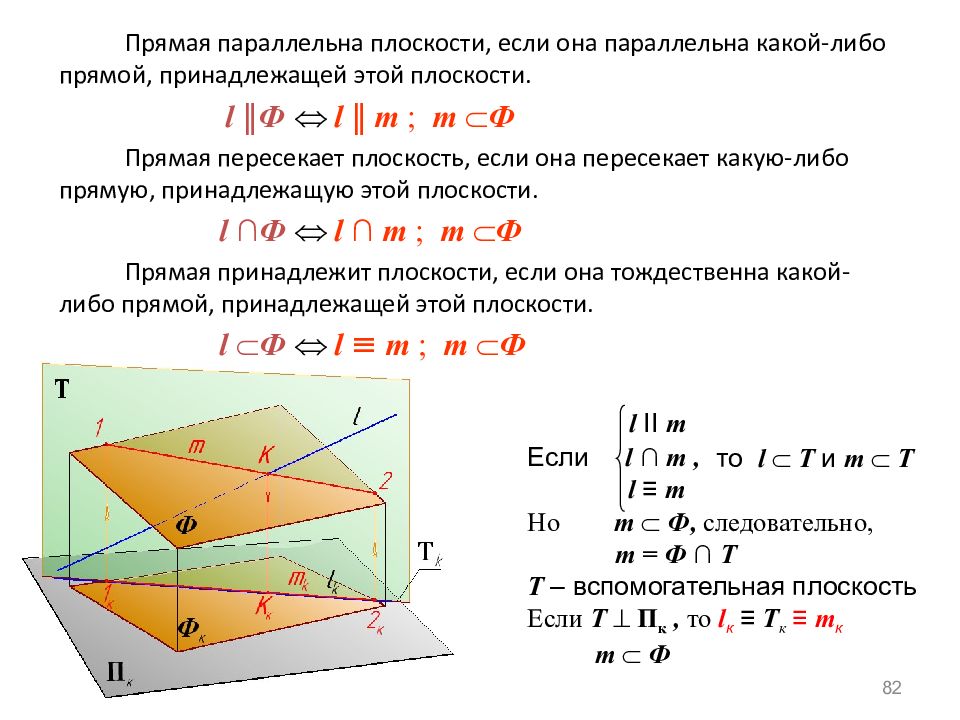
82 Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости. l ‖ Ф l ‖ m ; m Ф Прямая пересекает плоскость, если она пересекает какую-либо прямую, принадлежащую этой плоскости. l ∩ Ф l ∩ m ; m Ф Прямая принадлежит плоскости, если она тождественна какой-либо прямой, принадлежащей этой плоскости. l Ф l ≡ m ; m Ф l II m Если l ∩ m, l ≡ m Но m Ф, следовательно, m = Ф ∩ T T – вспомогательная плоскость Если T П к, то l к ≡ T к ≡ m к m Ф то l T и m T
Слайд 83: Пример 1
83 Пример 1 Дана прямая l. Определить ее положение относительно плоскости АВ С 1.Зададим m 2 ≡ l 2 2. m ( 1,2 ); 1 = m∩ АВ; 2= m ∩ ВС ; 3. Находим m 1. 4. Сравниваем положение проекций m 1 и l 1, m 1 ‖ l 1 5. Вывод: l ‖ Ф
Слайд 84: Построение точки пересечения прямой и плоскости
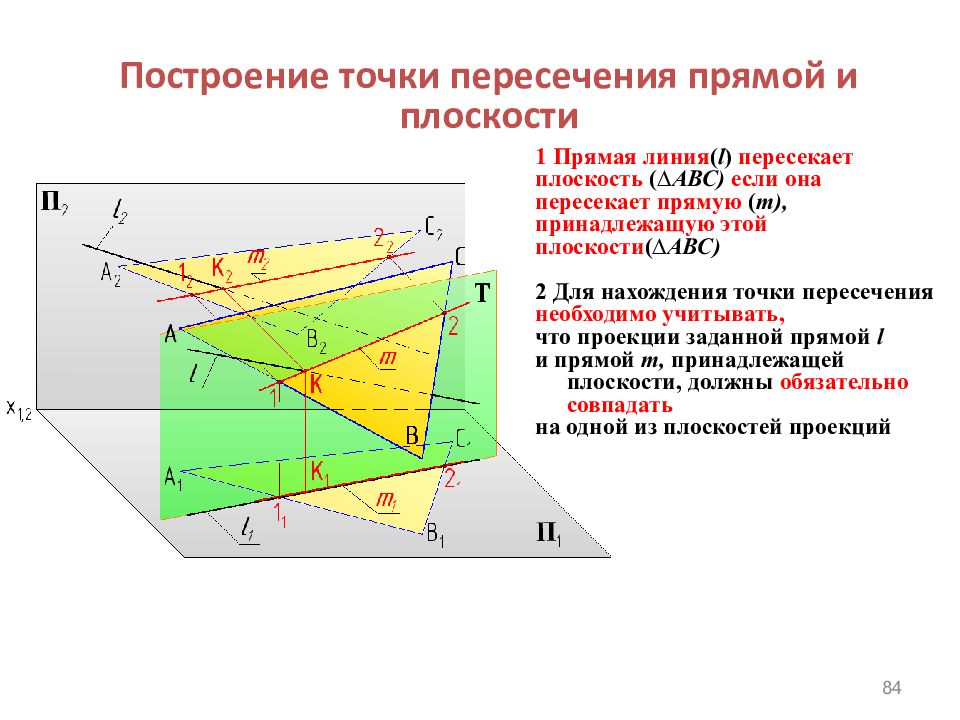
84 Построение точки пересечения прямой и плоскости 1 Прямая линия ( l ) пересекает плоскость ( ∆ АВС ) если она пересекает прямую ( m), принадлежащую этой плоскости ( ∆ АВС ) 2 Для нахождения точки пересечения необходимо учитывать, что проекции заданной прямой l и прямой m, принадлежащей плоскости, должны обязательно совпадать н а одной из плоскостей проекций
Слайд 85: Для нахождения точки пересечения прямой l с плоскостью Ф ( ABC ) выполним :
85 Для нахождения точки пересечения прямой l с плоскостью Ф ( ABC ) выполним : 1. Проведем m, учитывая, что l 1 ≡ m 1 2. Отметим прямую m в плоскости двумя точками m ( 1,2 ); 1 = m∩ АВ; 2= m ∩ ВС 3. Построим m 2 ( 1 2,2 2 ) 4. Сравним положение проекций m 2 и l 2, m 2 ∩ l 2 = К 2 5. Вывод: l ∩ Ф=К – точка пересечения прямой l и плоскости Ф Дана прямая l. Определить ее положение относительно плоскости АВС Пример 2
Слайд 86
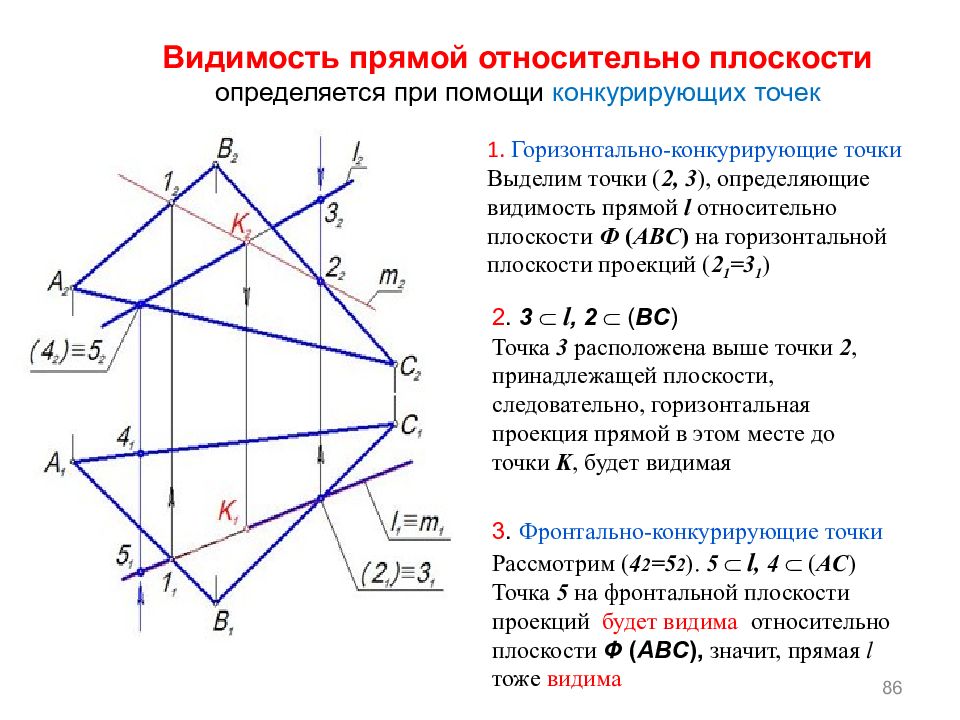
86 Видимость прямой относительно плоскости определяется при помощи конкурирующих точек 2. 3 l, 2 ( BC ) Точка 3 расположена выше точки 2, принадлежащей плоскости, следовательно, горизонтальная проекция прямой в этом месте до точки K, будет видимая 3. Фронтально-конкурирующие точки Рассмотрим ( 4 2 =5 2 ). 5 l, 4 ( AC ) Точка 5 на фронтальной плоскости проекций будет видима относительно плоскости Ф ( ABC ), значит, прямая l тоже видима 1. Горизонтально-конкурирующие точки Выделим точки ( 2, 3 ), определяющие видимость прямой l относительно плоскости Ф ( ABC ) на горизонтальной плоскости проекций ( 2 1 =3 1 )
Последний слайд презентации: НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
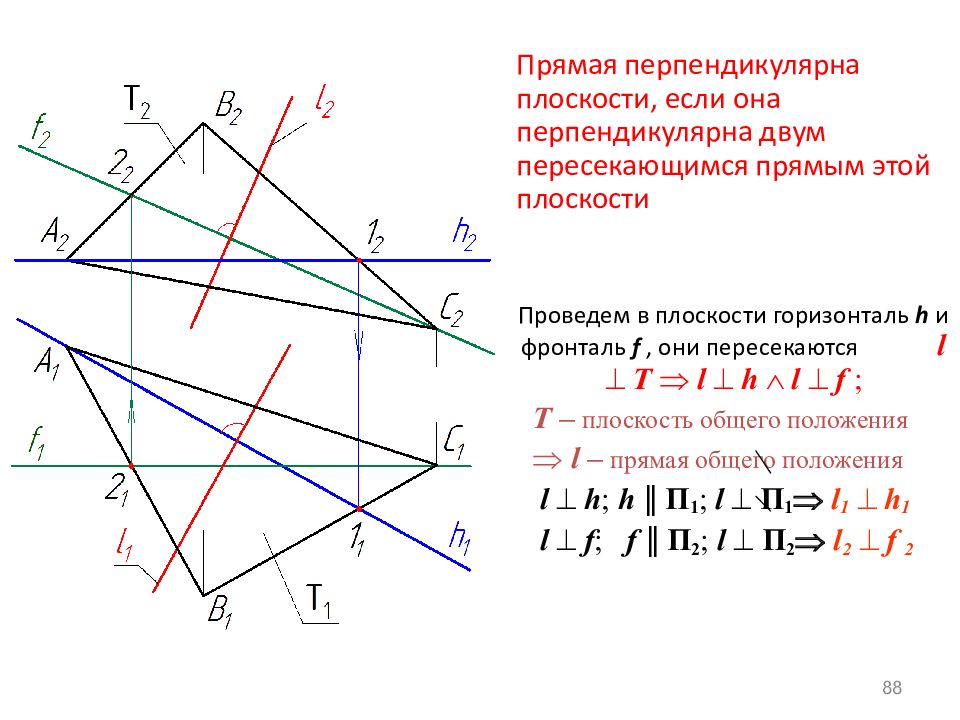
88 Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости Проведем в плоскости горизонталь h и фронталь f, они пересекаются l T l h l f ; Т – плоскость общего положения l – прямая общего положения l h ; h ‖ П 1 ; l П 1 l 1 h 1 l f ; f ‖ П 2 ; l П 2 l 2 f 2