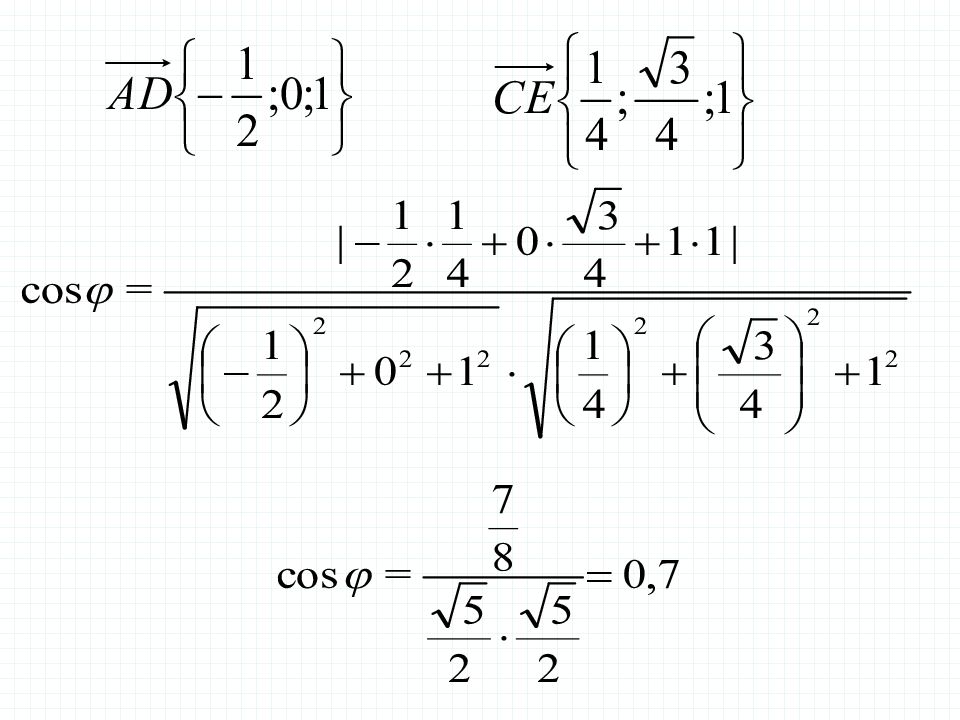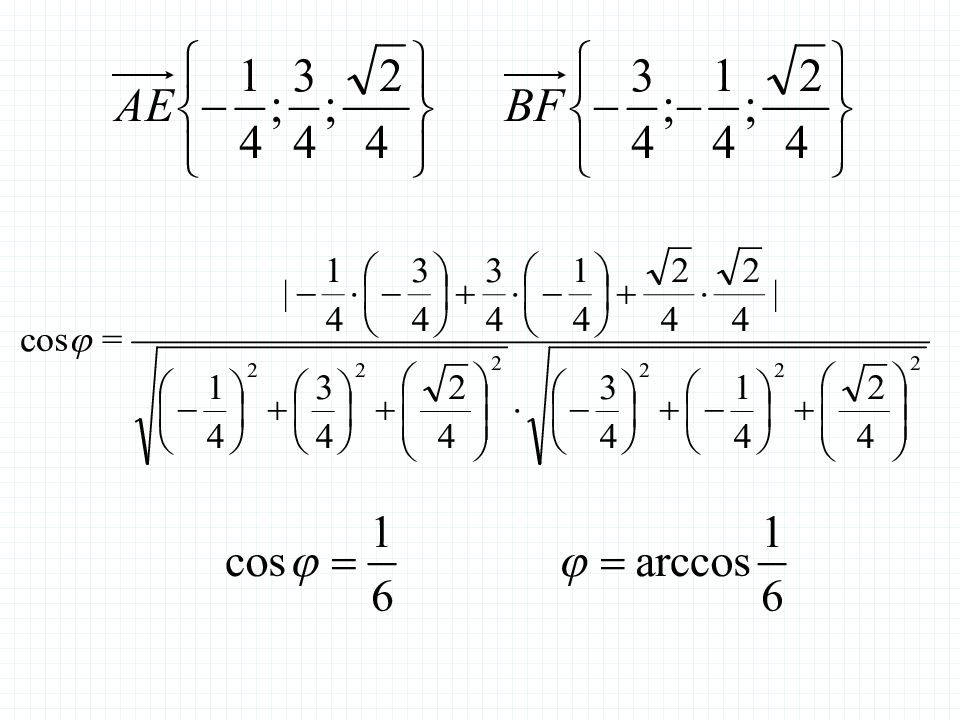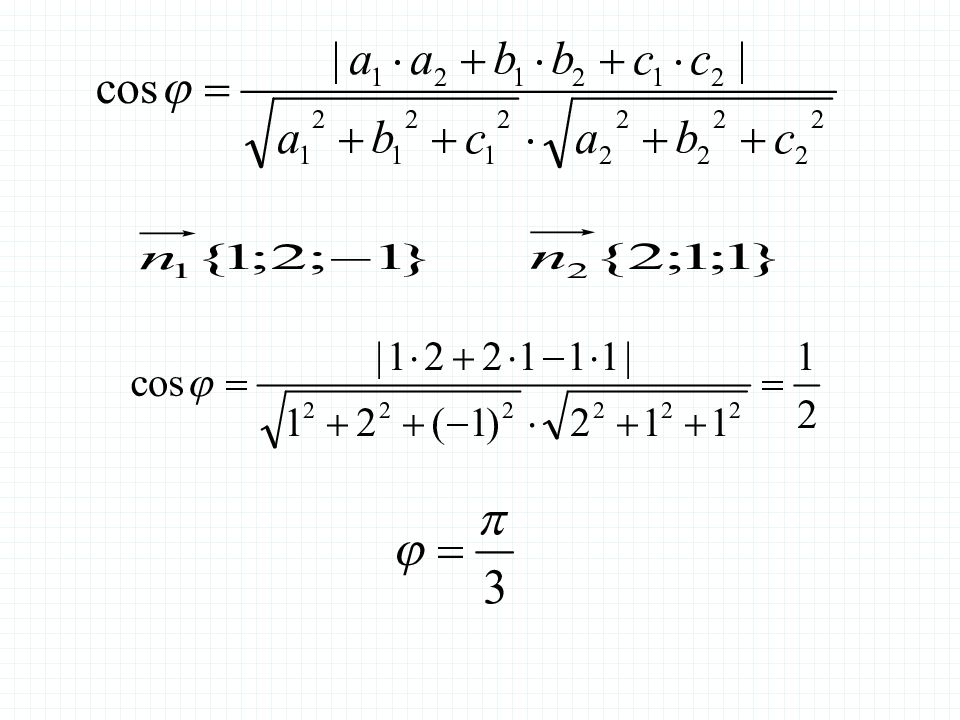Метод координат в задачах С2 Стереометрия
Угол между прямыми - направляющий вектор прямой а - направляющий вектор прямой b - угол между прямыми
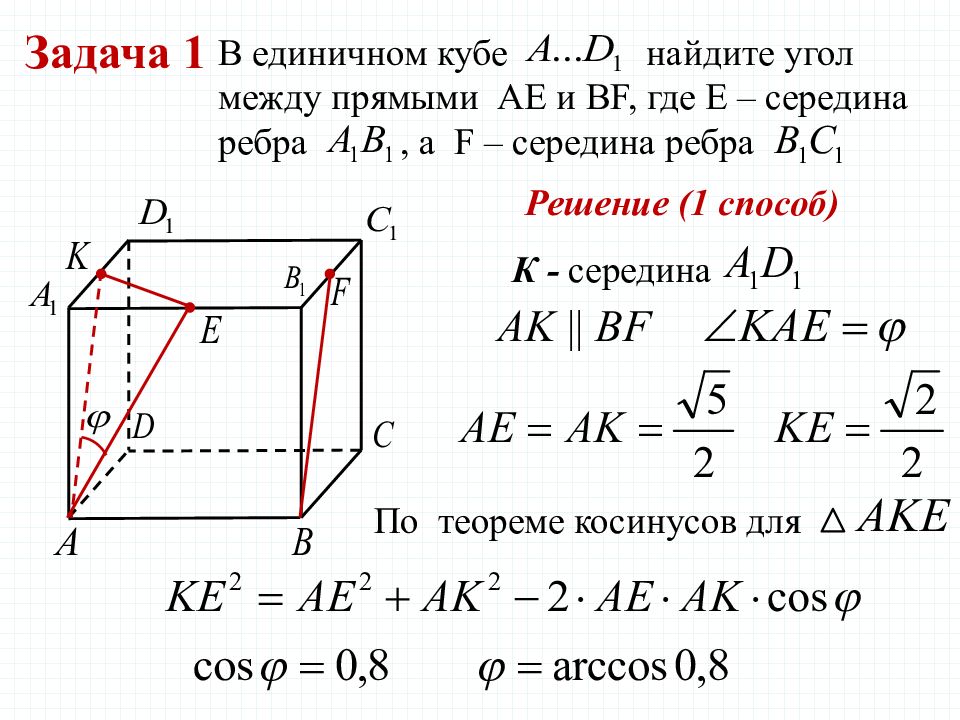
Задача 1 В единичном кубе найдите угол между прямыми AE и BF, где Е – середина ребра, а F – середина ребра К - середина Решение (1 способ) По теореме косинусов для
Решение (2 способ)
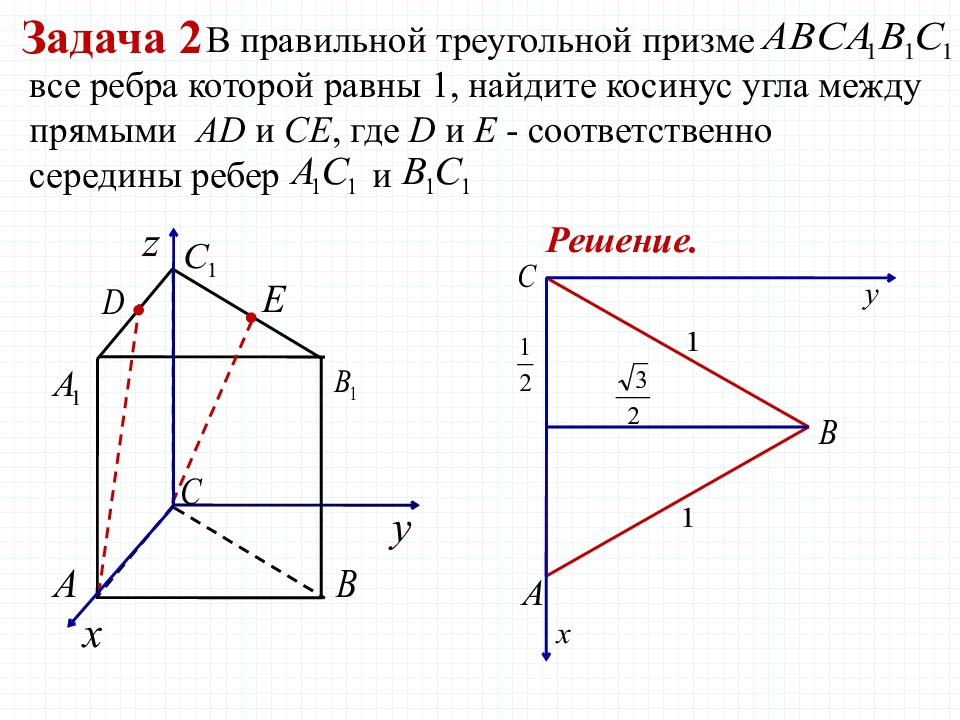
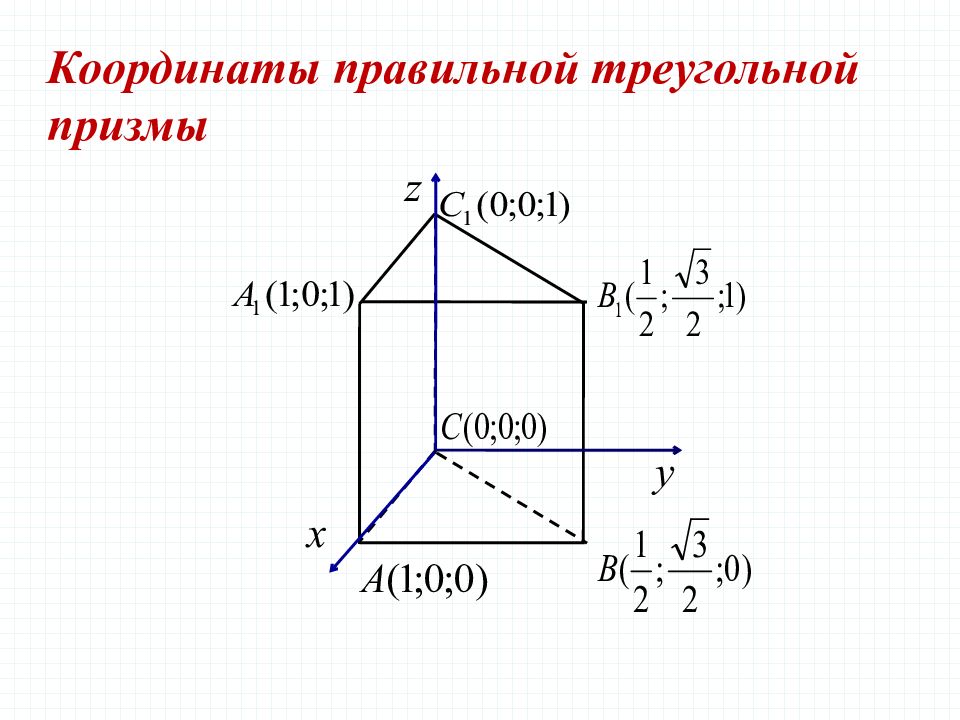
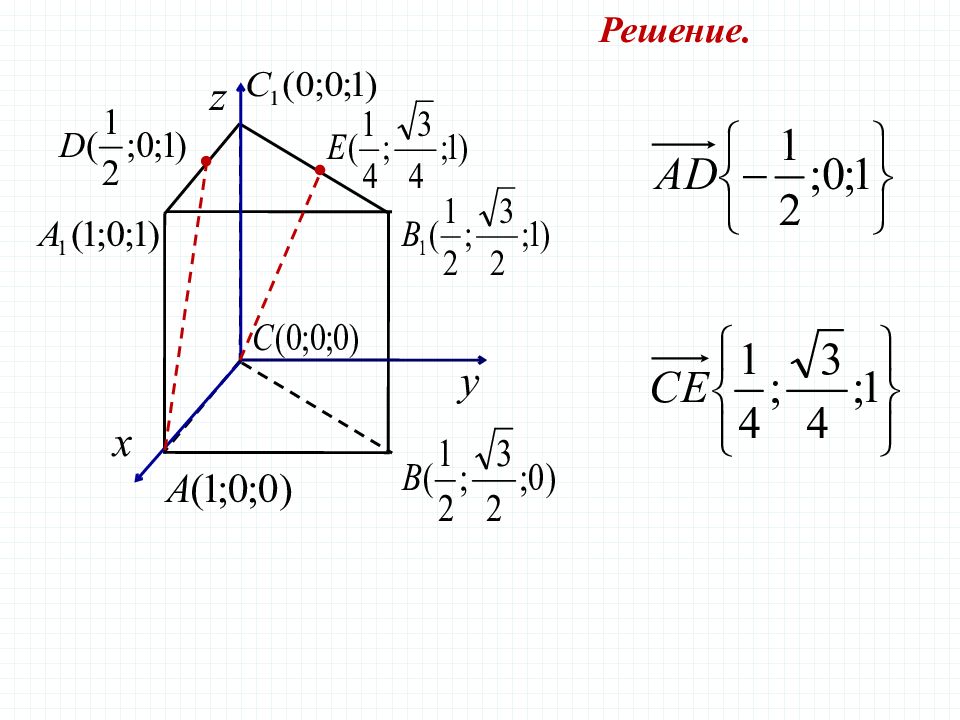
В правильной треугольной призме все ребра которой равны 1, найдите косинус угла между прямыми AD и CE, где D и E - соответственно середины ребер и Задача 2 Решение.
Координаты правильной треугольной призмы
Решение.
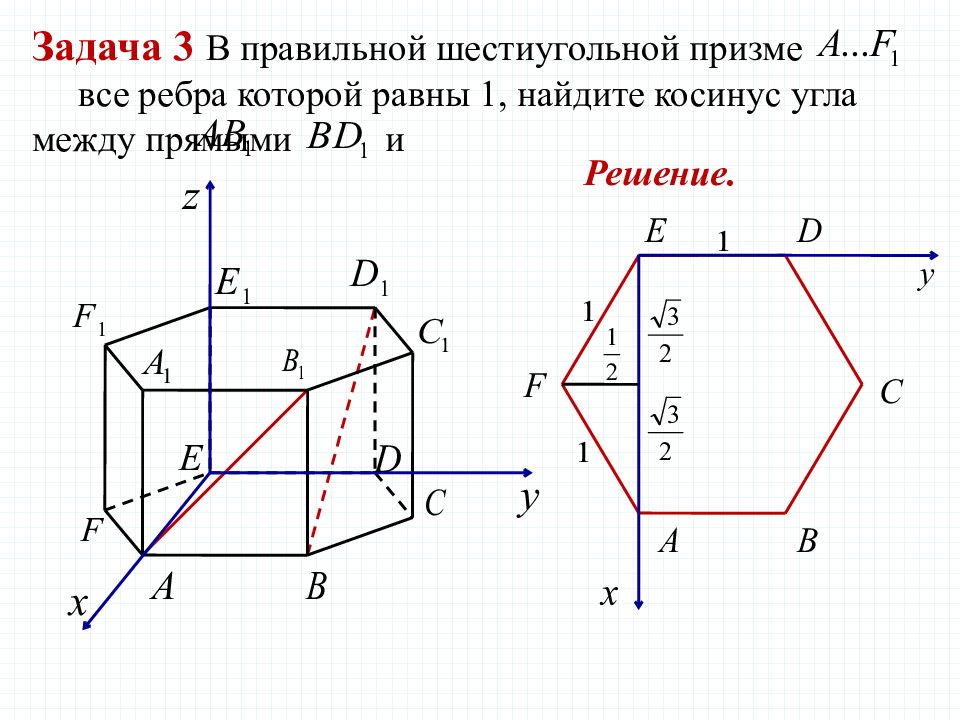
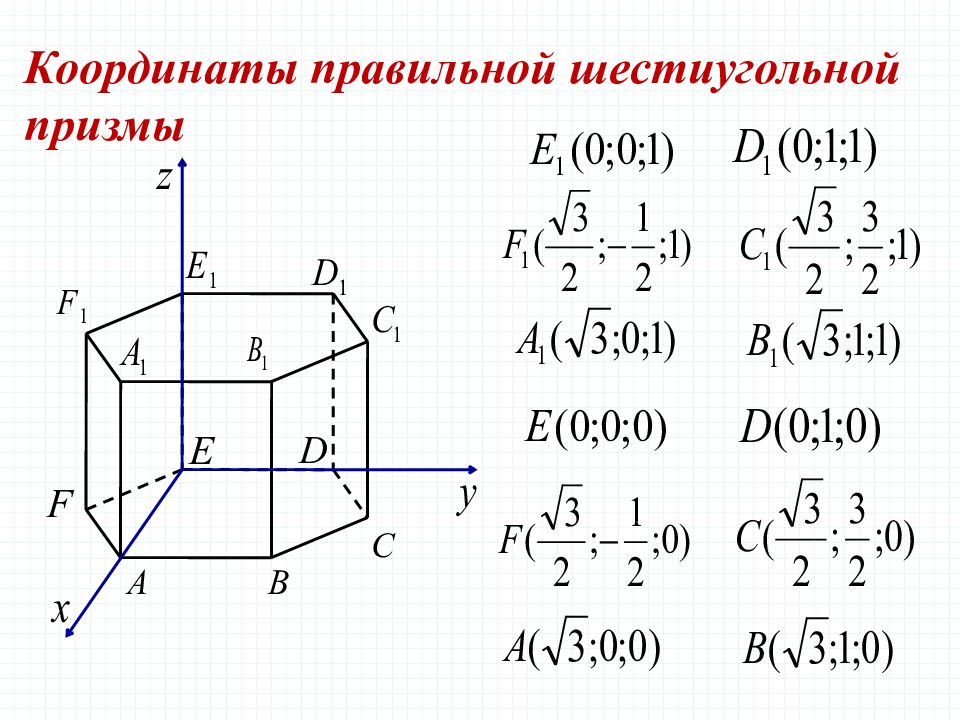
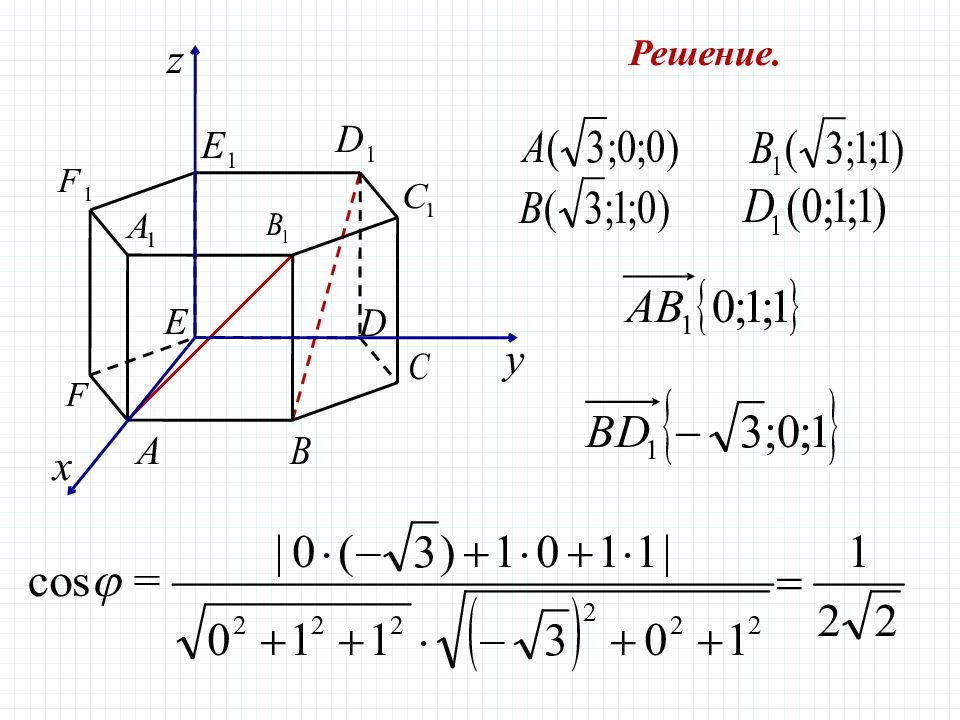
Задача 3 В правильной шестиугольной призме все ребра которой равны 1, найдите косинус угла между прямыми и Решение.
Координаты правильной шестиугольной призмы
Решение.
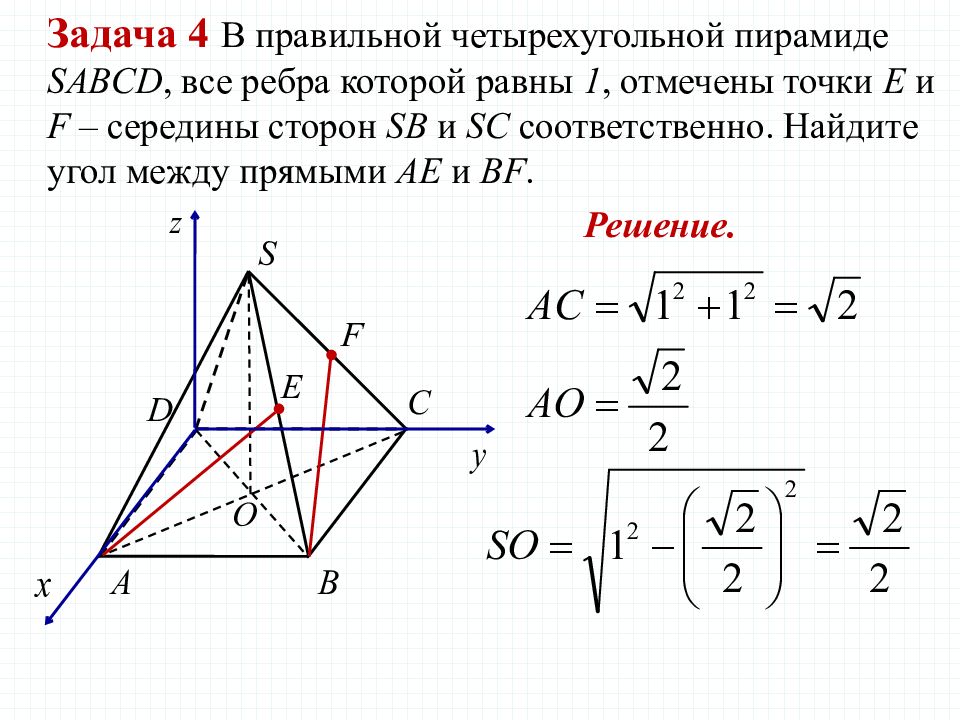
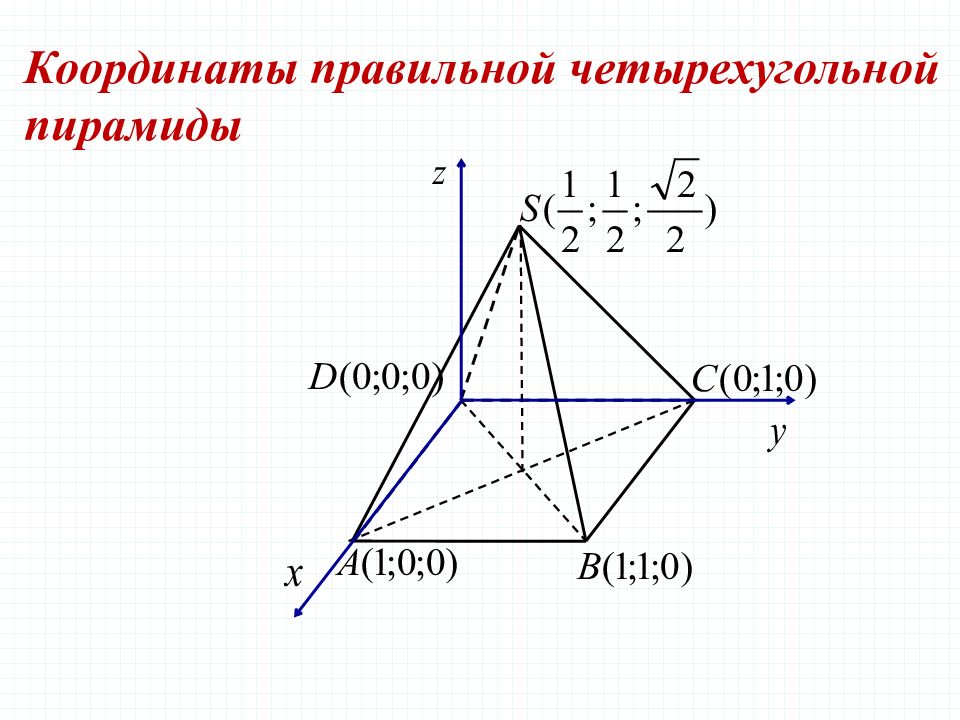
Задача 4 В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки Е и F – середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF. Решение.
Координаты правильной четырехугольной пирамиды
Е - середина SB F - середина SC Решение.
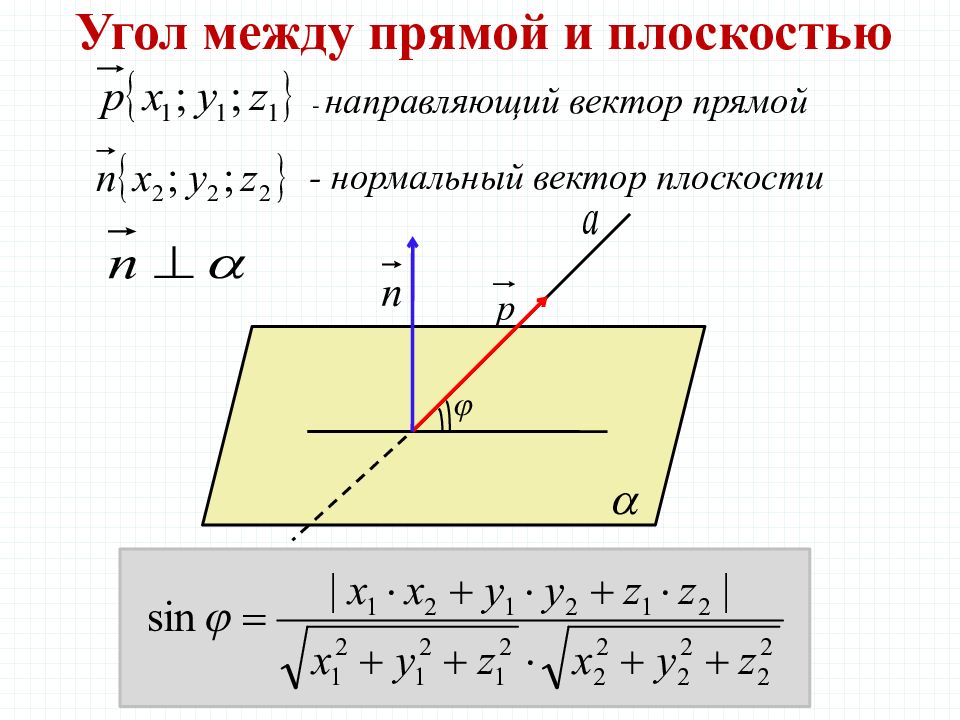
Угол между прямой и плоскостью - направляющий вектор прямой - нормальный вектор плоскости
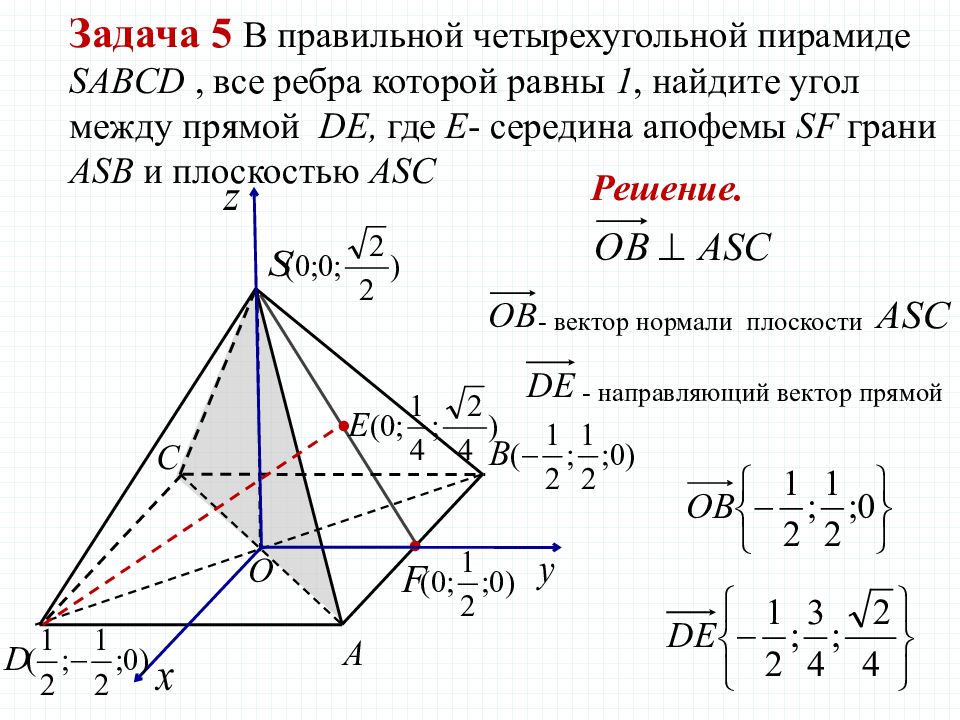
Задача 5 В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите угол между прямой DE, где Е - середина апофемы SF грани ASB и плоскостью ASC Решение. - вектор нормали плоскости - направляющий вектор прямой
- вектор нормали плоскости - направляющий вектор прямой DE
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору -нормальный вектор плоскости , где
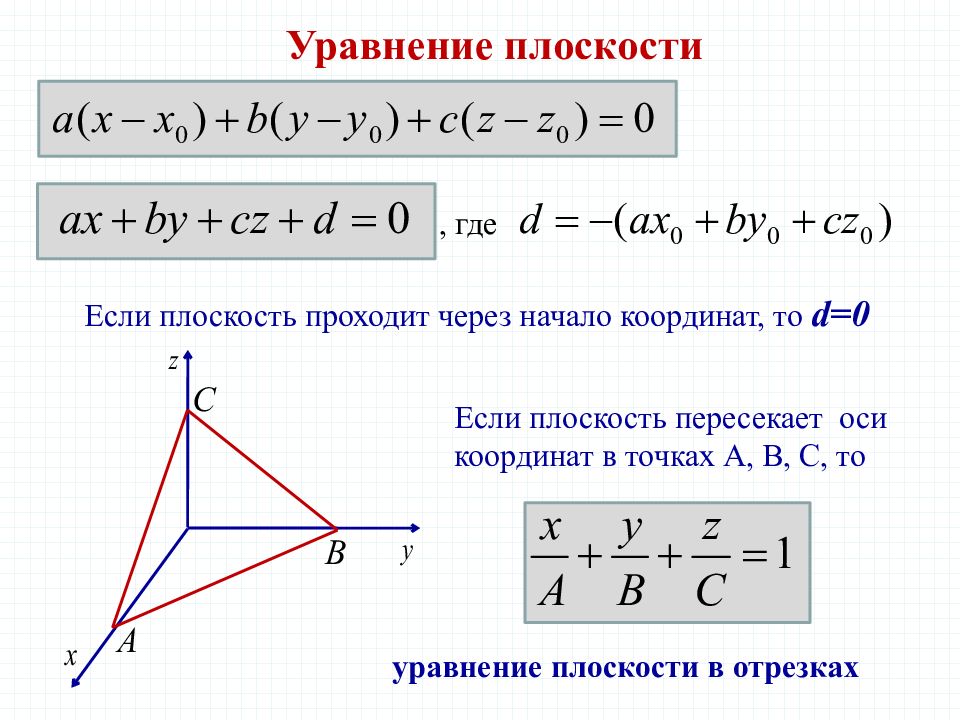
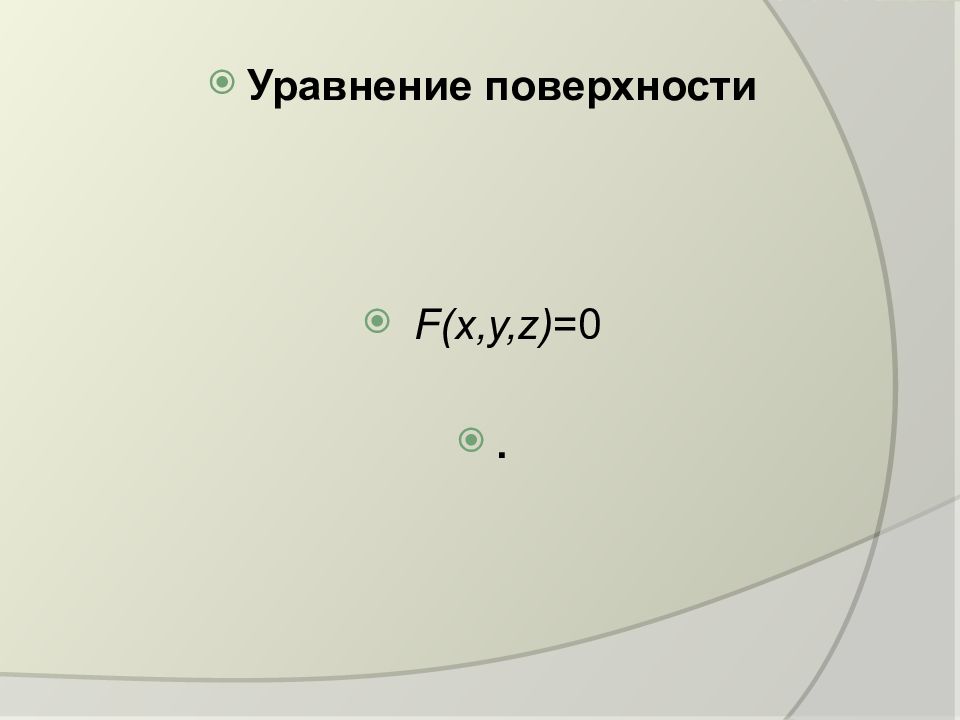
Уравнение плоскости Если плоскость проходит через начало координат, то d=0 Если плоскость пересекает оси координат в точках А, В, С, то , где уравнение плоскости в отрезках
Задача 6 Составить уравнение плоскости, проходящей через точки А(-2;3;5), В(4;-3;0), С(0;6;-5) и найти координаты вектора нормали. Решение.
Расстояние от точки до плоскости
Расстояние между параллельными плоскостями
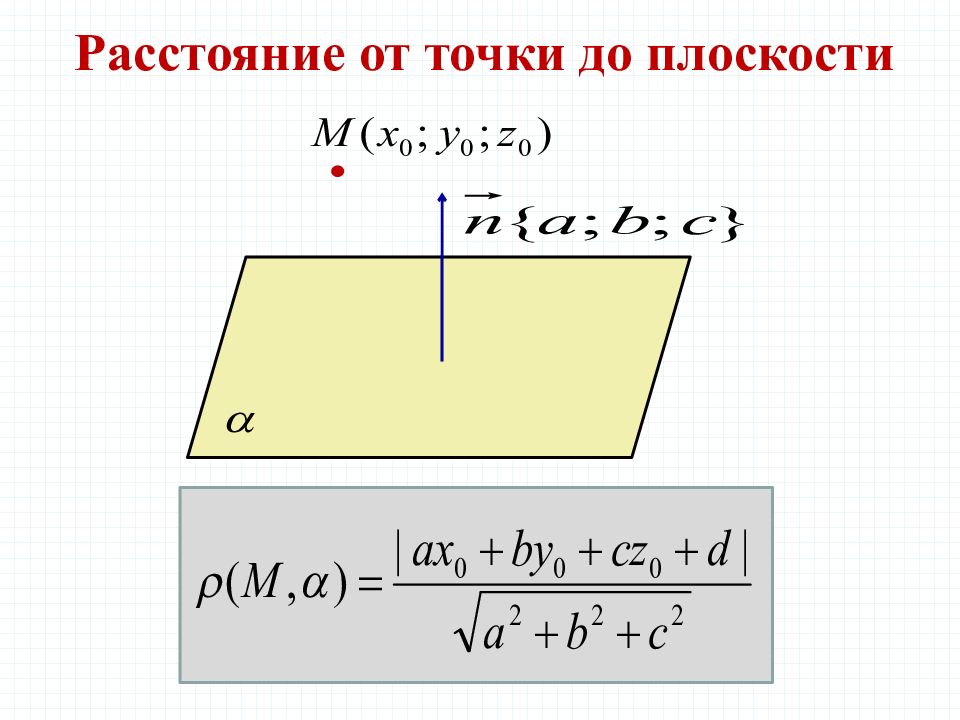
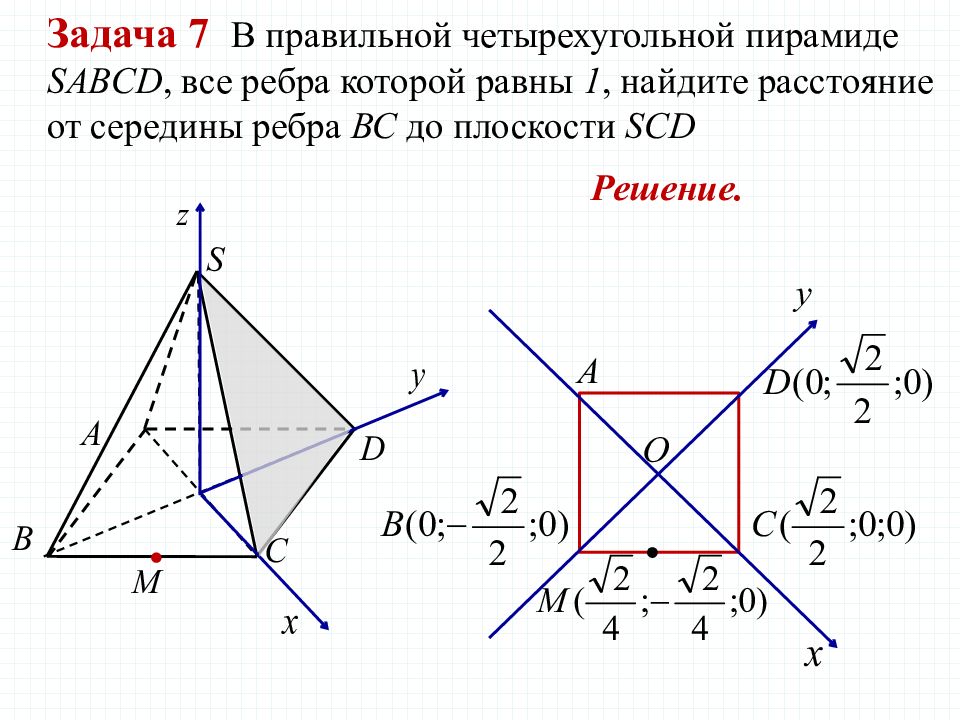
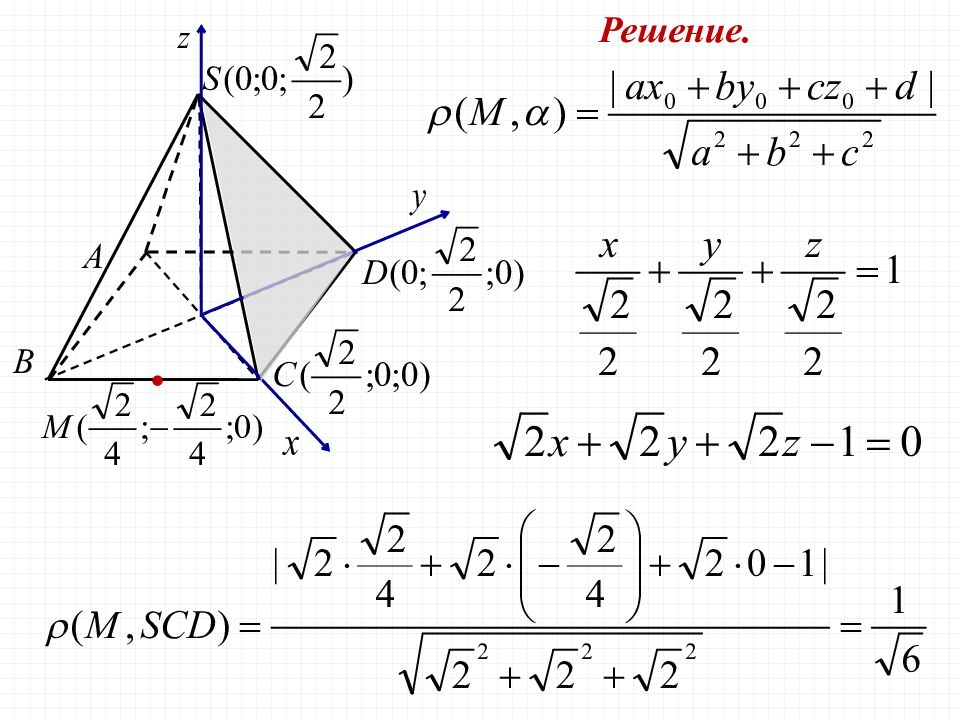
Задача 7 В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от середины ребра ВС до плоскости SCD Решение.
Решение.
Угол между плоскостями Вектор нормали плоскости Вектор нормали плоскости
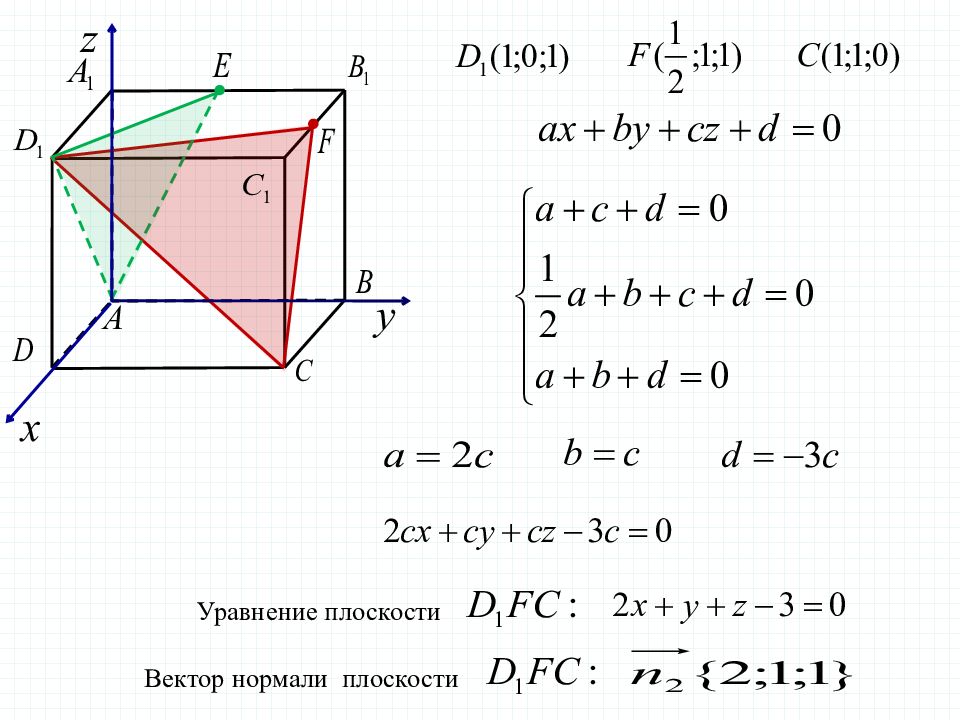
Задача 8 В единичном кубе найдите угол между плоскостями и, где Е – середина ребра, а F – середина ребра Решение. Уравнение плоскости Вектор нормали плоскости
Уравнение плоскости Вектор нормали плоскости
