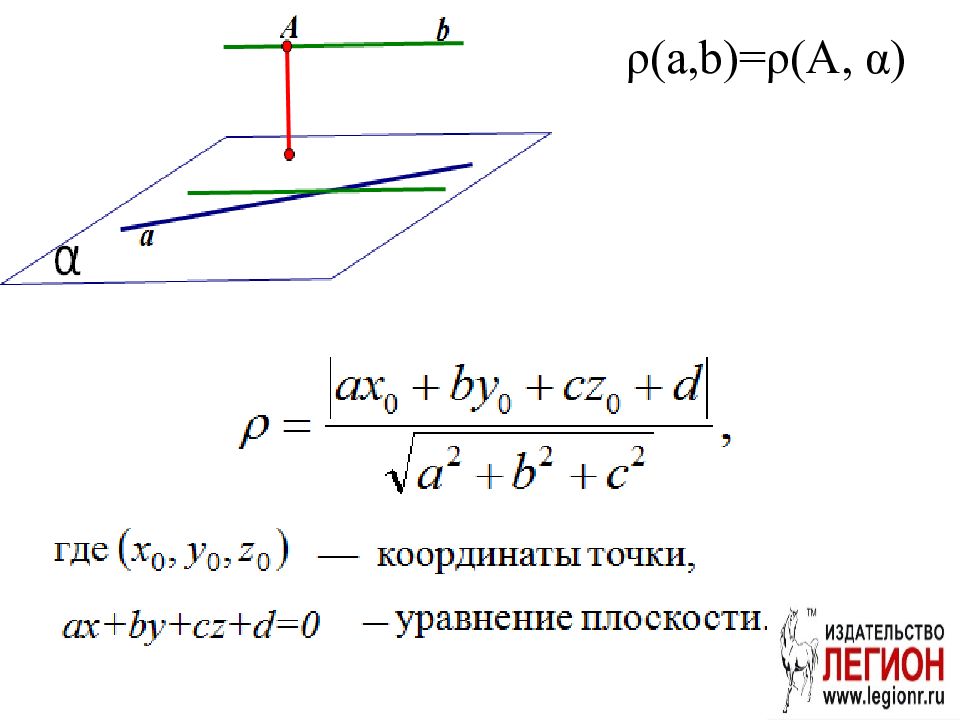
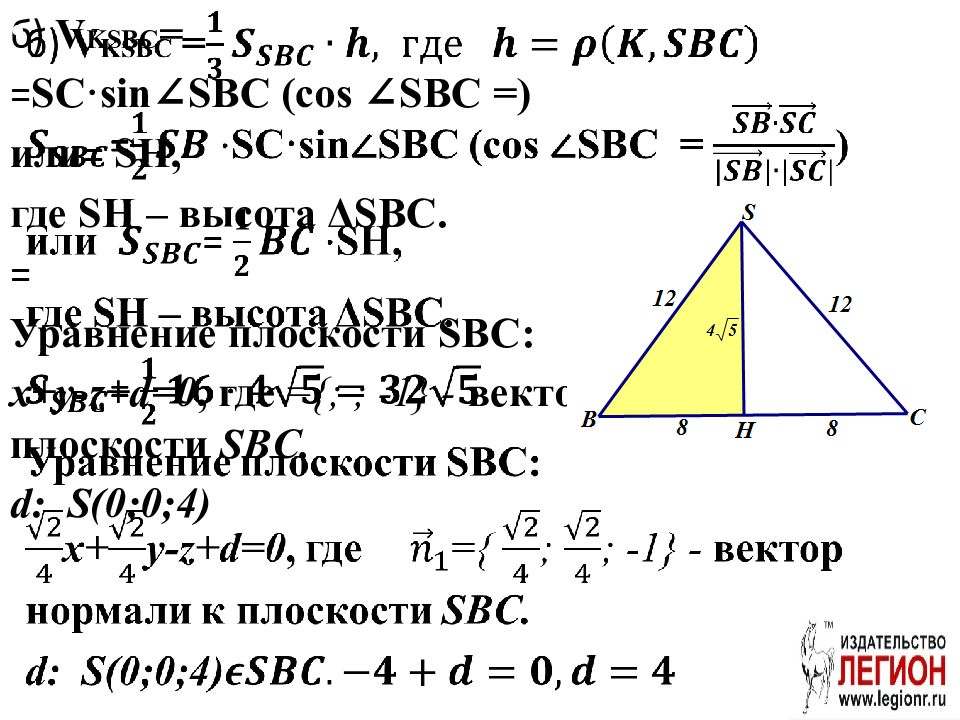Первый слайд презентации: Методы решения задач повышенной сложности по геометрии (ЕГЭ). Семинар с практической частью
Фридман Елена Михайловна Издательство «Легион»
Метод дополнительных построений Метод геометрических преобразований Метод подобия Метод площадей Метод вспомогательной окружности Метод геометрического видения Метод координат Векторный метод
Слайд 3: Основные факторы успеха
Время (чем больше времени на подготовку, тем лучше) Система (работа по плану, а не от случая к случаю) Желание подготовиться
Незнание и/или непонимание аксиом, определений, теорем, а также методов решения задач; неумение их применять, (в том числе, применять их неверно) ; невнимательное чтение условия и вопроса задания; вычислительные ошибки ; нарушения логики в рассуждениях; принятие ошибочных гипотез ; недостатки в работе с рисунком.
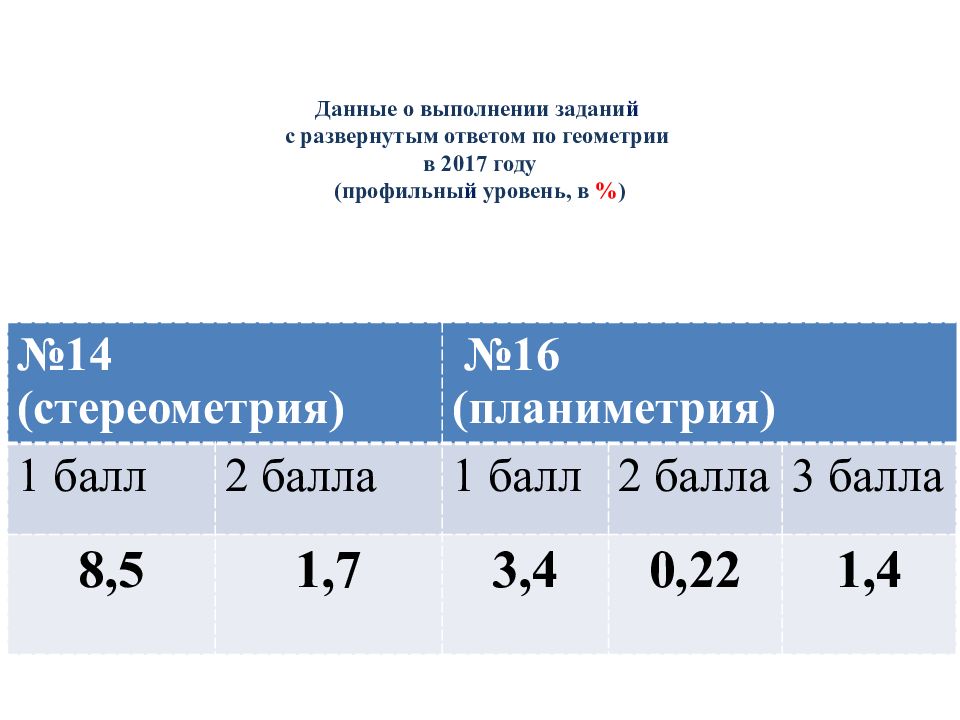
№14 (стереометрия) №16 (планиметрия) 1 балл 2 балла 1 балл 2 балла 3 балла 8,5 1,7 3,4 0,22 1,4
Слайд 9: Что нужно знать
Аксиомы и теоремы стереометрии и планиметрии Правила изображения (проектирования) пространственных фигур на плоскость Основные методы построения сечений многогранников
Слайд 10: Что нужно уметь
Применять знания в процессе решения задачи: Увидеть, что нужно построить на каждом шаге построения сечения Предложить способ построения Построить (точку, линию, плоскость и т.д.) Veni, vidi, vici ( пришел, увидел, победил)
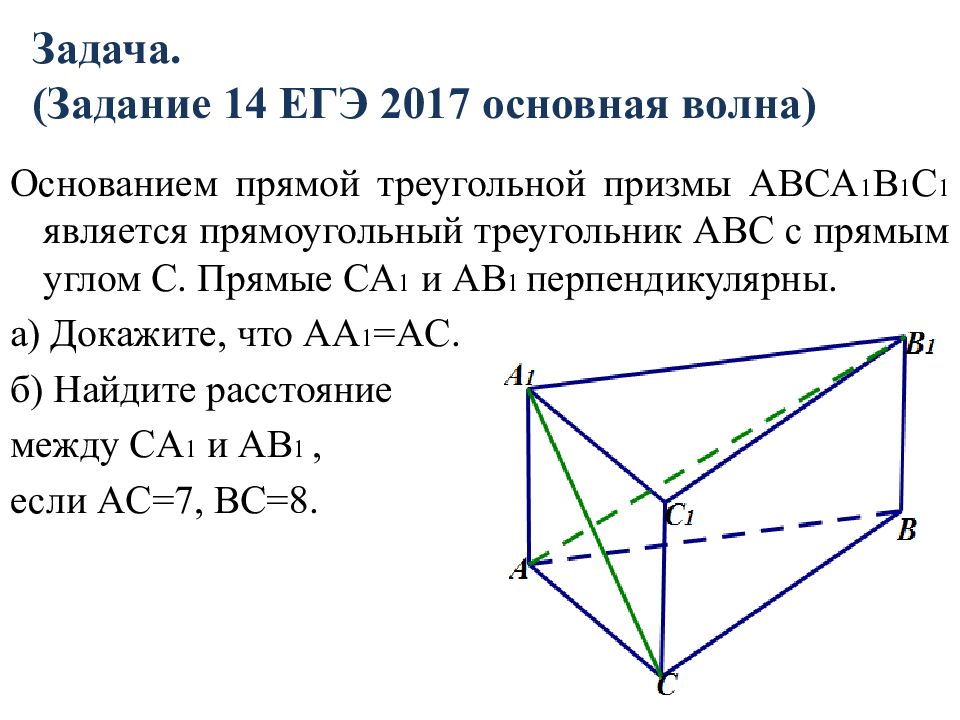
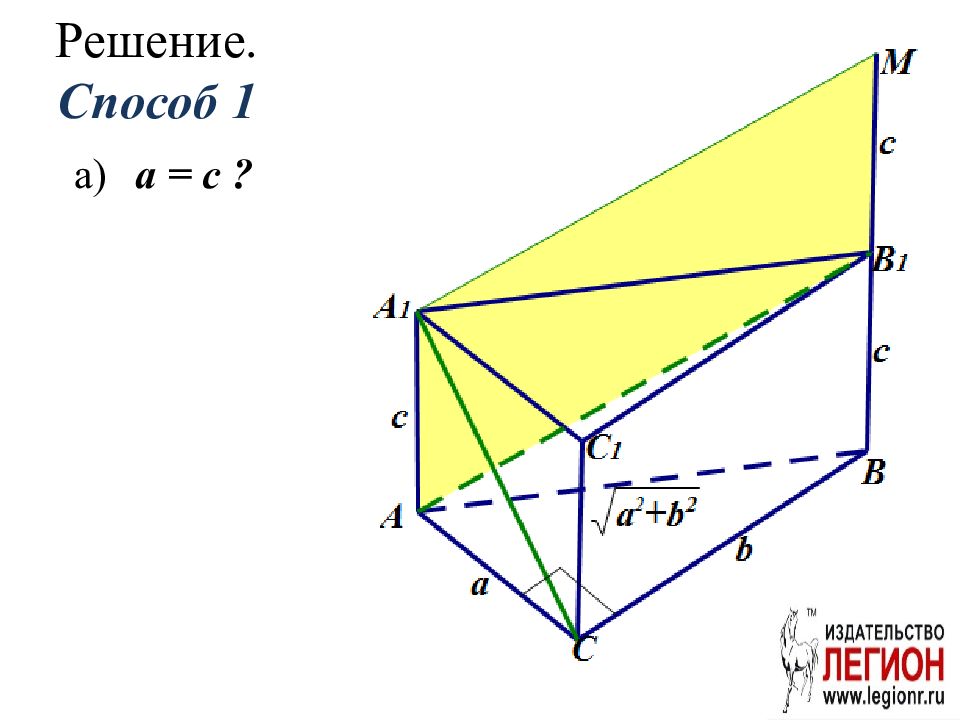
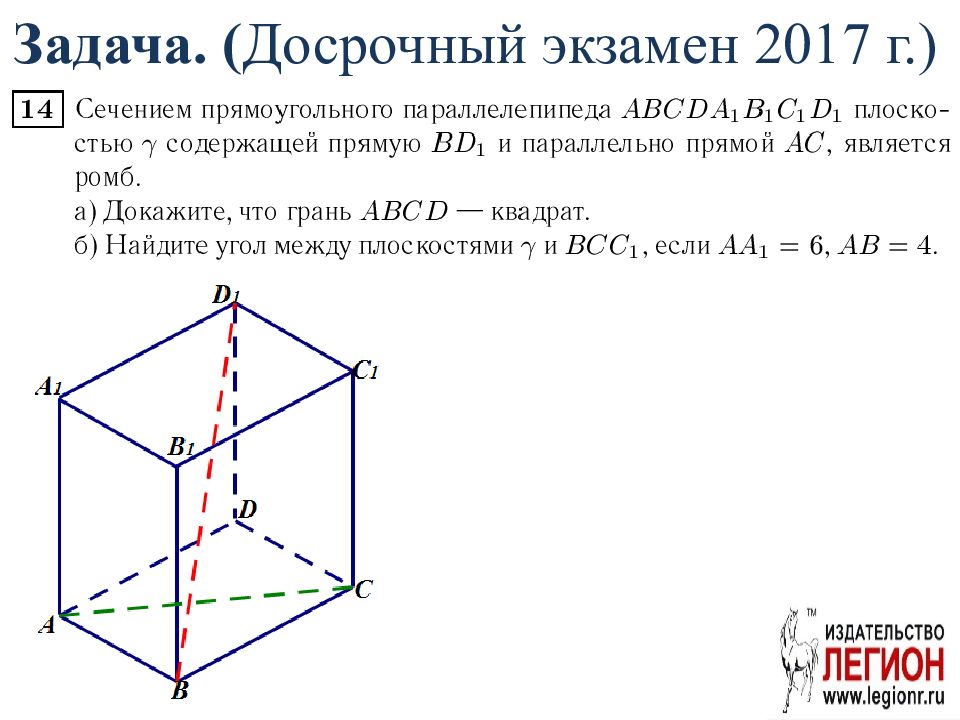
Слайд 11: Задача. (Задание 14 ЕГЭ 2017 основная волна)
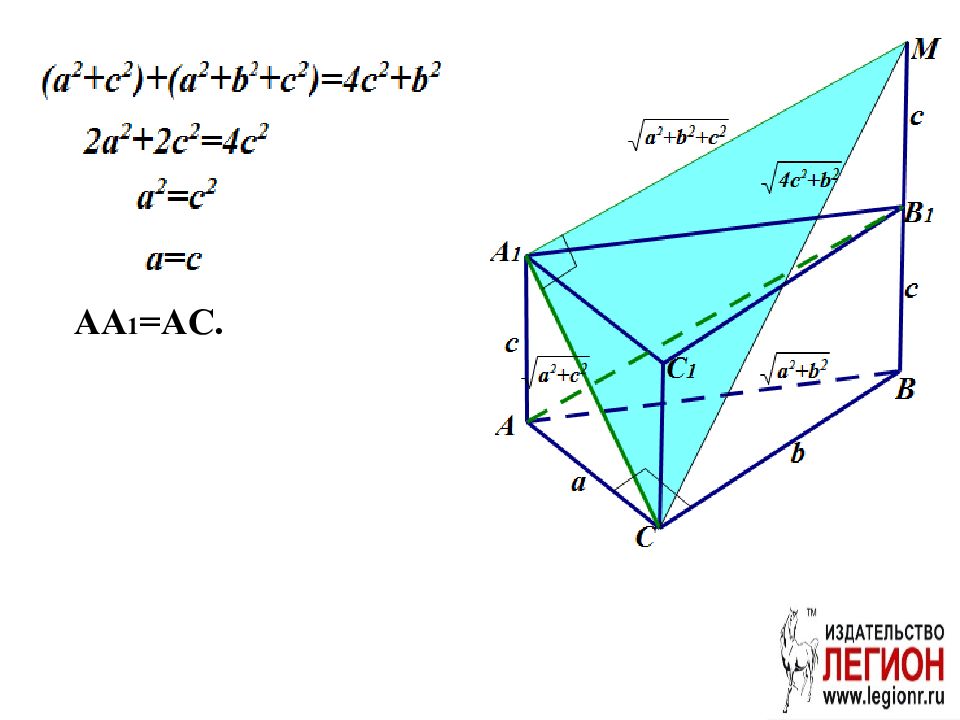
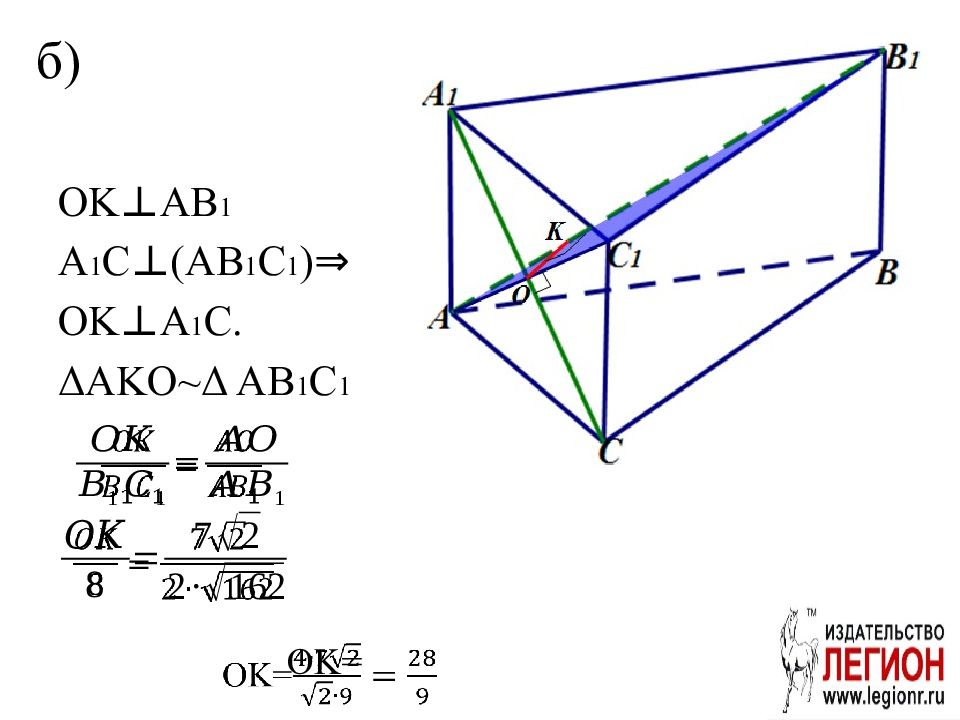
Основанием прямой треугольной призмы ABCA 1 B 1 C 1 является прямоугольный треугольник ABC с прямым углом С. Прямые CA 1 и AB 1 перпендикулярны. а) Докажите, что AA 1 = AC. б) Найдите расстояние между CA 1 и AB 1, если AC=7, BC=8.
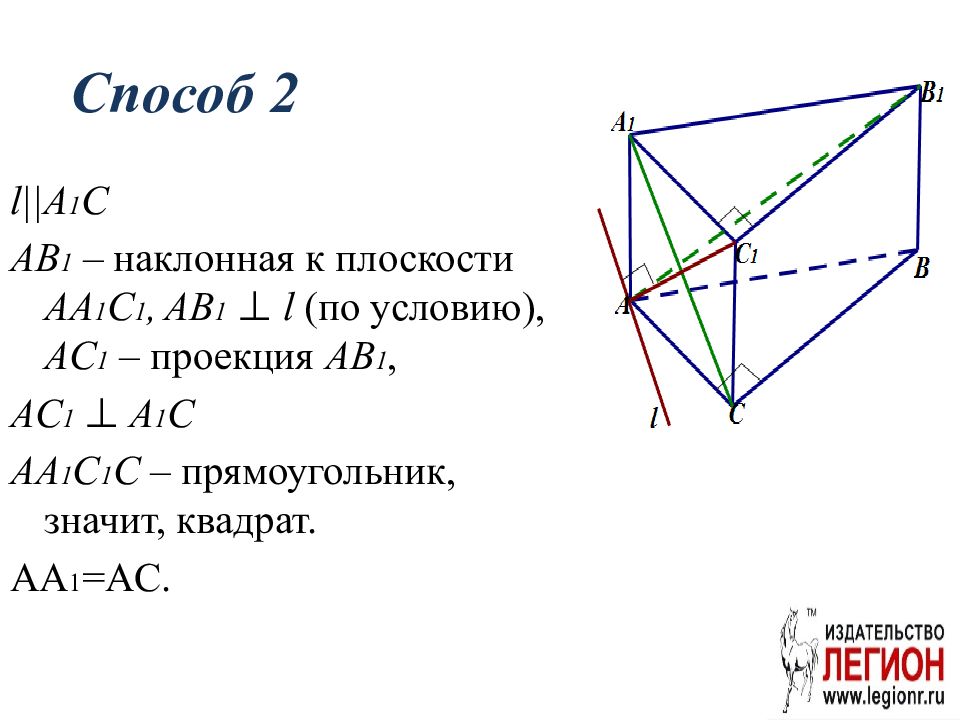
Слайд 14: Способ 2
l||A 1 C AB 1 – наклонная к плоскости AA 1 C 1, AB 1 ⊥ l ( по условию ), AC 1 – проекция AB 1, AC 1 ⊥ A 1 C AA 1 C 1 C – прямоугольник, значит, квадрат. AA 1 = AC.
Слайд 17
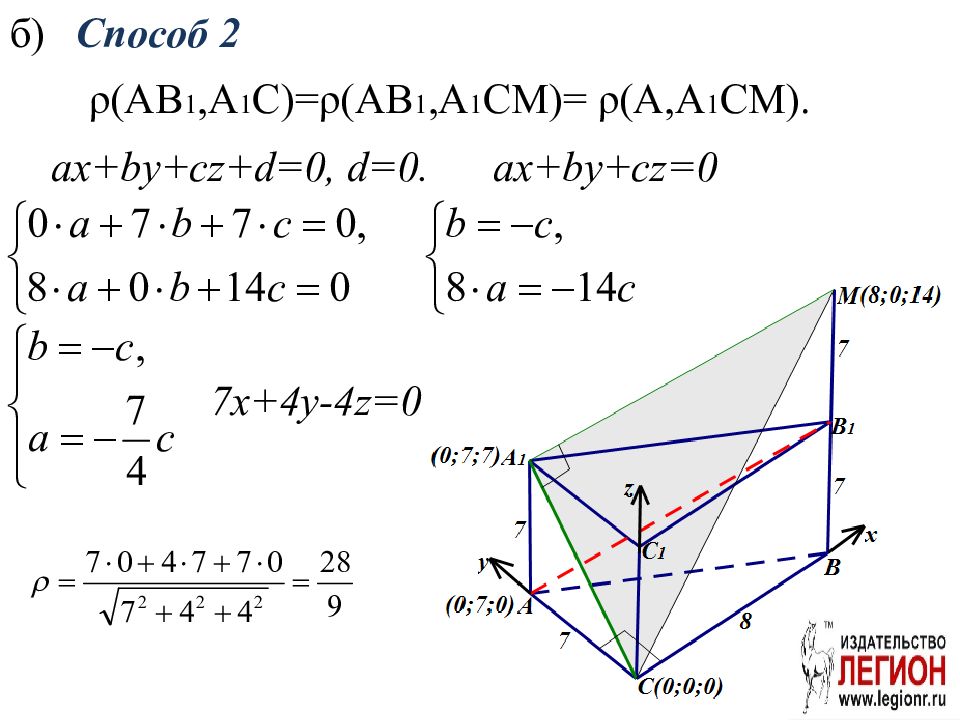
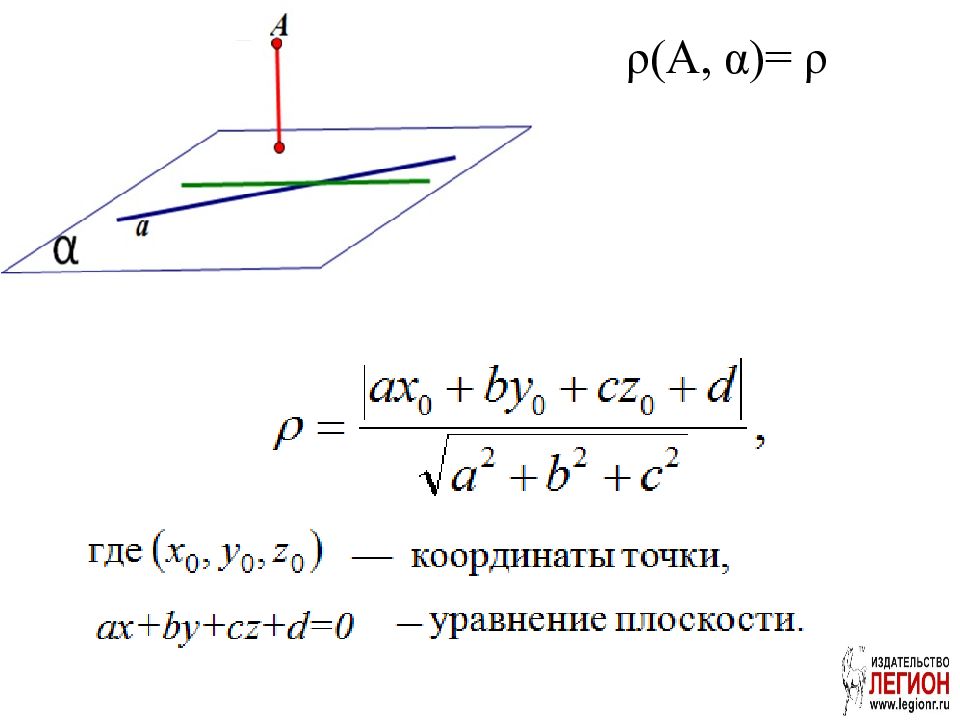
ρ (AB 1,A 1 C)= ρ (AB 1,A 1 CM)= ρ (A,A 1 CM). б) ax+by+cz+d =0, d=0. ax+by+cz =0 7x+4y-4z=0 Способ 2
Слайд 18: Основные методы построения сечений многогранников
Аксиоматический Метод следов Метод вспомогательных сечений (метод внутреннего проектирования) Комбинированный метод
Слайд 19: Метод следов
Понятие следа Линия пересечения плоскости сечения и плоскости грани многогранника называется следом секущей плоскости на плоскости этой грани многогранника. Точка пересечения плоскости сечения и прямой, содержащей ребро многогранника, называется следом секущей плоскости на прямой, содержащей это ребро многогранника.
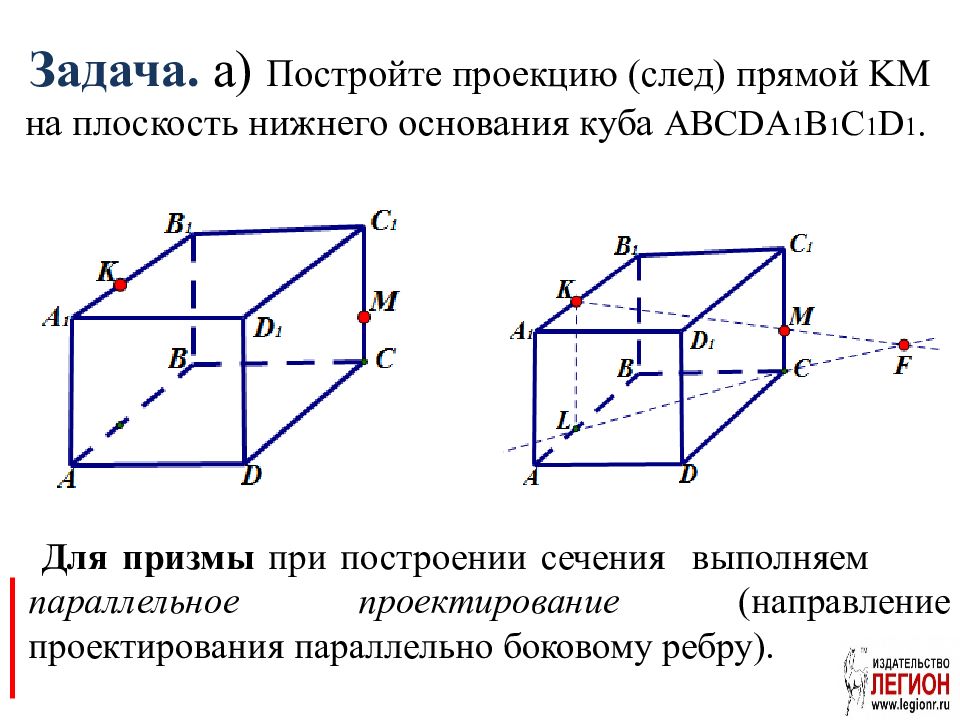
Слайд 20: Задача. а) Постройте проекцию (след) прямой KM на плоскость нижнего основания куба ABCDA 1 B 1 C 1 D 1
Для призмы при построении сечения выполняем параллельное проектирование (направление проектирования параллельно боковому ребру).
Слайд 21
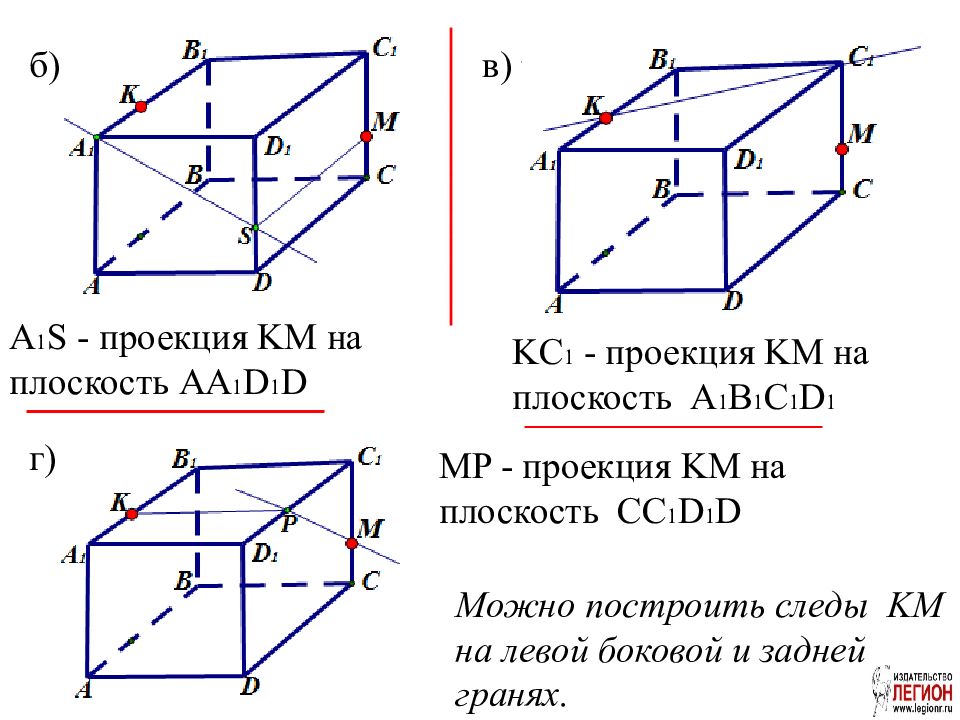
A 1 S - проекция KM на плоскость AA 1 D 1 D KC 1 - проекция KM на плоскость A 1 B 1 C 1 D 1 MP - проекция KM на плоскость CC 1 D 1 D б) в) г) Можно построить следы KM на левой боковой и задней гранях.
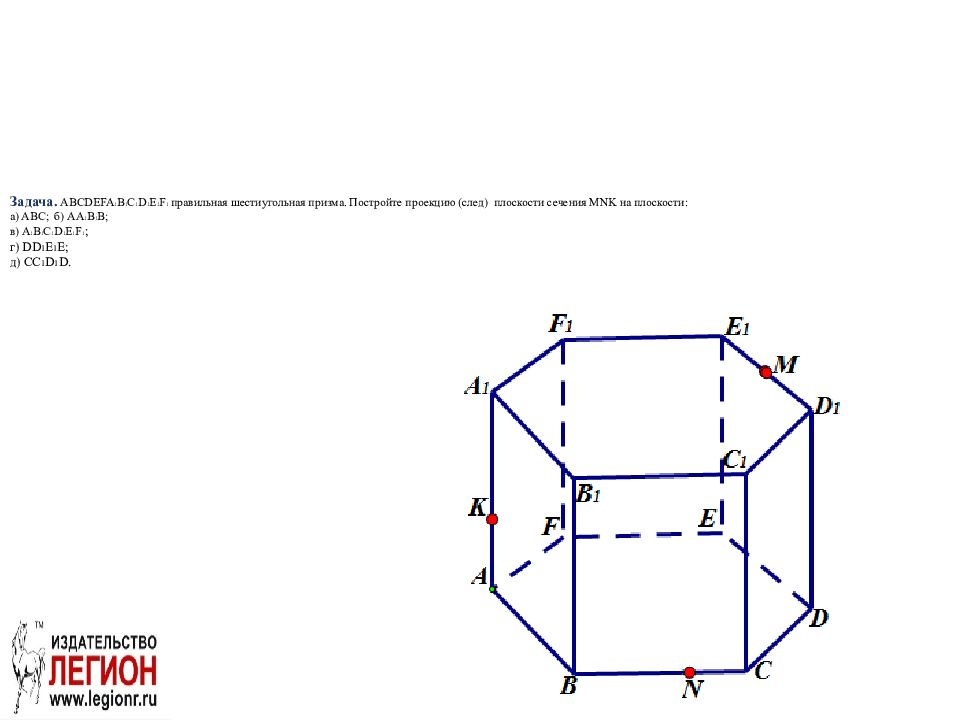
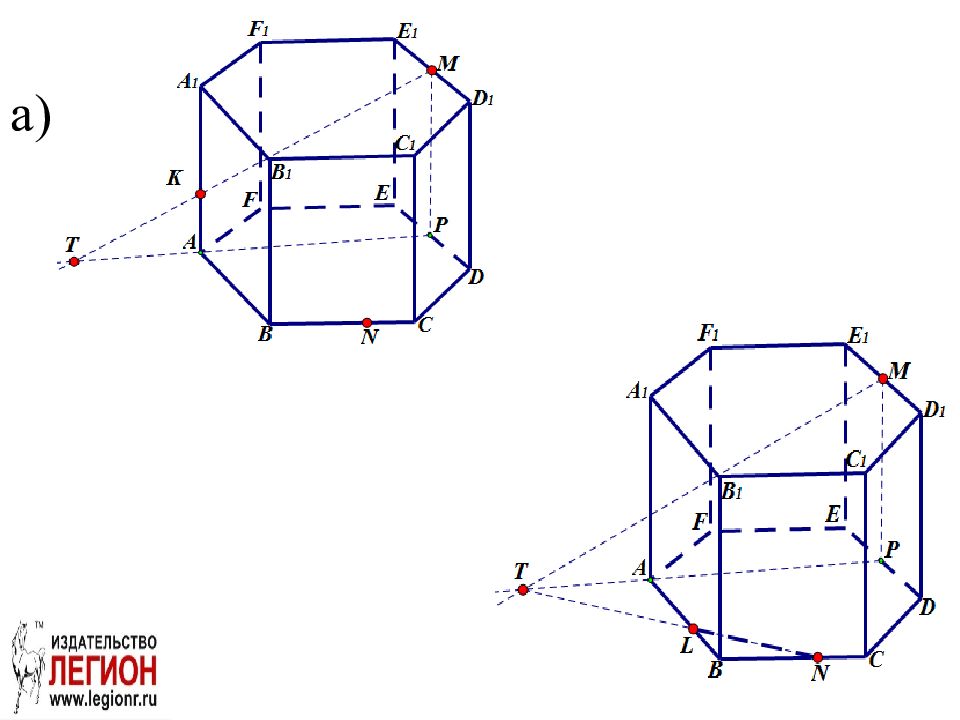
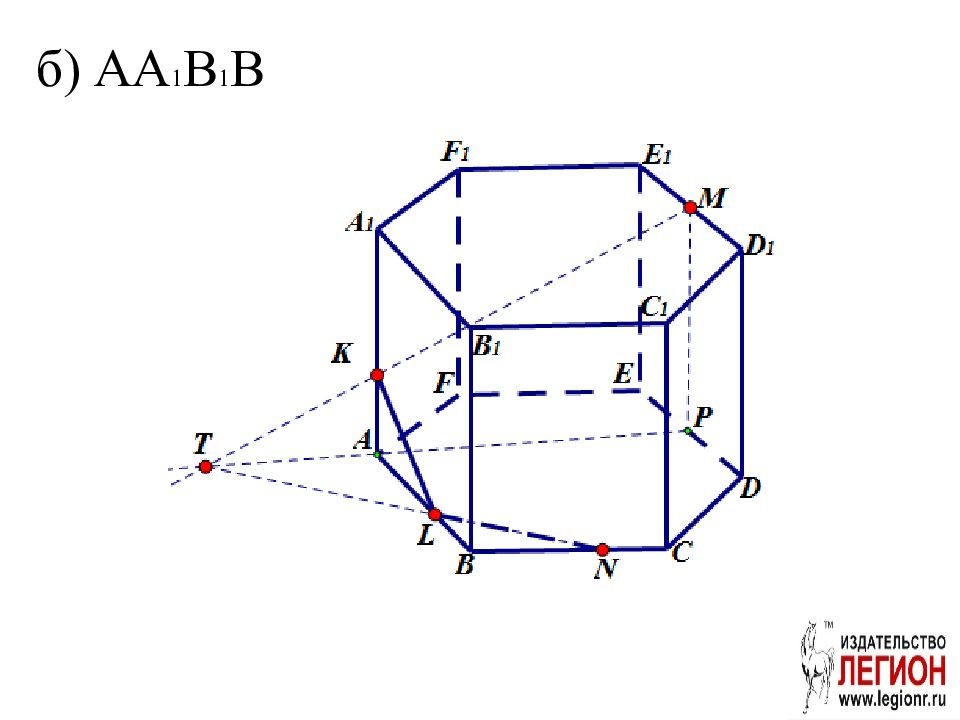
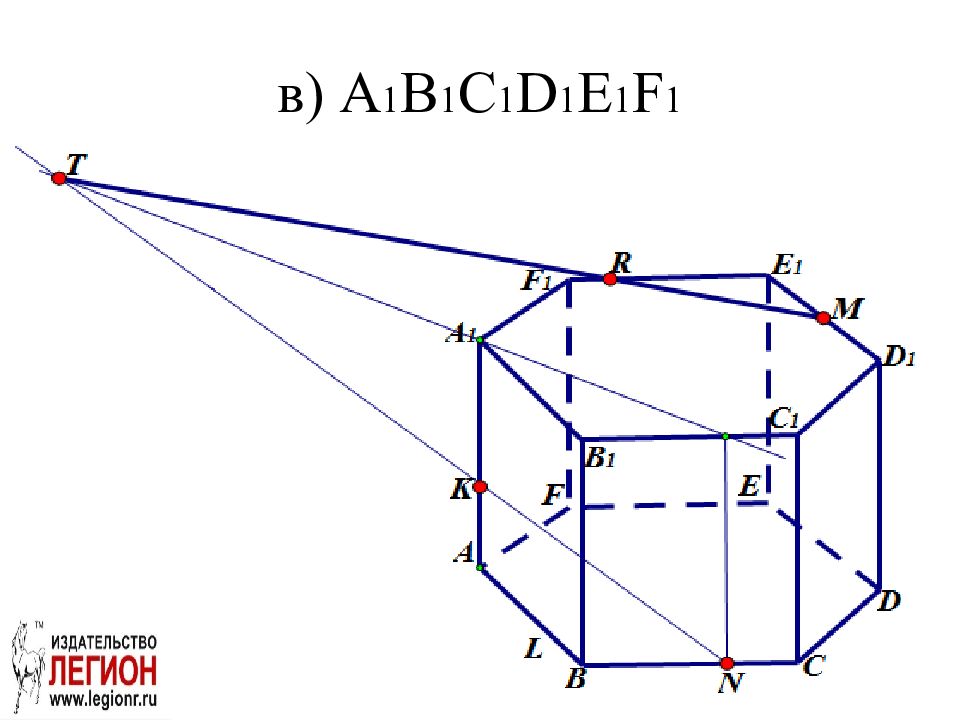
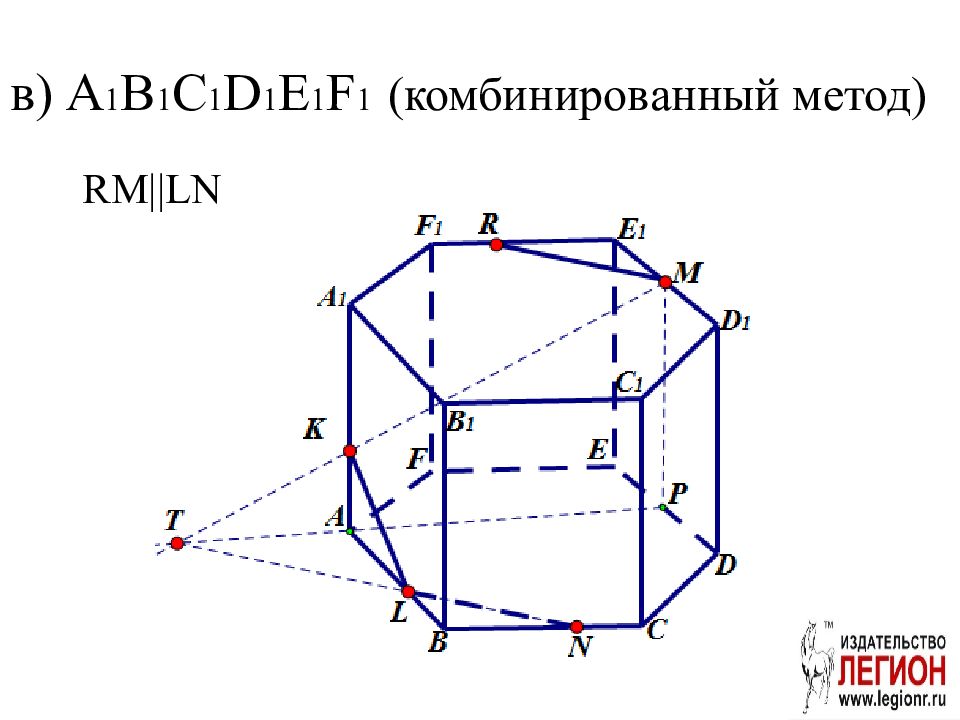
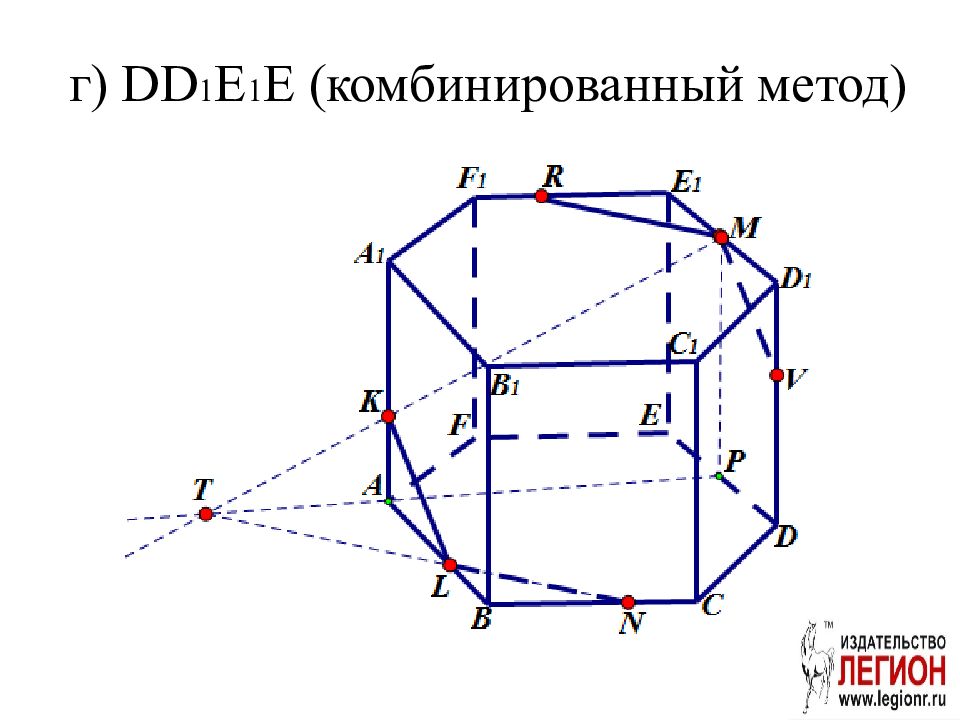
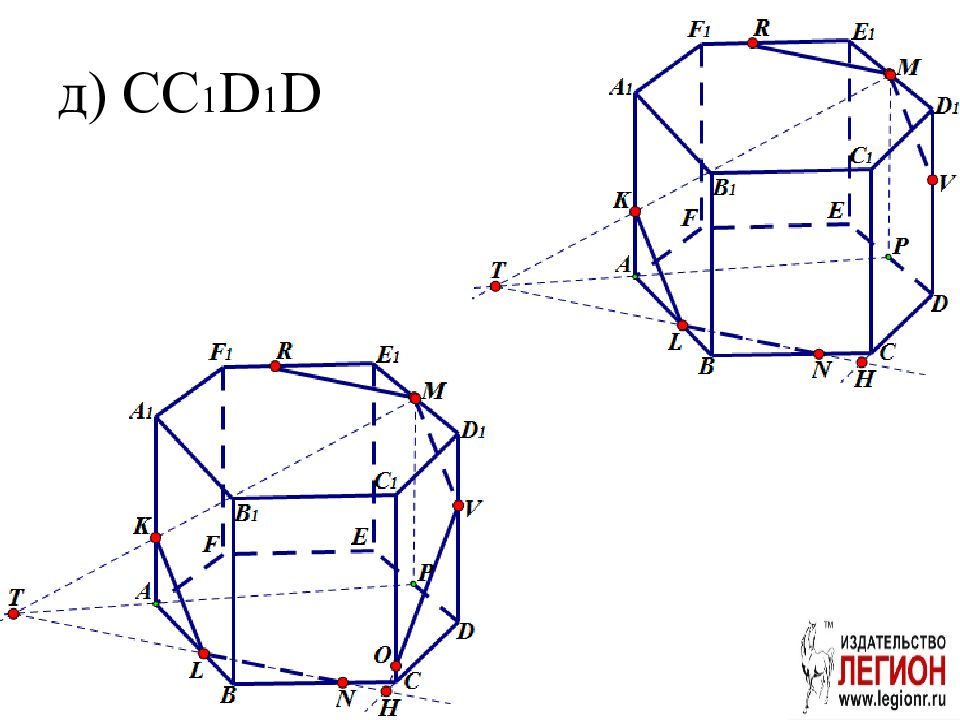
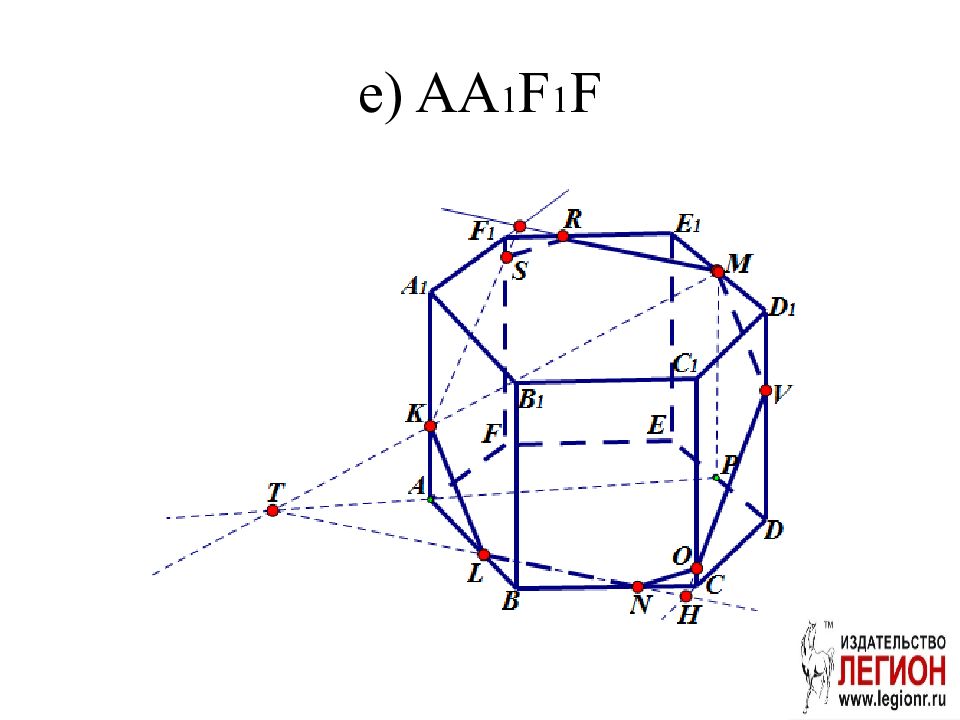
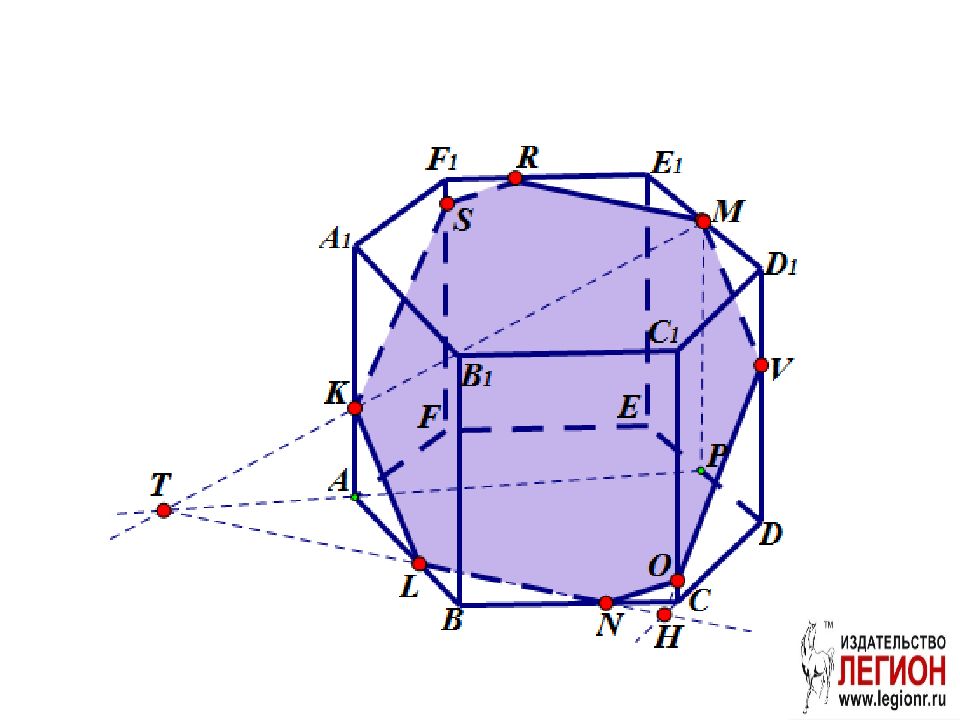
Слайд 22: Задача. ABCDEFA 1 B 1 С 1 D 1 E 1 F 1 правильная шестиугольная призма. Постройте проекцию (след) плоскости сечения MNK на плоскости: а) ABC; б) AA 1 B 1 B; в) A 1 B 1 С 1 D 1 E 1 F 1 ; г) DD 1 E 1 E; д ) CC 1 D 1 D
Слайд 26: Комбинированный метод
Сочетание применения теорем о параллельности прямых и плоскостей в пространстве и аксиоматического метода.
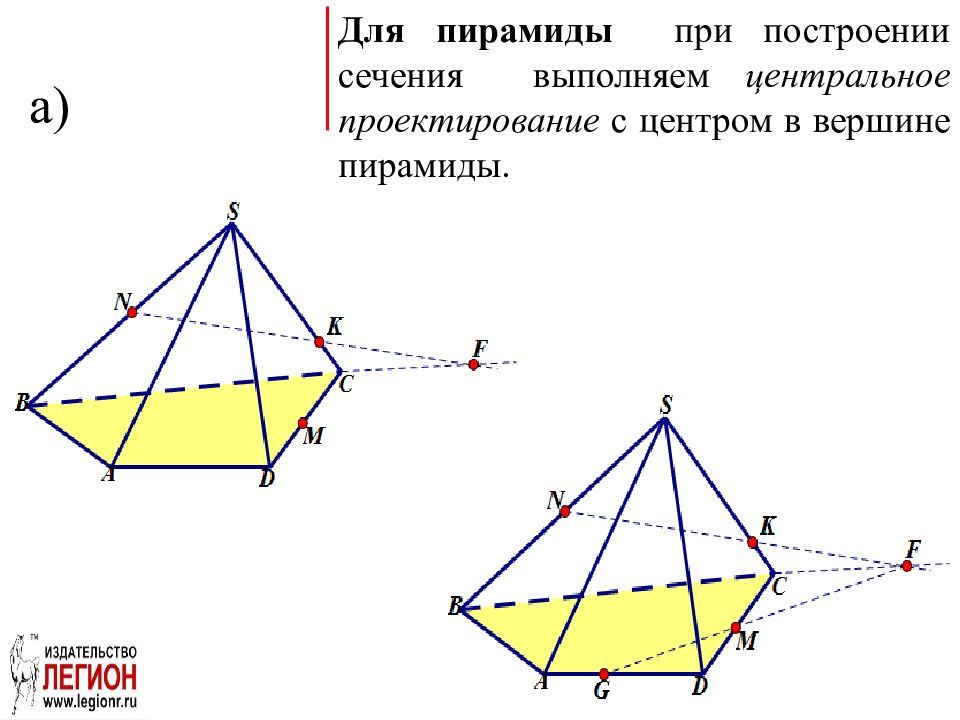
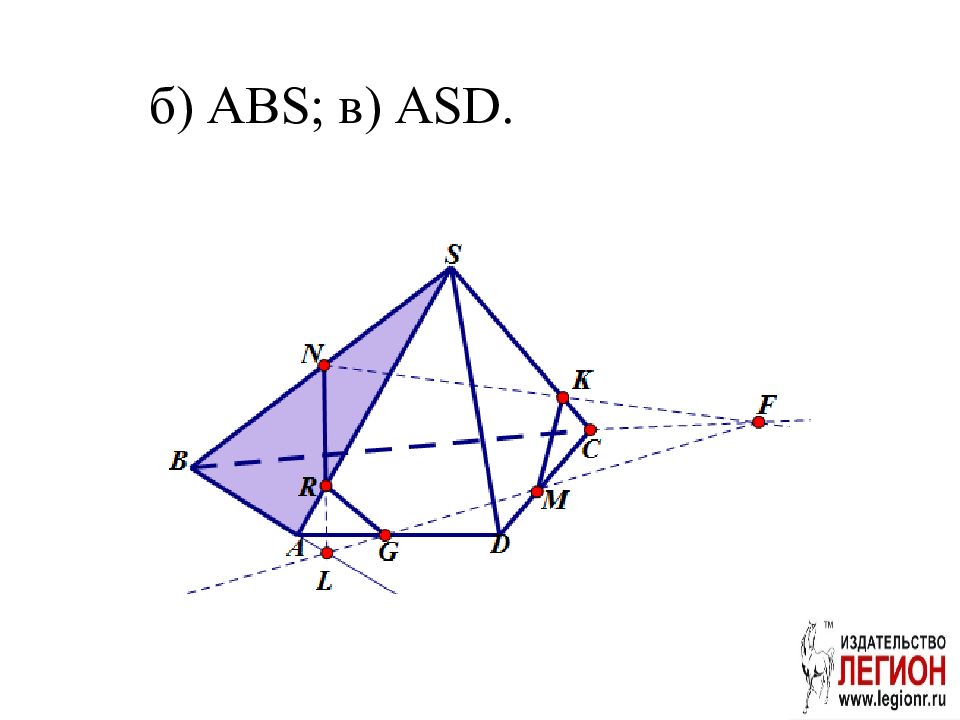
Слайд 32: Задача. Постройте проекцию (след) плоскости сечения MNK на плоскости: а) ABC ; б) ABS ; в) ASD
Слайд 33
а) Для пирамиды при построении сечения выполняем центральное проектирование с центром в вершине пирамиды.
Слайд 36: Метод вспомогательных сечений (метод внутреннего проектирования)
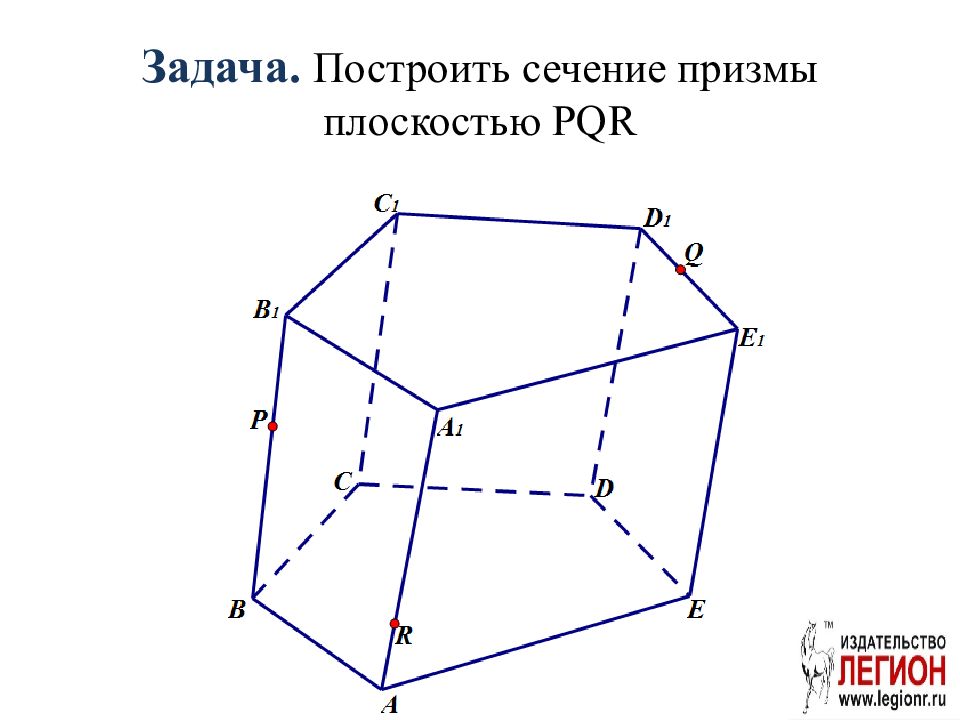
Универсальный метод, основанный на построении вспомогательных плоскостей, не выходящих за пределы многогранника.
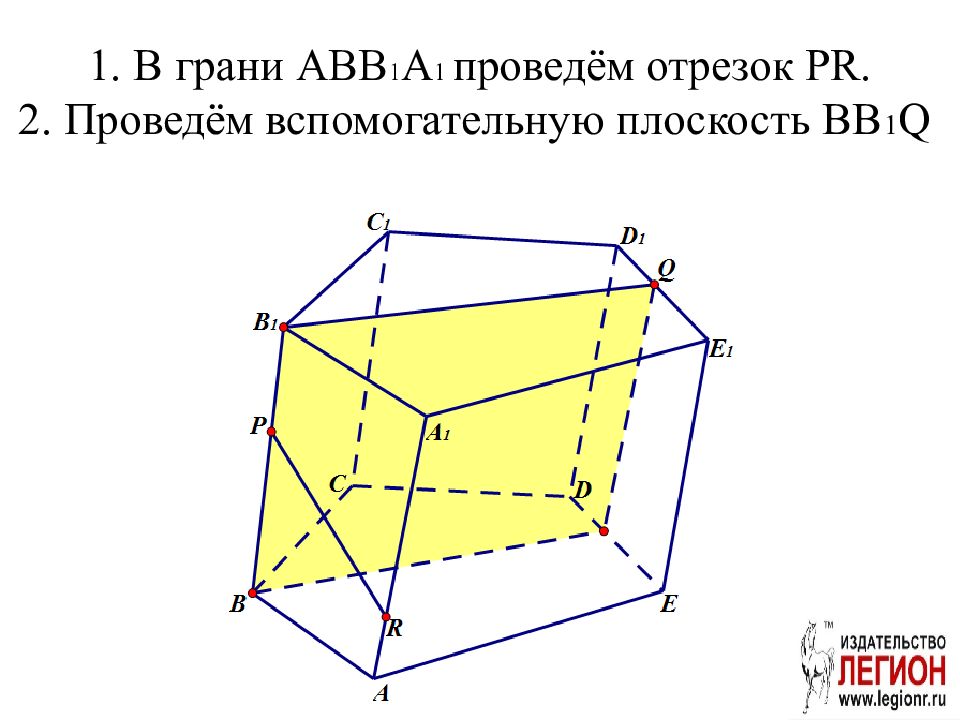
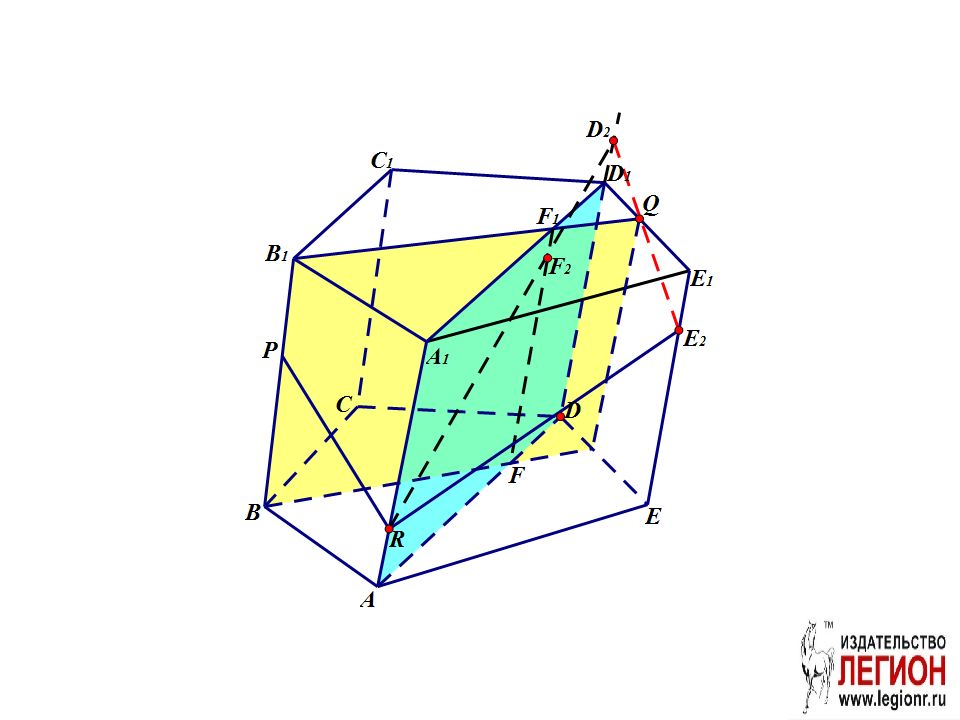
Слайд 38: 1. В грани ABB 1 A 1 проведём отрезок PR. 2. Проведём вспомогательную плоскость BB 1 Q
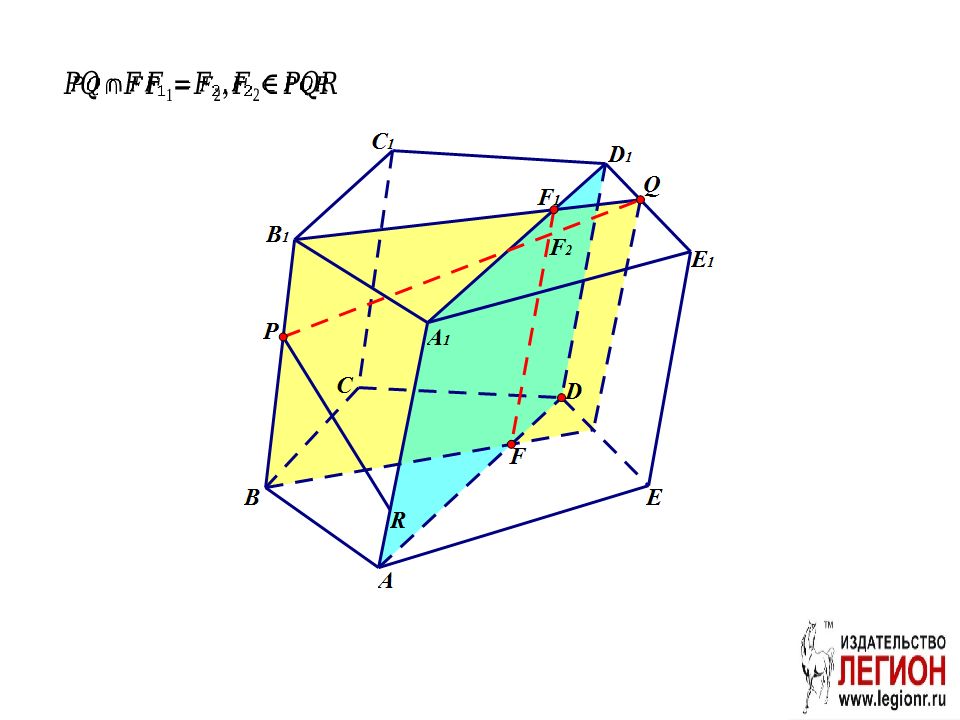
Слайд 39
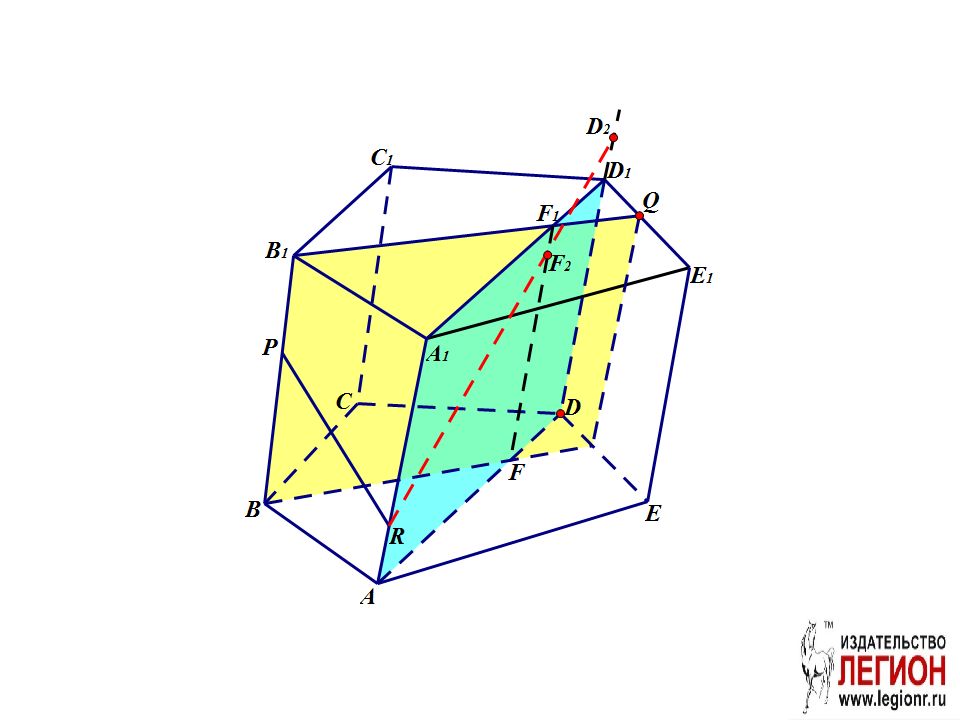
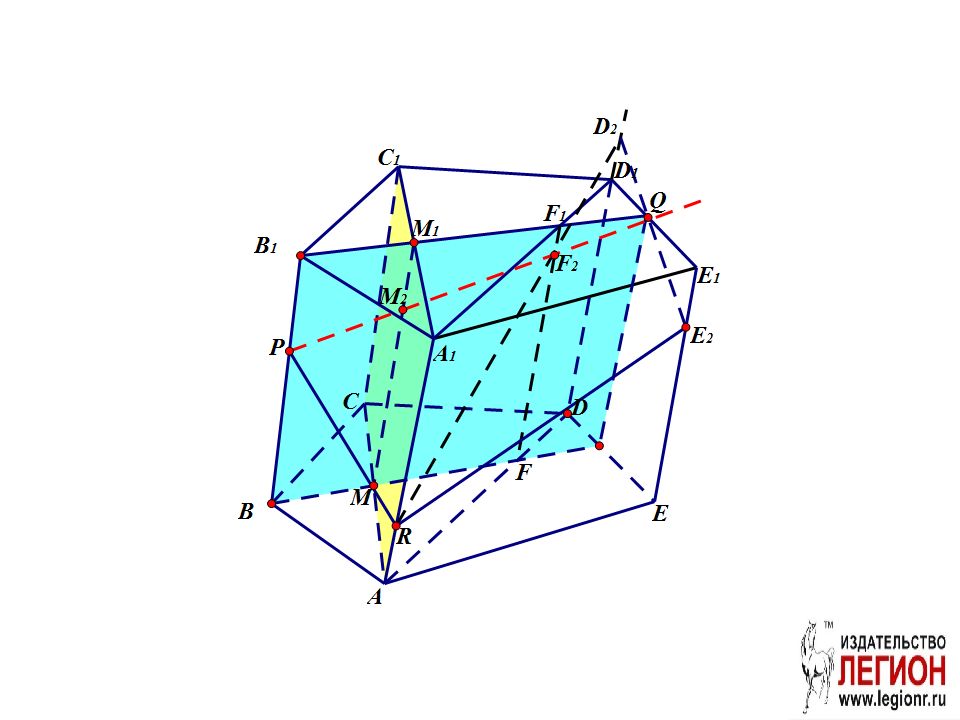
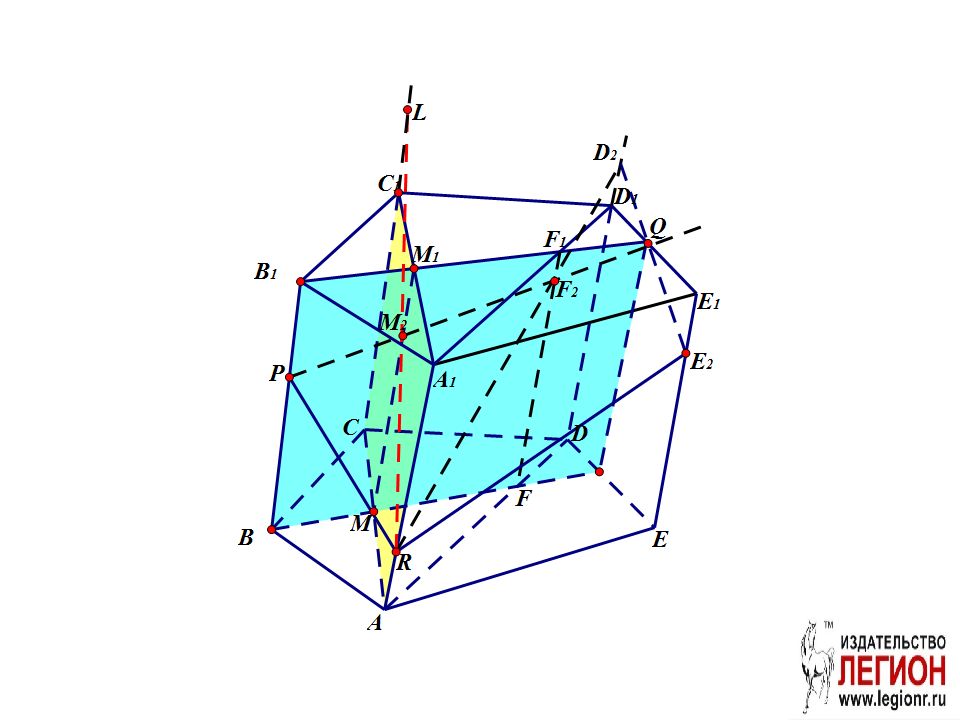
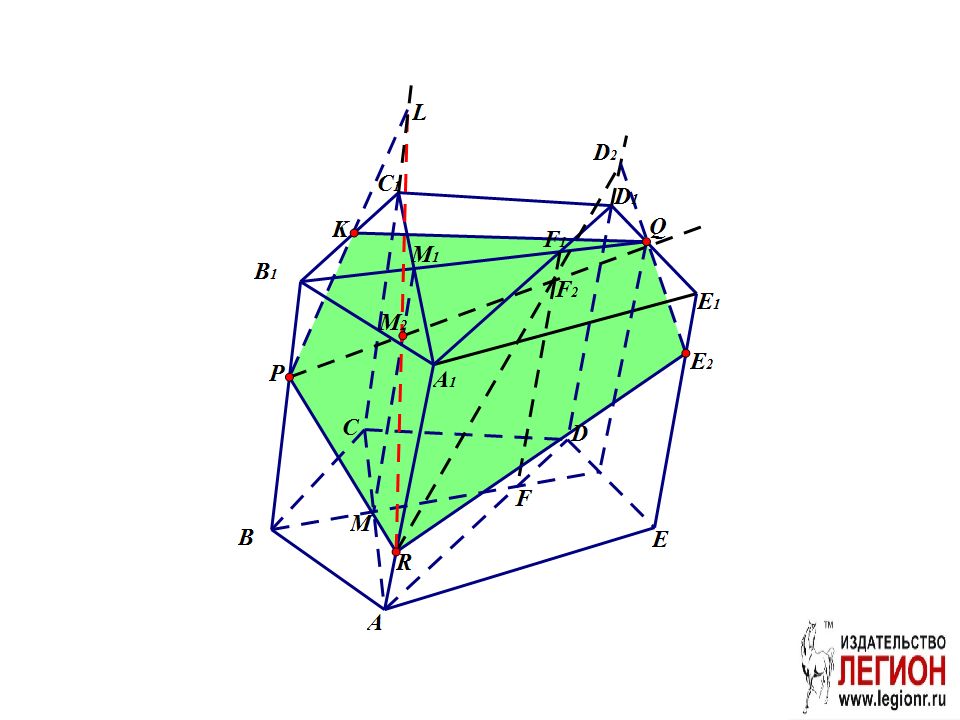
Проведем вспомогательную плоскость ADD 1. FF 1 – линия пересечения ADD 1 и BB 1 Q.
Слайд 47
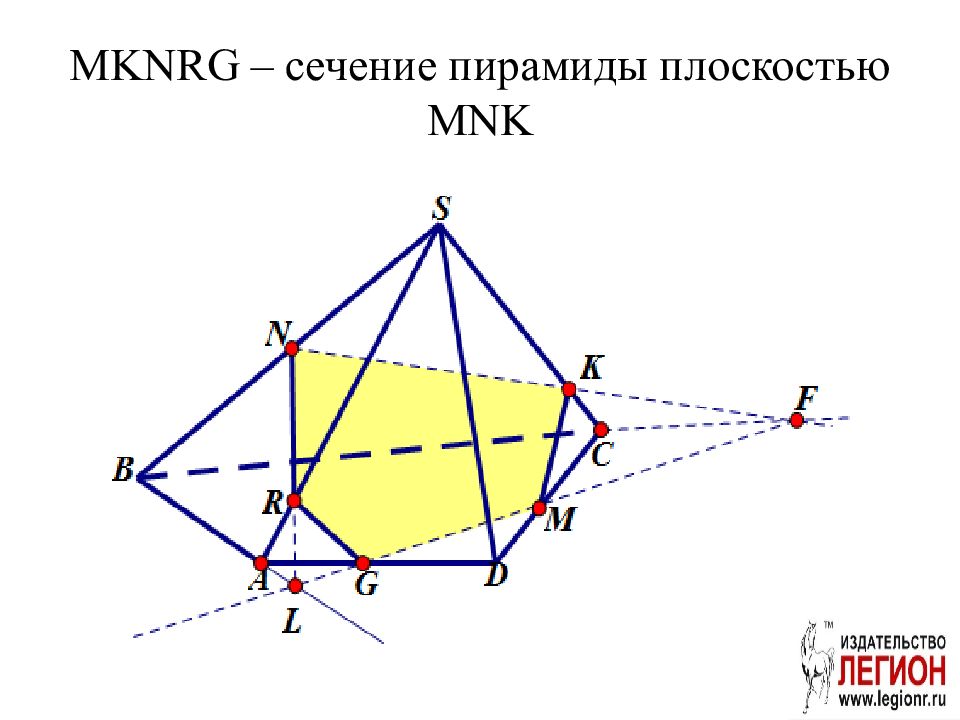
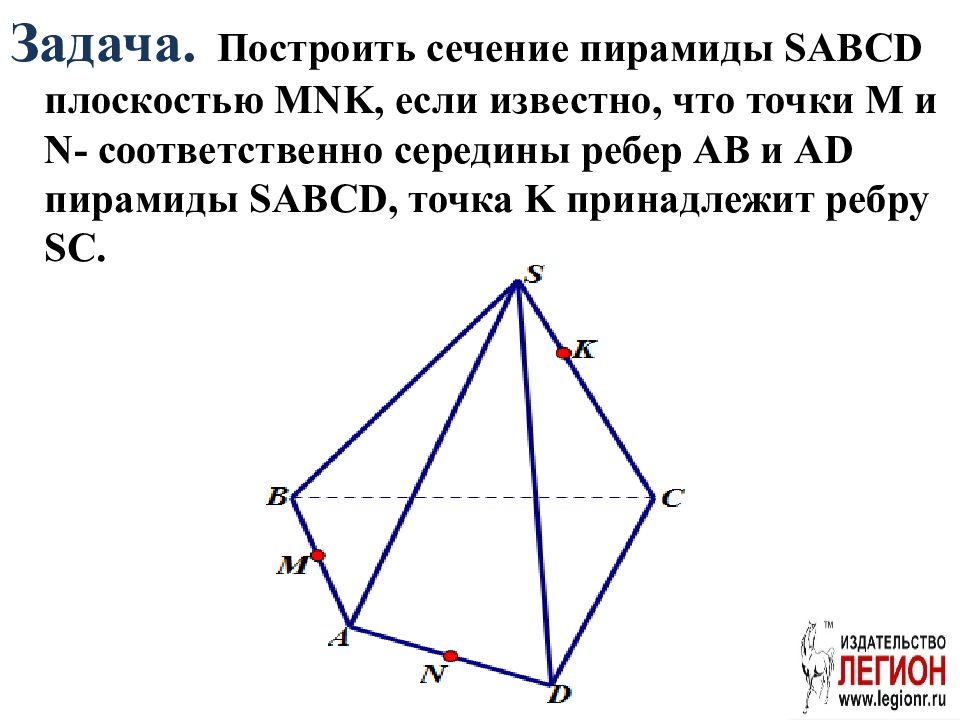
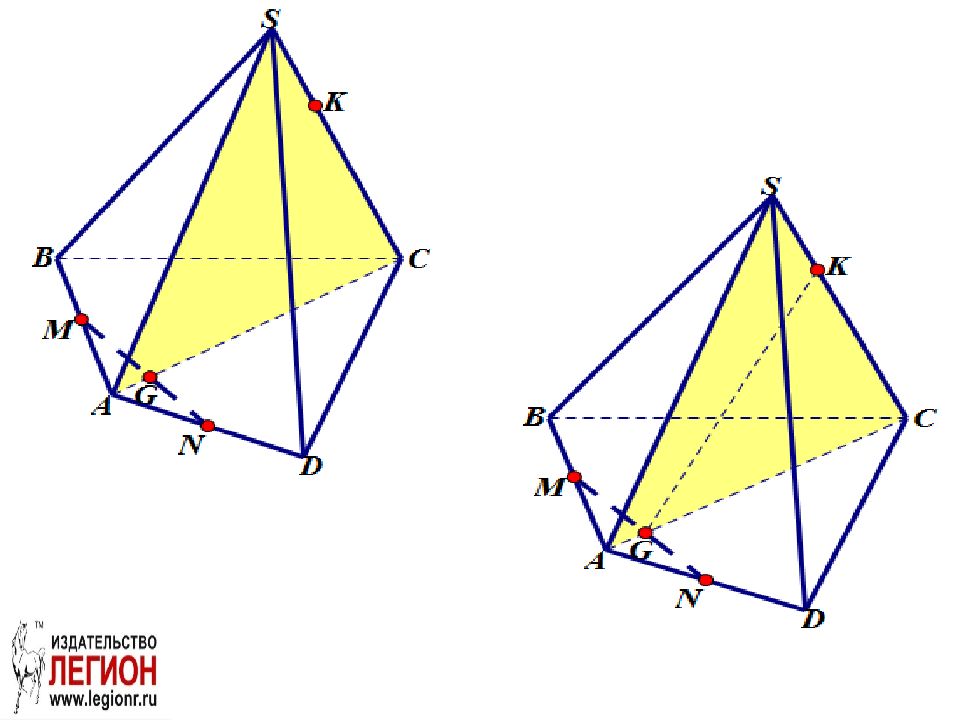
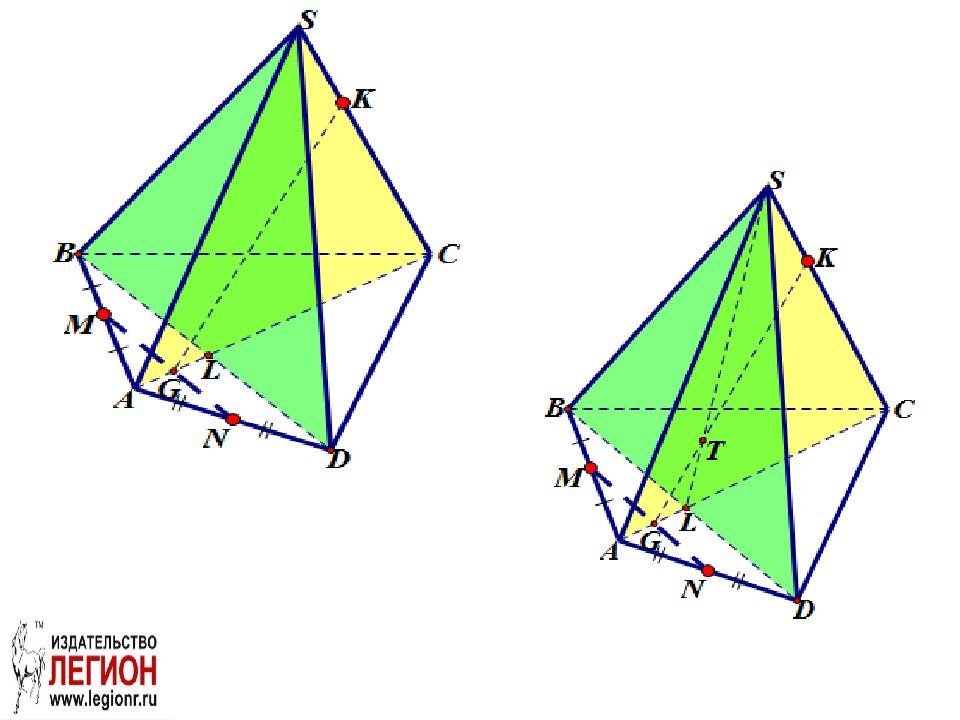
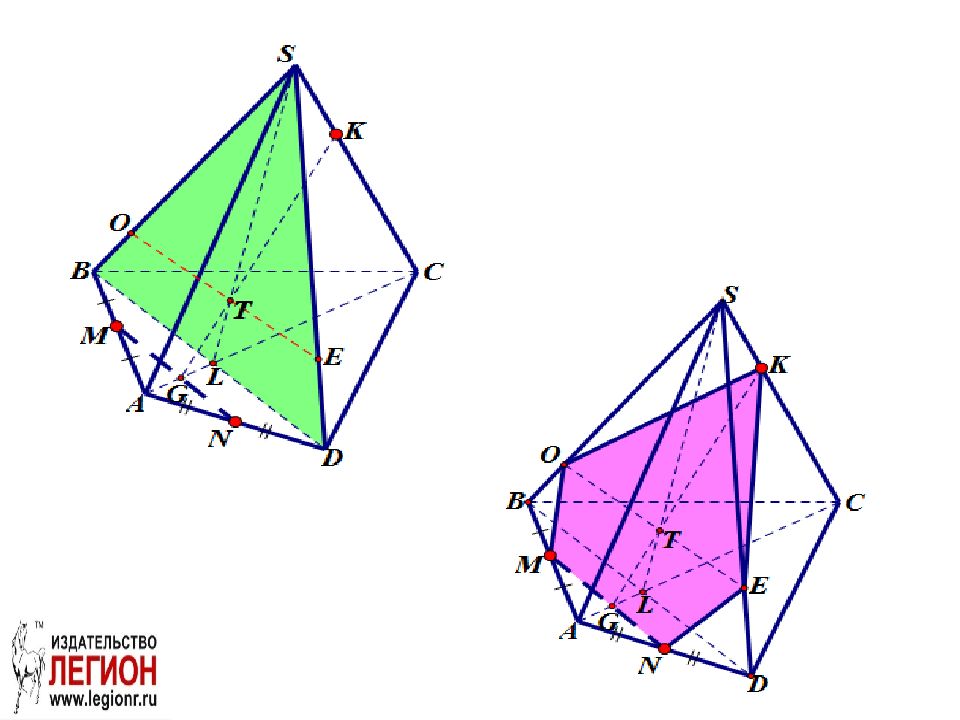
Задача. Построить сечение пирамиды SABCD плоскостью MNK, если известно, что точки M и N - соответственно середины ребер AB и AD пирамиды S ABCD, точка K принадлежит ребру S C.
Слайд 51: Задача
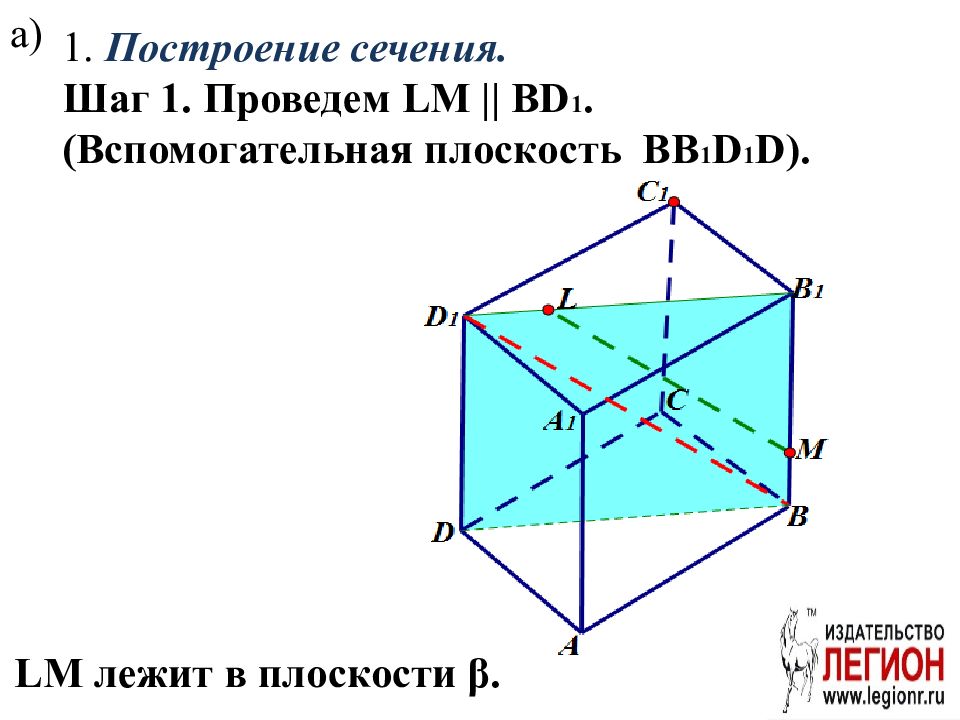
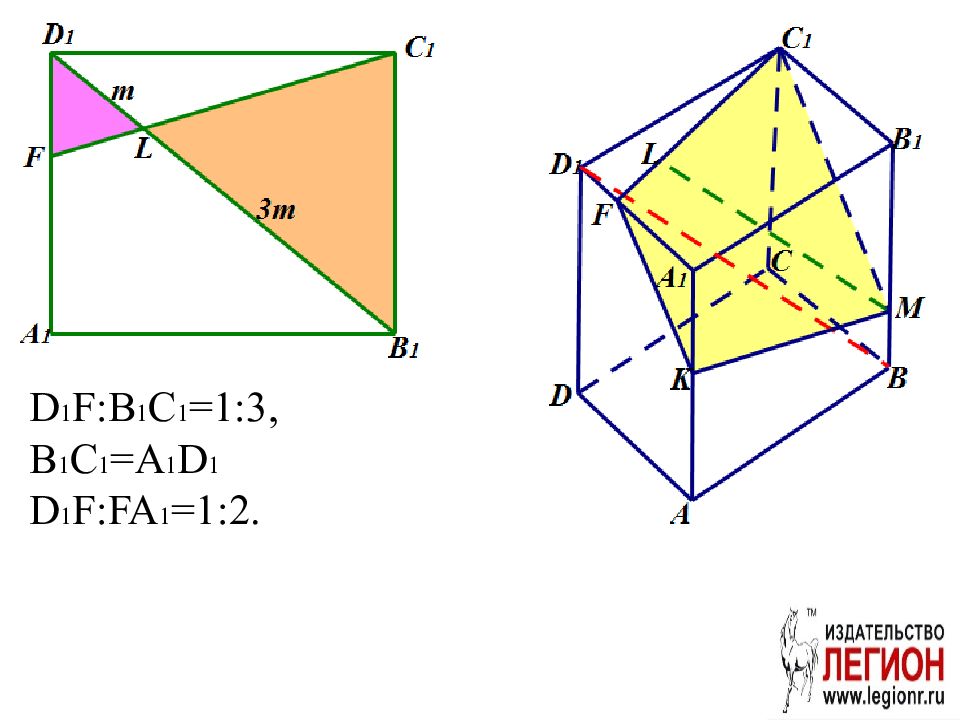
В кубе ABCDA 1 B 1 C 1 D 1 точка M лежит на ребре BB 1 так, что BM:MB 1 =1:3. Через точки M и С 1 параллельно BD 1 проведена плоскость. а) Докажите, что плоскость проходит через середину ребра AA 1. б) Найдите площадь сечения куба плоскостью, если AB=12.
Слайд 52
а) 1. Построение сечения. Шаг 1. Проведем LM || BD 1. ( Вспомогательная плоскость BB 1 D 1 D). LM лежит в плоскости β.
Слайд 53
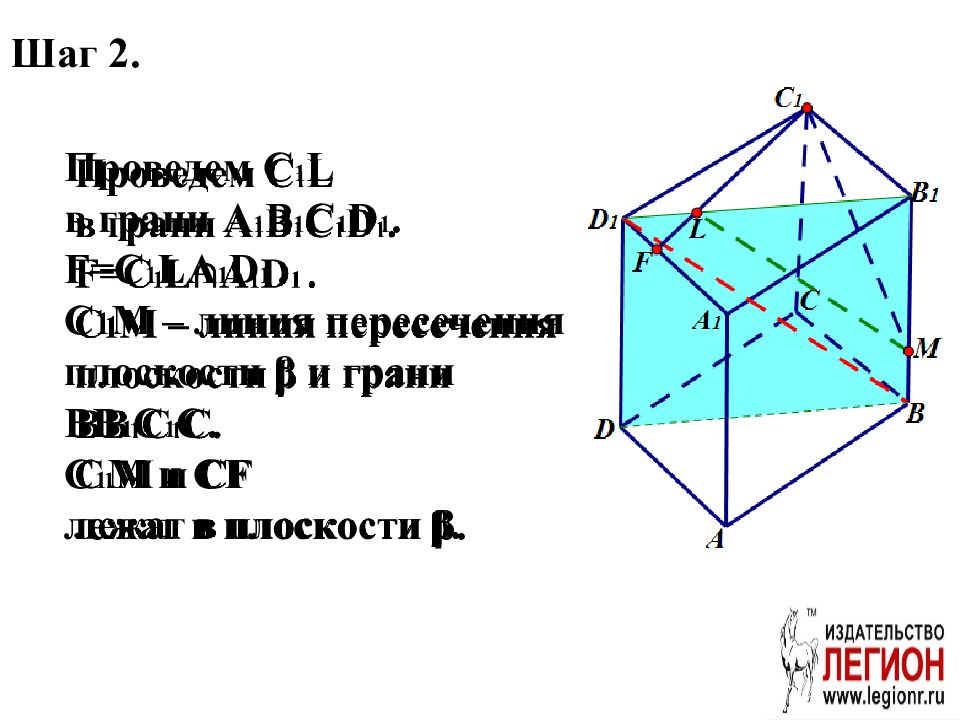
Шаг 2. Проведем С 1 L в грани A 1 B 1 C 1 D 1. F= С 1 L A 1 D 1. С 1 М – линия пересечения плоскости β и грани BB 1 C 1 C. C 1 M и CF лежат в плоскости β.
Слайд 54
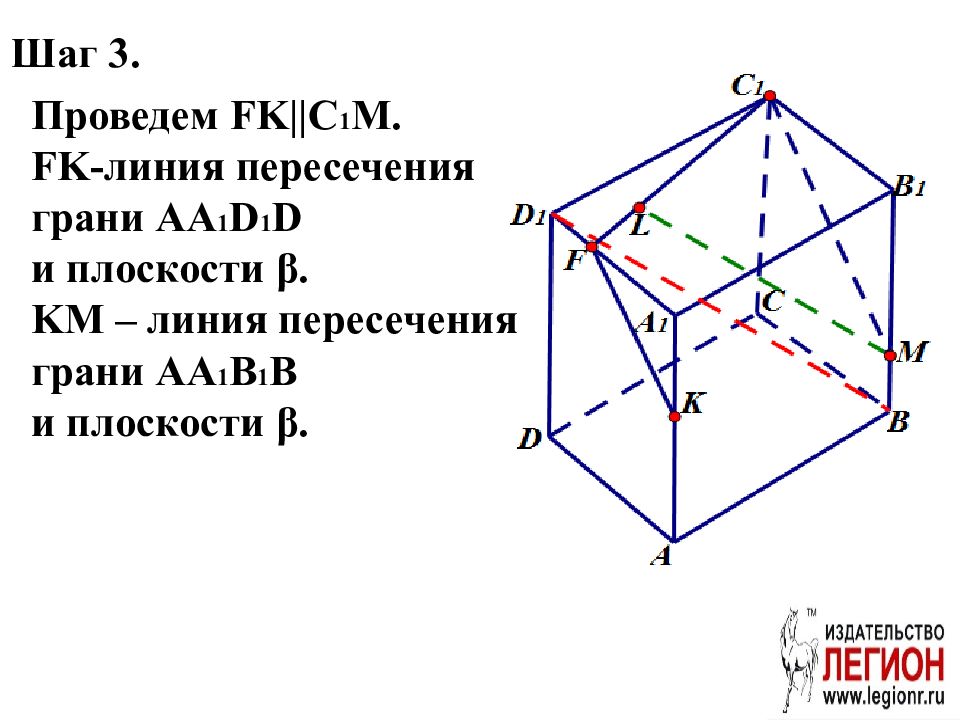
Шаг 3. Проведем FK||C 1 M. FK -линия пересечения грани AA 1 D 1 D и плоскости β. KM – линия пересечения грани AA 1 B 1 B и плоскости β.
Слайд 58
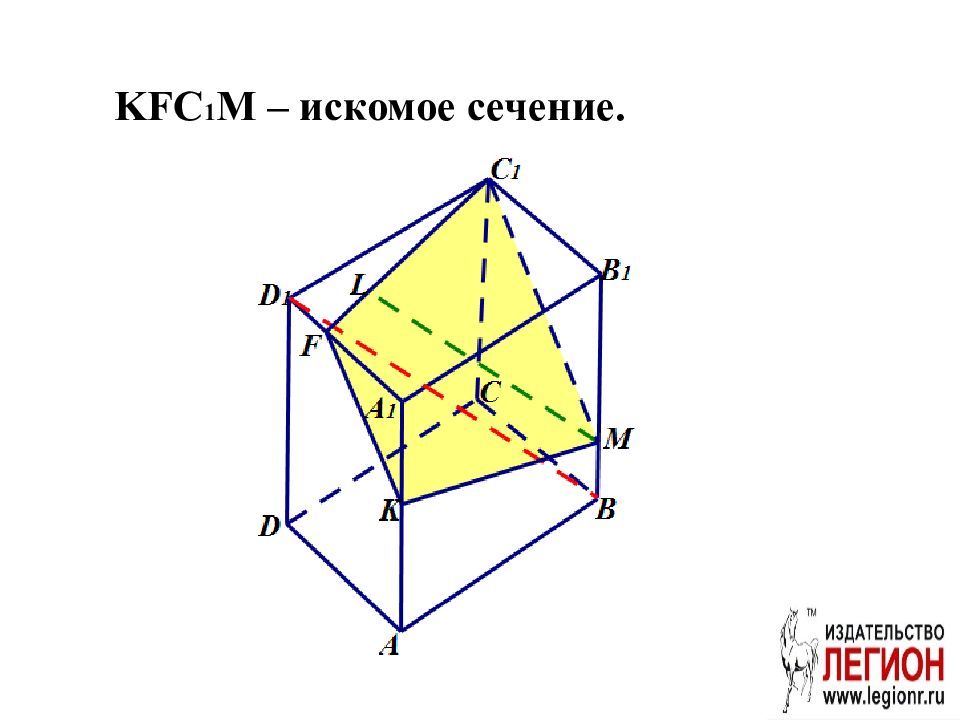
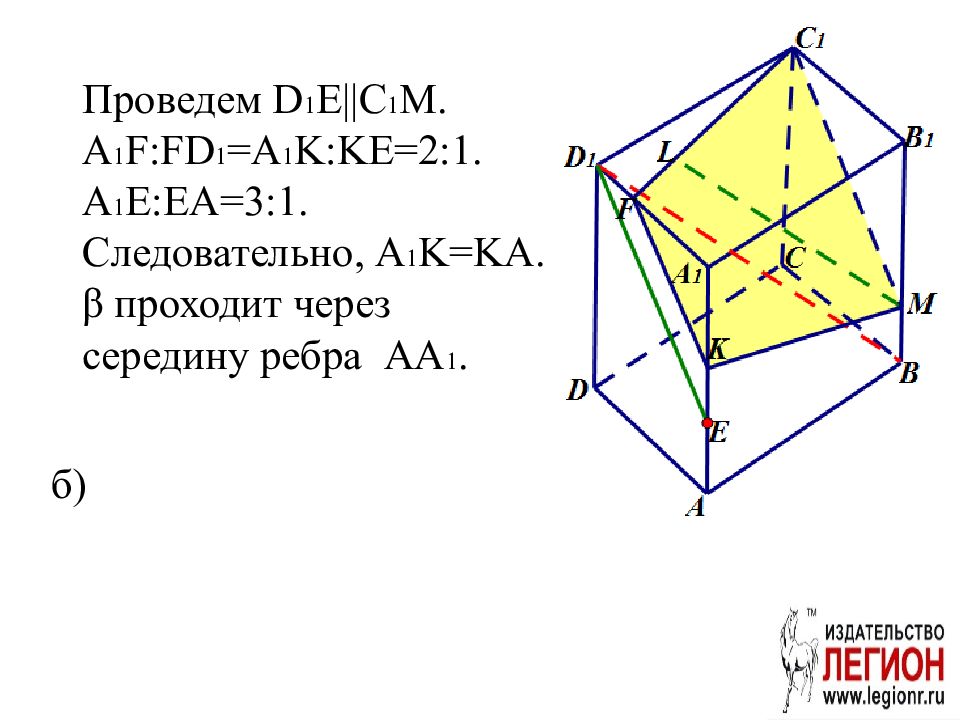
Проведем D 1 E||C 1 M. A 1 F:FD 1 =A 1 K:KE=2:1. A 1 E:EA=3:1. Следовательно, A 1 K=KA. β проходит через середину ребра AA 1. б )
Слайд 59
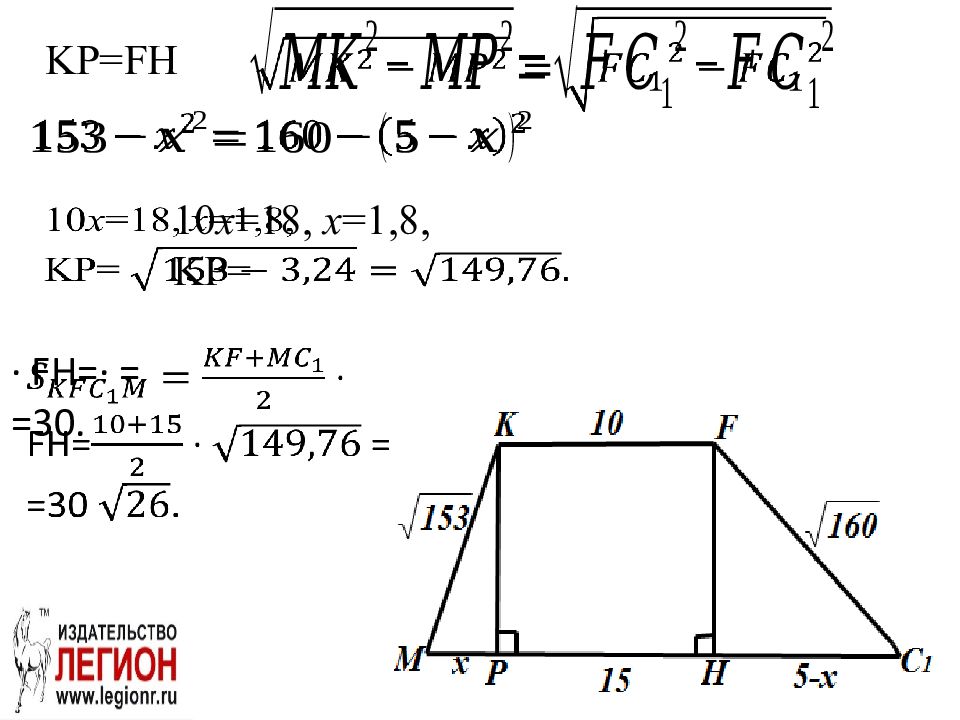
Сечение KFC 1 M – трапеция, AB=12 по условию. · FH : KF= KF=10. : = : F = KM
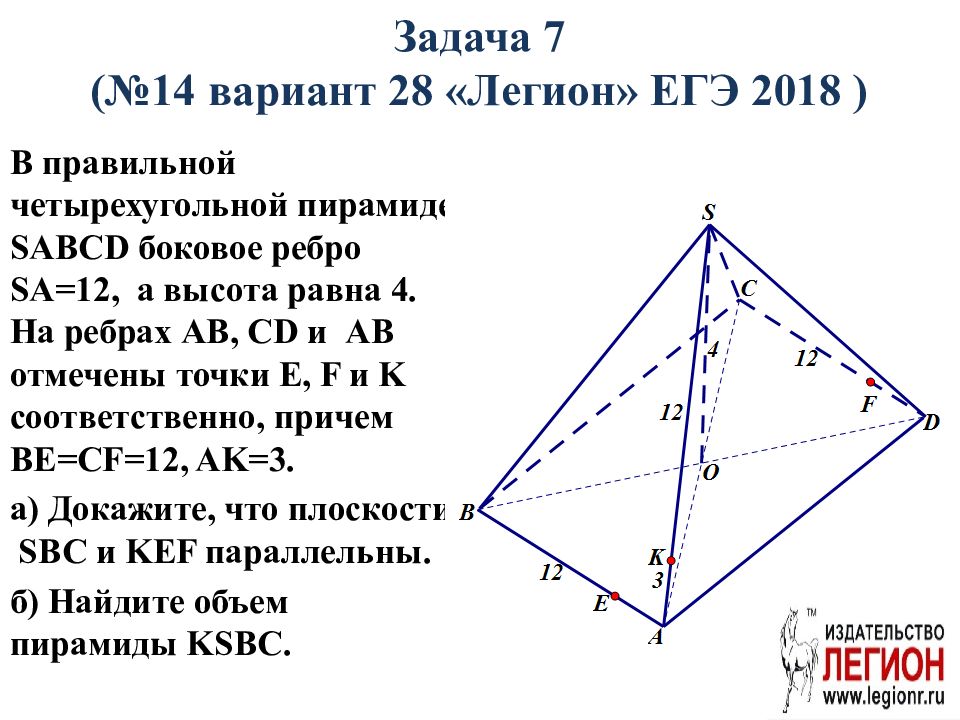
Слайд 61: Задача 7 (№ 1 4 вариант 28 «Легион» ЕГЭ 2018 )
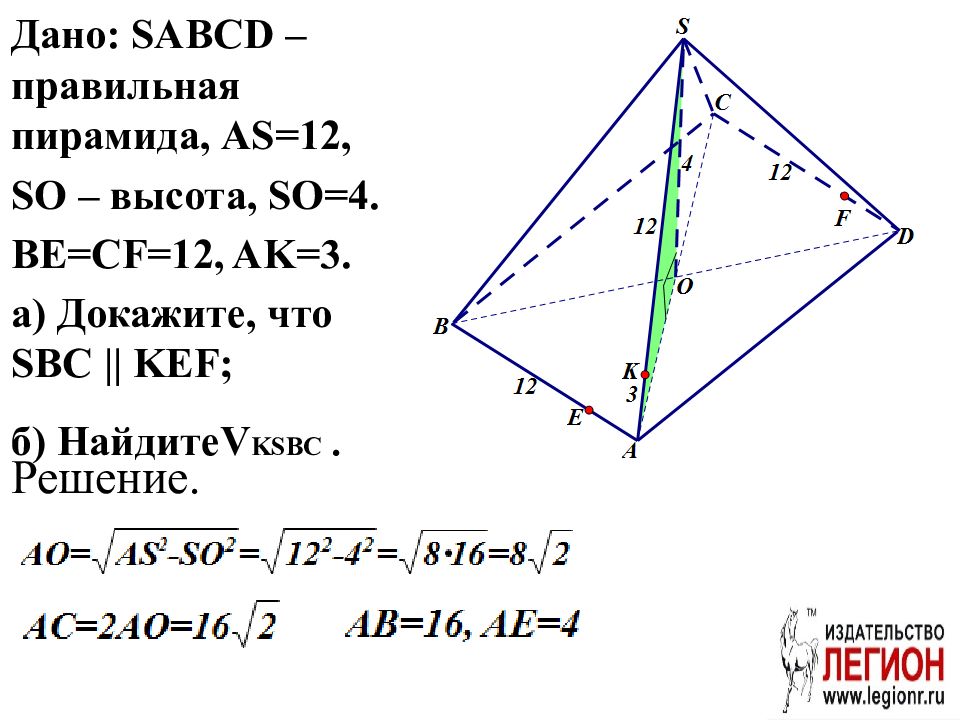
В правильной четырехугольной пирамиде SABCD боковое ребро SA=12, а высота равна 4. На ребрах AB, CD и AB отмечены точки E, F и K соответственно, причем BE=CF=12, AK=3. а ) Докажите, что плоскости SBC и KEF параллельны. б ) Найдите объем пирамиды KSBC.
Слайд 62
Дано: SABCD – правильная пирамида, AS=12, SO – высота, SO=4. BE=CF=12, AK=3. а ) Докажите, что SBC || KEF; б ) Найдите V KSBC. Решение.
Слайд 64: Решение
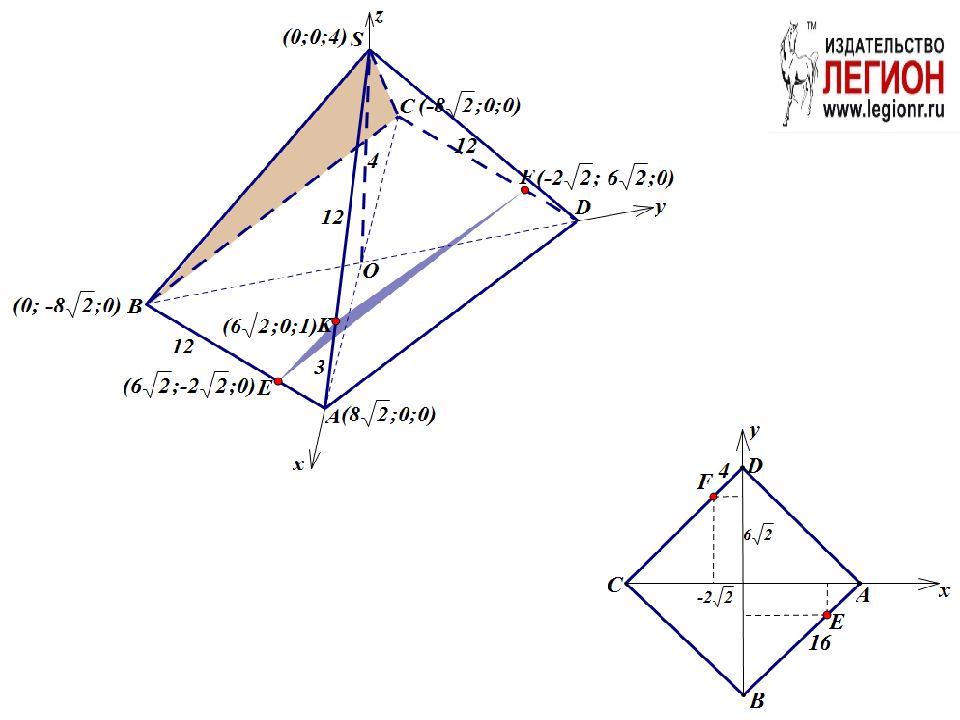
SBC || KEF ( векторы нормалей). = {l; m; n} = { ; ; -1} = { ; ; -1} Способ 1 ⇔
Слайд 65: Способ 2
SBC ||KEF ⇔ (SB||EK и BC||EF) Δ SBA~ Δ AEK:, ∠ SAB – общий, ⇒ SB||EK. AE=FD=4, ⇒ EF||BC.
Слайд 66
б) V KSBC = = SC·sin ∠ SBC ( cos ∠ SBC = ) или = SH, где SH – высота Δ SBC. = Уравнение плоскости SBC: x+ y-z+d=0, где = { ; ; -1 } - вектор нормали к плоскости SBC. d : S(0;0;4)
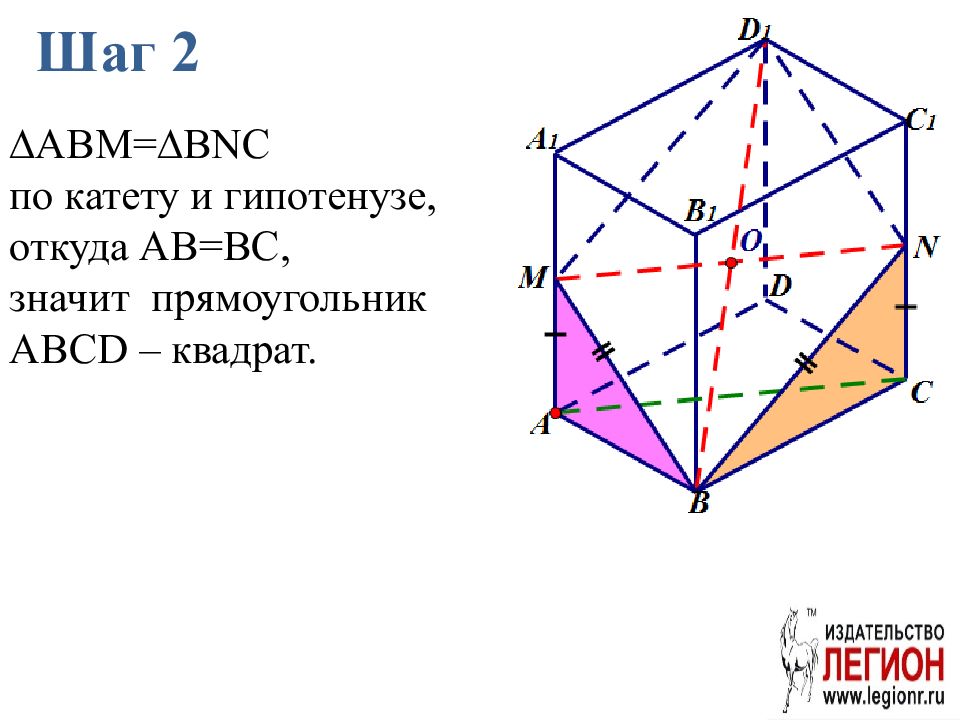
Слайд 71: Шаг 2
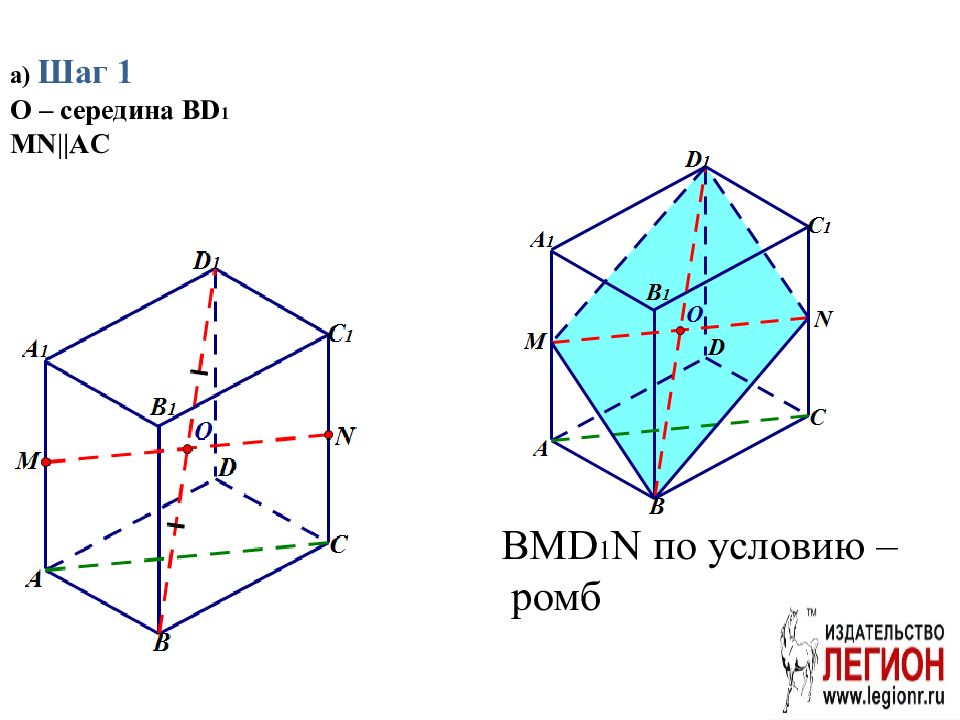
∆ ABM=∆BNC по катету и гипотенузе, откуда AB=BC, значит прямоугольник ABCD – квадрат.
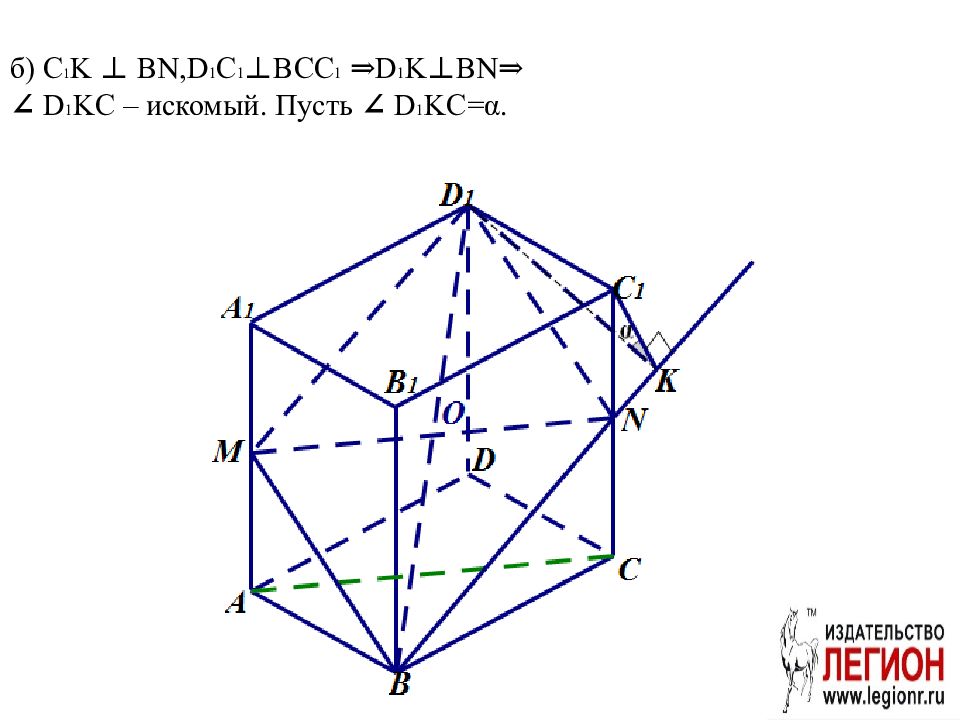
Слайд 72: б) C 1 K ⊥ BN,D 1 C 1 ⊥ BCC 1 ⇒D 1 K ⊥ BN⇒ ∠ D 1 KC – искомый. Пусть ∠ D 1 KC = α
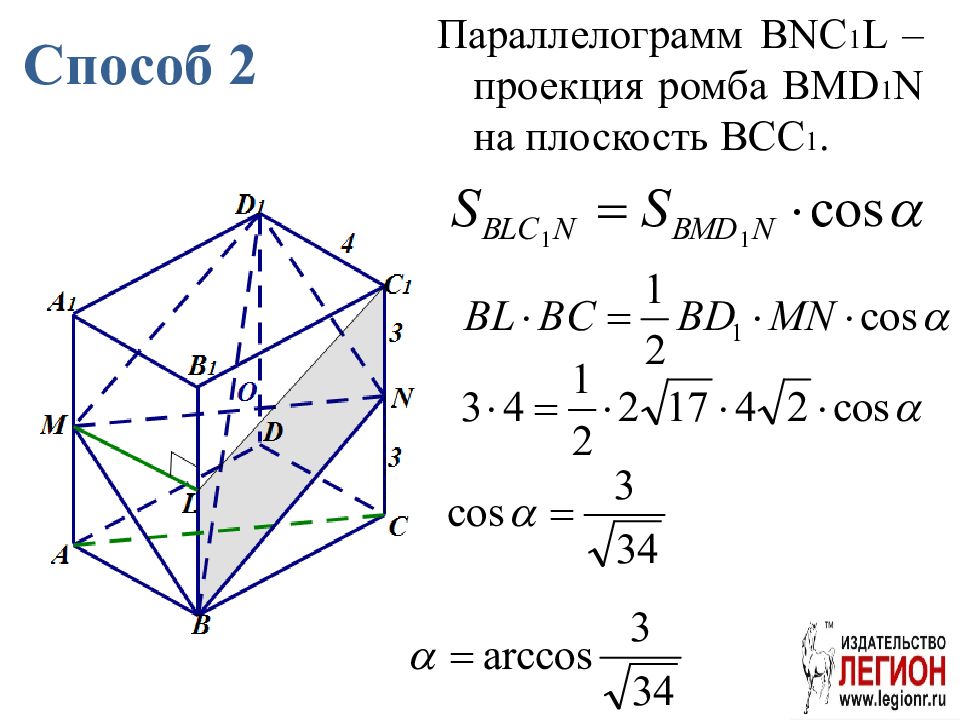
Слайд 74: Способ 2
Параллелограмм BNC 1 L – проекция ромба BMD 1 N на плоскость BCC 1.
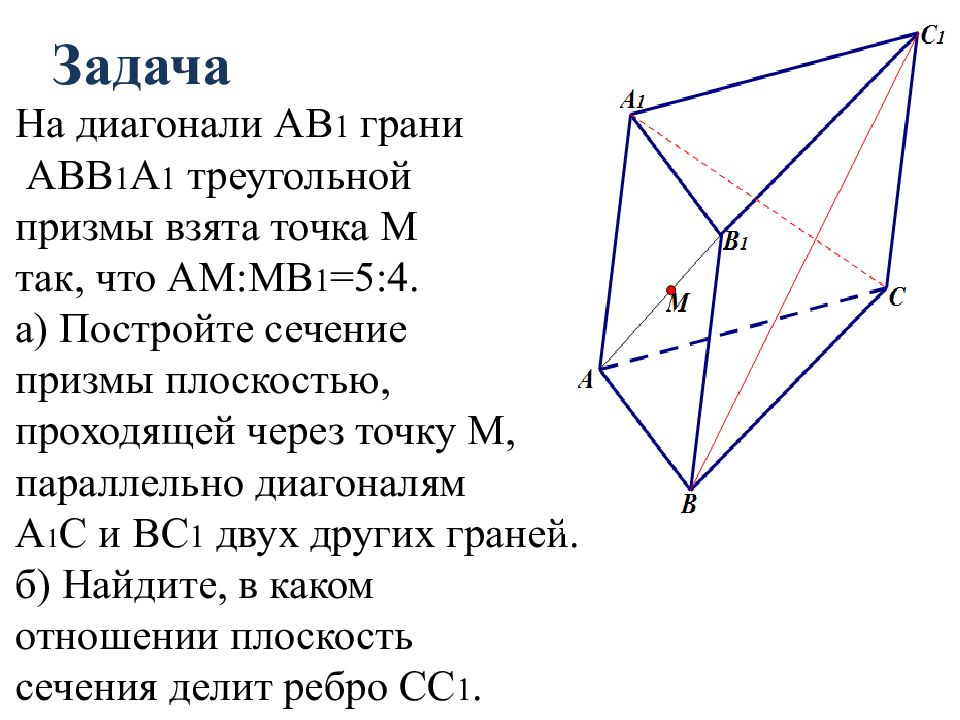
Слайд 77: Задача
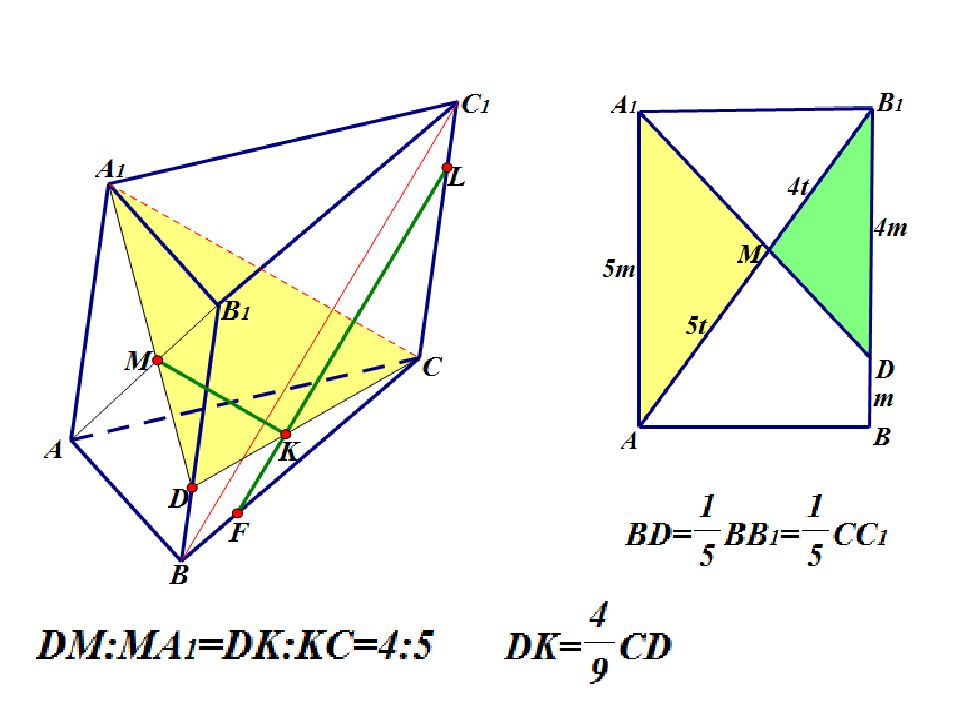
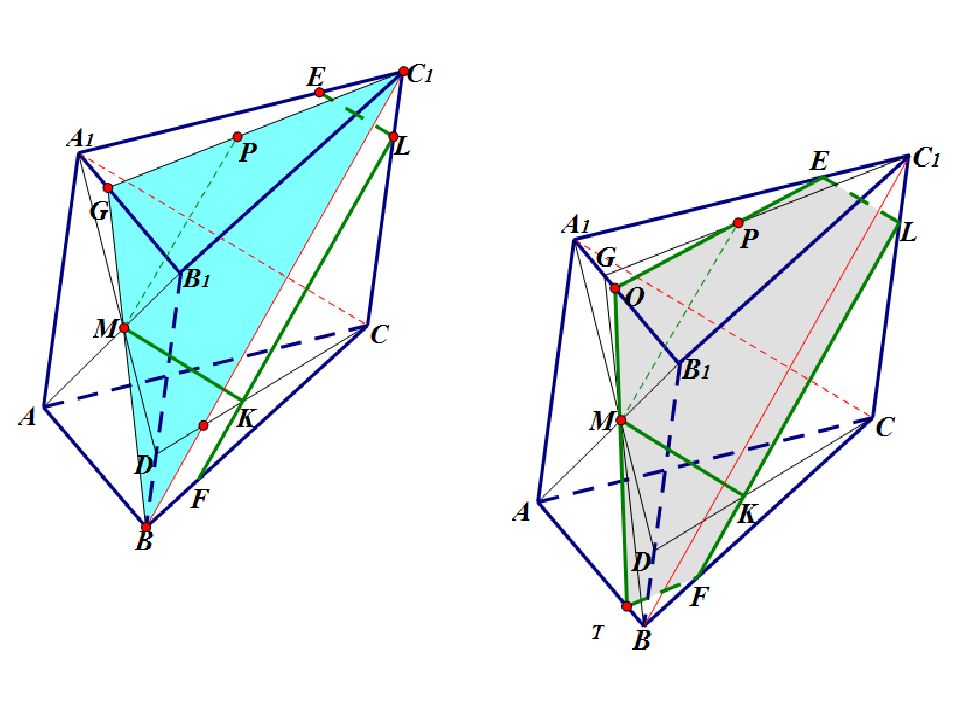
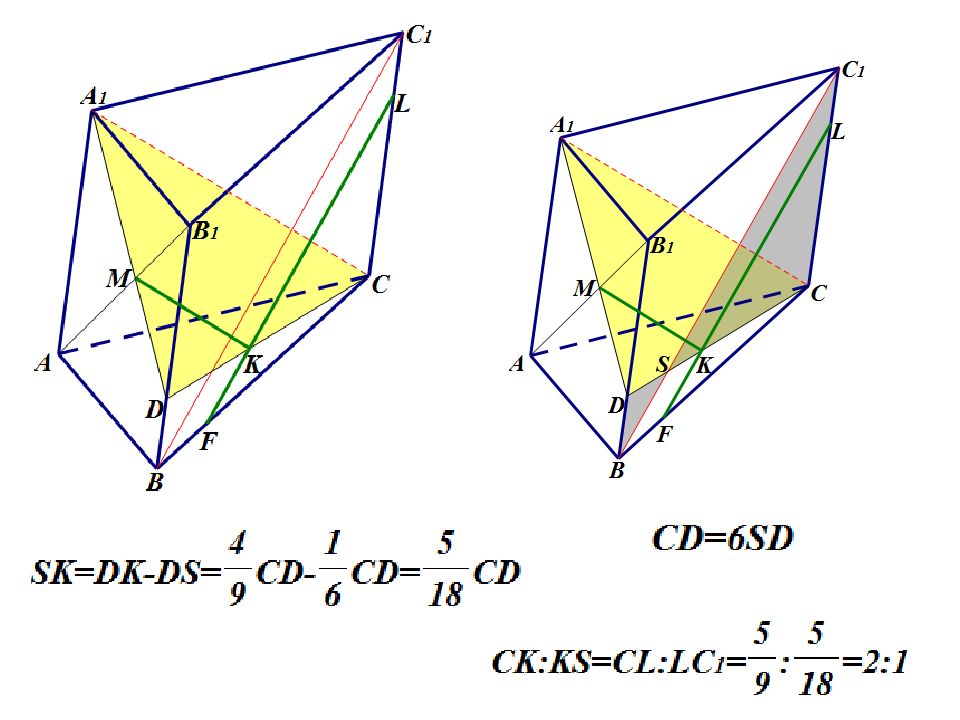
На диагонали AB 1 грани ABB 1 А 1 треугольной призмы взята точка M так, что AM:MB 1 =5:4. а ) Постройте сечение призмы плоскостью, проходящей через точку M, параллельно диагоналям A 1 С и BC 1 двух других граней. б ) Найдите, в каком отношении плоскость сечения делит ребро СС 1.
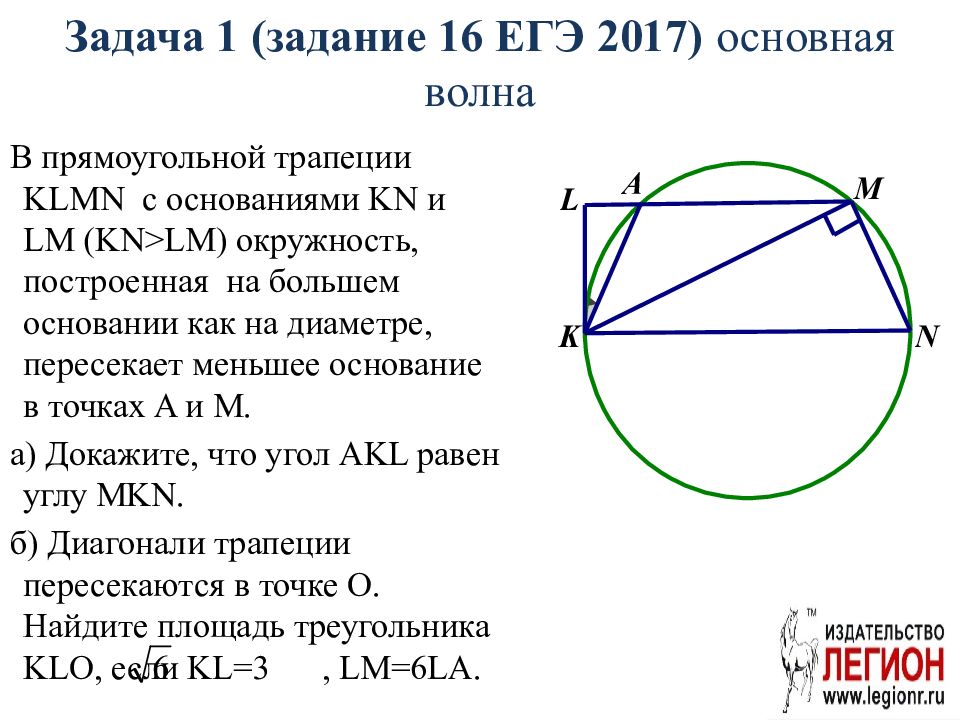
Слайд 84: Задача 1 (задание 16 ЕГЭ 2017) основная волна
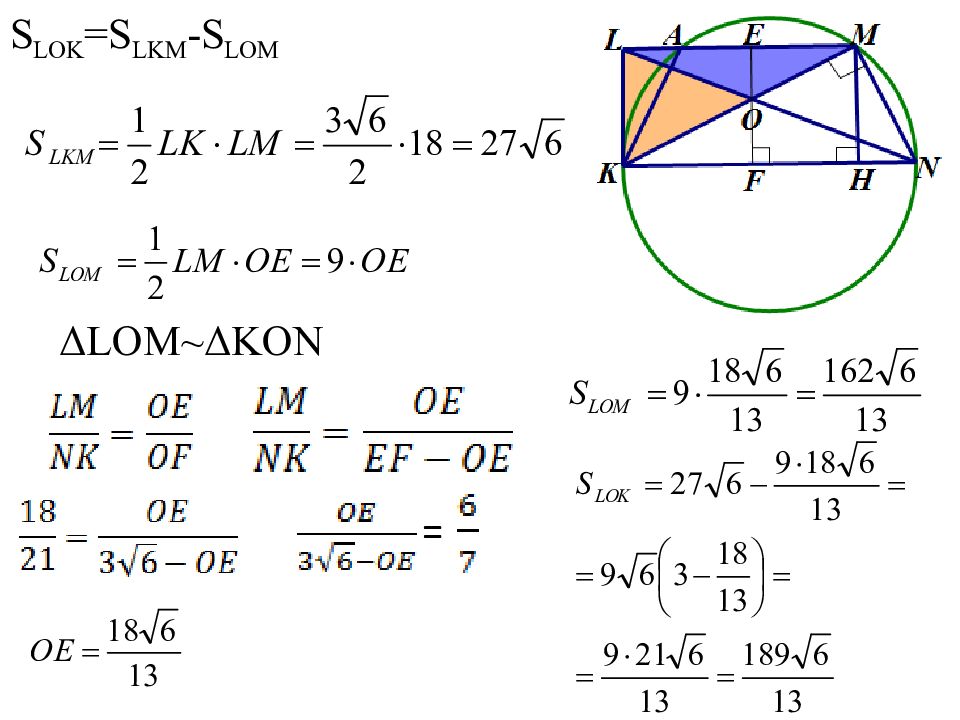
В прямоугольной трапеции KLMN с основаниями KN и LM ( KN > LM ) окружность, построенная на большем основании как на диаметре, пересекает меньшее основание в точках A и M. а) Докажите, что угол AKL равен углу MKN. б) Диагонали трапеции пересекаются в точке O. Найдите площадь треугольника KLO, если KL =3, LM =6 LA.
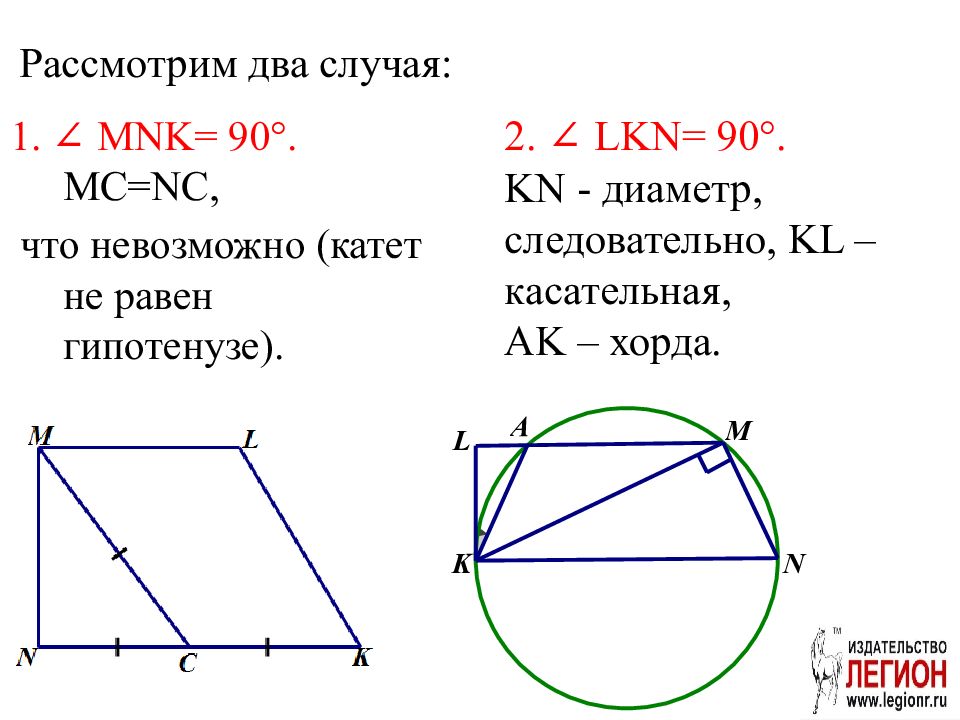
Слайд 85: Рассмотрим два случая:
1. ∠ MNK = 90°. MC=NC, что невозможно (катет не равен гипотенузе). 2. ∠ LKN = 90°. KN - диаметр, следовательно, KL – касательная, AK – хорда.
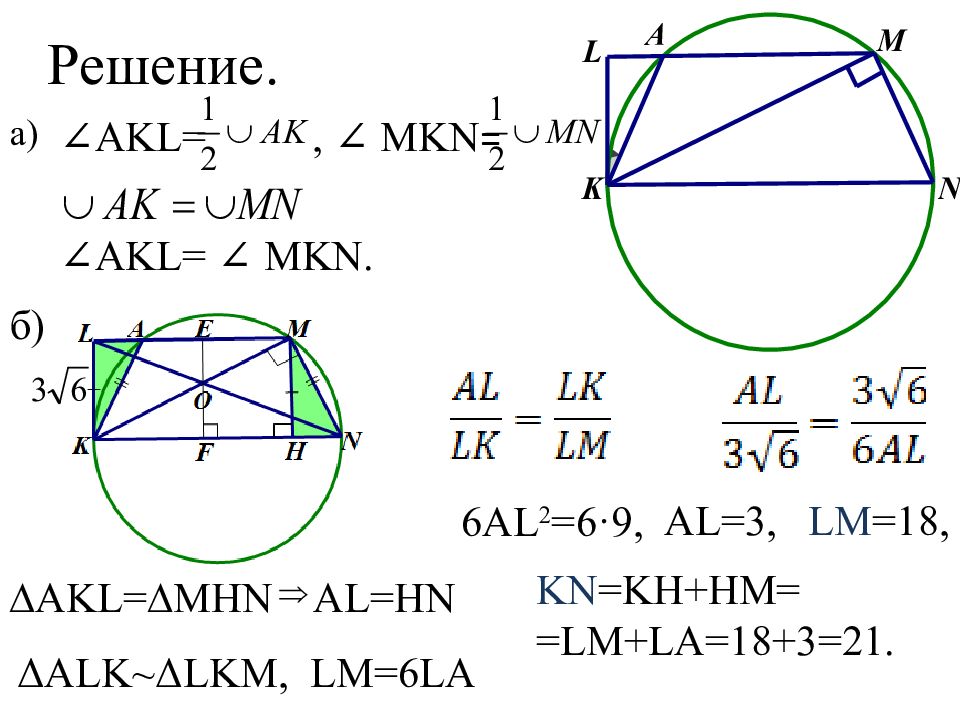
Слайд 86: Решение
∠ AKL =, ∠ MKN = ∠ AKL = ∠ MKN. а) б) ∆AKL=∆MHN AL = HN ΔALK ~ ΔLKM, LM=6LA 6AL 2 =6·9, AL=3, LM =18, KN =KH+HM= =LM+LA=18+3=21.
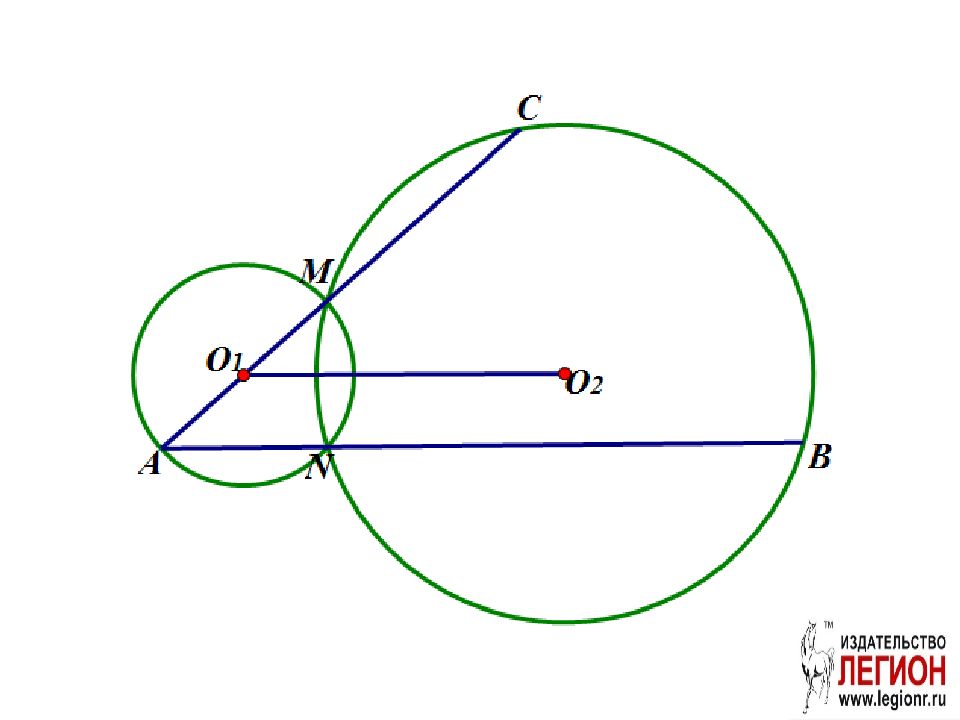
Слайд 88: Задача (№ 16 вариант 15 «Легион» ЕГЭ 2018 )
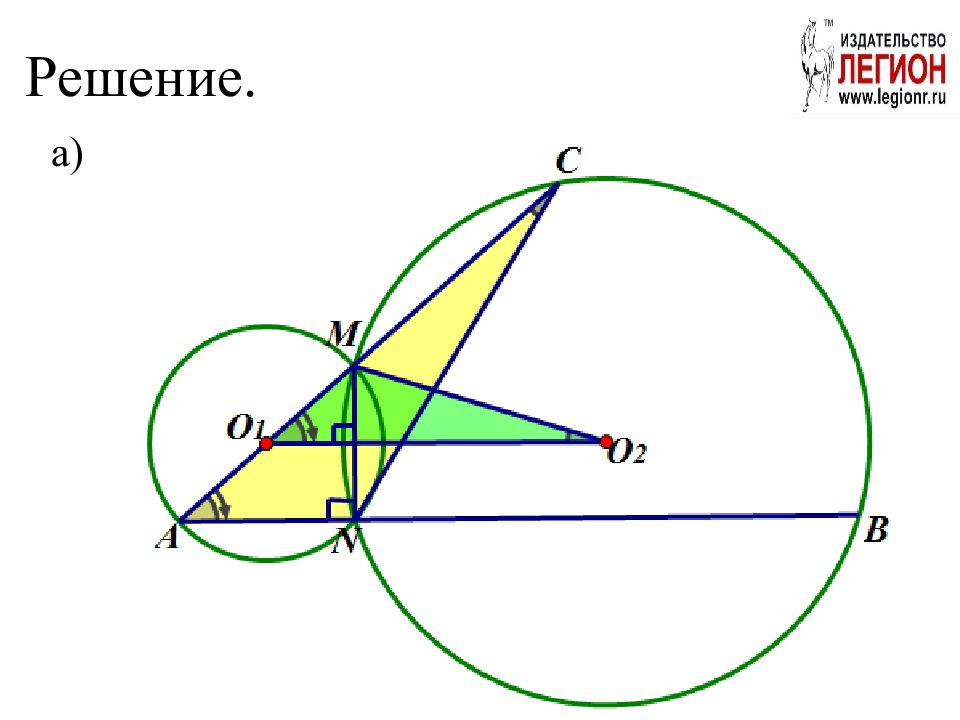
Две окружности с центрами O 1 и O 2 пересекаются в точках M и N, причем точки O 1 и O 2 лежат по разные стороны от прямой MN. Продолжение диаметра AM первой окружности и хорды AN этой же окружности пересекают вторую окружность в точках C и B соответственно. а ) Докажите, что треугольники ANC и O 1 MO 2 подобны; б) Найдите MC, если ∠ CMB= ∠ NMA, а радиус второй окружности в 2,5 раза больше радиуса первой и MN=2.
Слайд 92
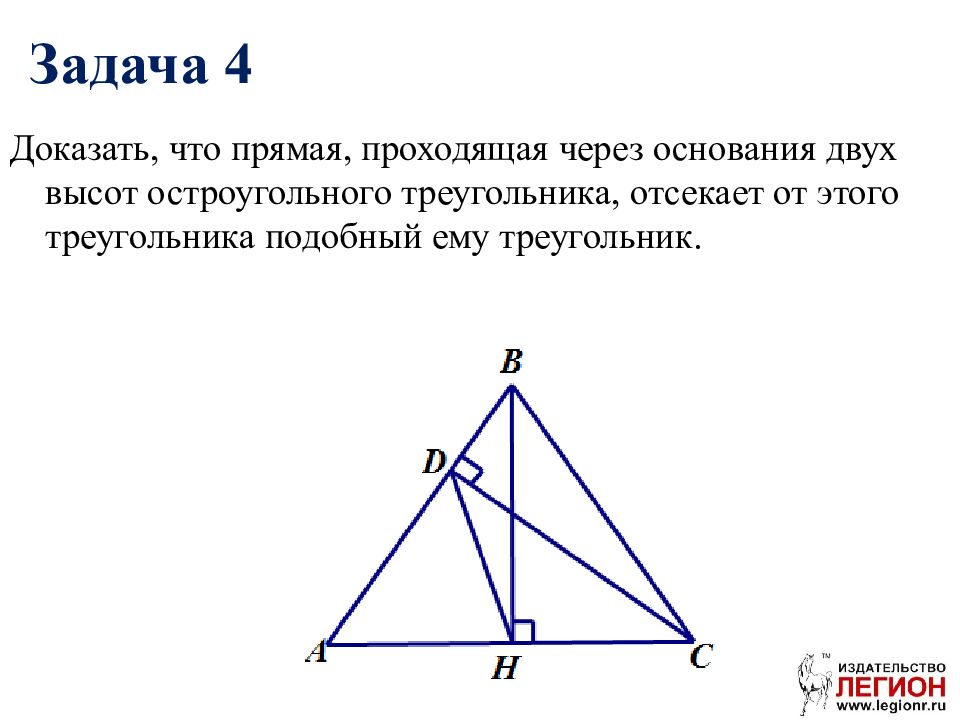
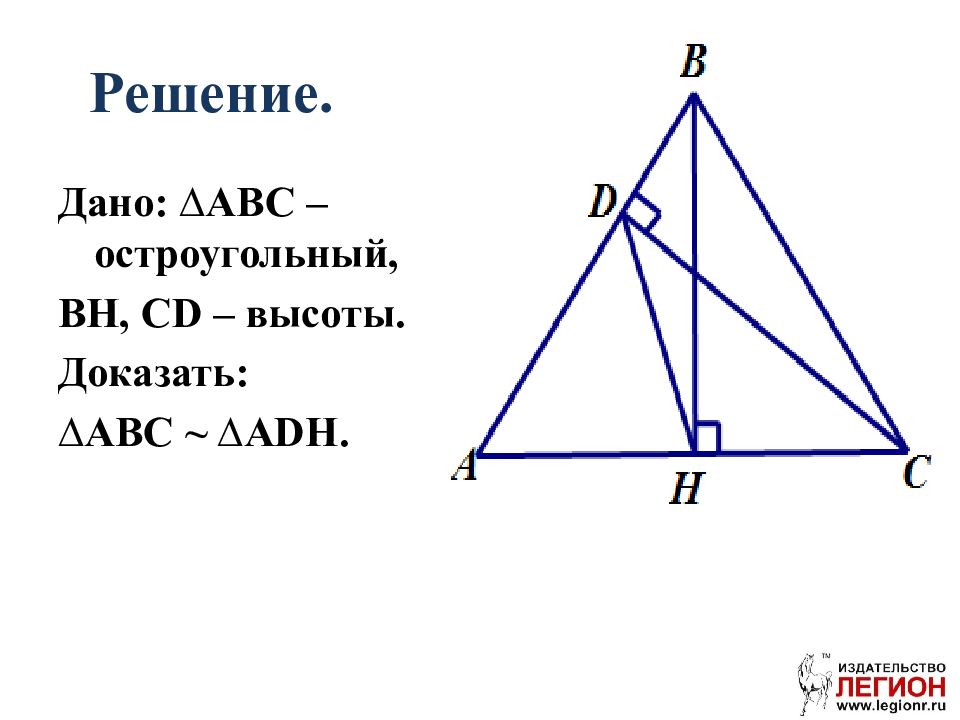
Доказать, что прямая, проходящая через основания двух высот остроугольного треугольника, отсекает от этого треугольника подобный ему треугольник. Задача 4
Слайд 93: Решение
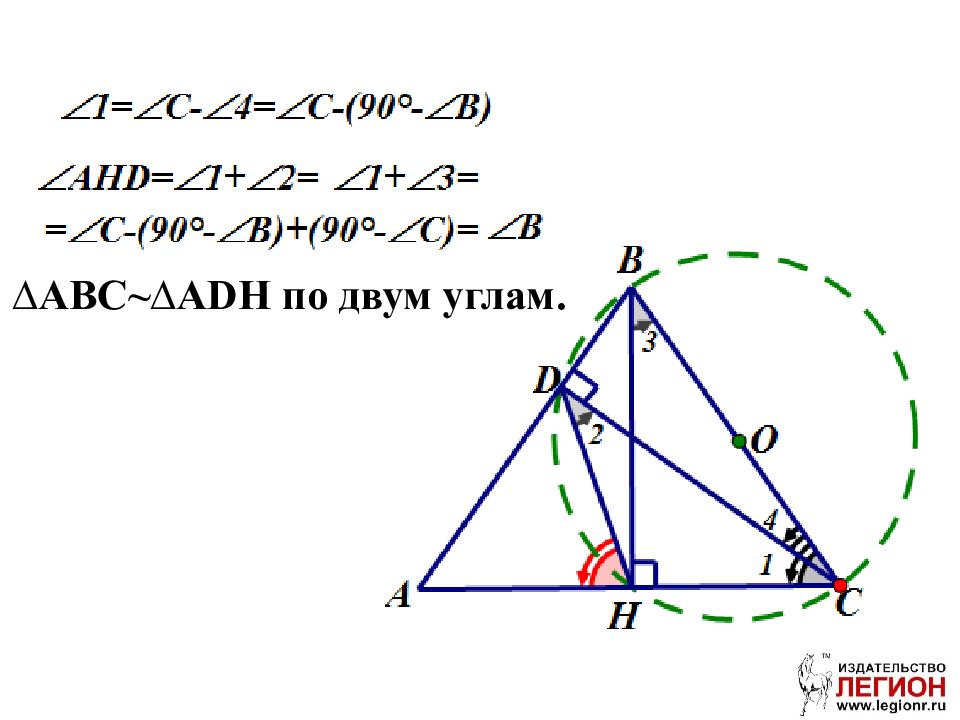
Дано: ∆ ABC – остроугольный, BH, CD – высоты. Доказать: ∆ ABC ~ ∆ ADH.
Слайд 94
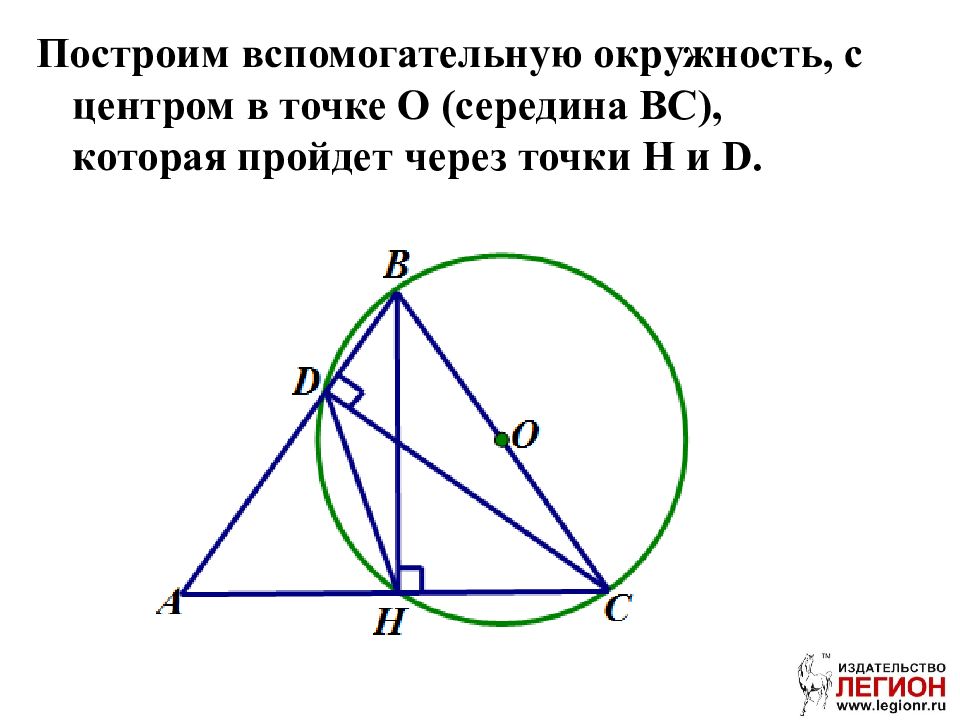
Построим вспомогательную окружность, с центром в точке О (середина ВС), которая пройдет через точки H и D.
Слайд 96: Задача
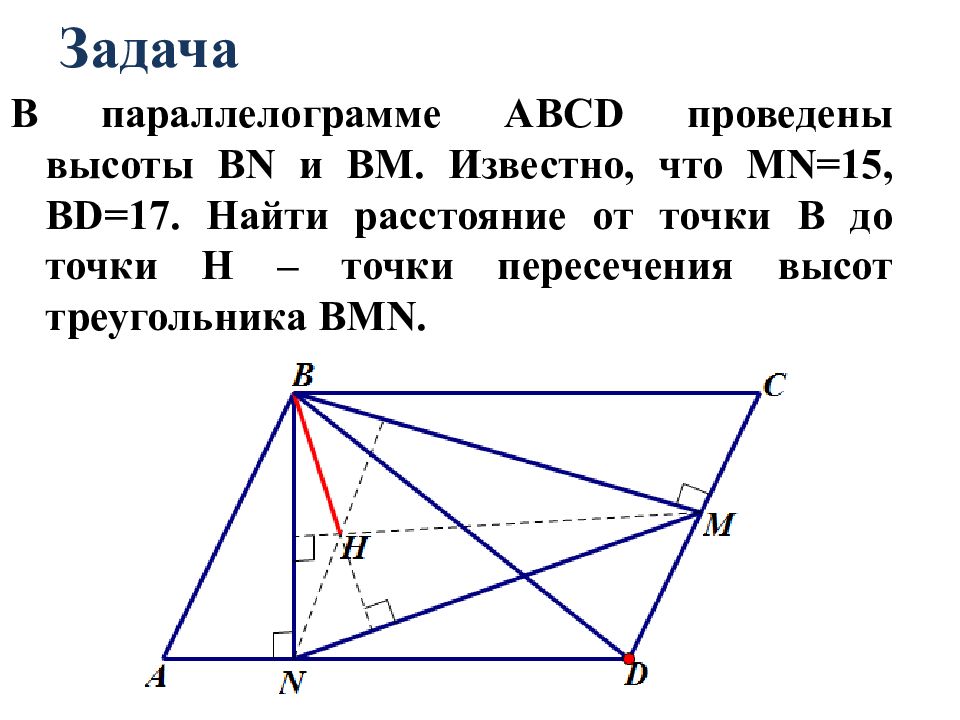
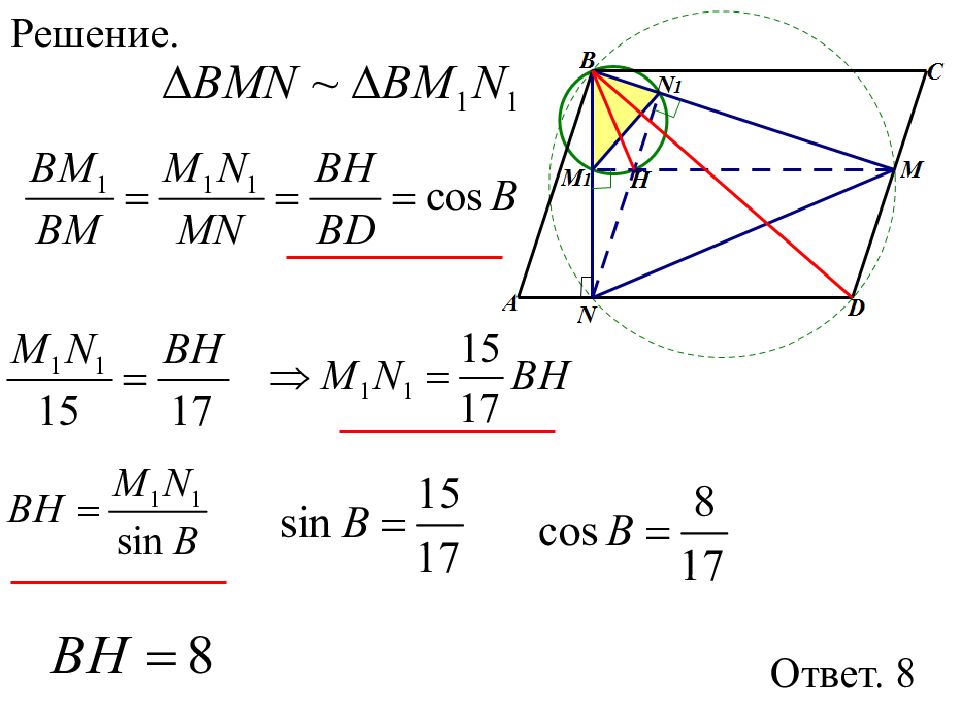
В параллелограмме АВСD проведены высоты ВN и ВМ. Известно, что МN=15, ВD=17. Найти расстояние от точки В до точки Н – точки пересечения высот треугольника ВМ N.
Слайд 98: Задача
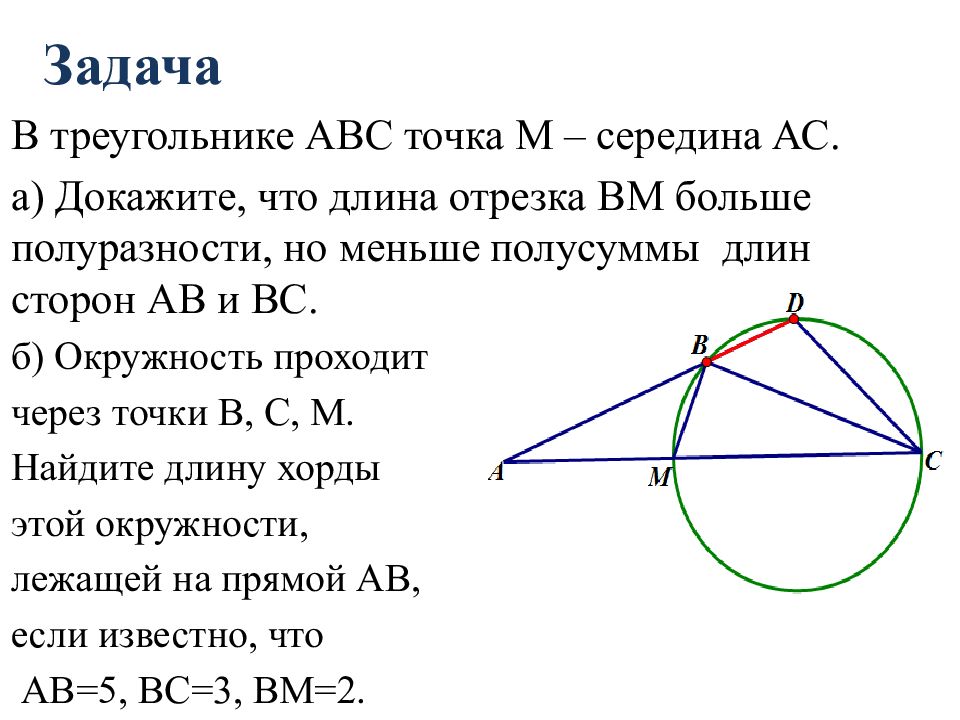
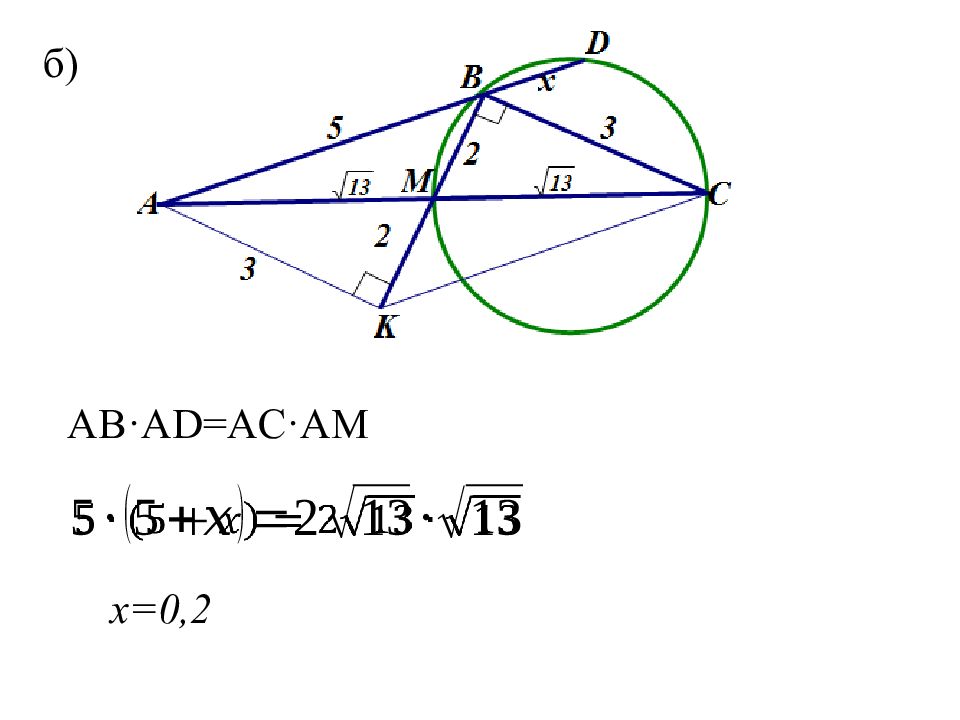
В треугольнике АВС точка М – середина АС. а) Докажите, что длина отрезка ВМ больше полуразности, но меньше полусуммы длин сторон АВ и ВС. б ) Окружность проходит через точки В, С, М. Найдите длину хорды этой окружности, лежащей на прямой АВ, если известно, что АВ=5, ВС=3, ВМ=2.