Пусть дана бесконечная последовательность . Определение. Выражение называется рядом, а числа - членами ряда. Краткая запись. - общий член ряда. Ряд считается заданным, если задана функция
1). 2). Иногда ряд задают рекуррентной формулой. Пример. Тогда и т.д.
Образуем последовательность частичных сумм Определение. Если существует предел последовательности то ряд сходящийся и - его сумма. Если последовательность не стремится к пределу, то ряд расходящийся. Последнее имеет место в двух случаях: 1) 2) не существует
1) 2) 3) не существует.
1) Если ряд сходится, то сходится ряд. Доказательство. 2) Если ряды и сходятся, то сходится ряд Доказательство. 3) Если ряд сходится, то сходится и ряд, в котором выброшено конечное число членов.
Если ряд сходится, то сходится и любой его остаток.
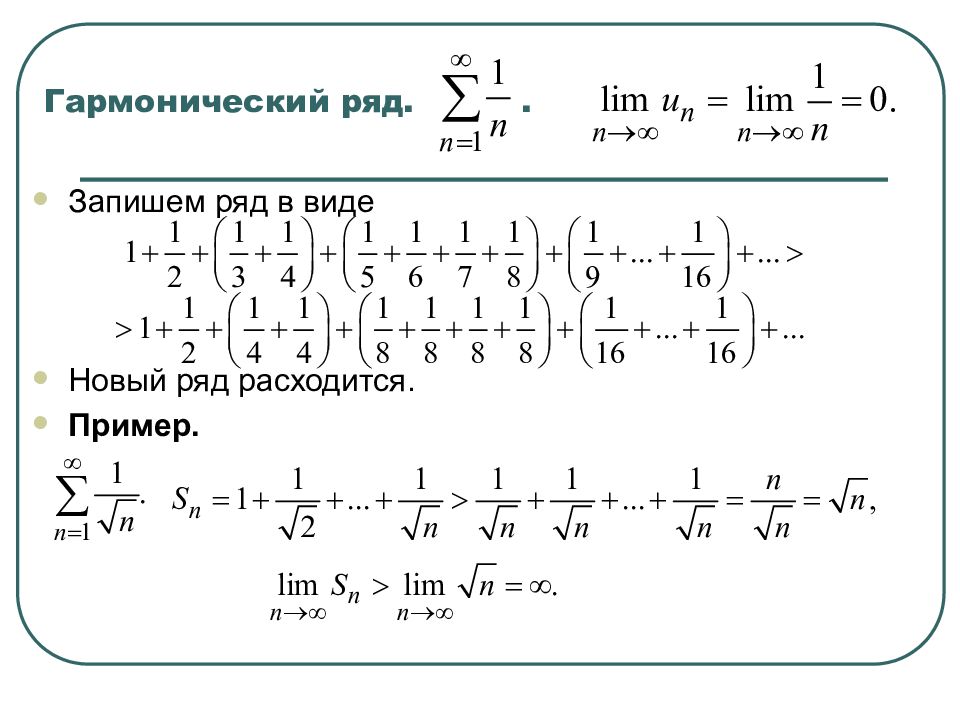
Необходимый признак. Если ряд сходится, то Доказательство. Если то ряд расходится. Пример. Ряд расходится. Вообще стремление не означает сходимости ряда.
Запишем ряд в виде Новый ряд расходится. Пример.
Рассмотрим ряд такой, что Лемма. Если частичные суммы ряда с положительными членами ограничены сверху то ряд сходится. Доказательство. т.к. Если последовательность монотонно возрастает и ограничена сверху, то по признаку сходимости Вейерштрасса она имеет предел Если ряд сходится, то Если ряд с положительными членами расходится, то
Пусть даны два ряда с положительными членами Тогда: 1) если сходится ряд (2), то сходится ряд(1); 2) если расходится ряд (1), то расходится ряд(2). Доказательство. 1) В силу леммы ряд (1) сходится. 2) Признак справедлив, если условие (*) выполняется с какого-либо номера в силу 3-го свойства сходящихся рядов.
Сравним с расходящимся рядом. исходный ряд расходится.
Если то ряды (1) и (2) сходятся или расходятся одновременно. Доказательство. или Пусть ряд (2) сходится. Тогда по свойству 1 сходящихся рядов сходится ряд и т.к. следовательно ряд (1) сходится. Если ряд (2) расходится, то в силу ряд (1) расходится.
Сравним с расходящимся рядом Исходный ряд расходится.
Пусть дан ряд Если существует предел то при - ряд сходится, при - ряд расходится, при - ряд может сходится или расходиться.
Пусть. Следовательно Тогда т.е. Т.к. последний ряд есть бесконечно убывающая геометрическая прогрессия, то исходный ряд сходится. Пусть и т.е. ряд расходится.
1) Применим признак д’Аламбера. Ряд сходится. 2) Применим признак д’Аламбера. О сходимости ряда ничего сказать нельзя. Необходимо применить другой достаточный признак сходимости.
Пусть дан ряд Если существует предел то при - ряд сходится, при - ряд расходится, при - ряд может сходится или расходиться.
Применим радикальный признак Коши. Ряд сходится.
