Первый слайд презентации: Синус и косинус острого угла
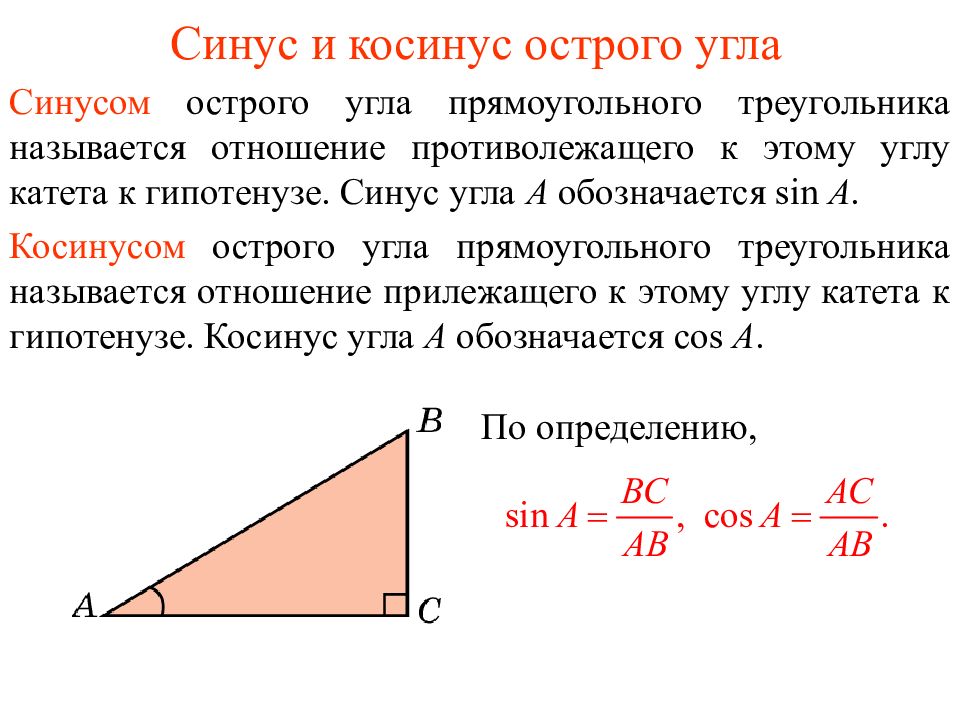
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе. Синус угла А обозначается sin A. Кос инусом острого угла прямоугольного треугольника называется отношение п ри лежащего к этому углу катета к гипотенузе. Кос инус угла А обозначается cos A. По определению,
Слайд 2: Тангенс и котангенс острого угла
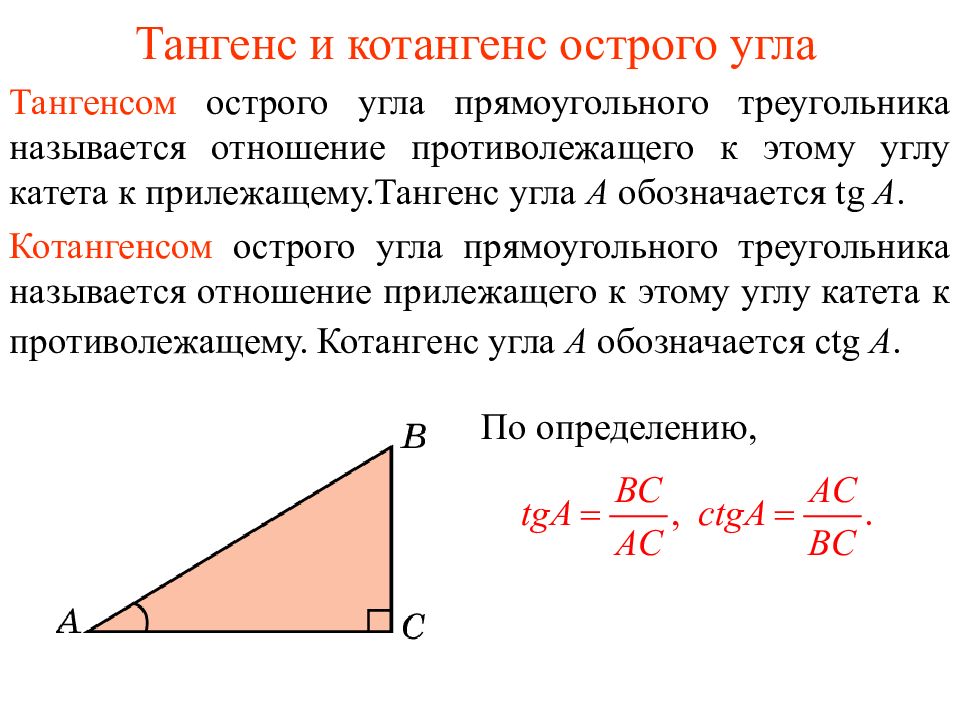
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к прилежащему.Тангенс угла А обозначается tg A. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к противолежащему. Котангенс угла А обозначается с tg A. По определению,
Слайд 3: Тригонометрические функции
Синус, косинус, тангенс и котангенс называют тригонометрическими функциями острого угла. Из определения тригонометрических функций следует: 1) катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего угла; 2) катет прямоугольного треугольника равен произведению гипотенузы на косинус прилежащего угла; 3) катет прямоугольного треугольника равен произведению второго катета на тангенс противолежащего угла; 4) катет прямоугольного треугольника равен произведению второго катета на котангенс прилежащего угла.
Слайд 4: Упражнение 1
Найдите значения тригонометрических функций угла в 3 0 о. Ответ:
Слайд 5: Упражнение 2
Найдите значения тригонометрических функций угла в 45 о. Ответ:
Слайд 6: Упражнение 3
Найдите значения тригонометрических функций угла в 60 о. Ответ:
Слайд 7: Упражнение 4
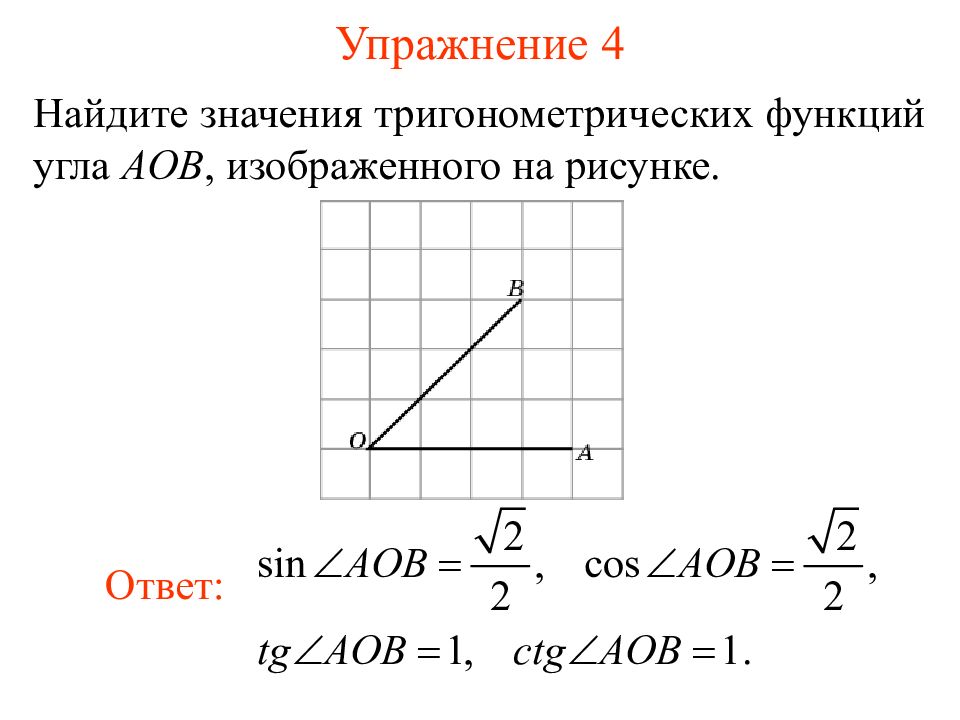
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке. Ответ:
Слайд 8: Упражнение 5
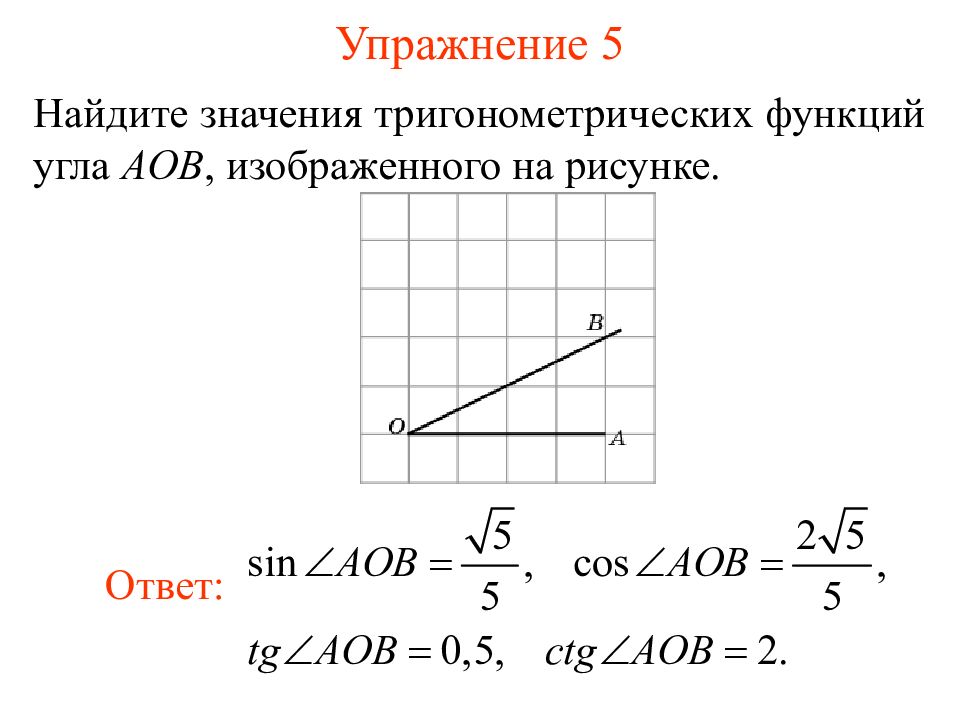
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке. Ответ:
Слайд 9: Упражнение 6
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке. Ответ:
Слайд 10: Упражнение 7
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке. Ответ:
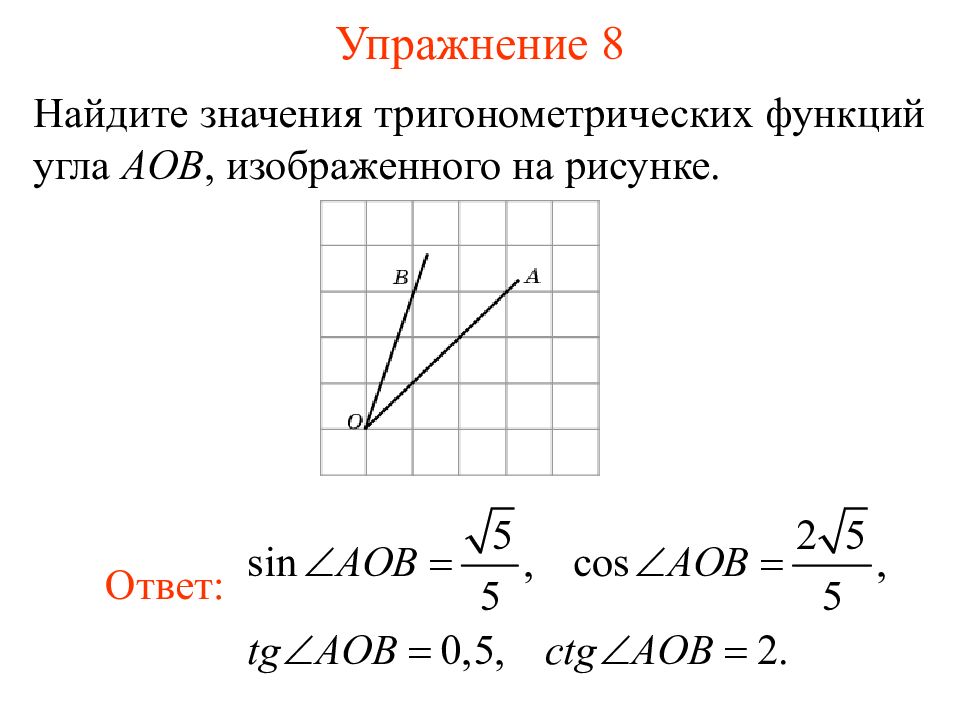
Слайд 11: Упражнение 8
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке. Ответ:
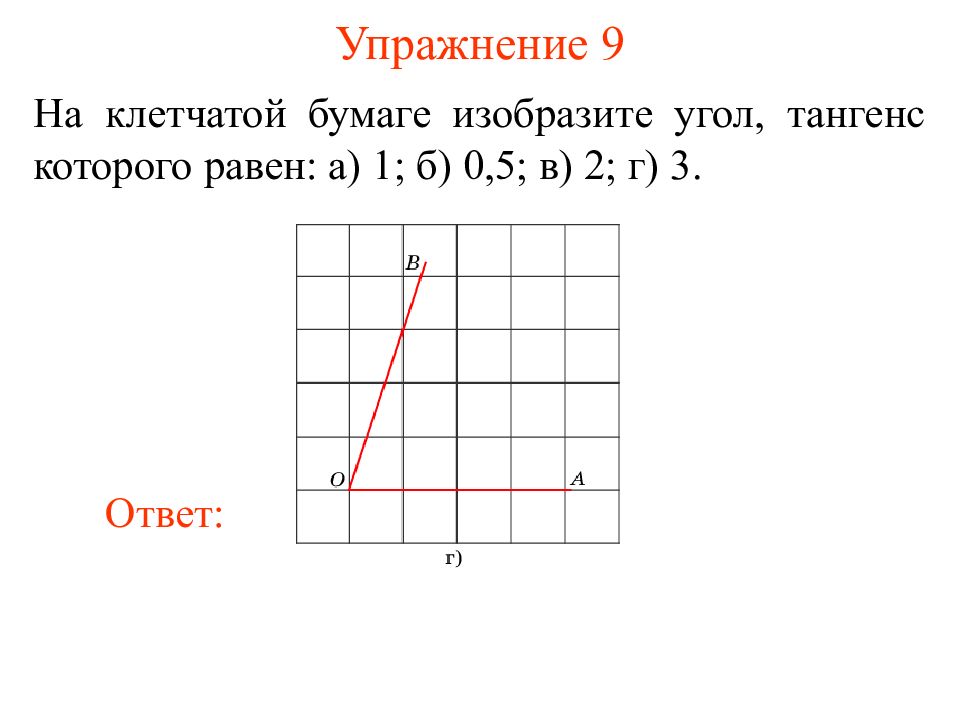
Слайд 12: Упражнение 9
На клетчатой бумаге изобразите угол, тангенс которого равен: а) 1; б) 0,5; в) 2; г) 3. Ответ:
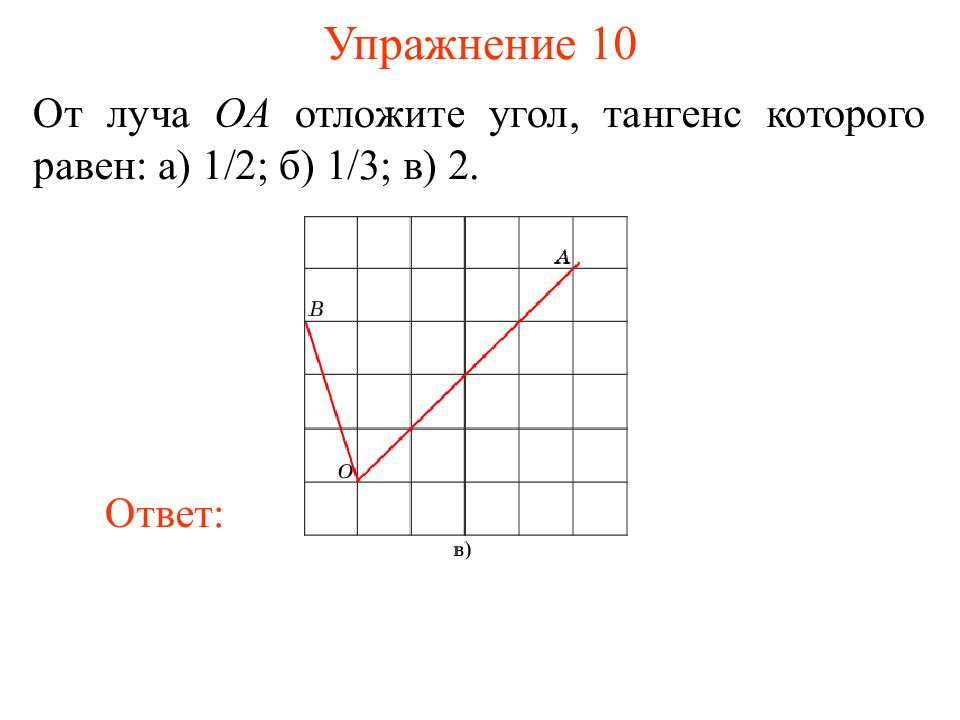
Слайд 13: Упражнение 10
От луча OA отложите угол, тангенс которого равен: а) 1 /2 ; б) 1/3 ; в) 2. Ответ:
Слайд 14: Упражнение 11
Может ли синус (косинус) угла быть равен ? Ответ: Нет, значения синуса и косинуса меньше единицы.
Слайд 15: Упражнение 12
Может ли тангенс (ко тангенс ) угла быть равен ? Ответ: Да.
Слайд 16: Упражнение 1 3
Катеты прямоугольного треугольника равны 12 см и 5 см. Найдите все тригонометрические функции его меньшего угла A. Ответ:
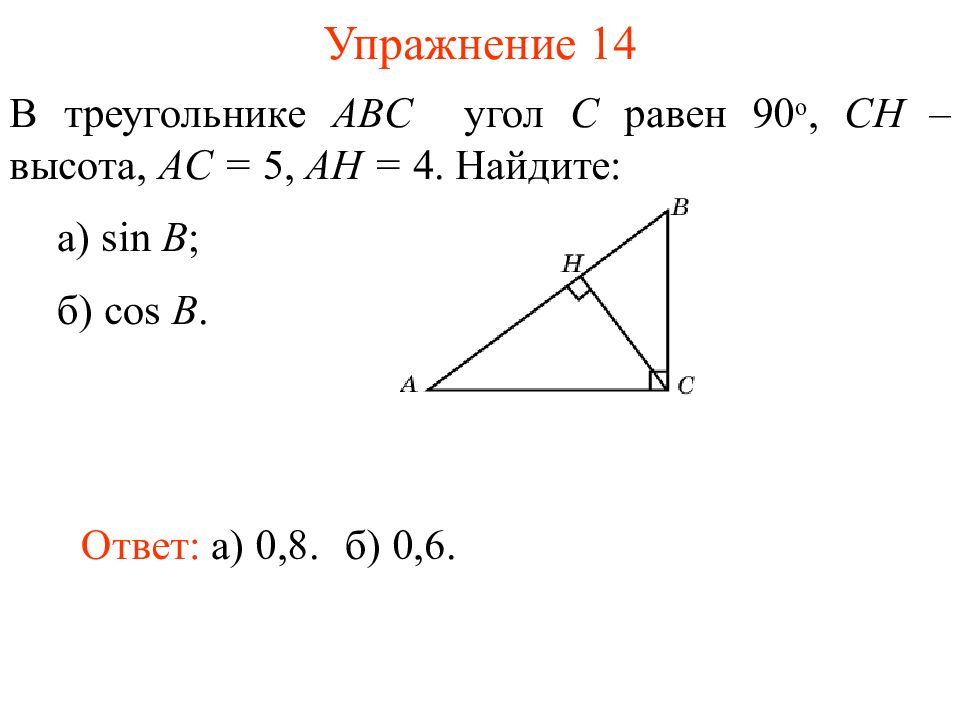
Слайд 17: Упражнение 1 4
В треугольнике ABC угол C равен 90 о, CH – высота, AC = 5, AH = 4. Найдите : а) sin B ; б) cos B. Ответ: а ) 0,8. б ) 0, 6.
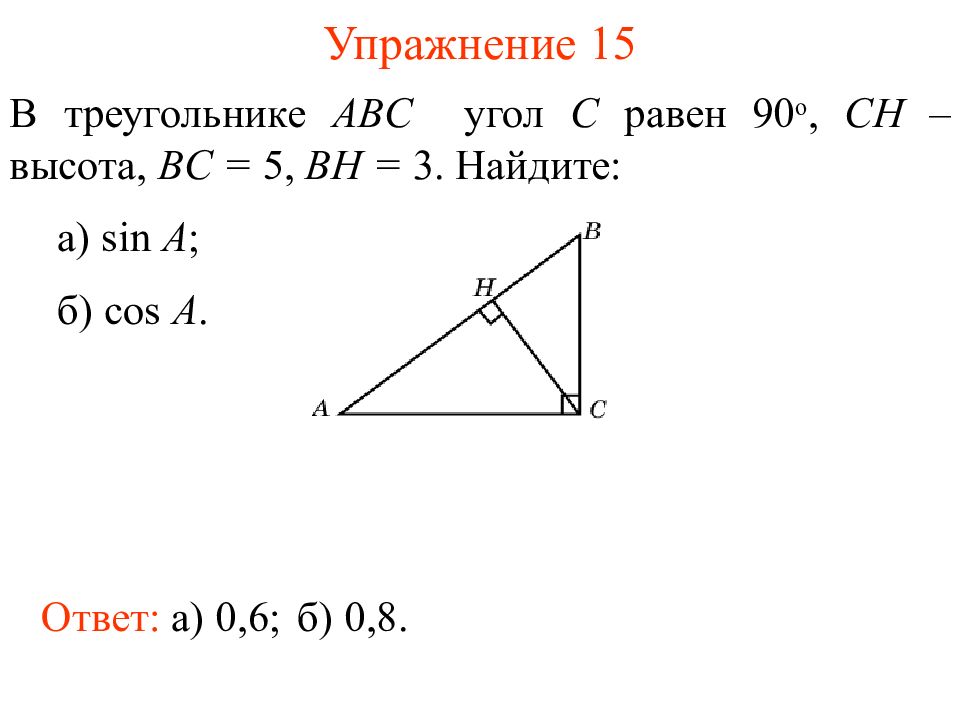
Слайд 18: Упражнение 1 5
В треугольнике ABC угол C равен 90 о, CH – высота, BC = 5, BH = 3. Найдите : а) sin A ; б) cos A. Ответ: а) 0,6 ; б) 0, 8.
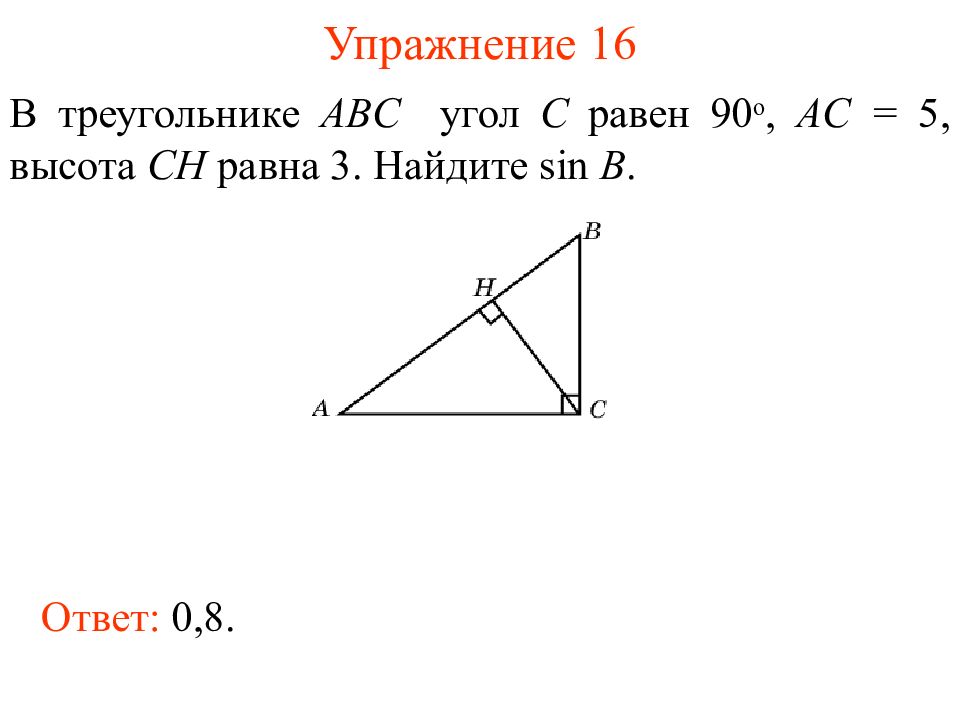
Слайд 19: Упражнение 1 6
В треугольнике ABC угол C равен 90 о, AC = 5, высота CH равна 3. Найдите sin B. Ответ: 0,8.
Слайд 20: Упражнение 1 7
В треугольнике ABC угол C равен 90 о, BC = 5, высота CH равна 4. Найдите sin A. Ответ: 0,6.
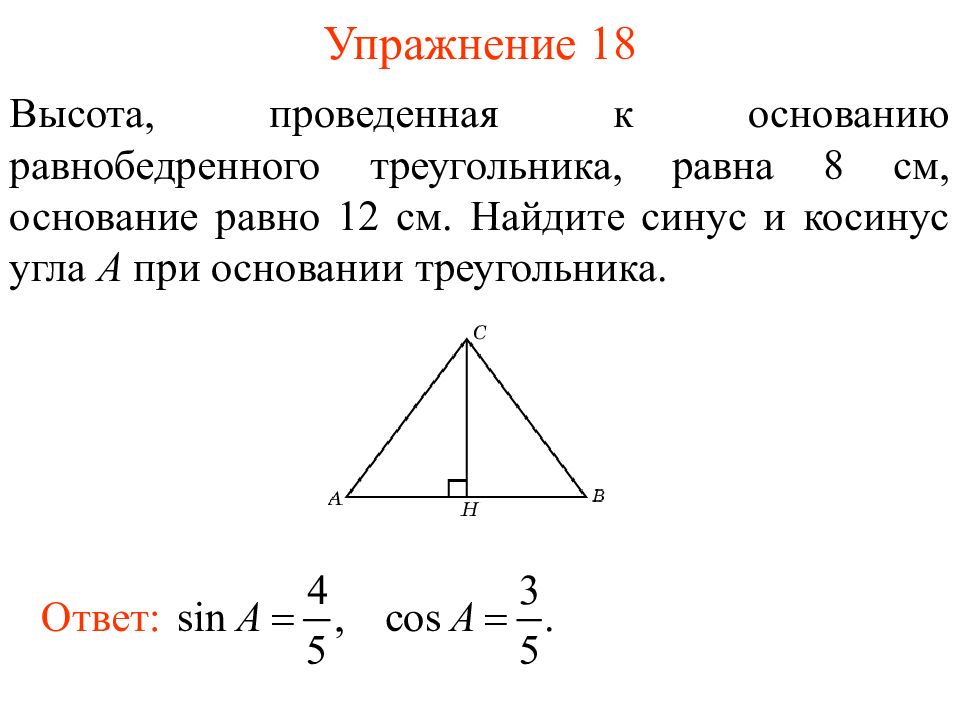
Слайд 21: Упражнение 1 8
Высота, проведенная к основанию равнобедренного треугольника, равна 8 см, основание равно 12 см. Найдите синус и косинус угла A при основании треугольника. Ответ:
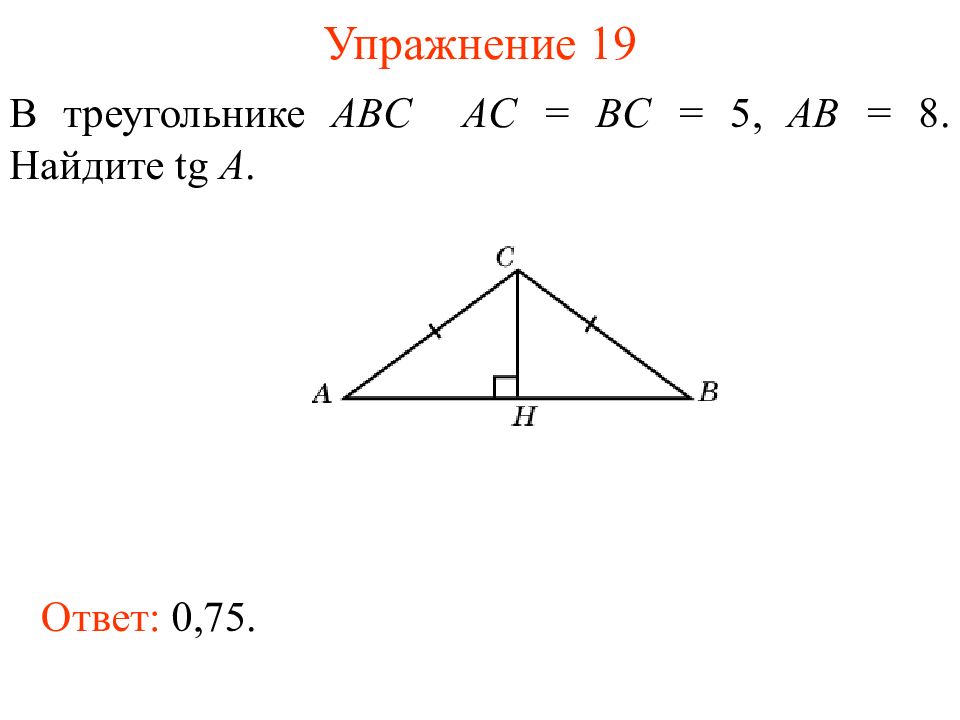
Слайд 22: Упражнение 19
В треугольнике ABC AC = BC = 5, AB = 8. Найдите tg A. Ответ: 0,75.
Слайд 23: Упражнение 20
В треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите sin A. Ответ: 0,8.
Слайд 24: Упражнение 2 1
В треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите cos A. Ответ: 0,6.
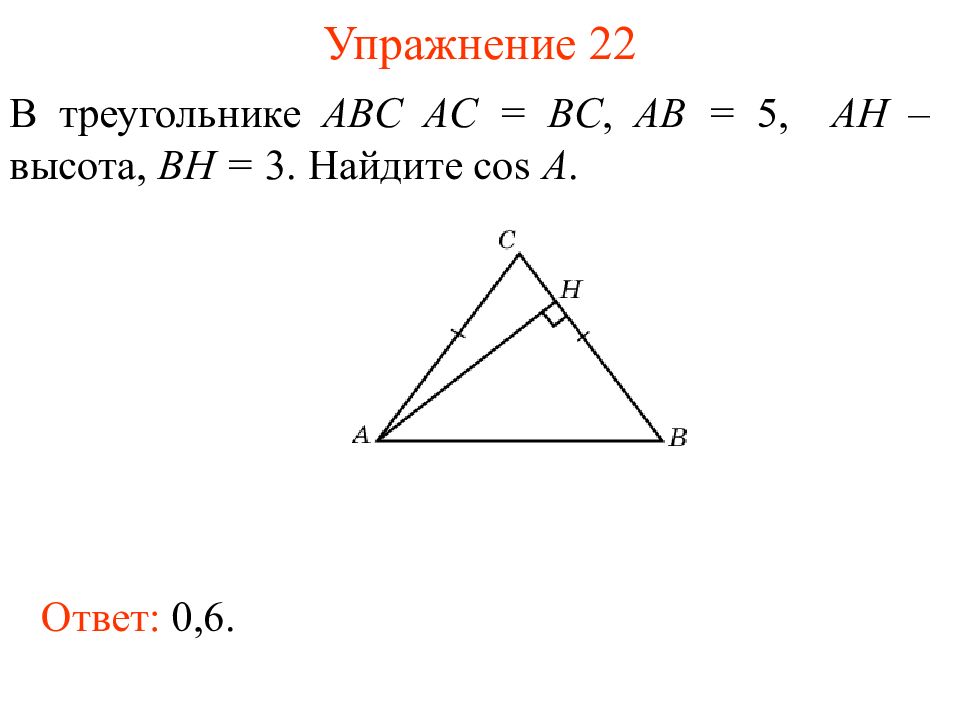
Слайд 25: Упражнение 2 2
В треугольнике ABC AC = BC, AB = 5, AH – высота, BH = 3. Найдите cos A. Ответ: 0,6.
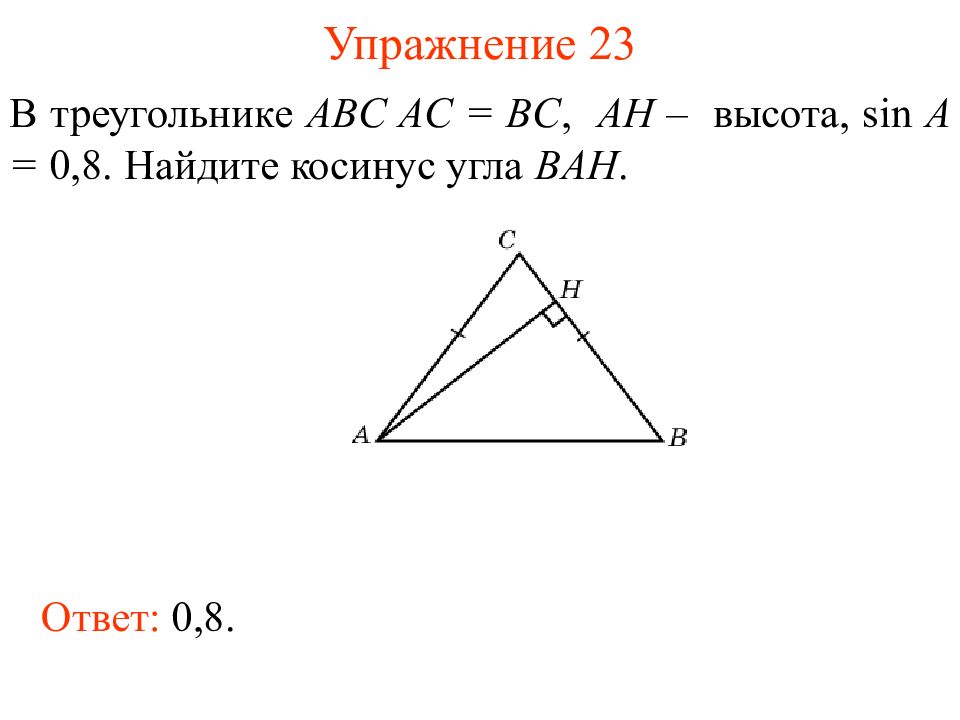
Слайд 26: Упражнение 2 3
В треугольнике ABC AC = BC, AH – высота, sin A = 0,8. Найдите косинус угла BAH. Ответ: 0,8.
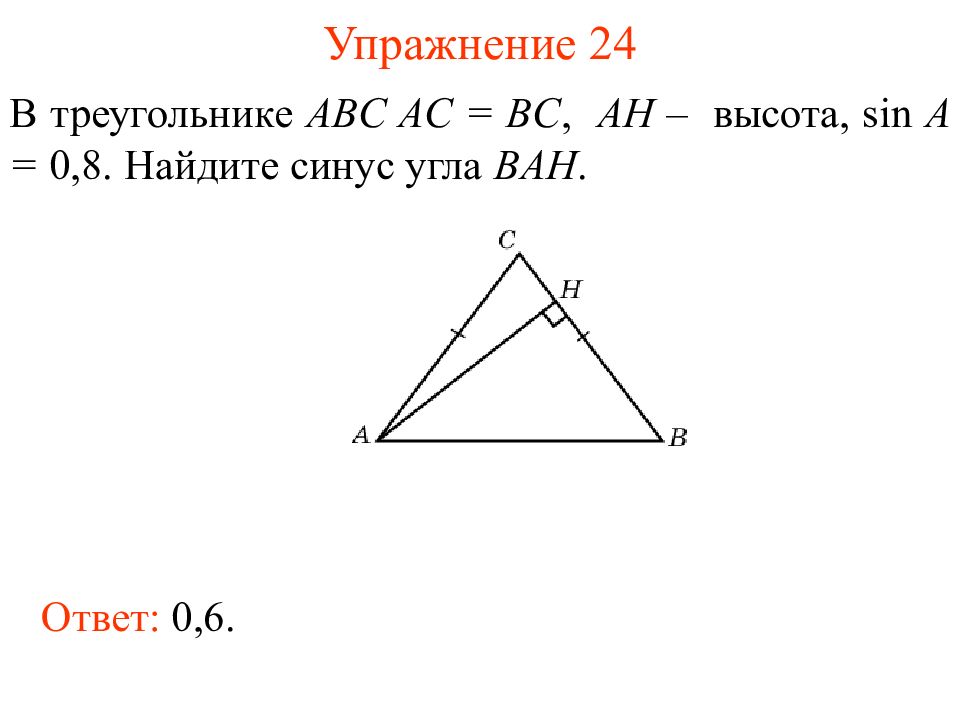
Слайд 27: Упражнение 2 4
В треугольнике ABC AC = BC, AH – высота, sin A = 0,8. Найдите синус угла BAH. Ответ: 0,6.
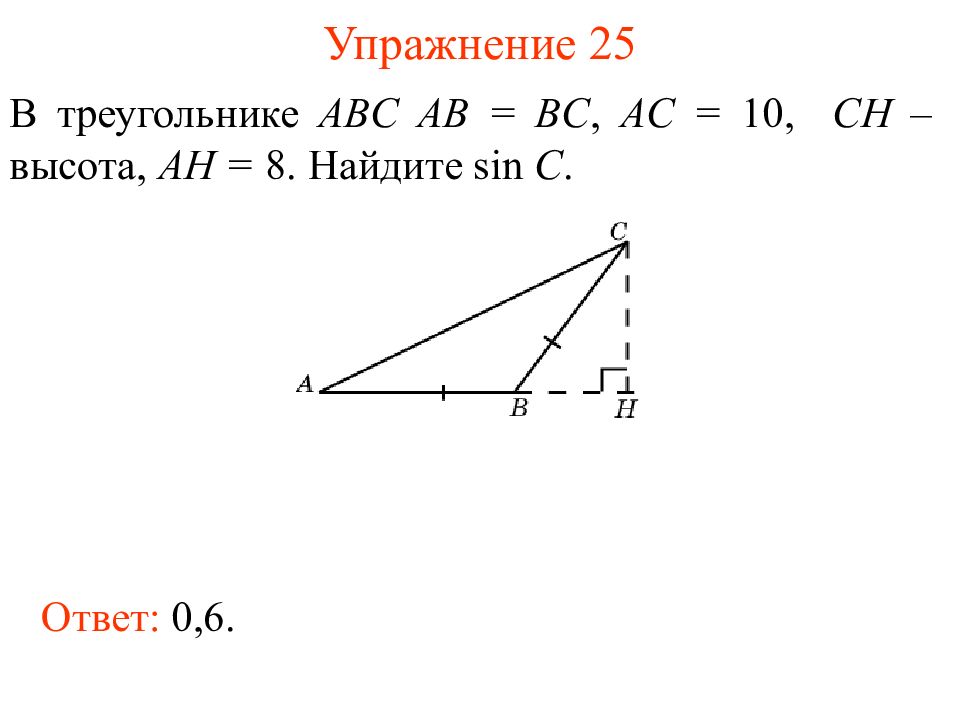
Слайд 28: Упражнение 2 5
В треугольнике ABC AB = BC, AC = 10, CH – высота, AH = 8. Найдите sin C. Ответ: 0,6.
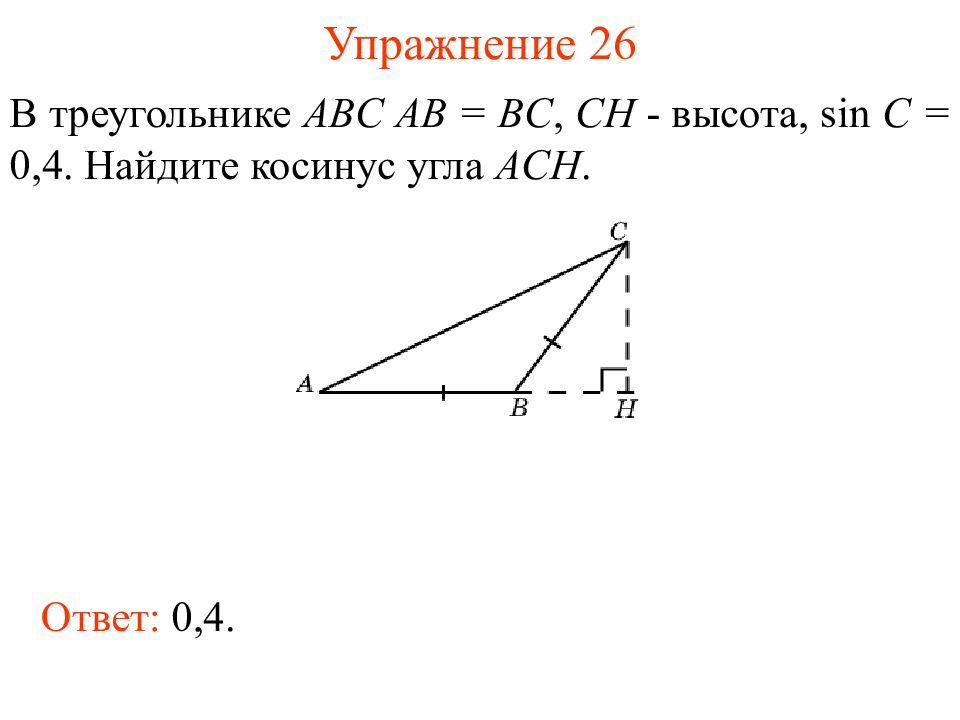
Слайд 29: Упражнение 26
В треугольнике ABC AB = BC, CH - высота, sin C = 0,4. Найдите косинус угла ACH. Ответ: 0,4.
Слайд 30: Упражнение 31
Ответ: 37 о. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. Под каким углом к направлению на запад он должен идти, чтобы вернуться домой? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций.)
Слайд 31: Упражнение 32
Ответ: 37 о. Грибник, войдя в лес, в течение двух часов шел в направлении на север, а затем с той же скоростью в течение полутора часов – на восток. Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций.)
Слайд 32: Упражнение 34
Ответ: 2 о. Горная железная дорога поднимается на 1 м на каждые 30 м пути. Используя таблицу тригонометрических функций, найдите угол подъема в градусах. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Слайд 33: Упражнение 35
Ответ: 5 о. Человек, пройдя вверх по склону холма 1000 м, поднялся на 90 м над плоскостью основания холма. Используя таблицу тригонометрических функций, найдите (в среднем) угол наклона холма в градусах. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Слайд 34: Упражнение 36
Ответ: 2 о. Использую таблицу тригонометрических функций, найдите приближенное значение угла, под которым виден столб высотой 3 м, находящийся от наблюдателя на расстоянии 100 м. В ответе укажите целое число градусов.
Слайд 35: Упражнение 37
Ответ: 50 о. Высота башни главного здания МГУ имени М.В. Ломоносова равна 240 м. Под каким углом видна эта башня с расстояния 200 м? В ответе укажите приближенное значение, равное целому числу градусов.
Слайд 36: Упражнение 38
Ответ: 15 о. Высота Останкинской телевизионной башни – 540 м. Используя таблицу тригонометрических функций, найдите угол в градусах, под которым видна башня с расстояния 2000 м.
Слайд 37: Упражнение 39
Ответ: 34 о. Строение высоты 30 м бросает тень длиной 45 м. Используя таблицу тригонометрических функций, найдите угол наклона солнечных лучей. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Слайд 38: Упражнение 40
Ответ: 64 о. Используя таблицу тригонометрических функций, найдите угол наклона солнечных лучей, если длина тени стоящего человека в два раза меньше его роста. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Слайд 39: Упражнение 41
Ответ: 31 о. Лестница имеет ступеньки, ширина которых равна 30 см, а высота – 18 см. Используя таблицу тригонометрических функций, найдите угол подъема лестницы. В ответе укажите приближенное значение, выражаемое целым числом градусов.
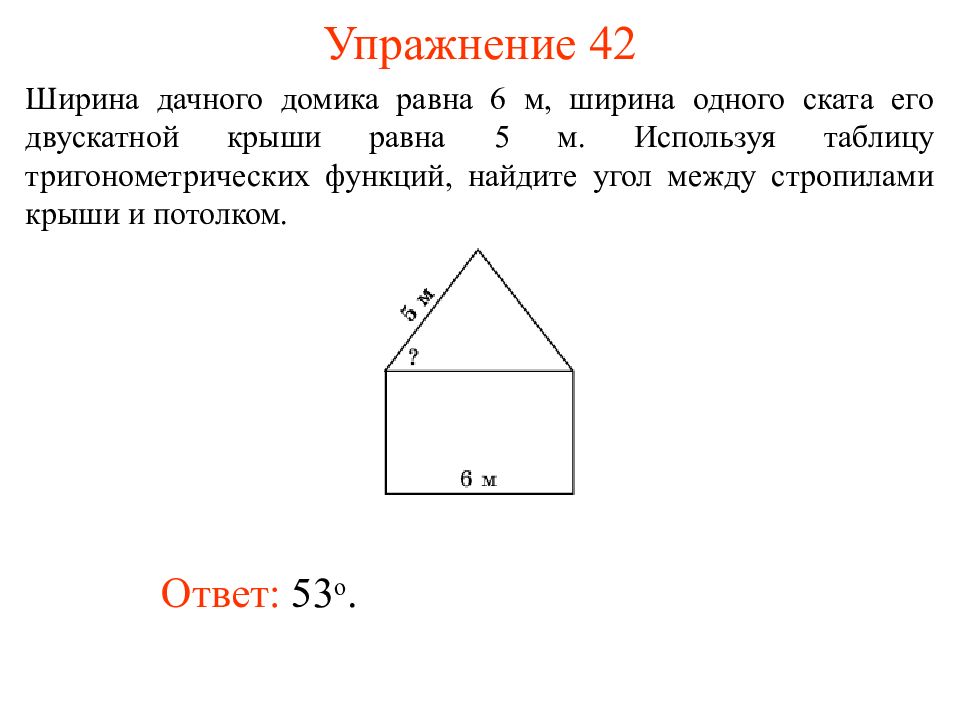
Слайд 40: Упражнение 42
Ответ: 53 о. Ширина дачного домика равна 6 м, ширина одного ската его двускатной крыши равна 5 м. Используя таблицу тригонометрических функций, найдите угол между стропилами крыши и потолком.
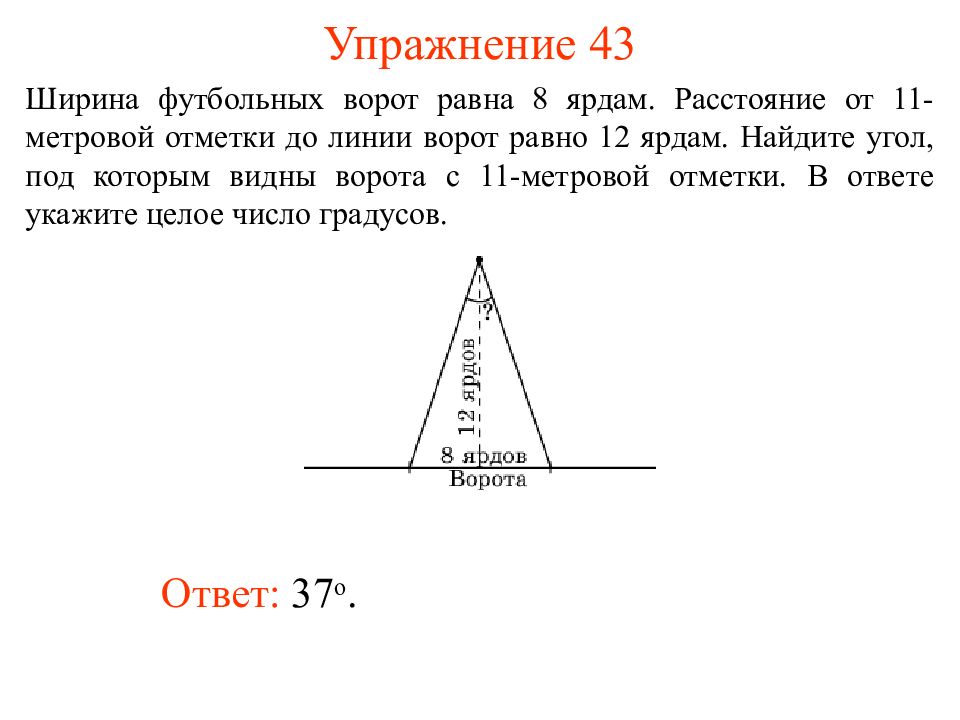
Слайд 41: Упражнение 43
Ответ: 37 о. Ширина футбольных ворот равна 8 ярдам. Расстояние от 11-метровой отметки до линии ворот равно 12 ярдам. Найдите угол, под которым видны ворота с 11-метровой отметки. В ответе укажите целое число градусов.
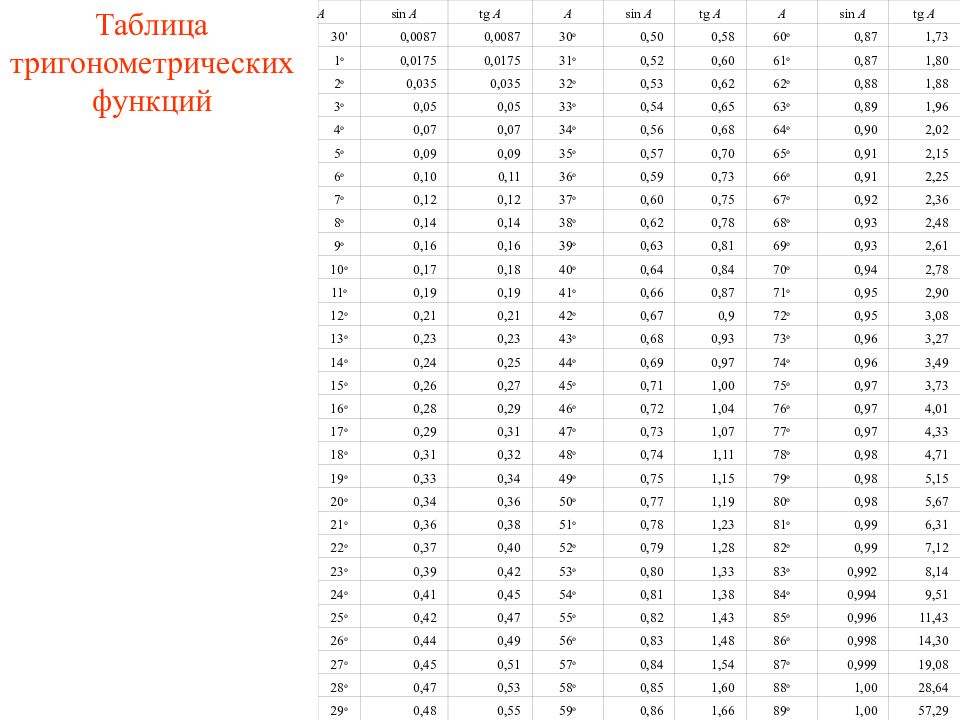
Последний слайд презентации: Синус и косинус острого угла: Таблица тригонометрических функций
A sin A tg A A sin A tg A A sin A tg A 30' 0,0087 0,0087 30 о 0,50 0,58 60 о 0,87 1,73 1 о 0,0175 0,0175 31 о 0,52 0,60 61 о 0,87 1,80 2 о 0,035 0,035 32 о 0,53 0,62 62 о 0,88 1,88 3 о 0,05 0,05 33 о 0,54 0,65 63 о 0,89 1,96 4 о 0,07 0,07 34 о 0,56 0,68 64 о 0,90 2,02 5 о 0,09 0,09 35 о 0,57 0,70 65 о 0,91 2,15 6 о 0,10 0,11 36 о 0,59 0,73 66 о 0,91 2,25 7 о 0,12 0,12 37 о 0,60 0,75 67 о 0,92 2,36 8 о 0,14 0,14 38 о 0,62 0,78 68 о 0,93 2,48 9 о 0,16 0,16 39 о 0,63 0,81 69 о 0,93 2,61 10 о 0,17 0,18 40 о 0,64 0,84 70 о 0,94 2,78 11 о 0,19 0,19 41 о 0,66 0,87 71 о 0,95 2,90 12 о 0,21 0,21 42 о 0,67 0,9 72 о 0,95 3,08 13 о 0,23 0,23 43 о 0,68 0,93 73 о 0,96 3,27 14 о 0,24 0,25 44 о 0,69 0,97 74 о 0,96 3,49 15 о 0,26 0,27 45 о 0,71 1,00 75 о 0,97 3,73 16 о 0,28 0,29 46 о 0,72 1,04 76 о 0,97 4,01 17 о 0,29 0,31 47 о 0,73 1,07 77 о 0,97 4,33 18 о 0,31 0,32 48 о 0,74 1,11 78 о 0,98 4,71 19 о 0,33 0,34 49 о 0,75 1,15 79 о 0,98 5,15 20 о 0,34 0,36 50 о 0,77 1,19 80 о 0,98 5,67 21 о 0,36 0,38 51 о 0,78 1,23 81 о 0,99 6,31 22 о 0,37 0,40 52 о 0,79 1,28 82 о 0,99 7,12 23 о 0,39 0,42 53 о 0,80 1,33 83 о 0,992 8,14 24 о 0,41 0,45 54 о 0,81 1,38 84 о 0,994 9,51 25 о 0,42 0,47 55 о 0,82 1,43 85 о 0,996 11,43 26 о 0,44 0,49 56 о 0,83 1,48 86 о 0,998 14,30 27 о 0,45 0,51 57 о 0,84 1,54 87 о 0,999 19,08 28 о 0,47 0,53 58 о 0,85 1,60 88 о 1,00 28,64 29 о 0,48 0,55 59 о 0,86 1,66 89 о 1,00 57,29