Первый слайд презентации: Теория вероятностей и математическая статистика
Кракашова Ольга Анатольевна доцент, канд. экон. наук, доцент кафедры « Математическая статистика, эконометрика и актуарные расчеты » РГЭУ (РИНХ)
Слайд 2: Лекция № 2
Классическое и статистическое определение вероятности. Основные теоремы теории вероятностей
Слайд 3: Классическое определение вероятности
Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементарных исходов. Обозначим число благоприятствующих событию А исходов через М, а число всех исходов – N. где M - целое неотрицательное число, 0≤ M≤N.
Другой тип объективной вероятности определяется исходя из относительной частоты ( частости ) по явления события. Относительной частотой события называется отношение числа испытаний m, при которых со- бытие появилось, к общему числу проведенных испытаний n. Статистической вероятностью события А называется относительная частота ( частость ) этого события, вычисленная по результатам большого числа испытаний. При большом числе испытаний статистическая вероятность приближенно равна классической вероятности, т.е.
Слайд 6: Последовательность решения задач по определению вероятности события
Определить состав эксперимента. Определить элементарное событие в данном опыте. Определить полную группу событий, найти число элементарных событий, составляющих полную группу событий. Определить интересующее нас событие, найти число элементарных событий, составляющих интересующее нас событие. Найти вероятность события по формуле (1).
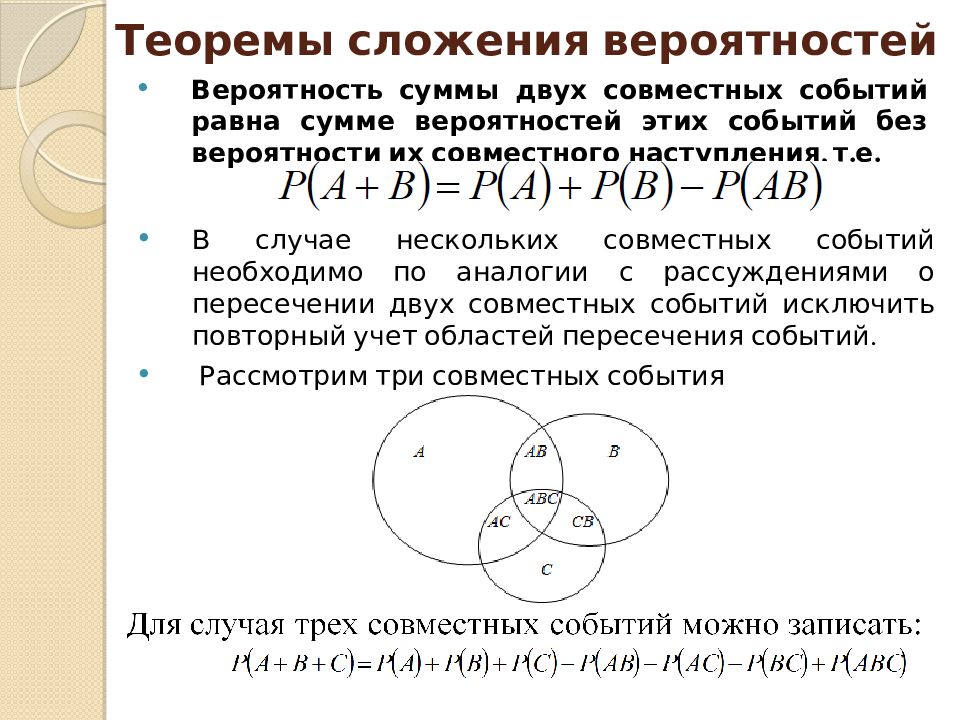
Слайд 8: Теоремы сложения вероятностей
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления, т.е. В случае нескольких совместных событий необходимо по аналогии с рассуждениями о пересечении двух совместных событий исключить повторный учет областей пересечения со бытий. Рассмотрим три совместных события
Слайд 10: Теоремы сложения вероятностей
Вероятность суммы несовместных событий. Для несовместных событий их совместное наступление есть невозможное событие, т.е. Следовательно, вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Правило сложения вероятностей справедливо и для конечного числа n попарно несовместных событий, т.е.