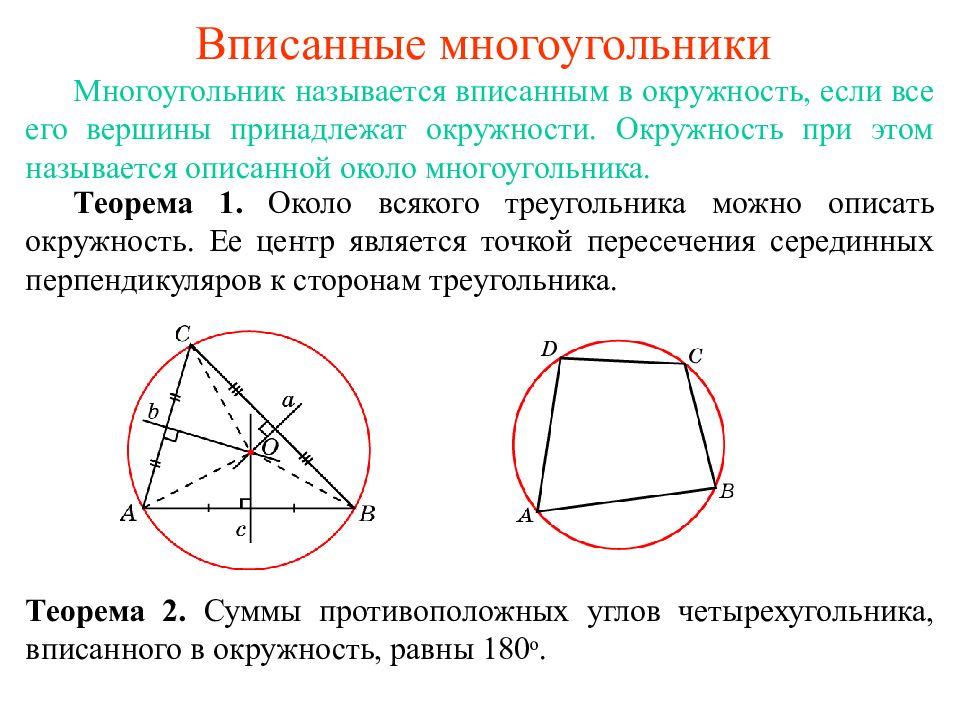
Первый слайд презентации: Трапеция
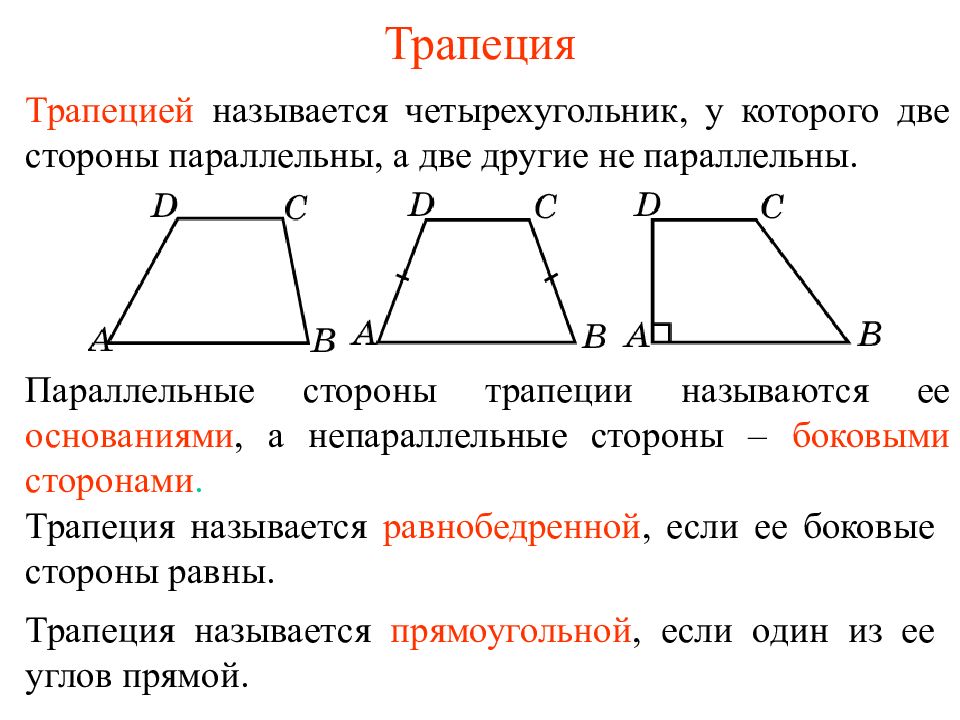
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Трапеция называется равнобедренной, если ее боковые стороны равны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны – боковыми сторонами. Трапеция называется прямоугольной, если один из ее углов прямой.
Слайд 2: Средняя линия трапеции
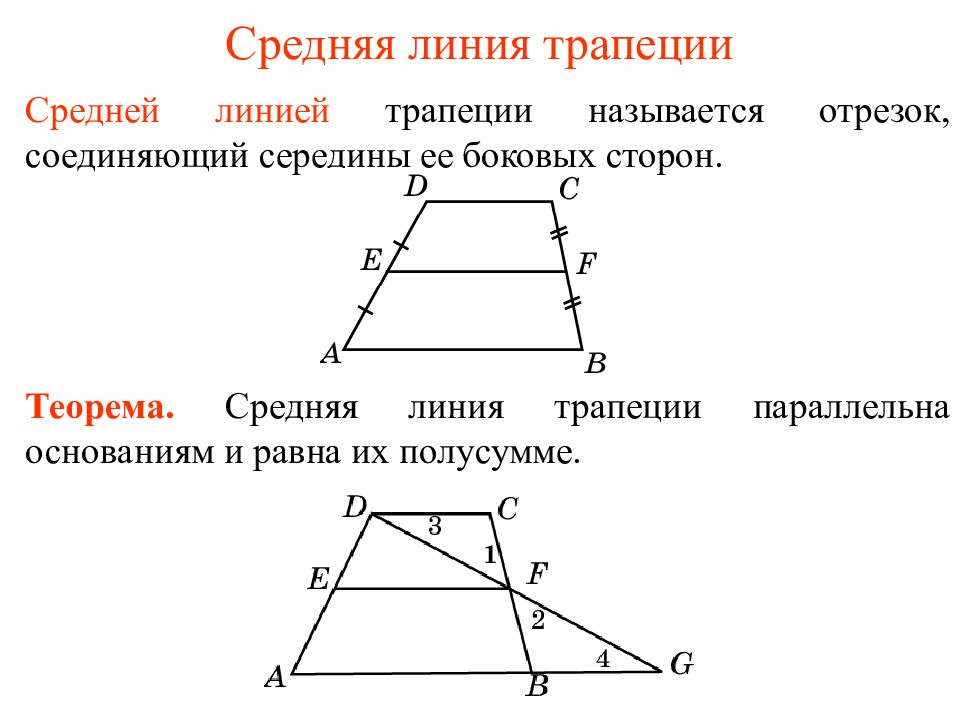
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Слайд 3: Вопрос 1
Какой четырехугольник называется трапецией? Ответ: Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Слайд 4: Вопрос 2
Какие стороны трапеции называются: а) основаниями; б) боковыми сторонами? Ответ: а) Основаниями трапеции называются ее п араллельные стороны ; б) боковыми сторонами трапеции называются ее непараллельные стороны.
Слайд 5: Вопрос 3
Какая трапеция называется : а) равнобедренной; б) прямоугольной? Ответ: а) Трапеция называется равнобедренной, если ее боковые стороны равны ; б) т рапеция называется прямоугольной, если один из ее углов прямой.
Слайд 6: Вопрос 4
Что называется средней линией трапеции? Ответ: Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Слайд 7: Вопрос 5
Сформулируйте теорему о средней линии трапеции. Ответ: Средняя линия трапеции параллельна основаниям и равна их полусумме.
Слайд 8: Упражнение 1
Могут ли углы, прилежащие к основанию трапеции, быть один острым, а другой тупым? Ответ: Да.
Слайд 9: Упражнение 2
Может ли у трапеции быть: а) три прямых угла; б) три острых угла? Ответ: а) Нет; б) нет.
Слайд 10: Упражнение 3
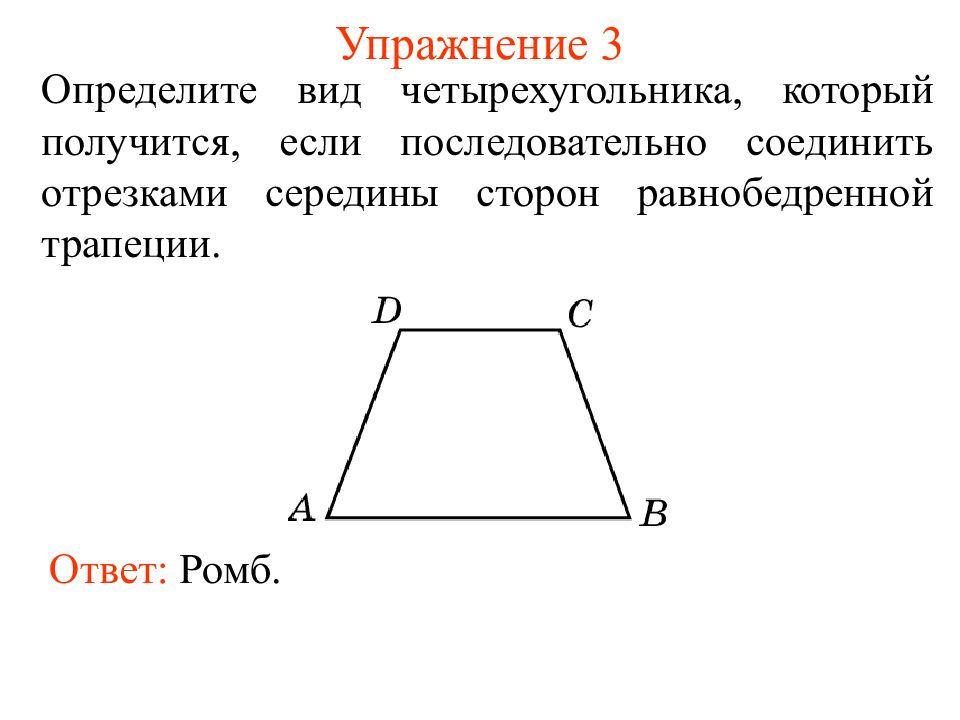
Определите вид четырехугольника, который получится, если последовательно соединить отрезками середины сторон равнобедренной трапеции. Ответ: Ромб.
Слайд 11: Упражнение 4
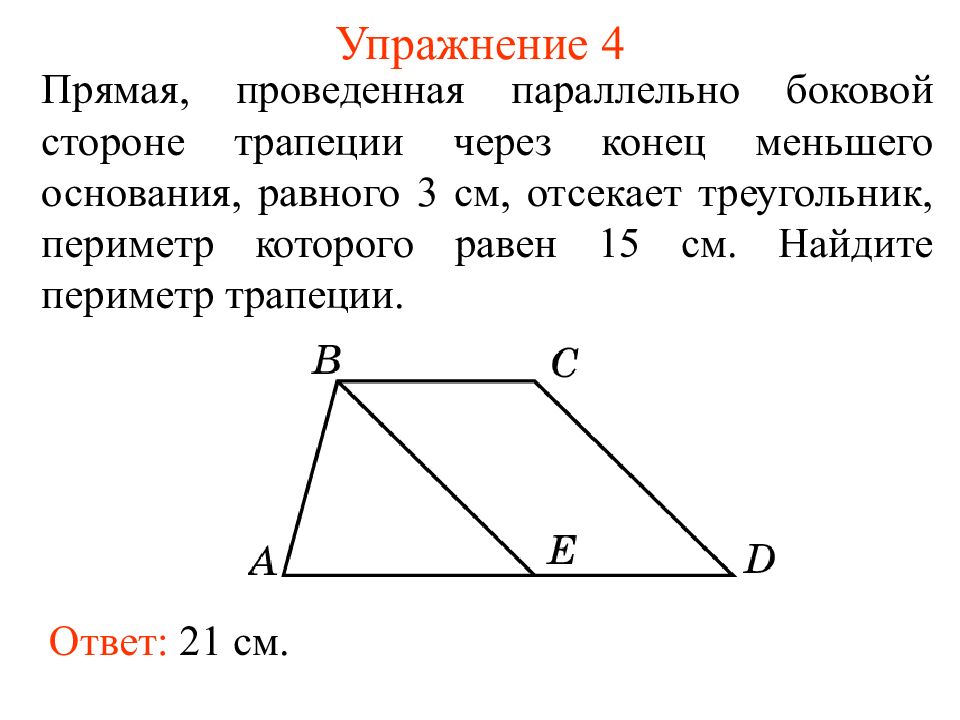
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 3 см, отсекает треугольник, периметр которого равен 15 см. Найдите периметр трапеции. Ответ: 21 см.
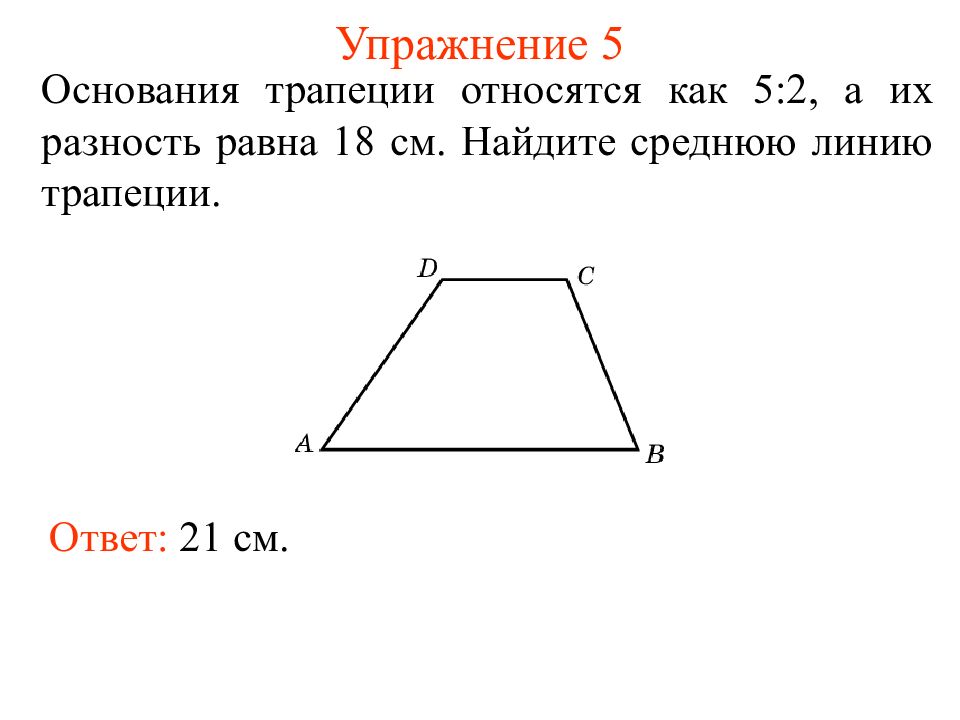
Слайд 12: Упражнение 5
Основания трапеции относятся как 5:2, а их разность равна 18 см. Найдите среднюю линию трапеции. Ответ: 21 см.
Слайд 13: Упражнение 6
Периметр трапеции равен 50 см, а сумма непараллельных сторон равна 20 см. Найдите среднюю линию трапеции. Ответ: 15 см.
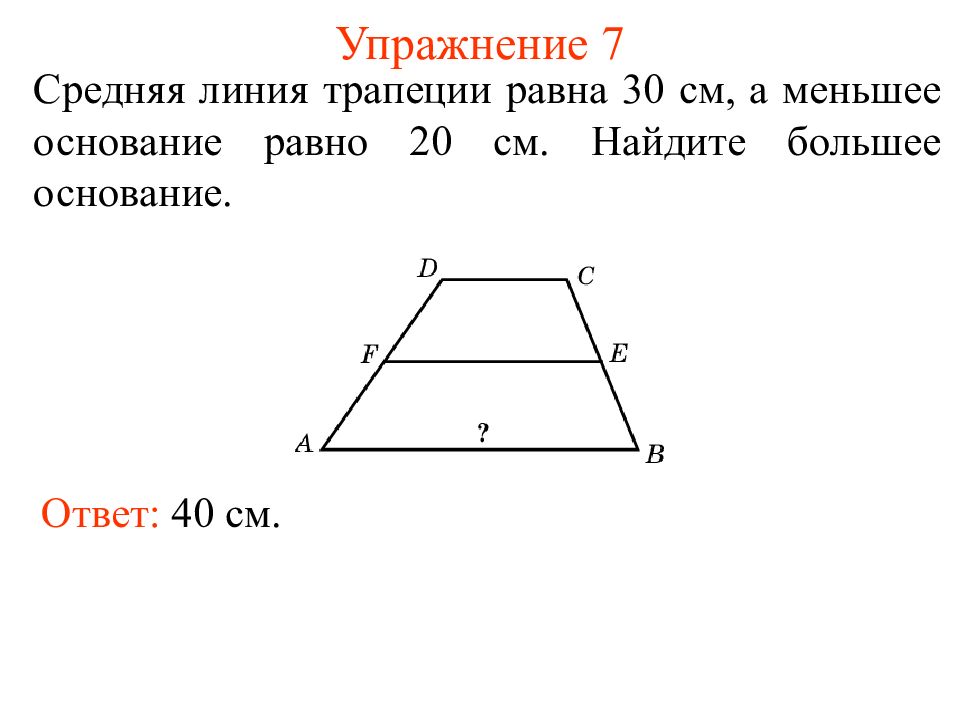
Слайд 14: Упражнение 7
Средняя линия трапеции равна 30 см, а меньшее основание равно 20 см. Найдите большее основание. Ответ: 40 см.
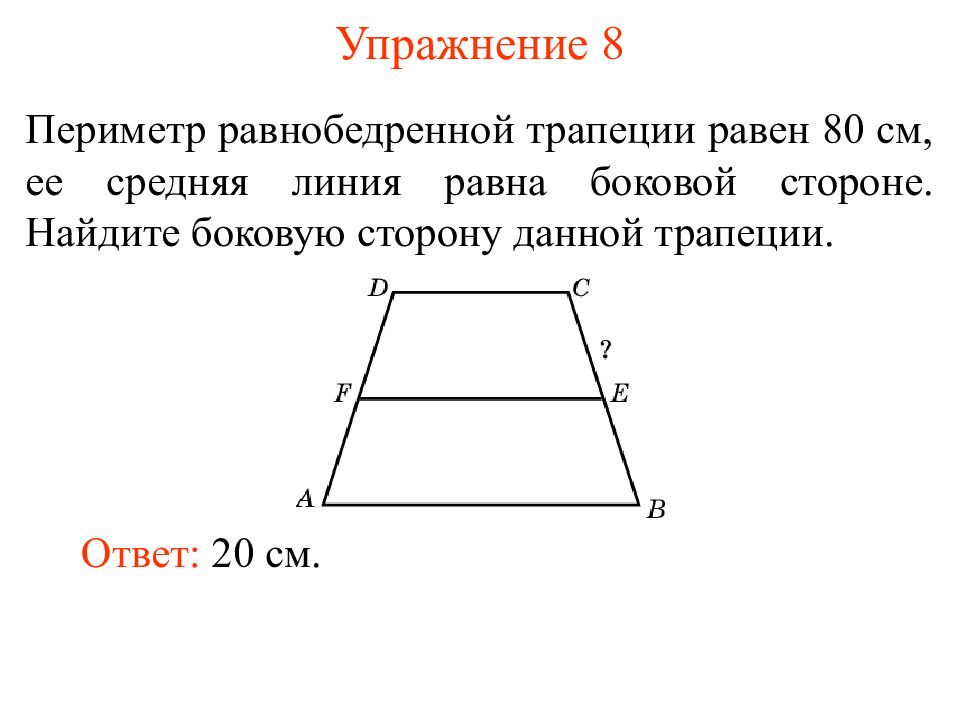
Слайд 15: Упражнение 8
Периметр равнобедренной трапеции равен 80 см, ее средняя линия равна боковой стороне. Найдите боковую сторону данной трапеции. Ответ: 20 см.
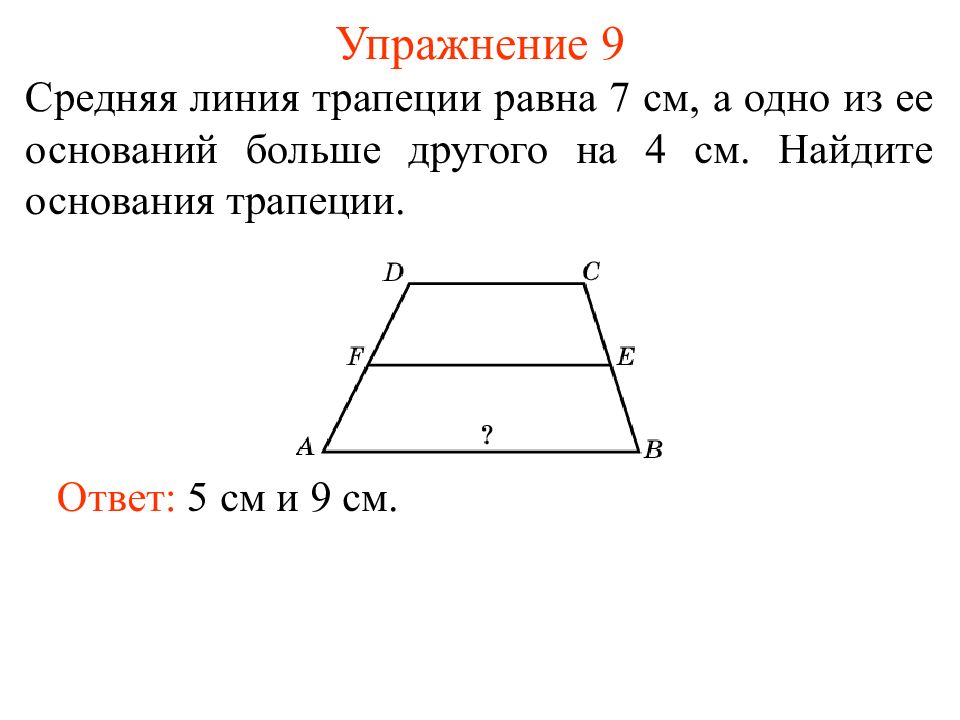
Слайд 16: Упражнение 9
Средняя линия трапеции равна 7 см, а одно из ее оснований больше другого на 4 см. Найдите основания тр а пеции. Ответ: 5 см и 9 см.
Слайд 17: Упражнение 10
Основания трапеции относятся как 2 : 3, а средняя линия равна 5 м. Найдите основания. Ответ: 4 м и 6 м.
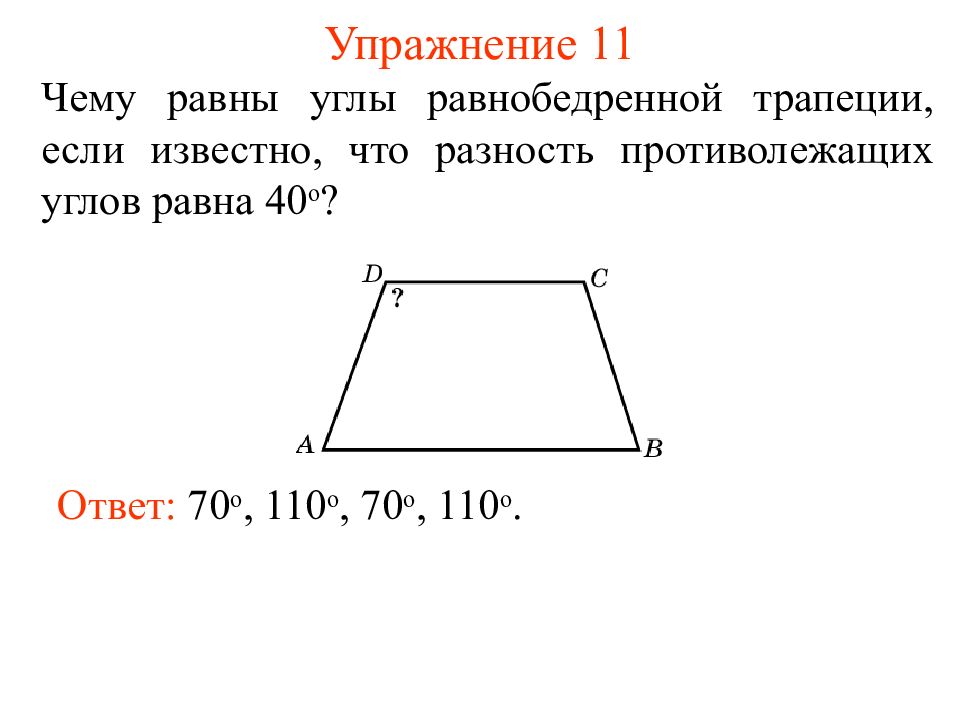
Слайд 18: Упражнение 11
Чему равны углы равнобедренной трапеции, если известно, что разность противолежащих углов равна 40 о ? Ответ: 7 0 о, 11 0 о, 7 0 о, 11 0 о.
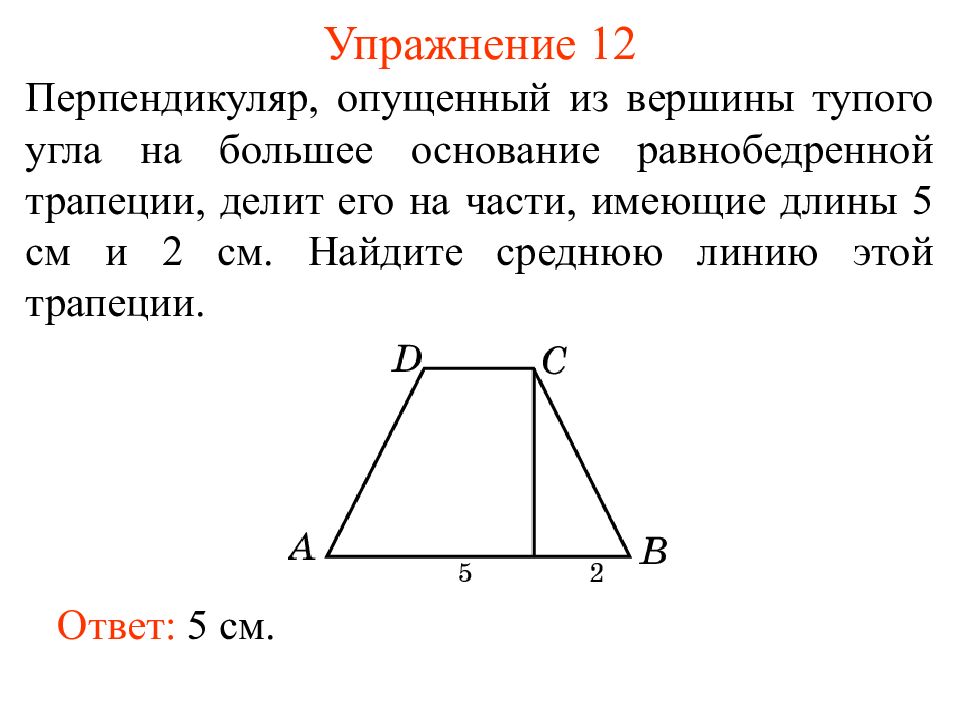
Слайд 19: Упражнение 12
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 5 см и 2 см. Найдите среднюю линию этой трапеции. Ответ: 5 см.
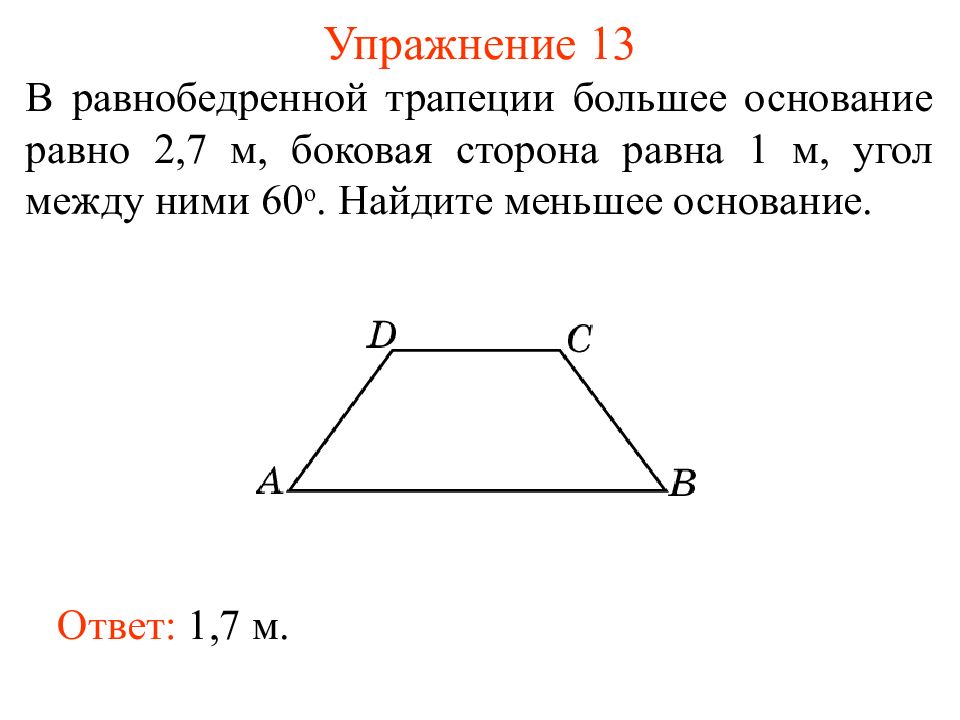
Слайд 20: Упражнение 13
В равнобедренной трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60 о. Найдите меньшее основание. Ответ: 1,7 м.
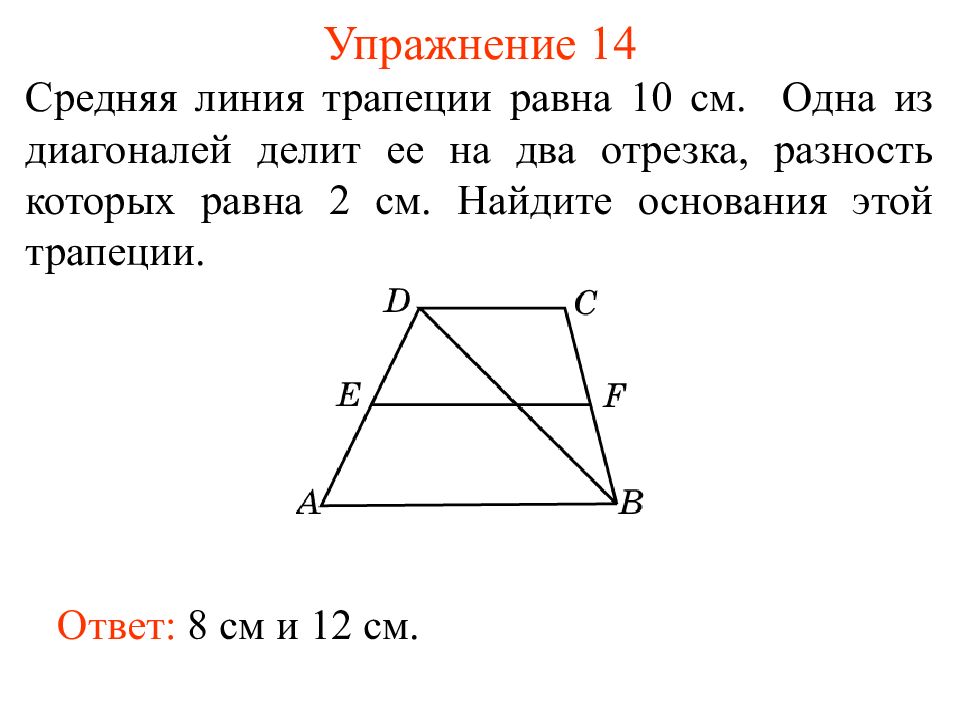
Слайд 21: Упражнение 14
C редняя линия трапеции равна 10 см. Одна из диагоналей делит ее на два отрезка, разность которых равна 2 см. Найдите основания этой трапеции. Ответ: 8 см и 12 см.
Слайд 22: Упражнение 15
Основания трапеции равны 4 см и 10 см. Найдите отрезки, на которые делит среднюю линию этой трапеции одна из ее диагоналей. Ответ: 2 см и 5 см.
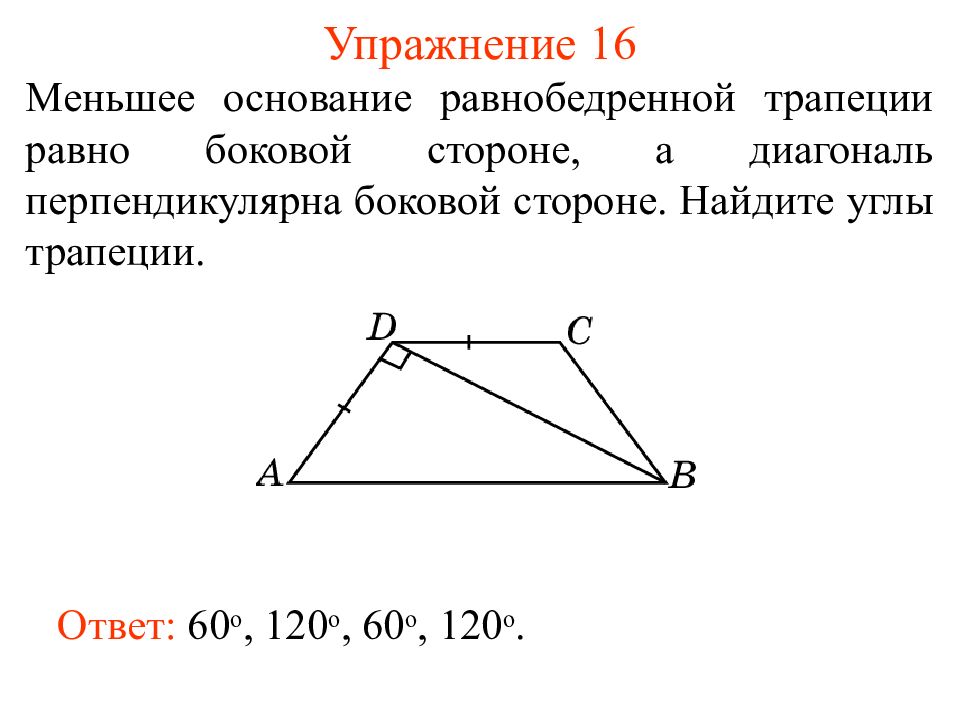
Слайд 23: Упражнение 16
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции. Ответ: 60 о, 120 о, 60 о, 120 о.
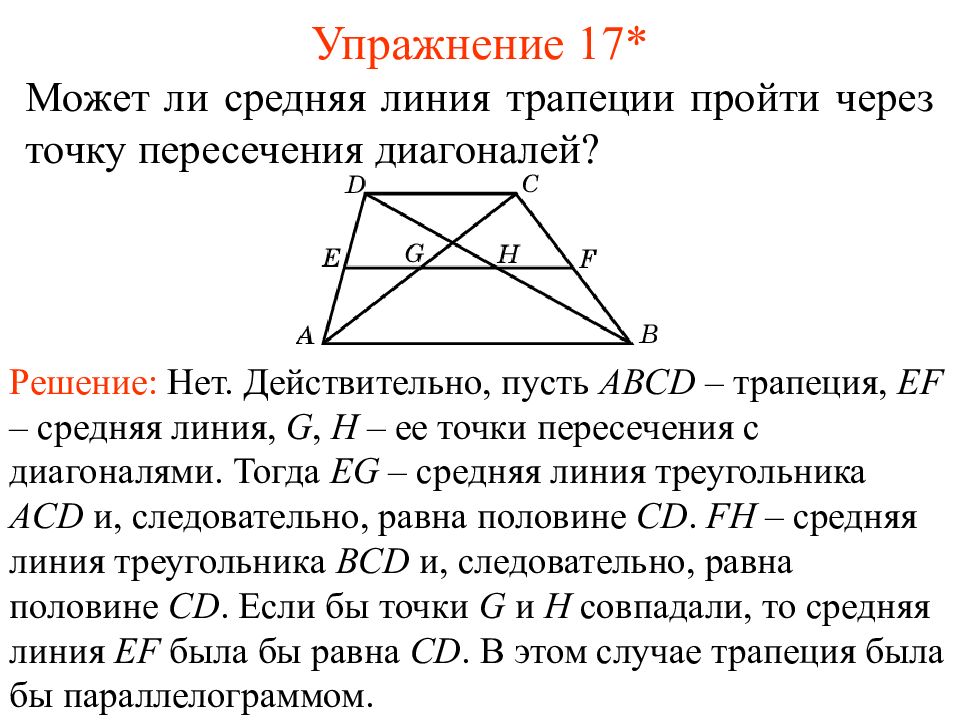
Слайд 24: Упражнение 17*
Может ли средняя линия трапеции пройти через точку пересечения диагоналей? Решение: Нет. Действительно, пусть ABCD – трапеция, EF – средняя линия, G, H – ее точки пересечения с диагоналями. Тогда EG – средняя линия треугольника ACD и, следовательно, равна половине CD. FH – средняя линия треугольника BCD и, следовательно, равна половине CD. Если бы точки G и H совпадали, то средняя линия EF была бы равна CD. В этом случае трапеция была бы параллелограммом.
Последний слайд презентации: Трапеция: Упражнение 18*
В выпуклом пятиугольнике ABCDE AE = 4. Середины сторон AB и CD, BC и ED соединены отрезками. Середины H и K этих отрезков снова соединены отрезками. Найдите длину отрезка HK. Решение: Пусть M, N, P, R, L – середины соответствующих сторон. Тогда HK = ML = AE = 1.