Первый слайд презентации: УСТНО:
Какая прямая называется перпендикулярной плоскости? Сформулировать признак перпендикулярности прямой и плоскости.
Слайд 4: Через сторону АС треугольника АВС проведена плоскость Найдите: площадь треугольника АВС, если
А С В В 1
Слайд 5
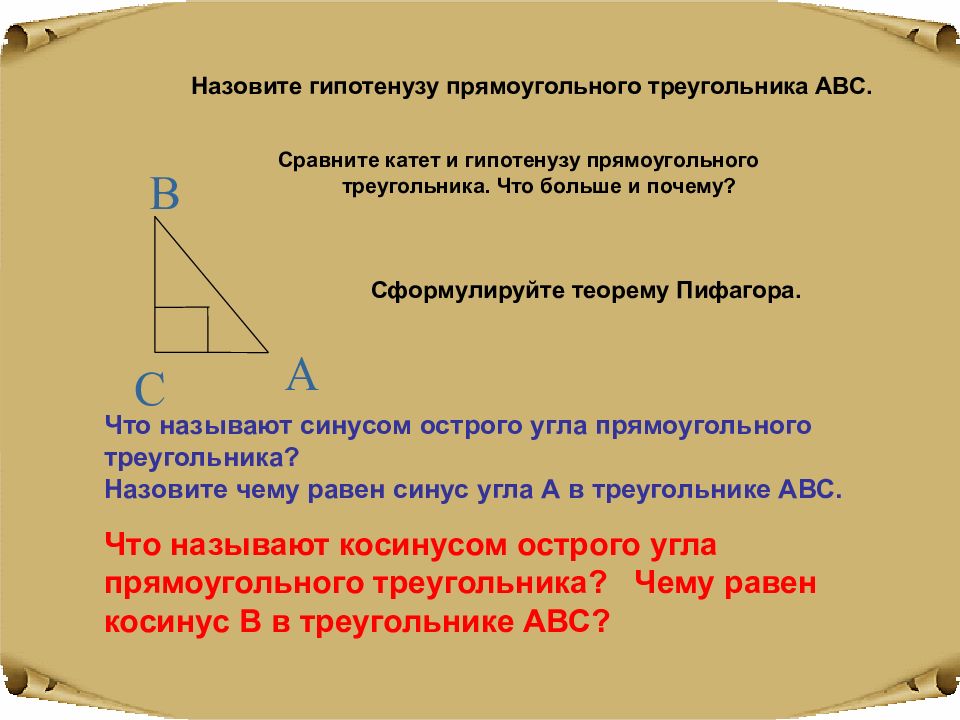
Сравните катет и гипотенузу прямоугольного треугольника. Что больше и почему? C B A Сформулируйте теорему Пифагора. Назовите гипотенузу прямоугольного треугольника АВС. Что называют синусом острого угла прямоугольного треугольника? Назовите чему равен синус угла А в треугольнике АВС. Что называют косинусом острого угла прямоугольного треугольника? Чему равен косинус В в треугольнике АВС?
Слайд 6
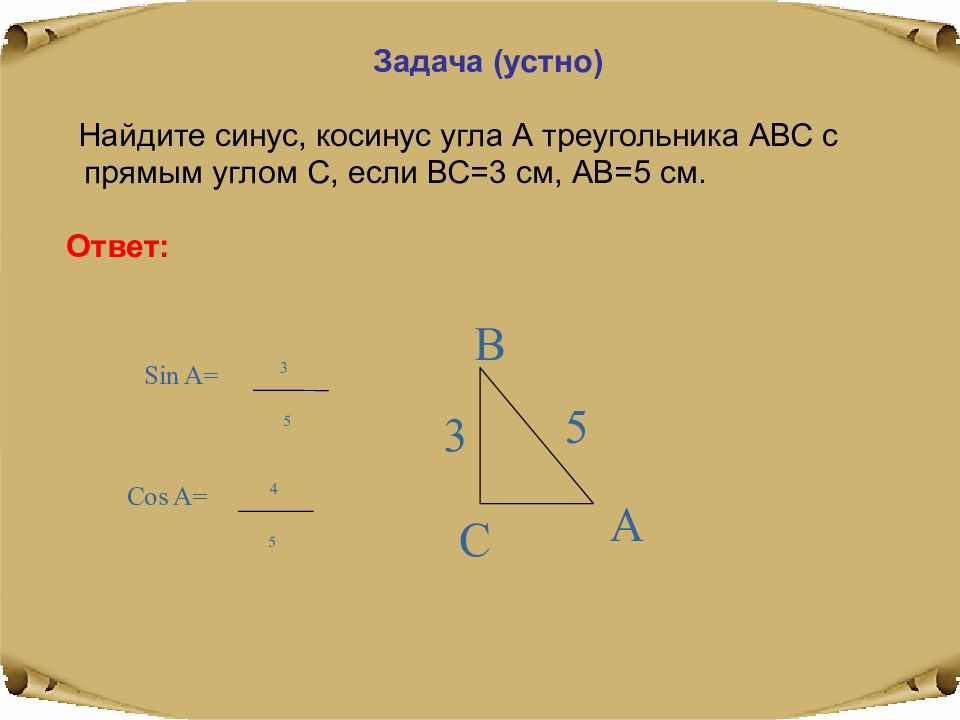
Задача (устно) Найдите синус, косинус угла А треугольника АВС с прямым углом С, если ВС=3 см, АВ=5 см. Ответ: 3 C 5 B A 3 5 Sin A= 4 5 Cos A=
Слайд 7: Введение нового материала
Слайд 8
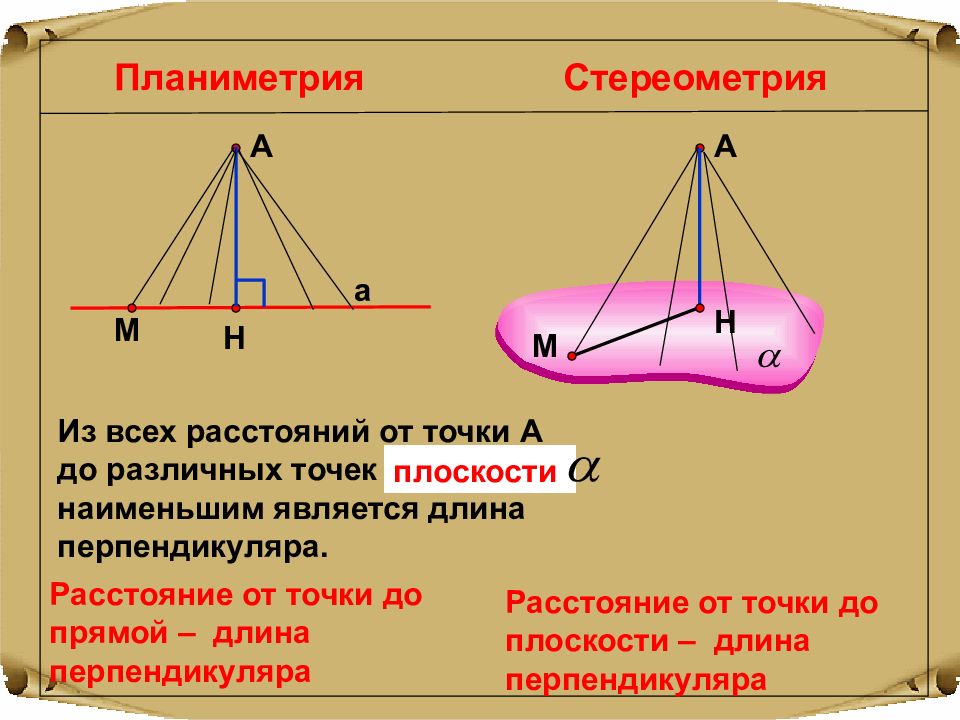
Планиметрия Стереометрия Расстояние от точки до прямой – длина перпендикуляра Н А а А Н М М Расстояние от точки до плоскости – длина перпендикуляра Из всех расстояний от точки А до различных точек прямой а наименьшим является длина перпендикуляра. плоскости
Слайд 9
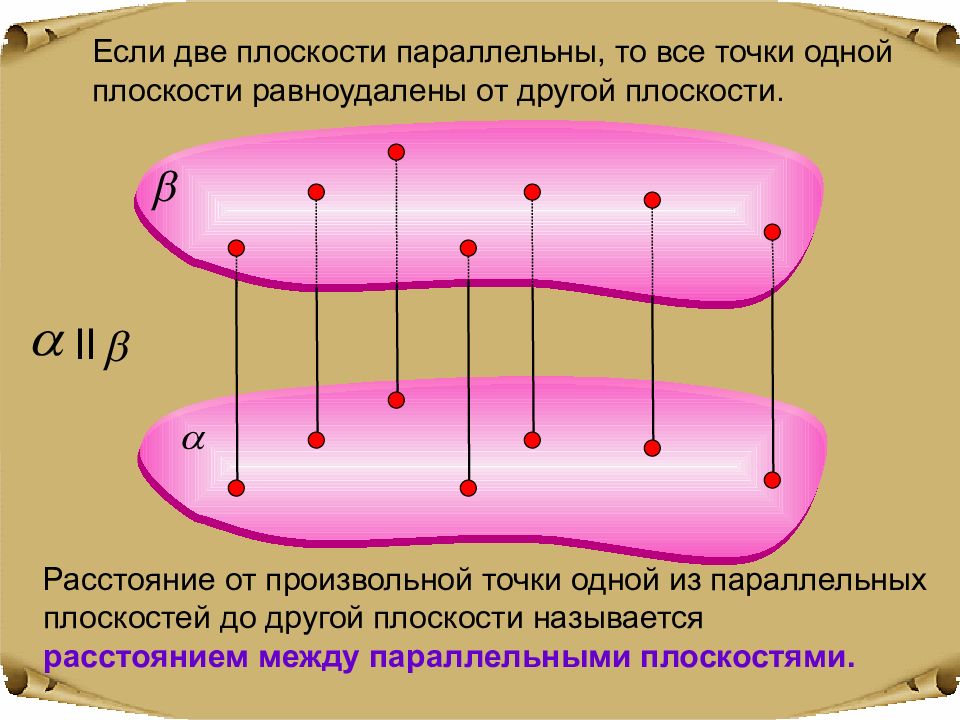
Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями. II
Слайд 10
Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. a II a Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
Слайд 11
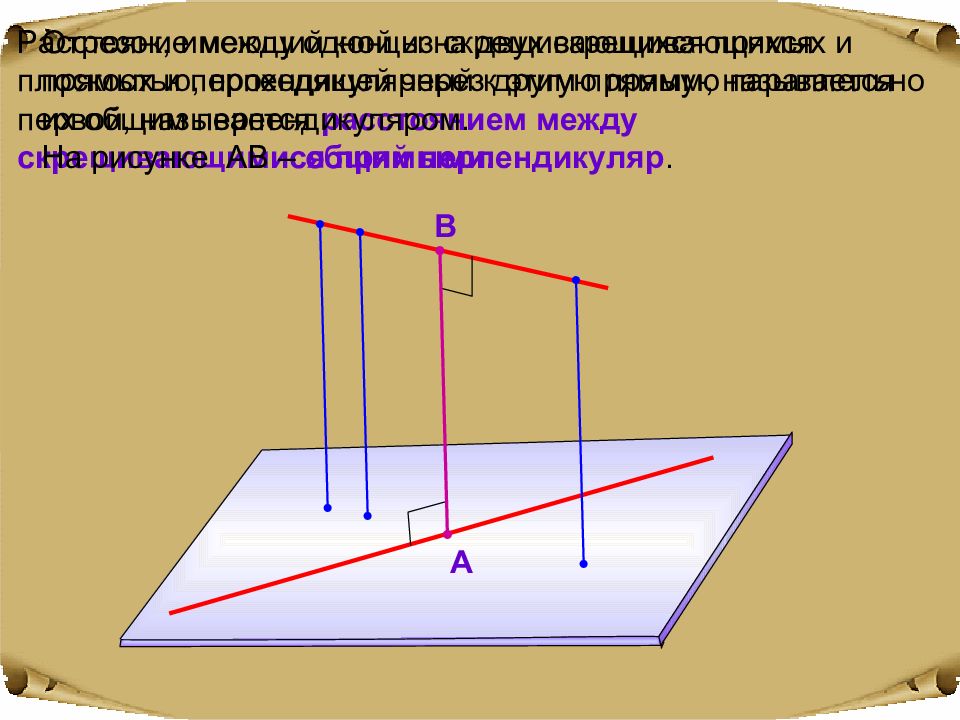
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к этим прямым, называется их общим перпендикуляром. На рисунке АВ – общий перпендикуляр. А В
Слайд 12
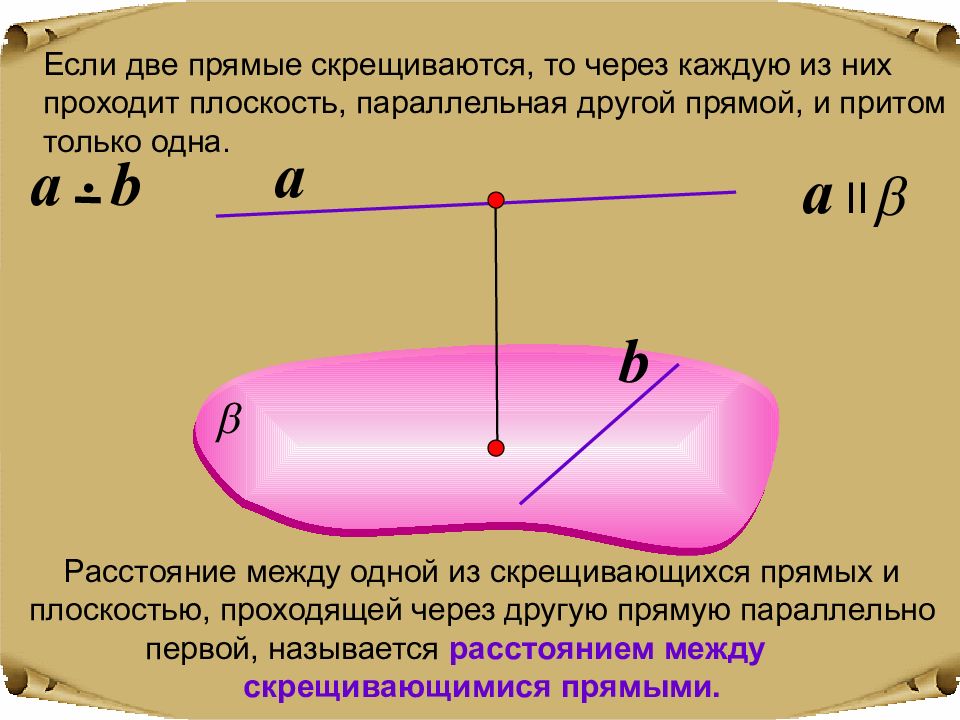
a II Если две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна. a Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. b a b
Слайд 13
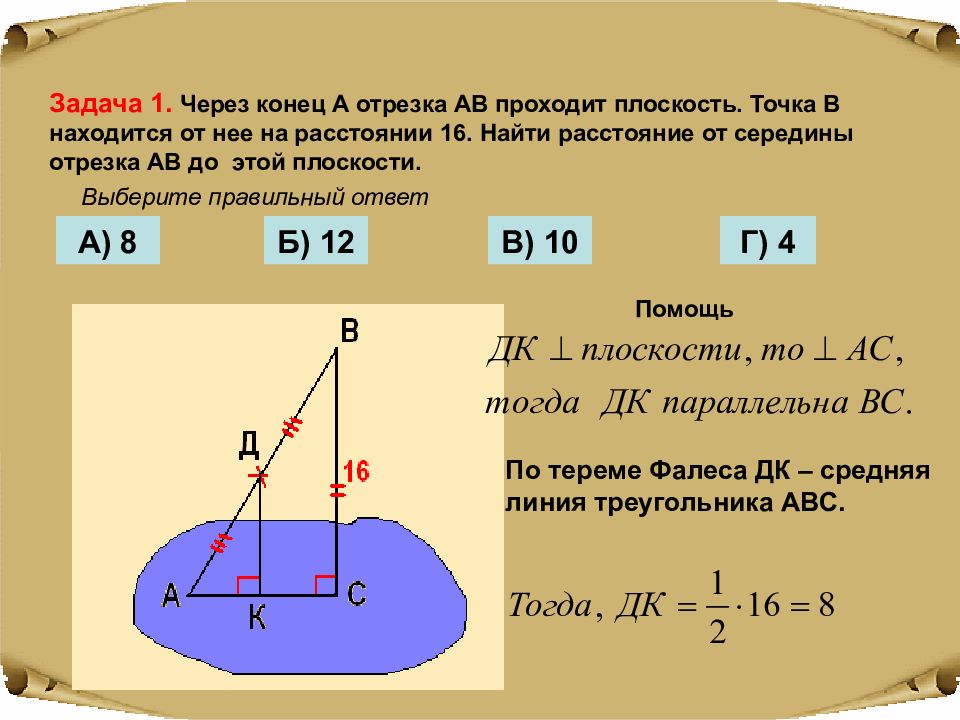
Задача 1. Через конец А отрезка АВ проходит плоскость. Точка В находится от нее на расстоянии 16. Найти расстояние от середины отрезка АВ до этой плоскости. А) 8 Б) 12 В) 10 Г) 4 Выберите правильный ответ Помощь По тереме Фалеса ДК – средняя линия треугольника АВС.
Слайд 14
Задача 2. Отрезок длиной 10 своими концами упирается в две параллельные плоскости, расстояние между которыми равно 8. Найти проекции отрезка на эти плоскости. А)6 и 6 Б)6 и 5 В)8 и 8 Г)8 и 5 Помощь 8 По теореме Пифагора
Слайд 15
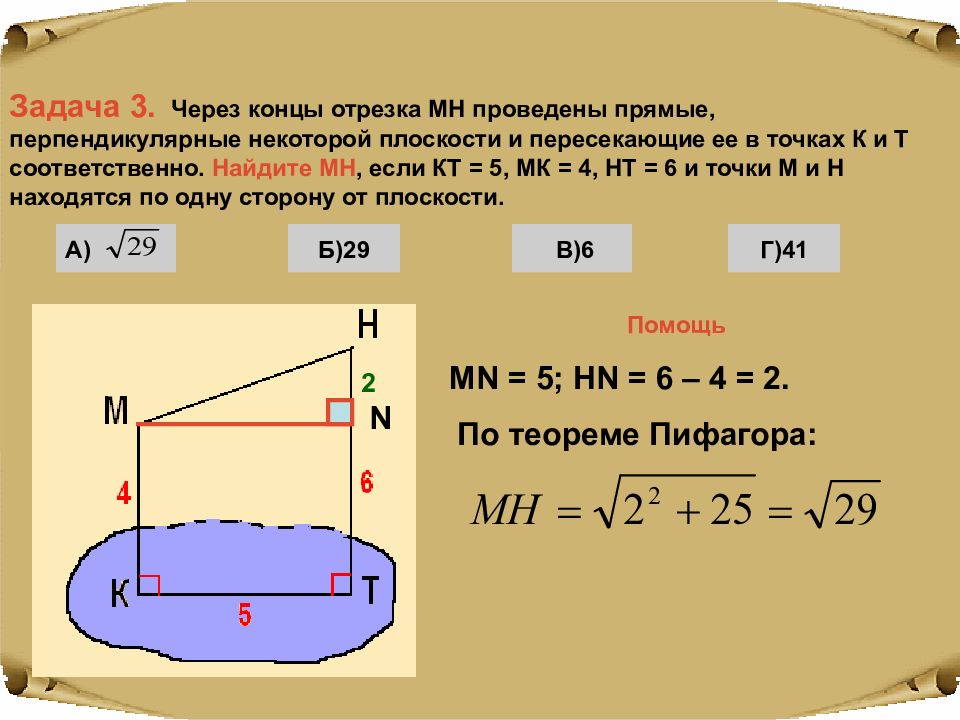
Задача 3. Через концы отрезка МН проведены прямые, перпендикулярные некоторой плоскости и пересекающие ее в точках К и Т соответственно. Найдите МН, если КТ = 5, МК = 4, НТ = 6 и точки М и Н находятся по одну сторону от плоскости. Б)29 В)6 Г)41 Помощь А) N MN = 5; HN = 6 – 4 = 2. 2 По теореме Пифагора:
Слайд 16
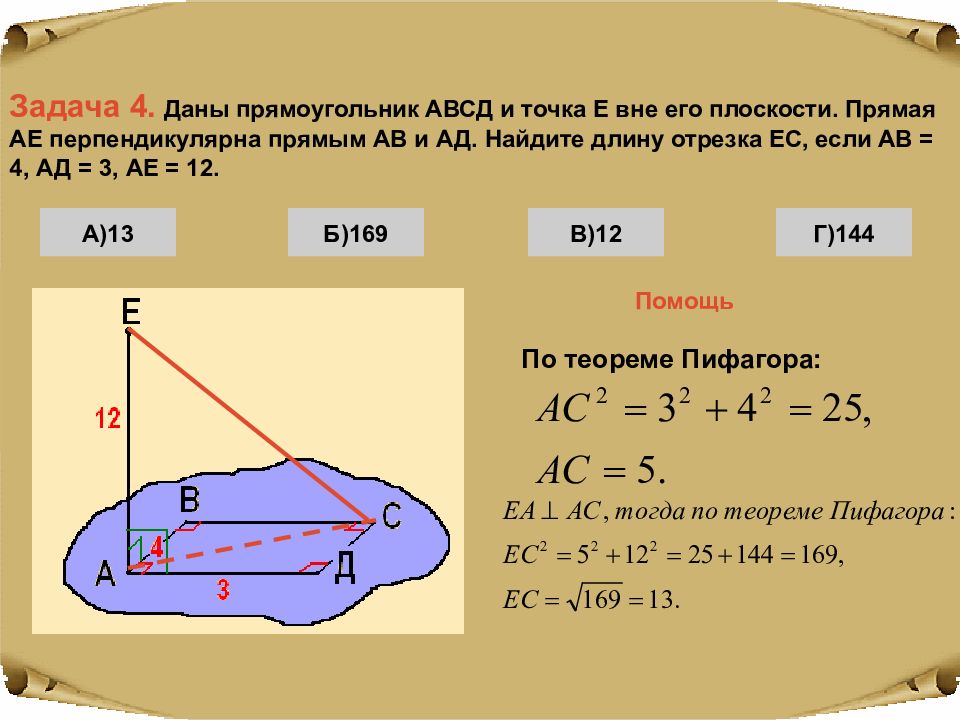
Задача 4. Даны прямоугольник АВСД и точка Е вне его плоскости. Прямая АЕ перпендикулярна прямым АВ и АД. Найдите длину отрезка ЕС, если АВ = 4, АД = 3, АЕ = 12. Г)144 Помощь В)12 Б)169 А)13 По теореме Пифагора:
Слайд 19
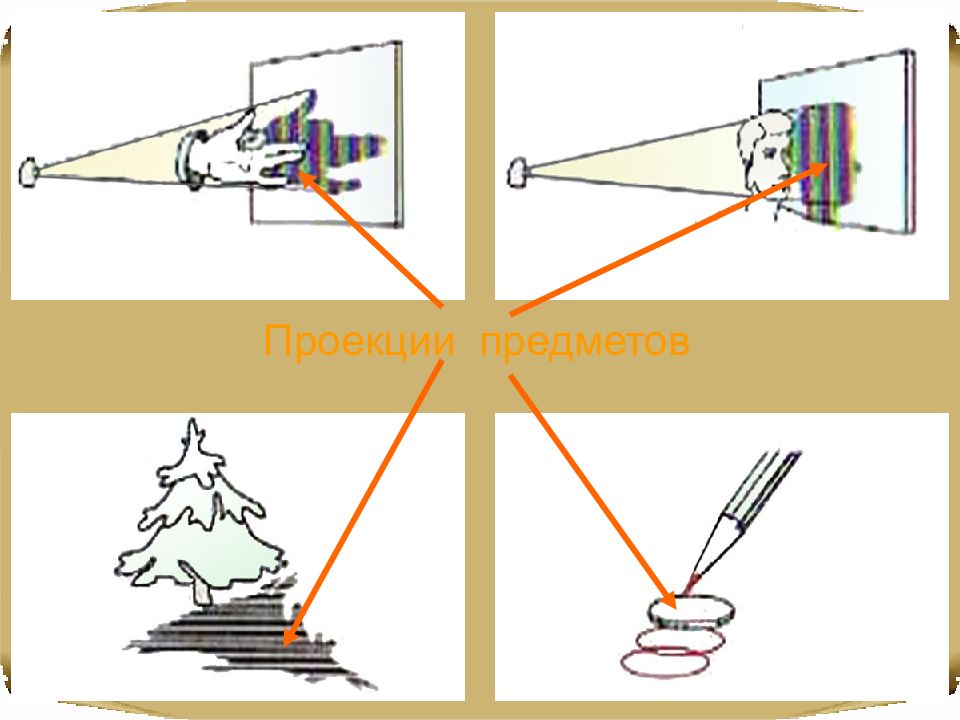
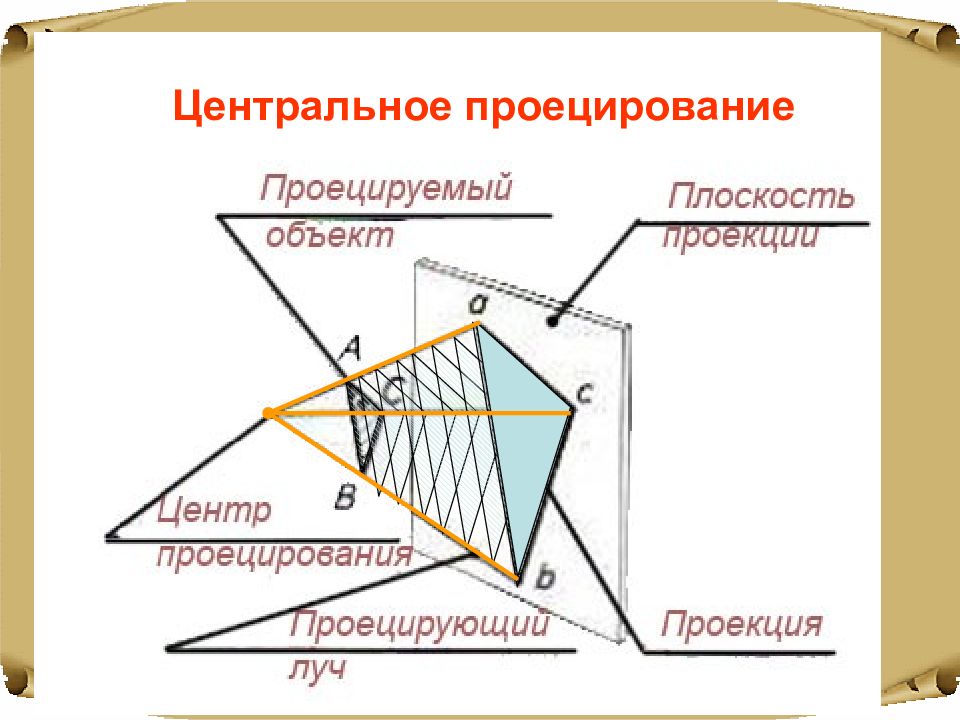
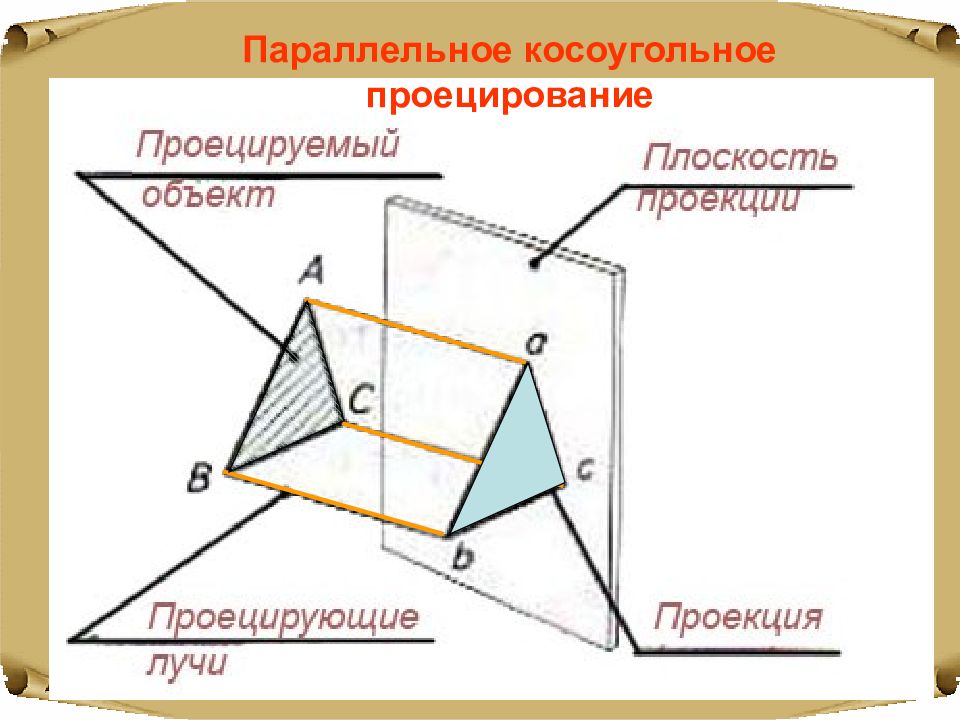
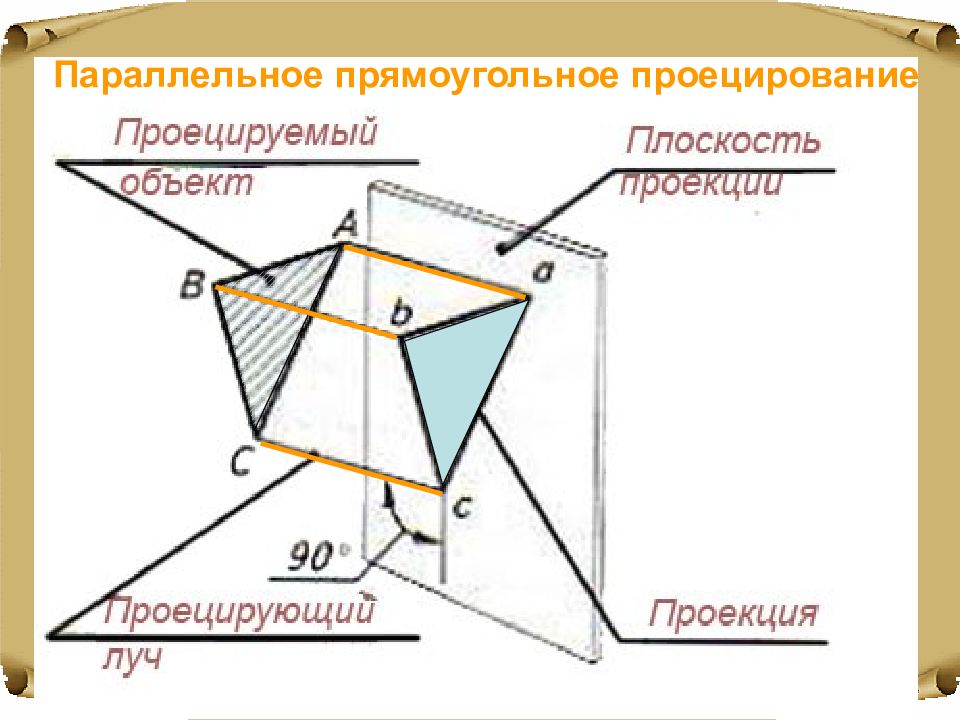
Рисунки, чертежи, фотографии или контуры, полученные посредством обводки предмета, - все это проекции предметов. Плоскостью проекций может быть стена, лист бумаги, поверхность земли ит.д.
Слайд 24
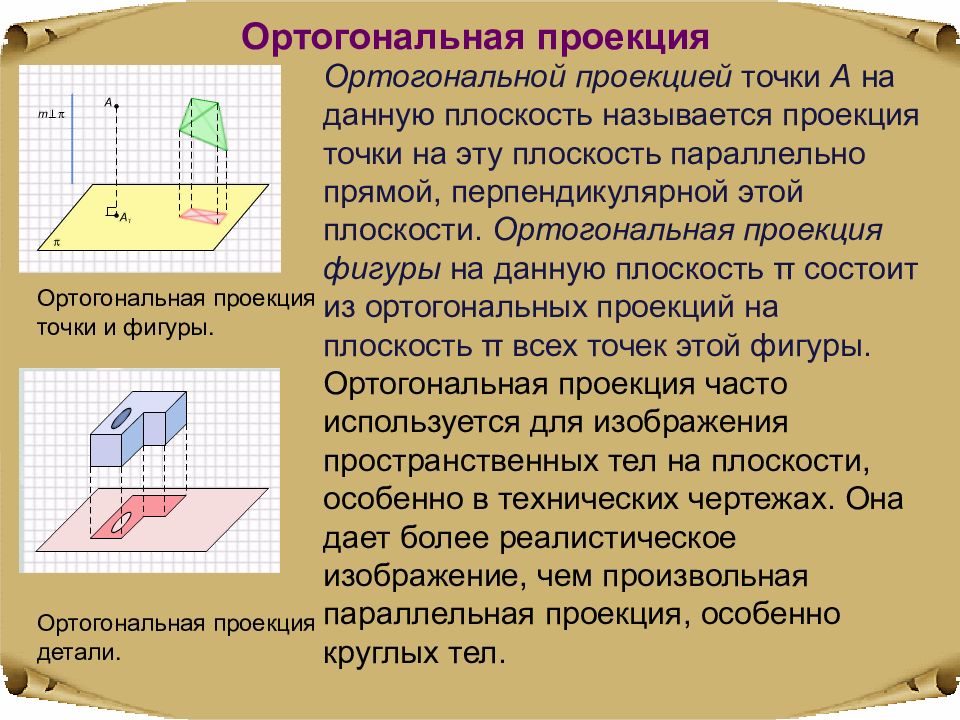
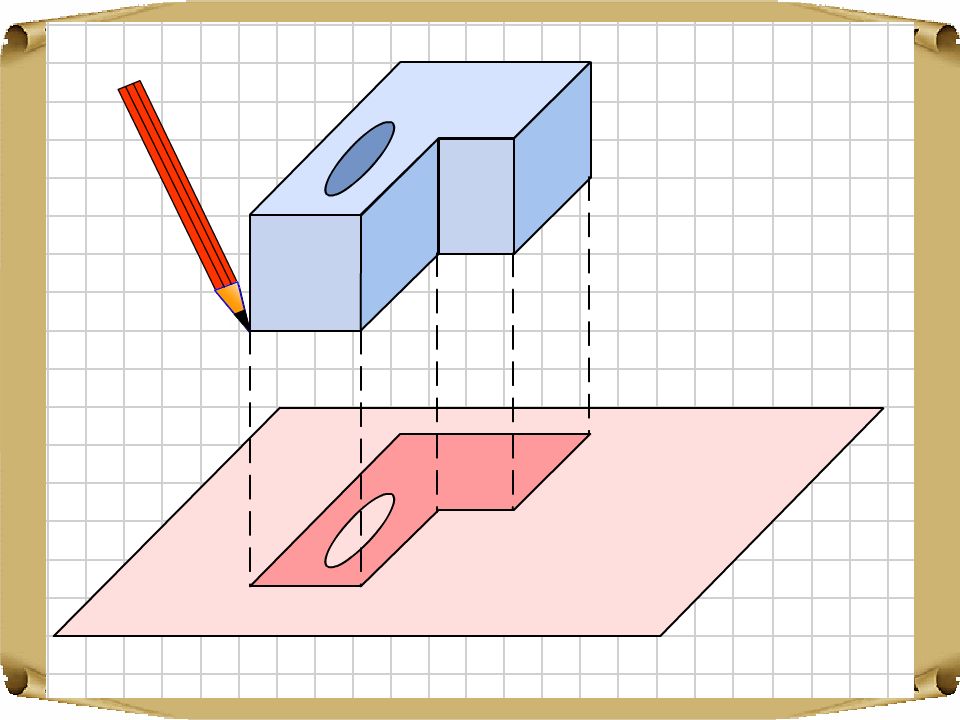
Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту плоскость параллельно прямой, перпендикулярной этой плоскости. Ортогональная проекция фигуры на данную плоскость π состоит из ортогональных проекций на плоскость π всех точек этой фигуры. Ортогональная проекция часто используется для изображения пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистическое изображение, чем произвольная параллельная проекция, особенно круглых тел. Ортогональная проекция Ортогональная проекция точки и фигуры. Ортогональная проекция детали.
Слайд 27
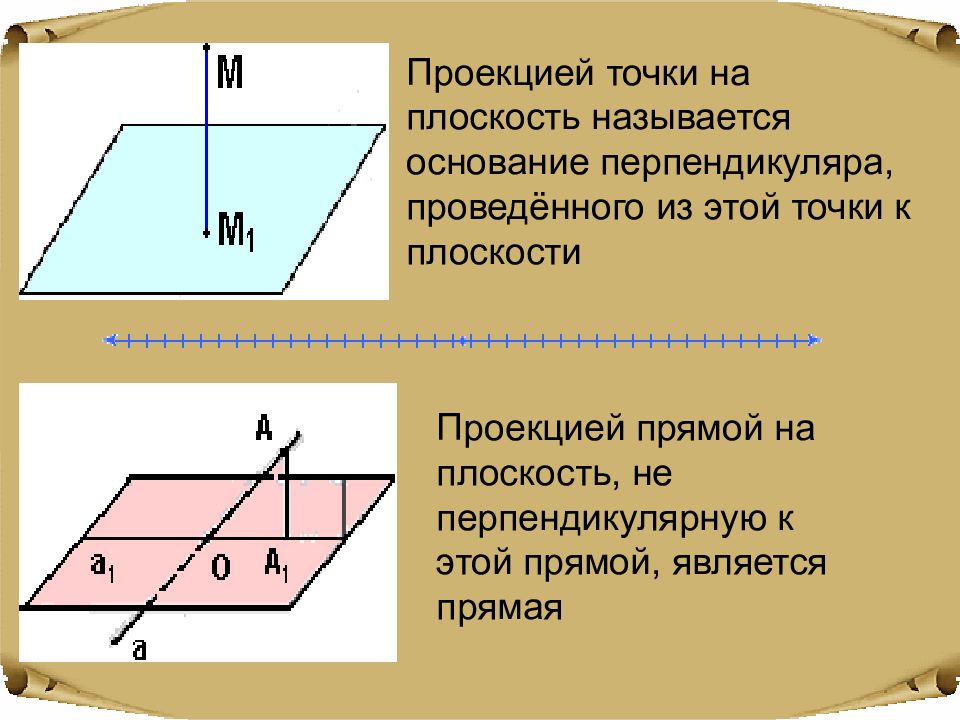
Проекцией точки на плоскость называется основание перпендикуляра, проведённого из этой точки к плоскости Проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая
Слайд 28
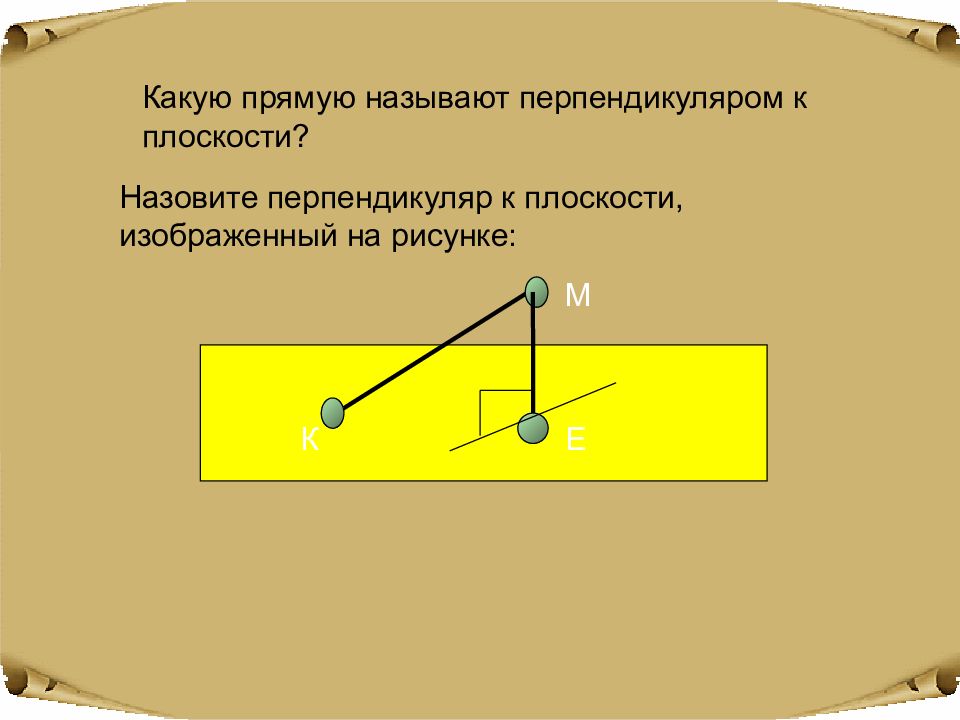
Какую прямую называют перпендикуляром к плоскости? Назовите перпендикуляр к плоскости, изображенный на рисунке: М К Е
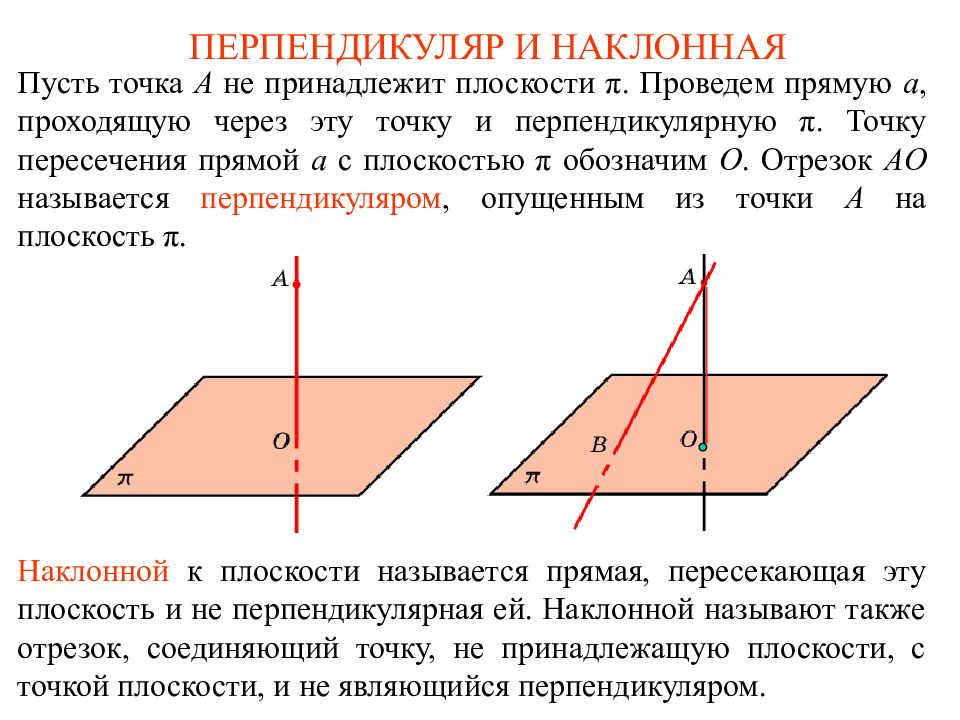
Слайд 29: Перпендикуляр и наклонная
Слайд 30
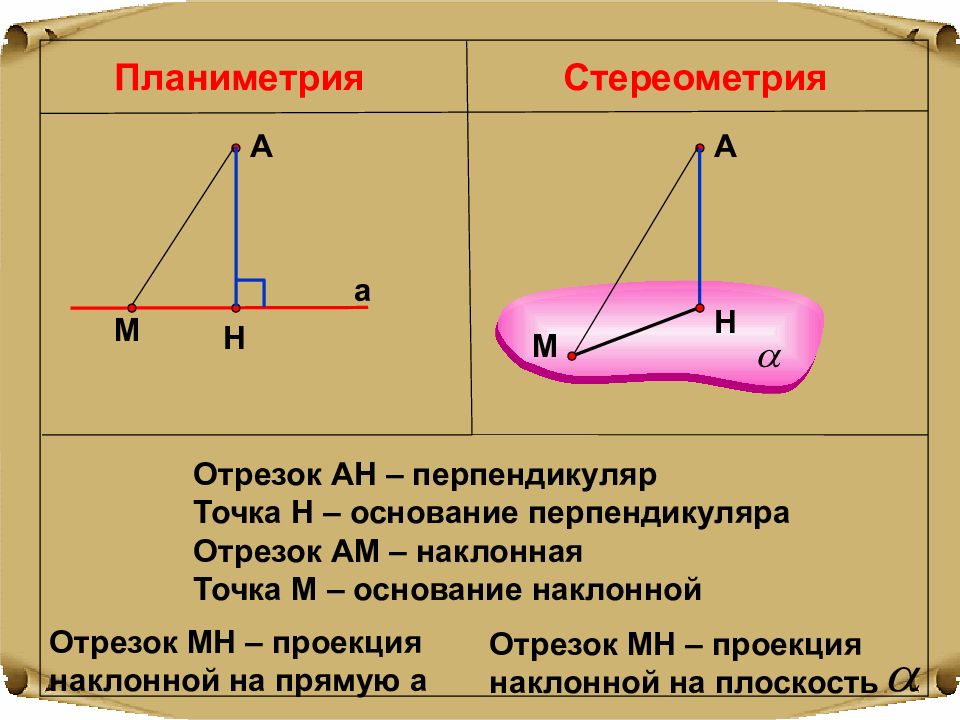
Планиметрия Стереометрия Отрезок АН – перпендикуляр Точка Н – основание перпендикуляра Отрезок АМ – наклонная Точка М – основание наклонной Н А а А Н М М Отрезок МН – проекция наклонной на прямую а Отрезок МН – проекция наклонной на плоскость
Слайд 31
Расстояние от лампочки до земли измеряется по перпендикуляру, проведенному от лампочки к плоскости земли Н а к л о н н а я Н а к л о н н а я П Е Р П Е Н Д И К У Л Я Р Проекция Проекция
Слайд 32
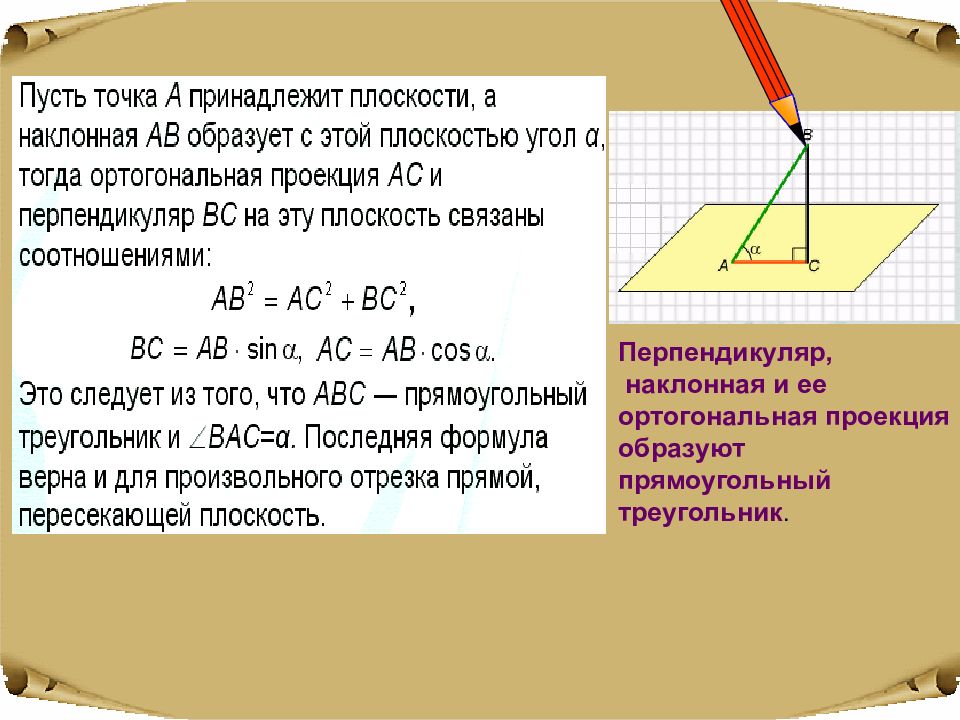
Перпендикуляр, наклонная и ее ортогональная проекция образуют прямоугольный треугольник.
Слайд 34
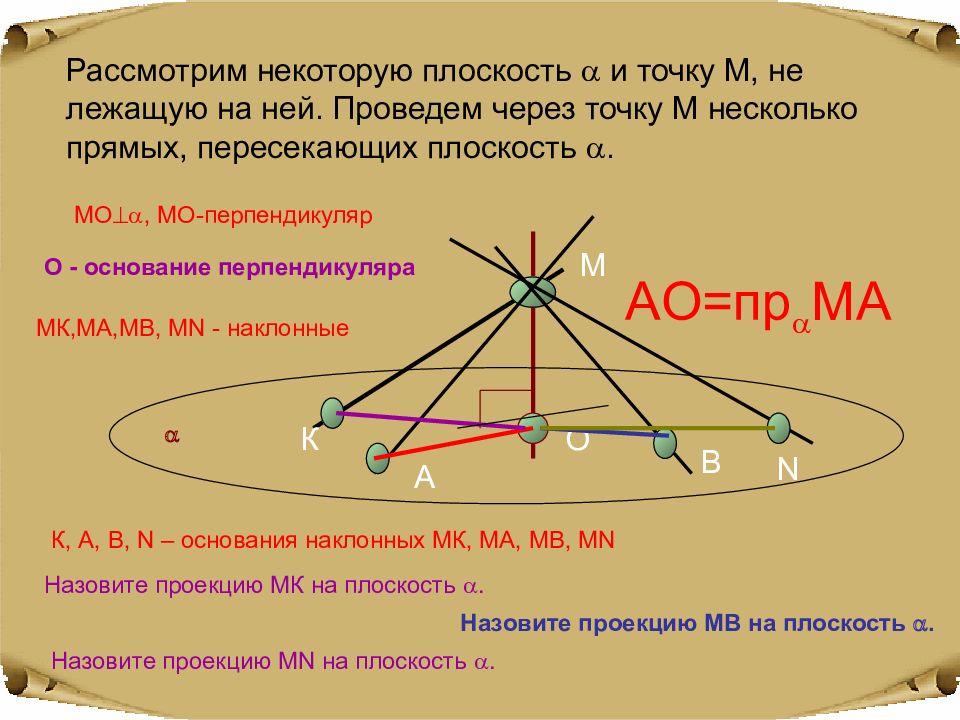
Рассмотрим некоторую плоскость и точку М, не лежащую на ней. Проведем через точку М несколько прямых, пересекающих плоскость . МО , МО-перпендикуляр О - основание перпендикуляра К О М А В N МК,МА,МВ, М N - наклонные К, А, В, N – основания наклонных МК, МА, МВ, М N AO= пр МА Назовите проекцию МК на плоскость . Назовите проекцию МВ на плоскость . Назовите проекцию М N на плоскость .
Слайд 35: Свойства наклонных, выходящих из одной точки
1. Перпендикуляр всегда короче наклонной, если они проведены из одной точки. 2. Если наклонные равны, то равны и их проекции, и наоборот. 3. Большей наклонной соответствует большая проекция и наоборот.
Слайд 36
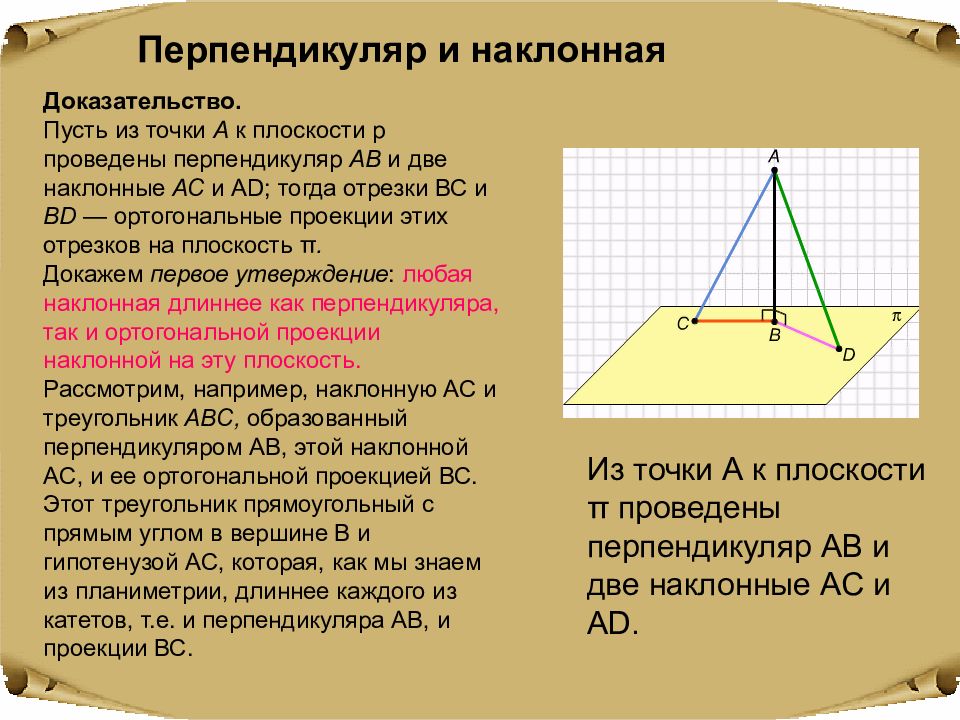
Перпендикуляр и наклонная Доказательство. Пусть из точки А к плоскости p проведены перпендикуляр АВ и две наклонные АС и AD ; тогда отрезки ВС и BD — ортогональные проекции этих отрезков на плоскость π. Докажем первое утверждение : любая наклонная длиннее как перпендикуляра, так и ортогональной проекции наклонной на эту плоскость. Рассмотрим, например, наклонную A С и треугольник ABC, образованный перпендикуляром A В, этой наклонной A С, и ее ортогональной проекцией ВС. Этот треугольник прямоугольный с прямым углом в вершине В и гипотенузой A С, которая, как мы знаем из планиметрии, длиннее каждого из катетов, т.е. и перпендикуляра A В, и проекции ВС. Из точки А к плоскости π проведены перпендикуляр АВ и две наклонные AC и AD.
Слайд 37
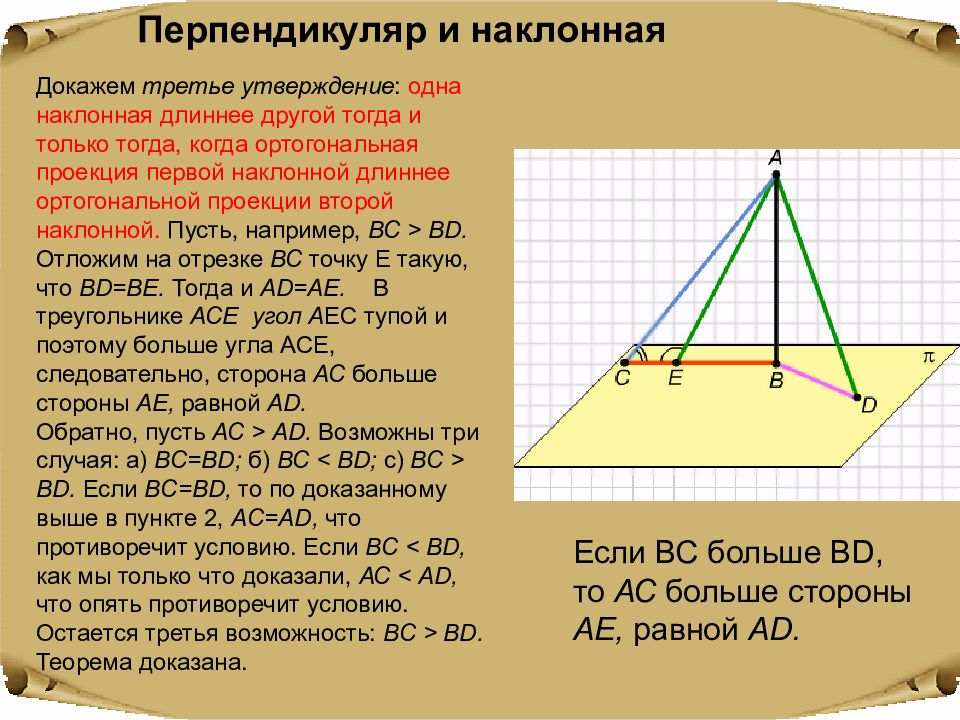
Перпендикуляр и наклонная Докажем третье утверждение : одна наклонная длиннее другой тогда и только тогда, когда ортогональная проекция первой наклонной длиннее ортогональной проекции второй наклонной. Пусть, например, ВС > BD. Отложим на отрезке ВС точку Е такую, что BD=BE. Тогда и AD=AE. В треугольнике АСЕ угол A EC тупой и поэтому больше угла ACE, следовательно, сторона АС больше стороны АЕ, равной AD. Обратно, пусть АС > AD. Возможны три случая: a) BC=BD; б) ВС < BD; с) ВС > BD. Если BC=BD, то по доказанному выше в пункте 2, AC=AD, что противоречит условию. Если ВС < BD, как мы только что доказали, АС < AD, что опять противоречит условию. Остается третья возможность: ВС > BD. Теорема доказана. Если ВС больше BD, то АС больше стороны АЕ, равной AD.
Слайд 39
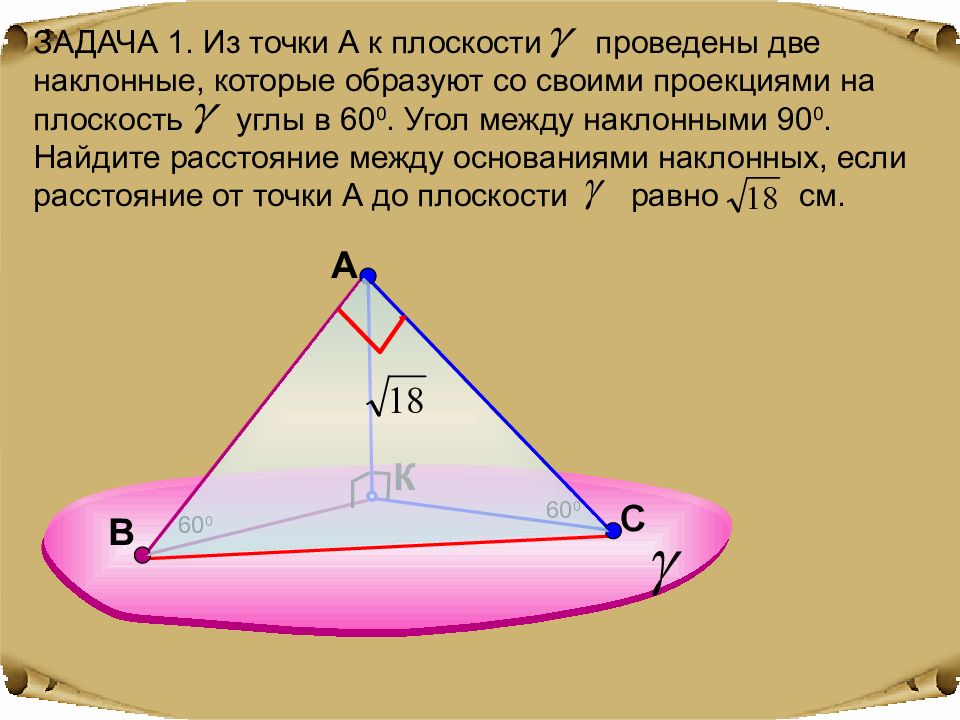
A К ЗАДАЧА 1. Из точки А к плоскости проведены две наклонные, которые образуют со своими проекциями на плоскость углы в 60 0. Угол между наклонными 90 0. Найдите расстояние между основаниями наклонных, если расстояние от точки А до плоскости равно см. 60 0 60 0 С В
Слайд 40
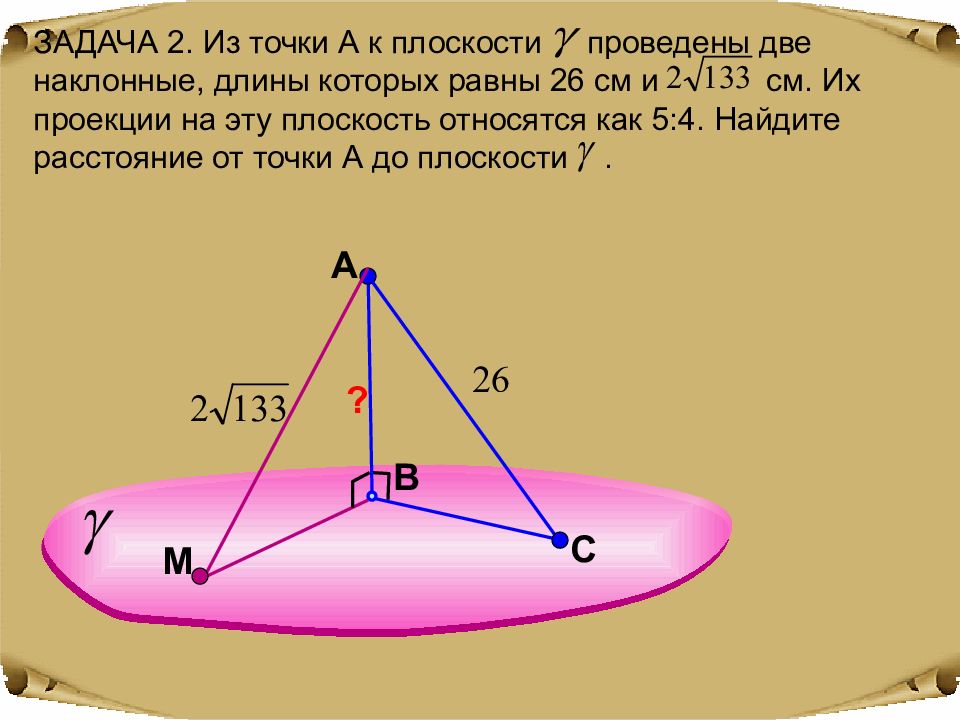
A В ЗАДАЧА 2. Из точки А к плоскости проведены две наклонные, длины которых равны 26 см и см. Их проекции на эту плоскость относятся как 5:4. Найдите расстояние от точки А до плоскости. С М ?
Слайд 41: Домашнее задание
Выучить теорию ( конспект или §2, п.19 ), № 138, № 140, № 141, № 142
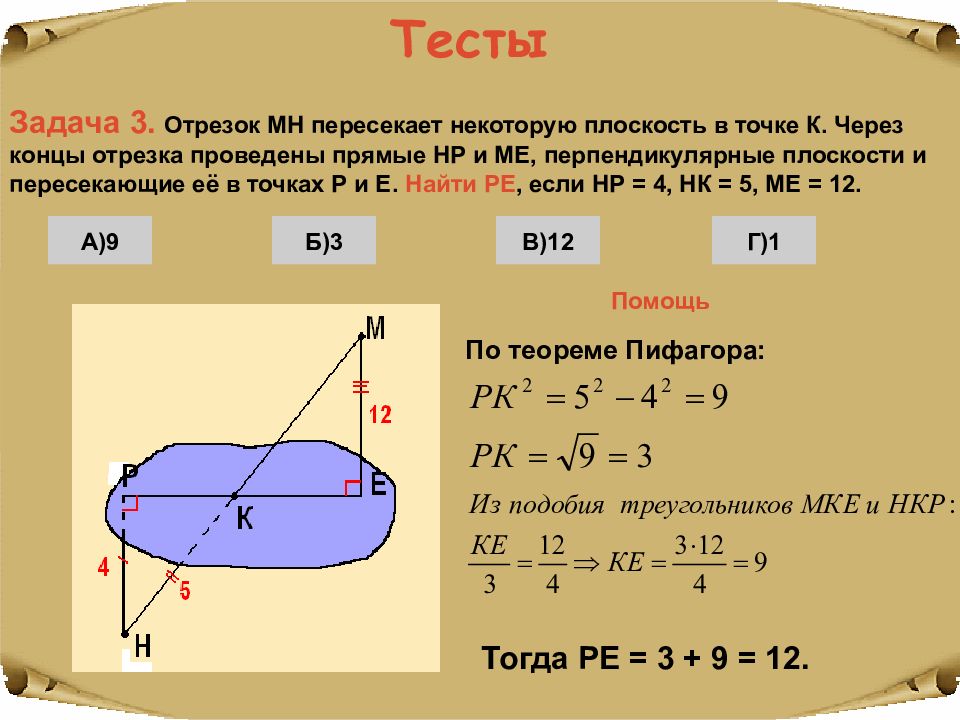
Последний слайд презентации: УСТНО:: Тесты
Задача 3. Отрезок МН пересекает некоторую плоскость в точке К. Через концы отрезка проведены прямые НР и МЕ, перпендикулярные плоскости и пересекающие её в точках Р и Е. Найти РЕ, если НР = 4, НК = 5, МЕ = 12. А)9 Б)3 Г)1 В)12 Помощь По теореме Пифагора: Тогда РЕ = 3 + 9 = 12.