Первый слайд презентации: Перпендикулярность прямых и плоскостей
Автор Календарева Н.Е. © 2011 г.
Слайд 2: План
Перпендикулярность прямых Перпендикулярность прямой и плоскости Признак перпендикулярности прямой и плоскости Перпендикуляр и наклонная Расстояние от точки до плоскости Теорема о трех перпендикулярах 2
Слайд 3: Продолжение плана
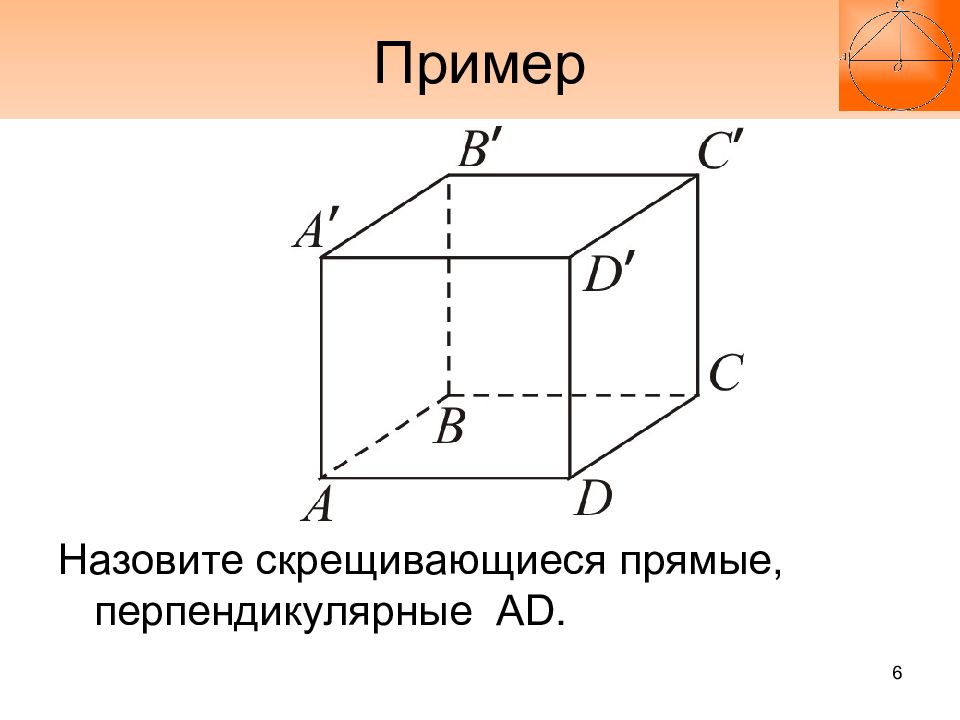
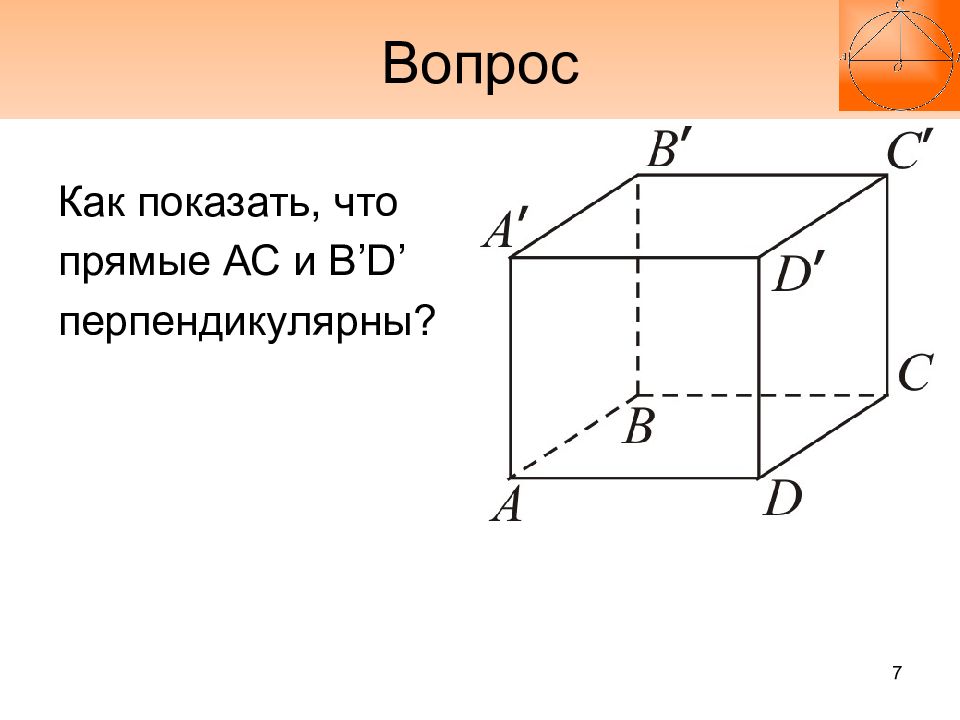
7. Куб, его перпендикулярные прямые, наклонные и их проекции 8. Треугольная пирамида, прямая призма и проектирование точек на плоскость 9. Перпендикулярность плоскостей 10. Признак перпендикулярности плоскостей 3
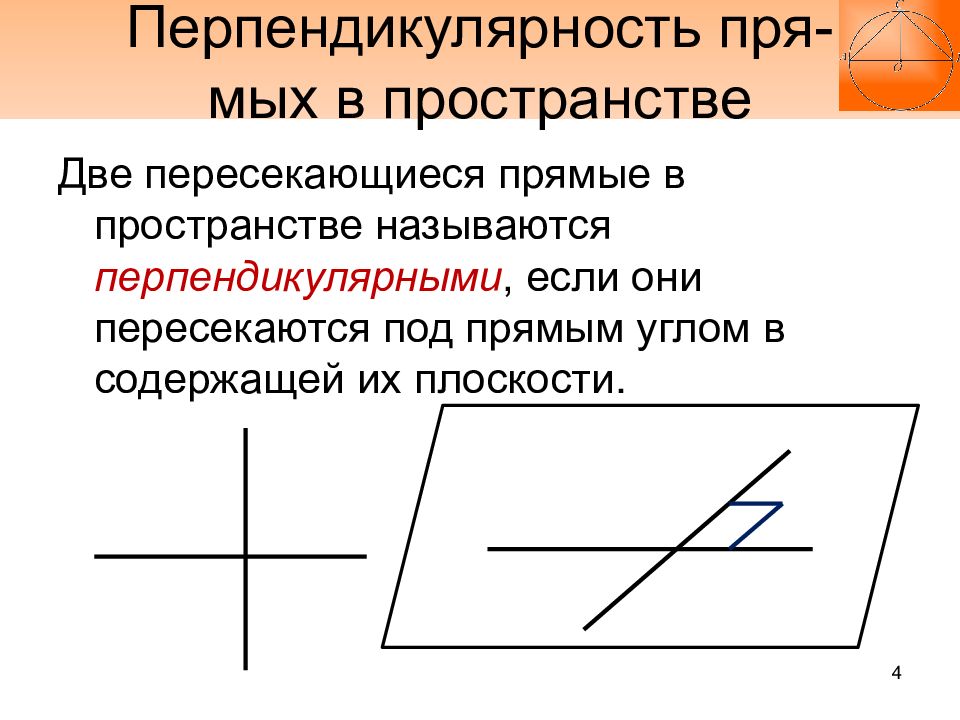
Две пересекающиеся прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом в содержащей их плоскости. 4
Слайд 5: Перпендикулярные прямые
Две скрещивающиеся прямые называются перпендикулярными, если параллельные им пересекающиеся прямые перпендикулярны. А b b’ a 5
Слайд 8: Теорема
Если две пересекающиеся прямые соответственно параллельны двум перпендикулярным прямым, то они тоже перпендикулярны. Доказательство в Погорелове в параграфе «Перпендикулярность прямых и плоскостей», теорема 17.1 8
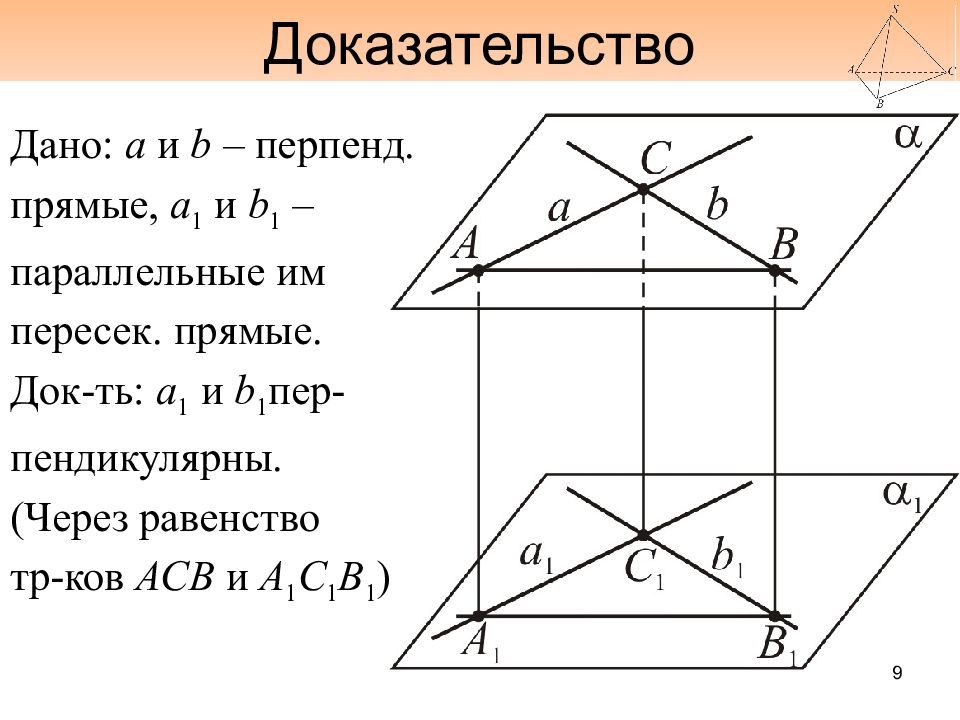
Слайд 9: Доказательство
Дано: а и b – перпенд. прямые, а 1 и b 1 – параллельные им пересек. прямые. Док-ть : а 1 и b 1 пер- пендикулярны. (Через равенство тр-ков АСВ и А 1 С 1 В 1 ) 9
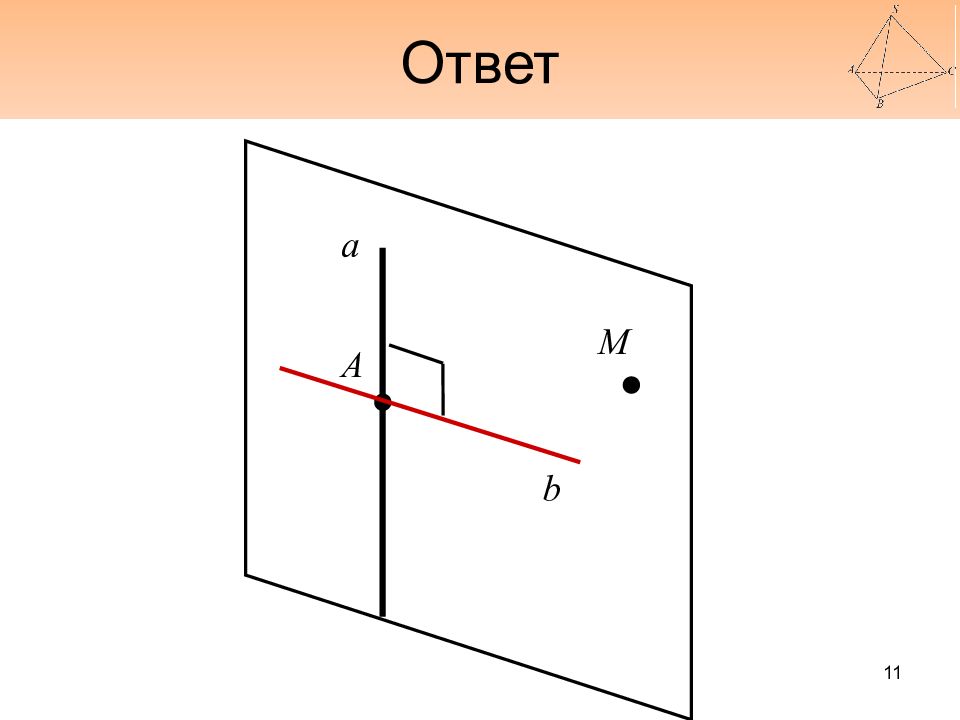
Слайд 10: 1. Задача на построение
Можно ли через любую точку прямой в пространстве провести перпендикулярную ей прямую? Если да, то сколько? 10
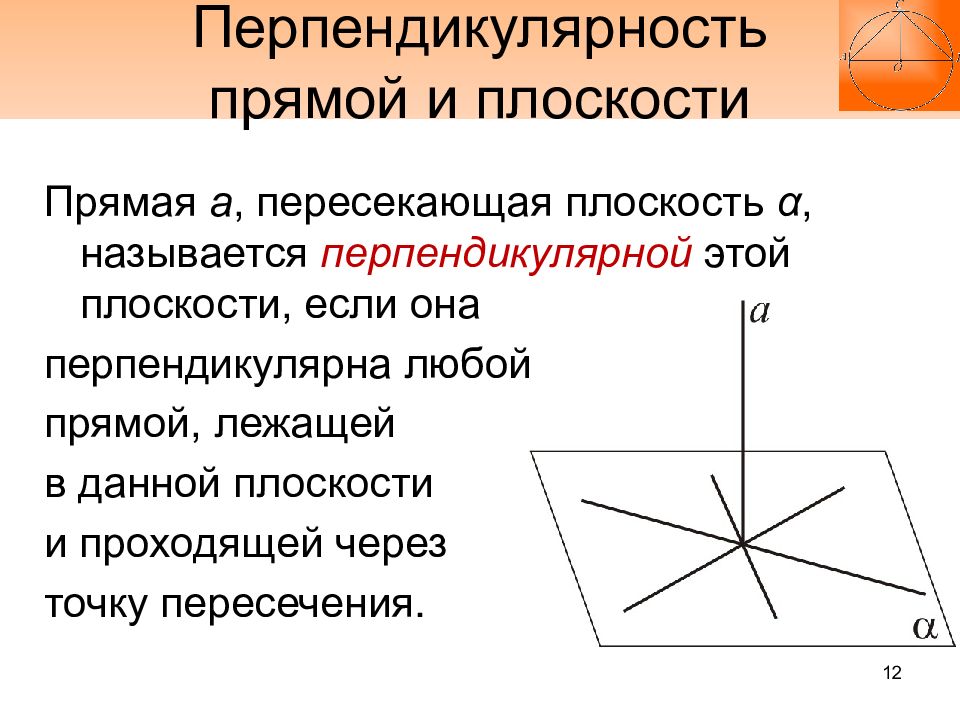
Слайд 12: Перпендикулярность прямой и плоскости
Прямая а, пересекающая плоскость α, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, лежащей в данной плоскости и проходящей через точку пересечения. 12
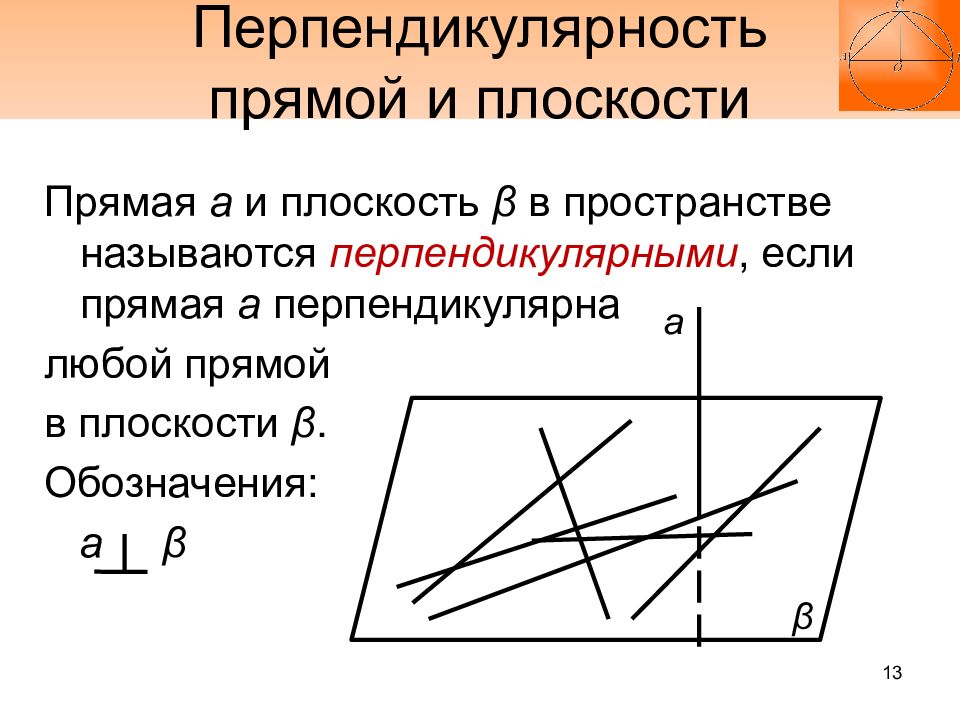
Слайд 13: Перпендикулярность прямой и плоскости
Прямая а и плоскость β в пространстве называются перпендикулярными, если прямая а перпендикулярна любой прямой в плоскости β. Обозначения: а β β а 13
Слайд 15: Признак перпендикулярности прямой и плоскости
Если две пересекающие прямые, лежащие в плоскости β, перпендикулярны прямой а, то а β. Другая формулировка. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости. 15
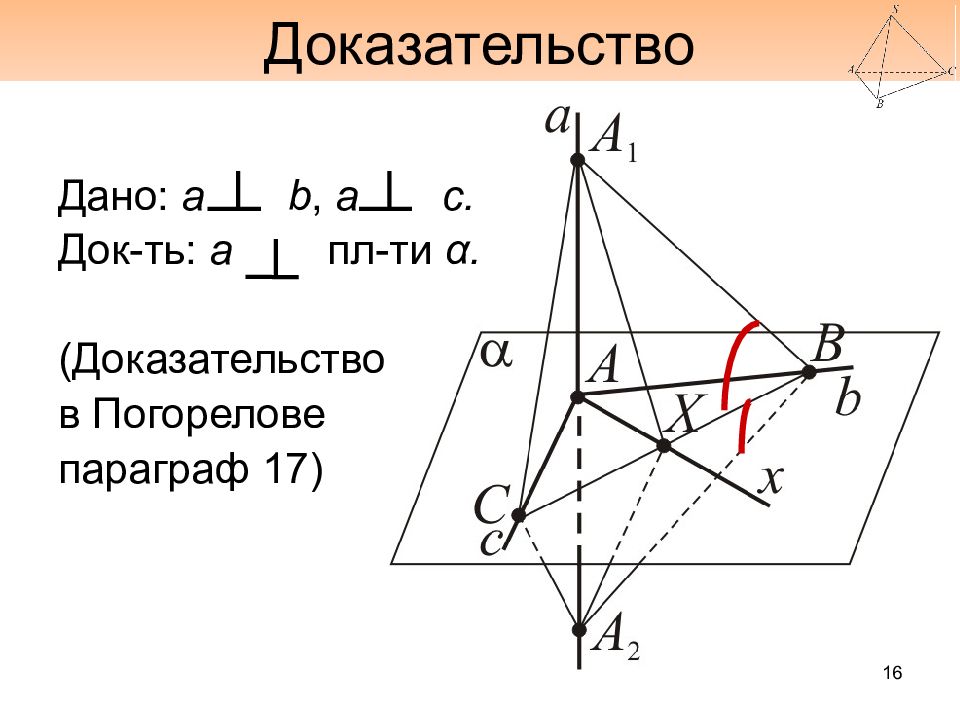
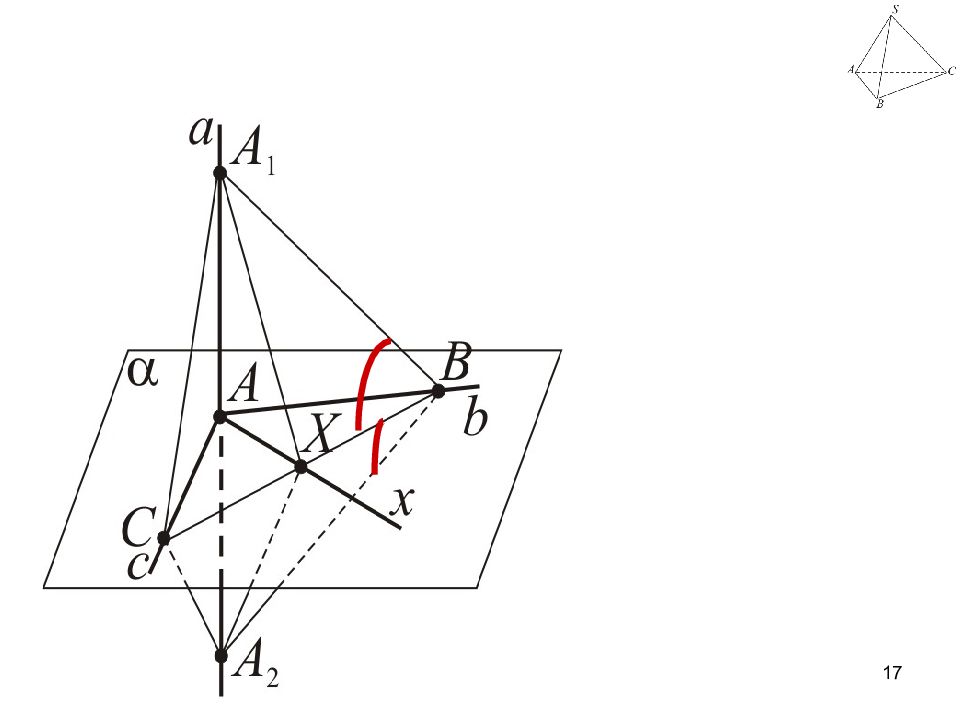
Слайд 16: Доказательство
Дано: а b, а c. Док-ть : а пл-ти α. (Доказательство в Погорелове параграф 17) 16
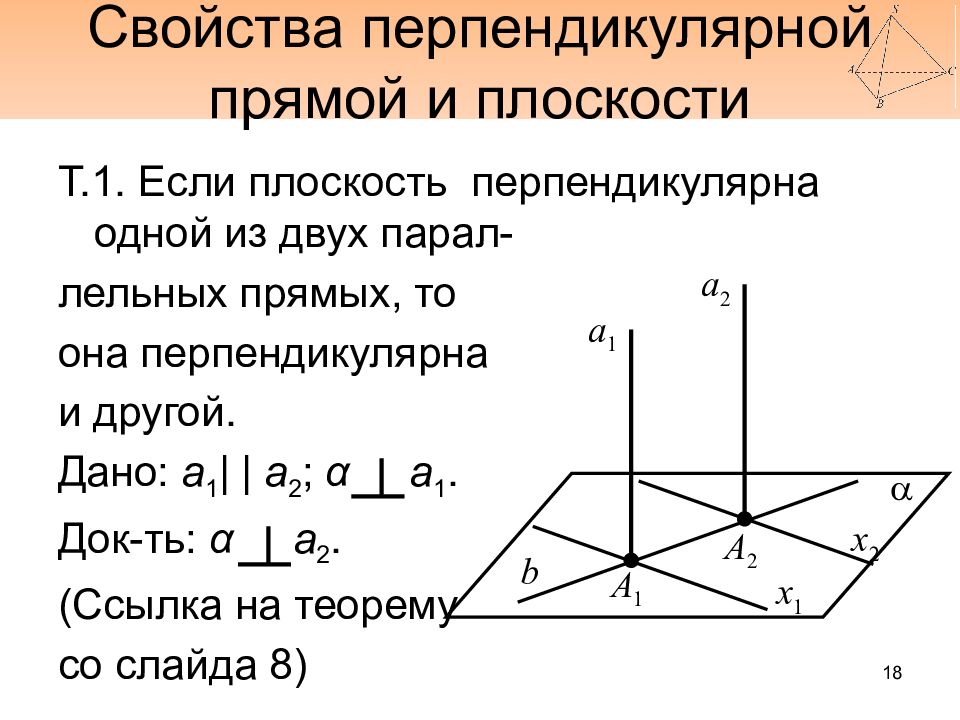
Слайд 18: Свойства перпендикулярной прямой и плоскости
Т.1. Если плоскость перпендикулярна одной из двух парал - лельных прямых, то она перпендикулярна и другой. Дано: а 1 | | a 2 ; α а 1. Док-ть : α а 2. (Ссылка на теорему со слайда 8) a 1 a 2 x 2 x 1 A 2 A 1 b a 18
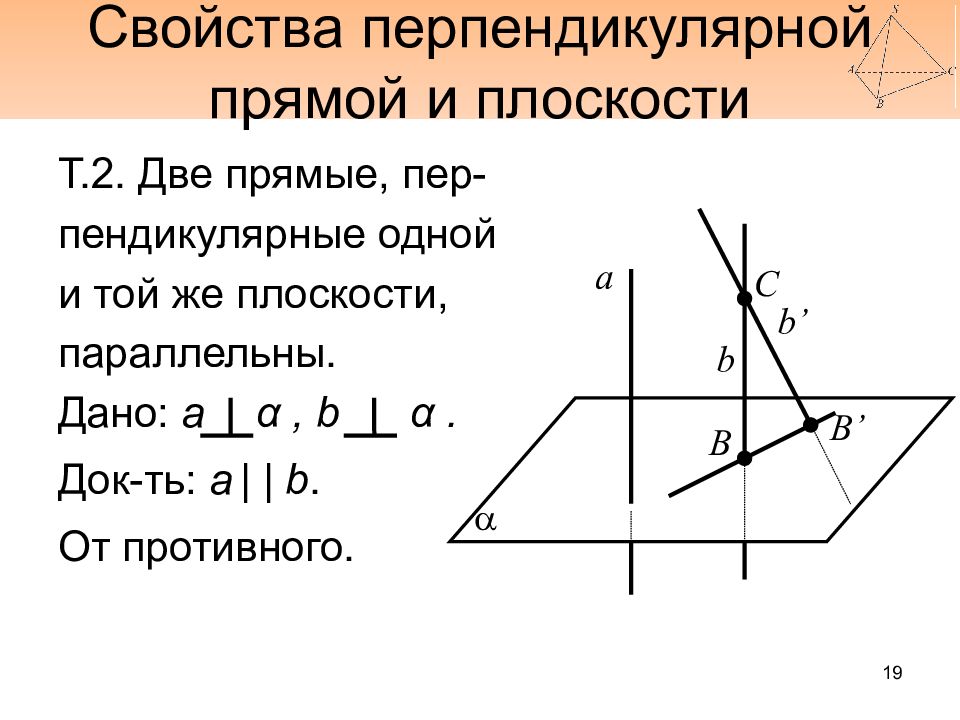
Слайд 19: Свойства перпендикулярной прямой и плоскости
Т.2. Две прямые, пер- пендикулярные одной и той же плоскости, параллельны. Дано: а α, b α. Док-ть : а | | b. От противного. a a b b’ C B B’ 19
Слайд 20
Теорема 3. Если пря-мая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости. 20
Слайд 21: Обратное утверждение
Верно обратное свойство. Если прямая перпендикулярна двум различным плоскостям, то эти плоскости параллельны. 21
Слайд 22: Задача на построение
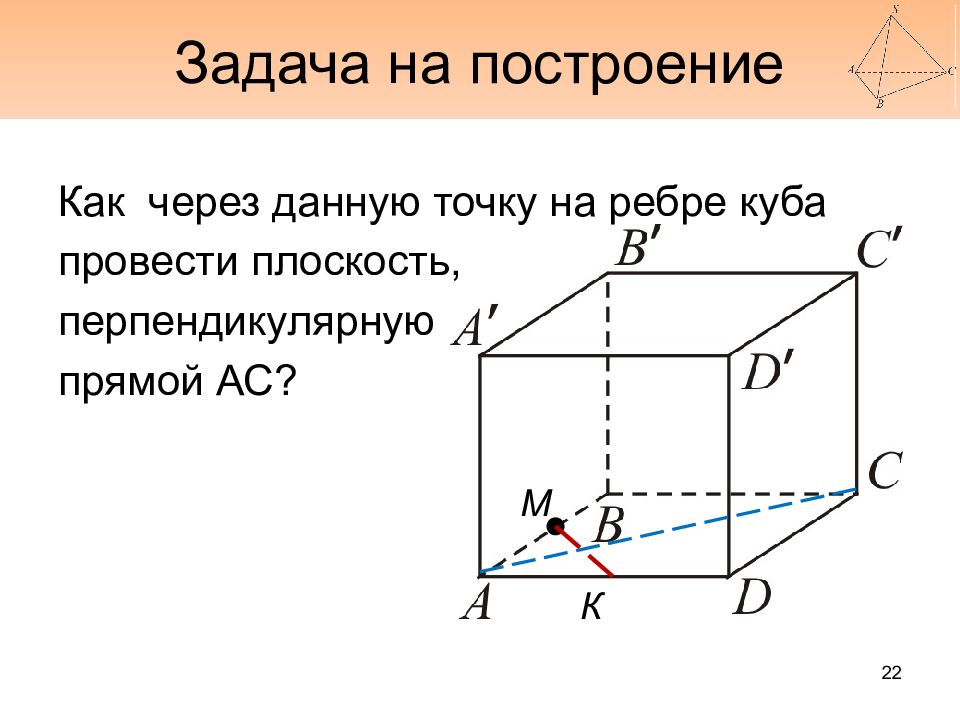
Как через данную точку на ребре куба провести плоскость, перпендикулярную прямой АС? 22 М К
Слайд 23: Перпендикуляр и наклонная
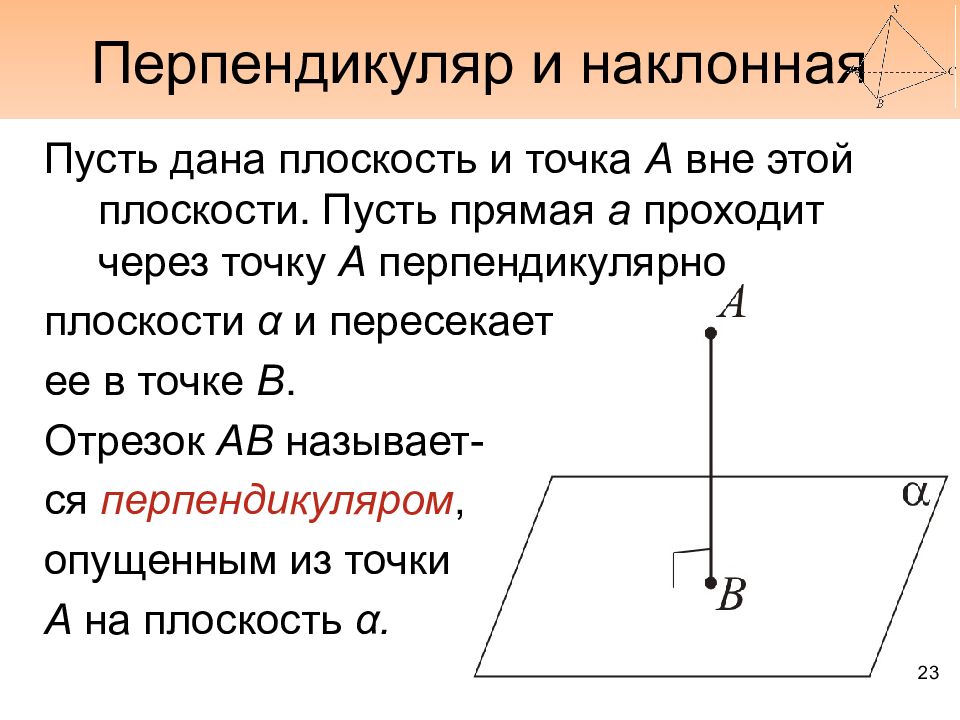
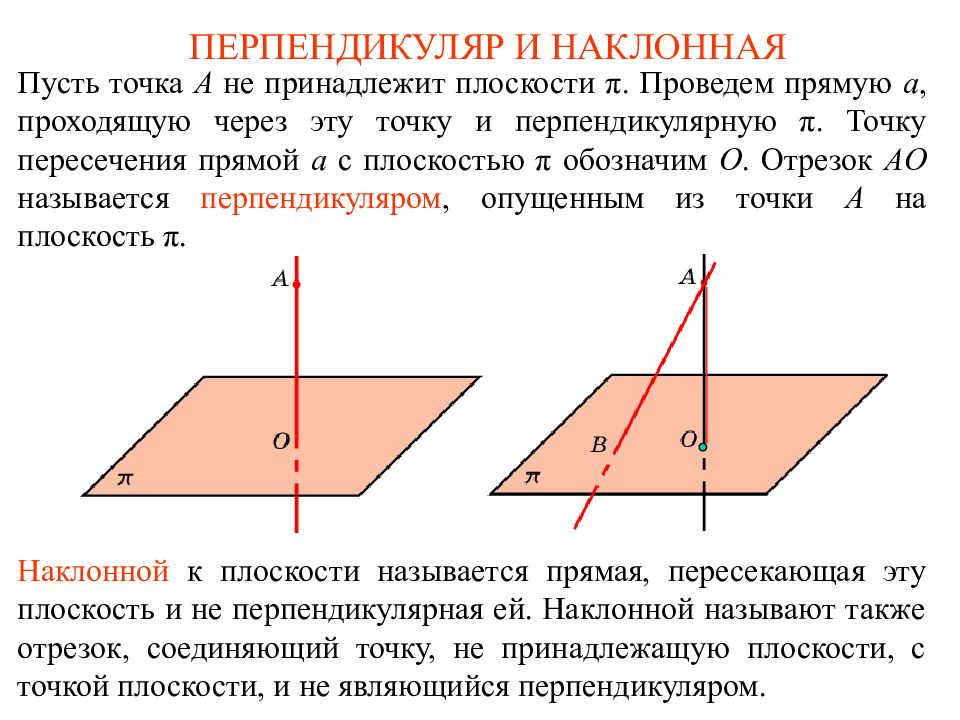
Пусть дана плоскость и точка А вне этой плоскости. Пусть прямая а проходит через точку А перпендикулярно плоскости α и пересекает ее в точке В. Отрезок АВ называет- ся перпендикуляром, опущенным из точки А на плоскость α. 23
Слайд 24: Перпендикуляр и наклонная
Точка В называется основанием этого перпендикуляра. Пусть С – любая точка плоскости, отличная от В. Отрезок АС называет- ся наклонной, прове - денной из точки А к плоскости α. 24
Слайд 25: Перпендикуляр и наклонная
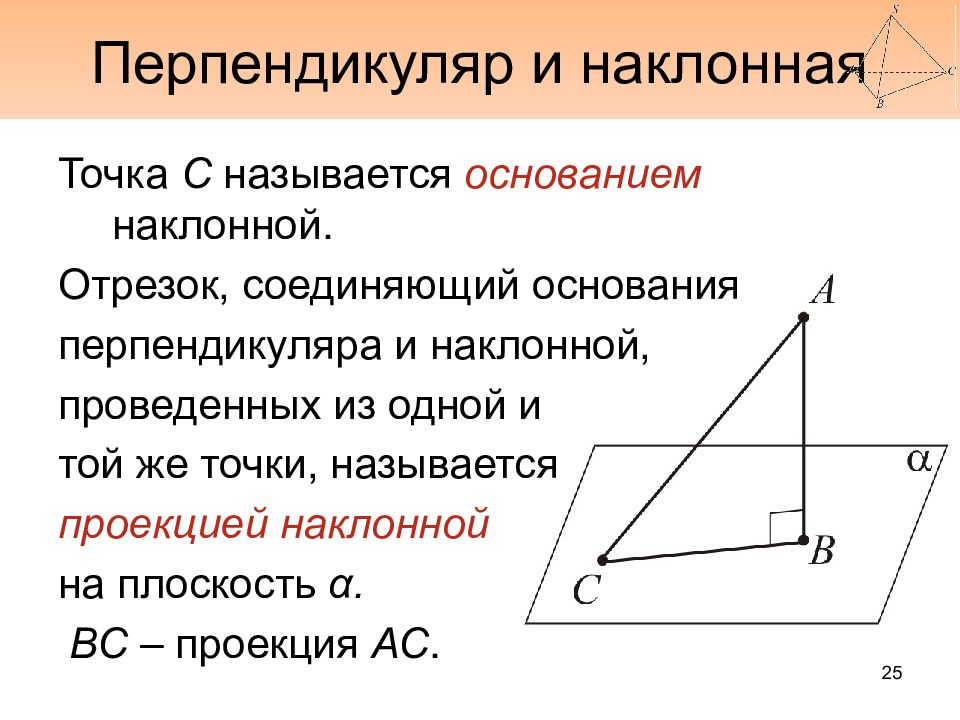
Точка С называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной на плоскость α. ВС – проекция АС. 25
Слайд 26: Определение наклонной
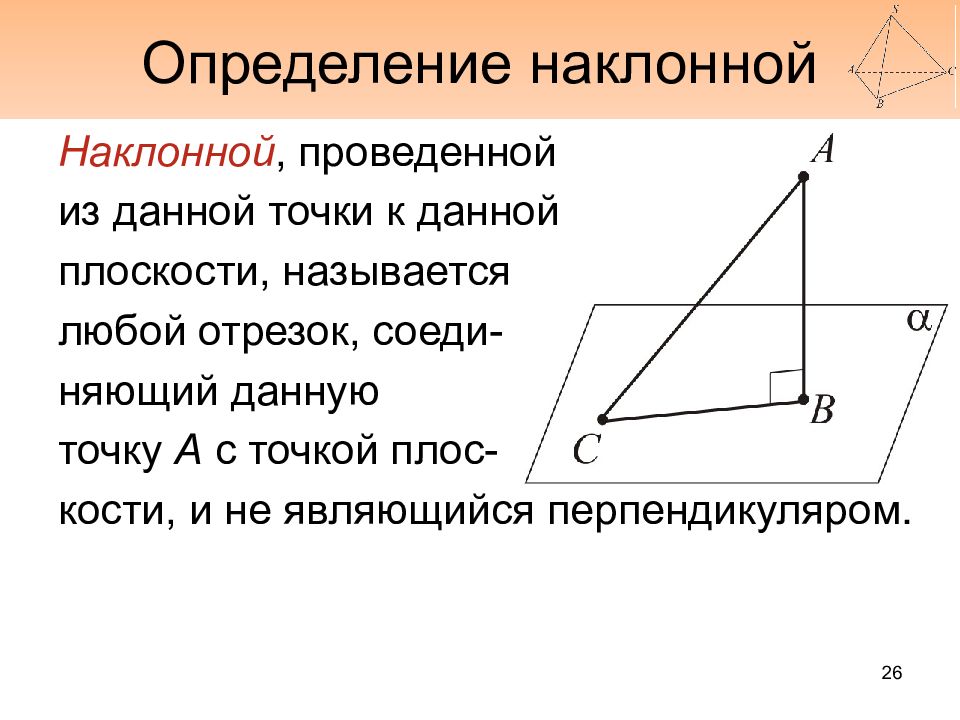
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соеди - няющий данную точку А с точкой плос - кости, и не являющийся перпендикуляром. 26
Слайд 27: Свойство перпендикуляра и наклонной
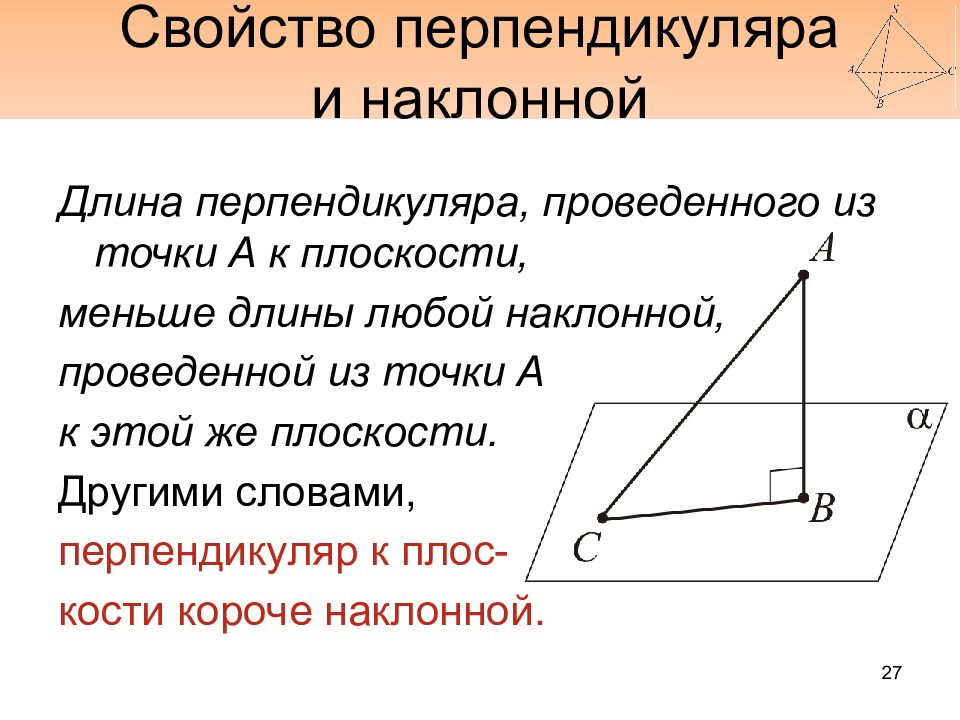
Длина перпендикуляра, проведенного из точки А к плоскости, меньше длины любой наклонной, проведенной из точки А к этой же плоскости. Другими словами, перпендикуляр к плос - кости короче наклонной. 27
Слайд 28: Расстояние от точки до плоскости
Расстоянием от точки М, не лежащей в плоскости, до плоскости α называется длина перпендикуляра, проведенного из точки М на данную плоскость. Найти расстояние от точки до плоскости – это значит найти длину перпендикуляра. 28
Слайд 29: Вопросы
Дана точка М и плоскость α. Сколько можно построить перпендикуляров из точки М к плоскости α ? Сколько можно построить наклонных из точки М к этой плоскости? Сколько можно построить наклонных из точки М заданной длины? Где лежат основания таких наклонных? 29
Слайд 30: Задача
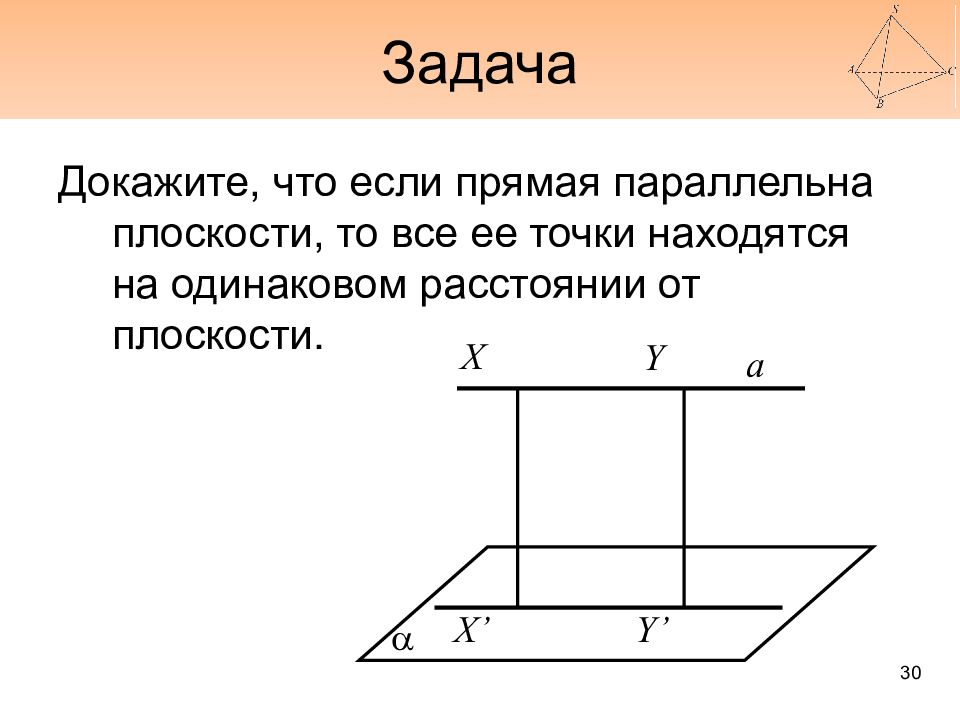
Докажите, что если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости. X Y X’ Y’ a a 30
Слайд 31: Теорема о трех перпендикулярах
Прямая теорема. Прямая, проведенная на плоскости через основание наклон- ной перпендикулярно ее проекции, перпендикулярна и самой наклонной. 31
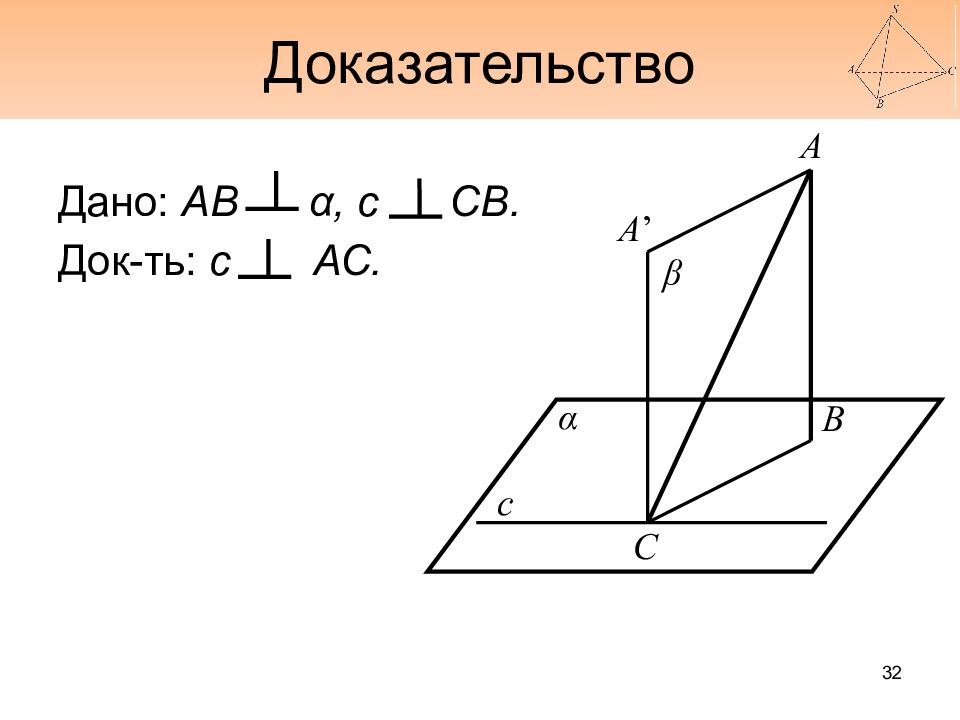
Слайд 33: Обратная теорема
Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна проекции наклонной на эту плоскость. 33 А А ’ В C с α β