«Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать». Галилео Галилей
Задание 1: Заполнить пропуски так, чтобы получились предложения, соответствующие данному чертежу. 1.Градусная мера углов < A, < B равна сорока пяти градусам. Чему равна градусная мера углов АСН и ВСН? 2. На чертеже изображено три равных отрезка AH, CH и ? Ответ пояснить. длина каждого из которых равна ? см. 3. Изображенные на чертеже треугольники : ∆АНС, ∆ САВ ??? Так как они имеют по ??? (два случая ) .
Задание 2: Выделите условие и заключение в перечисленных утверждениях. 1. Если треугольники равны, то в них равны соответственные углы. Условие: Заключение: 2. Если треугольники равны, то равен и их периметр. Условие: Заключение: 3. В равнобедренном треугольнике найдутся две равные стороны. Условие: Заключение: 4. В равнобедренном треугольник углы при основании равны. Условие: Заключение: 5. В равнобедренном треугольнике медианы, проведённые к боковым сторонам равны между собой. Условие: Заключение:
Устно: Вставьте в предложения подходящие слова так, чтобы получились верные утверждения. 1. Периметр равностороннего треугольника в ??? раза больше длины его стороны 2. Если треугольник ABC и MNK равны, то в треугольнике ABC найдётся угол ??? углу NMK 3. Если AK и BN – медианы треугольника ABC, то третья медиана этого треугольника пройдёт через точку пересечения ???. 4. Если две стороны и угол между ними одного треугольника ??? и углу между ними ??? треугольника то такие треугольники ???.
Если сторона и прилежащие к ней углы одного треугольника соответственно равны, стороне и прилежащим к ней углам другого треугольника то такие треугольники равны. Дано: ∆ ABC, ∆ MNK AB = MN, < A = < M, < B = < N Доказать: ∆ ABC = ∆ MNK Доказательство: Наложим ∆ ABC на ∆ MNK, так чтобы AB совместилось с MN, вершины C и K лежали по одну сторону от MN. Так как AB = MN, то A совместится с M, вершина B – с вершиной N. Луч AC совместится с MK, так как < A = < M, луч BC совместится с NK так как < B = < N. Точка пересечения AC и BC совместится с точкой пересечения лучей MK и NK то есть C совместится с K. ∆ ABC и ∆ MNK полностью совместится, следовательно ∆ ABC равен ∆ MNK. Ч.Т.Д.
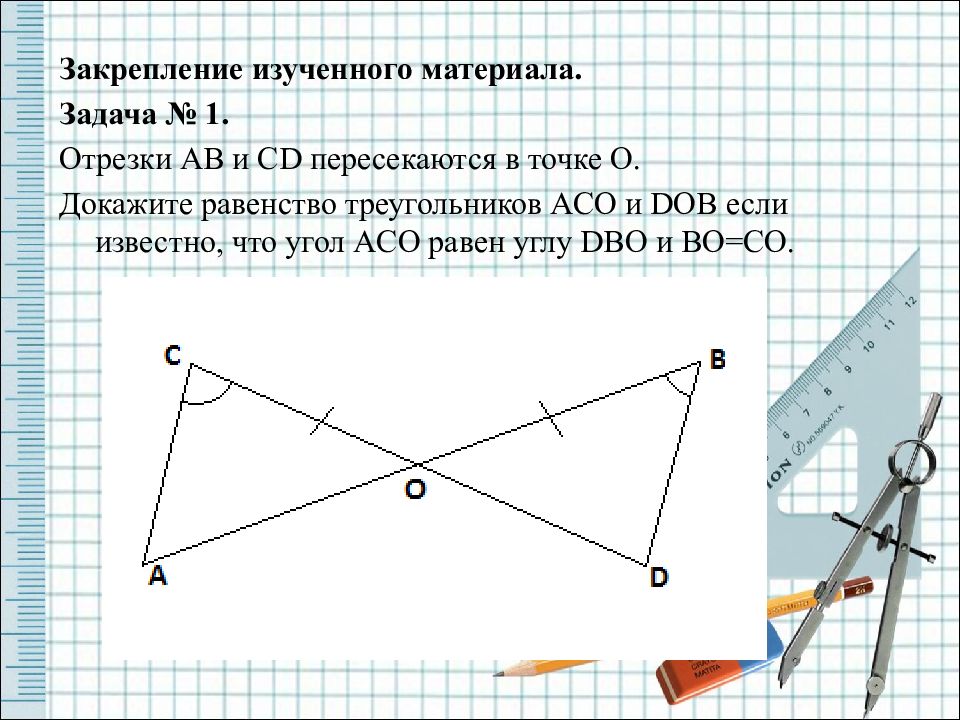
Закрепление изученного материала. Задача № 1. Отрезки AB и CD пересекаются в точке O. Докажите равенство треугольников ACO и DOB если известно, что угол ACO равен углу DBO и BO = CO.
Решение: Рассмотрим ∆ ACO и ∆ DBO : BO = CO (по условию) < ACO = < DBO (по условию) < AOC = < DOB (вертикальные) Следственно ∆ ACO = ∆ DBO по стороне и двум прилежащим к ней углам.
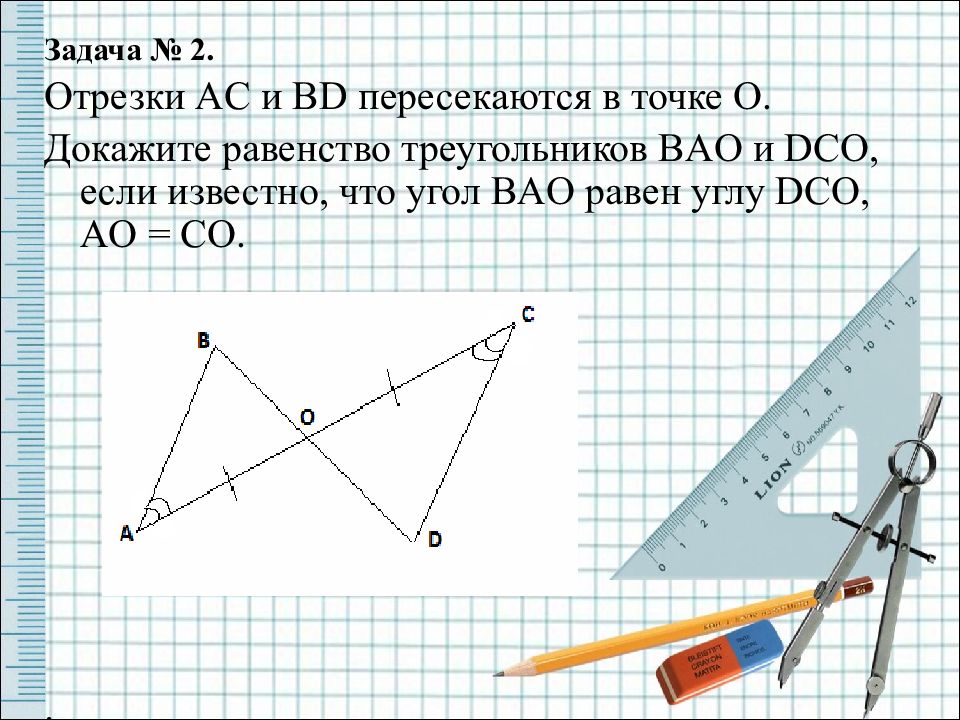
Задача № 2. Отрезки AC и BD пересекаются в точке O. Докажите равенство треугольников BAO и DCO, если известно, что угол BAO равен углу DCO, AO = CO. .
Решение: Рассмотрим ∆ BAO и ∆ DCO. AO = CO (по условию) < BAO = < DCO (по условию) < AOB = < COD (по вертикальные) ∆ BAO = ∆ DCO по стороне и двум прилежащим к ней углам.
