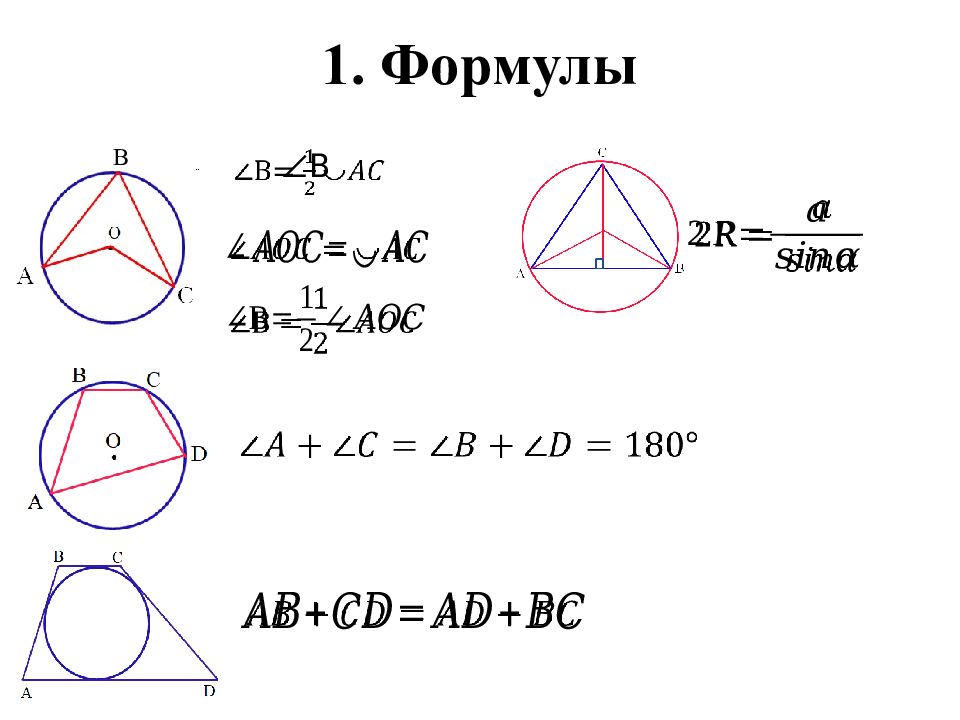
Первый слайд презентации: Задачи ЕГЭ по теме: « О писанная окружность»
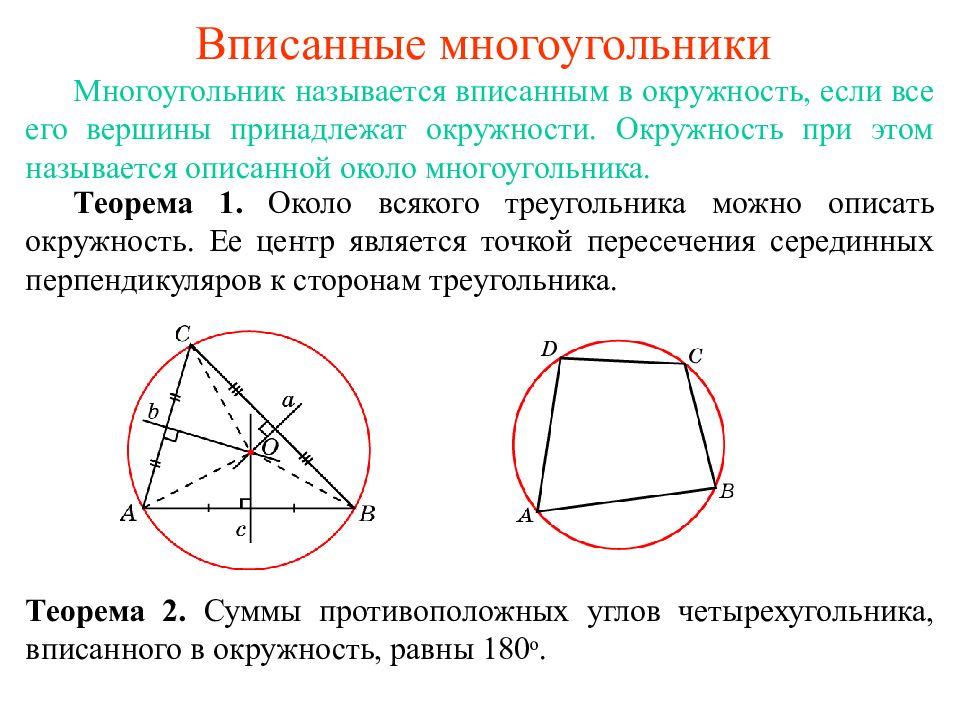
Слайд 3: 2. Описанная окружность
Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1 : 3 : 5. Найдите больший угол треугольника ABC. Ответ дайте в градусах. Решение. Пусть меньшая часть окружности равна x, тогда Больший угол опирается на большую дугу ⇒ ◡ B писанный угол равен половине дуги, на которую он опирается. ⇒ ⇒ Ответ : 100 x 3x 5x
Слайд 4: Первый способ
Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах. Cумма противоположных углов четырехугольника, вписанного в окружность, равна 180°, поэтому Ответ : 122. 58
Слайд 5: Второй способ
∠ A вписанный и опирается на ◡ BCD ⇒ ∠ ⇒ Градусная мера ∠ C вписанный и опирается на ◡ BAD ⇒ ∠ C. Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах. Ответ: 122. 58
Слайд 6
Вписанный угол равен половине дуги, на которую он опирается, значит ∠ Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95, 49, 71, 145. Найдите угол B этого четырехугольника. Ответ дайте в градусах. Ответ: 1 08 95 49 71 145
Слайд 7
5x Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4 : 2 : 3 : 6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах. Решение. 4 x 2x 3x 6x Пусть, тогда ∠ A – в писанный, равен половине дуги, на которую он опирается ⇒ ∠ ∠ Ответ: 60
Слайд 8
Четырехугольник ABCD вписан в окружность. ∠ ABD = 75°, ∠ CAD = 35 °. Найдите ∠ ABC. Ответ дайте в градусах. 75 35 Решение. Вписанный угол равен половине дуги, на которую он опирается, значит, + ABD + Ответ: 110
Слайд 9
Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите ∠ CAD. Ответ дайте в градусах. 70 Решение. Вписанный ∠, на которую он опирается, следовательно, найдем ∠ ⇒ Ответ: 4 0
Слайд 10
H • O Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника. Решение. Треугольник ABC правильный, значит, все углы равны по 60. По теореме синусов имеем: Ответ: 2
Слайд 11
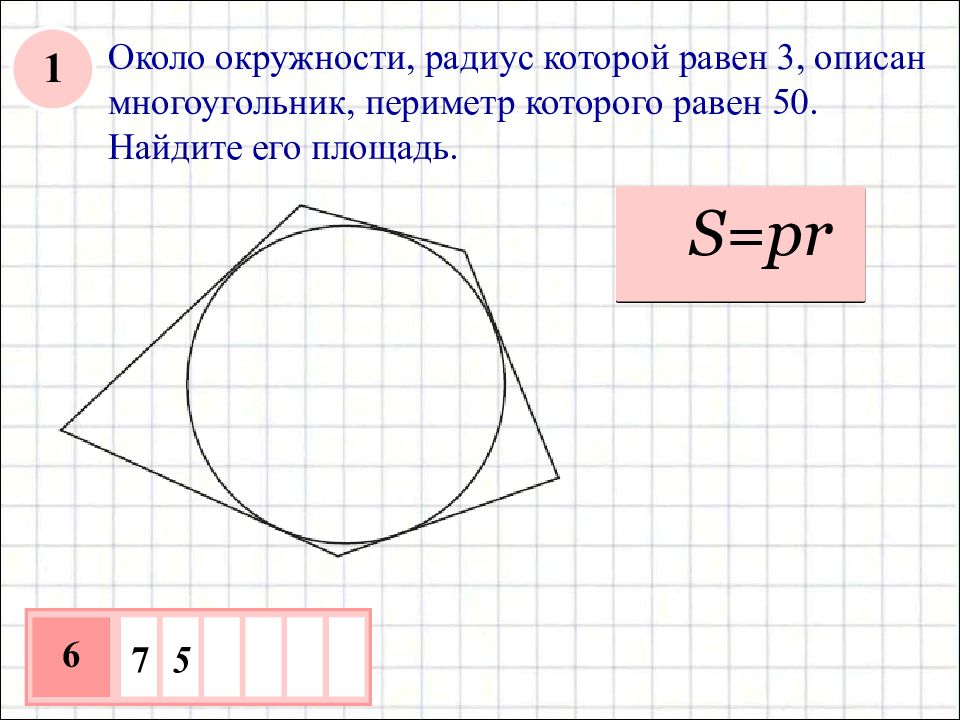
S=pr 7 5 6 Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 50. Найдите его площадь. 1
Слайд 12
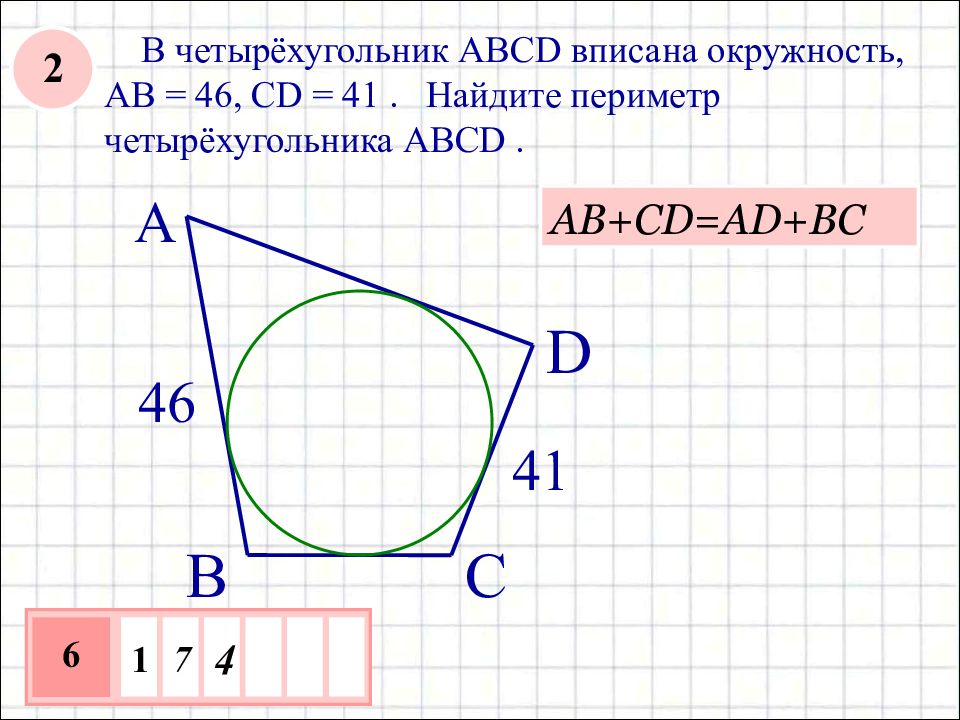
В четырёхугольник ABCD вписана окружность, AB = 46, CD = 41. Найдите периметр четырёхугольника ABCD. A 41 B C D 46 АВ+С D=AD+BC 1 7 4 6 2
Слайд 13
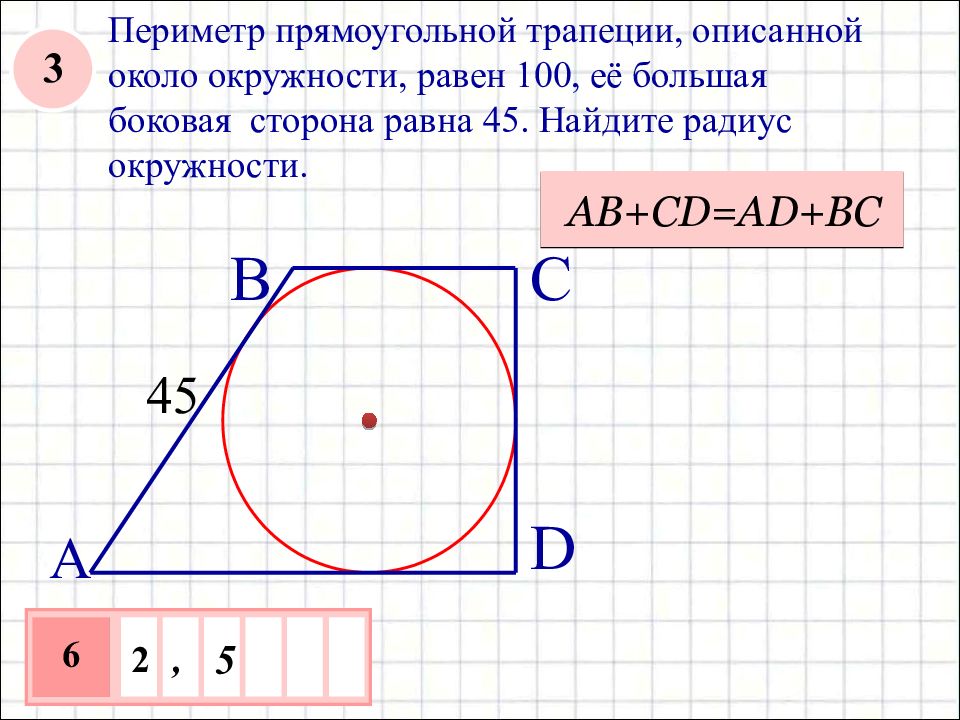
Периметр прямоугольной трапеции, описанной около окружности, равен 100, её большая боковая сторона равна 45. Найдите радиус окружности. 45 A B C D АВ+С D=AD+BC 2 , 5 6 3
Слайд 14
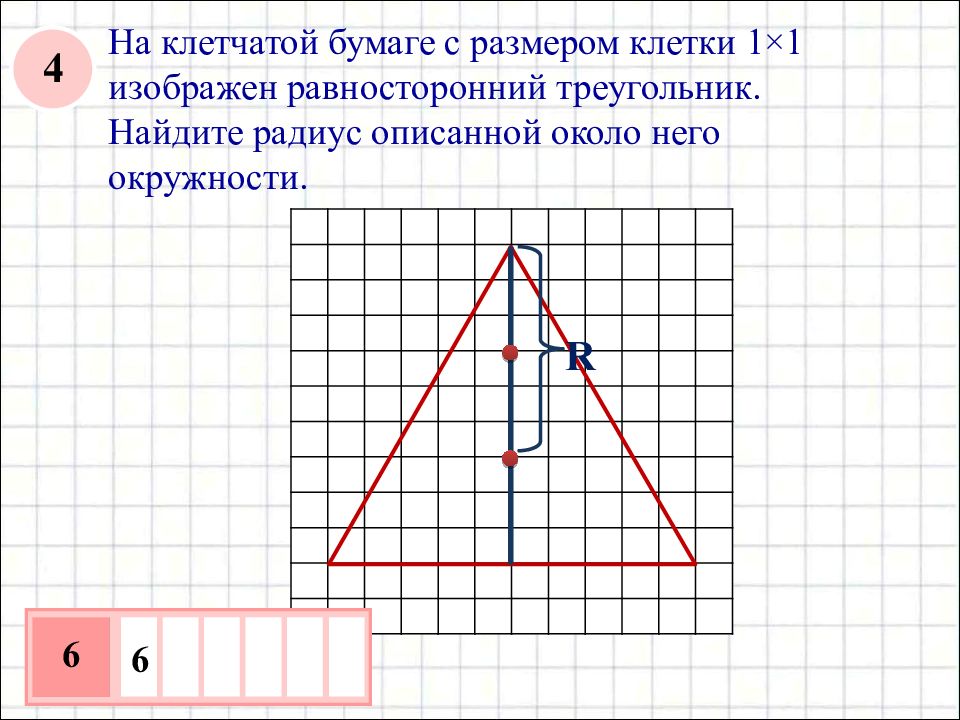
На клетчатой бумаге с размером клетки 1×1 изображен равносторонний треугольник. Найдите радиус описанной около него окружности. 6 6 R 4
Слайд 15
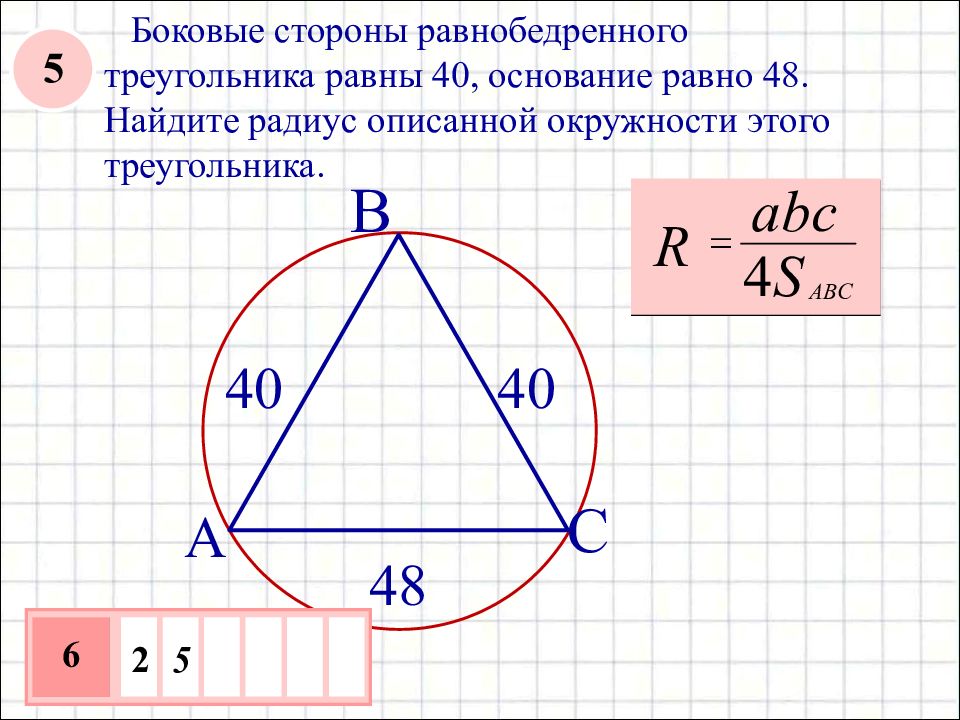
Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника. A B C 40 40 48 2 5 6 5
Слайд 16
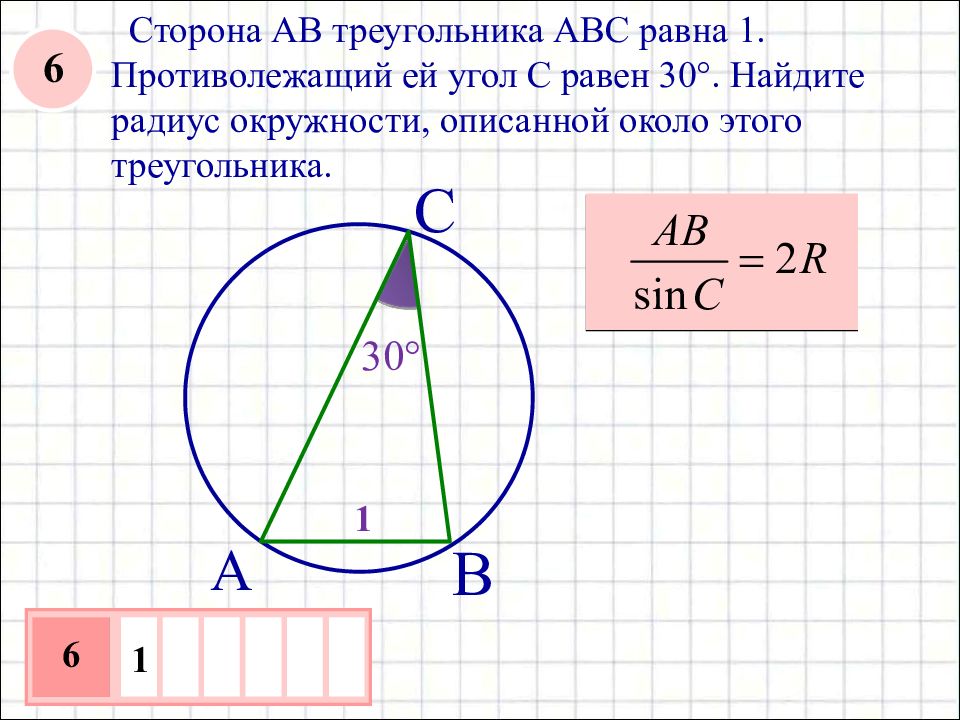
Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 30°. Найдите радиус окружности, описанной около этого треугольника. C A B 30° 1 1 6 6
Слайд 18
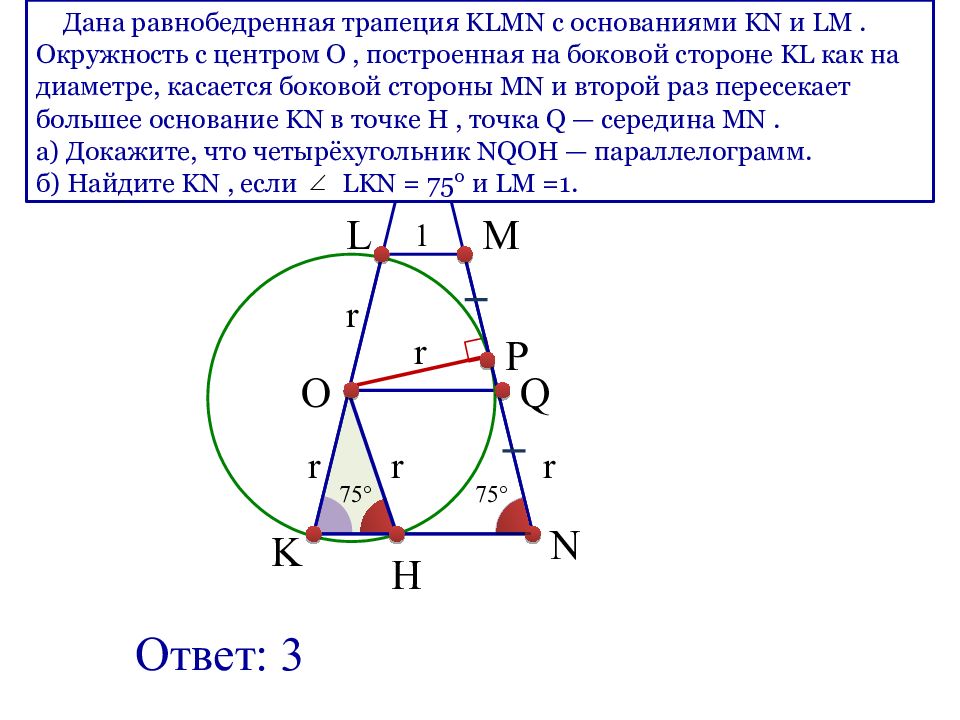
O K H N Q L P M T r r r r 1 r 30° 75° r 75° Ответ: 3 Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром O, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке H, точка Q — середина MN. а) Докажите, что четырёхугольник NQOH — параллелограмм. б) Найдите KN, если LKN = 75° и LM =1.
Слайд 19
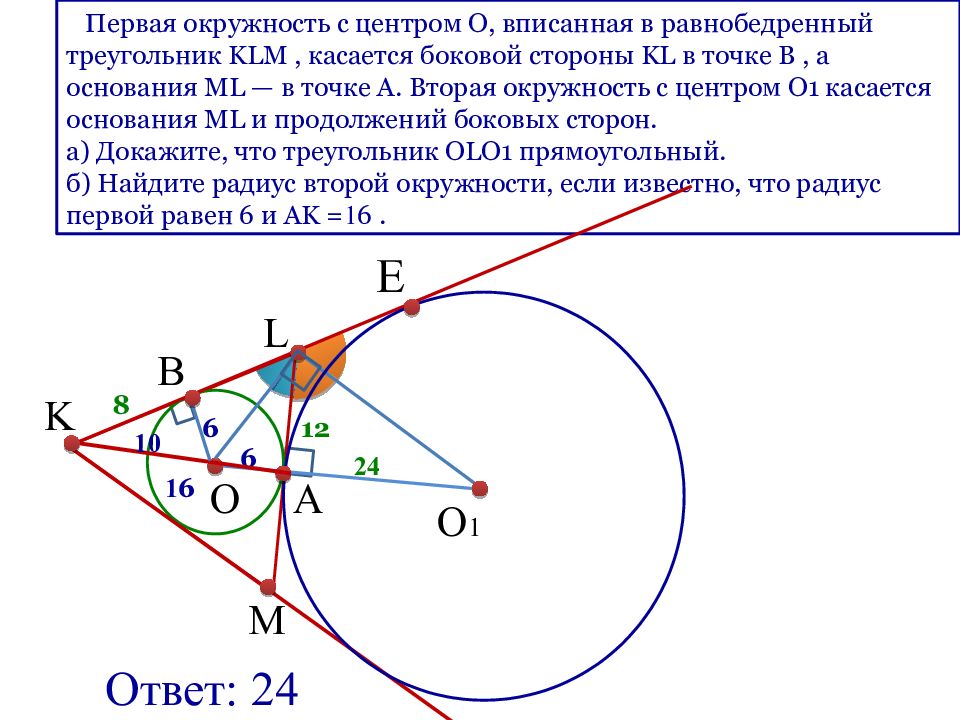
Первая окружность с центром O, вписанная в равнобедренный треугольник KLM, касается боковой стороны KL в точке B, а основания ML — в точке A. Вторая окружность с центром O1 касается основания ML и продолжений боковых сторон. а) Докажите, что треугольник OLO1 прямоугольный. б) Найдите радиус второй окружности, если известно, что радиус первой равен 6 и AK = 1 6. K M L B A O O 1 6 1 6 1 0 8 6 12 24 Ответ: 24 Е
Слайд 20
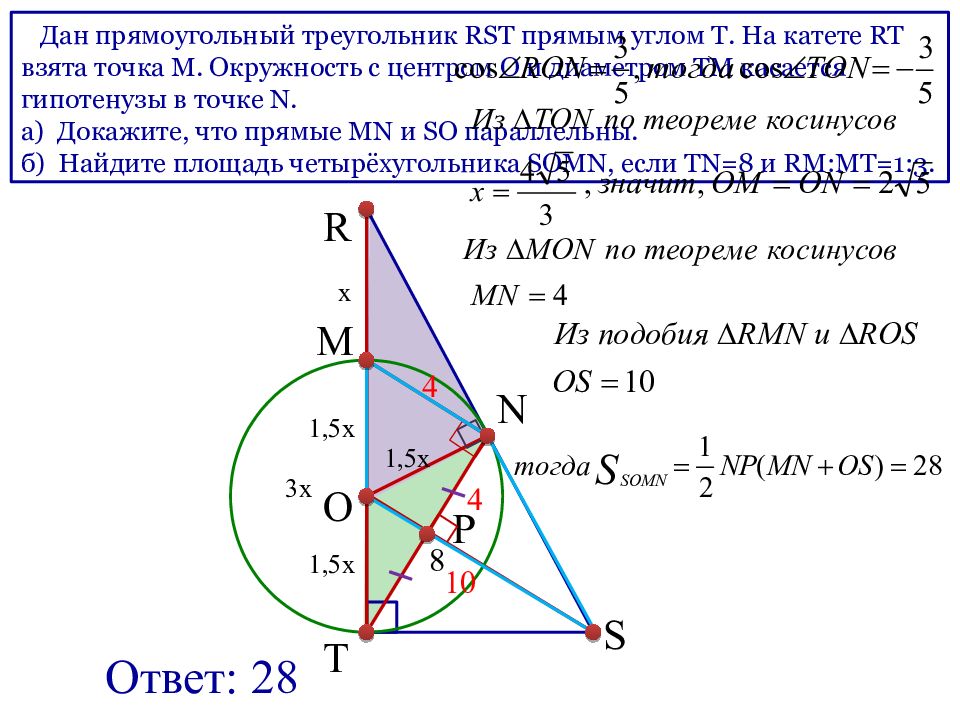
Дан прямоугольный треугольник RST прямым углом Т. На катете RT взята точка М. Окружность с центром О и диаметром ТМ касается гипотенузы в точке N. а) Докажите, что прямые MN и SO параллельны. б) Найдите площадь четырёхугольника SOMN, если TN= 8 и RM : MT =1:3. N R T S M O P 1,5x 1,5x x 3x 1,5x 8 4 4 10 Ответ: 28