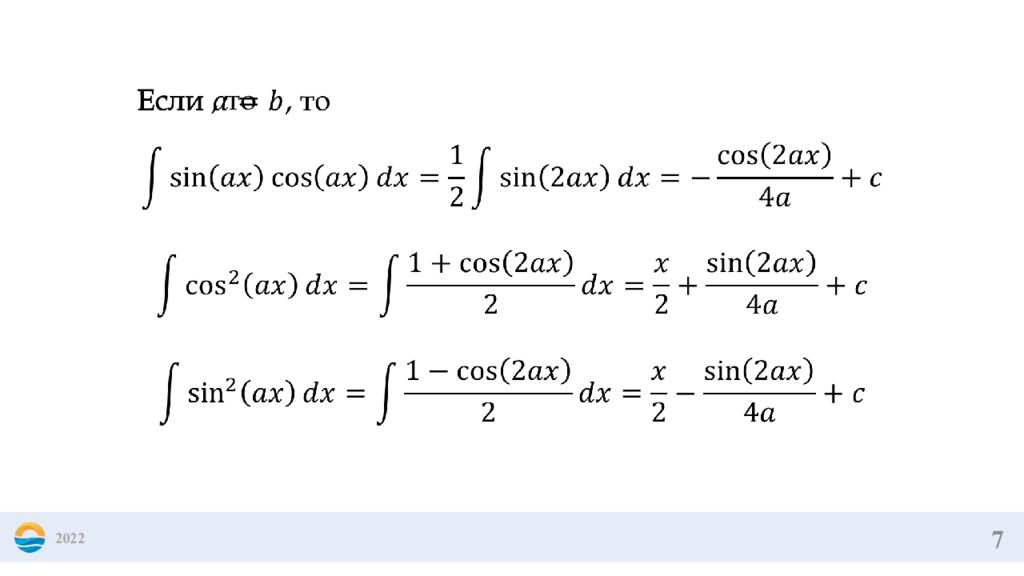2022 ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ И ИРРАЦИОНАЛЬНЫХ МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ЛИНЕЙНАЯ АЛГЕБРА БФУ имени И. Канта
2 2022 ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Обозначим через рациональную функцию от и.
3 2022 Интегралы вида приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки. В результате этой подстановки имеем Примечание: универсальная подстановка во многих случаях приводит к сложным вычислениям, поэтому применяется только тогда, когда нельзя применить другие подстановки, вид которых зависит от свойств функции.
4 2022 Если – четная функция относительно и, т.е., то подстановка преобразует исходный интеграл в интеграл от рациональной функции аргумента. При этом используются формулы. Если – нечетная функция относительно, т.е., то интеграл рационализируется с помощью подстановки. Если – нечетная функция относительно, т.е., то подстановка рационализирует интеграл.
5 2022 Интегралы вида рационализируются с помощью подстановки, а интегралы вида – с помощью подстановки. Интегралы вида находят с помощью универсальной тригонометрической подстановки.
6 2022 При нахождении интегралов вида применяются тригонометрические формулы
7 2022 Если, то
8 2022 Интегралы вида где, вычисляются с помощью подстановки при нечетном, а при нечетном – с помощью подстановки. В случаях четных и используются тригонометрические формулы
9 2022 ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ Если подынтегральная функция иррациональна, то ее с помощью замены переменной во многих случаях можно привести к рациональному виду или к табличному интегралу. Этот способ называется интегрированием посредством рационализации подынтегрального выражения.
10 2022 В интегралах вида где – рациональная функция, – натуральное число и – постоянные, рационализации подынтегрального выражения достигается одной из трех подстановок: если если в остальных случаях.
11 2022 Интегралы вида где – целые числа, преобразуются в интегралы от рациональной функции с помощью подстановки, где – наименьшее общее кратное чисел, то есть.
12 2022 Интегралы вида рационализируется подстановкой, где – наименьшее общее кратное чисел
13 2022 С помощью тригонометрических подстановок к рациональному тригонометрическому виду приводятся соответственно интегралы
14 2022 Интегралы вида могут быть найдены с помощью таких же подстановок, так как после выделения полного квадрата в квадратном трехчлене и применения подстановки получают интегралы от выражений
15 2022 Интегралы вида находятся с помощью подстановки.
16 2022 Интегралы от дифференциальных биномов где – рациональные числа, выражаются через элементарные функции только в трех случаях: 1) если р – целое число, то используем подстановку, где – наименьшее общее кратное знаменателей дробей, то есть ; 2) если – целое число,, то, где – знаменатель дроби ; 3) если – целое число,, то, где – знаменатель дроби.
2022 Спасибо за внимание! МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ЛИНЕЙНАЯ АЛГЕБРА БФУ имени И. Канта
