2022 ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ЛИНЕЙНАЯ АЛГЕБРА БФУ имени И. Канта
2 2022 ОПРЕДЕЛЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ Рассмотрим дифференциальное уравнение где – некоторый постоянный коэффициент пропорциональности. Интегрирование этого уравнение приводит к общему решению в виде показательной функции
3 2022 Если задать начальные условия при, то можно определить произвольную постоянную и, таким образом, найти частное решение которое представляет собой интегральный закон рассматриваемого процесса.
4 2022 Наряду с отдельными показательными функциями в математике и ее приложениях находят применение различные комбинации показательных функций, среди которых особое значение имеют некоторые линейные и дробно-линейные комбинации функций и, которые имеют название гиперболические функции.
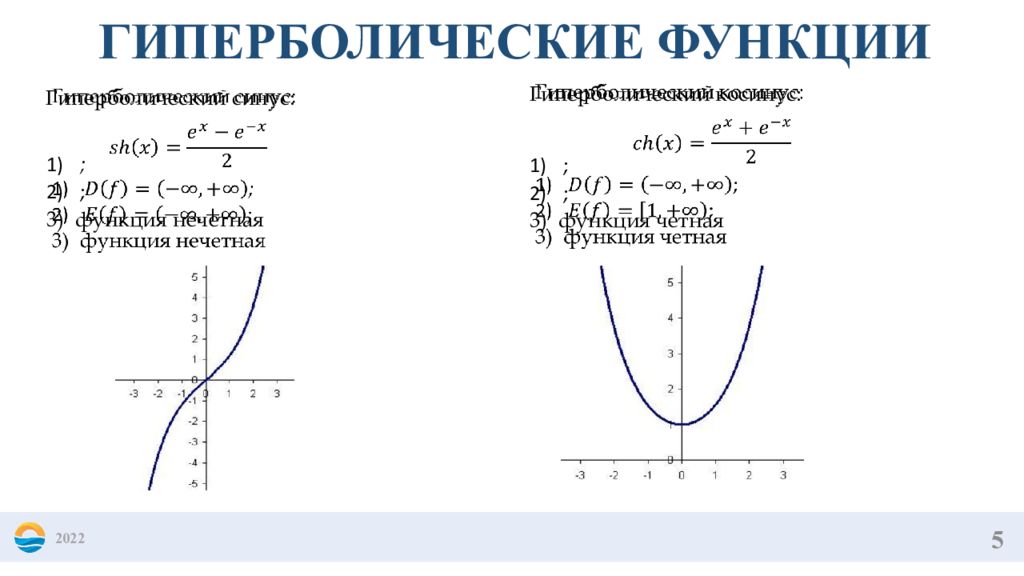
5 2022 ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ Гиперболический синус: ; ; функция нечетная Гиперболический косинус: ; ; функция четная
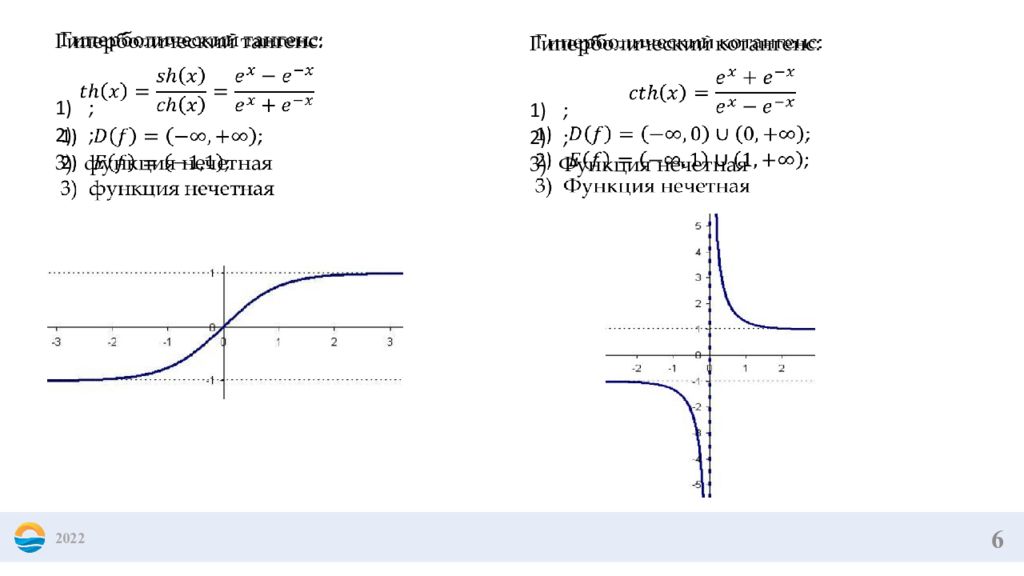
6 2022 Гиперболический тангенс : ; ; функция нечетная Гиперболический котангенс : ; ; Функция нечетная
7 2022 СООТНОШЕНИЯ МЕЖДУ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ
8 2022
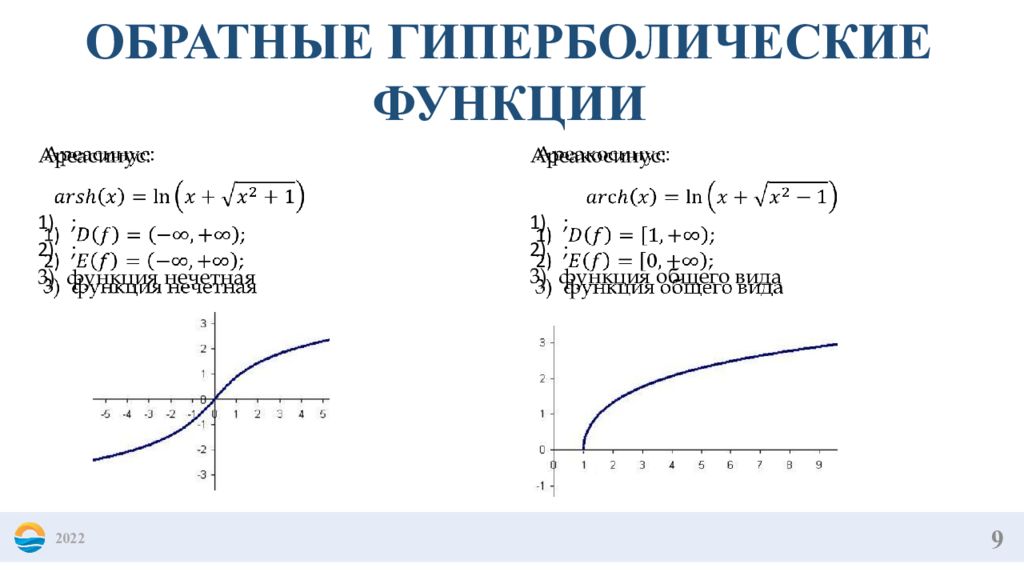
9 2022 ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ Ареасинус : ; ; функция нечетная Ареакосинус : ; ; функция общего вида
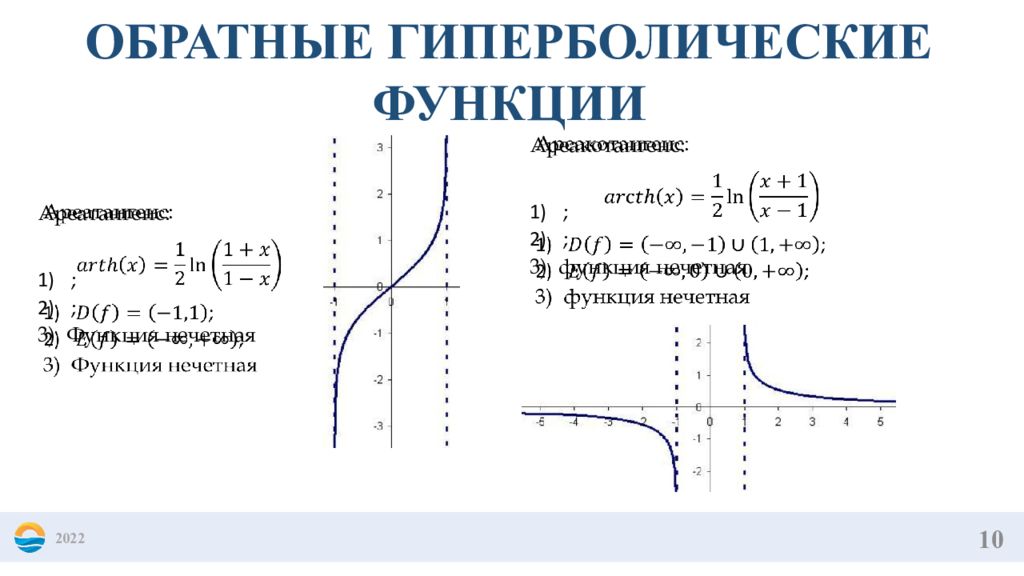
10 2022 ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ Ареатангенс : ; ; Функция нечетная Ареакотангенс : ; ; функция нечетная
11 2022 ПРОИЗВОДНЫЕ И ИНТЕГРАЛЫ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
12 2022
2022 Спасибо за внимание! МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ЛИНЕЙНАЯ АЛГЕБРА БФУ имени И. Канта
