Первый слайд презентации: Особенности решения тригонометрических уравнений
Учитель математики МАОУ лицей № 48 г.Краснодара Гаврилова Маргарита Петровна
Слайд 2
Знать определение тригонометрического уравнения, их виды и способы решения; Иметь представление о методах решения тригонометрических уравнений; Уметь применять тригонометрические формулы для упрощения выражений Знать способы, позволяющие сделать отбор корней при решении тригонометрических уравнений; Уметь распознавать вид тригонометрического уравнения, требующих для своего решения отбора корней; Уметь правильно изображать на единичной окружности точки, соответствующие значениям тригонометрических функций, и в случае «табличных» значений уметь определять значения аргументов этих функций; Владеть аппаратом способов решения тригонометрических уравнений, требующих для своего решения отбора корней.
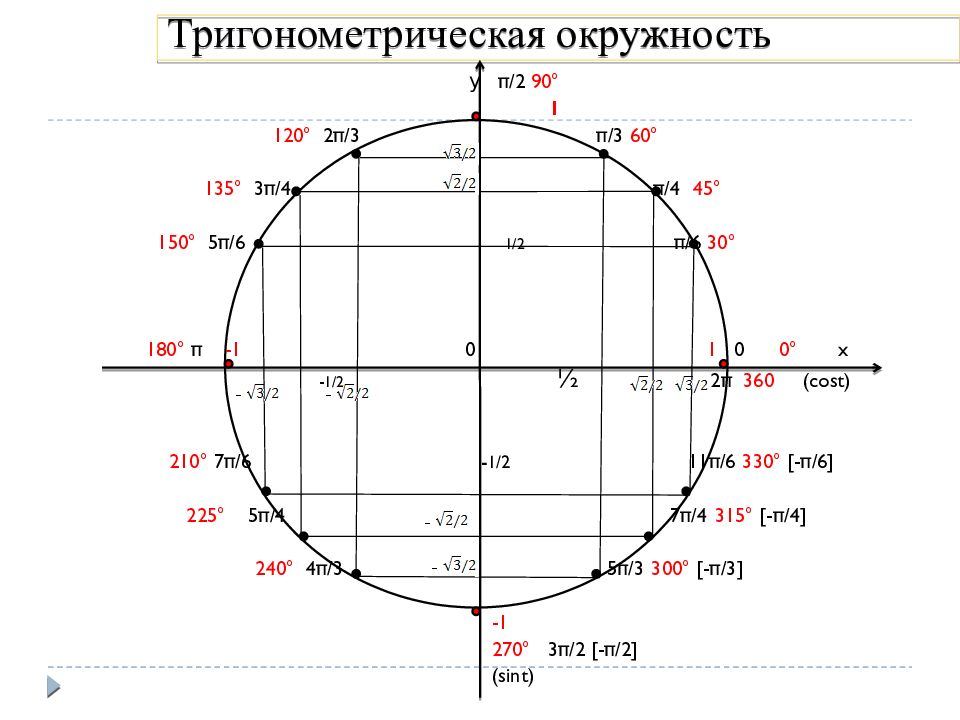
Слайд 3: Тригонометрическая окружность
у π /2 90° 1 120° 2 π /3 π /3 60° 135° 3 π /4 π /4 45° 150° 5 π /6 1/2 π /6 30° 180° π -1 0 1 0 0° x - 1/2 ½ 2 π 360 (cost) 210° 7 π /6 - 1/2 11 π /6 330° [- π /6] 225° 5 π /4 7 π /4 315° [- π /4] 240° 4 π /3 5 π /3 300° [- π /3] -1 270° 3 π /2 [- π /2] ( sint )
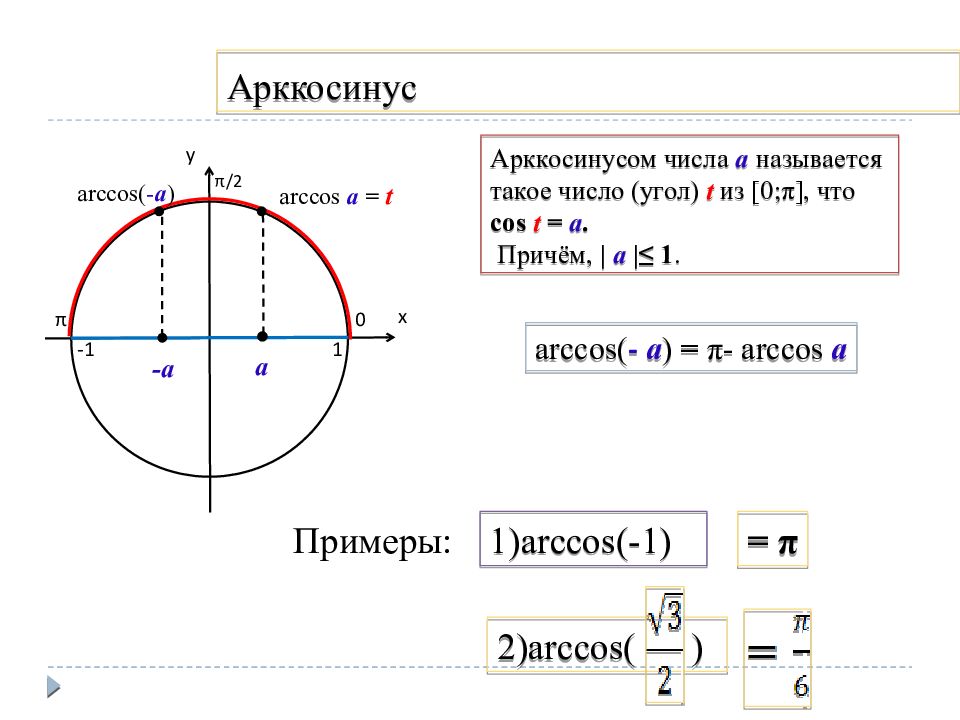
Слайд 4: Арккосинус
у х π/2 0 π 1 -1 -а а arccos а = t arccos( - а ) Арккосинусом числа а называется такое число (угол) t из [0; π ], что cos t = а. Причём, | а |≤ 1. arccos ( - а ) = π - arccos а Примеры: 1) arccos (-1) = π 2) arccos ( )
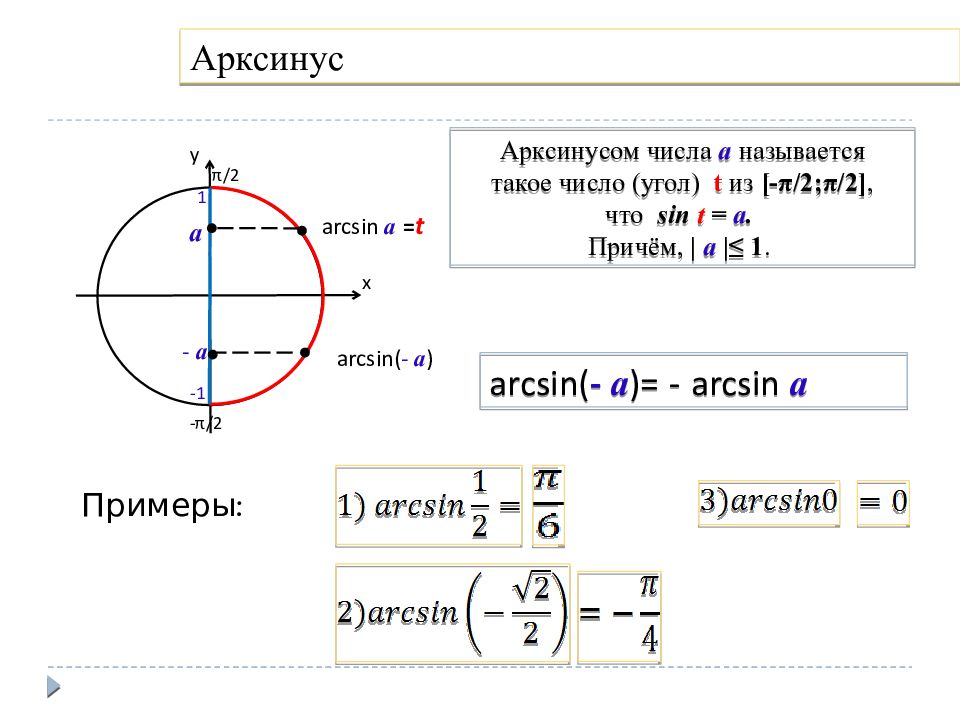
Слайд 5: Арксинус
Примеры: у х π/2 - π/2 -1 1 а arcsin а = t - а arcsin ( - а )= - arcsin а arcsin( - а ) Арксинусом числа а называется такое число (угол) t из [- π/2 ; π/2 ], что sin t = а. Причём, | а |≤ 1.
Слайд 6: Арктангенс
у π/2 - π/2 х 0 а arctg а = t Арктангенсом числа а называется такое число (угол) t из (- π/2;π/2 ), что tg t = а. Причём, а Є R. arctg ( - а ) = - arctg а - а arctg( - а ) Примеры: 1) arctg√3/3 = π/6 2) arctg (-1) = - π/4
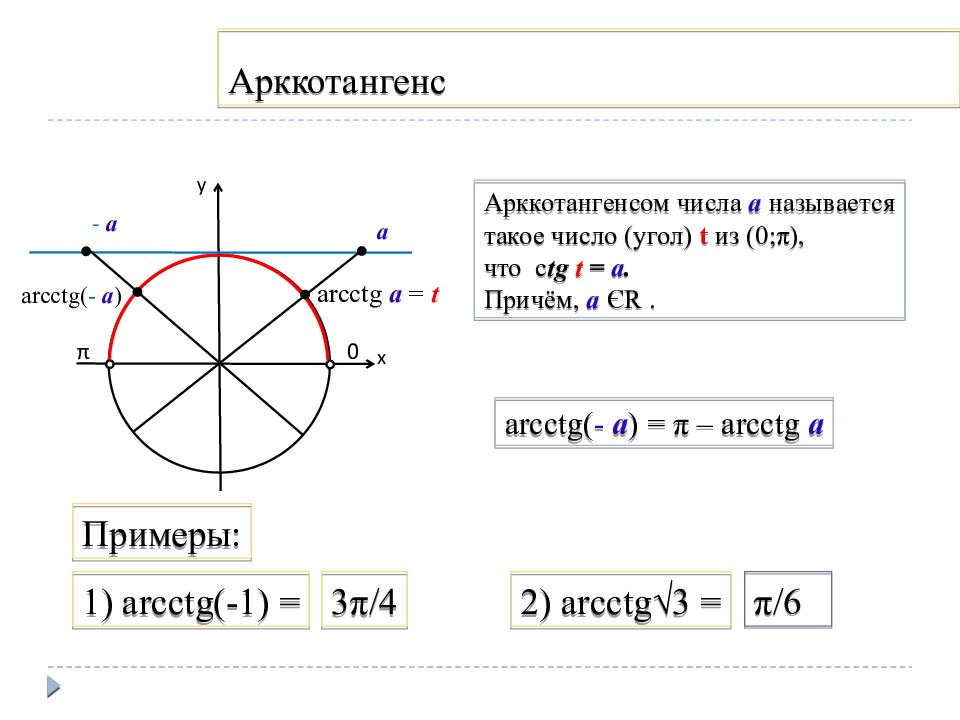
Слайд 7: Арккотангенс
у х 0 π а arcctg а = t Арккотангенсом числа а называется такое число (угол) t из (0; π ), что c tg t = а. Причём, а Є R. arcctg ( - а ) = π – arcctg а - а arcctg( - а ) 1) arcctg (-1) = Примеры: 3 π/4 2) arcctg√3 = π/6
1.cost = а, где | а| ≤ 1 или Частные случаи 1) cost=0 t = π/2+π k‚ k Є Z 2) cost=1 t = 2 π k‚ k Є Z 3) cost = -1 t = π+2π k‚ k Є Z
Слайд 9: Формулы корней простейших тригонометрических уравнений
2. sint = а, где | а |≤ 1 или Частные случаи 1) sint=0 t = π k‚ k Є Z 2) sint=1 t = π/2+2π k‚ k Є Z 3) sint = - 1 t = - π/2+2π k‚ k Є Z
Слайд 10: Формулы корней простейших тригонометрических уравнений
3. tgt = а, а Є R t = arctg а + π k‚ k Є Z 4. ctgt = а, а Є R t = arcctg а + π k‚ k Є Z
Слайд 14
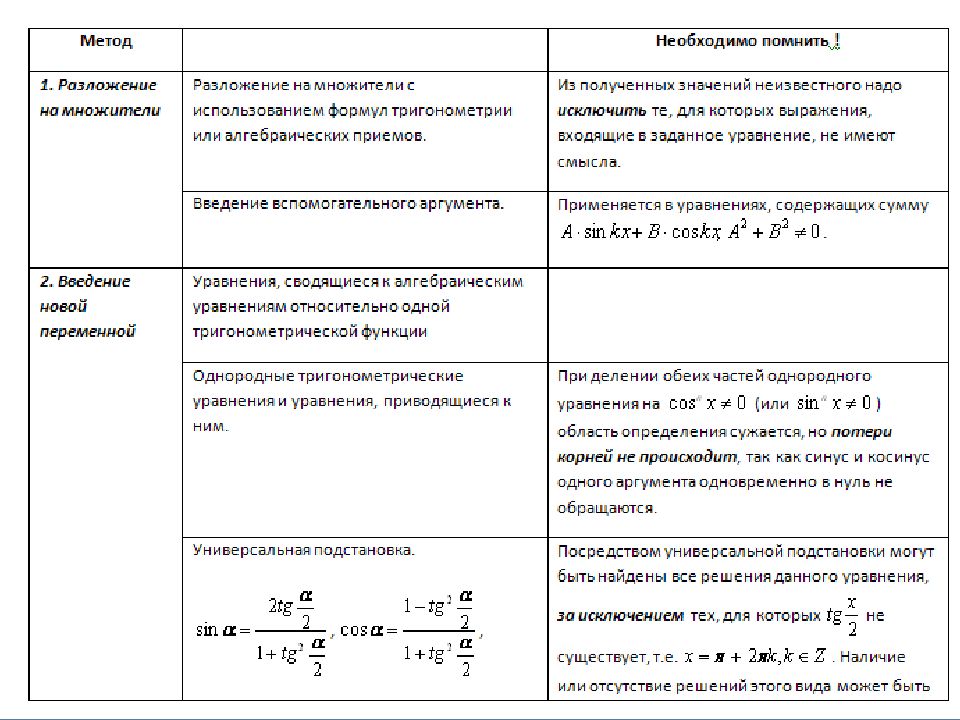
1.Сводимые к квадратным Решаются методом введения новой переменной a∙sin²x + b∙sinx + c=0 Пусть sinx = p, где |p| ≤1, тогда a∙p² + b∙p + c = 0 Найти корни, вернуться к замене и решить простые уравнения. 2. Однородные 1)Первой степени: Решаются делением на cos х (или sinx ) и методом введения новой переменной. a∙sinx + b∙cosx = 0 Т.к. sinx и cosx одновременно не равны нулю, то разделим обе части уравнения на cosx (или на sinx ). Получим: простое уравнение a∙tgx + b = 0 или tgx = m
Слайд 15
2) Однородные уравнения второй степени: Решаются делением на cos² х (или sin²x ) и методом введения новой переменной. a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0 Разделим обе части на cos²x. Получим квадратное уравнение: a∙tg²x + b∙tgx + c = 0. 3).Уравнение вида: А sinx + B cosx = C. А, В, С 0
Слайд 16
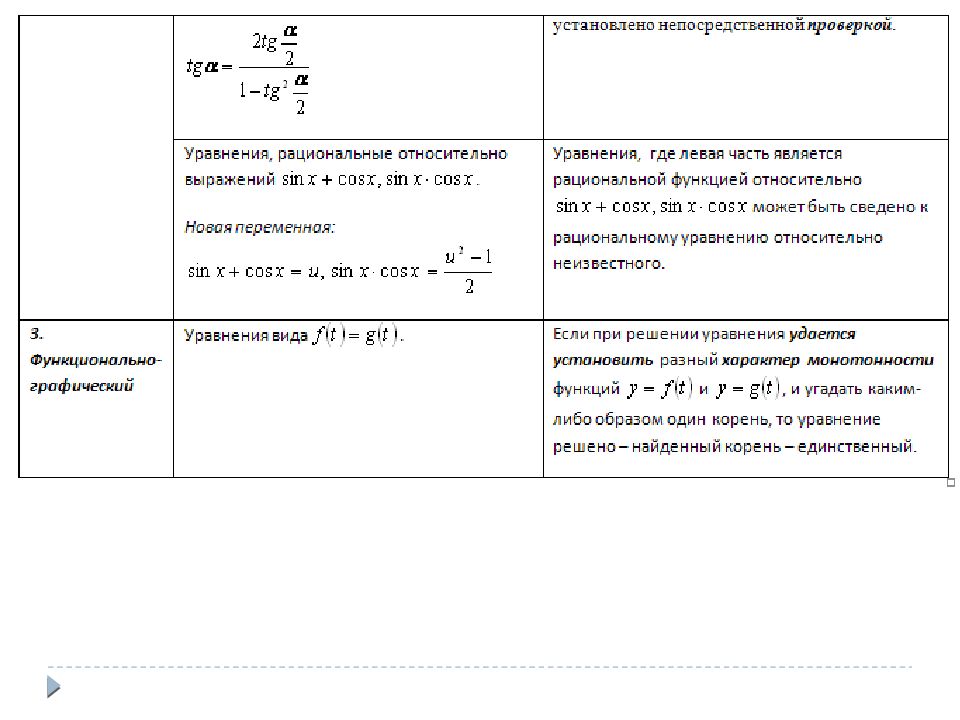
Формулы. a cosx + b sinx заменим на C sin ( x + ), где sin = cos = - вспомогательный аргумент. Универсальная подстановка. х + 2 n ; Проверка обязательна! Понижение степени. = (1 + cos2x ) : 2 = (1 – cos 2x) : 2 Метод вспомогательного аргумента.
Слайд 17
Так как, то существует такое значение, что , тогда последнее уравнение может быть переписано в виде , где 1 способ. Путем введения вспомогательного аргумента.
Слайд 23: 4 способ Возведение обеих частей равенства в квадрат и приведение к однородному уравнению
Слайд 25
Простые советы. Увидел квадрат – понижай степень. Увидел произведение – делай сумму. Увидел сумму – делай произведение.
Слайд 26
1.Потеря корней: делим на g (х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2. Лишние корни: возводим в четную степень. умножаем на g (х) (избавляемся от знаменателя). Этими операциями мы расширяем область определения. Потеря корней, лишние корни.
Слайд 27: Способы отбора корней
Арифметический способ Алгебраический способ Геометрический способ Функционально-графический способ