Урок геометрии в 7 классе
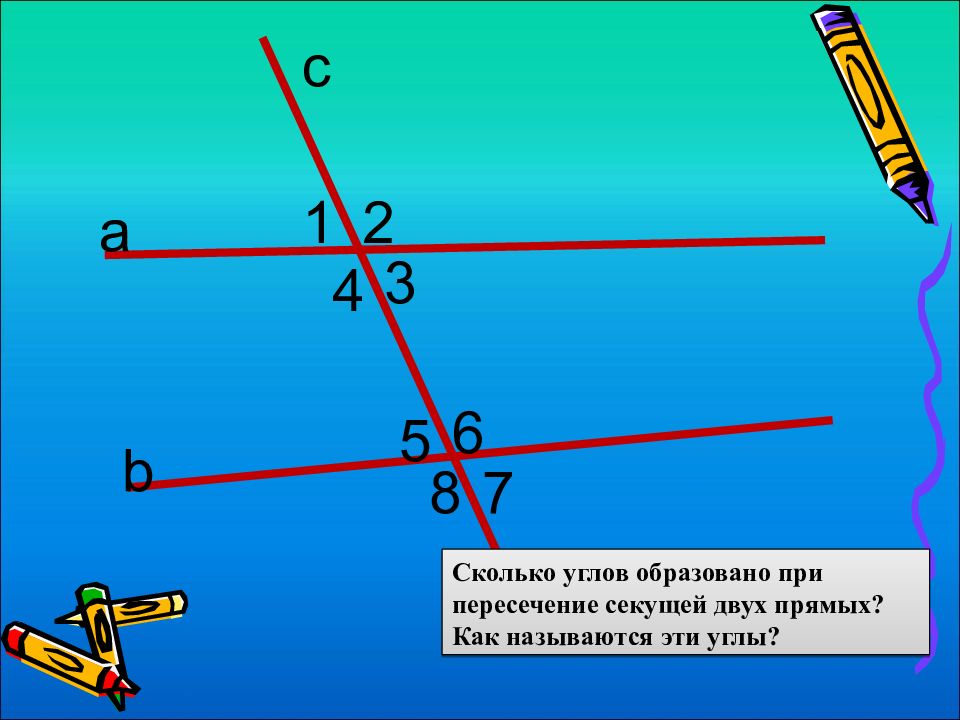
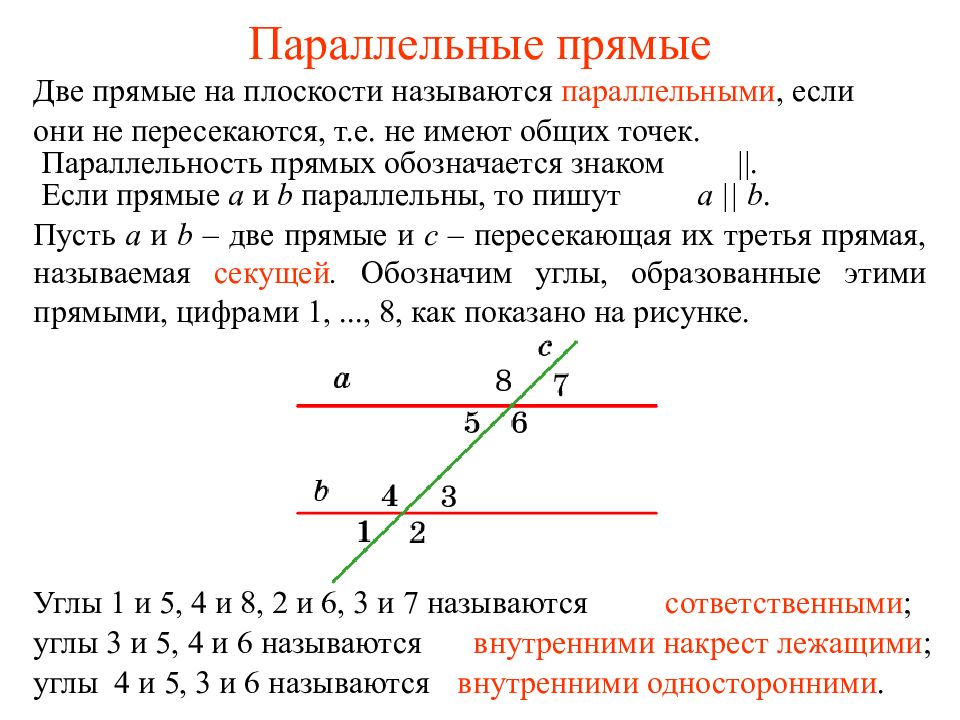
с а b Сколько углов образовано при пересечение секущей двух прямых? Как называются эти углы? 1 2 3 4 5 6 7 8
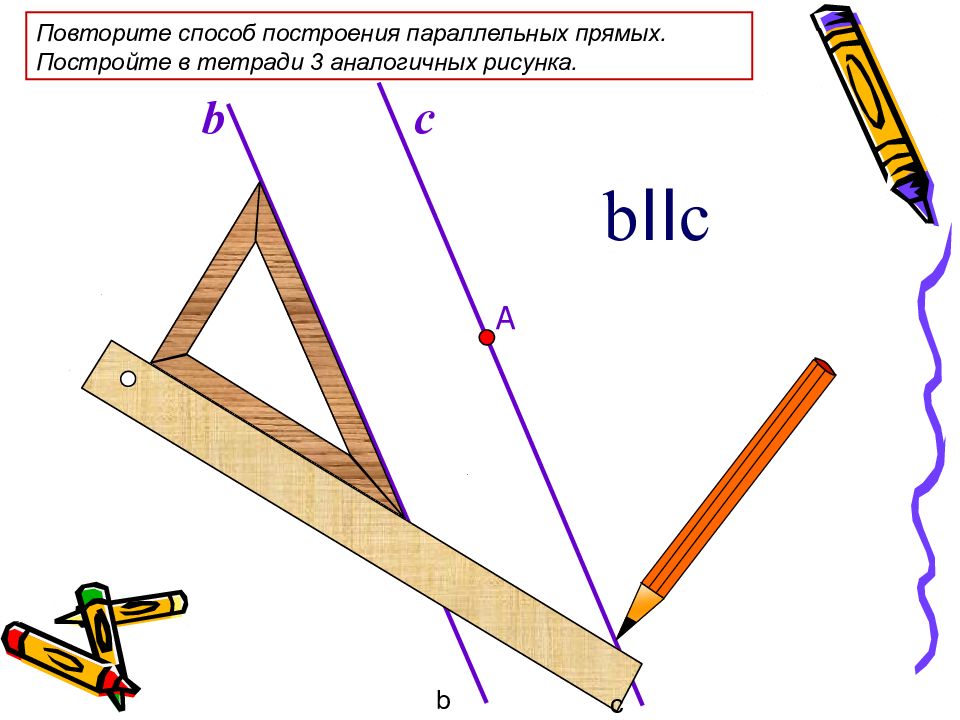
b b II c c А b c Повторите способ построения параллельных прямых. Постройте в тетради 3 аналогичных рисунка.
Аксиома параллельных прямых
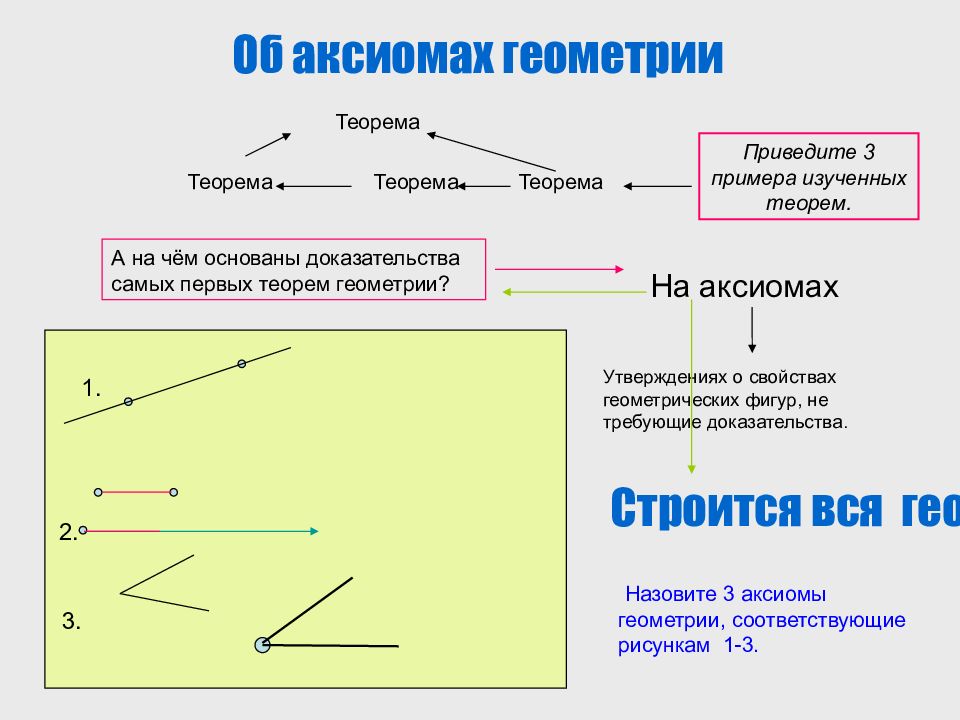
Теорема Теорема Теорема Теорема Об аксиомах геометрии А на чём основаны доказательства самых первых теорем геометрии? На аксиомах Утверждениях о свойствах геометрических фигур, не требующие доказательства. 2. Приведите 3 примера изученных теорем. Назовите 3 аксиомы геометрии, соответствующие рисункам 1-3. 1. 3. Строится вся геометрия
Сначала формулируются исходные положения - аксиомы На их основе, путём логических рассуждений доказываются другие утверждения Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида 365 – 300 гг. до н.э. Геометрия, изложенная в «Началах», называется евклидовой геометрией Некоторые из аксиом Евклида (часть из них он называл постулатами ) и сейчас используются в геометрии Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».
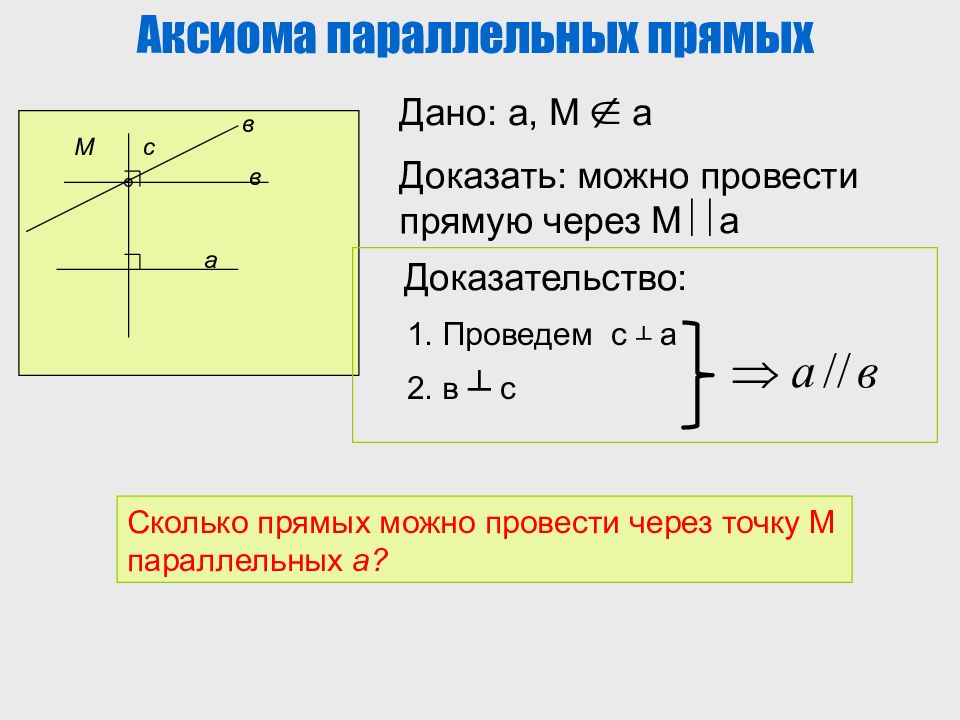
Аксиома параллельных прямых М а в с в Сколько прямых можно провести через точку М параллельных а? Дано: а, М а Доказать: можно провести прямую через М а Доказательство: 1. Проведем с ┴ а 2. в ┴ с
Нам представляется, что через т. М нельзя провести прямую (отличную от прямой в ), параллельную прямой а. А можем ли мы это доказать? Ответ на этот непростой вопрос дал великий русский математик Н.И. Лобачевский. Он выяснил, что это утверждение доказать нельзя, т.к. само является аксиомой.
Аксиома параллельных прямых А Через точку, не лежащую на прямой проходит только одна прямая, параллельная данной. Опр. Следствие – это утверждение, которое выводится непосредственно из аксиом и теорем.
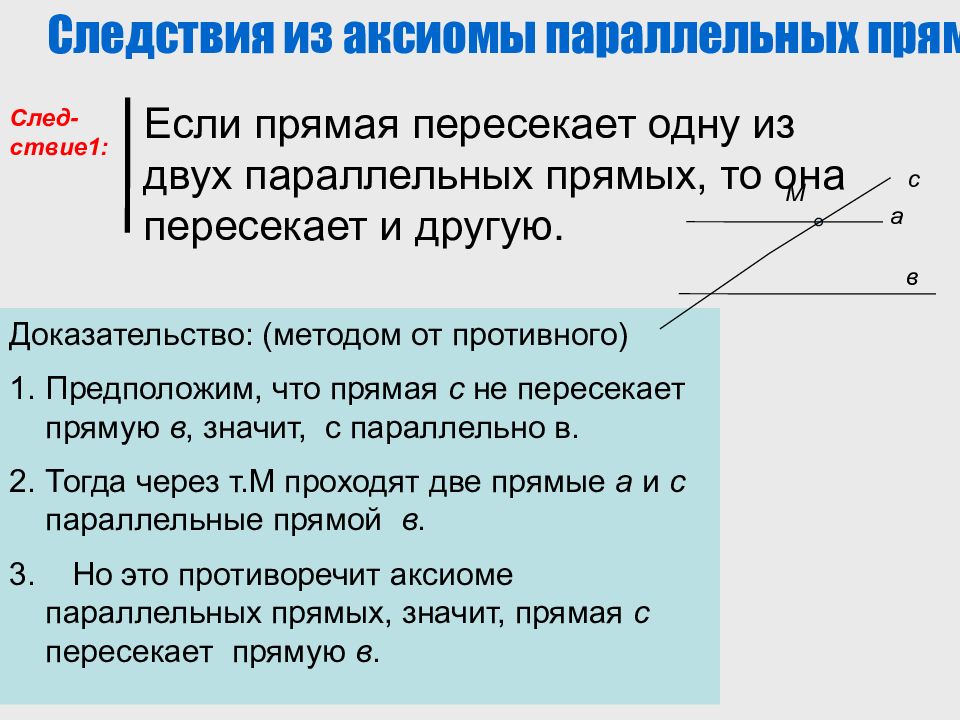
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Следствия из аксиомы параллельных прямых Доказательство: (методом от противного) Предположим, что прямая с не пересекает прямую в, значит, с параллельно в. Тогда через т.М проходят две прямые а и с параллельные прямой в. 3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в. а в М с След-ствие1:
Если две прямые параллельны третьей прямой, то они параллельны. Доказательство: (метод от противного) Предположим, что прямая а и прямая в пересекаются. 2. Тогда через т.М проходят две прямые а и в параллельные прямой с 3. Но это противоречит аксиоме параллельных прямых. 4. Значит прямые а и в параллельны. а в с След- ствие 2:
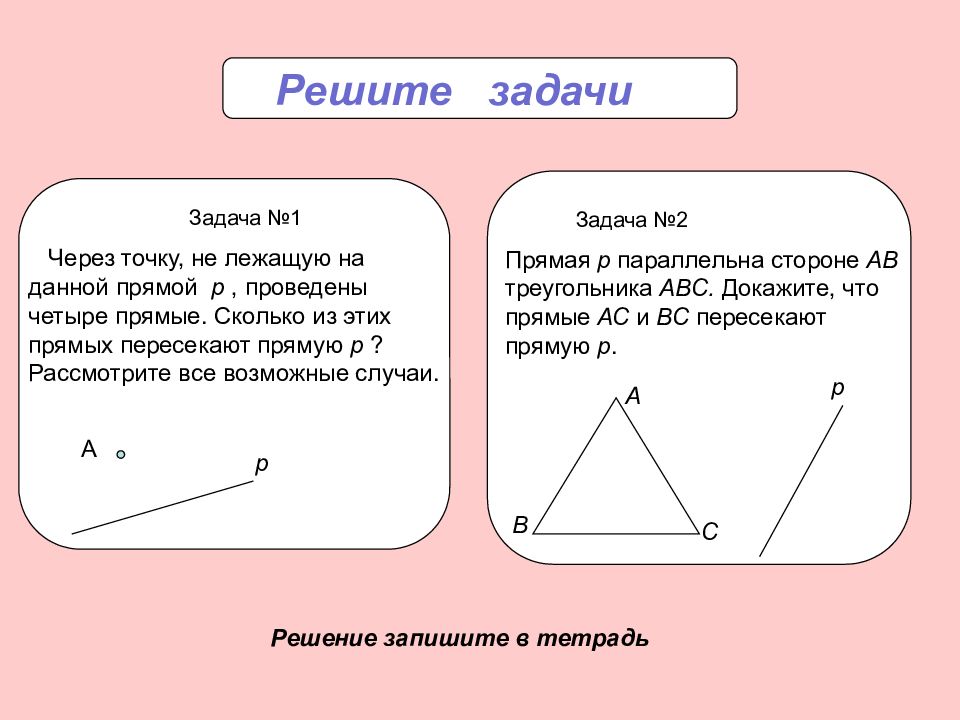
Решите задачи Задача №1 Через точку, не лежащую на данной прямой p, проведены четыре прямые. Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи. А р Задача №2 Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые АС и ВС пересекают прямую р. А В С р Решение запишите в тетрадь
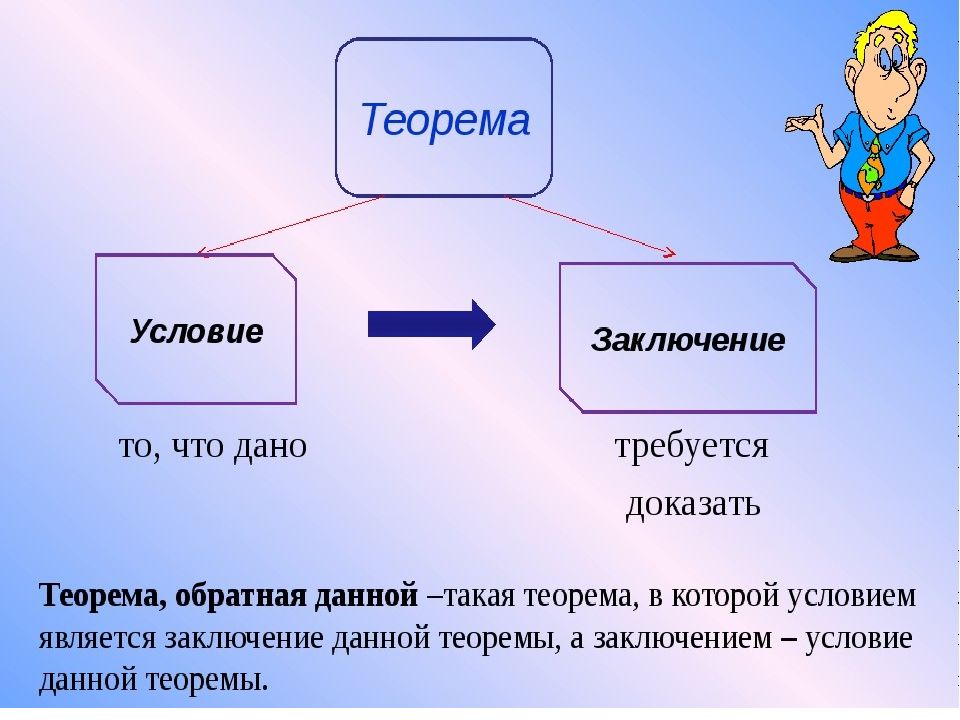
Прямая и обратная теоремы Каждая теорема состоит из УСЛОВИЯ и ЗАКЛЮЧЕНИЯ
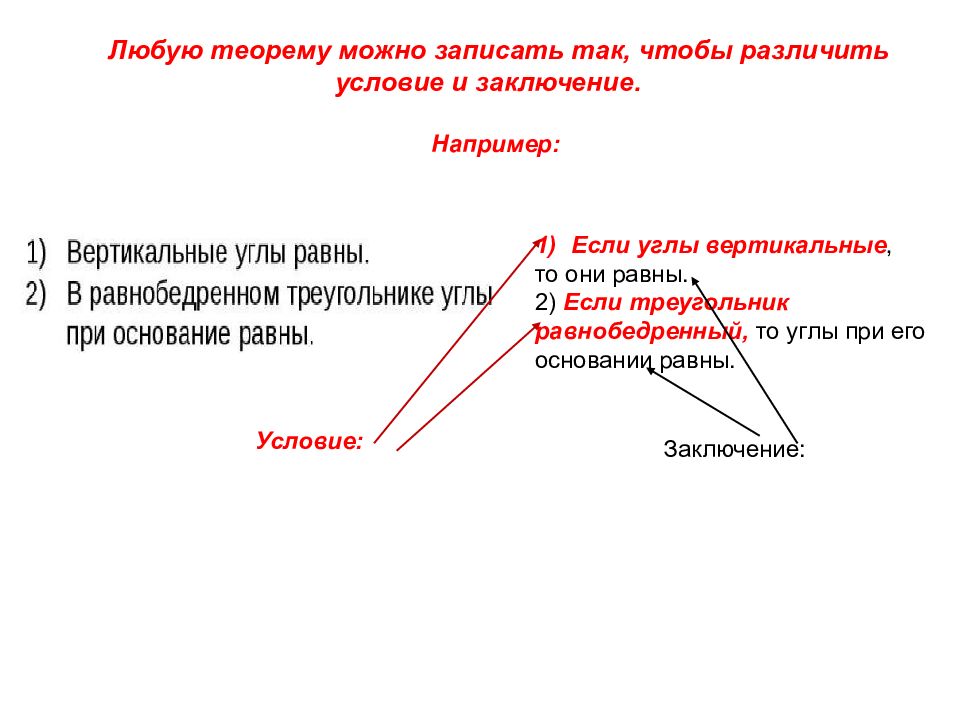
Любую теорему можно записать так, чтобы различить условие и заключение. Например: Если углы вертикальные, то они равны. 2) Если треугольник равнобедренный, то углы при его основании равны. Условие: Заключение:
Опр. Теорема называется обратной, в случае когда условие является заключением. Например: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны Пря - мая теорема Обрат- ная теорема Если две прямые параллельные прямые пересечены секущей, то накрест лежащие углы равны
Выполните тест, ответы запишите в тетрадь. Тест по теме «Аксиомы» 1. Основные объекты геометрии – это… 2. Аксиома – это утверждение, а) получаемое путем логического доказательства, б) истинность которых принимается без доказательства, в) которое требуется доказать 3. Теорема – это утверждение, … 4.Кто автор работы «Начала»? 5. Из каких частей состоит теорема? 6. Назовите условие и заключение в 1 признаке параллельности прямых. Спасибо за внимание! Успехов в работе по изучению геометрии!
