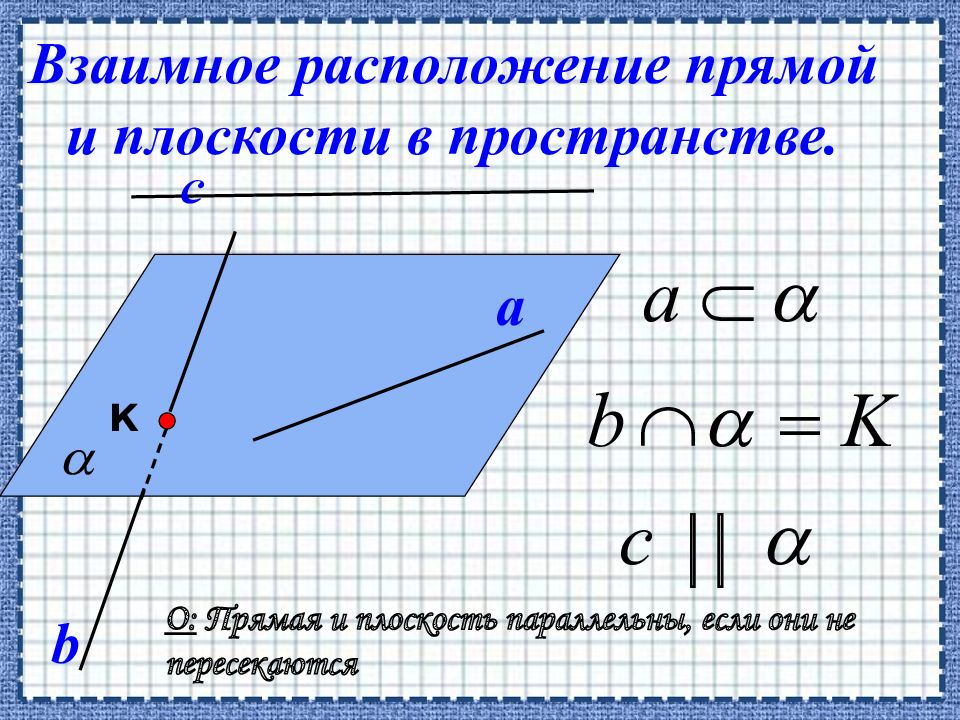
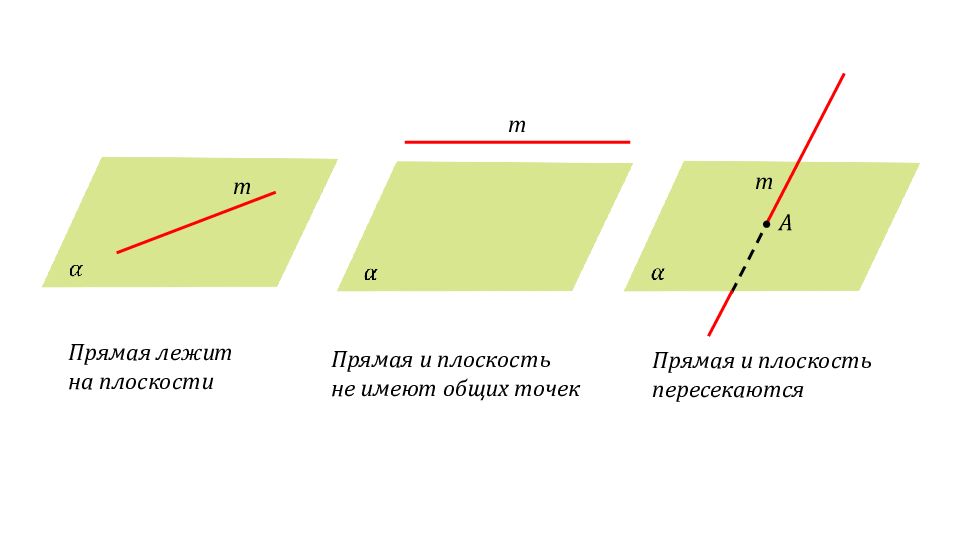
Слайд 2: Содержание:
Аксиомы стереометрии и их простейшие следствия Параллельность прямых и плоскостей Перпендикулярность прямых и плоскостей
Слайд 3
С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. Аксиомы стереометрии С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. С3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Слайд 4
Простейшие следствия из аксиом стереометрии Теорема 15.1: Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Теорема 15.2: Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. Теорема 15.3: Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Слайд 5
Параллельность прямых и плоскостей Теорема 16.1: Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну. Теорема 16.2: Две прямые, параллельные третьей прямой, параллельны Теорема 16.3: Если прямая, не принадлежащая плоскости, параллельна какой - нибудь прямой в этой плоскости, то она параллельна и самой плоскости. Теорема 16.4: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Теорема 16.5: Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Слайд 6
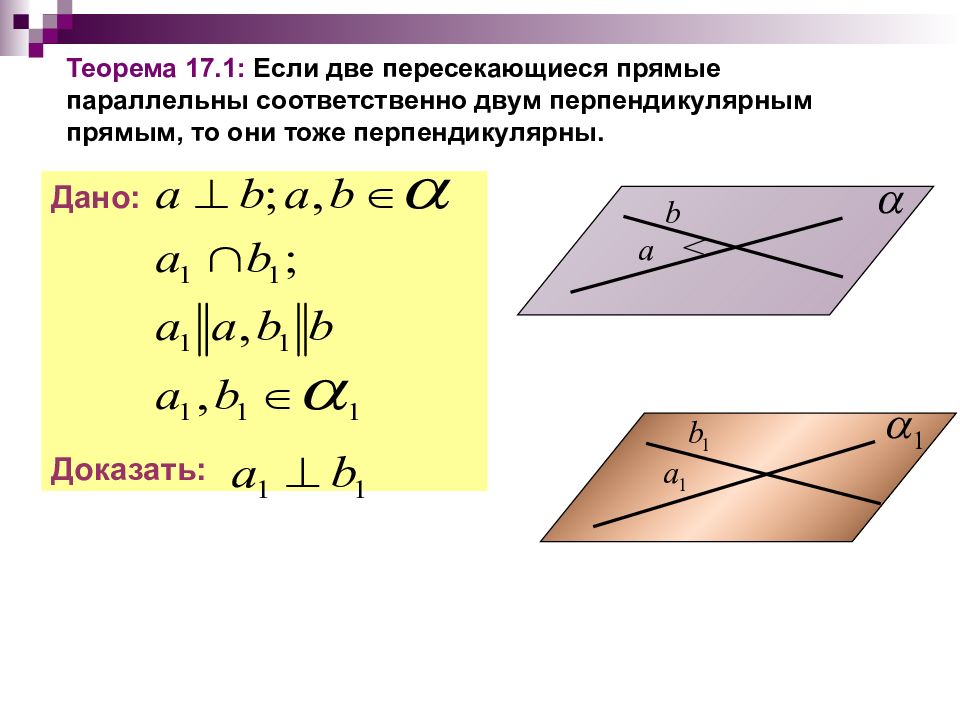
Перпендикулярность прямых и плоскостей Теорема 17.1: Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны. Теорема 17.2: Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости. Теорема 17. 3 : Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой. Теорема 17.4: Две прямые, перпендикулярные одной и той же плоскости, параллельны. Теорема 17.5: Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна наклонной. Теорема 17. 6 : Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Слайд 7
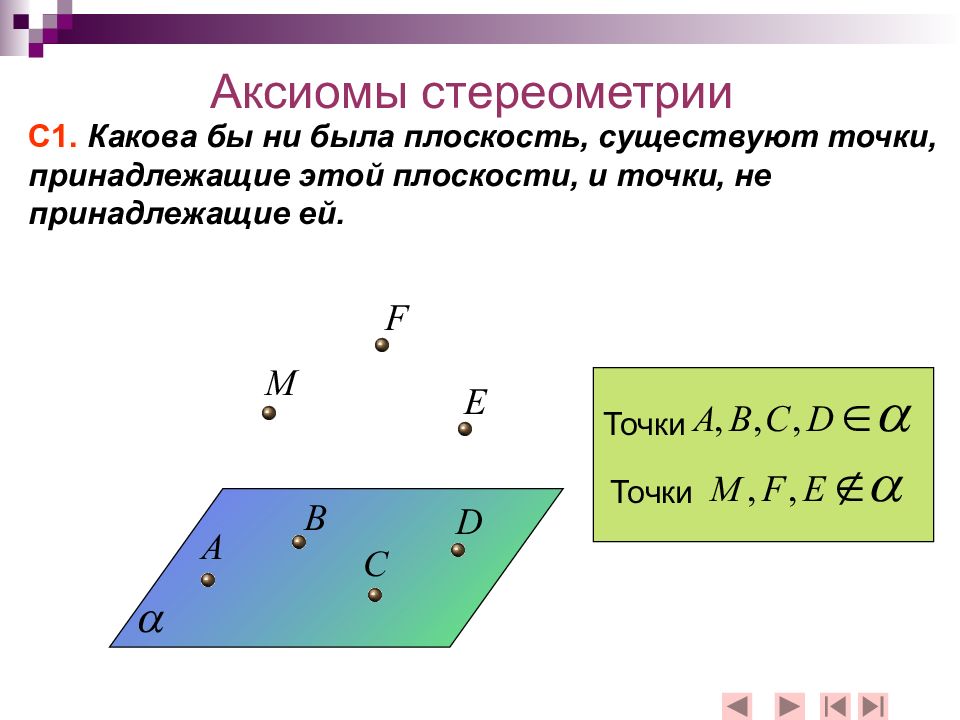
С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. Аксиомы стереометрии Точки Точки
Слайд 8
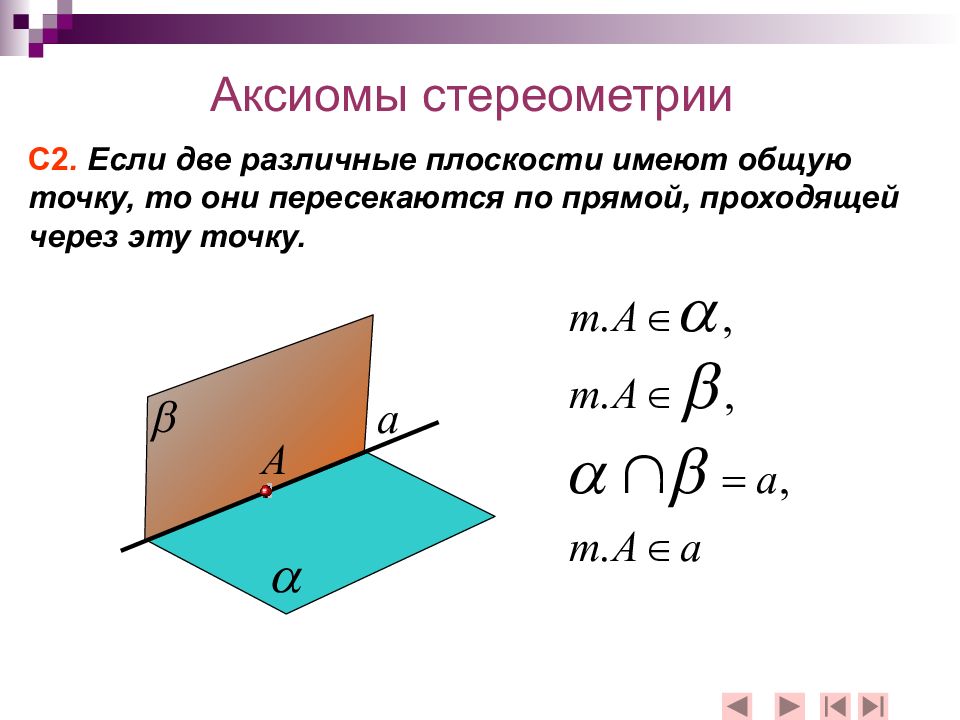
С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Аксиомы стереометрии
Слайд 9
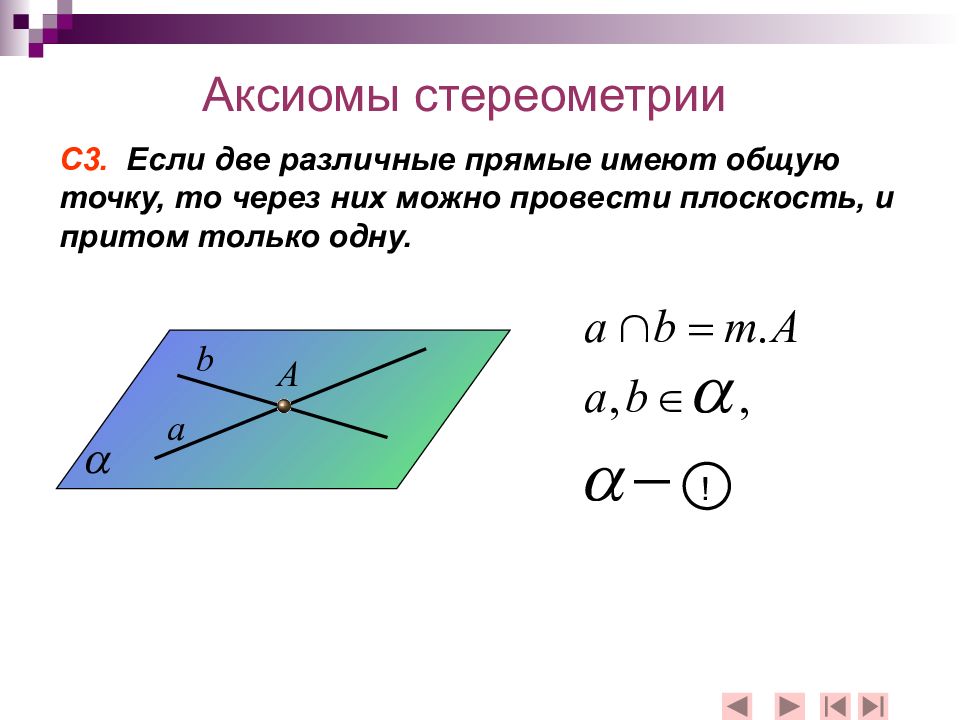
С3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну. Аксиомы стереометрии !
Слайд 10
Теорема 15.1: Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Дано: прямая а, Доказать: Доказательство: 1)Возьмём (по I) 2) Проведём прямую АВ, 3) Через прямые АВ и а проведём плоскость - (по С 3 ) Теорема доказана. ! !
Слайд 11
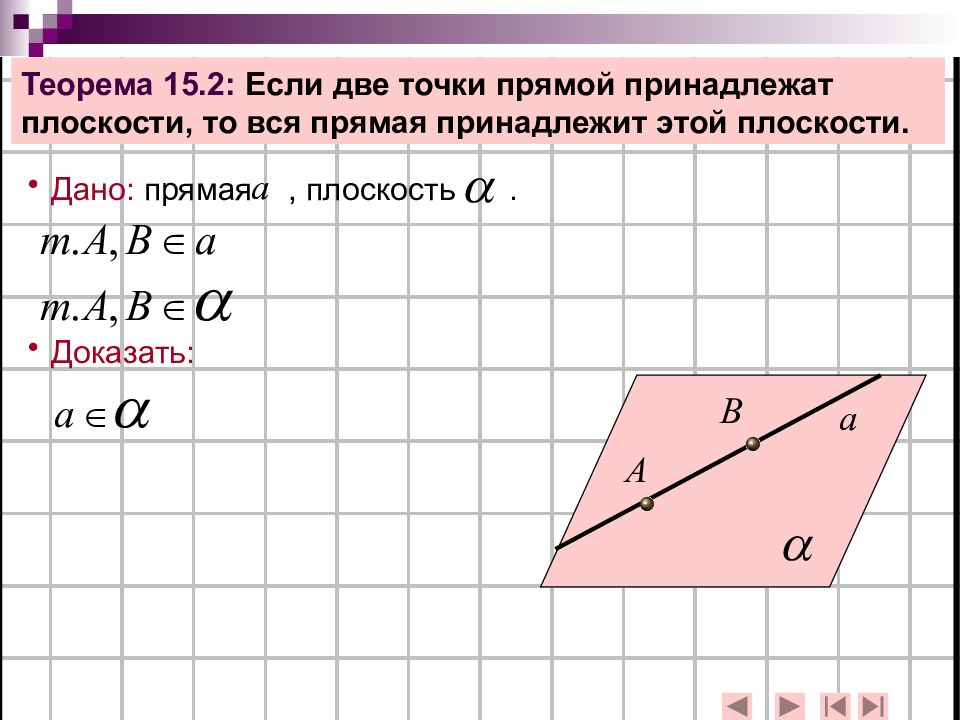
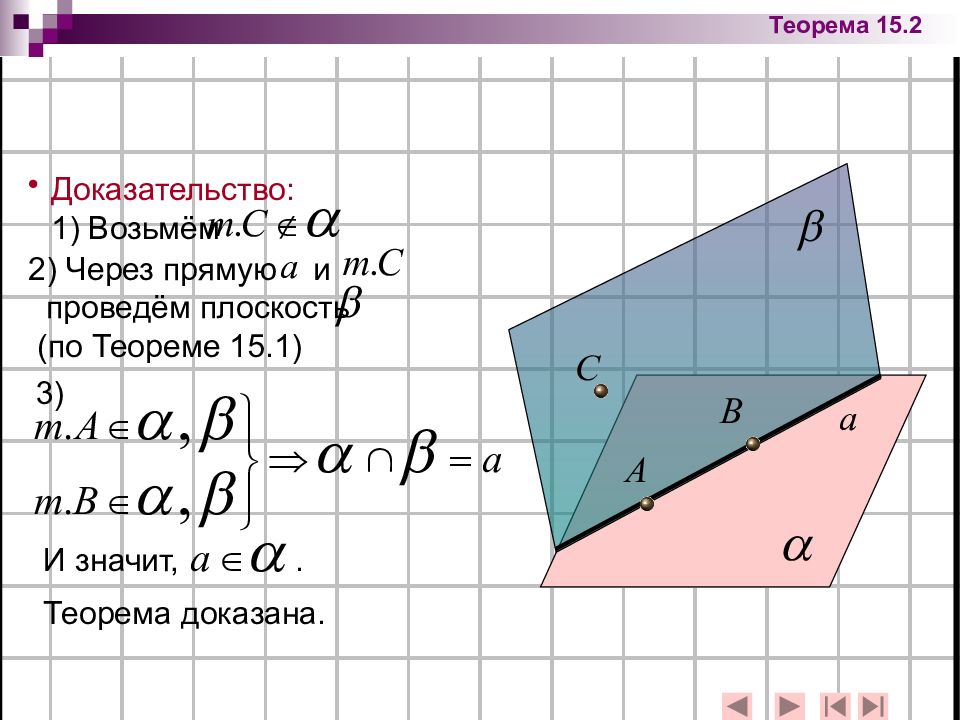
Теорема 15.2: Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. Дано: прямая, плоскость. Доказать:
Слайд 12
Доказательство: 1) Возьмём 2) Через прямую и проведём плоскость (по Теореме 15.1) 3) И значит,. Теорема доказана. Теорема 15.2
Слайд 13
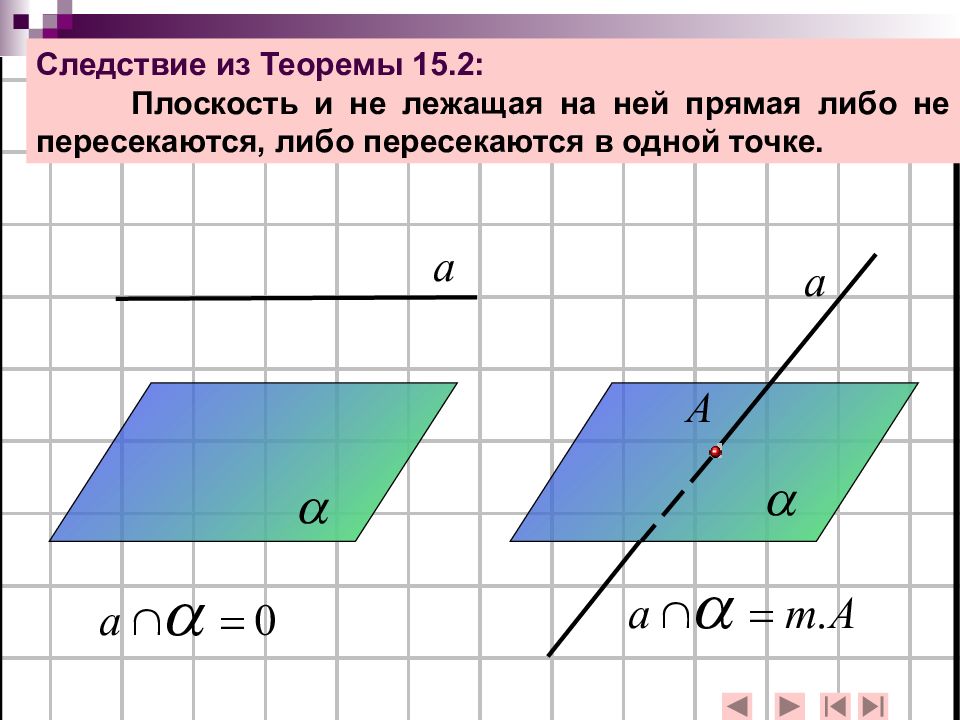
Следствие из Теоремы 15.2: Плоскость и не лежащая на ней прямая либо не пересекаются, либо пересекаются в одной точке.
Слайд 14
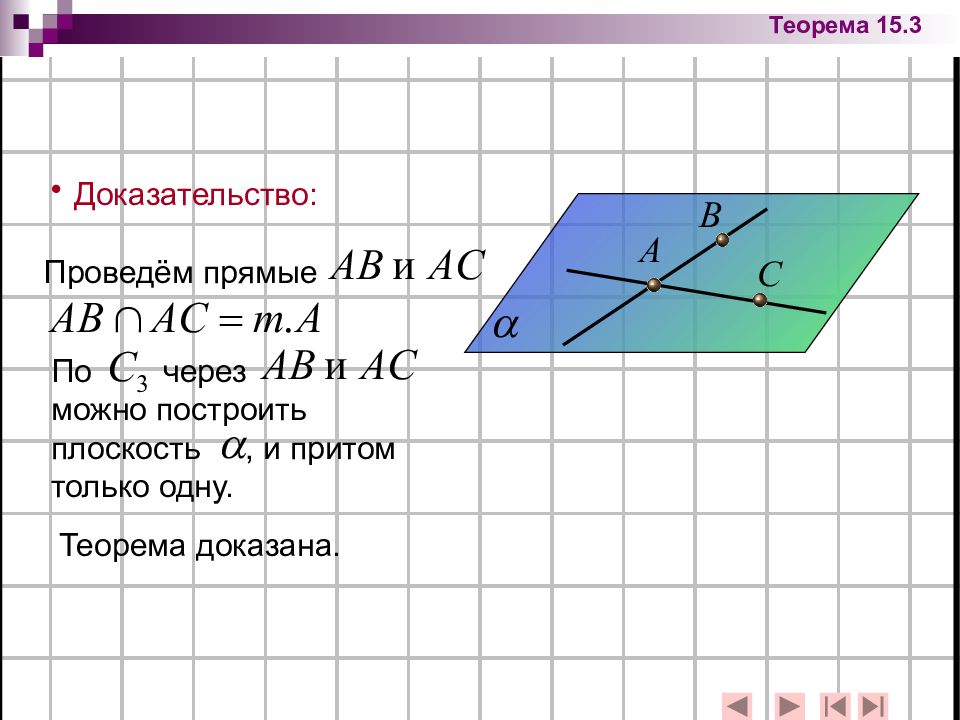
Теорема 15.3: Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну. Дано: Доказать: !
Слайд 15
Доказательство: Проведём прямые По через можно построить плоскость, и притом только одну. Теорема доказана. Теорема 15.3
Слайд 16
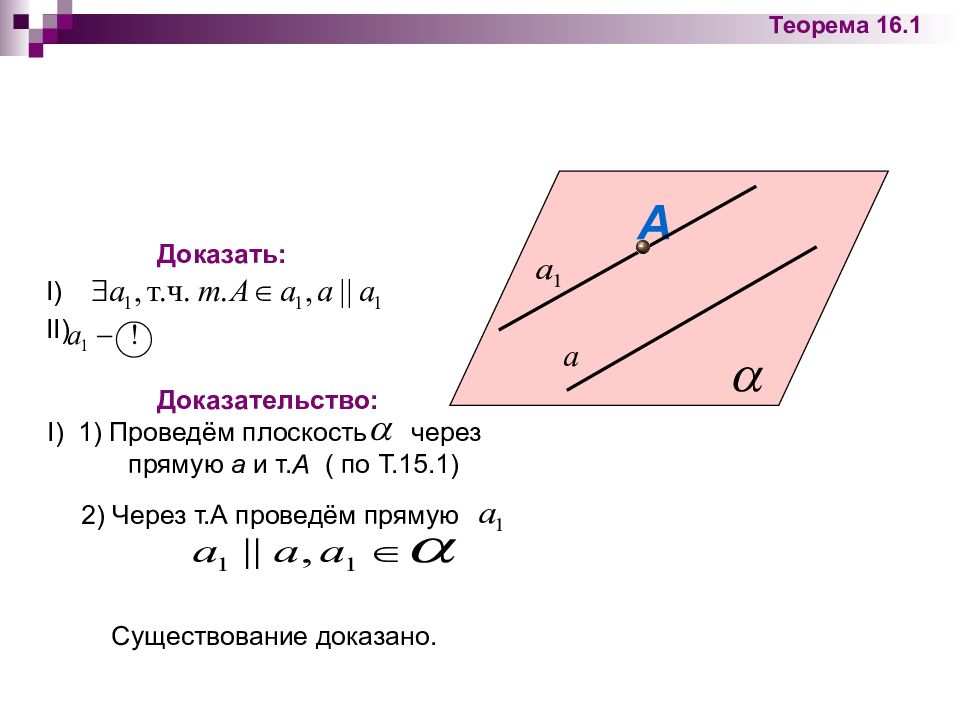
Дано: прямая a, т.А а А Доказать: I) II) Теорема 16.1: Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.
Слайд 17
Доказательство : I) 1) Проведём плоскость через прямую а и т. А ( по Т.15.1) Доказать: I) II) А 2) Через т.А проведём прямую Существование доказано. Теорема 16.1
Слайд 18
А 5) Получили, что через прямую а и точку А проходит 2 различные плоскости, а по Т.15.1 через прямую и не принадлежащую ей точку можно провести единственную плоскость, значит, II) 3) Предположим, 4) Проведём через прямые плоскость Теорема доказана. Теорема 16.1
Слайд 19: Признак параллельности прямых
Теорема 16.2: Две прямые, параллельные третьей прямой, параллельны. b c Рассмотрим случай, когда прямые не принадлежат одной плоскости. Дано: Доказать:
Слайд 20
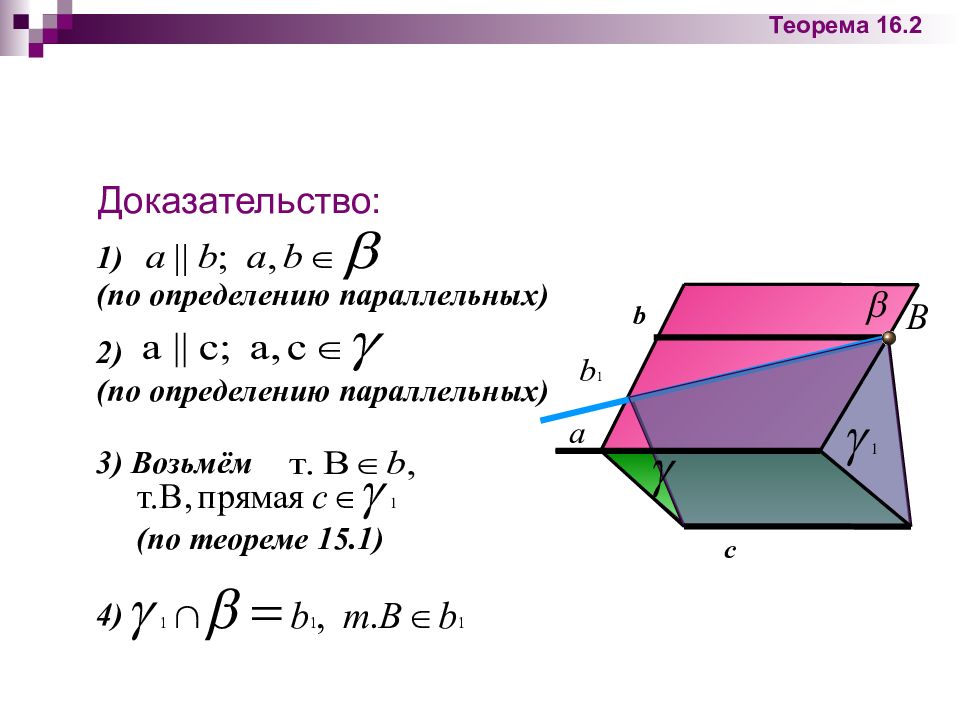
Доказательство: b c 1) (по определению параллельных) 2) (по определению параллельных) 3) Возьмём (по теореме 15.1) 4) Теорема 16.2
Слайд 21
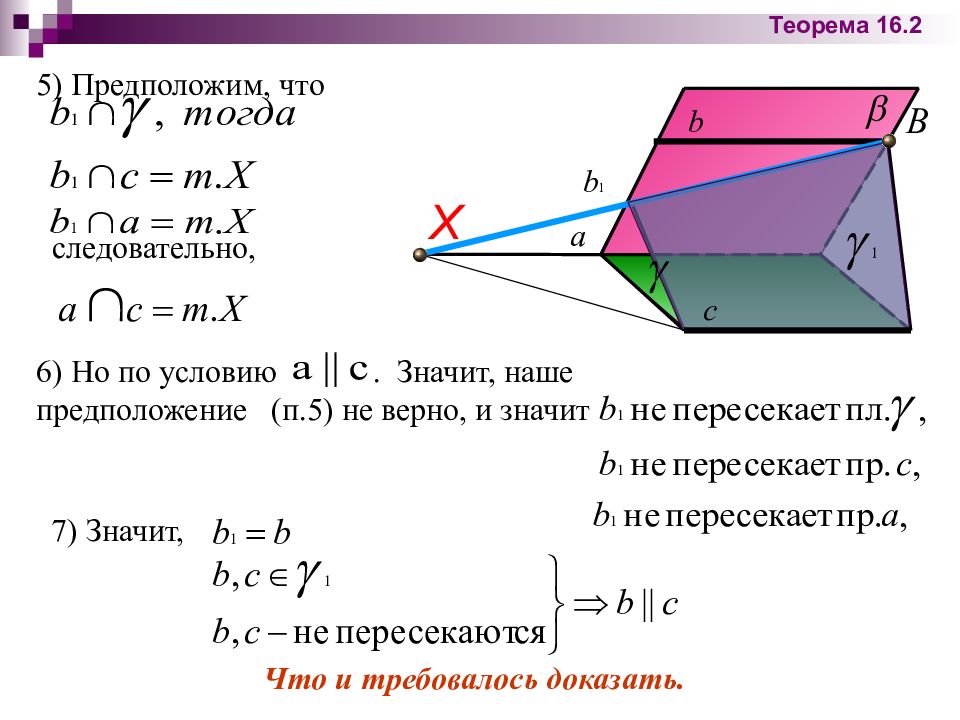
5) Предположим, что следовательно, Что и требовалось доказать. Х 6) Но по условию. Значит, наше предположение (п.5) не верно, и значит 7) Значит, Теорема 16.2
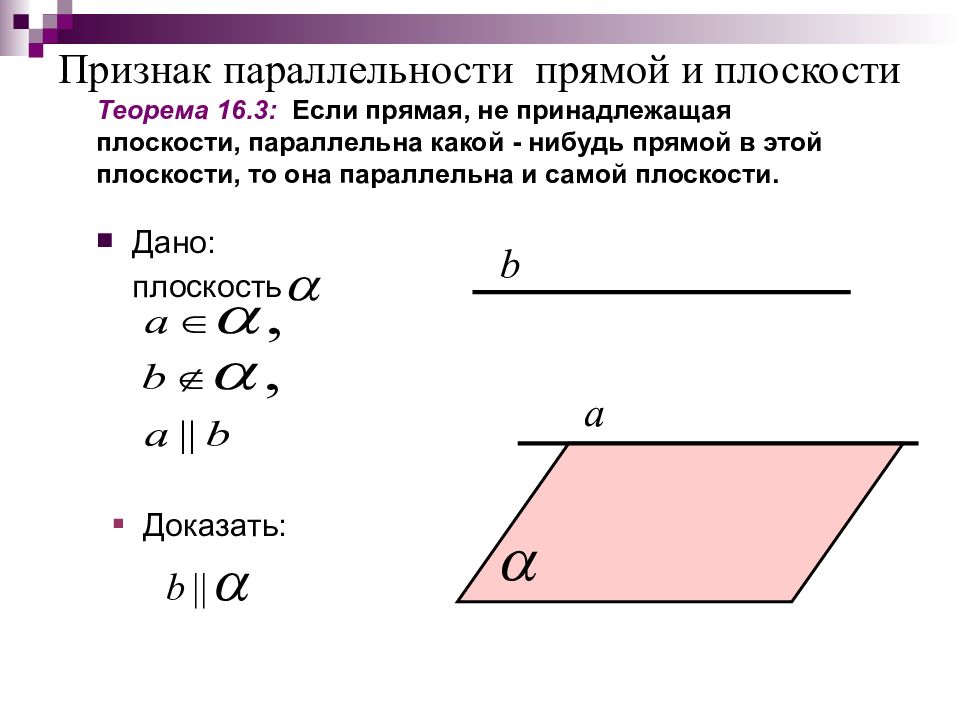
Дано: плоскость Теорема 16.3: Если прямая, не принадлежащая плоскости, параллельна какой - нибудь прямой в этой плоскости, то она параллельна и самой плоскости. Доказать:
Слайд 23
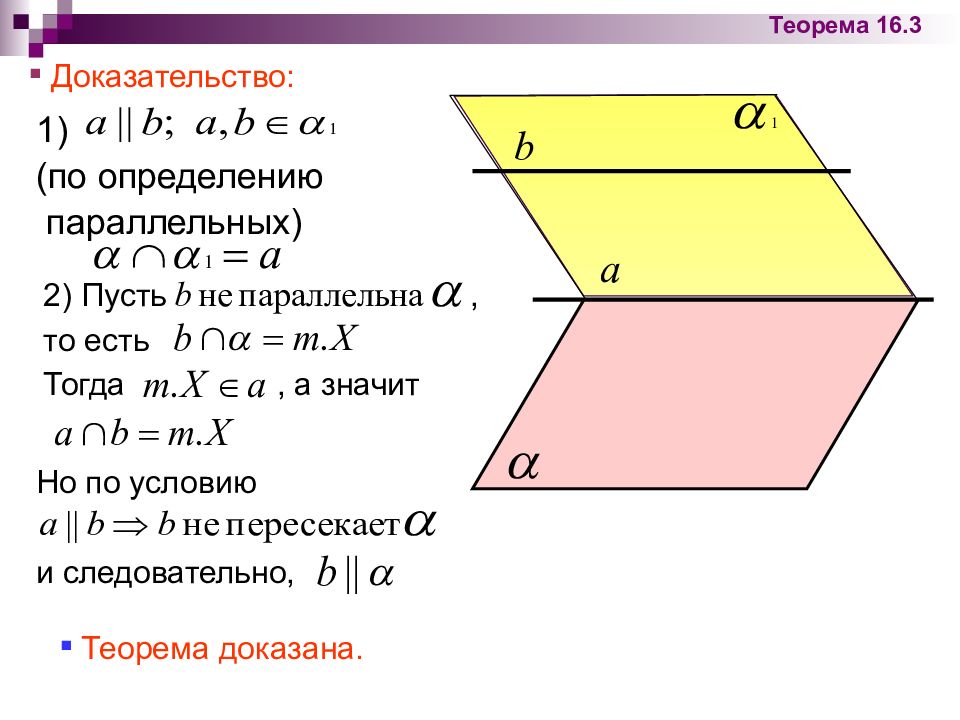
1) (по определению параллельных) Доказательство: 2) Пусть, то есть Тогда, а значит Но по условию и следовательно, Теорема доказана. Теорема 16.3
Слайд 24
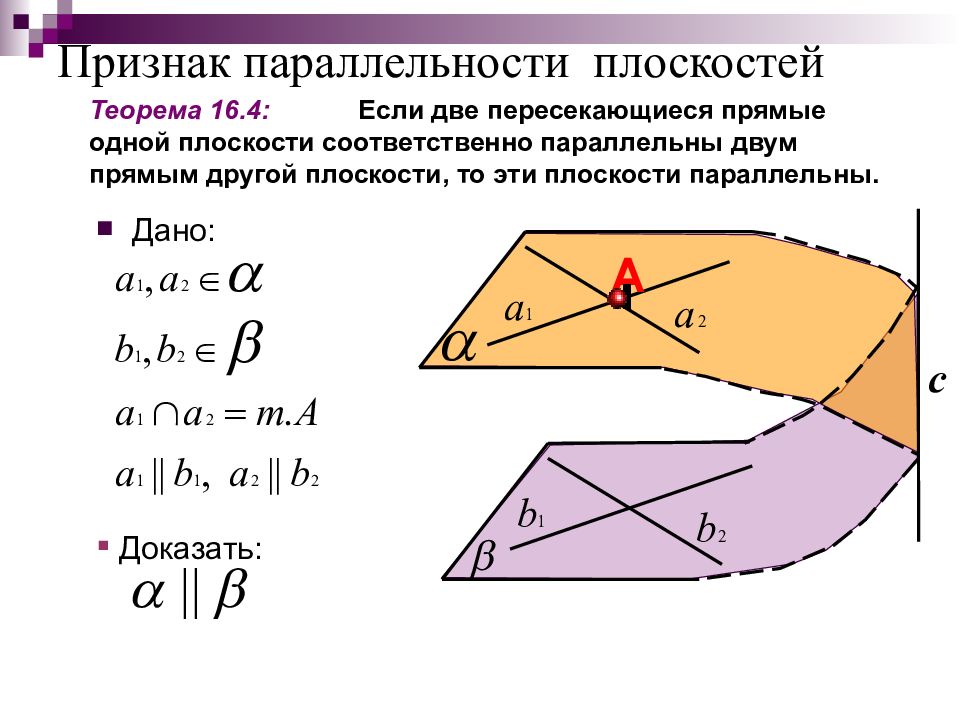
А c Признак параллельности плоскостей Дано: Теорема 16.4: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Доказать:
Слайд 25
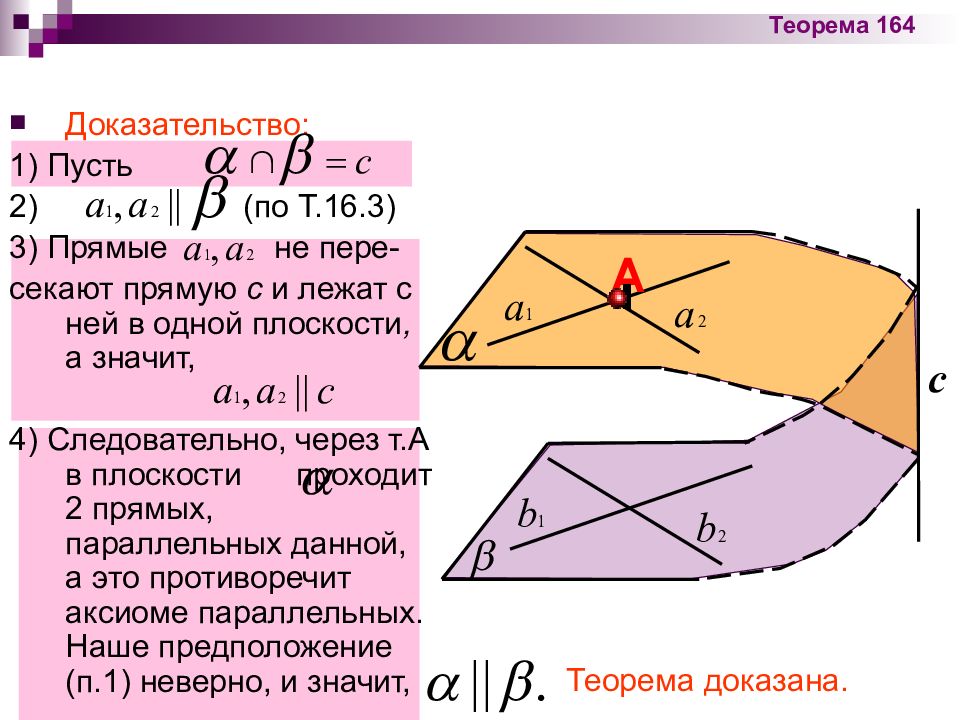
Доказательство: 1) Пусть 2) (по Т.16.3) 3) Прямые не пере- секают прямую с и лежат с ней в одной плоскости, а значит, 4) Следовательно, через т.А в плоскости проходит 2 прямых, параллельных данной, а это противоречит аксиоме параллельных. Наше предположение (п.1) неверно, и значит, А c Теорема доказана. Теорема 164
Слайд 26
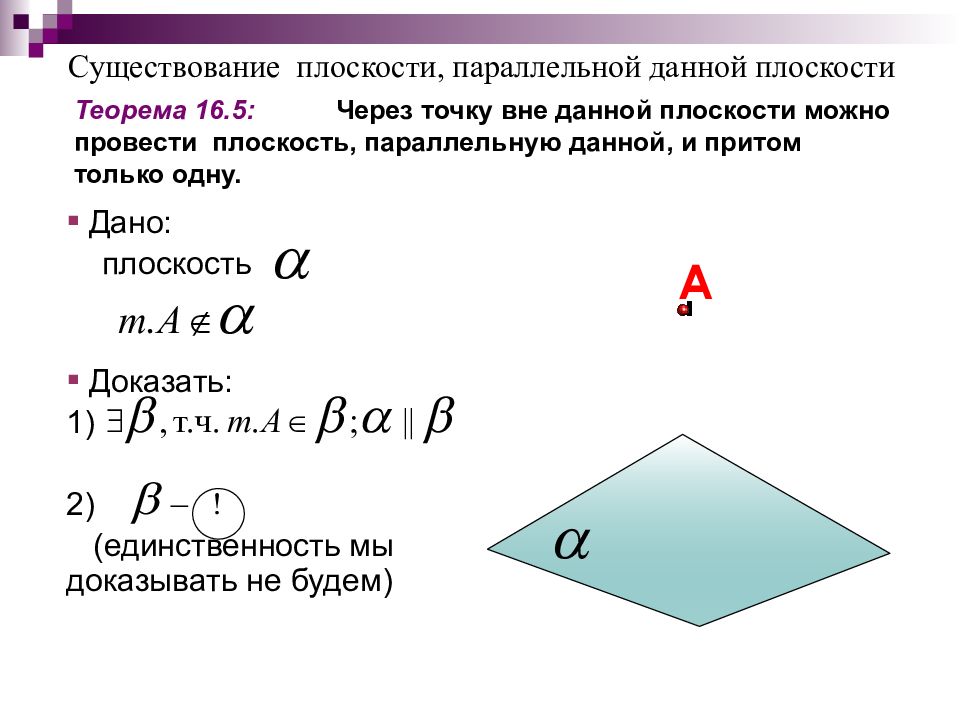
Существование плоскости, параллельной данной плоскости Теорема 16.5: Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну. А Дано: плоскость Доказать: 1) 2) (единственность мы доказывать не будем)
Слайд 27
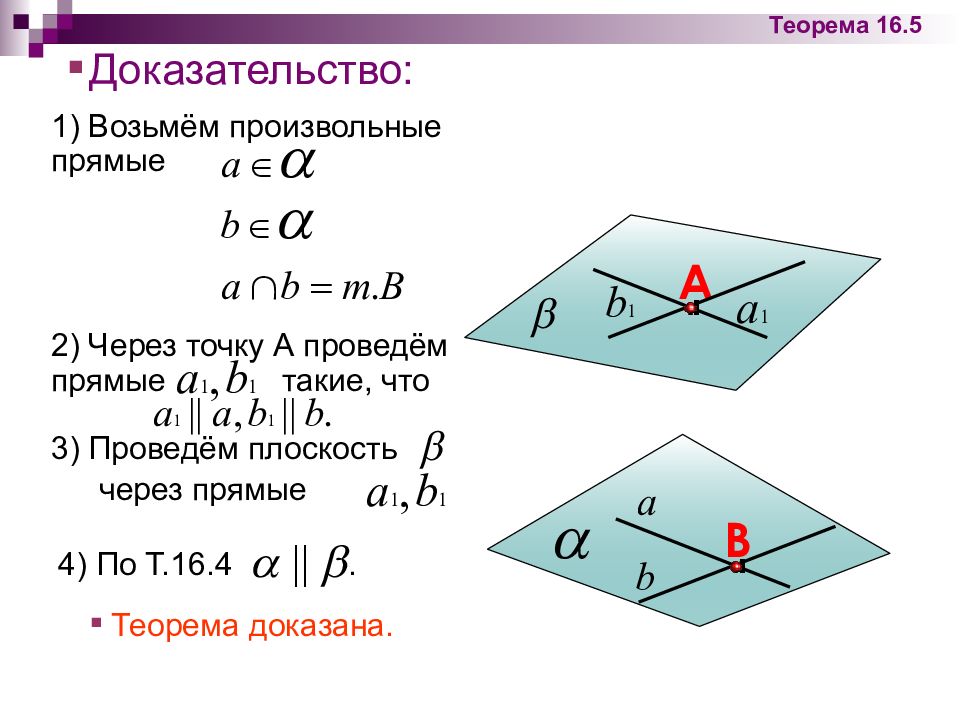
1) Возьмём произвольные прямые 2) Через точку А проведём прямые такие, что 3) Проведём плоскость через прямые 4) По Т.16.4. Теорема доказана. Доказательство: А В Теорема 16.5
Слайд 28
Теорема 17.1: Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны. Дано: Доказать:
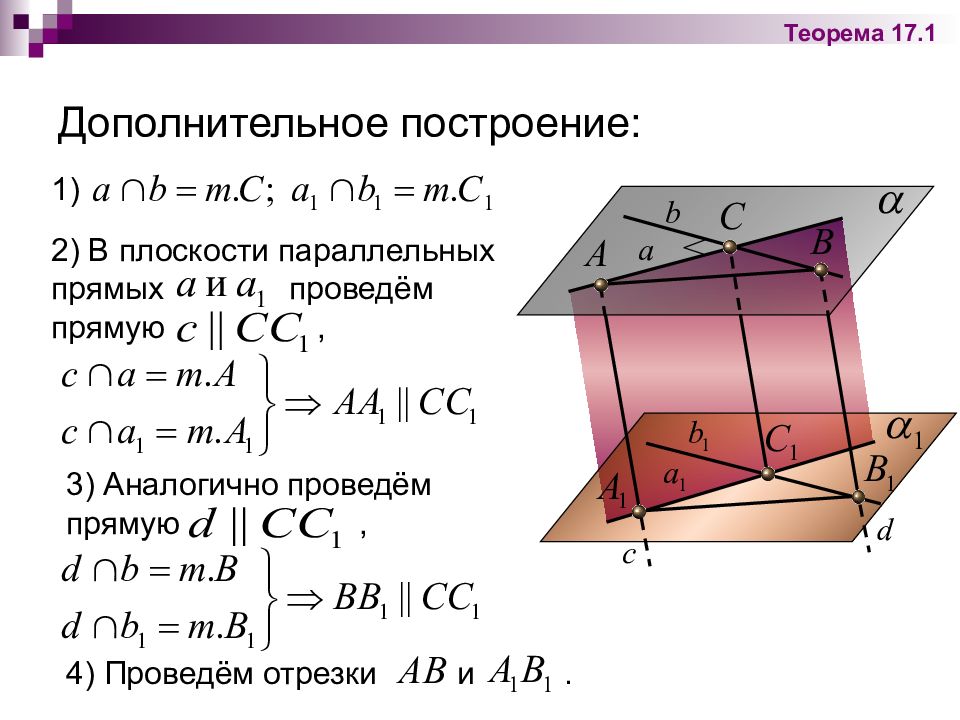
Слайд 29: Дополнительное построение:
1) 2) В плоскости параллельных прямых проведём прямую, 3) Аналогично проведём прямую, 4) Проведём отрезки и. Теорема 17.1
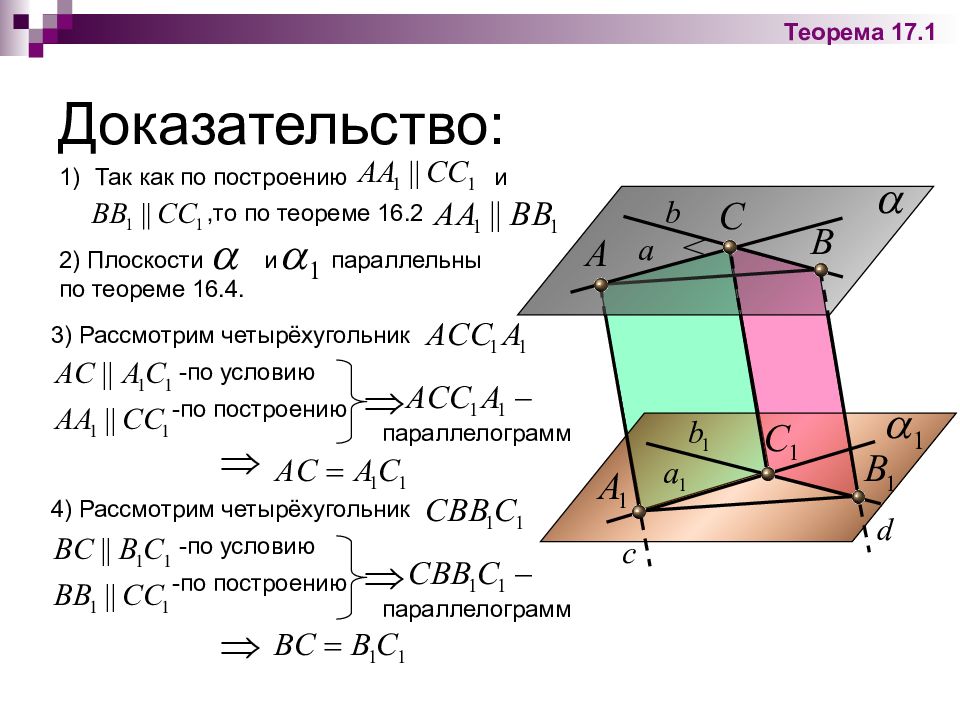
Слайд 30: Доказательство:
4) Рассмотрим четырёхугольник -по условию -по построению Доказательство: Теорема 17.1 Так как по построению и ,то по теореме 16.2 2) Плоскости и параллельны по теореме 16.4. 3) Рассмотрим четырёхугольник -по условию -по построению параллелограмм параллелограмм
Слайд 31
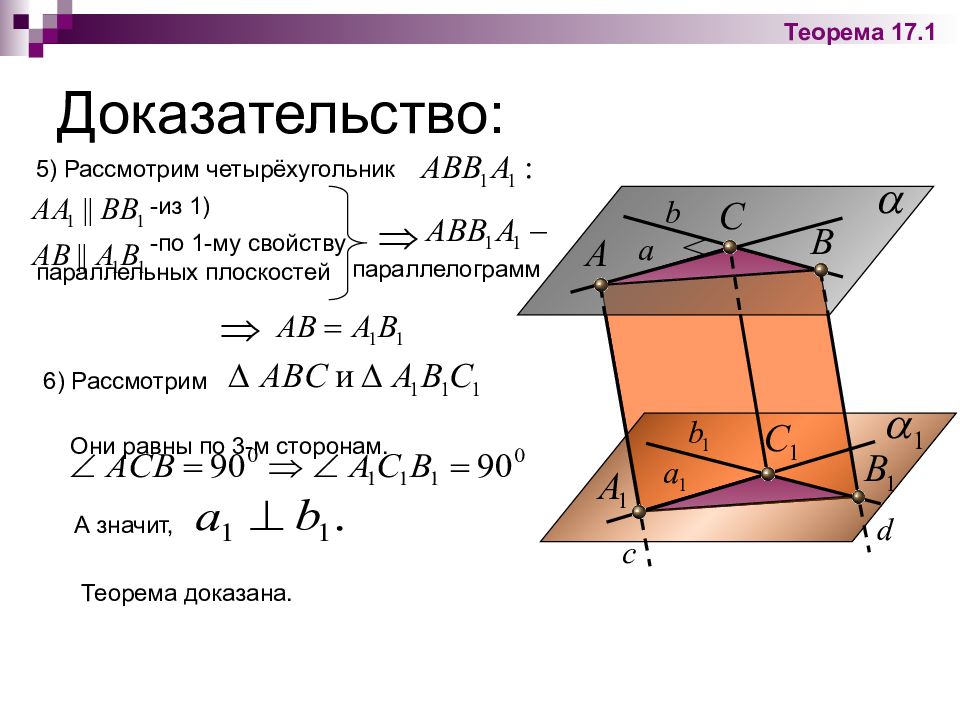
Доказательство: Теорема 17.1 5) Рассмотрим четырёхугольник -из 1) -по 1-му свойству параллельных плоскостей параллелограмм 6) Рассмотрим Они равны по 3-м сторонам. А значит, Теорема доказана.
Слайд 32
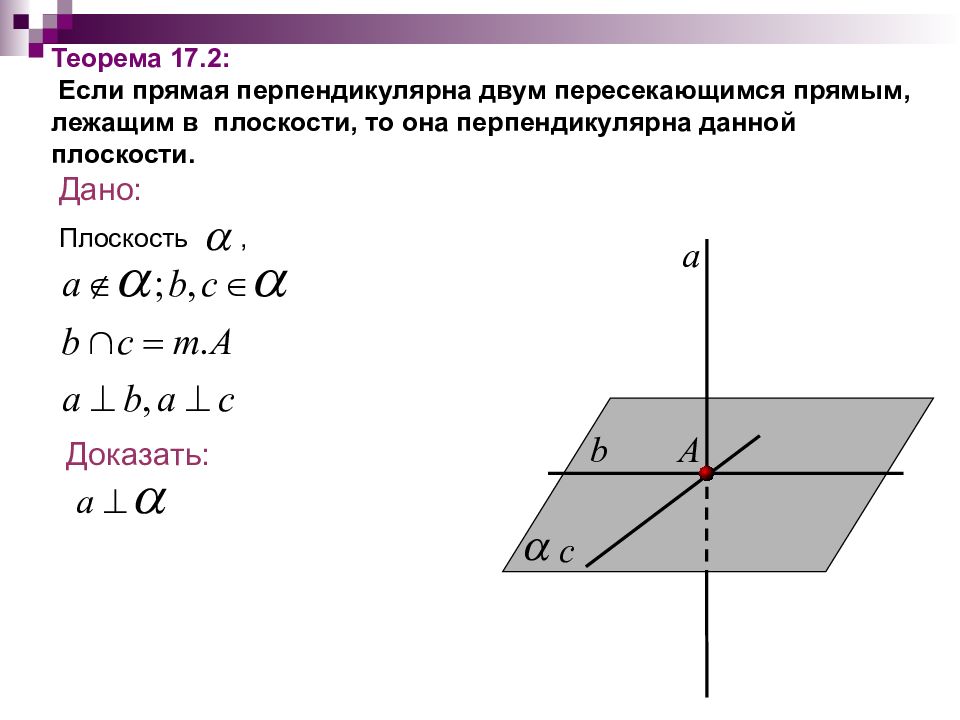
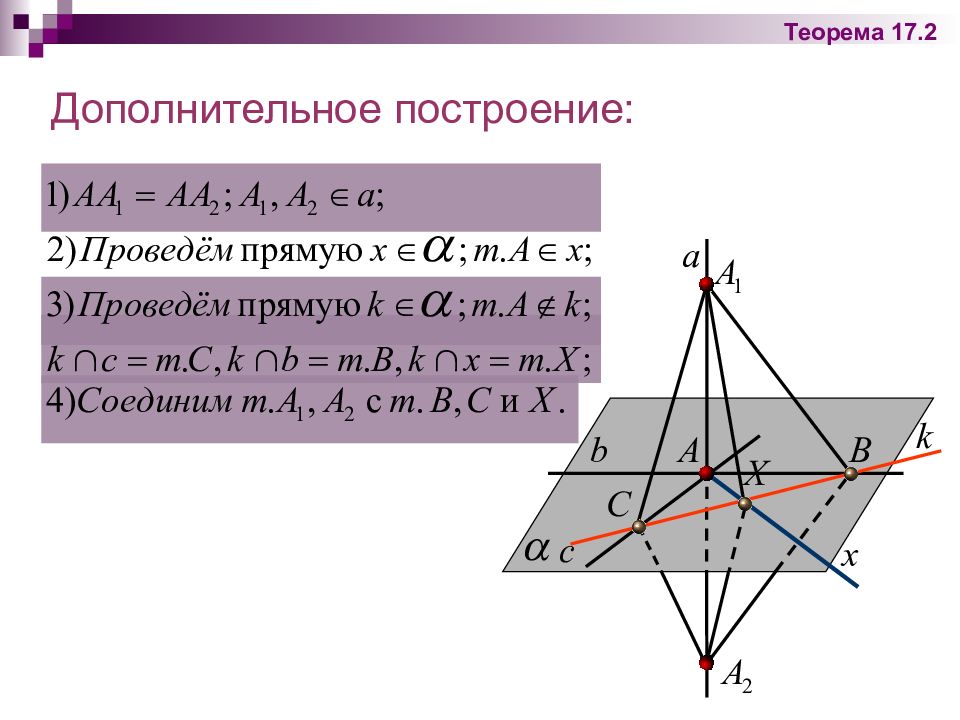
Теорема 17.2: Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости. Дано: Плоскость, Доказать:
Слайд 34: Доказательство:
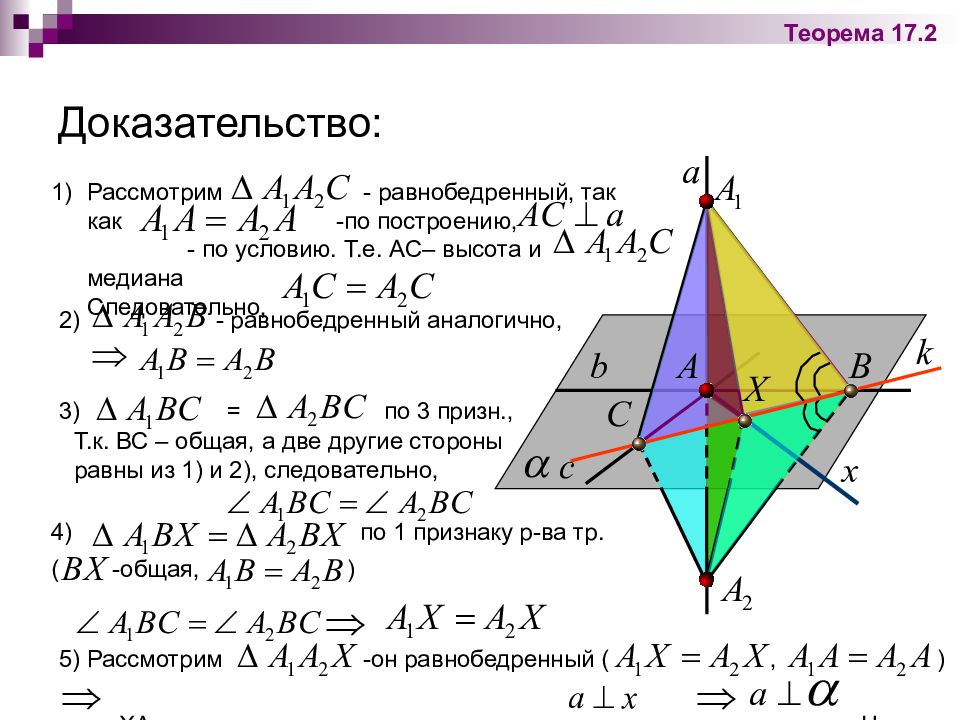
Рассмотрим - равнобедренный, так как -по построению, - по условию. Т.е. АС– высота и медиана Следовательно, Доказательство: - равнобедренный аналогично, 3) = Т.к. ВС – общая, а две другие стороны равны из 1) и 2), следовательно, 5) Рассмотрим -он равнобедренный (, ) ХА- медиана, высота, а значит, прямая, и. Ч.и т.д. 4) по 1 признаку р-ва тр. ( -общая, ) по 3 призн., Теорема 17.2
Слайд 35
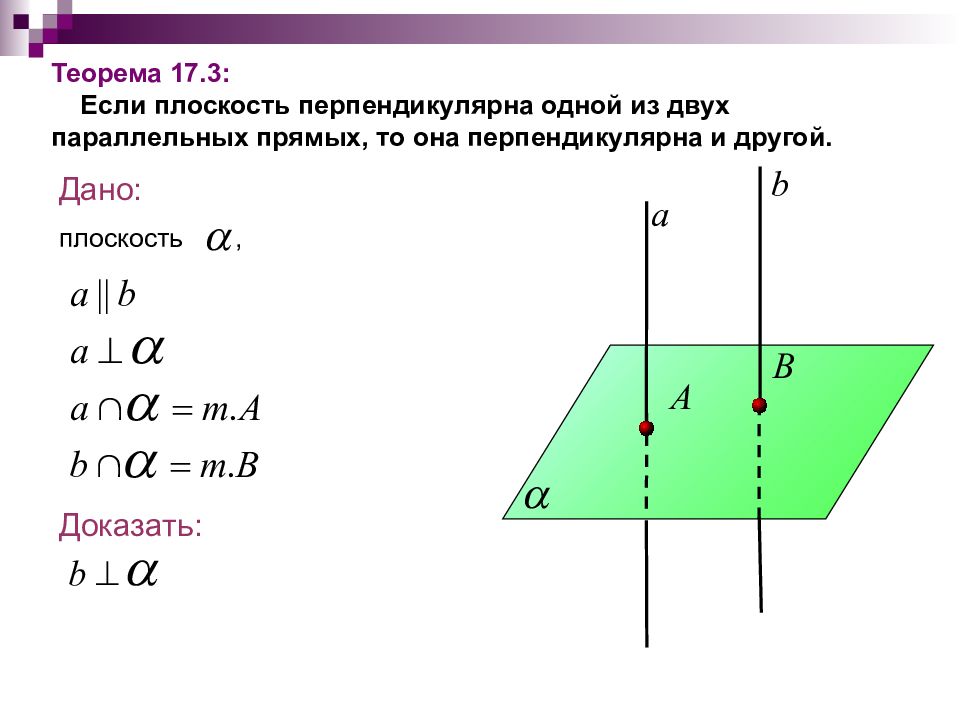
Теорема 17. 3 : Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой. Дано: плоскость, Доказать:
Слайд 36
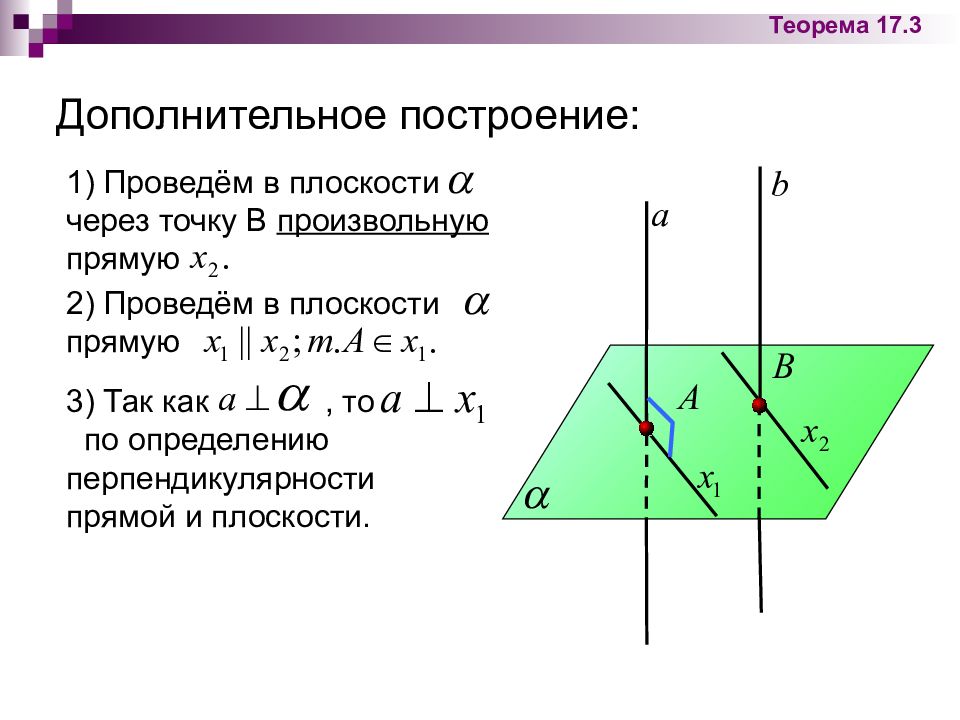
2) Проведём в плоскости прямую Дополнительное построение: Теорема 17. 3 1) Проведём в плоскости через точку В произвольную прямую 3) Так как, то по определению перпендикулярности прямой и плоскости.
Слайд 37
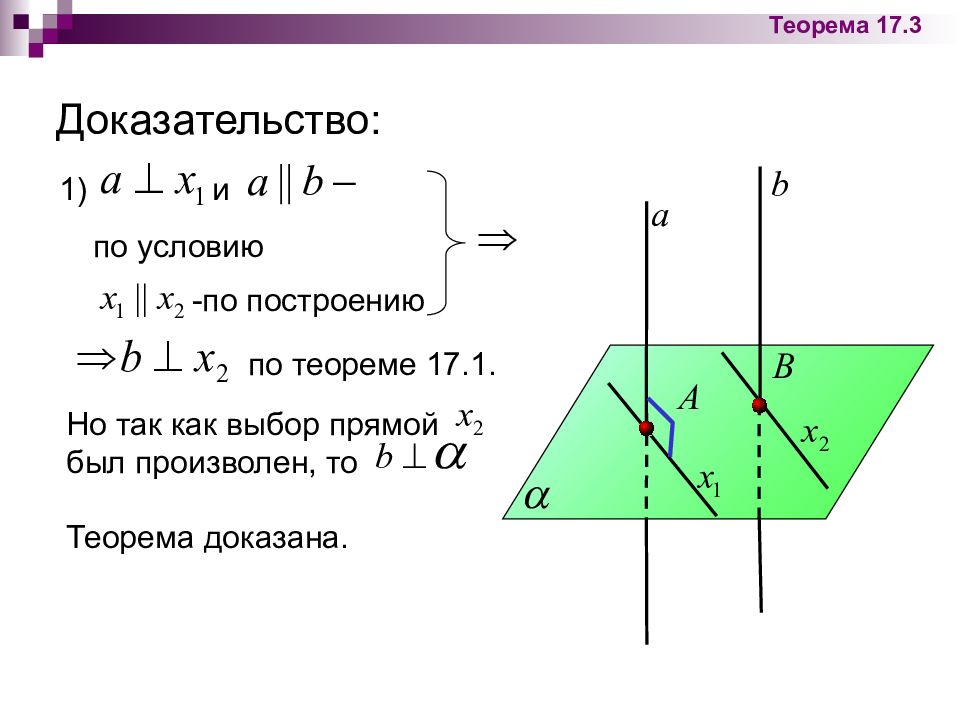
Доказательство: Теорема 17. 3 по условию -по построению по теореме 17.1. 1) и Но так как выбор прямой был произволен, то Теорема доказана.
Слайд 38
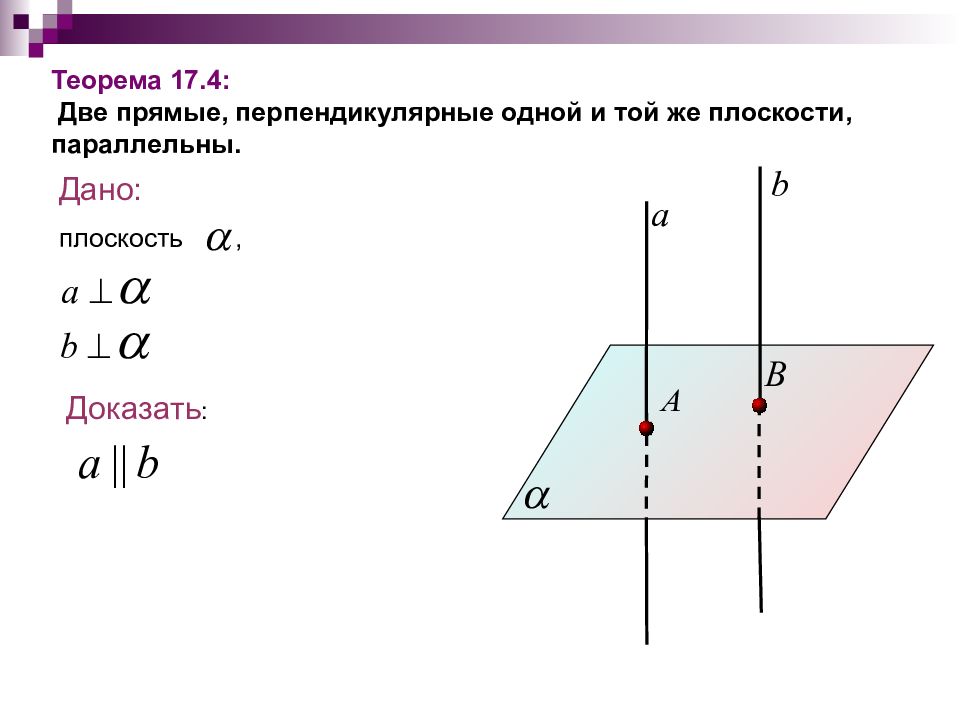
Дано: плоскость, Теорема 17.4: Две прямые, перпендикулярные одной и той же плоскости, параллельны. Доказать :
Слайд 39
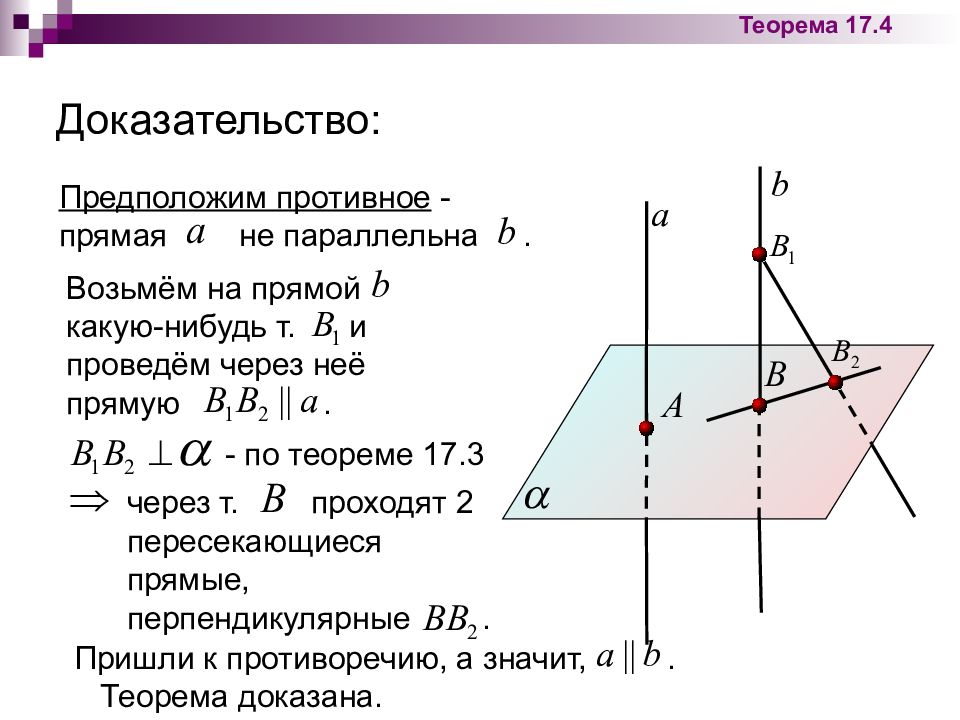
Доказательство: Теорема 17.4 Предположим противное - прямая не параллельна. Возьмём на прямой какую-нибудь т. и проведём через неё прямую. - по теореме 17.3 через т. проходят 2 пересекающиеся прямые, перпендикулярные. Пришли к противоречию, а значит,. Теорема доказана.
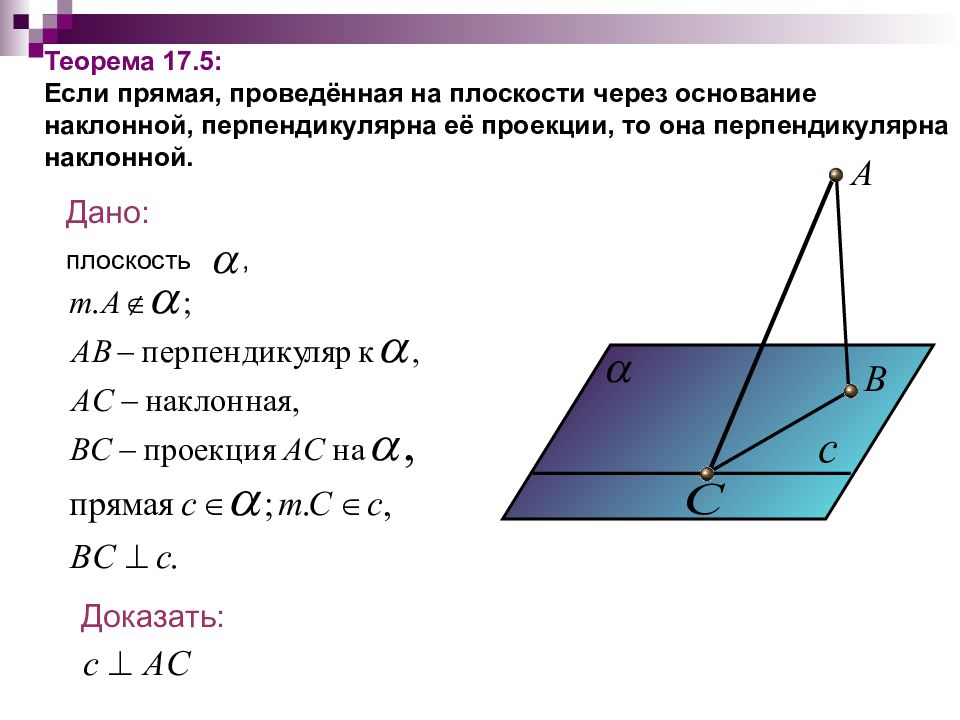
Слайд 40: Теорема 17.5: Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна наклонной
Дано: плоскость, Доказать:
Слайд 41
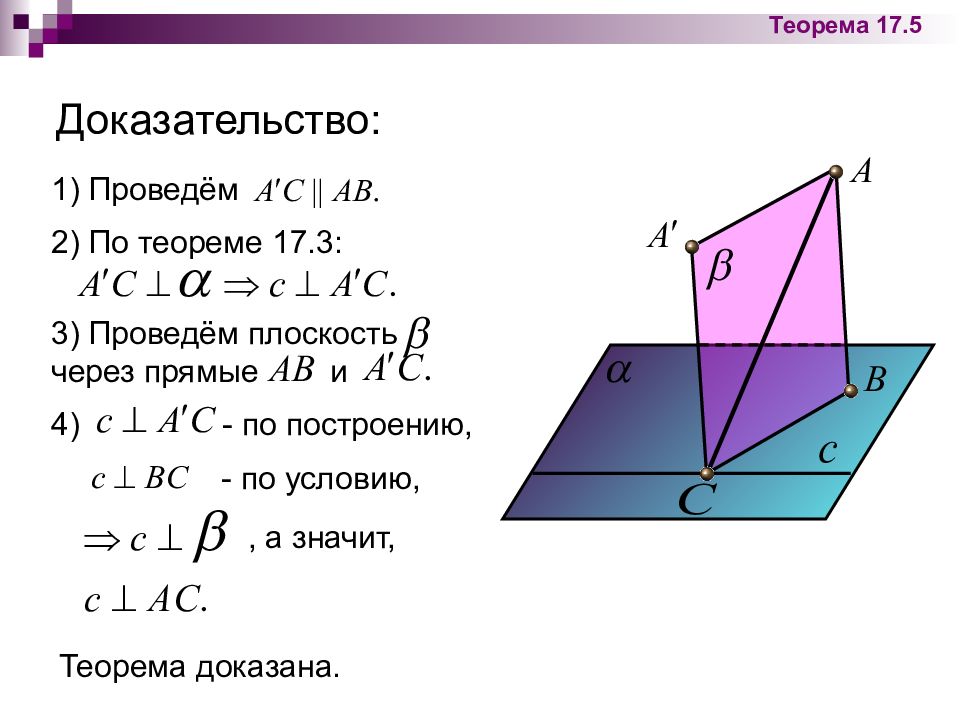
Доказательство: Теорема 17.5 1) Проведём 2) По теореме 17.3: 3) Проведём плоскость через прямые и 4) - по построению, - по условию, , а значит, Теорема доказана.
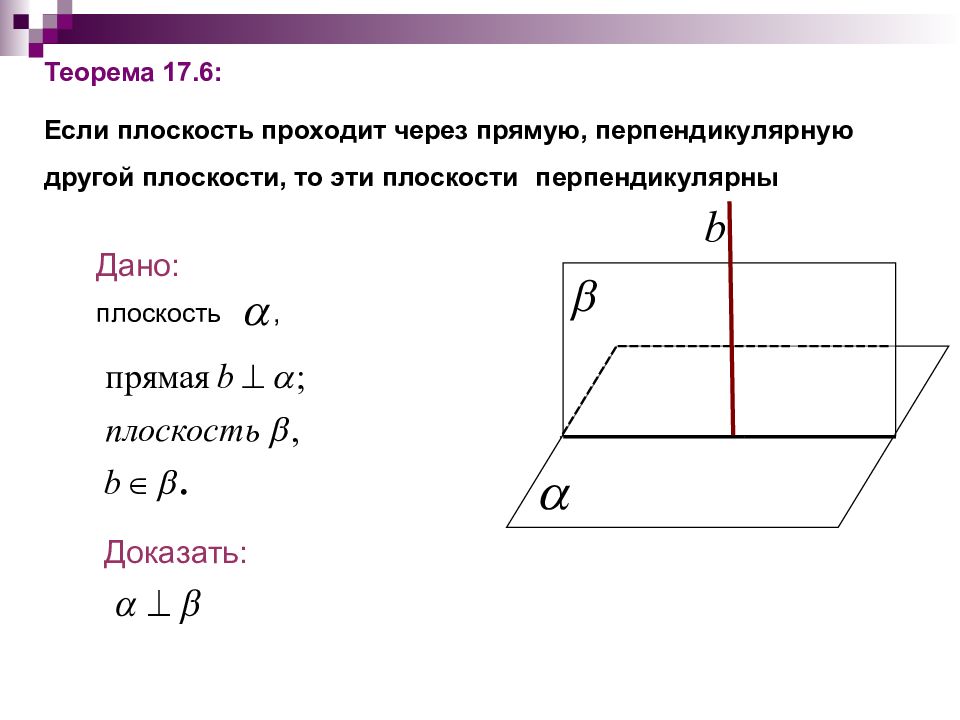
Слайд 42: Теорема 17. 6 : Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны
Дано: плоскость, Доказать: Теорема 17. 6 : Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны
Последний слайд презентации: Все аксиомы и теоремы стереометрии
Доказательство: Теорема 17. 6 1) 2) Проведём на пл. через т. О прямую 3) Проведём плоскость через прямые и. - по построению - по условию, (т.к. ), а значит, пл. пересекает пл-ти и по перпендикулярным прямым, по определению перпендикулярности плоскостей. Теорема доказана.