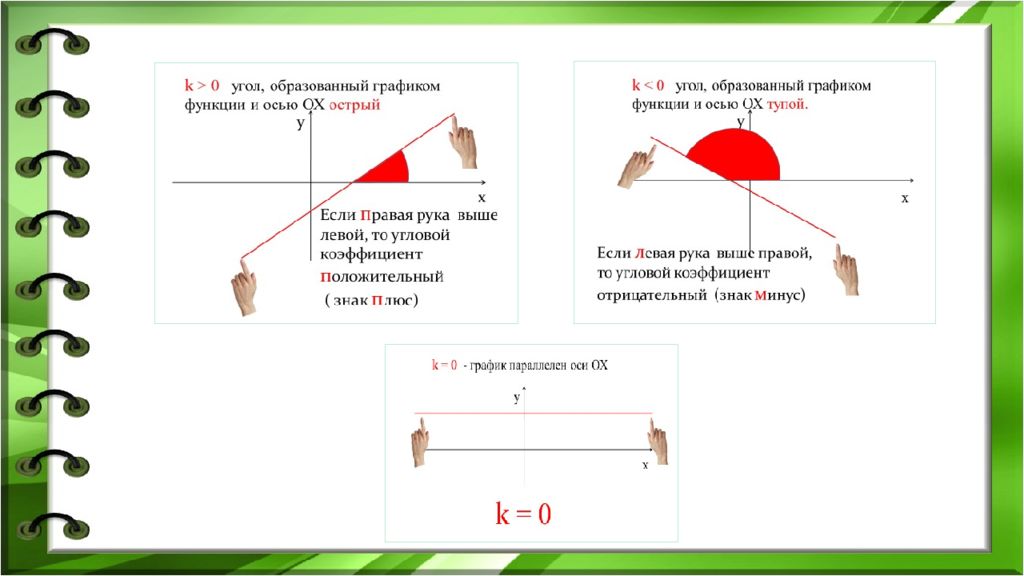
«Расскажи мне и я забуду. Покажи мне и я пойму. Позволь мне сделать самому, и я научусь» Конфуций Конфуций-древнекитайский проповедник, писатель, философ.
1 9 задание На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения. 1 2 Решение Уравнение прямой у= kx+b. Первая прямая проходит через точки (-4;1) и (-2;4), k=. Найдем b,подставив координаты одной из точек в уравнение 1=1,5·(-4)+ b, b =7. у =1,5х+7-уравнение1 прямой. 2) Вторая прямая проходит через точки (-1;0) и (2;3), k=. Найдем b,подставив координаты одной из точек в уравнение 0=1·(-1)+ b, b =1.Тогда у=х+1-уравнение2 прямой. 3)Решим систему уравнений Вычтем из 1 уравнения 2 уравнение, получим 0=0,5х+6.Отсюда х=-12.Тогда у=-11. Ответ:-11
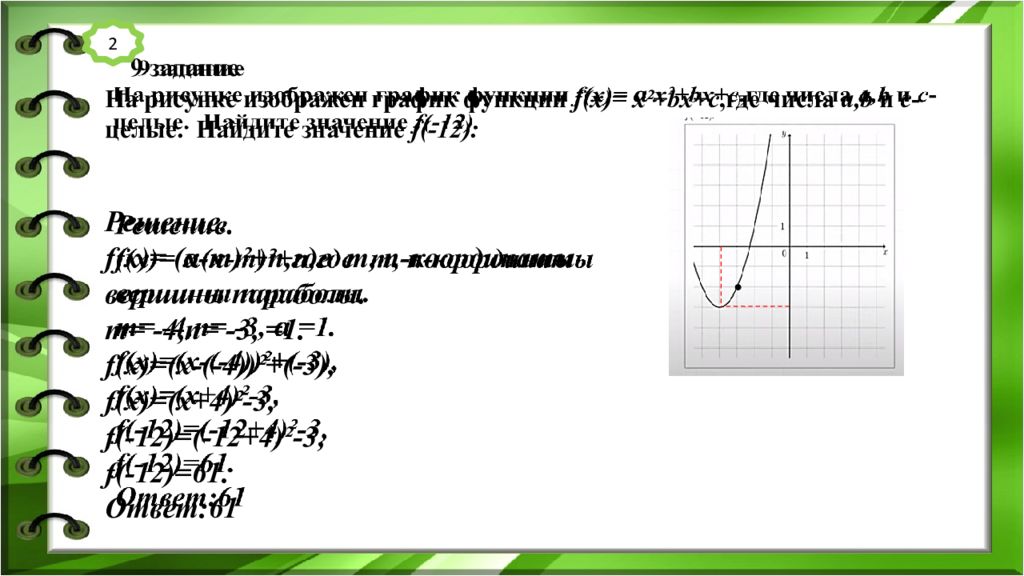
9 задание На рисунке изображен график функции f(x)= x²+bx+c,где числа a, b и c -целые. Найдите значение f(-12). Решение. f (x)= (x-m)²+n, где m, n -координаты вершины параболы. m= -4,n= -3, =1. f (x)=(x-(-4))²+(-3), f (x)=(x+4)²-3, f (-12)=(-12+4)²-3, f (-12)=61. Ответ:61 2
9 задание На рисунке изображен график функции f(x)= + bx+c, где числа, b и c -целые. Найдите значение f(4). Решение. f(x)= (x-m)²+n, где ( m, n )-координаты вершины параболы. По графику m= -2,n= 11, = -2. (Введем новую систему координат через вершину параболы, тогда график ф ункции f(x ) = проходит через точку (2;-2). Подставив в формулу f(x) =,найдем а) f(x)= - (x+2)²+11= - x²-2x+9, значит, = - 2, b=-2, c=9. Тогда f(4)= - +11= - 18+11= - 7. Ответ:- 7 3
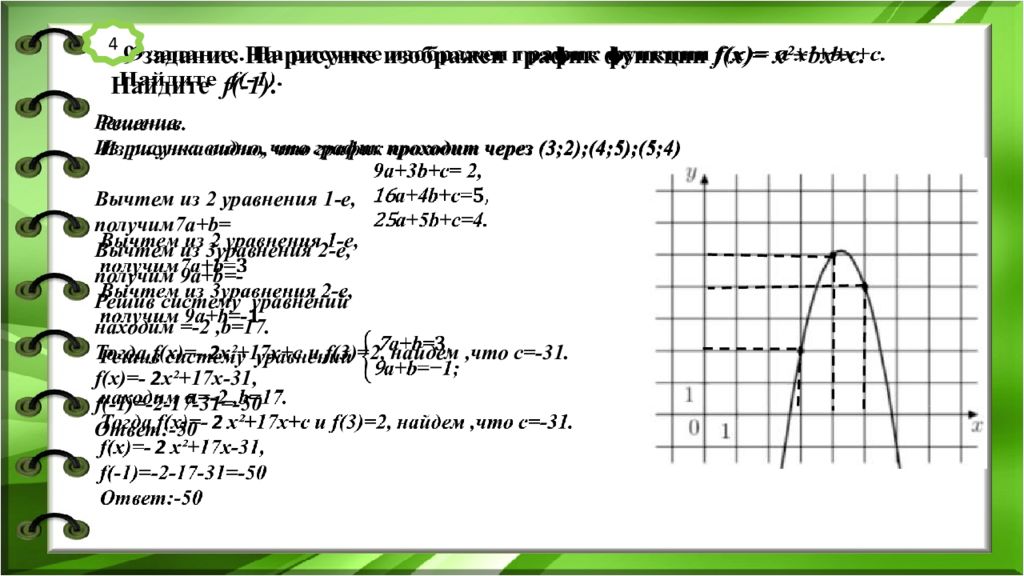
9 задание. На рисунке изображен график функции f(x)= x²+bx+c. Найдите f( -1 ). Решение. Из рисунка видно, что график проходит через (3;2);(4;5);(5;4) В ычтем из 2 уравнения 1-е, п олучим7 a + b = Вычтем из 3уравнения 2 -е, получим 9 a + b=- Решив систему уравнений находим =-2, b =17. Тогда f(x )= - 2 x²+ 17 x+c и f( 3 ) = 2, найдем,что с=-31. f(x)= - 2 x²+ 17 x -31, f( -1 ) =-2-17-31=-50 Ответ:-50 4
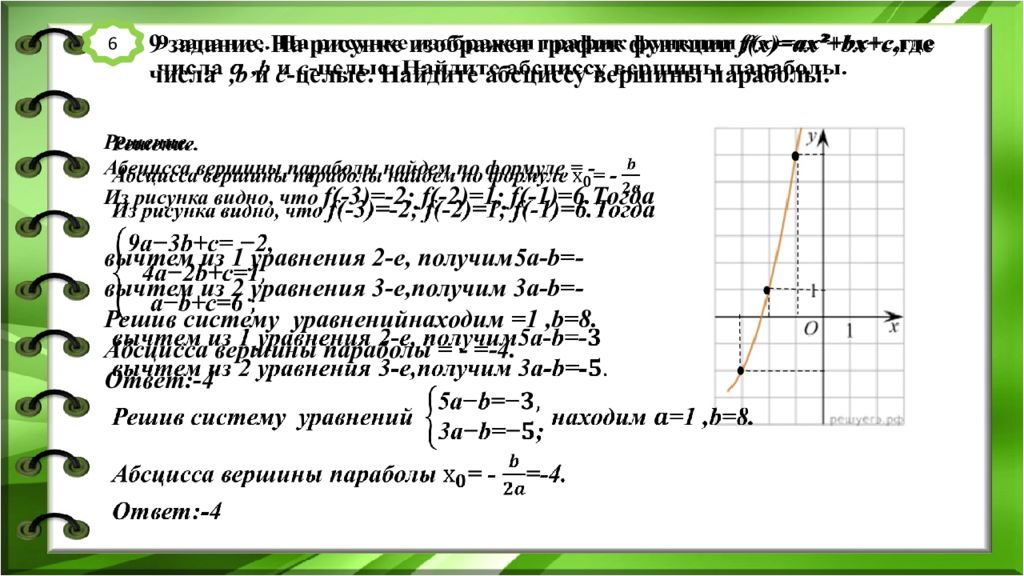
9 задание. На рисунке изображен график функции f(x)= ах ² + bx+c,где числа, b и c -целые. Найдите абсциссу вершины параболы. Решение. Абсцисса вершины параболы найдем по формуле = - Из рисунка видно, что f ( -3 ) =-2; f ( -2 ) =1; f( -1 ) =6.Тогда вычтем из 1 уравнения 2-е, получим 5a-b=- вычтем из 2 уравнения 3-е,получим 3 a-b=- Решив систему уравнений находим =1, b =8. Абсцисса вершины параболы = - =-4. Ответ:-4 6
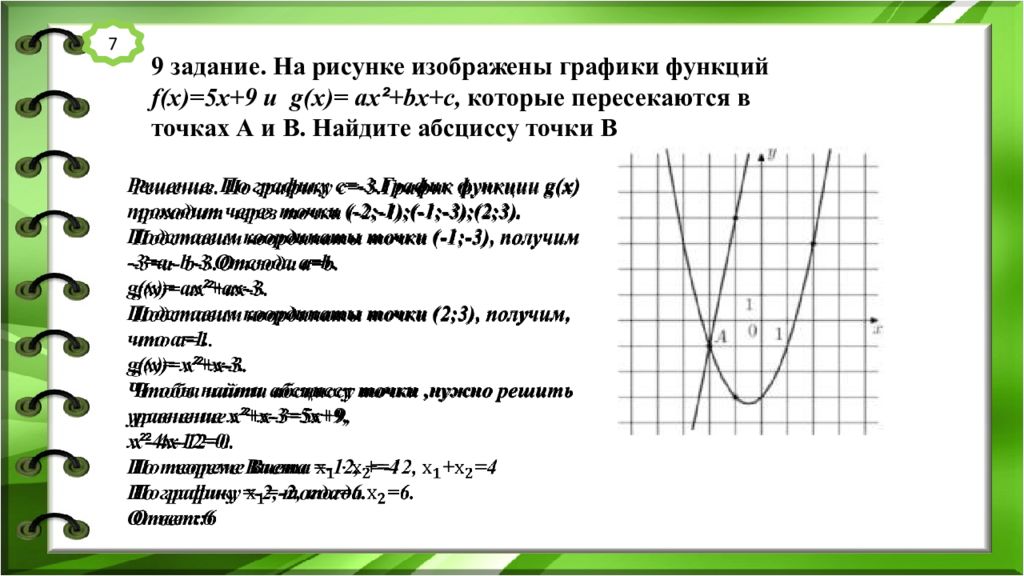
7 9 задание. На рисунке изображены графики функций f(x )= 5х+9 и g(x)= ах ² + bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки B Решение. По графику с=-3.График функции g(x ) проходит через точки (-2;-1);(-1;-3);(2;3). Подставим координаты точки (-1;-3), получим -3=а- b -3.Отсюда а= b. g(x)= ах ² + а x -3. Подставим координаты точки (2;3 ), получим, что а=1. g(x)= х ² +x -3. Чтобы найти абсциссу точки,нужно решить уравнение х ² +x -3=5х+9, х ² -4 x -12=0. По теореме Виета =-12, + =4 По графику =-2, тогда =6. Ответ:6
Решение. f(x )= ( x-m)²+n, где m, n -координаты вершины параболы. m =- 3,n=3, =1. f(x)=(x- (- 3 ))²+3 f(x)=( x+ 3) ² +3, f(x )= х ²+ 6х+12, так как f(x )= 0. то х ² +6х+12=0 D=6²-4·1·12= -12. Ответ:-12 Решите 9 задание На рисунке изображен график функции f(x)= x²+bx+c,где числа, b и c -целые. Найдите значение дискриминанта уравнения f(x)= 0. 8
Решение. |bx+c| =0 в точке излома. Значит, bx+c =0 при х=2. Ответ:2 9 9 задание На рисунке изображен график функции вида = x+|bx+c|+d, где числа, b, c и d -целые. Найдите корень уравнения bx+c =0
9 задание. На рисунке изображён график функции вида f(x )= ax + | bx + c| + d, где числа a, b, c и d — целые. Найдите корень уравнения ax + d=0. Решение. | bx + c |=0 в точке излома при х=1, Если х<1,то f(x)= ax - bx - c + d=(а-b)х+ d-с, где (а-b)-угловой коэффициент, (d-с)-ордината точки пересечения прямой с осью Ох. По графику а-b=-4; d-с=5. Если х>1,то f(x)= ax + bx + c +d=( а+b ) х+с + d, где а+b-угловой коэффициент, по графику а+b =2. Продолжив прямую до пересечения с осью Оу, получим, что с+ d =-1. Решив эти системы получим,что a =-1;b=3;c=-3;d=2. Подставив найденные значения в уравнение ax +d=0, получим -x + 2=0, х =2. Ответ:2 10 5 -1
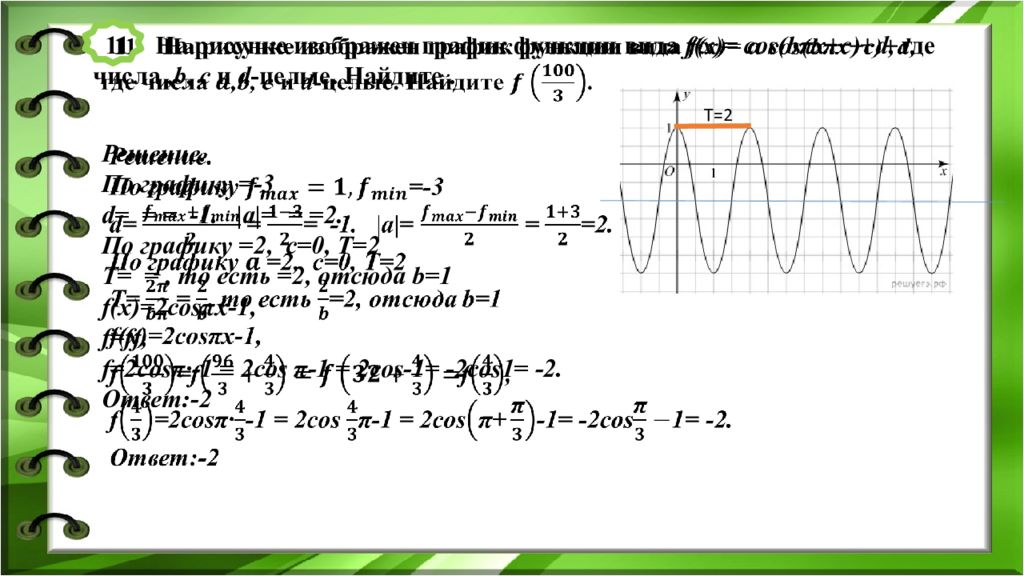
11 На рисунке изображен график функции вида f(x )= cos(b π x+c )+d, где числа, b, c и d -целые. Найдите. Решение. По графику =-3 d = = = -1. |a|= = =2. По графику =2, c=0, T=2 T= =, то есть =2, отсюда b=1 f (x)=2cos π x-1, f =f f, f =2cos π· -1 = 2cos π -1 = 2cos -1= -2cos 1= -2. Ответ:-2 Т=2
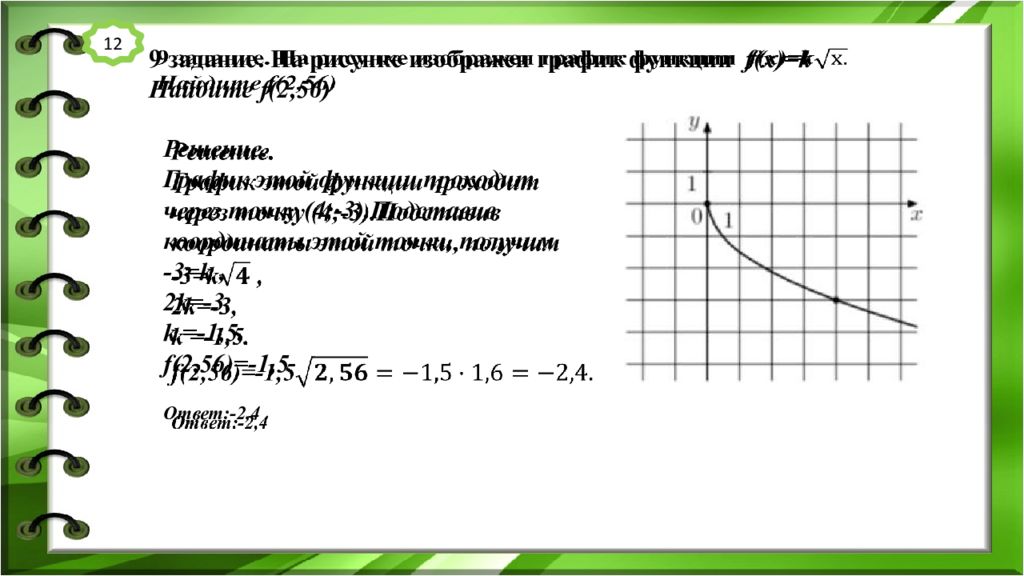
9 задание. На рисунке изображен график функции f(x)=k Найдите f(2,56) Решение. График этой функции проходит через точку (4;-3).Подставив координаты этой точки, получим -3= k, 2 k =-3, k =-1,5. f(2,56 ) =-1,5 Ответ:-2,4 12
9 задание. На рисунке изображен график функции f(x)= +a. Найдите f (0,25) Решение. График функции имеет горизонтальную асимптоту y =-2, значит, а=-2. ( График функции f(x)= + a получается сдвигом графика функции f(x )= вдоль оси Оу на величину |а| вверх, если а >0 и вниз если a<0 ) По графику а= -2 и проходит через точку (3;-3). -3= -2 отсюда k=-3.Значит, f(x)= -2, f( 0,25 )= -2= -14. Ответ:- 14 13
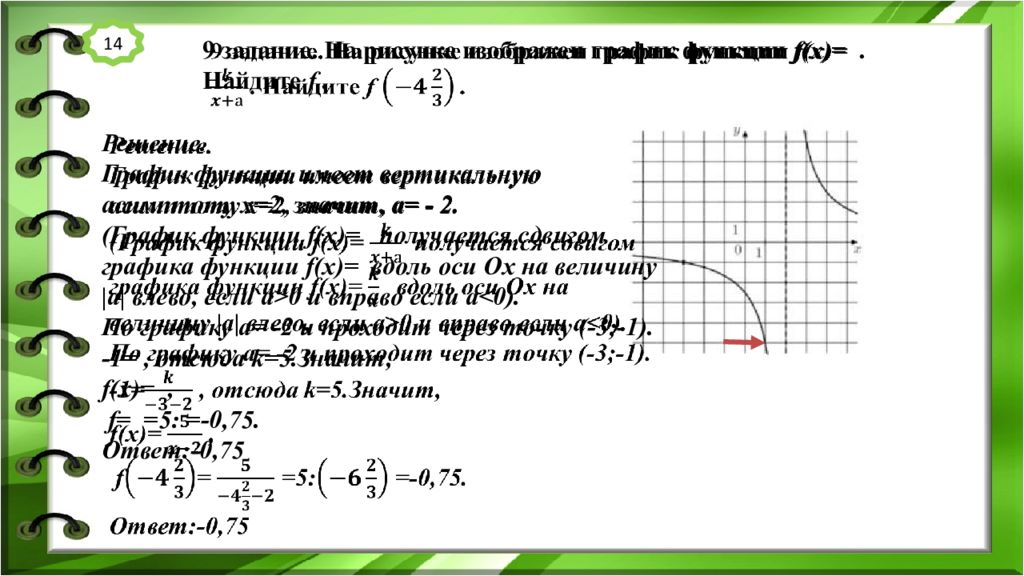
14 9 задание. На рисунке изображен график функции f(x)=. Найдите f. Решение. График функции имеет вертикальную асимптоту x=2, значит, а= - 2. (График функции f(x)= получается сдвигом графика функции f(x)= вдоль оси Ох на величину |а| влево, если а >0 и вправо если a<0 ). По графику а= -2 и проходит через точку (-3;-1). -1=, отсюда k= 5.Значит, f(x)=, f = =5: =-0,75. Ответ:-0,75
9 задание. На рисунке изображён график функции вида f(x )= +c, где числа a, b и c — целые. Найдите f(13). Решение. График функции имеет горизонтальную асимптоту y=2, значит, c=2. График функции имеет вертикальную асимптоту x=3, значит, b= - 3. По графику f(2)=1, тогда +2=1, отсюда a=1. Таким образом, f(x)= +2 Найдём f(13 )= +2=2,1. f(13)=2,1. Ответ:2,1 15
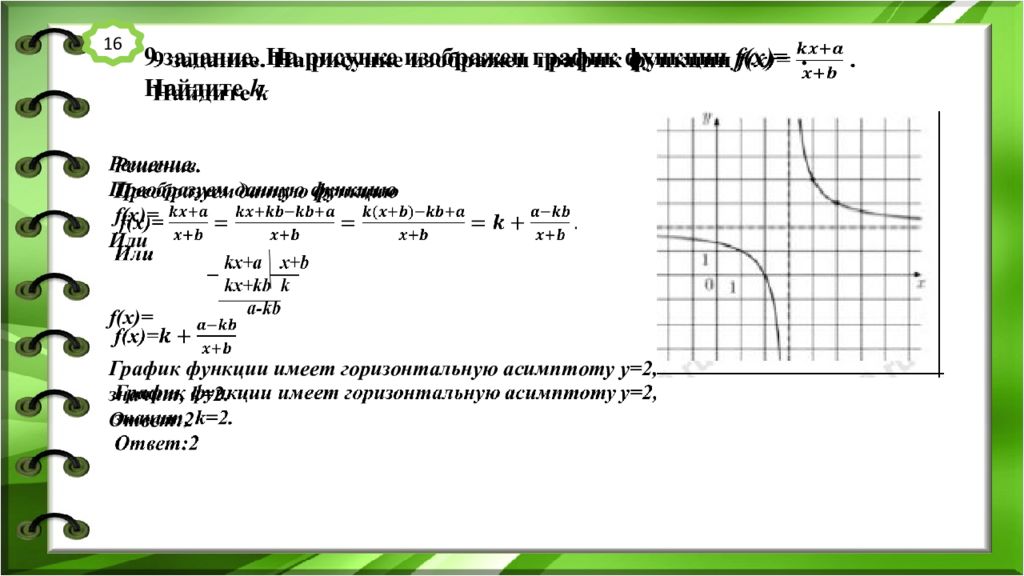
9 задание. На рисунке изображен график функции f(x)=. Найдите k Решение. Преобразуем данную функцию f(x)= Или f(x ) = График функции имеет горизонтальную асимптоту y=2, значит, k =2. Ответ:2 16
9 задание. На рисунке изображен график функции f(x)=. Найдите a Решение. Преобразуем данную функцию f(x)= Или График функции имеет горизонтальную асимптоту y=2, значит, k =2. График функции имеет вертикальную асимптоту x=3, значит, b= - 3. По графику f( 5 )= 3, тогда 3=, отсюда а=-4. Ответ:-4 17 f(x) =
18 9 задание. На рисунке изображен график функции f(x )=b+ x. Найдите значение х при котором f(x )=2. Решение. График функции f(x)= b+ x получается сдвигом графика функции f(x)= x. вдоль оси Оу на величину |b| вверх, если b > 0 и вниз если b <0. По графику b = -2 и проходит через точку (3;- 1 ). -1= - 2 +, отсюда а =3.Значит, f(x)= - 2 x, найдем х при котором f(x )= 2. 2=-2 x, x =4, значит, х=81. Ответ:81
19 9 задание. На рисунке изображен график функции f(x )=. Найдите значение х при котором f (-5 ). Решение. График функции f(x)= получается сдвигом графика функции f(x)= вдоль оси Ох на величину | b | влево, если b>0 и вправо если b<0. По графику b = - -1 и проходит через точку ( 3 ; 2 ). отсюда а =. Значит, f ( -5 )= = = Ответ:0,125
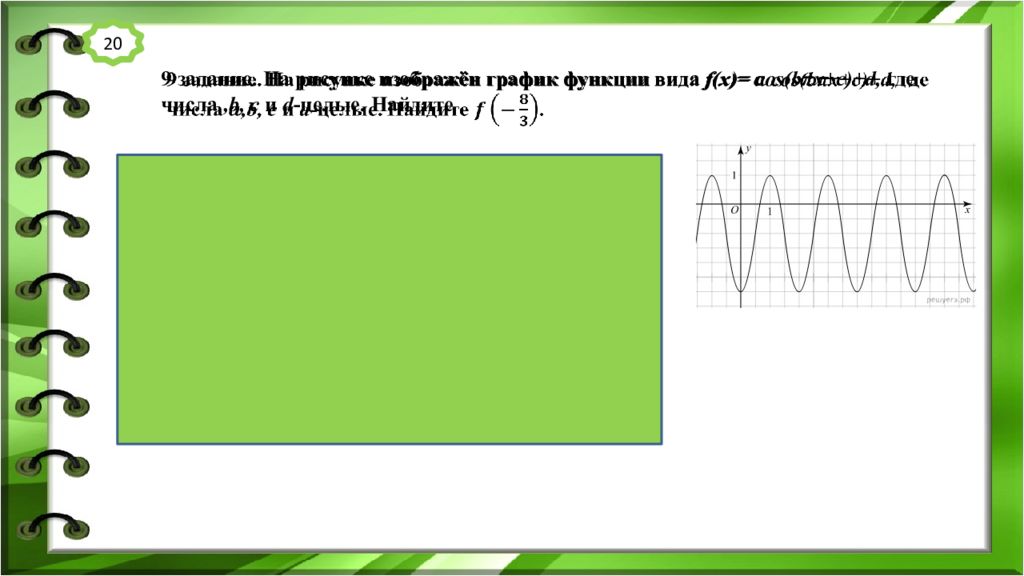
9 задание. На рисунке изображён график функции вида f(x)= cos(b π x+c )+d, где числа, b, c и d -целые. Найдите. Решение. По графику =-3 d= = = -1. |a|= = =2. По графику = - 2, c=0, T=2 T= =, то есть =2, отсюда b=1 f(x )= - 2cos π x-1, f =f f, f = - 2cos π· -1 = - 2cos π -1 = - 2cos -1= 2cos 1= 0. Ответ:0 20
1.ПРОЕКТ. Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2022 года по МАТЕМАТИКЕ. Профильный уровень. ФИПИ 2.Статград. Новое ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами. 3.Образовательный портал «СДАМ ГИА» Математика профильного уровня.
