задание 7. Применение производной к исследованию функций. Готовимся к ЕГЭ
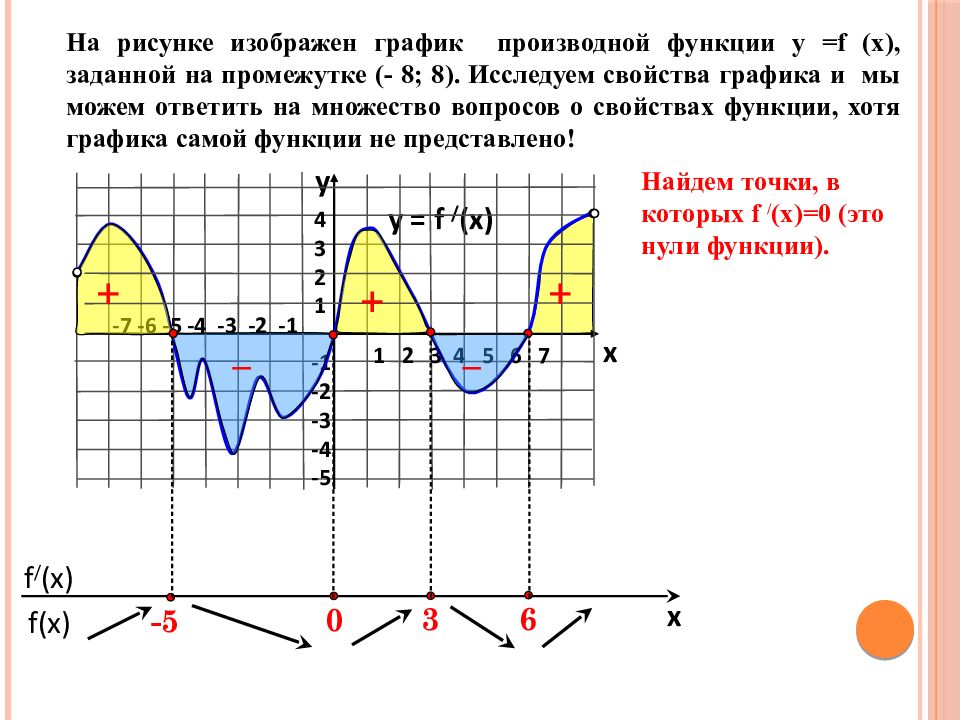
f(x) f / (x) x На рисунке изображен график производной функции у = f (x), заданной на промежутке (- 8; 8). Исследуем свойства графика и мы можем ответить на множество вопросов о свойствах функции, хотя графика самой функции не представлено! y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x 6 3 0 -5 Найдем точки, в которых f / (x) =0 (это нули функции). + – – + +
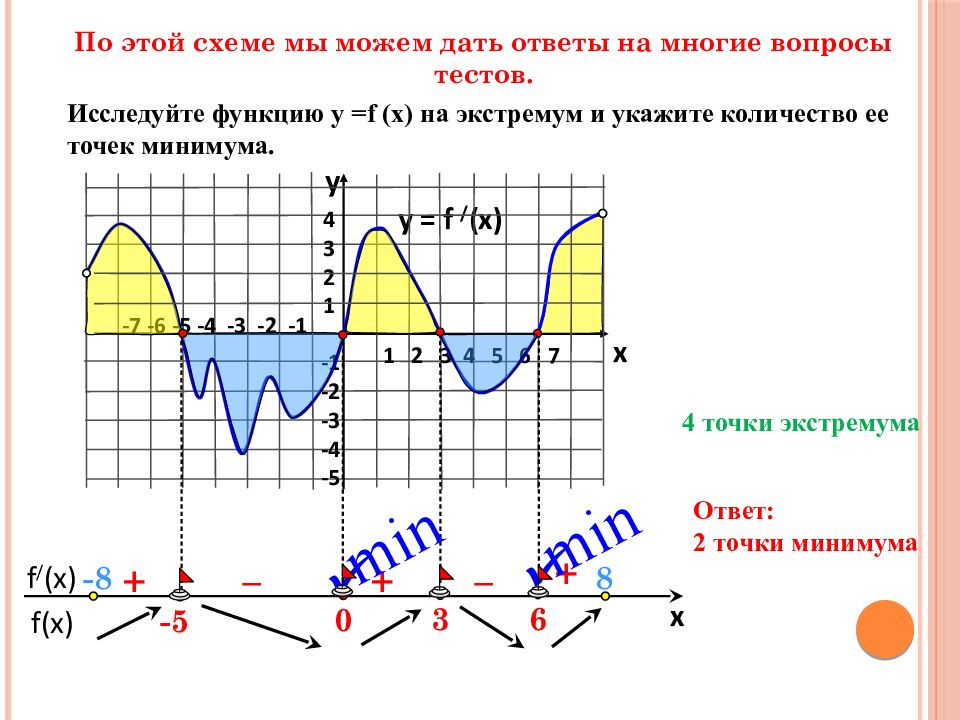
f(x) f / (x) x По этой схеме мы можем дать ответы на многие вопросы тестов. y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x 6 3 0 -5 + – – + + Исследуйте функцию у = f (x) на экстремум и укажите количество ее точек минимума. 4 точки экстремума Ответ: 2 точки минимума min min - 8 8
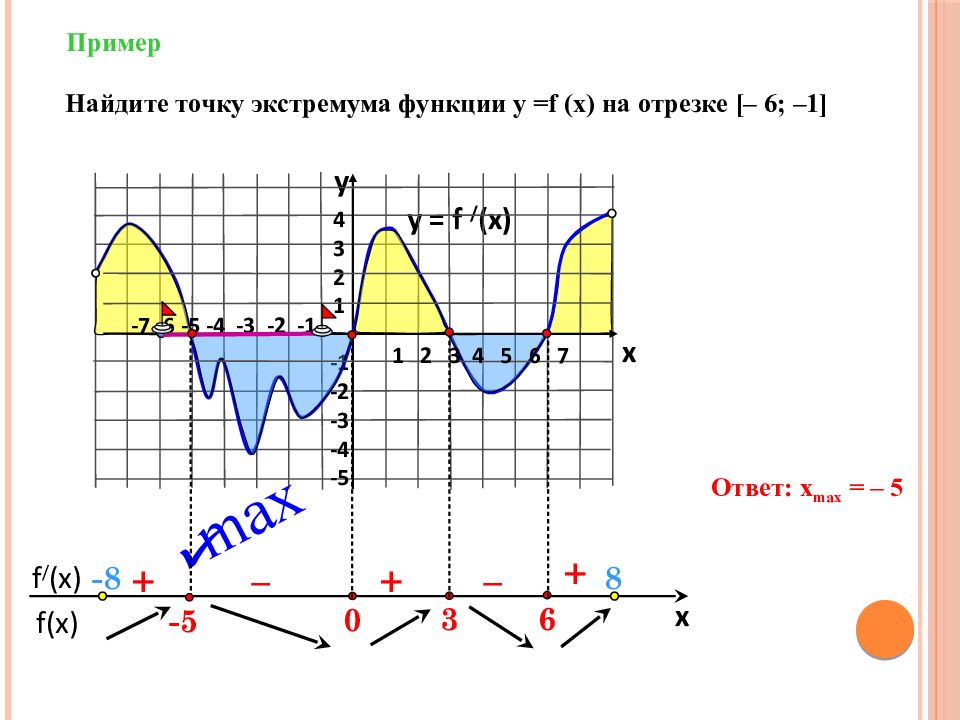
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + Найдите точку экстремума функции у = f (x) на отрезке [ – 6; –1 ] Ответ: x max = – 5 max 6 3 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 - 8 8
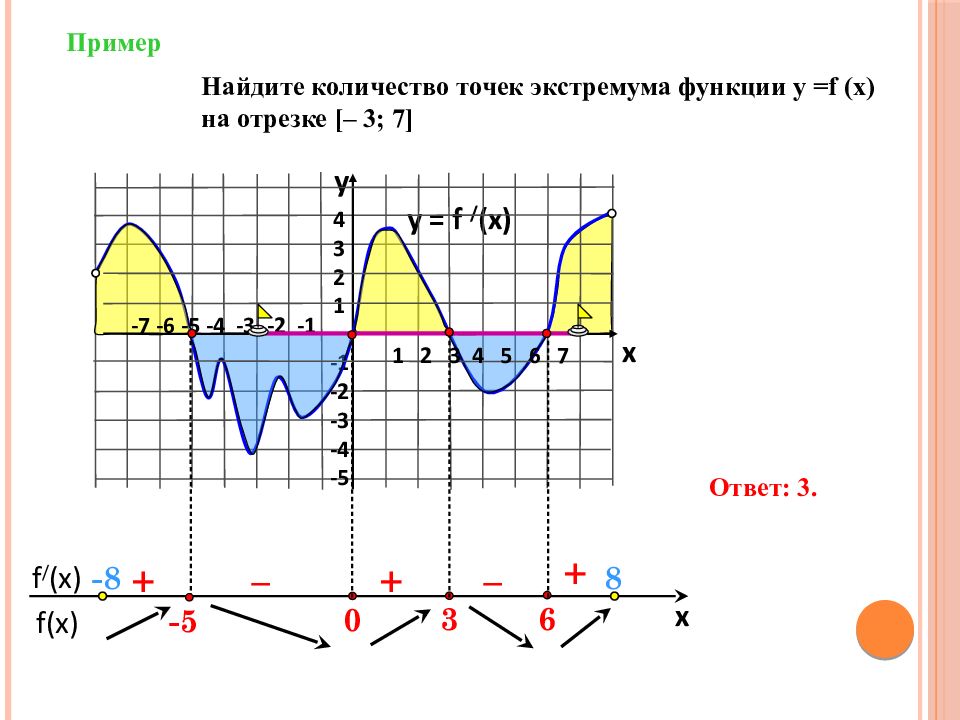
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + Найдите количество точек экстремума функции у = f (x) на отрезке [ – 3; 7 ] Ответ: 3. 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 - 8 8 6 3 0
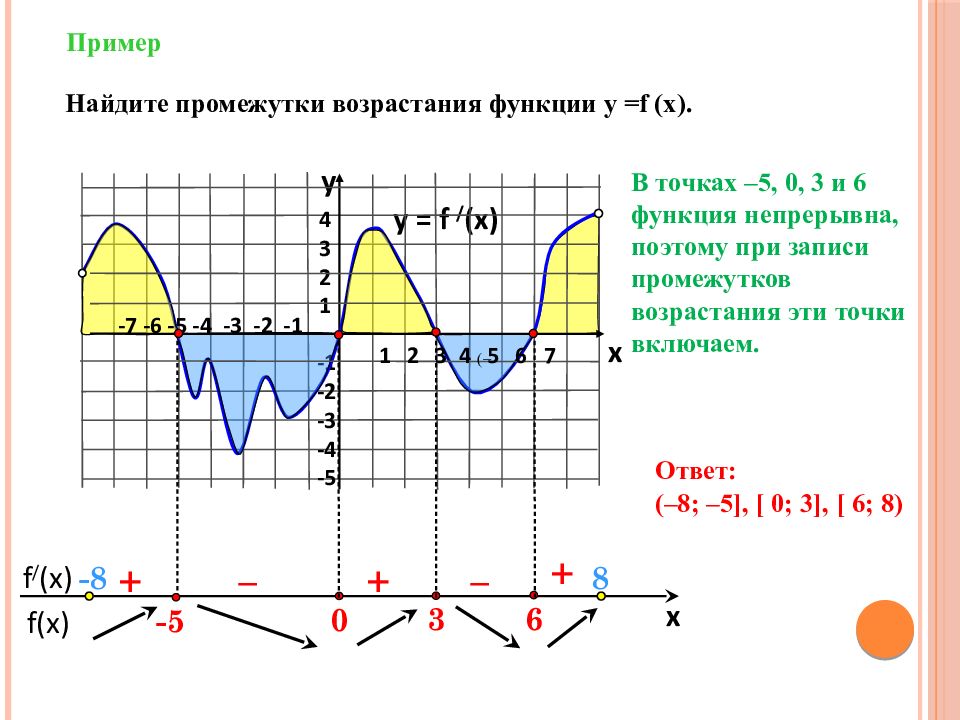
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + Найдите промежутки возрастания функции у = f (x). В точках –5, 0, 3 и 6 функция непрерывна, поэтому при записи промежутков возрастания эти точки включаем. 6 3 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 Ответ: (–8; –5 ], [ 0 ; 3], [ 6 ; 8) - 8 8
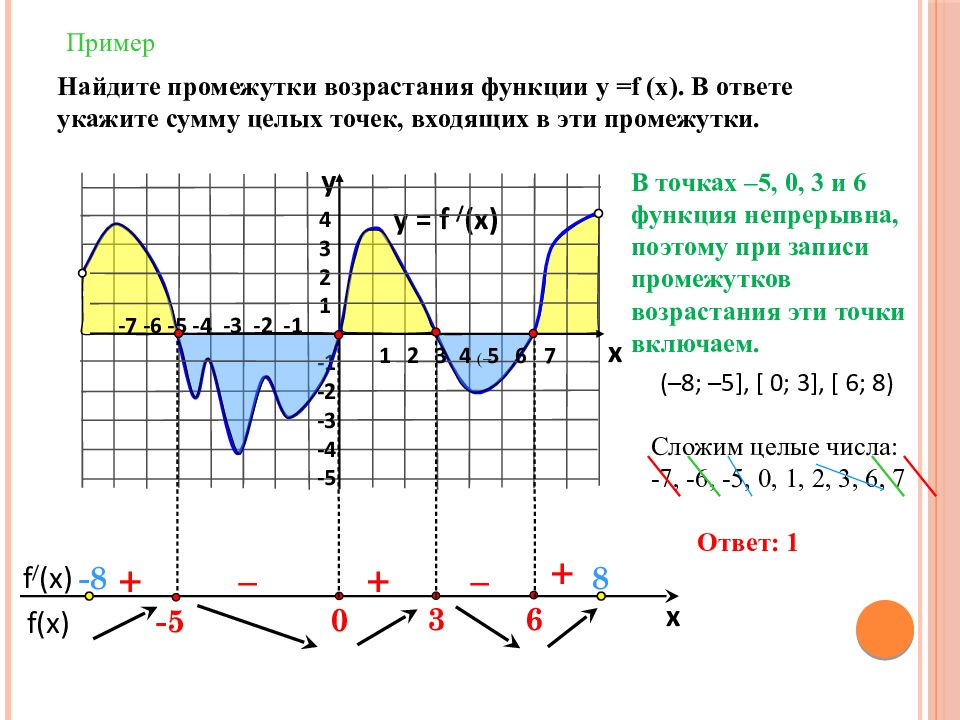
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + Найдите промежутки возрастания функции у = f (x). В ответе укажите сумму целых точек, входящих в эти промежутки. В точках –5, 0, 3 и 6 функция непрерывна, поэтому при записи промежутков возрастания эти точки включаем. 6 3 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 Сложим целые числа: -7, -6, -5, 0, 1, 2, 3, 6, 7 - 8 8 (–8; –5 ], [ 0 ; 3], [ 6 ; 8) Ответ: 1
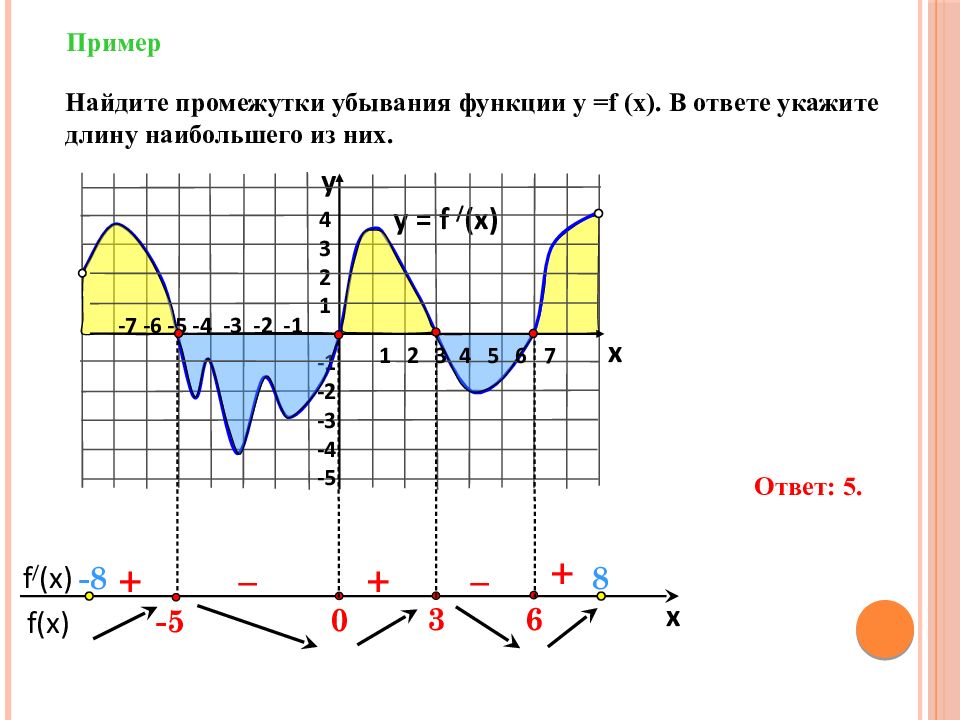
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + Найдите промежутки убывания функции у = f (x). В ответе укажите длину наибольшего из них. 6 3 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 Ответ: 5. - 8 8
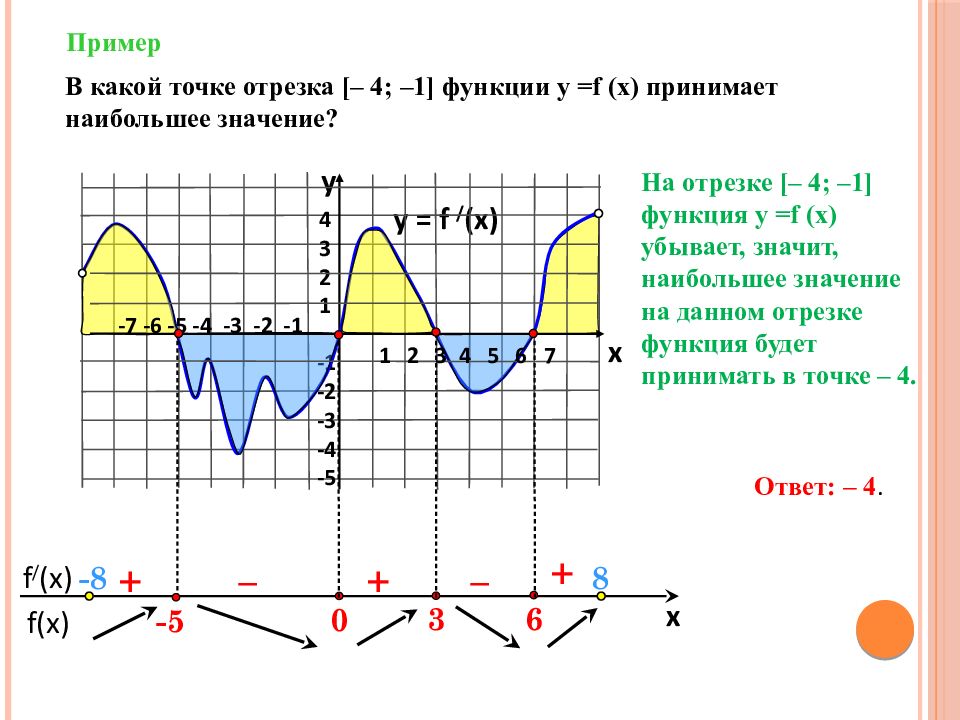
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + В какой точке отрезка [ – 4; –1 ] функции у = f (x) принимает наибольшее значение? 6 3 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 Ответ: – 4. - 8 8 На отрезке [ – 4; –1 ] функция у = f (x) убывает, значит, наибольшее значение на данном отрезке функция будет принимать в точке – 4.
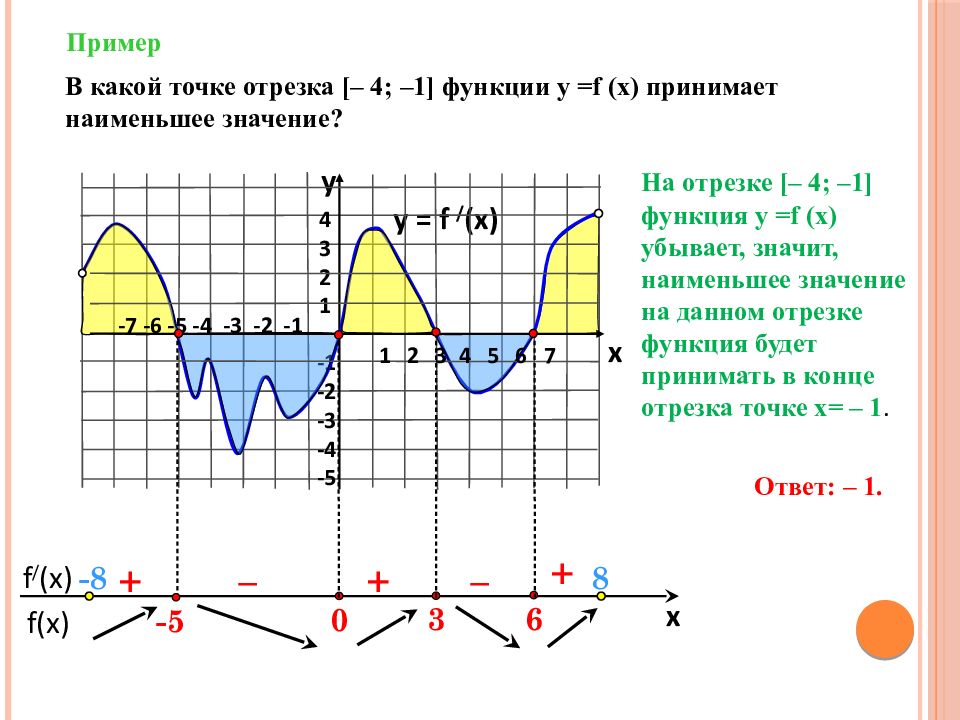
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + В какой точке отрезка [ – 4; –1 ] функции у = f (x) принимает наименьшее значение? 6 3 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 Ответ: – 1. - 8 8 На отрезке [ – 4; –1 ] функция у = f (x) убывает, значит, наименьшее значение на данном отрезке функция будет принимать в конце отрезка точке х= – 1.
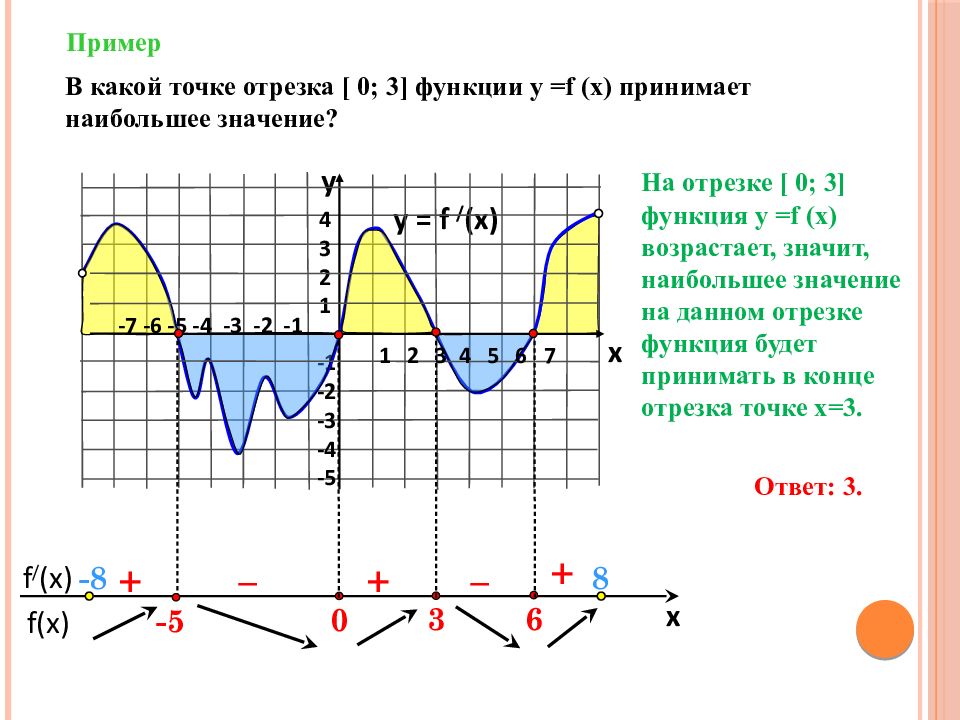
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + В какой точке отрезка [ 0; 3 ] функции у = f (x) принимает наибольшее значение? 6 3 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 Ответ: 3. - 8 8 На отрезке [ 0; 3 ] функция у = f (x) возрастает, значит, наибольшее значение на данном отрезке функция будет принимать в конце отрезка точке х=3.
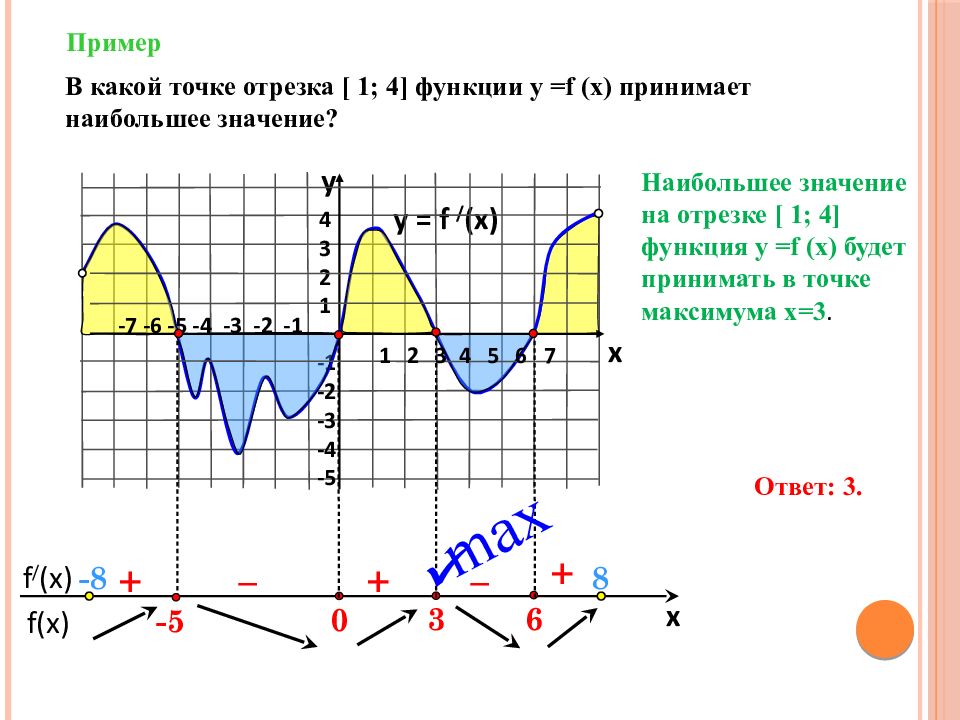
f(x) f / (x) x Пример y = f / (x) 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + В какой точке отрезка [ 1; 4 ] функции у = f (x) принимает наибольшее значение? 6 3 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -5 Ответ: 3. - 8 8 Наибольшее значение на отрезке [ 1; 4 ] функция у = f (x) будет принимать в точке максимума х=3. max
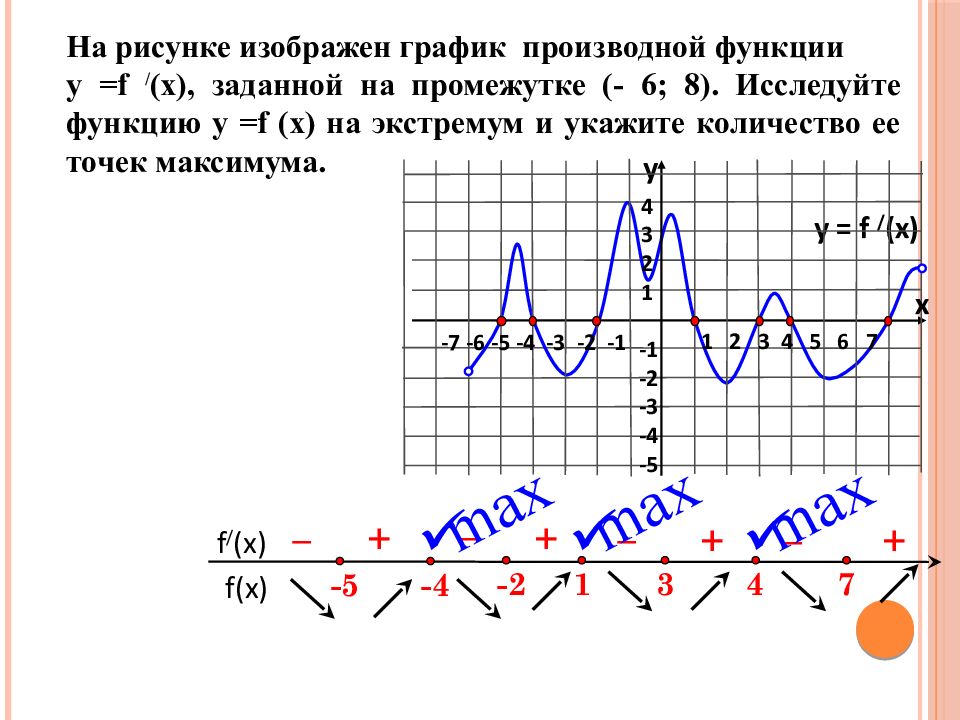
На рисунке изображен график производной функции у = f / (x), заданной на промежутке (- 6 ; 8). Исследуйте функцию у = f (x) на экстремум и укажите количество ее точек максимума. f(x) f / (x) y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x 3 1 -2 -5 -4 4 7 + – + – – – + + max max max
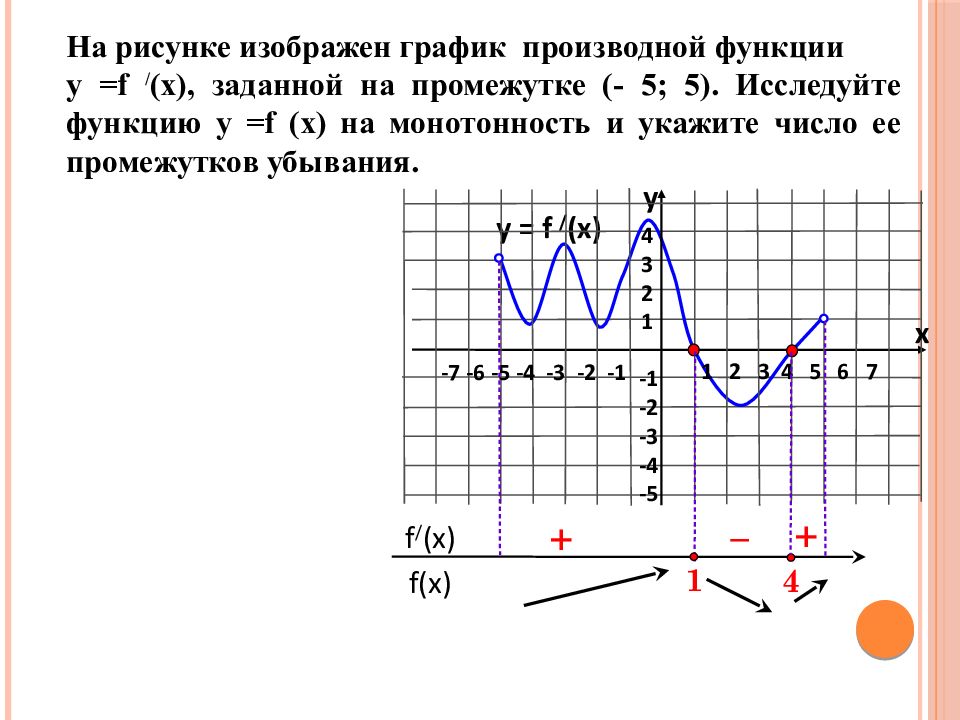
На рисунке изображен график производной функции у = f / (x), заданной на промежутке (- 5 ; 5 ). Исследуйте функцию у = f (x) на монотонность и укажите число ее промежутков убывания. f(x) f / (x) 4 + – y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x + 1
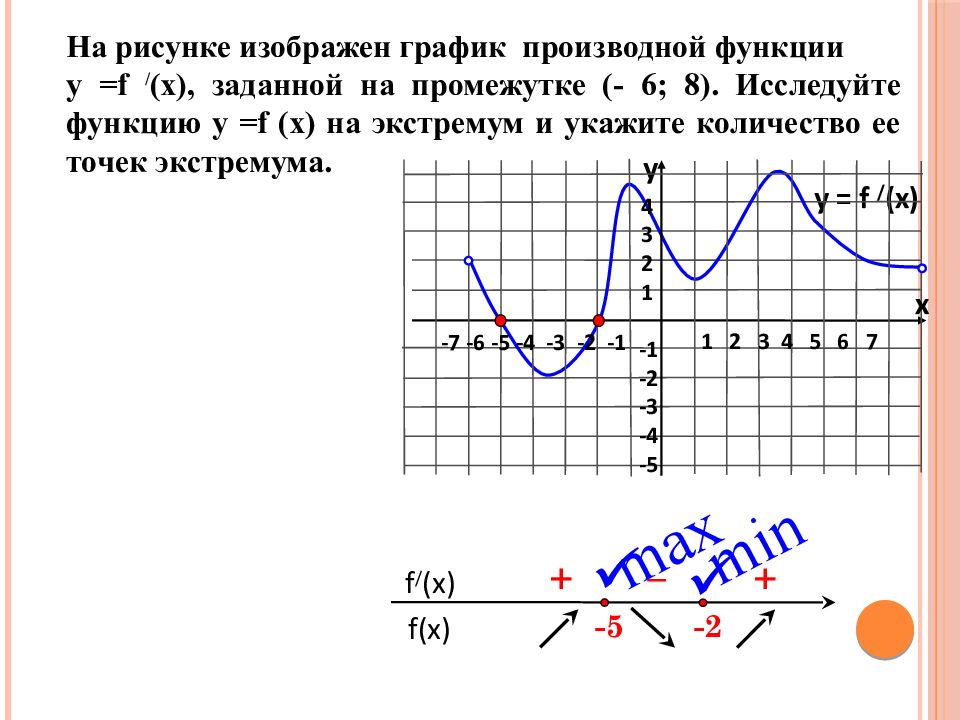
На рисунке изображен график производной функции у = f / (x), заданной на промежутке (- 6; 8). Исследуйте функцию у = f (x) на экстремум и укажите количество ее точек экстремума. f(x) f / (x) -2 + – y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x -5 + min max
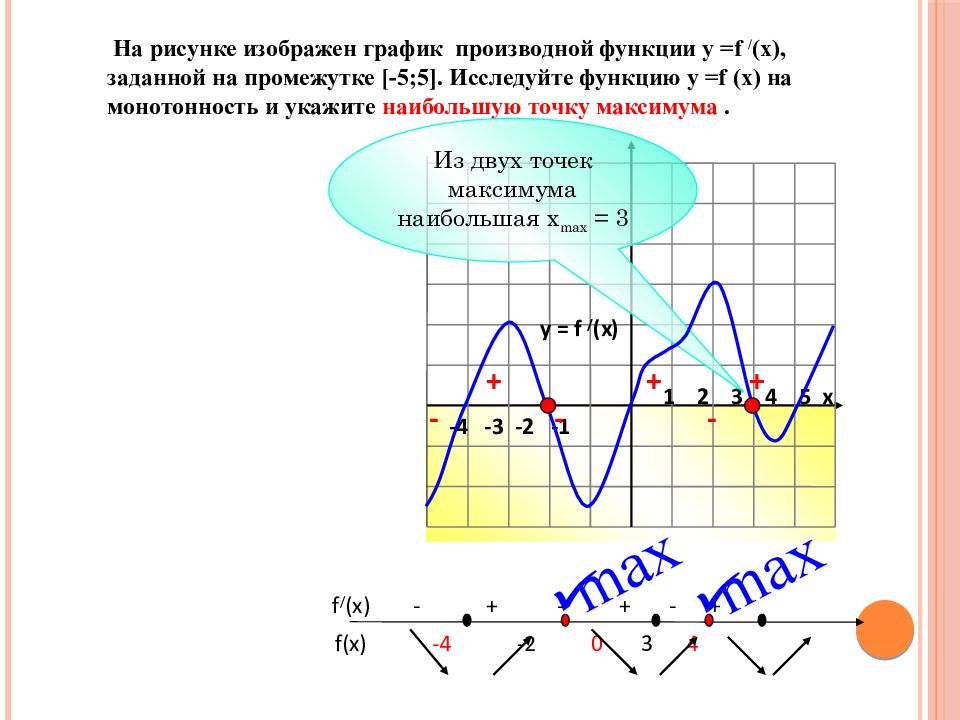
-4 -3 -2 -1 1 2 3 4 5 х На рисунке изображен график производной функции у = f / (x), заданной на промежутке [-5;5]. Исследуйте функцию у = f (x) на монотонность и укажите наибольшую точку максимума. y = f / (x) + + + - - - f / (x) - + - + - + f(x) -4 -2 0 3 4 Из двух точек максимума наибольшая х max = 3 max max
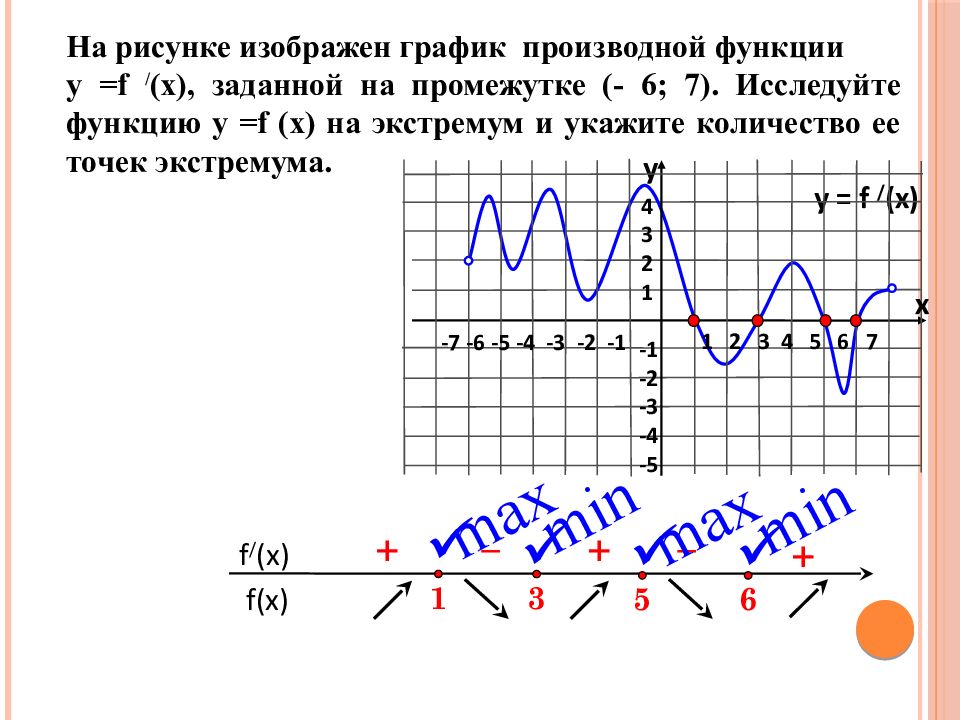
На рисунке изображен график производной функции у = f / (x), заданной на промежутке (- 6; 7). Исследуйте функцию у = f (x) на экстремум и укажите количество ее точек экстремума. f(x) f / (x) 3 + – y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x 1 + 5 6 – + min max max min
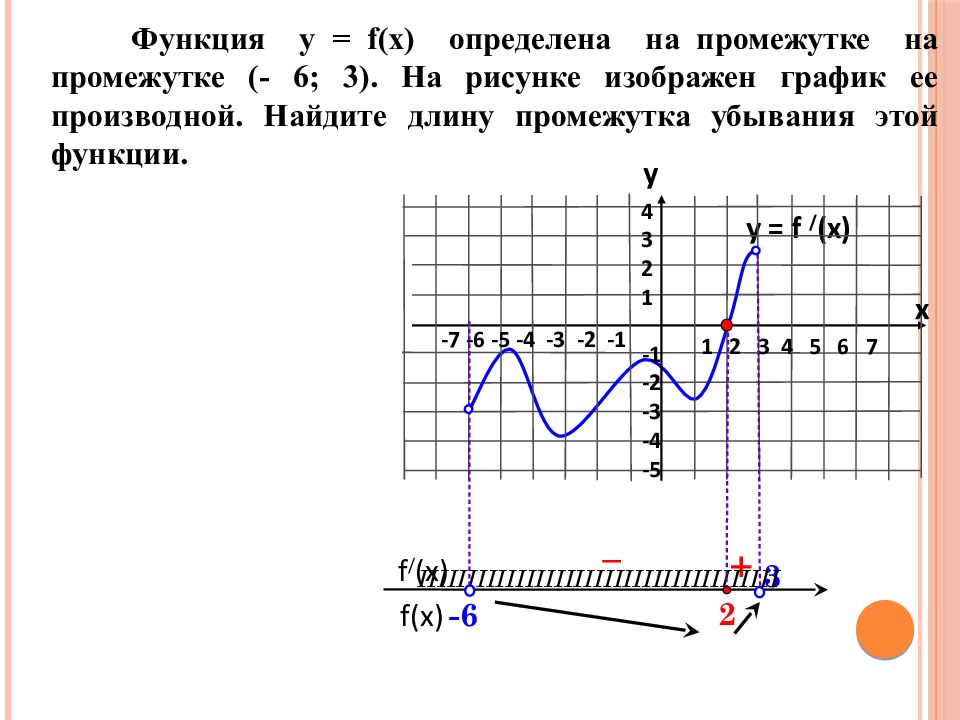
y = f / (x) f(x) f / (x) Функция у = f(x) определена на промежутке на промежутке (- 6 ; 3 ). На рисунке изображен график ее производной. Найдите длину промежутка убывания этой функции. + – 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 3 IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII y x -6 2
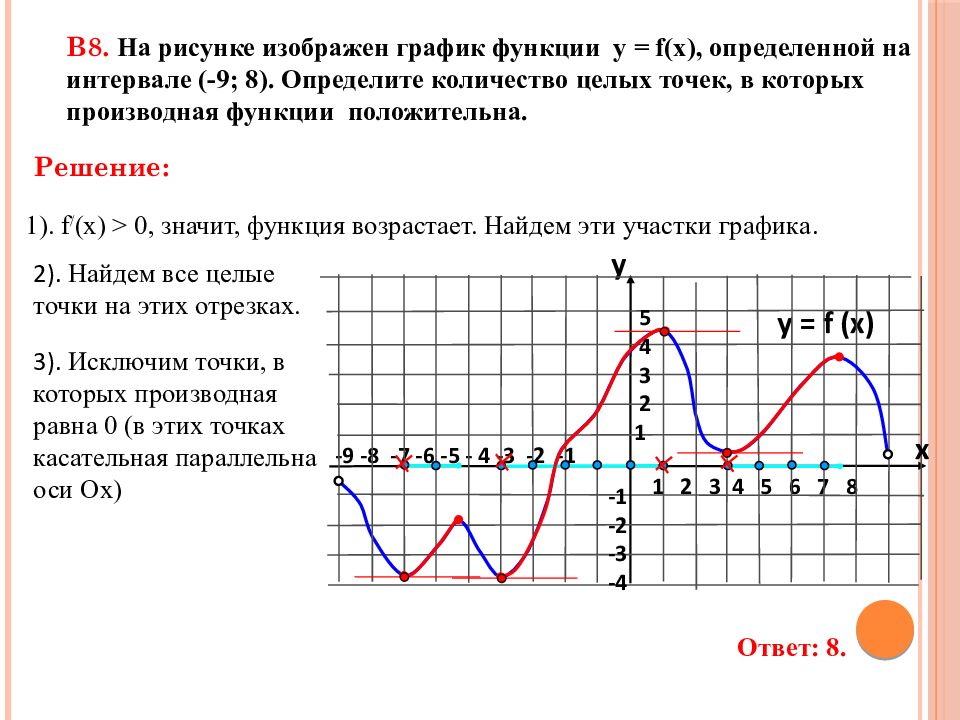
3). Исключим точки, в которых производная равна 0 (в этих точках касательная параллельна оси Ох) -9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 В8. На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции положительна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1). f / (x) > 0, значит, функция возрастает. Найдем эти участки графика. 2). Найдем все целые точки на этих отрезках. Ответ: 8. Решение:
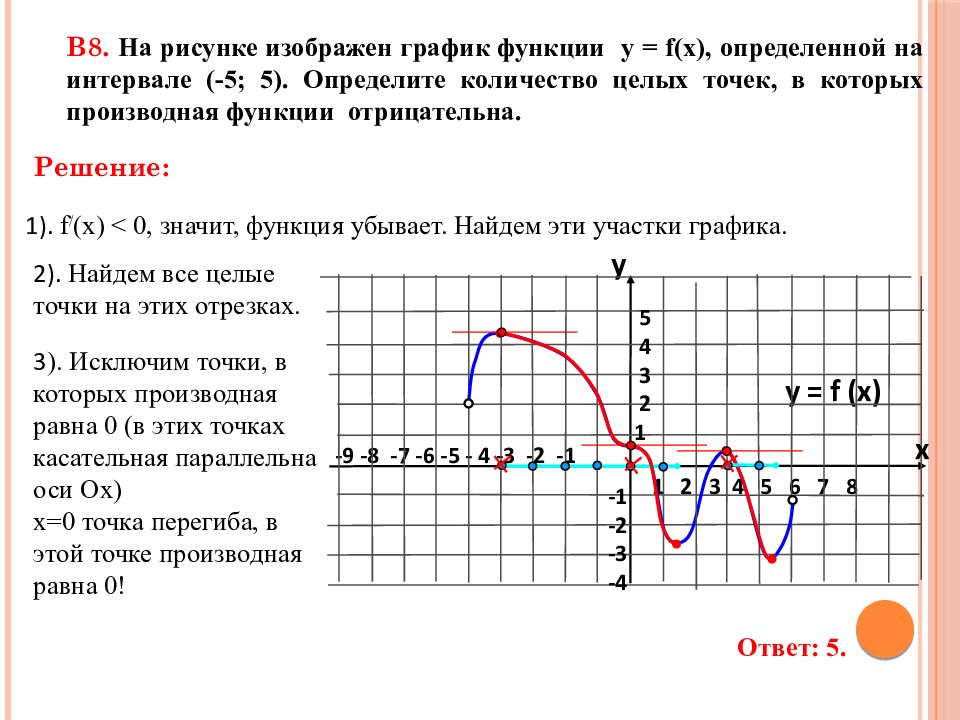
3 ). Исключим точки, в которых производная равна 0 (в этих точках касательная параллельна оси Ох) х=0 точка перегиба, в этой точке производная равна 0! -9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 В8. На рисунке изображен график функции у = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции отрицательна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1). f / (x) < 0, значит, функция убывает. Найдем эти участки графика. 2). Найдем все целые точки на этих отрезках. Ответ: 5. Решение:
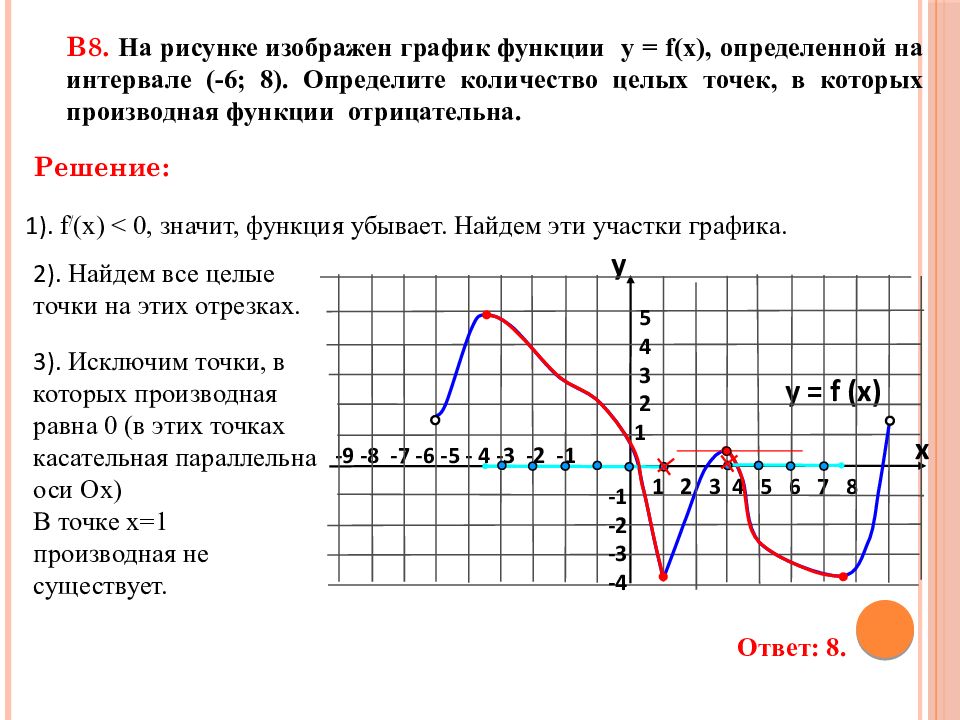
3). Исключим точки, в которых производная равна 0 (в этих точках касательная параллельна оси Ох) В точке х=1 производная не существует. -9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 В8. На рисунке изображен график функции у = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции отрицательна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1). f / (x) < 0, значит, функция убывает. Найдем эти участки графика. 2). Найдем все целые точки на этих отрезках. Ответ: 8. Решение:
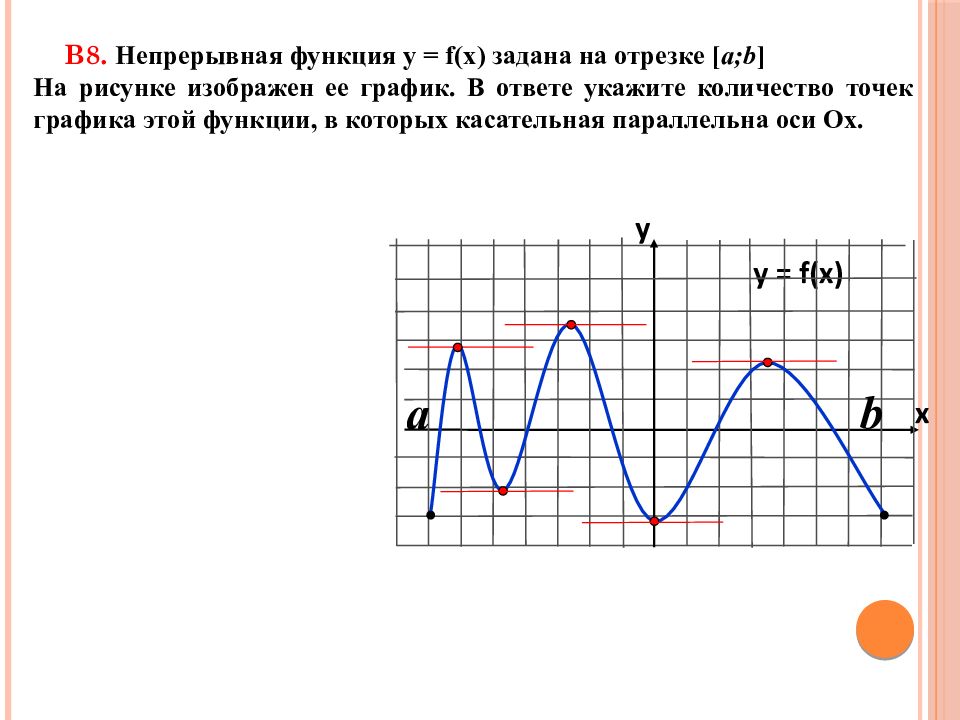
В8. Непрерывная функция у = f(x) задана на отрезке [ a;b ] На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. y = f(x) y x a b
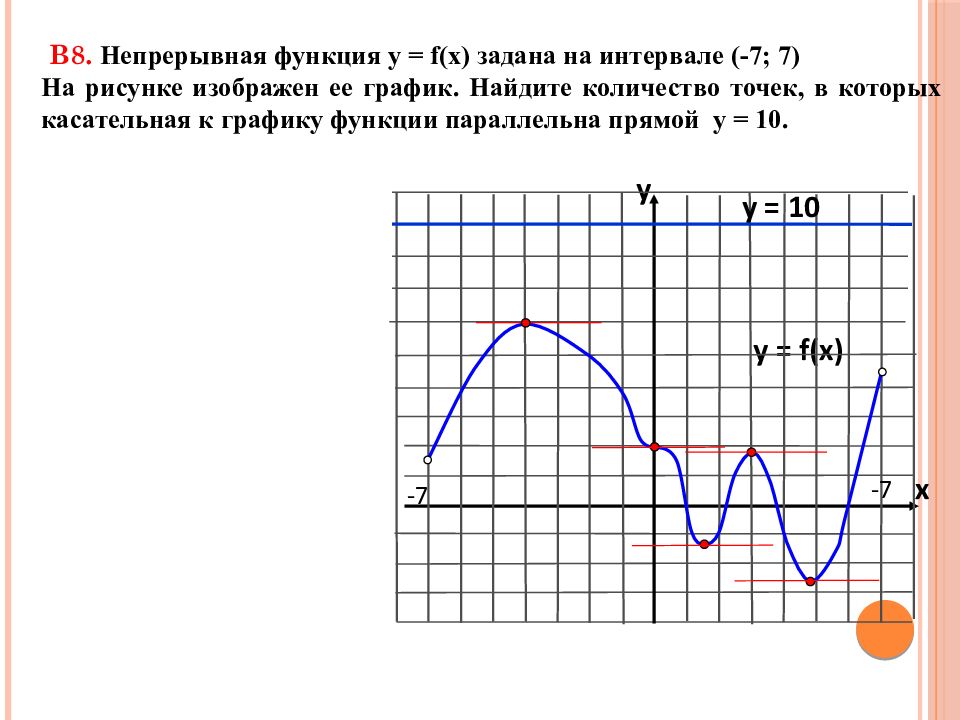
В8. Непрерывная функция у = f(x) задана на интервале (-7; 7) На рисунке изображен ее график. Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 10. y = f(x) y x -7 -7 y = 10
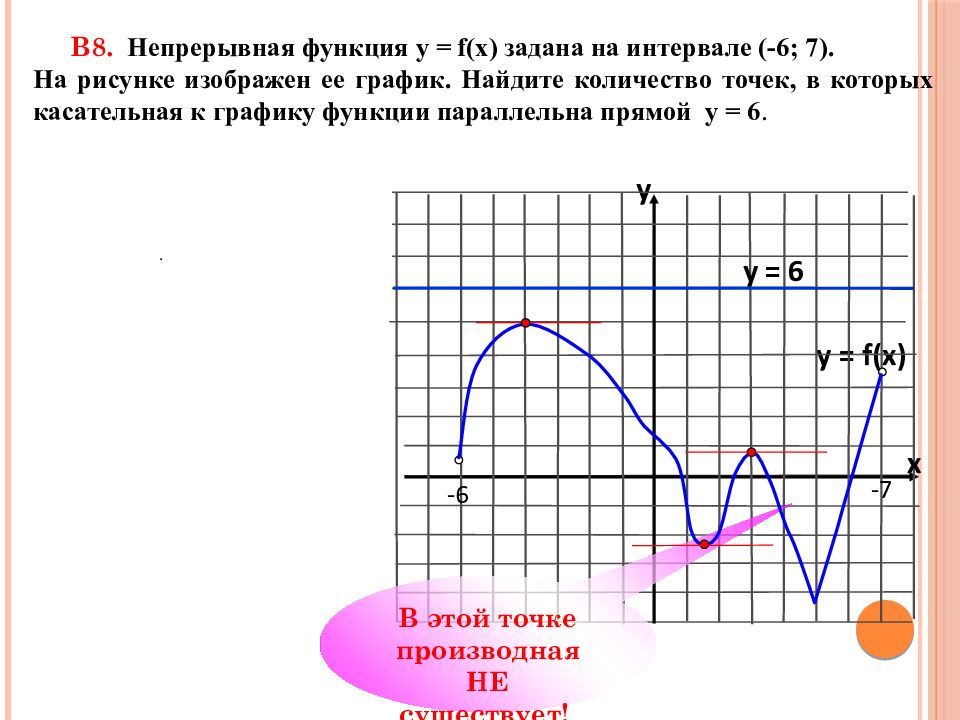
В8. Непрерывная функция у = f(x) задана на интервале (-6; 7). На рисунке изображен ее график. Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6. y = f(x) y x - 6 -7 y = 6 . В этой точке производная НЕ существует!
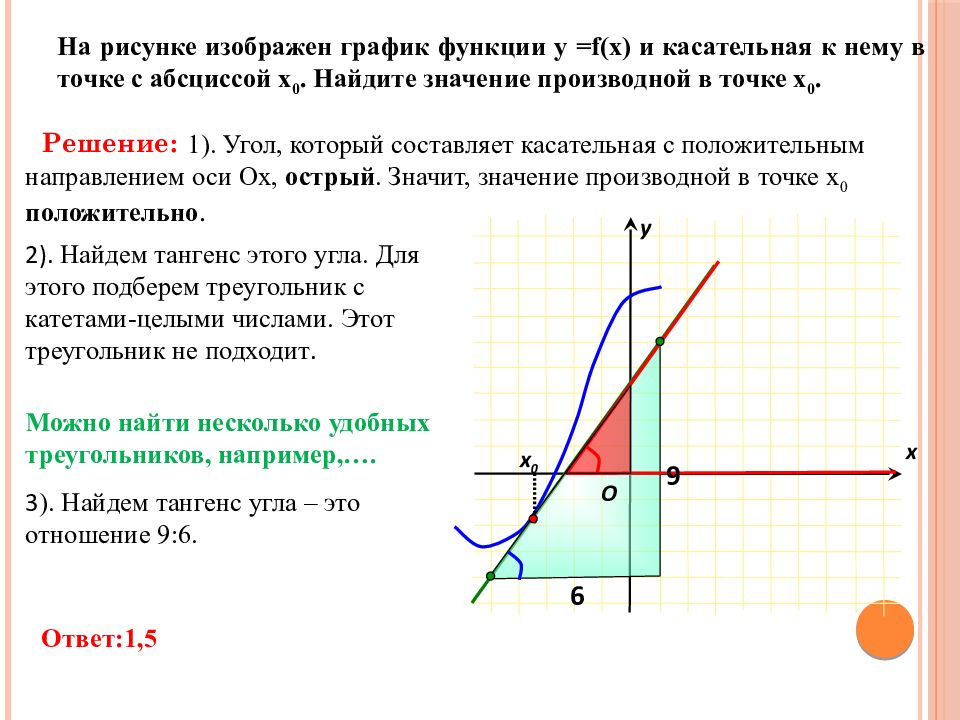
На рисунке изображен график функции у = f(x) и касательная к нему в точке с абсциссой х 0. Найдите значение производной в точке х 0. х х 0 у 1). Угол, который составляет касательная с положительным направлением оси Ох, острый. Значит, значение производной в точке х 0 положительно. Решение: 2). Найдем тангенс этого угла. Для этого подберем треугольник с катетами-целыми числами. Этот треугольник не подходит. Можно найти несколько удобных треугольников, например,…. 3 ). Найдем тангенс угла – это отношение 9:6. Ответ:1,5 O 9 6
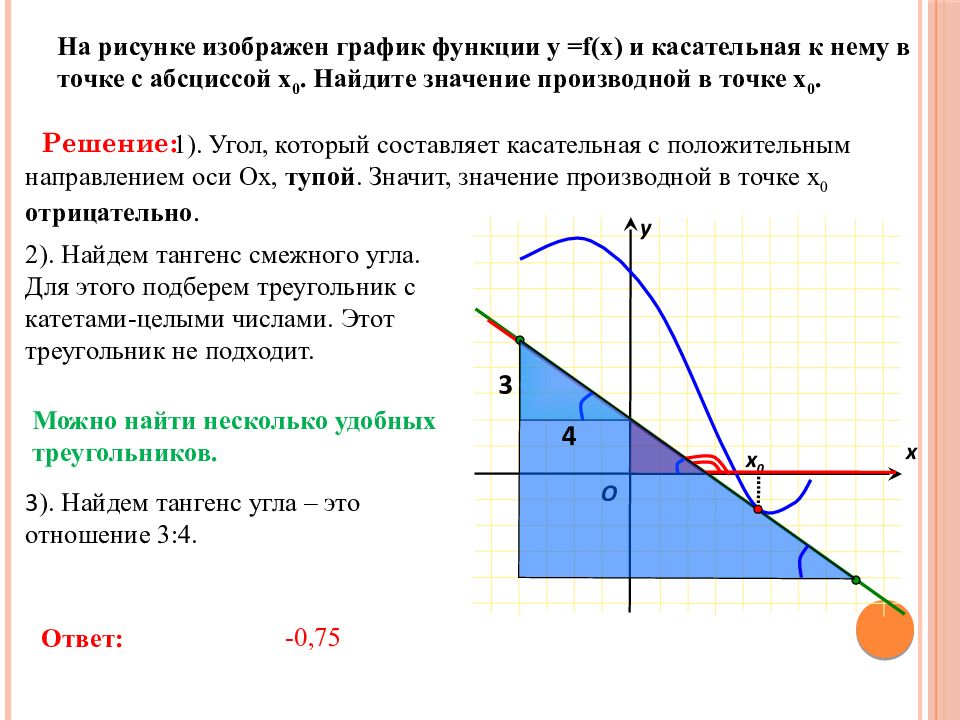
На рисунке изображен график функции у = f(x) и касательная к нему в точке с абсциссой х 0. Найдите значение производной в точке х 0. х х 0 у O 1). Угол, который составляет касательная с положительным направлением оси Ох, тупой. Значит, значение производной в точке х 0 отрицательно. Решение: 2). Найдем тангенс смежного угла. Для этого подберем треугольник с катетами-целыми числами. Этот треугольник не подходит. Можно найти несколько удобных треугольников. 3 ). Найдем тангенс угла – это отношение 3:4. Ответ: -0,75 3 4
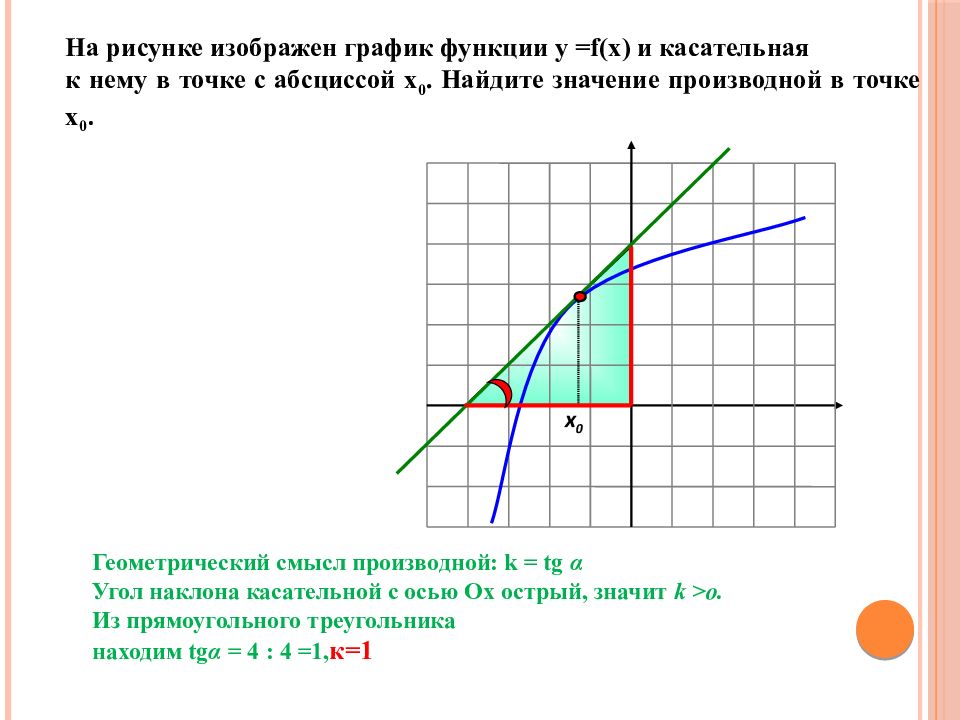
На рисунке изображен график функции у = f(x) и касательная к нему в точке с абсциссой х 0. Найдите значение производной в точке х 0. х 0 Геометрический смысл производной: k = tg α Угол наклона касательной с осью Ох острый, значит k >o. Из прямоугольного треугольника находим tg α = 4 : 4 =1, к=1
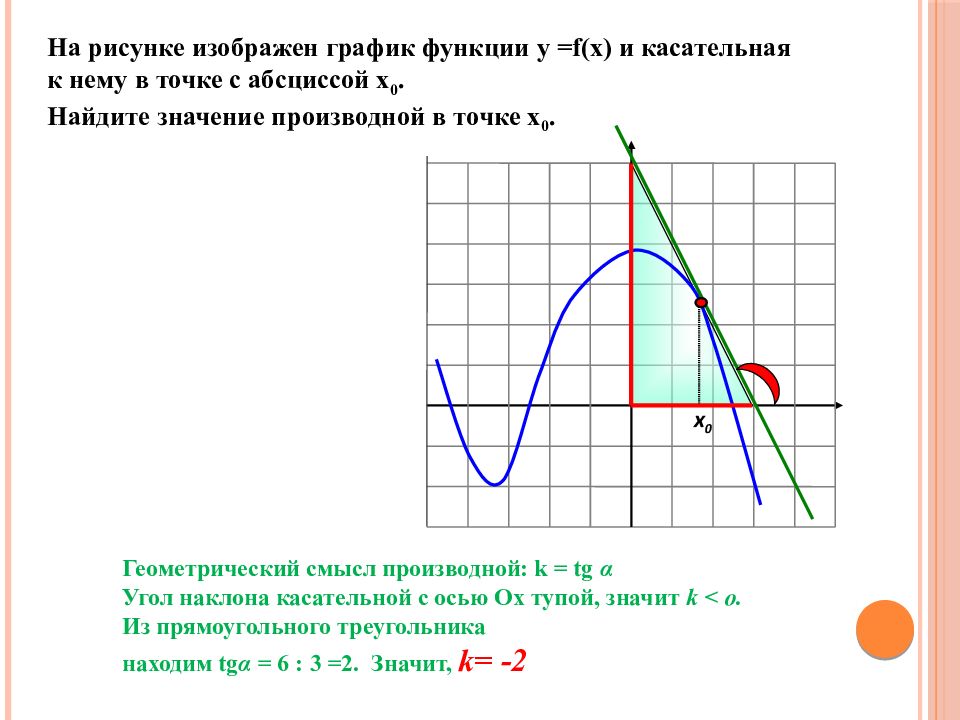
На рисунке изображен график функции у = f(x) и касательная к нему в точке с абсциссой х 0. Найдите значение производной в точке х 0. х 0 Геометрический смысл производной: k = tg α Угол наклона касательной с осью Ох тупой, значит k < o. Из прямоугольного треугольника находим tg α = 6 : 3 =2. Значит, k = -2
