Преобразование графиков тригонометрических функций

Первый слайд презентации: Преобразование графиков тригонометрических функций

Изображение слайда

Слайд 2: Содержание

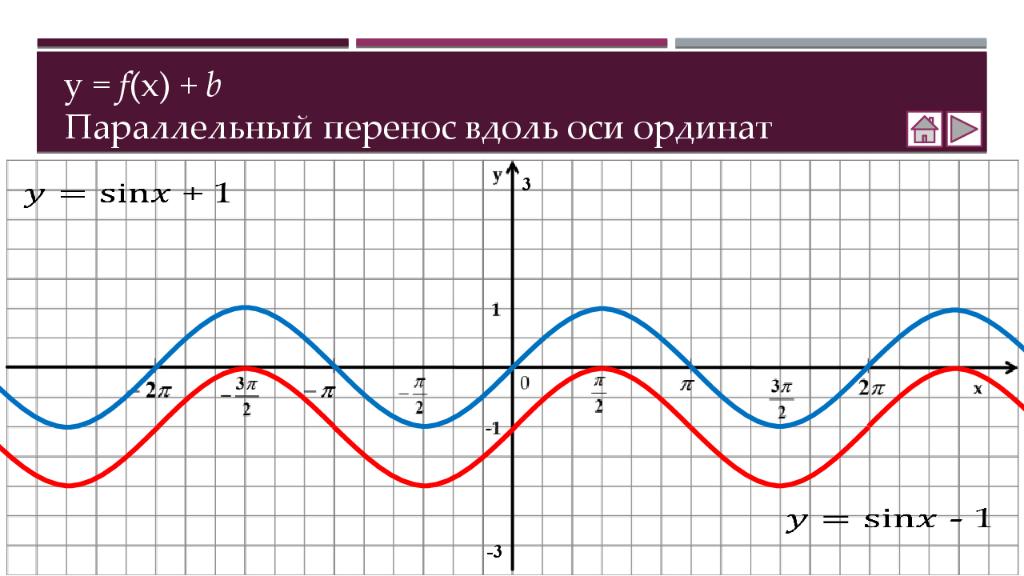
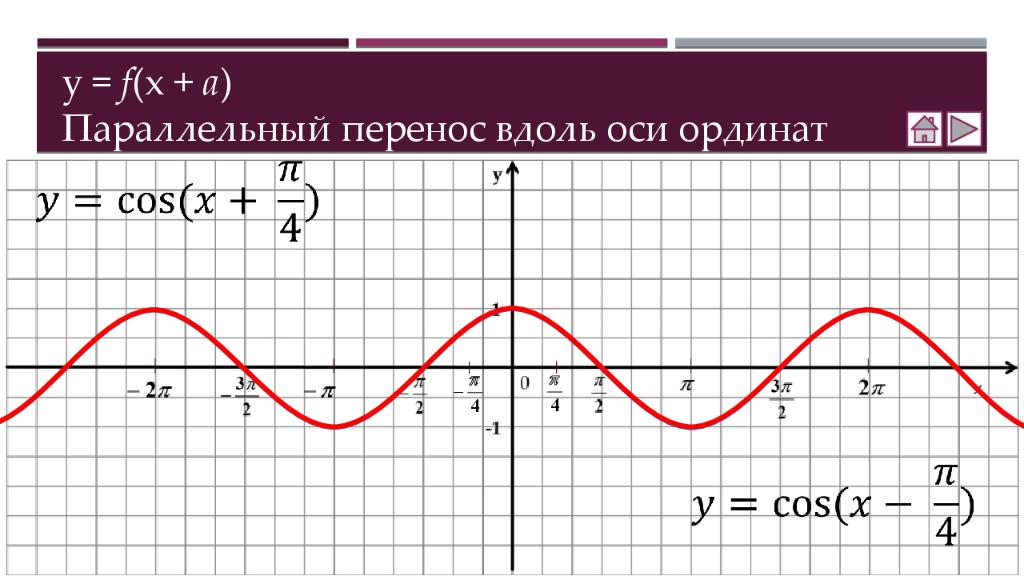
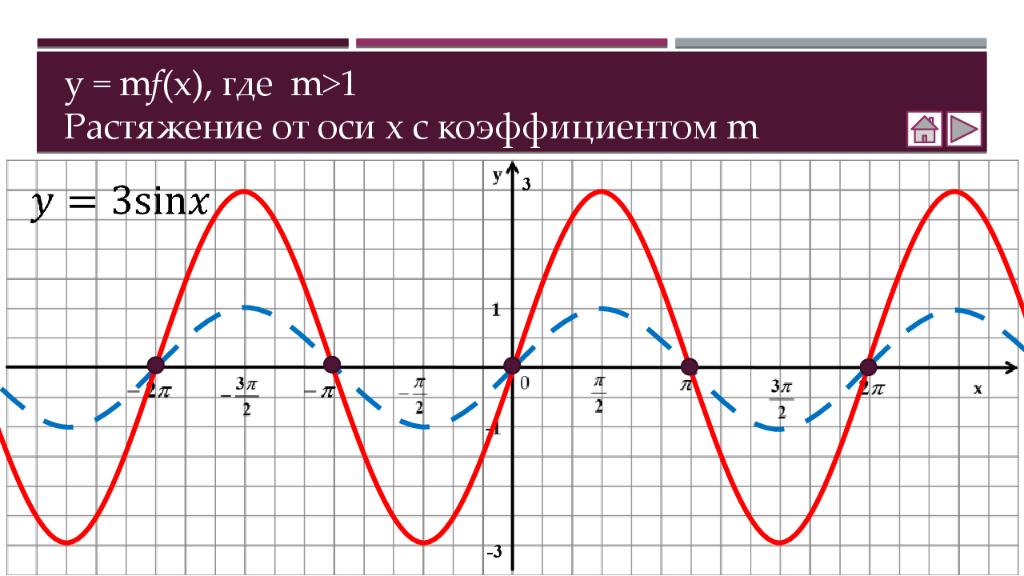
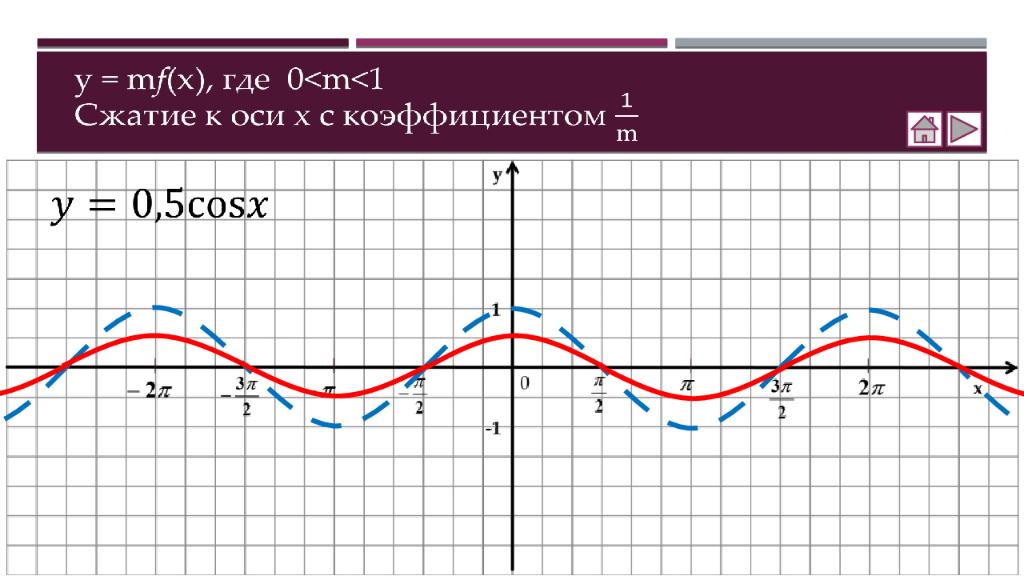
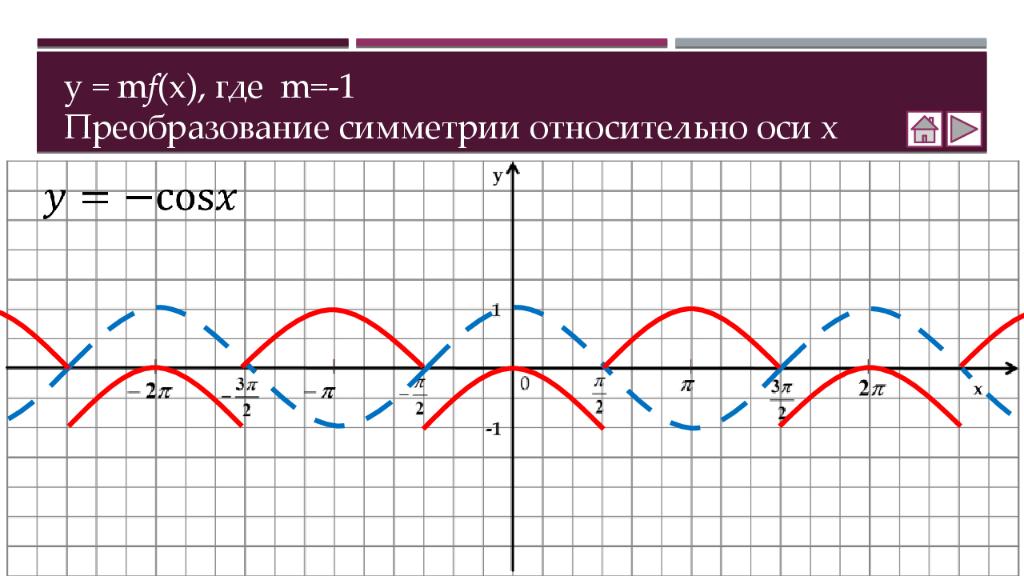
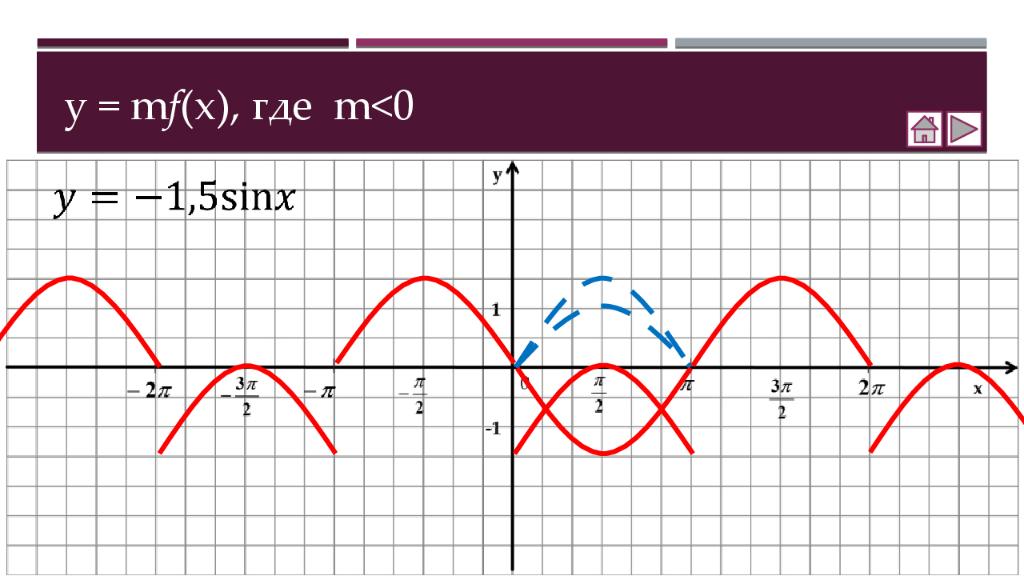
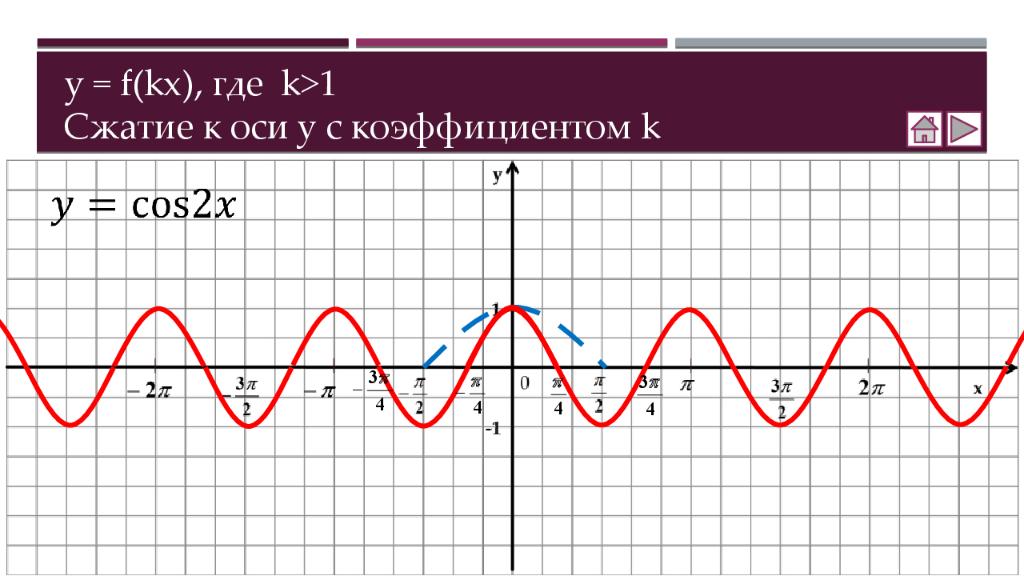
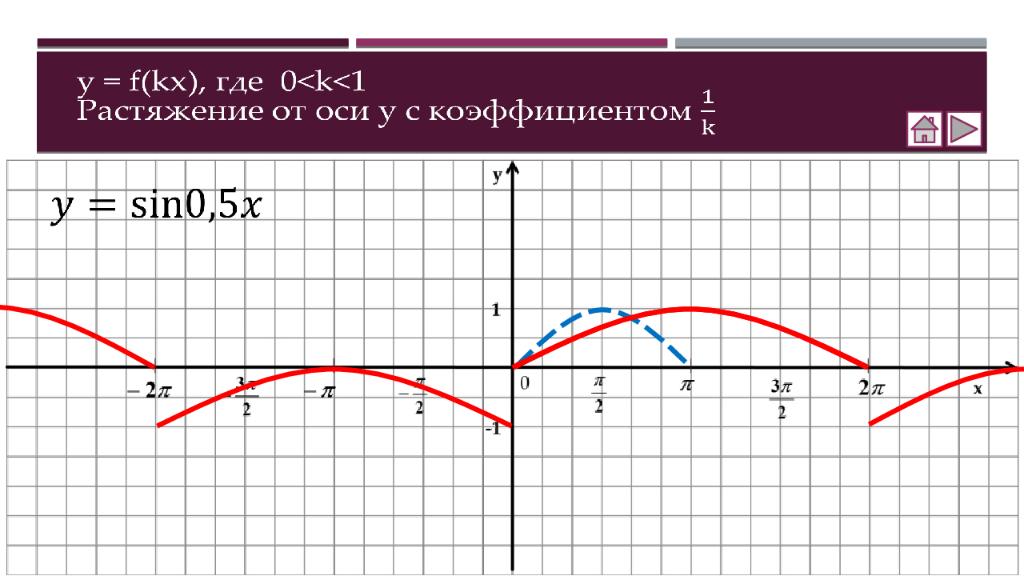
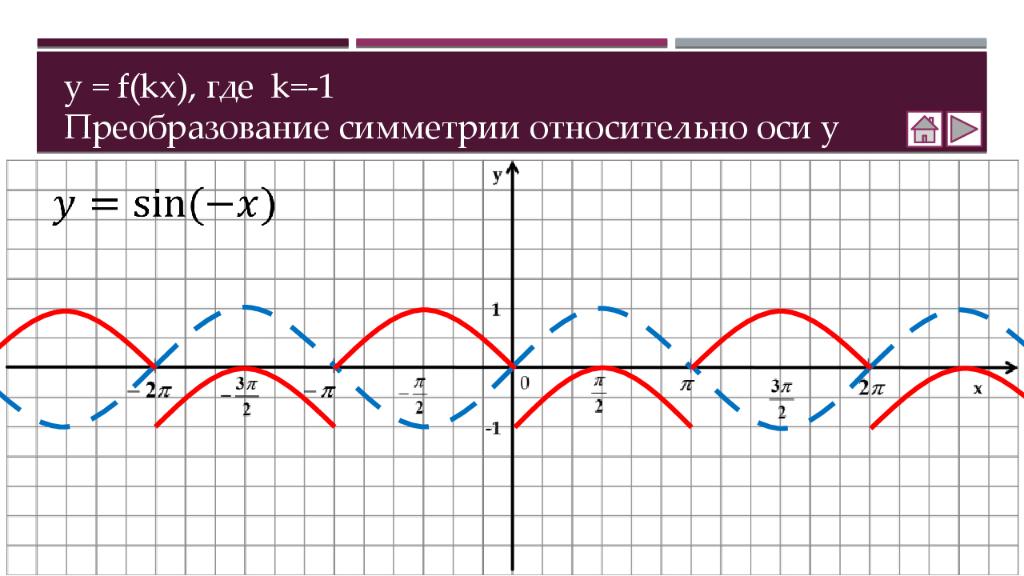
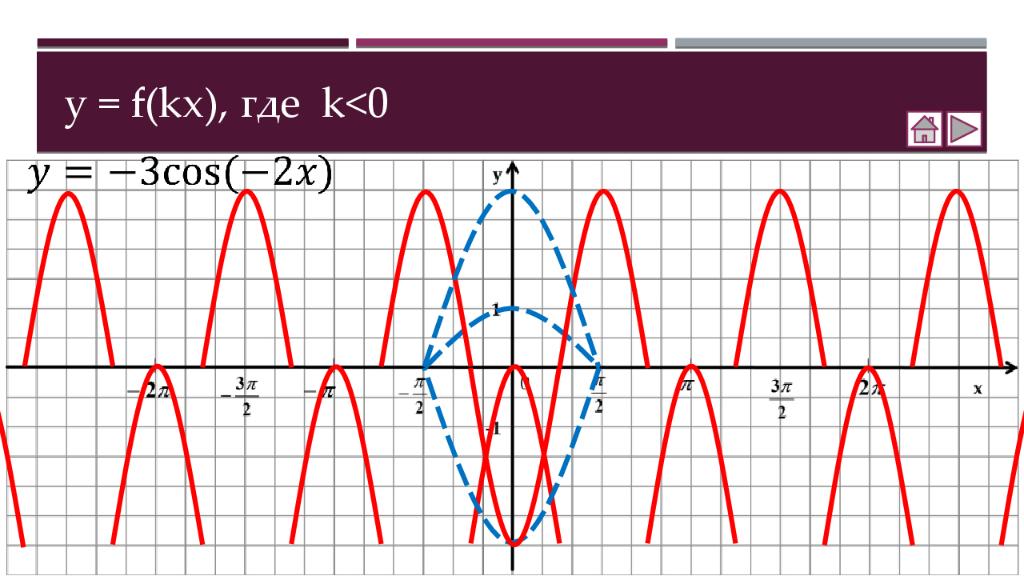
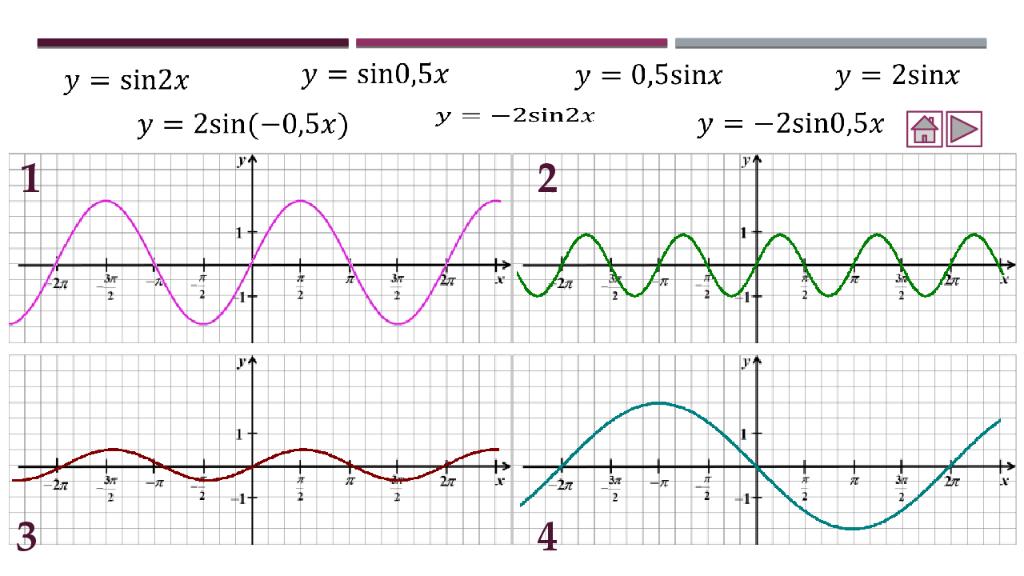
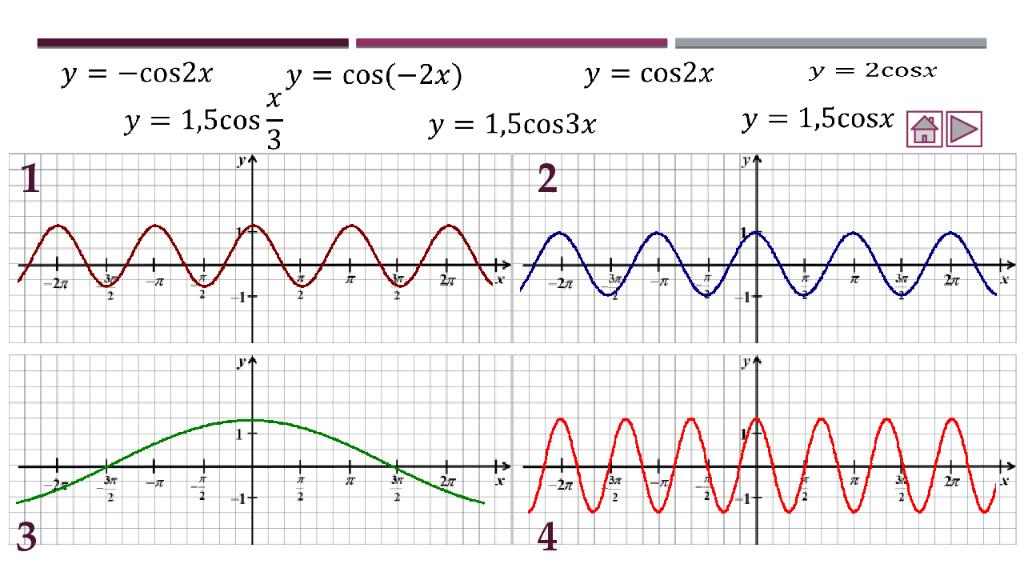
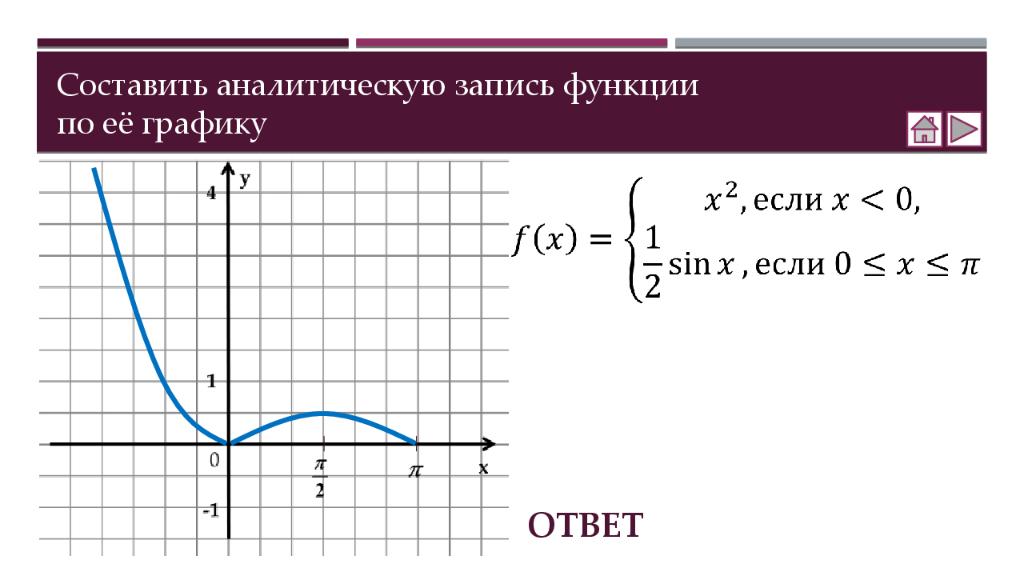
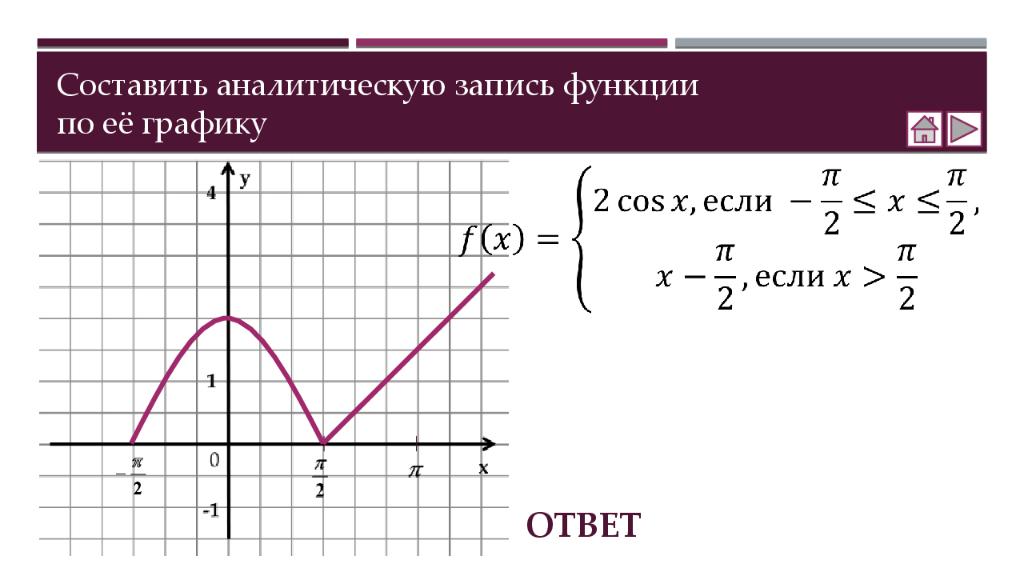
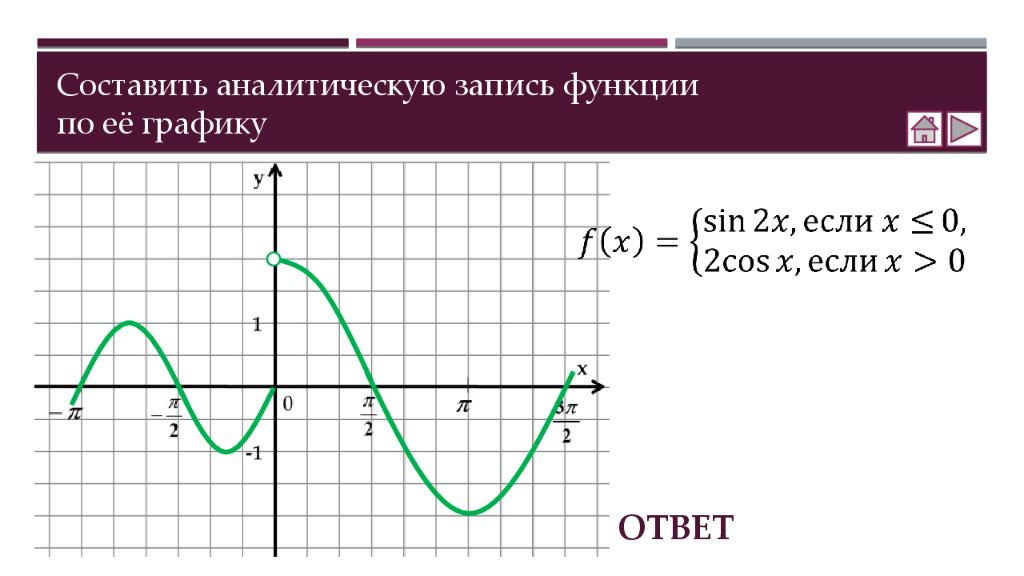
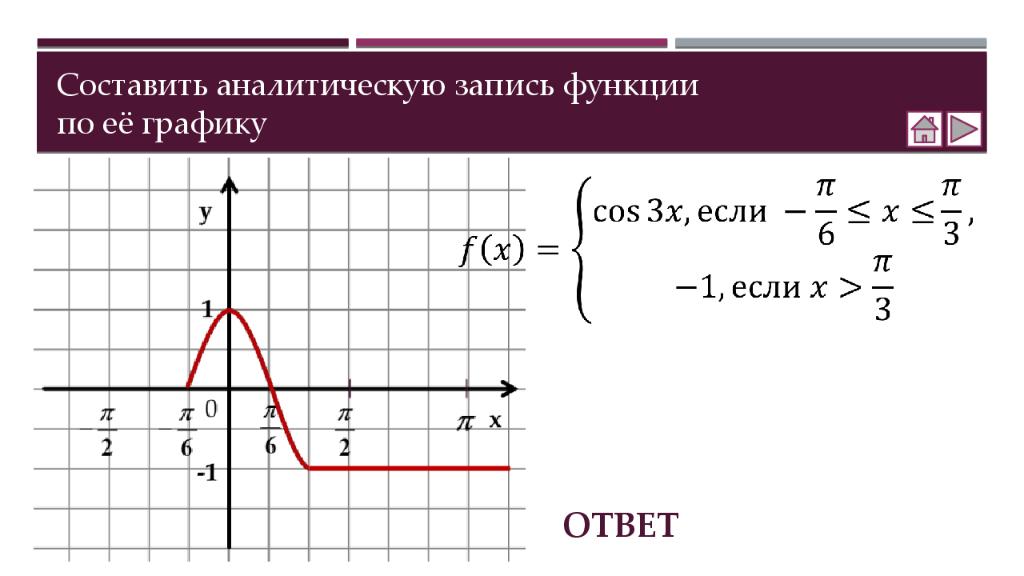
Теория Как построить график функции y = f (x ) + b Как построить график функции y = f (x + a ) Как построить график функции y = m f (x) Как построить график функции y = f(kx) Практика Соотнесение графиков функций с их формулами Построение графиков функций Составление аналитической записи функции по её графику Самостоятельная работа

Изображение слайда

Слайд 3: y = f (x) + b Параллельный перенос вдоль оси ординат

3 -3

Изображение слайда

Слайд 4: y = f (x + a ) Параллельный перенос вдоль оси ординат

Изображение слайда

Слайд 5: y = m f (x), где m>1 Растяжение от оси х с коэффициентом m

3 -3

Изображение слайда

Слайд 6

Изображение слайда

Слайд 7: y = m f (x), где m =- 1 Преобразование симметрии относительно оси х

Изображение слайда

Слайд 8: y = m f (x), где m<0

Изображение слайда

Слайд 9: y = f( kx ), где k>1 Сжатие к оси у с коэффициентом k

Изображение слайда

Слайд 10

Изображение слайда

Слайд 11: y = f(kx), где k =- 1 Преобразование симметрии относительно оси y

Изображение слайда

Слайд 12: y = f(kx), где k<0

Изображение слайда

Слайд 13

1 2 3 4

Изображение слайда

Слайд 14

1 2 3 4

Изображение слайда

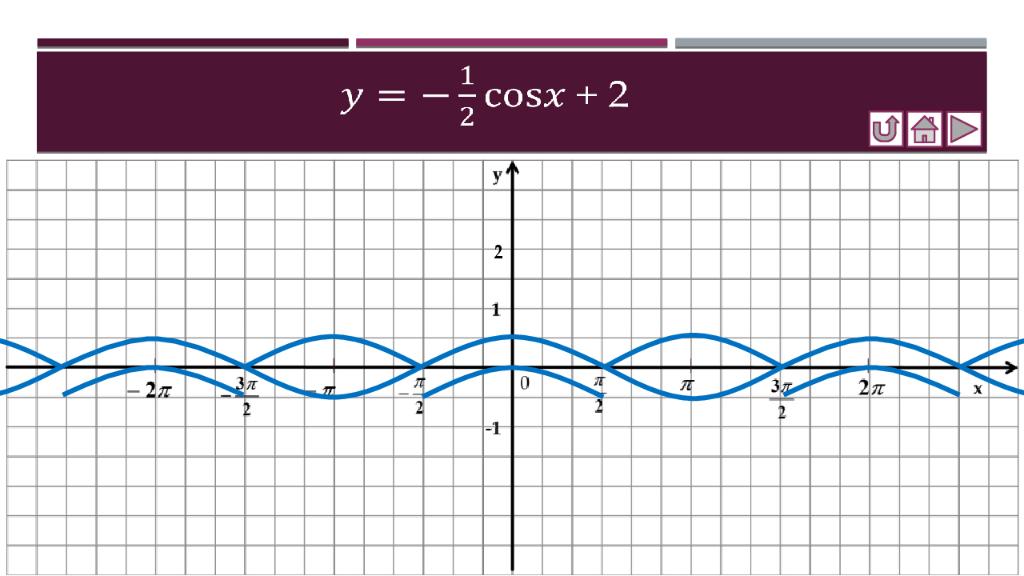
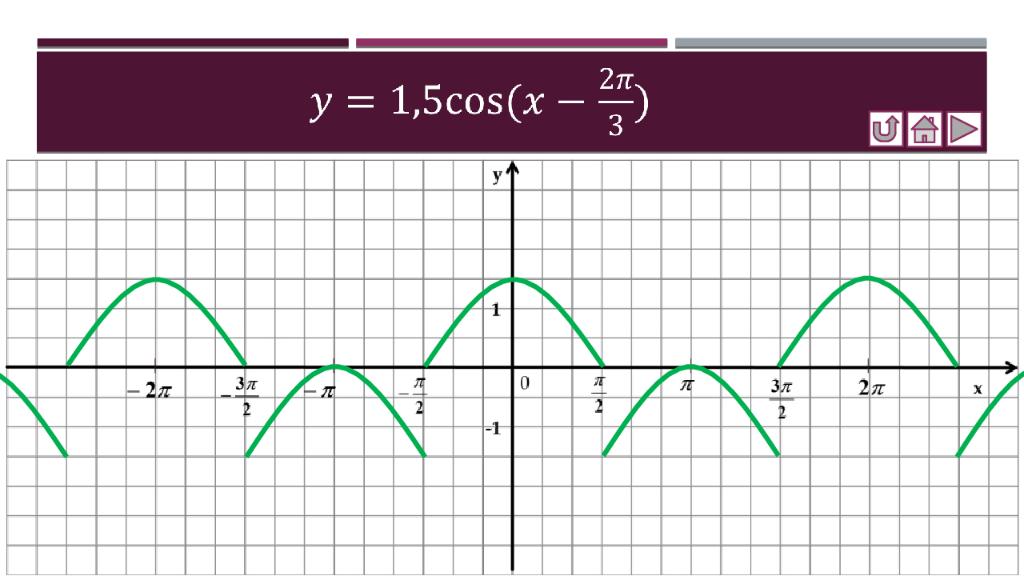
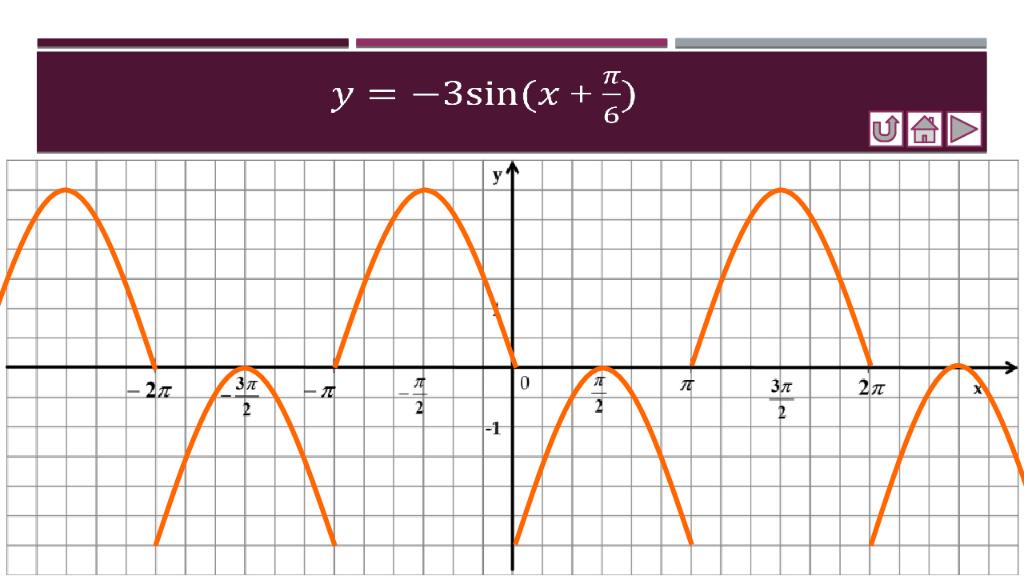
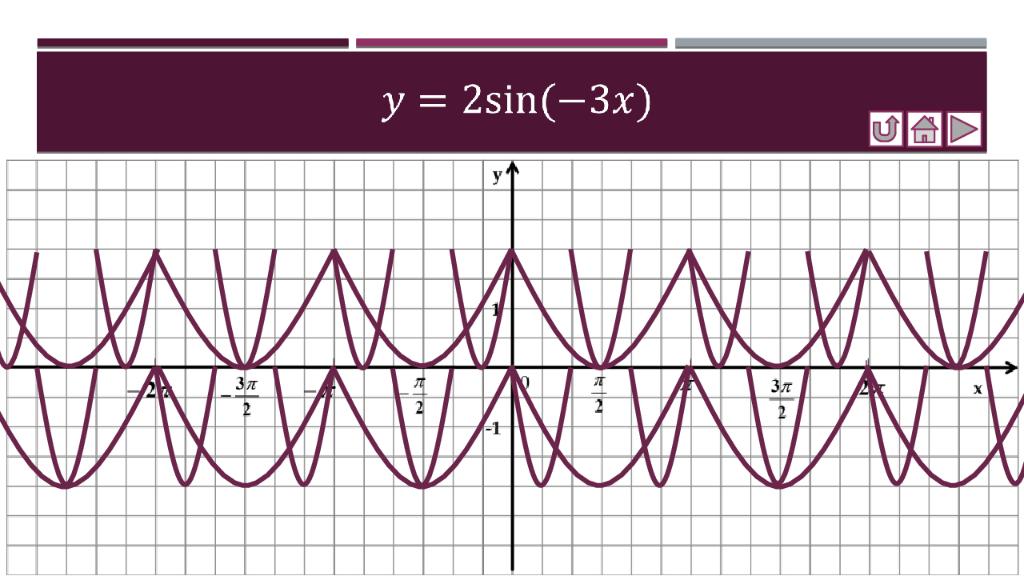
Слайд 15: Построить графики функций

Изображение слайда

Слайд 16

2

Изображение слайда

Слайд 17

Изображение слайда

Слайд 18

Изображение слайда

Слайд 19

Изображение слайда

Слайд 20: Составить аналитическую запись функции по её графику

Ответ

Изображение слайда

Слайд 21: Составить аналитическую запись функции по её графику

Ответ

Изображение слайда

Слайд 22: Составить аналитическую запись функции по её графику

Ответ

Изображение слайда

Слайд 23: Составить аналитическую запись функции по её графику

Ответ

Изображение слайда

Слайд 24: Самостоятельная работа

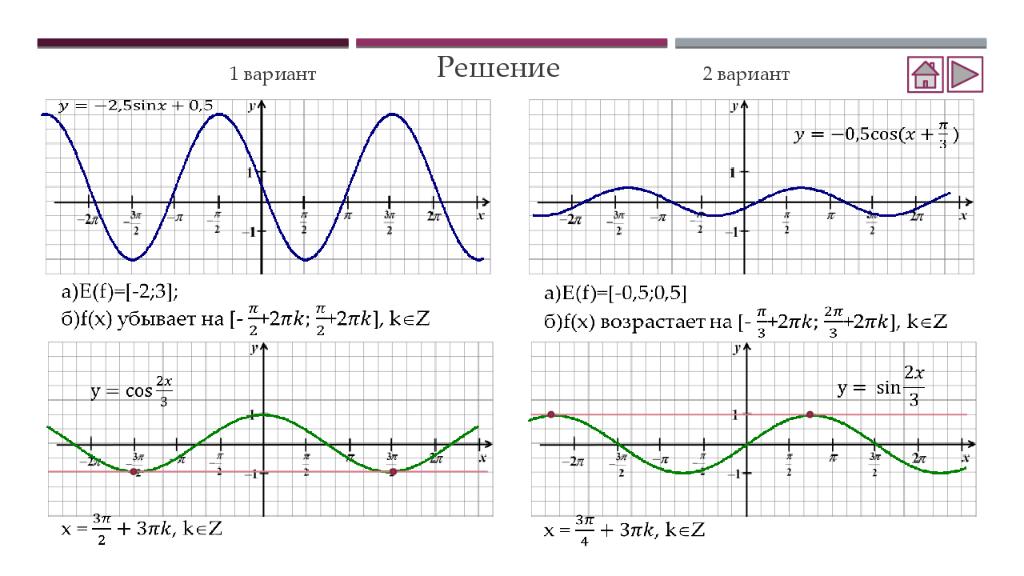
Вариант 1 Вариант 2 а) область значений функции; б) промежутки убывания функции. 1. Постройте график функции 2. Решите графически уравнение По графику найдите: а) область значений функции; б) промежутки возрастания функции.

Изображение слайда

Слайд 25

1 вариант 2 вариант Решение

Изображение слайда

Последний слайд презентации: Преобразование графиков тригонометрических функций: литература

Мордкович А. Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень). М. : Мнемозина. Мордкович А. Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений (базовый уровень). М. : Мнемозина. Александрова Л. А. Алгебра и начала математического анализа. 10 класс. Самостоятельные работы для учащихся общеобразовательных учреждений. М. : Мнемозина.

Изображение слайда

Преобразование графиков тригонометрических функций — презентация

Первый слайд презентации: Преобразование графиков тригонометрических функций

Слайд 2: Содержание

Слайд 3: y = f (x) + b Параллельный перенос вдоль оси ординат

Слайд 4: y = f (x + a ) Параллельный перенос вдоль оси ординат

Слайд 5: y = m f (x), где m>1 Растяжение от оси х с коэффициентом m

Слайд 6

Слайд 7: y = m f (x), где m =- 1 Преобразование симметрии относительно оси х

Слайд 8: y = m f (x), где m<0

Слайд 9: y = f( kx ), где k>1 Сжатие к оси у с коэффициентом k

Слайд 10

Слайд 11: y = f(kx), где k =- 1 Преобразование симметрии относительно оси y

Слайд 12: y = f(kx), где k<0

Слайд 13

Слайд 14

Слайд 15: Построить графики функций

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20: Составить аналитическую запись функции по её графику

Слайд 21: Составить аналитическую запись функции по её графику

Слайд 22: Составить аналитическую запись функции по её графику

Слайд 23: Составить аналитическую запись функции по её графику

Слайд 24: Самостоятельная работа

Слайд 25

Последний слайд презентации: Преобразование графиков тригонометрических функций: литература

Похожие презентации