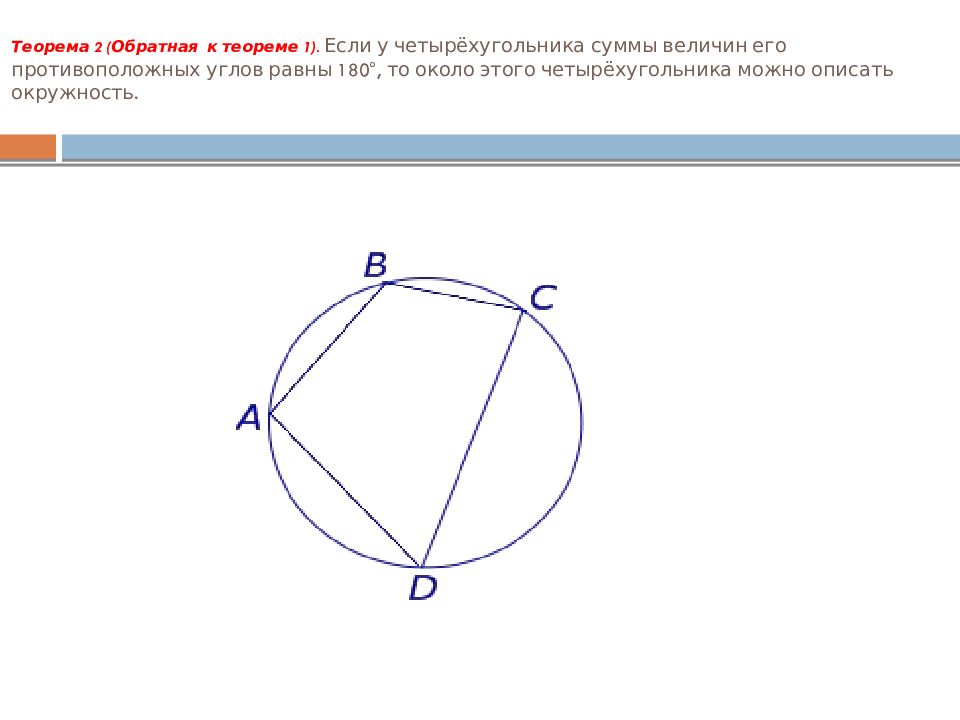
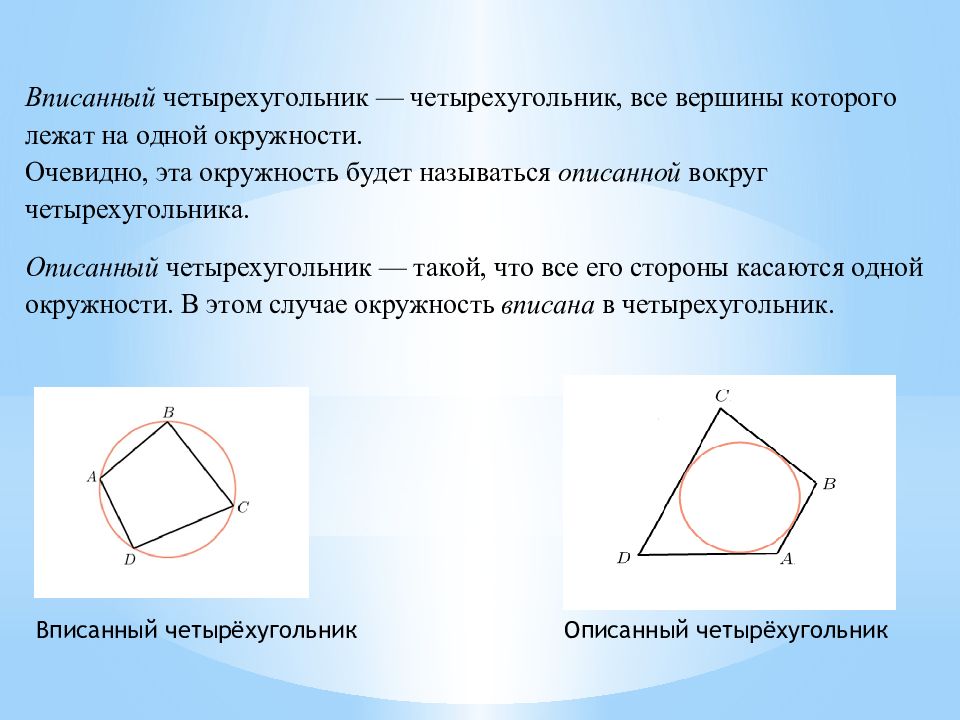
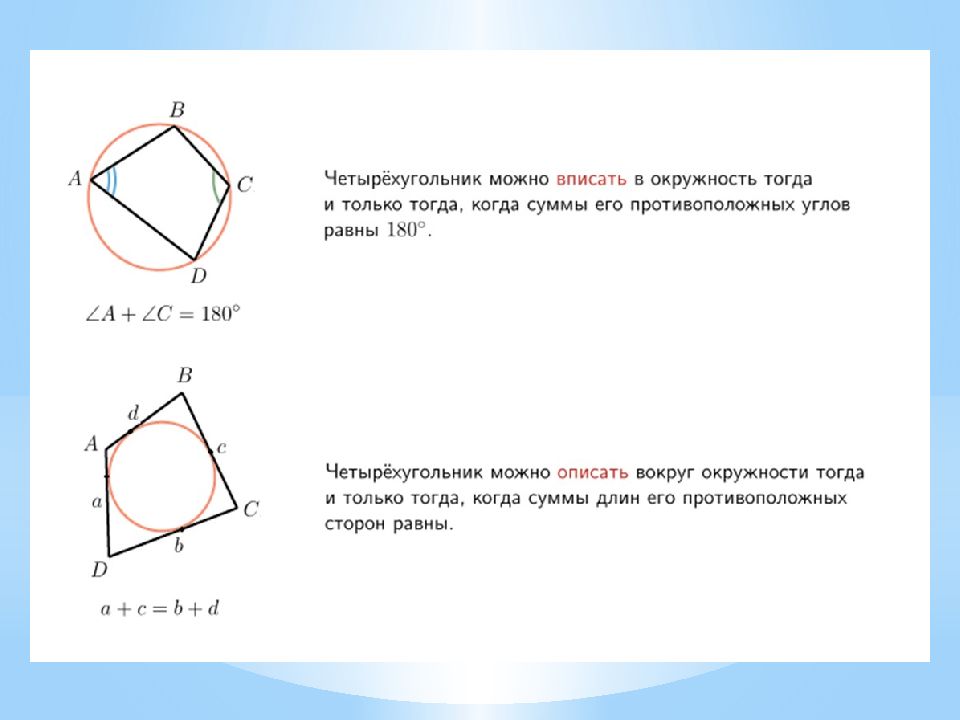
Определение 1. Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника. В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.
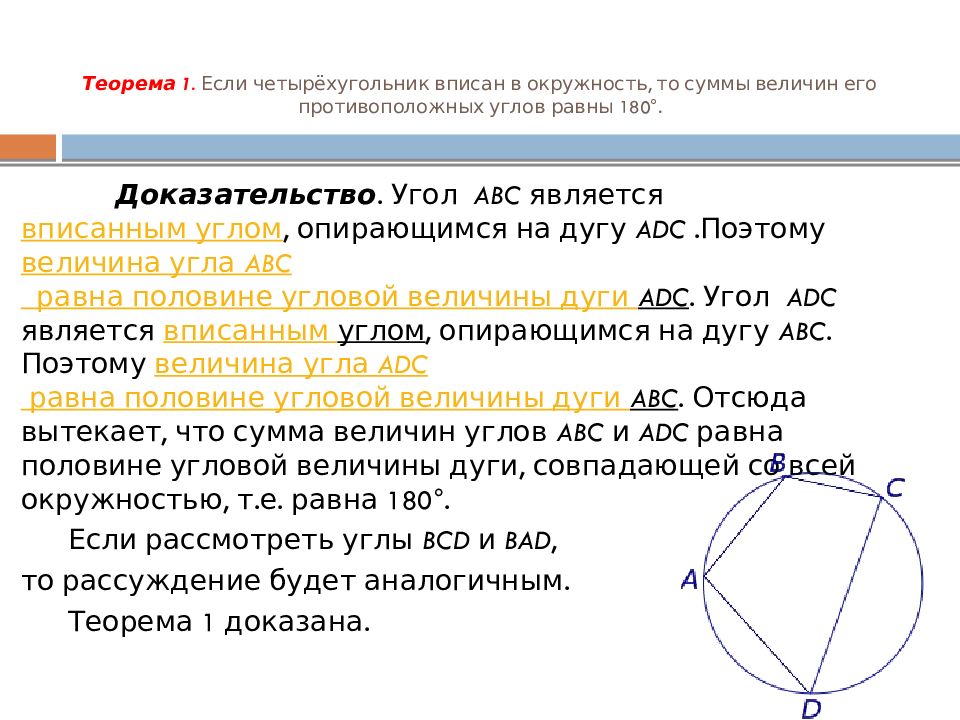
Доказательство. Угол ABC является вписанным углом, опирающимся на дугу ADC .Поэтому величина угла ABC равна половине угловой величины дуги ADC. Угол ADC является вписанным углом, опирающимся на дугу ABC. Поэтому величина угла ADC равна половине угловой величины дуги ABC. Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180°. Если рассмотреть углы BCD и BAD, то рассуждение будет аналогичным. Теорема 1 доказана.
справедливо равенство : AC∙BD=AB∙CD+AD∙BC
Вписанный четырёхугольник Описанный четырёхугольник
