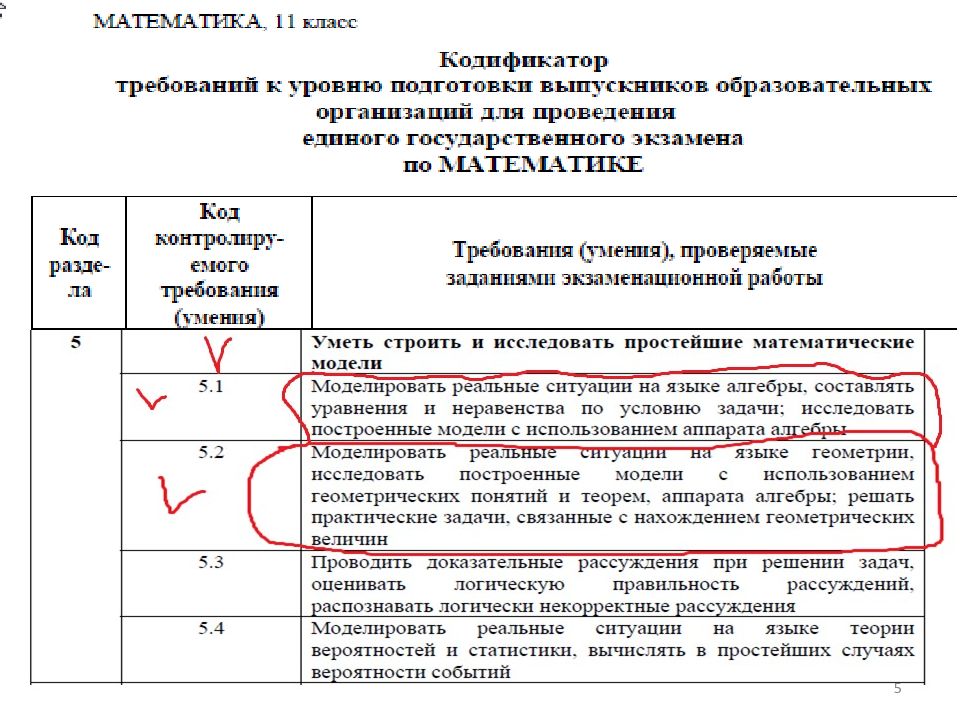
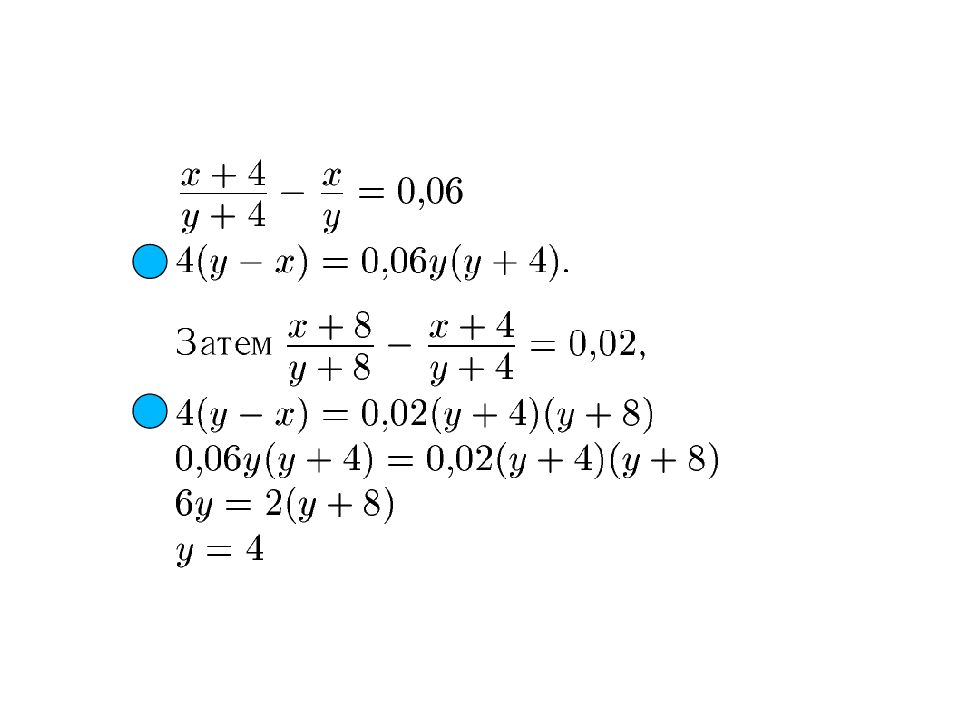Первый слайд презентации: Экономическая» задача в ЕГЭ по математике (профильны й уровень № 17)
Фридман Елена Миха йловна Издательство «Легион»
Слайд 4
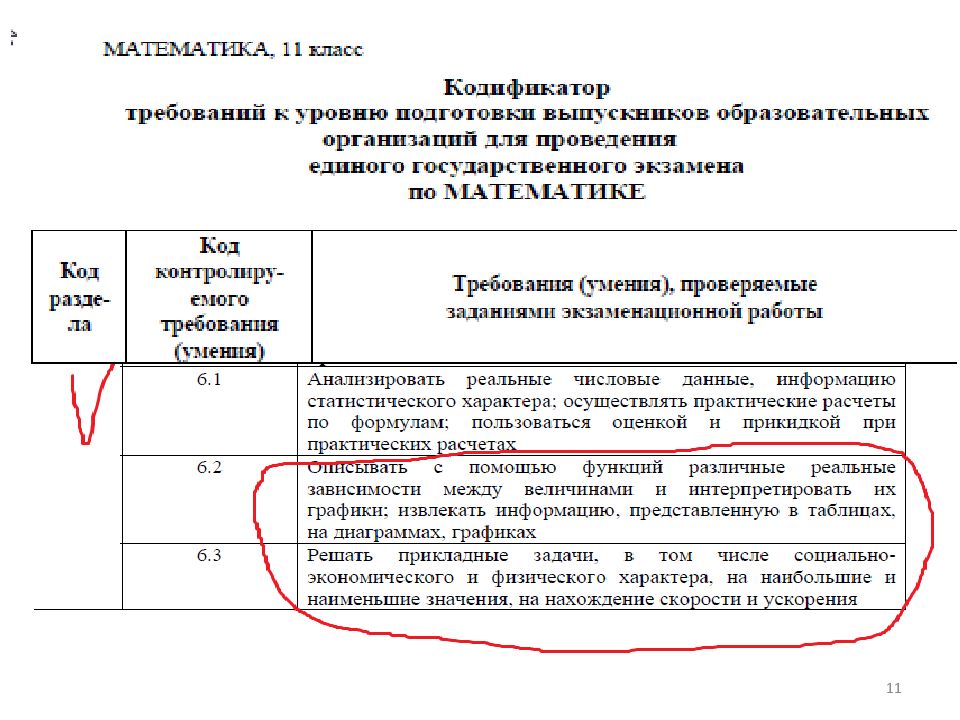
Задачи на оптимальны й выбор Банки, вклады, кредиты Производственные задачи 4
Слайд 6: Задача 1
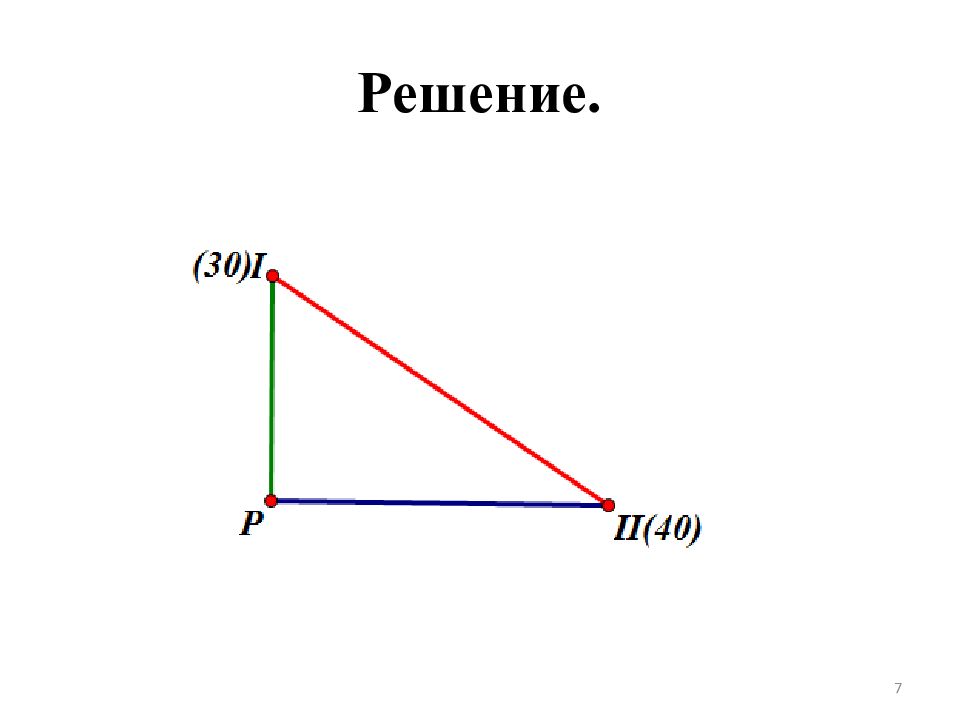
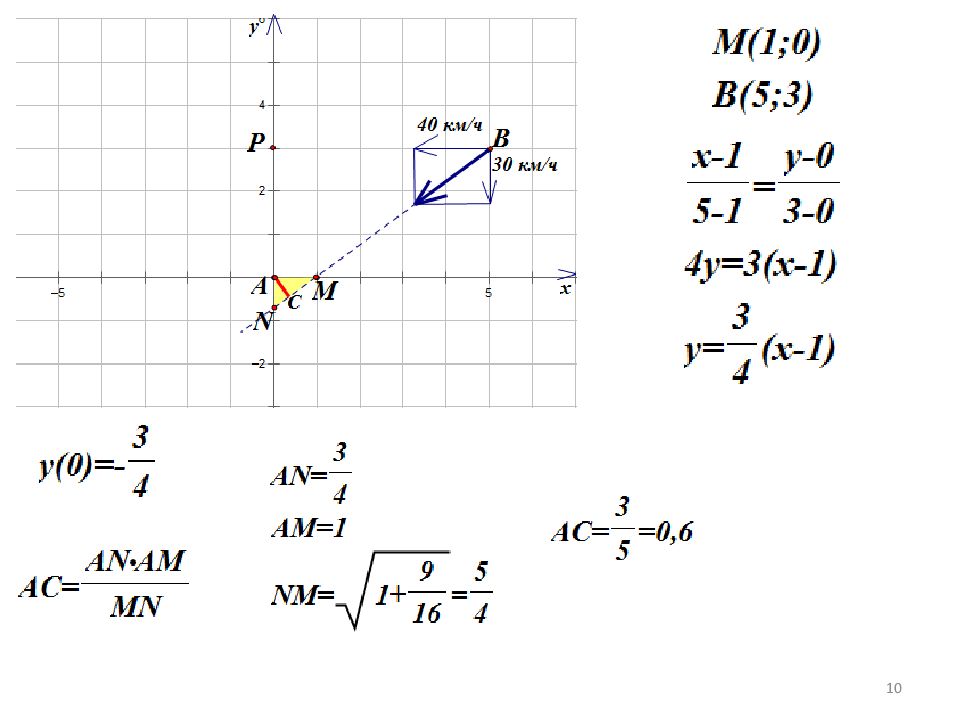
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние? 6
Слайд 8
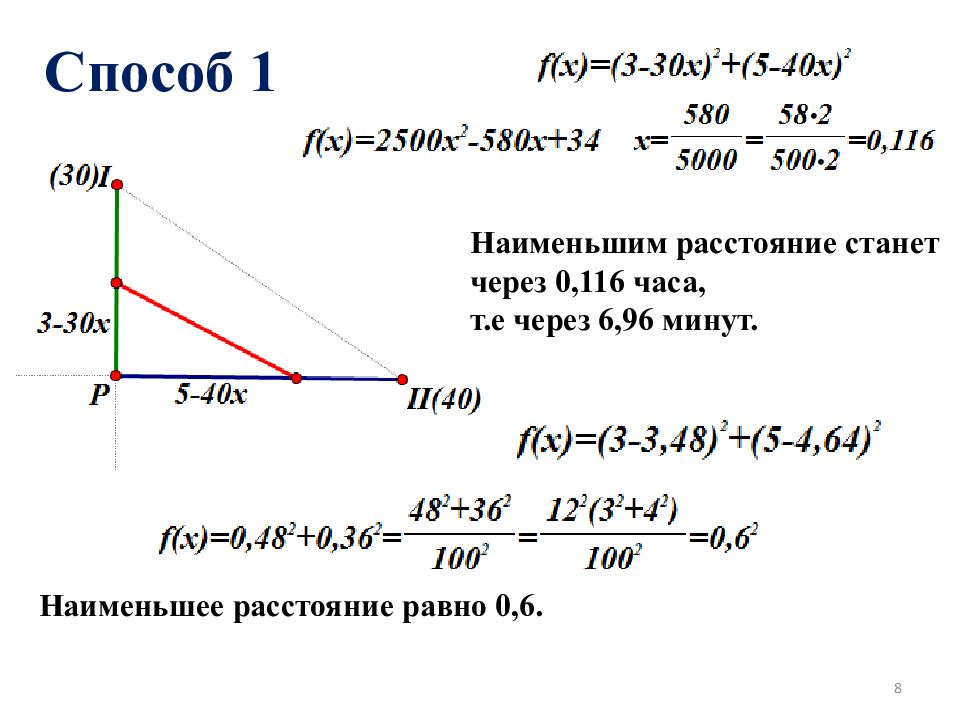
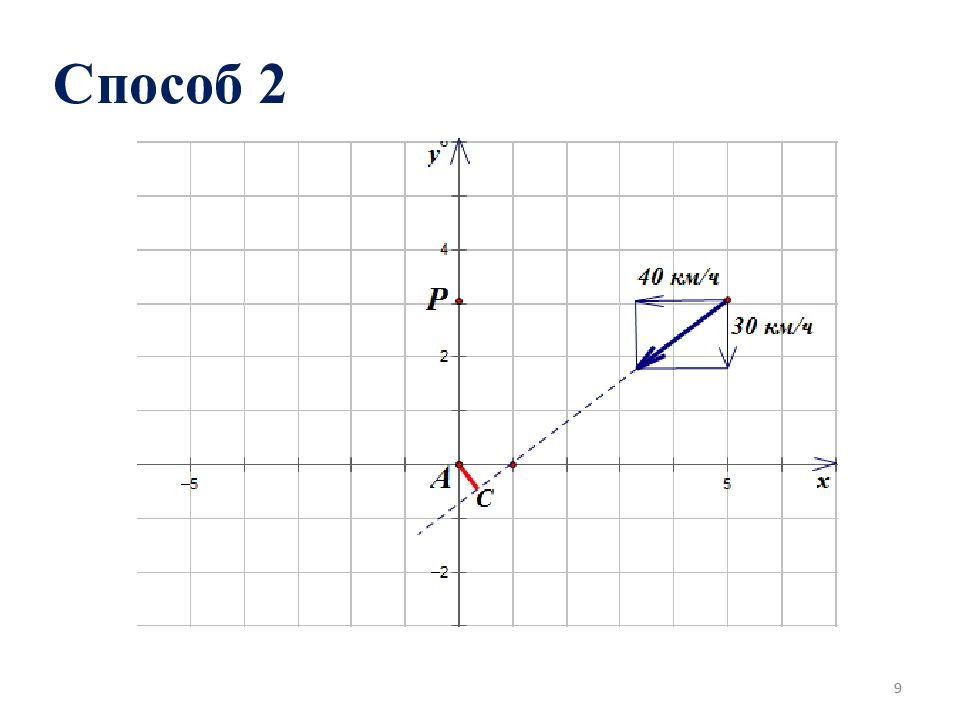
Способ 1 Наименьшее расстояние равно 0,6. Наименьшим расстояние станет через 0,116 часа, т.е через 6,96 минут. 8
Слайд 12: Задача 2
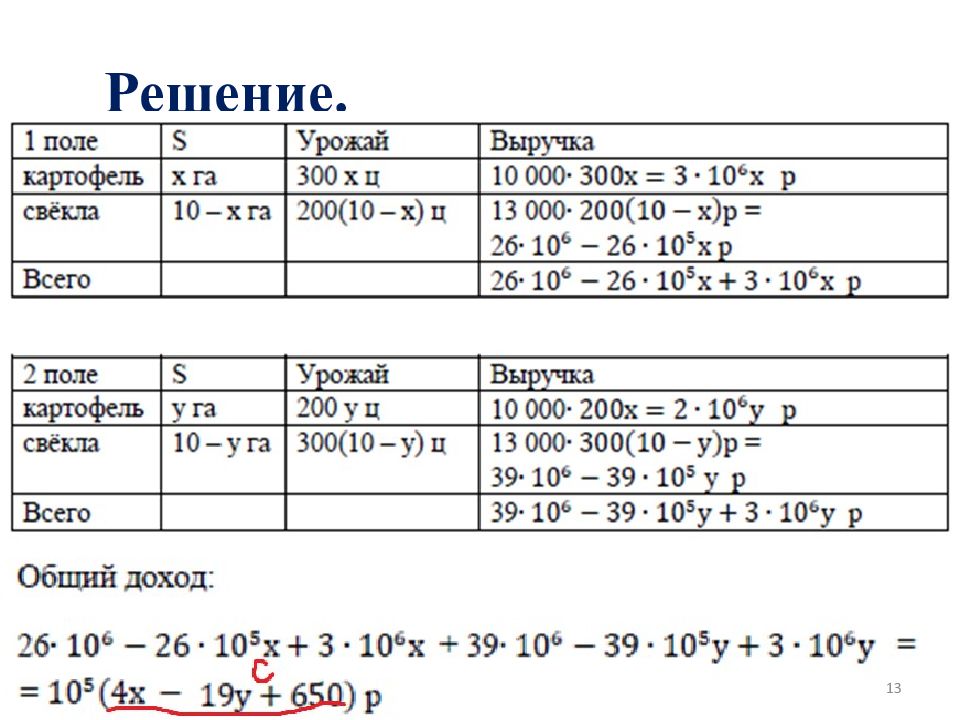
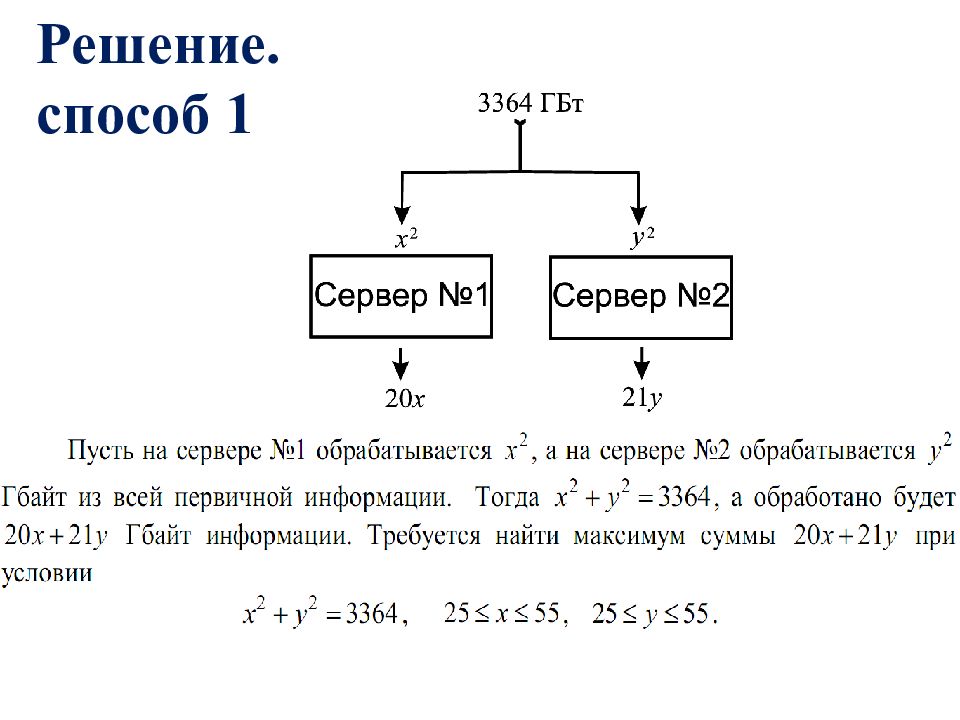
У фермера есть два поля площадью 10 га. На каждом поле можно выращивать картофель и свеклу. Поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц /га, а на втором - 200 ц /га Урожайность свеклы на первом поле составляет 200 ц /га, а на втором – 300 ц /га. Фермер может продавать картофель по цене 10 000 р / ц, а свеклу – по цене 13 000 р / ц. Какой наибольший доход может получить фермер? 12
Слайд 14
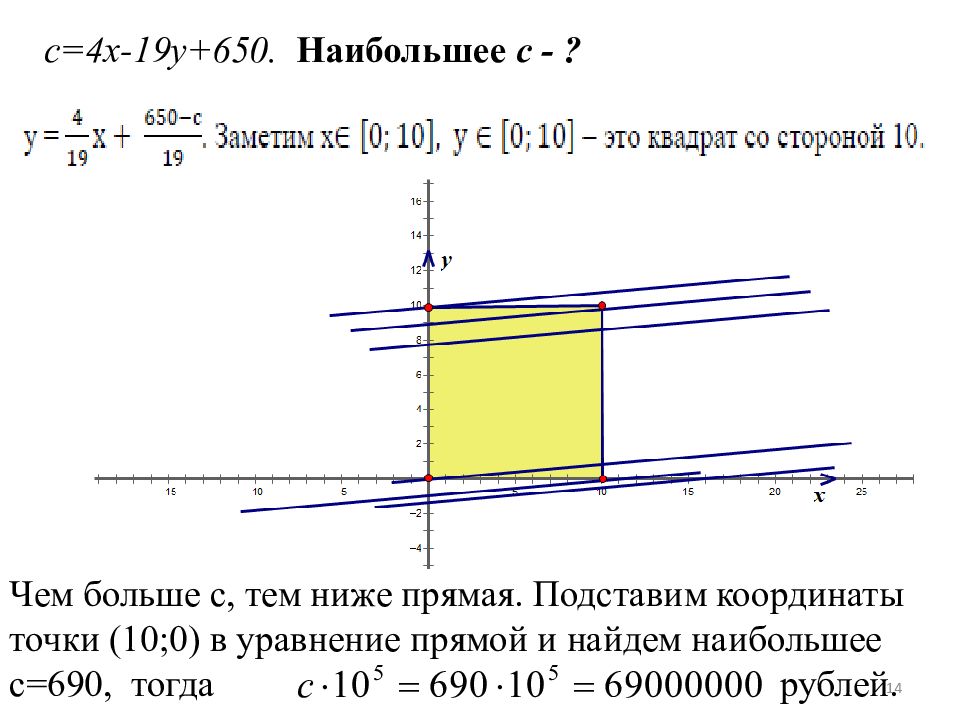
с=4х-19у+650. Наибольшее с - ? Чем больше с, тем ниже прямая. Подставим координаты точки (10;0) в уравнение прямой и найдем наибольшее с=690, тогда рублей. 14
Слайд 15: Задача 3
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель? 15
Слайд 16: Решение
Пусть в отеле x обычных номеров и y номеров «люкс» 21 x+49y=1099. f( x,y )= 2000x+4500y=500(4x+9y). f наиб- ? f(y) – убывающая. Если y=1, то x=50. f наиб= f(50) =2000·50+4500·1= 104500 ( руб. ) 16
Слайд 17: Задача 4
Вкладчик положил две одинаковые суммы под r % годовых в банки «А» и «Б». Через год условия по вкладу «А» изменились, и он понизил годовую ставку до 8 % годовых, в то время как банк «Б» оставил годовую ставку на прежнем уровне. На й дите, при каком наименьшем целом r вклад в банке «Б» через три года будет по кра й не й мере на 16 % больше, чем вклад в банке «А». 17
Слайд 18: Решение
Годы Вклад в банк «А» Вклад в банк «Б» % Сумма в начале года Сумма в конце года % Сумма в начале года Сумма в конце года 1 r n r n 2 8 r 3 8 r r = 17 18
Слайд 19: Задача 5
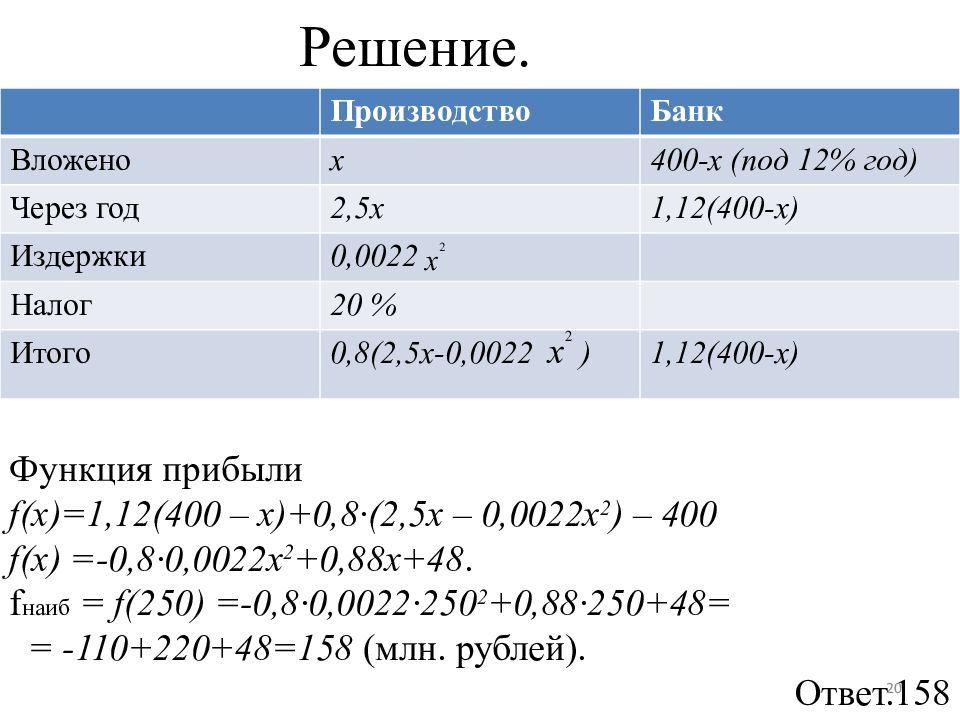
Часть денег от суммы 400 млн. рублей размещена в банке под 12% годовых, а другая часть инвестирована в производство, причем через год эффективность вложения ожидается в размере 250% (т.е. вложенная сумма х млн. рублей оборачивается в капитал 2,5х млн. рублей), затем отчисляются деньги на издержки, которые задаются квадратичной зависимостью 0,0022х 2. Разность между капиталом и издержками в производстве облагается налогом в 20%. Как распределить капитал между банком и производством, чтобы через год получить общую максимальную прибыль от размещения денег в банк и вложения денег в производство? Сколько млн. рублей составит эта прибыль? 19
Слайд 20: Решение
Производство Банк Вложено x 400-x (под 12% год) Через год 2,5x 1,12(400-x) Издержки 0,0022 Налог 20 % Итого 0,8(2,5x-0,0022 ) 1,12(400-x) Функция прибыли f ( x )=1,12(400 – х )+0,8·(2,5х – 0,0022х 2 ) – 400 f ( x ) =-0,8·0,0022х 2 +0,88х+48. f наиб = f (250) =-0,8·0,0022·250 2 +0,88·250+48= = -110+220+48=158 (млн. рублей). Ответ.158 20
Слайд 27: Задача 7
В банк помещён вклад 64 000 рублей под 25% годовых. В конце каждого из первых трёх лет (после начисления процентов) вкладчик дополнительно положил на счёт одну и ту же фиксированную сумму. К концу четвёртого года после начисления процентов оказалось, что он составляет 385 000 рублей. Какую сумму (в рублях) ежегодно добавлял вкладчик? 27
Слайд 28: Решение
Пусть x рублей вкладчик добавлял в конце каждого из первых трёх лет. Тогда на счету в конце 1-го года 1,25·64 000+ x =80 000+ x рублей, в конце 2-го года – 1,25(80 000+x)+x рублей, в конце 3-го года – 1,25 ( 1,25(80 000+x)+x )+ х рублей, в конце 4-го года – 1,25(1,25 ( 1,25(80 000+x)+x )+ х ) =385 000 рублей 28
Слайд 34: Задача 10
Семен Петрович положил 8000 рубле й в сберегательны й банк. По истечении года к его вкладу были добавлены деньги, начисленные в качестве процентов, и, помимо этого, Семен Петрович увеличил сво й вклад на 1360 рубле й. Еще через год он решил снять 1440 рубле й, а остальные 9360 рубле й положил на новы й срок. Чему равна процентная ставка в этом банке? 34
Слайд 42: Задача 13
Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен возвращать банку часть денег в конце каждого месяца. В конце каждого месяца к оставшейся сумме основного долга добавляется r% этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы сумма долга уменьшалась на одну и ту же величину каждый месяц ( на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27% больше, чем сумма, взятая им в долг. Найдите r. 42
Слайд 43: Решение
Месяц C умма Начислено Отдал Должен 1 N N+ N+ 2 3 … … … … … 17 0 Ответ. 3 43
Слайд 48
48 Решение. n – срок кредита (целое число лет), 1-ая составляющая выплат – ежегодны й платеж по кредиту x. Тогда 10 10- x 10-2x …, 10-nx – последовательность выплат 1-о й составляюще й по кредиту. 10 - nx =0, откуда
Слайд 51
51 Содержание критерия, задание 17 Баллы Обоснованно получен верный ответ 3 Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: — неверный ответ из-за вычислительной ошибки; — верный ответ, но решение недостаточно обосновано 2 Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено 1 Решение не соответствует ни одному из критериев, перечисленных выше 0 Максимальный балл 3 Критерии
Слайд 54
Решение. Пусть S – сумма кредита. 1,04 (S+0,9S+0,8S+0,7S+0,6S+0,5S)- -(S+0,9S+0,8S+0,7S+0,6S+0,5S)= = 0,04 (S+0,9S+0,8S+0,7S+0,6S+0,5S) = 0,04·4,5S=0,1 8 S. Переплата составит 18%. Ответ. 18 % 54
Слайд 59
Книги можно заказать в нашем интернет-магазине на сайте: www.legionr.ru Спрашивайте в книжных магазинах города! 59