Первый слайд презентации
Кафедра математики и моделирования Старшие преподаватели Е.Д. Емцева и Е.Г. Гусев Курс «Высшая математика» Лекция 1 3. Тема: Формула полной вероятности. Формула Бейеса. Цель: Разъяснить формулу полной вероятности и как следствие из неё – формулу Бейеса.
Слайд 2: Терминология
Допустим, что об условиях опыта можно сделать n исключающих друг друга предположений (гипотез): H 1,H 2,…,H n, где H i H j = Ø, i ≠ j H i – несовместные, образующие полную группу события.
Слайд 3: Формула полной вероятности
Заданы условные вероятности события А, при каждой из гипотез P ( A ׀ H 1 ),…, P ( A ׀ H n ). Событие А может появиться только вместе с одной из гипотез. Найдем вероятность события А. A= H 1 A +H 2 A + …+ H n A, H i A – несовместные события, значит, P(H i A) = P(H i )∙P(A ׀ H i ) Отсюда – формула полной вероятности
Слайд 4: Формула полной вероятности
Применяется, когда опыт со случайными исходами распадается на два случая: розыгрыш условий опыта розыгрыш результата
Слайд 5: Пример1
Имеются два одинаковых ящика с карандашами. В 1-ом ящике – 2 зеленых и 1 синий карандаш, во 2-ом – 1 зеленый и 3 синих. Наудачу выбирают один из ящиков и вынимают из него карандаш. Какова вероятность вынуть зеленый карандаш?
Слайд 6: Решение
H i – выбор i ящика P ( H 1 ) = P ( H 2 )=1 /2 P ( A ׀ H 1 ) =2/3 P ( A ׀ H 2 ) = ¼ P ( A ) =
Слайд 7: Пример 2
Предположим, что 0,5% всех мужчин и 0,025% всех женщин дальтоники. Найти вероятность того, что наугад выбранное лицо страдает дальтонизмом. Фразу из песни считать верной : «На 10 девчонок по статистике 9 ребят».
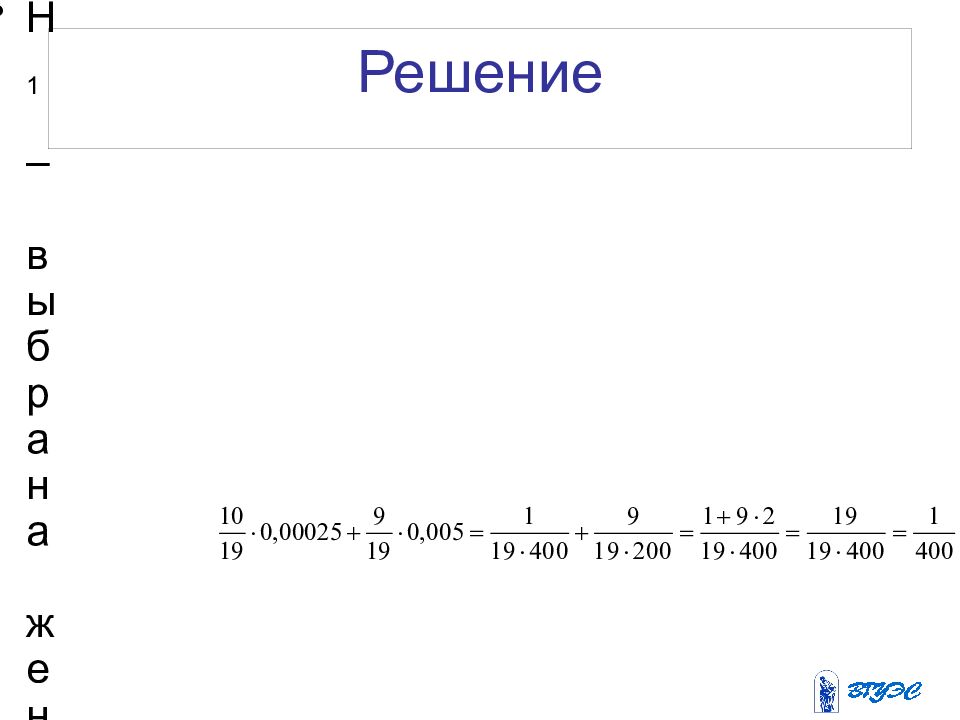
Слайд 8: Решение
H 1 – выбрана женщина H 2 – выбран мужчина P(H 1 ) = 10 /19; P(H 2 ) = 9/19; P(A ׀ H 1 ) = 0.00025 P(A ׀ H 2 ) = 0.005 P ( A ) =
Слайд 9: Формула Бейеса
До опыта о его условиях можно было сделать ряд гипотез H 1, H 2,…,H n ; ∑H i = Ω ; H i H j = Ø Вероятности гипотез до опыта «априорные вероятности» заданы: P(H 1 ),….,P(H n ); Пусть опыт проведен, в результате его появилось событие А. Найдем вероятность гипотез, при условии, что А произошло (найти «апостериорные» вероятности гипотез, при условии, что опыт дал результат А).
Слайд 10: Формула Бейеса
P(H 1 ׀ A); P(H 2 ׀ A)…. P(H n ׀ A) P(H i A) = P(H i )∙ P(A ׀ H i ) =P(A)∙ P(H i ׀ A) P ( H i |A ) = =
Слайд 11: Пример 1
Три барабана с лотереями: в 1-ом 50 билетов, из которых два выигрышных; во 2-ом 100 билетов – 4 выигрышных; в 3-ем 300 билетов – 5 выигрышных. Изымают 1 билет – выигрышный. Из какого барабана менее вероятно этот билет ?
Слайд 12: Решение
P ( H i ) = 1 /3; P ( A ׀ H 1 ) = 2/50=1/25; P ( A ׀ H 2 ) = 4/100=1/25; P ( A ׀ H 3 ) = 5/300=1/60; P(A) = P(H 1 ׀ A) = P(H 2 ׀ A) = 12/29 P(H 3 ׀ A)= 5/29
Слайд 13: Пример 2
2. Два студента на практике в налоговой полиции проверяют правильность заполнения налоговых деклараций членами правительства РФ. 1 студент обрабатывает 60% деклараций, 2-ой – 40%. Вероятность того, что 1-ый допустит ошибку при обработке 0.01, 2-ой – 0.03. Руководитель практики для контроля проверил одну декларацию и выявил ошибку проверки. Определить вероятность того, что ошибся 1-ый студент.
Слайд 14: Решение
H 1 – проверил 1-ый студент Н 2 – проверил 2-ой студент А – «студент ошибся» P(H 1 ׀ A) =